Programmable multivalent DNA-origami tension probes for reporting cellular traction forces

Abstract

Mechanical forces are central to most, if not all, biological processes including cell development, immune recognition, and metastasis. Because the cellular machinery mediating mechano-sensing and force generation is dependent on the nanoscale organization and geometry of protein assemblies, a current need in the field is the development of force-sensing probes that can be customized at the nanometer lengthscale. In this work, we describe a DNA origami tension sensor that maps the piconewton (pN) forces generated by living cells. As a proof-of-concept, we engineered a novel library of six-helix-bundle DNA-origami tension probes (DOTPs) with a tailorable number of tension-reporting hairpins (each with their own tunable tension response threshold) and a tunable number of cell-receptor ligands. We used single-molecule force spectroscopy to determine the probes’ tension response thresholds and used computational modeling to show that hairpin unfolding is semi-cooperative and orientation-dependant. Finally, we use our DOTP library to map the forces applied by human blood platelets during initial adhesion and activation. We find that the total tension signal exhibited by platelets on DOTP-functionalized surfaces increases with the number of ligands per DOTP, likely due to increased total ligand density, and decreases exponentially with the DOTP’s force-response threshold. This work opens the door to applications for understanding and regulating biophysical processes involving cooperativity and multivalency.

Graphical abstract

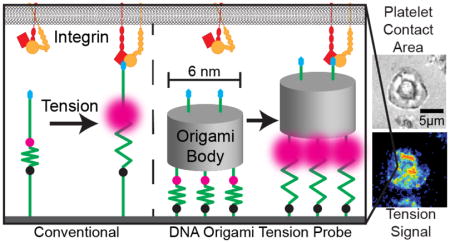
Mechanical cues are essential for a wide range of cellular processes including cell adhesion, immune recognition, metastasis, and clotting.^1–4 Cells sense the mechanical properties of the extracellular matrix (ECM) through integrin receptors that transmit forces bidirectionaly between the cellular cytoskeleton and the ECM. There are several different methods for studying integrin mechanics. For example, single-molecule force spectroscopy techniques, including atomic force spectroscopy, magnetic tweezers, and optical tweezers, are used to probe the interactions between cell receptors and their ligands.^{5, 6} These methods capture the physical chemistry of ligand-receptor interactions, but often poorly recapitulate biological processes because many membrane receptors function within oligomers rather than operating as isolated molecules. For example, groups of integrins assemble into focal adhesions (FAs) containing hundreds of different structural and signaling proteins that physically bridge the ECM to the cytoskeleton.⁷ Another complementary method for studying cell mechanobiology is traction force microscopy (TFM), which measures the cell-driven deformation of polymer substrates⁸. With micrometer spatial resolution and nanonewton sensitivity,⁹ TFM is capable of mapping the forces generated by mature FAs but cannot resolve the forces by nascent adhesions or focal complexes that precede the formation of mature FAs. To bridge the gap between these two types of methods, we developed molecular tension-based fluorescence microscopy (MTFM) for imaging cell traction forces with piconewton (pN) resolution.^{10, 11} The technological center-piece of MTFM is a molecular reporter comprised of an extendable, “spring-like” unit that is flanked by a fluorophore and quencher and anchored to a substrate. Tension transmitted to the probe leads to its extension, which separates the fluorophore from the quencher and results in a drastic increase (up to 100 fold) in fluorescence intensity.^{12, 13}

Over the past few years, we and others have developed several different classes of MTFM probes that include polytheylene glycol,^{12, 14–16} protein,^17–19 and DNA-based probes.^{13, 20–25} Among these, DNA-based MTFM probes exhibit several advantages including ease of synthesis, modular design, and the best reported signal-to-noise ratio.²⁰ These probes are typically comprised of three oligonucleotides. The first secures the probe to an underlying substrate. The second is a stem-loop hairpin with a well-characterized force-extension relationship. The third oligonucelotide presents a ligand that binds to a cell surface receptor (e.g. cyclic Arg-Gly-Asp-Phe-Lys (cRGDfK), a synthetic peptide engineered to have high affinity towards α_vβ₃ integrin receptors). Importantly, the arms flanking the hairpin are complementary to the other two oligonucleotides which also carry a fluorophore (e.g. Cy3B) and quencher (e.g. BHQ-1). When folded the probe is highly quenched (~97–99% quenching efficiency). Tension applied to the probe unfolds the DNA hairpin, resulting in a significant increase in fluorescence. Within a fluorescence tension image, the fluorescence intensity is directly proportional to the number of unfolded hairpins per unit area. The F_1/2 of a given DNA-hairpin probe, which is defined as the equilibrium force at which the hairpin spends half of its time in an unfolded state, can be tuned from ~2 to 19 pN by modifying the GC content and length of the stem region of the hairpin.^{20, 22, 26, 27}

The tunability of the probe F_1/2 is important as it enables determination of the magnitude of receptor forces. For example, we found that the T cell receptor (TCR) applies between 12 and 19 pN to its antigen in CD8⁺ mouse T-cells,¹³ while human platelet integrins apply a range of forces that can exceed 19 pN.²⁸ We also found that TCR forces were enhanced to >19 pN and spatially reorganized by enabling surface adhesion of the Lymphocyte function-associated antigen 1 (LFA-1), demonstrarting the importance of cooperative interactions in receptor mechanics.¹³ Accordingly, it is highly desirable to engineer a new generation of MTFM probes that can present multiple ligands for testing the role of multivalency in force transmission and access a broader range of force response thresholds.

DNA origami can be used to create complex nanoscale 3D structures by using the well-characterized properties of Watson-Crick base-pairing.²⁹ Such approaches have formerly been used to design complex DNA nanostructures including lattices, tubes, boxes, polyhedra, and functional machines.^30–34 DNA origami nanostructures allow for highly-defined integration of molecular components, enabling the creation of nanostrcutures with prescribed geometric, chemical, optical, and mechanical properties.^35–44 Furthermore, the integration of mechanosensitive biomolecules into DNA origami nanostructures has enabled several novel single-molecule force spectroscopy techniques.^45–50 For example, a recently developed DNA origami force-clamp was used in conjunction with single-molecule fluorescence imaging to study transitions between folded and unfolded states in biomolecules under a constant, structurally-specified force⁴⁹. These mechanically-informed designs are enabled in part by recent computational tools such as CanDo,^51–53 which applies finite element methods to the prediction of the 3D shape and mechanical properties of DNA nanostructures, and OxDNA,^54–57 a coarse-grain molecular dynamics platform for oligonucleotide and small origami systems.

In this work, we present DNA origami tension probes (DOTPs) that can multiplex adhesive peptides and force-sensitive hairpins in a parallel fashion (Figure 1a), enabling the first use of DNA origami to study molecular mechanics in living cells. Using the biomembrane force probe (BFP), we measure the unfolding forces (F_unfold, the average force required to unfold a tension sensor) of DOTPs with one, two, or three hairpins in parallel and observe that F_unfold correlates positively both with the number of hairpins and with the F_1/2 of the constituent hairpins. We then compare our experimental results to theoretical models and perform finite element simulations which suggest that the hairpins unfold in a semi-coopertative, orientation-dependant manner. Finally, we use DOTPs in live-cell experiments with human platelets. These live-cell experiments show that the inclusion of multiple ligands increases cell-spreading and tension signal, which we attribute to a two-fold increase in the total ligand density. Additionally, we observed that the use of multiple hairpins in parallel increases F_unfold and therefore decreases cellular tension signal. We quantitatively compare these results from previous live-cell studies of platelent traction forces using conventional DNA-based tension probes²⁸ and observe similar trends with respect to F_unfold. This new class of nanoscale tension probes opens the door toward more complex and sophisticated reporters of molecular mechanics.

Figure 1.

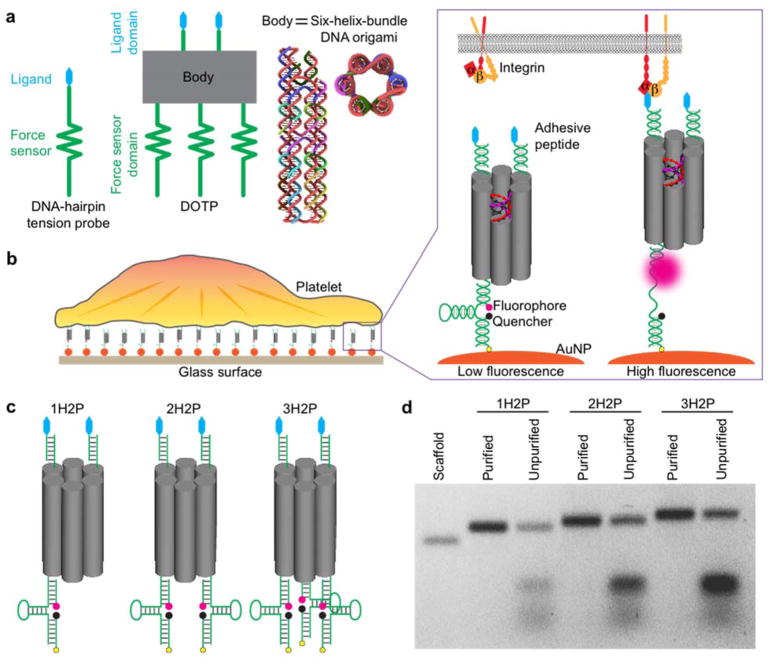
Design and characterization of DNA origami-based tension probes (DOTPs). (a) Schematic showing three components of a DOTP: a ligand presenting domain, an origami body, and a force sensing domain. The body is comprised of a six-helix-bundle DNA origami (side and top view), in which six parallel double-helices are packed on a honeycomb lattice. (b) Illustration of a platelet spreading on a glass surface functionalized with DOTPs. The zoomed-in scheme shows the mechanism of tension-to-fluorescence transduction. The origami constructs are conjugated to gold nanoparticle (AuNP)-coated glass surfaces utilizing thiol–Au binding. Upon receptor (integrin) engagement to the adhesive peptide (cRGDfk) and application of sufficient tension the hairpin unfolds, separating the fluorophore from the AuNP and organic quencher and dequenching the dye. (c) Schematic of DOTPs with two adhesive peptides (blue) on the ligand presenting domain (top end) and one, two or three hairpin(s) on the force sensor domain (bottom end), denoted 1H2P, 2H2P and 3H2P, respectively. (d) Agarose gel electrophoresis of purified and unpurified 1H2P, 2H2P and 3H2P. The scaffold band contains the 425 nucleotide scaffold strand.

The DOTP is comprised of three components: a ligand-presenting domain with one or more cRGDfk peptides, an origami body, and a force-sensor unit consisting of one or more DNA hairpins arrayed in parallel (Figure 1a). The origami body of the tension sensor consists of a 425-nucleotide single-stranded DNA scaffold folded by 17 staples through hybridization using the DNA origami technique.²⁹ The resulting structure is a six-helix bundle packed on a honeycomb lattice (Figures 1a and S2–S3, see Supporting Information for details on design and synthesis). The six-helix bundle is ~45 nm long and ~6 nm in diameter and presents its ligand-presenting domain at one end and its force-sensor domain at the other end. The 3′ termini of the strands displaying the force-sensor domain are modified with thiol groups, which anchor the construct onto an AuNP-coated glass surface. The force-sensor domain includes one or more DNA hairpins, each tagged with a fluorophore-quencher pair (Cy3B and BHQ1) near the base of the hairpin stem (Figure 1b). As in conventional DNA hairpin-based tension probes, each Cy3B molecule is dual-quenched by BHQ1 and the AuNP.¹³ Engagement of the ligand-presenting domain by a receptor with a tensile force exceeding the F_unfold of the DOTP results in cooperative unfolding of all hairpins, which in turn dequenches the fluorophore(s) and generates increased fluorescence signal (Figure 1b). For this proof-of-concept study, we generated four DOTPs with differing numbers of peptide ligands and hairpins: one-hairpin and one-peptide (1H1P), one-hairpin and two-peptide (1H2P), two-hairpin and two-peptide (2H2P) and three-hairpin and two-peptide (3H2P) (Figures 1c and S2). We confirmed the successful incorporation of multiple hairpins within the DNA origami scaffold using agarose gel electrophoresis (Figure 1d).

To measure the F_unfold values of different DOTP constructs, we performed single-molecule force spectroscopy using the BFP technique⁵⁸ (Figure 2a). In this technique, a streptavidin-coated probe bead is attached to a red blood cell (RBC). The RBC is then lightly aspirated into and held with a micropipette tip as shown in Figure 2a. A microparticle coated with biotin-presenting DOTP is then brought into contact with the probe bead and the formation of a biotin-streptavidin bond bridges the two particles together via the DOTP. The target bead is then retracted to stretch the RBC, resulting in a tensile force ramp applied to the DOTP at a rate of 500 pN/s. The displacement of the interface between the probe bead and RBC is optically monitored and transduced to force, generating a force vs. time curve (Figures 2b and S4).⁵⁹ Note that the extension is halted upon irreversible separation (either through shearing of the DNA handles or mechanical rupture of the biotin-streptavidin bond), as indicated by a reduction of force to baseline. Within this force vs. time curve, we measured the force at which a sharp, substantial dip in the force level occurred (Figure 2b, inset). We attribute this sharp drop to a rapid elongation of the tension sensor due to unfolding of the hairpin(s). We repeated this experiment several times (n > 30) and averaged the dip-force across all trials to obtain F_unfold for each construct. We performed this experiment on 1H, 2H, and 3H DOTPs with hairpins of 22% GC-content stems and 77% GC-content stems (Figure 2c, d and S5). Because all hairpins were of identical length (25 bp) and loop size (7 T bases), we anticipated that hairpins with higher GC-content would display a higher F_unfold.^{26, 27}

Figure 2.

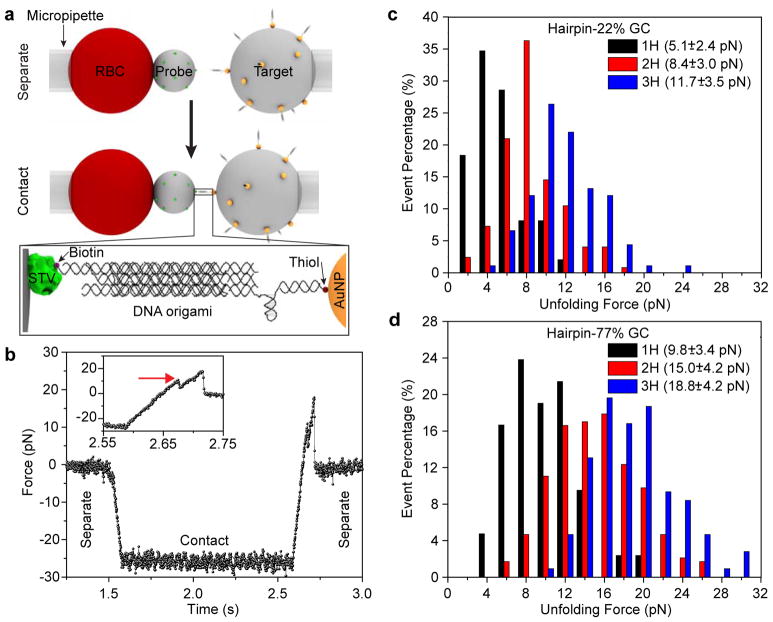
DOTP calibration with BFP single-molecule force spectroscopy. (a) Schematic showing BFP setup. A micropipette-aspirated red blood cell (RBC) is affixed to a streptavidin (STV, green)-coated probe bead. A DOTP-coated target bead, which itself is aspirated by another micropipette, is brought into contact with the STV-coated bead. The ligand-presenting domains each present one biotin (purple sphere), resulting in biotin-STV binding between the two beads. The target bead is then retracted to apply tension to the DOTP. Zoom-in shows the assembled DOTP between the two beads. (b) Representative trace of a single molecule unfolding event showing unfolding of a 1H-77% GC DOTP. Zoom-in of the trace (inset) shows the unfolding event. The red arrow indicates the opening of the hairpin at ~10 pN. (c) Histogram of unfolding events for 1H-22% GC (black, n = 50), 2H-22% GC (red, n = 100) and 3H-22% GC (blue, n = 90) DOTPs. (d) Histogram of unfolding events for 1H-77% GC (black, n = 42), 2H-77% GC (red, n = 230) and 3H-77% GC (blue, n = 98). The legends in (c) and (d) show the corresponding F_unfold with standard deviation for each probe.

With a loading rate of 500 pN/s, we found that the F_unfold of the DOTPs with 1H, 2H and 3H containing 22% GC-content stems were 5.1 ± 2.4 pN (hairpin attached to helix-3; n = 50), 8.4 ± 3.0 pN (hairpins attached to helix-1 and -3; n = 100), and 11.7 ± 3.5 pN (hairpins attached to helix-1, -3 and -5; n = 90), respectively (Figures 2c). For the DOTPs with 77% GC-content stems, the thresholds were 9.8 ± 3.4 pN (n = 42), 15.0 ± 4.2 pN (n = 230) and 18.8 ± 4.2 pN (n = 98), respectively (Figures 2d). In all cases mentioned above, increasing the number of hairpins or the GC content resulted in statistically significant increases in F_unfold (comparisons performed using two-sample t-tests, Table S1). The F_unfold of 5.1 ± 2.4 pN observed in the 1H-22% GC DOTP, agreed with the F_unfold of an individual hairpin (4.8 ± 1.9 pN, n = 36, p < 0.01), suggesting that incorporation of the bulky origami structure does not significantly alter the mechanical response of a single hairpin probe (Figure S7). This agreement of F_unfold also suggests that it is the single 22% GC hairpin in the origami sensor that unfolds rather than other elements within the origami scaffold. We also found that moving the postion of the 22% GC hairpin from helix-3 to helix-1 or from helix-3 to helix-5 did not greatly alter the F_unfold (Figures S6a and S7a, b, p = 0.345 and 0.179 respectively), suggesting a weak or negligible influence of hairpin location on F_unfold. Note that it is also possible to assemble different types of hairpins with different GC-contents (such as 22% and 77%) on a single origami sensor (Figures S6b and S7a, c). The F_unfold of a 2H-mixed DOTP with one 22% GC hairpin and one 77% GC hairpin was 11.4 ± 4.1 pN (n = 57), which is higher than the F_unfold of the 2H-22% GC DOTP (p < 0.01) and lower than F_unfold of 2H-77% GC hairpins (p < 0.01). A 3H-mixed DOTP with one 77% GC hairpin and two 22% GC hairpin yielded an F_unfold of 12.1 ± 4.1 pN (n = 113), which is significantly lower than the 3H-77% construct (p < 0.01) but not significantly higher than the 3H-22% GC DOTP (p = 0.657) or the 2H-mixed DOTP (p = 0.291). Altogether, these measurments demonstrate that the F_unfold of a DOTP can be tuned by multiplexing the hairpin structures comprising the force-sensitive unit of the probe.

To obtain a deeper understanding how multiplexed DNA hairpins cooperate to increase F_unfold, we compared our experimental data to theoretical models of multi-bond rupture. Rupture of multiple molecular bonds in parallel has previously been studied using dynamic force spectroscopy^60–63 and these observations have been accompanied by quantitative theoretical models relating the number of bonds to unfolding force.⁶¹ The unzipping and parallel models represent two extreme cases, and differ in their assumption of the nature of cooperativity between bonds: In the unzipping model, only one hairpin is under tension at a time, so each hairpin unfolds sequentially at its own individual unfolding force and F_unfold is minimized due to the lack of cooperativity between the hairpins. In the parallel unfolding model, tension is equally divided between all hairpins and hairpins unfold cooperatively. Given the parallel arrangement of the hairpins, we anticipated that DOTPs would match predictions by the parallel unfolding model.

The results of our comparisons are shown in Table 1, and further details of our modeling methods are explained in the Supplemental Note. As expected, the unzipping model underpredicts F_unfold for all six DOTPs by an average of 21.7%. Surprisingly, the parallel model overpredicts F_unfold for all six DOTPs by an average of 18.8%. While we initially expected hairpins to unfold in a fully cooperative manner, it appears that hairpin unfolding is best described by a model which is intermediate between unzipping and parallel. Given the rigid nature of the six-helix bundle body of the probe,⁴³ we hypothesized that the discrepancy from the parallel model could be explained by imbalance of tension transmitted to the hairpins. In other words, force transmitted through the ligand may not be evenly distributed to each of the two or three hairpins at the bottom of the rigid six-helix bundle. A logical extension of this hypothesis is that the orientation of tension relative to the long axis of the DOTP could influence how tension is distributed amongst the hairpins.

Table 1.

Comparison of experimentall measured F_unfold to Theoretical Models, with Relative Errors

Tension Sensor	Experiment	Unzipping	Parallel	Orientation Dependent
2H-22%	8.4 ± 2.4	7.1 (−16%)	9.6 (+15%)	7.8 – 8.4 (−4%)*
3H-22%	11.7 ± 3.0	7.5 (−36%)	12.6 (+8%)*	9.9 – 10.8 (−11%)
2H-77%	15.5 ± 4.2	12.0 (−23%)	19.2 (+24%)	14.8 – 16.6 (1%)*
3H-77%	18.8 ± 4.2	13.0 (−31%)	26.5 (+41%)	18.3–20.9 (4%)*
2H-Mix	11.4 ± 4.1	10.2 (−11%)	12.0 (+6%)	10.8–11.3 (−2%)*
3H-Mix	12.1 ± 4.1	10.5 (−13%)	14.4 (+19%)	12.3–12.9 -+4%)*
Average Error		−21.7%	+18.8	−1.3%*

^*Model with lowest relative error

To illustrate the effect of tension imbalance, we performed Monte Carlo simulations of a 2H 77% GC DOTP in which the percentage of force experienced by one hairpin is varied from 0% to 50% (note that these two extreme cases approximate the unzipping and parallel models respectively). Our results indicate that more heterogeneous force distributions lead to a decrease in F_unfold (Figure 3a, b). We next examined how changes in the orientation of tension could modulate F_unfold of multivalent DOTPs by changing the heterogeneity of tension distributed to the hairpins. To do this, we used a finite element method derived from the previously mentioned CanDo software^{51, 52} combined with our Monte Carlo simulation method (Figures 3c and S9, Movie S1). We found that tension imbalance was substantial and dependant on the orientation of tension (Figures 3d–e and S10). We quantify force orientation using azimuthal angle ϕ (the angle around the long axis of the DOTP) and polar angle θ (the angle between tension and the long axis of the tension probe, Figure S12). We assume that forces are randomly distributed in ϕ and have an unknown distribution in θ which depends on the orientations of the force and the DOTP with respect to the sample plane (Figures S10c and S11a). The range of F_unfold reported in Table I reflects the range of F_unfold obtained after averaging with respect to ϕ, while the relative error is calculated using the midpoint of this range.

Figure 3.

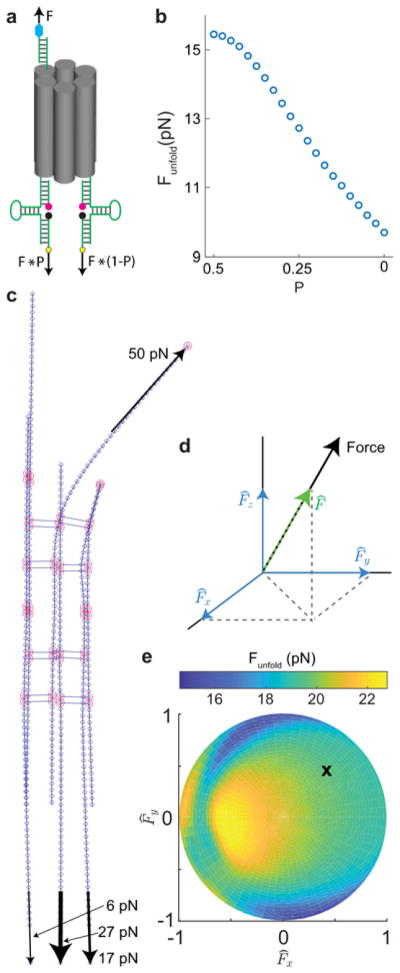
Uneven distribution of tension between hairpins influences F_unfold in an orientation-dependant manner. (a) Visual representation of force imbalance, where total force F is distributed between two hairpins according to constant P. (b) Results of Monte Carlo simulations showing that F_unfold decreases as P decreases from 0.5 to 0 due to increasing tension imbalance. (c) Snapshot of a 3H DOTP rendered as a finite element structure. Elements (short blue lines) are connected by nodes (blue diamonds). Nodes at crossover positions are circled in red. A 50 pN force applied at the site of the ligand, as well as resulting 27 pN, 17 pN, and 6 pN forces experienced at the hairpins, are denoted as black arrows. (d) Coordinate system showing force vector (black arrow), unit force vector (F̂, a vector of magnitude 1 that is parallel to the force denoted by the green dashed arrow), and the x, y, and z components of unit force vector (blue arrows). (e) Plot showing simulated F_unfold as a function of force orientation, as denoted by the x and y components of the unit force vector. The z component of the unit vector is related to radial position on plot. Black x denotes the orientation shown in c.

When accounting for the effect of tension imbalance, the F_unfold of our Monte Carlo simulations was only 1.3% lower than the experimentally measured F_unfold on average (Table 1). In addition, our orientation-dependant model was the most accurate model for five of the six DOTPs. Together, these results indicate that the combination of multiple hairpins increases F_unfold through partial cooperativity between the hairpins and that the unfolding of parallel tension sensors depends on the orientation of force.

Note that in the above simulations we assume that hairpin unfolding is irreversible. In reality, hairpin refolding is possible, particularly if the DOTP is still held closed by one or two folded hairpins. To examine the effect of refolding on the simulated F_unfold values, we modified the Monte Carlo simulations to allow hairpin refolding. We found that accounting for refolding slightly increased the simulated F_unfold values in a manner that depended on the number of hairpins in the DOTP and their GC content. We also found that, regardless of the parameters chosen to model refolding, refolding decreases the accuracy of the parallel bond rupture model and therefore reinforces our conclusion that F_unfold is orientation-dependent. As such, the values in Table I represent lower bounds. We refer readers to the Supplementary Note, Figure S18, and Table S3 for a more detailed discussion of the effect of hairpin refolding on the predicted F_unfold.

Application of DOTPs in living cells

To demonstrate DOTPs’ potential for use in biological applications, we used DOTPs presenting the α_vβ₃ integrin-binding peptide cRGDfK to map molecular tension exerted by human platelets. We chose human platelets as a model system because under our experimental conditions they produce bright tension signal with probes in the 5–19 pN range for extended durations and because mechanical contraction is a core function of platelet biology^{4, 20, 28, 64–66}. The cRGDfK ligand is a peptide that mimics the integrin receptor binding site of fibrinogen and fibronectin, which mediate platelet aggregation by targeting mechanosensitive integrin proteins on the platelet surface⁶⁷. Human platelets were pre-activated with adenosine diphosphate (ADP) and seeded onto a surface coated with 1H2P-22% GC (F_unfold = 5.1 pN) DOTPs. The platelets attached to the surface within 3 minutes and unfolded the 5.1 pN DOTPs, resulting in increased fluorescence intensity under the cell body (Figures 4a, S15 and Movie S2). Tension signal continued to increase as the platelets further spread out for 5 min, at which point the tension signal reached a plateau (Figure 4b) and the cells stopped spreading (Figure 4a). This experiment demonstrates that DOTPs can be used to map integrin traction forces in living cells.

Figure 4.

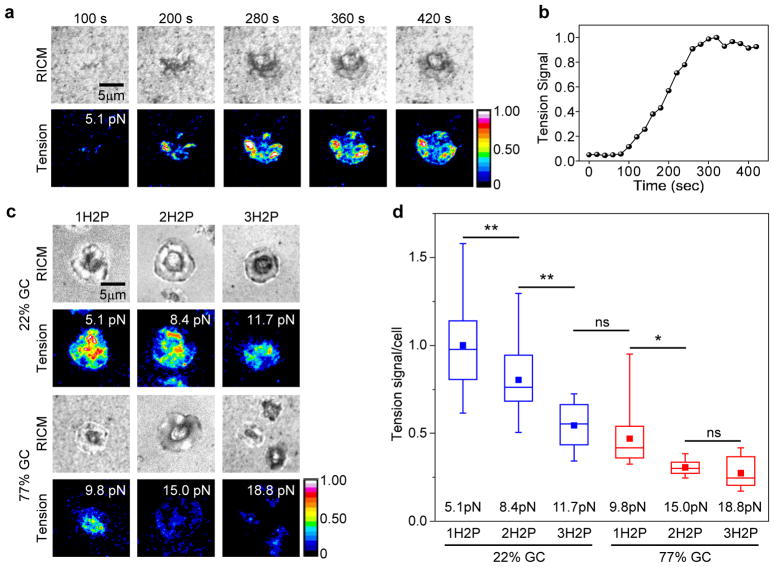
Platelet mechanics measured by DOTPs. (a) Representative time-lapse images of platelet spreading imaged in the reflection interference contrast microscopy (RICM) channel and tension signal in total internal reflection fluorescence (TIRF) channel on a glass surface coated with 1H2P-22% GC origami tension sensors. Scale bar: 5 μm. (b) Plot of whole-cell tension signal as a function of time for the platelet shown in (a). (c) Representative platelet adhesion and corresponding tension signal of platelets activated on surfaces coated with DNA origami tension probes with one (1H2P), two (2H2P) and three (3H2P) hairpin(s) of 22% GC content and 77% GC content. For each tension signal image the F_unfold of the corresponding DOTP is shown in the top-right corner. (d) Comparison of the tension signal from platelets activated on DNA origami tension probes with one, two and three hairpin(s) of 22% GC content and 77% GC content. Mean tension signal for 1H2P with 22% GC was normalized to 1 and all the others were calculated relative to it. Each mean value (solid square) represents averaged signal from more than 20 individual cells (whiskers indicate the range of the data, while the line and box represent the median ± quartile). Corresponding BFP-calibrated F_unfold values are shown. (* p < 0.05; ** p < 0.01; ns: non-significant (p > 0.05); ANOVA).

We next examined the effect of multiplexed ligands by comparing platelets on 1H1P and 1H2P surfaces (Figures S16). Surfaces functionalized with the two different types of tension probes showed similar background intensity, indicating that the two surfaces present the probes at similar densities. ADP activated-platelets were added to these two surfaces and cell adhesion density and tension signal were measured after 20 minutes of incubation. When compared to the 1H1P sensor, the 1H2P sensor supported ~62% higher platelet adhesion and ~50% higher platelet spreading area (Figure S16e–g). In addition, platelets spreading on 1H2P-functionalized surfaces exhibited fluorescent tension signal that was twice as high as platelets on 1H1P surfaces (Figure S16d). To confirm that the increased adhesion was indeed a result of ligand multiplexing, we compared adhesion density and fluorescent tension signal of 1H1P sensors presenting peptides on helix-6 and 1H1P sensors presenting peptides on helix-4 and found little difference between the two constructs (Figure S16). Note that because the ~6 nm separation between the two peptides is smaller than the ~10 nm diameter of an individual integrin, it is unlikely that two integrins can engage two ligands of the same 1H2P sensor simultaneously⁶⁸. As such, we speculate that the increased adhesion and tension signal of the 1H2P probe arose due to increased ligand density and a correspondingly increased probability of each integrin binding to a DOTP. Furthermore, we posit that each individual integrin-DOTP bond is stabilized because stochastic cRGDfK-integrin dissociations are twice as likely to be rapidly followed with rebinding (this is known in the research literature as the “statistical effect” or “statistical rebinding”).⁶⁹

We next investigated the mechanical response of platelets when challenged with DOTPs with higher F_unfold. Platelets were seeded onto surfaces functionalized with 1H2P, 2H2P and 3H2P sensors containing either 22% GC or 77% GC hairpins. Representative cell spreading and tension signal images are shown in Figure 4c. The average whole-cell fluoresecence (normalized to area) for each construct is plotted in Figure 4d. Platelets adhered to and and spread on all substrates and generated tension signal regardless of F_unfold. As expected, average whole-cell fluorescence was negatively correlated with F_unfold, fitting well to the equation I=1.61exp(F_unfold/9.78 pN) (Figure S17). This trend is similar to that observed in previous work using conventional real-time DNA hairpin probes, which similarly fit the equation I=1.68exp(−F_unfold/9.86 pN) (Figure S17).²⁸ This general trend confirms that DOTPs with different numbers of hairpins generate different force response thresholds. These data also confirm previous observations that, within a single platelet, forces applied by integrins are highly heterogeneous and predominantly range from 5 to 19 pN.

We also observed that the 1H2P-77% GC probe reported a lower tension signal compared to the 2H2P-22% GC probe (p < 0.01), despite these two DNA origami sensors having similar calibrated tension thresholds (9.8 and 8.4 respectively). One potential explanation for this result may be the orientation dependence of F_unfold. In a recent study, we developed molecular force microscopy (MFM) to measure traction force orientation using conventional DNA-based tension sensors.⁶⁵ Using MFM, we estimated that platelet integrin forces are applied, on average, at an angle of ~45° from the z-axis. Interestingly, the F_unfold of the 2H sensors is generally expected to decrease at this force angle compared to forces aligned with the z-axis, while the F_unfold of 1H sensors is not expected to change with respect to force orientation. Such a decrease in F_unfold could be expected to result in an increase in intensity.

We emphasize that the calibrated F_unfold values do not provide a metric to quantify the results of live-cell experiments. The unfolding of DOTPs in live-cell experiments can differ from the unfolding of DOTPs in the BFP experiments due to many factors including differences in the distributions of orientations and loading rates experienced by the DOTPs. These factors are also expected to vary substantially spatially and temporally for a single live-cell. As such, we emphasize the importance of interpreting results of live-cell experiments in a relative manner; the exact F_unfold value measured with the BFP technique may not correspond directly to the force required for a cell to open a DOTP, but the scaling of F_unfold with the number of hairpins and hairpin GC content should persist for the live-cell experiment.

In conclusion, we present the first design of a DNA origami tension sensor and use platelet integrins as a model system to demonstrate the feasability of applying this new class of tension probe to the study of cellular forces. By multiplexing extensible hairpin domains, we demonstrate the ability to further tune the F_unfold of real-time DOTPs as measured using the BFP technique. Using a finite element method, we estimated the effect of force orientation on F_unfold. This application of CanDo represents, to the best of our knowledge, the first use of finite element simulations to estimate the response of a DNA origami nanostructure to tension applied via single molecule force spectroscopy. In future works we hope to use this approach to design tension sensors with orientation-dependant functions, mimicking cellular orientation-dependant mechanosensors such as the t-cell receptor³. Such structures could, in theory, be designed to release signaling molecules or therapeutics only when pulled in a specific direction. Such structures could also act as molecular orientation gates, dissociating from the surface when pulled at certain orientations and remaining anchored when pulled at other orientations.

In cell experiements, we observed that multiplexing DOTPs with greater F_unfold generates lower levels of tension signal. As a rough estimate, our results imply that ~70% of platelet integrins apply forces below 15 pN, while a small portion of integrins can exert forces surpassing 19 pN. Platelet tension maps also revealed that platelet tension is highly heterogeneous in space and time, an effect which may arise from variations in tension magnitude, orientation, and loading rate due to changing distributions of different force-mediating machinery across the cell suface.

In principle, DOTPs can be used in future work to study this effect and others by presenting multiple distinct ligands which target different interacting adhesion receptors (a phenomenon known as hetero-multivalency⁷⁰). For example, the T-cell receptor (TCR) is a mechanosensor that specifically detects foreign pathogens.³ Mechanical cooperativity between the TCR and the integrin LFA-1 is an active area of research for which the geometric and mechanical tunability of DOTPs could prove particularly useful. While the short (~6 nm) spacing between ligands in current DOTPs likely prevents simultaneous binding to multiple receptors, this limitation can be overcome in future designs by using differently-shaped origami bodies or flexible linkers. For example, inserting 10-base single-stranded DNA spacers between each ligand and the DOTP body would rroughly triple the maximum spacing between ligands from ~6 to ~18 nm. Alternatively, the six-helix bundle that composes the DOTP’s origami body could be replaced with a more sophisticated DNA origami design (e.g. a rigid Y-shaped nanostructure that presents two ligands at a precise distance from each other).

The geometric tunability of DOTPs may also prove useful in the study of cellular receptors which have multiple ligand-binding sites. For example, DNA origami tension sensors can be applied to study how the synergy site on fibronectin, located about 32 Å away from the RGD sequence, influences integrin mechanical force transmission^{15, 18, 71}. Previous studies have shown that molecular tension probes containing both the RGD sequence and the synergy site display increased fluorescence¹⁸, and DOTPs could be used to expand upon these results by showing the effect of spacing between the RGD sequence and the synergy site on integrin tension. With this work, we have taken an important step forward in the design of molecular probes for the study of molecular biomechanical functions including mechanosensation and mechanotransduction.