Hierarchical Clustering based optimal PMU placement for power system fault observability

Abstract

Optimal number and location of phasor measurement units (PMUs) in the power system networks faces challenges for achieving the full network observability during fault conditions. Achieving fault observability approach requires more constraints than normal system observability and consequently suffers from complex analysis and heavy computational burden for the large-scale networks. A new algorithm for determining the optimal PMU placement considering the network fault observability is introduced. The proposed algorithm is achieved through four stages. The first stage is achieved through the network fault simulation to obtain the post fault change in voltage (ΔV) at each bus. Then, the post fault change in voltage (ΔV) is used to build the network connectivity matrix (CM) and forming a new developed Faulted Connectivity Matrix (FCM) that describes the power system topology during the fault conditions. The correlation between the buses is obtained, in the second stage, by applying Pearson correlation coefficient. Hierarchical Clustering technique is given, in the third stage, to cluster the network into coherent zones to find the most correlated buses. Finally, the optimal location of the PMUs is identified within each zone based on simple proposed placement rules. The proposed algorithm is tested under a variety of fault events applied on different standard test systems. The results show the simplicity and the effectiveness of the proposed algorithm.

1. Introduction

Phasor Measurement Unit (PMU) is the principal element in synchronized phasor measurement system and should be installed in strategic and informative locations in the power system to gain the most possible information with minimum number of PMUs. Installing PMU at each bus of the network may achieve the full system observability [1]. However, the PMU and its deployment cost is expensive. Thus, it is necessary to minimize synchrophasor deployment cost through optimizing the number of PMUs in the network [2].

Minimizing the PMUs and maximizing the measurement redundancy lead the majority of researchers dealing with the PMU optimal placement as an optimization problem [1, 3, 4, 5, 6, 7, 8]. Therefore, the optimization problem of PMU placement is usually solved by the mathematical (conventional) techniques or the evolutionary (heuristic) algorithms [1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12].

Mathematical approaches are applied for solving the preformed linear mathematical equations using the integer linear programming (ILP). The appropriate constraints are necessary to be defined in this approach to guarantee the satisfaction of the desired objective that plays the major role in achieving the optimal solution [5].

Evolutionary algorithms are inspired from natural processes and have the capability to be combined with other methods to overcome the difficulties of achieving the local minima and handling the necessary constraints in the mathematical technique methods [6, 7]. However, the major disadvantage associated with meta-heuristic algorithms is that they consume significant time for the large problems and the solution is nearly optimal [6].

Clustering approaches are used in the power system research in many applications such as operation and control applications [13, 14], generators coherency identification [15, 16, 17], event location [18], power system vulnerability assessment [19], controlled islanding [20] and power system restoration [21]. Hierarchical Clustering [22] is applied in this paper to partition the power system network into specific zones that comprising the correlated system buses and identifying the optimal PMU location within each zone based on simple rules. Thus, applying the Hierarchical Clustering technique for optimal PMU placement overcomes the aforementioned difficulties and drawbacks in solving the optimization problem.

The network observability analysis is carried out either using numerical or topological approach. The numerical approaches suffer from the heavy computational burden in evaluating the rank of the Jacobian matrix and the difficulty rise for large-scale networks. Furthermore, the results are highly dependent on the cumulative errors effect. Therefore, the topological analysis is preferred and mostly used in literature [6].

Placing the PMU in a certain bus produces the voltage phasor of that bus and current phasors of the all branches connected to that bus. Thus, the PMU-equipped bus is said to be observable. The voltage phasors of all the adjacent buses to the PMU-equipped bus can be accurately estimated using a sequential linear minimum mean square error (LMMSE) estimator [23]. Hence, Placing PMU in a bus making that bus and all the adjacent connected buses are observable.

The concept of the observability as explained above shed the light into two different types of the system observability: normal observability and fault observability. The power system is defined to be normal observable if the voltage phasor of all the buses are determinable. On the other hand, the power system is defined to be fault observable if the voltage at two ends of each line and the current at any end of the line are determinable. Generally, if the system is normally observable may not be observable in fault condition [10].

Due to the constraints required for the fault observability purpose, the number of PMUs placed in any network for fault observability approach will be extra compared to the number of PMUs required for the normal observability for the same network.

The optimal PMU placement for fault observability [9, 10, 11, 12] issue has not been extensively discussed in research like the normal observability [1, 3, 4, 5, 6, 7, 8].

The authors in [9] minimized the PMUs number through mixing it with available flow measurements and considered the placement as an optimization problem by formulating it as a nonlinear integer programming problem then converted it into an equivalent integer linear programming problem through boolean implications. However, this work did not provide the minimum numbers of PMU compared to the method proposed in this paper. Furthermore, the conventional flow devices may not guarantee synchronized data.

Reference [10] applied the binary search algorithm to obtain the minimum number of PMUs and their locations considering initial assumption of the PMU numbers and the incipient locations and evaluating every possible combination of PMU installations to ensure the full system observability. Thus, this suggested method leading to increasing the number of PMUs due to evaluating the network pre and post fault location observability. Furthermore, the suggested method is failed to achieve the fault observability for all the branches of the network.

The PMU placement is introduced in [11] as an optimization problem. The placement problem is formulated based on the integer linear programming procedure and solved using the differential evolution method to ensure the global optimization of the placement problem. However, the performance of this method is highly affected with many parameters related to the differential evolution method and executed through excessive iterations.

Numerical fault observability is introduced in [12] while the problem is formulated as a binary semidefinite programming (BSDP) model with binary decision variables. Regardless the heavy computational burden of the numerical observability, the analysis and implementation methodology of the algorithm is very complicated.

This paper proposed a new method to identify the optimal PMU placement achieving the fault observability over the entire network based on the Hierarchical Clustering technique. Moreover, simple topological rules are proposed to avoid the difficulties of the numerical analysis. The proposed algorithm avoided dealing with the PMU placement as an optimization problem. Hence, overcoming the drawbacks of the optimization techniques such as excessive iterations, complicated analysis and the significant computational burden for the bulk large-scale networks.

The rest of the paper is organized as follows. The power system topological representation is described in Section 2. Section 3 depicts the proposed algorithm details. Section 4 verifies the proposed algorithm on a variety of test systems with different topologies. In Section 5, a comparison with previous works is provided. Finally, the conclusions are drawn out in Section 6.

2. Background

2.1. Power system topological representation

Topological representation done in this step is essential to describe the topological structure of any network configuration using the Connectivity Matrix (CM) [3, 4, 6, 10, 11].

The connectivity matrix (CM) is a binary square matrix with dimension equals to (N × N), where N is the total system buses. CM is defined as follow

$$C\text{M}=\{\begin{array}{c}1\text{if}\text{i}=\text{j}\hfill \\ 1\text{if}\text{bus}\text{i}\text{linked}\text{to}\text{bus}\text{j}\\ 0\text{otherwise}\hfill \end{array}$$ (1)

The binary elements of the connectivity matrix in Eq. (1) represent the linked buses of the network, where the binary one in the first line representing the main diagonal elements of the matrix and it implies the bus itself and it always one for any network. The binary one defined in the second line represents the off-diagonal elements and it implies the linked buses. While, the binary zero in the last line implies the non-linked buses in the network.

A simple example of the topological representation of the WSCC 3-machine 9-bus test system topology shown in Fig. 1 is described by the connectivity matrix (CM) given in Eq. (2).

$$C{M}_{\left(9x9\right)}=\left[\begin{array}{ccccccccc}1& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 1\\ 1& 0& 0& 1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 0& 1& 0& 0\\ 0& 0& 0& 1& 0& 1& 0& 0& 1\\ 0& 1& 0& 0& 1& 0& 1& 1& 0\\ 0& 0& 0& 0& 0& 0& 1& 1& 1\\ 0& 0& 1& 0& 0& 1& 0& 1& 1\end{array}\right]$$ (2)

Fig. 1.

WSCC 3-machine 9-bus test system.

The connectivity matrix (CM) described in this section will be used to form a new developed matrix describing the fault effect on the system buses as explained in details in the next section.

3. Methodology

The proposed algorithm consists of four stages. Firstly, the power system topological structure during fault condition is represented by the Faulted Connectivity Matrix (FCM). Pearson correlation coefficient (r) is applied on the FCM in the second stage to reveal the degree of coherency among all the system buses in second stage. Thirdly, Hierarchical Clustering technique is used to cluster the network into specific coherent zones that comprised the correlated system buses. The optimal PMU location is determined within each zone via applying simple proposed topological rules in the last stage. The details of each stage of the proposed algorithm are clarified as follows:

3.1. Topological representation of power system under fault condition

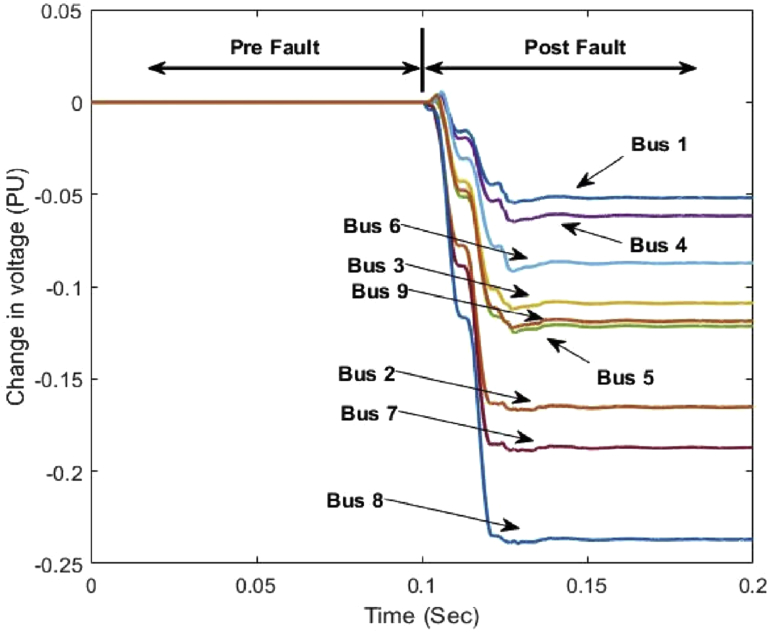
When a fault occurred in the power system network, rapidly the voltage dropped in all the network buses while the buses nearest to the faulted line will be the most affected buses and suffered from the maximum voltage drop among all the other network buses. For this reason, the change in voltage (ΔV) is used to describe the fault effect on all the system buses. To clarify this point a case study of a three phase fault on the line (7–8) on the WSCC 9-bus test system is simulated. The change in voltage (ΔV) on all the system buses due to that fault case is shown in Fig. 2.

Fig. 2.

Change in voltage (ΔV) due to fault on the line (7–8) on the WSCC 9-bus test system.

It is clear from the figure that the value of the (ΔV) of both buses 8 and 7 are the largest among the other buses. While the buses 2, 5 and 9 that are connected to the buses 7 and 8 will be then affected due to the fault. Consequently, the remote buses to the faulted line will be the less affected buses.

Therefore, the post fault change in voltage (ΔV) of each bus is utilized inside the connectivity matrix (CM) to represent the fault effect on all the system buses. The new reformed matrix, Faulted Connectivity Matrix (FCM), is defined as follow

$$F\text{CM}=\{\begin{array}{c}1\ast (\Delta {\text{V}}_{\text{i}}+\sum \Delta {\text{V}}_{\text{j}})\text{if}\text{i}=\text{j}\\ 1\ast \Delta {\text{V}}_{\text{j}}\text{if}\text{bus}\text{i}\text{linked}\text{to}\text{bus}\text{j}\hfill \\ 0\text{otherwise}\hfill \end{array}$$ (3)

where $\Delta V_i$ and $\Delta V_j$ is the change in voltage of bus_i and bus_j respectively.

The first line in Eq. (3) is the main diagonal element in the FCM. Each main diagonal element represents the change in voltage impact on each bus_i in the system and it is calculated by multiplying the binary one to the summation of the value of the change in voltage of the bus_i itself ($\Delta V_i$) and each change in the voltage value of each bus_j ($\Delta V_j$) connected to the bus_i. The second line represents the off-diagonal elements and it is calculated by multiplying the binary one to the change in voltage occurred in each bus_j ($\Delta V_j$) in the matrix. To clarify the FCM calculation procedure, the faulted connectivity matrix (FCM) is formed and detailed in Eq. (4) due to the fault condition on the line (7–8) on the WSCC 9-bus test system.

$${\text{FCM}}_{\left(9x9\right)}=\left[\begin{array}{ccccccccc}1\mathit{\ast }\left(\begin{array}{c}\Delta V1+\\ \Delta V4\end{array}\right)& 0& 0& 1\mathit{\ast }\Delta \mathit{V}4& 0& 0& 0& 0& 0\\ 0& 1\mathit{\ast }\left(\begin{array}{c}\Delta V2+\\ \Delta V7\end{array}\right)& 0& 0& 0& 0& 1\mathit{\ast }\Delta \mathit{V}7& 0& 0\\ 0& 0& 1\mathit{\ast }\left(\begin{array}{c}\Delta V3+\\ \Delta V9\end{array}\right)& 0& 0& 0& 0& 0& 1\mathit{\ast }\Delta \mathit{V}9\\ 1\mathit{\ast }\Delta \mathit{V}1& 0& 0& 1\mathit{\ast }\left(\begin{array}{c}\Delta V1+\\ \Delta V4+\\ \Delta V5+\\ \Delta V6\end{array}\right)& 1\mathit{\ast }\Delta \mathit{V}5& 1\mathit{\ast }\Delta \mathit{V}6& 0& 0& 0\\ 0& 0& 0& 1\mathit{\ast }\Delta \mathit{V}4& 1\mathit{\ast }\left(\begin{array}{c}\Delta V4+\\ \Delta V5+\\ \Delta V7\end{array}\right)& 0& 1\mathit{\ast }\Delta \mathit{V}7& 0& 0\\ 0& 0& 0& 1\mathit{\ast }\Delta \mathit{V}\text{4}& 0& 1\mathit{\ast }\left(\begin{array}{c}\Delta V4+\\ \Delta V6+\\ \Delta V9\end{array}\right)& 0& 0& 1\mathit{\ast }\Delta \mathit{V}9\\ 0& 1\mathit{\ast }\Delta \mathit{V}2& 0& 0& 1\mathit{\ast }\Delta \mathit{V}5& 0& 1\mathit{\ast }\left(\begin{array}{c}\Delta V2+\\ \Delta V5+\\ \Delta V7+\\ \Delta V8\end{array}\right)& 1\mathit{\ast }\Delta \mathit{V}8& 0\\ 0& 0& 0& 0& 0& 0& 1\mathit{\ast }\Delta \mathit{V}7& 1\mathit{\ast }\left(\begin{array}{c}\Delta V7+\\ \Delta V8+\\ \Delta V9\end{array}\right)& 1\mathit{\ast }\Delta \mathit{V}9\\ 0& 0& 1\mathit{\ast }\Delta \mathit{V}3& 0& 0& 1\mathit{\ast }\Delta \mathit{V}6& 0& 1\mathit{\ast }\Delta \mathit{V}8& 1\mathit{\ast }\left(\begin{array}{c}\Delta V3+\\ \Delta V6+\\ \Delta V8+\\ \Delta V9\end{array}\right)\end{array}\right]$$ (4)

The FCM provided from this stage will help in determining the correlated buses due to the fault condition as described in details in the second stage.

3.2. Determination of the correlated buses due to fault effect

The correlated system buses are determined using the Pearson correlation method described in [24]. Pearson correlation is applied on the FCM by calculating the pairwise correlation coefficient between each pair of the FCM rows.

The Pearson correlation coefficient (r) is defined in Eq. (5) as

$$r=\frac{{\sum \left(X-\overline{X}\right)\left(Y-\overline{Y}\right)}^{}}{\sqrt{{\left(X-\overline{X}\right)}^2}\sqrt{{\left(Y-\overline{Y}\right)}^2}}$$ (5)

where X and Y are the vector rows in the FCM, $\overline{X}$ is the mean value of vector X and $\overline{Y}$ is the mean value of vector Y.

The result of Pearson correlation produced a new correlation matrix whose elements varies between the specific range (−1 to 1). The value “−1” indicates a negative correlation between the system buses which mean in this paper that the buses are not topologically connected, while the value “1” indicates a positive correlation which mean the buses are topologically connected. The more the values nearer to “1” implies a higher change in voltage (ΔV) value in the connected buses and consequently indicating a higher correlation between these buses.

The results obtained from the correlation matrix identify the degree of coherency among the system buses. The correlation matrix elements obtained due to fault on the line (7–8) for the WSCC 9-bus system is shown in Fig. 3 as a scaled color figure to clarify the coherency between the system buses.

Fig. 3.

Color scaled figure clarify the correlation between buses due to fault condition.

Each colored box in Fig. 3 represents each element value in the FCM. Based on the color bar legend on the right side of the figure, the boxes with dark color (blue) implies that the buses indices marked on the figure axes are not topologically connected. The boxes colored with (yellow and light green) implies that both buses indices connected to that box are topologically connected and the degree of correlation between these buses due to the fault condition.

Based on the degree of coherency among the system buses specified in this stage, a set of particular zones comprising most correlated system buses will be identified using Hierarchical Clustering technique as illustrated in the next stage.

3.3. Coherent zones identification based on Hierarchical Clustering

Cluster analysis is one of the most common unsupervised machine learning techniques that used widely in statistics and data mining and applied in many applications in our daily life. There are many types of the clustering techniques such as K-means, fuzzy, density and Hierarchical clustering.

Clustering technique is used for obtaining the optimal PMU placement in terms of normal observability [25] only. While, the Hierarchical Clustering is used in this paper for obtaining the optimal PMU placement achieving fault observability approach. Hierarchical Clustering that described in [21] is a clustering technique that building groups of the input data in nested sets of multilevel clusters known as dendrogram that plotting the hierarchical relationship between clusters.

The Hierarchical Clustering technique is used in this stage of the algorithm to partition the power system network into specific coherent zones. Each zone comprises the most correlated buses obtained from the correlation matrix. The Hierarchical Clustering technique procedure is achieved through three sequential steps as follow:

3.3.1. Measuring the similarity between the correlated buses

The function of this step is to identify the most correlated buses in the system and the degree of correlation between the correlated system buses. The similarity measure between the buses is done by calculating the Euclidean distance between every two rows of the correlation matrix. Euclidean distance is defined in Eq. (6) by calculating the square root of the sum of the squares of the data differences [22] as follow:

$$d(p,q)=\sqrt{\sum _{i=1}^n{(p_i-q_i)}^2}$$ (6)

where p and q are each pairs of the row vectors of the correlation matrix, n is the total number of the correlation matrix rows.

3.3.2. Linking the correlated buses into hierarchical tree

In this step the relation between the correlated buses is viewed graphically in the dendrogram plot via starting building up the hierarchical tree from individual buses then progressively merging the most correlated buses in clusters until there is only a single cluster left.

There are many methods to merge the clusters with each other to represent the hierarchical tree in the dendrogram plot. Thus, choosing the type of linkage method will effect on the shape of linking the sets of the formed cluster groups in the dendrogram.

The main target in this algorithm is to join the correlated system buses accurately with each other while avoiding neither creating a large wide cluster including unmatched sets of uncorrelated of the system buses nor creating many small clusters that leading to separating the highly correlated buses into sets of small clusters.

The weighted average distance also known as Weighted Pair Group Method with Averaging (WPGMA) is defined in Eq. (7) and it is selected in this paper because it calculates the distance between the clusters as a simple average. Therefore, the matched correlated buses can be linked correctly in the dendrogram plot.

Another advantage of the weighted average distance method is that when different fault types and locations are simulated the resulted shape of the correlated buses as a hierarchical tree will not dramatically change in the dendrogram.

The weighted average distance [21] is defined as:

$$L\left(x,y\right)=\frac{(d\left(p,y\right)+d\left(q,y\right))}{2}$$ (7)

where cluster x combining both p and q clusters and L(x,y) is the distance between cluster x and cluster y.

To clarify the above two steps, the dendrogram plot due to the fault on the line (7–8) of the WSCC 9-bus system test is shown in Fig. 4.

Fig. 4.

Dendrogram plot for a fault on the line (7–8) at the WSCC 9-bus system.

The dendrogram shown in Fig. 4 clarifies the relation between the correlated buses. The cluster C1 is comprising the buses 2 and 7, which are the most correlated buses in the system, and both are topologically connected, then bus 1 is correlated and connected with bus 4 and comprised in C2, then bus 3 is correlated and connected with bus 9 in C3. Bus 5 is partially correlated with the buses in C1 and all are combined in C4. Bus 8 is partially correlated with C4 and so on. The group of buses in C6 are partially correlated with the buses in C2. Finally, both C2 and C6 are connected with C5 creating one cluster that comprising all the system buses.

The degree of the correlation between the connected buses is identified by the similarity index where the smaller value of similarity implies a smaller value of Euclidean distance and hence a higher degree of correlation.

3.3.3. Hierarchical tree cut off

The last step after plotting the dendrogram is to determine where to cut off the hierarchical tree to identify the optimal number of coherent zones that comprising the correlated buses. The Gap Statistic introduced in [26] is a common approach that widely used for determining the most appropriate number of clusters for any clustering method.

The main idea of the Gap Statistic approach is to compare the total within intra-cluster variation (W_k) defined by Eq. (8) for different values of k (where k is the number of clusters being evaluated) with their expected values under null reference distribution of the data (W_kb).

$${\text{W}}_{\text{k}}=\sum _{\text{c}=1}^{\text{k}}\frac{1}{2{\text{n}}_{\text{c}}}{\text{D}}_r$$ (8)

where n_c is the number of data points in cluster r and D_r is the sum of the pairwise distances for all points in cluster c.

Gap Statistic [24] is evaluated as defined by Eq. (9) to estimate the optimal number of clusters, where the optimal number is identified by the cluster that maximized the Gap value

$$Ga{p}_n\left(K\right)=E_n^{\ast }\{\log \left(W_k\right)\}-\log \left(W_k\right)$$ (9)

where E* denotes the expectation under a sample of size n from the reference distribution.

The Gap Statistic is evaluated graphically via plotting the Gap values versus the proposed numbers of clusters (k) and estimating the elbow location in the plot that indicating the number of clusters that give the largest gap value as shown in Fig. 5.

Fig. 5.

Gap values versus the proposed number of clusters.

The marked dendrogram is shown in Fig. 6, while each zone marked with different color to identify the set of the correlated and topologically connected buses within each specific zone.

Fig. 6.

Dendrogram divided into three zones due to fault on the line (7–8) at the WSCC 9-bus system.

The Hierarchical Clustering results applied on the WSCC 9-bus test system and the network clustered into three coherent zones as shown in Fig. 7, each zone comprised the correlated buses as identified in the marked dendrogram.

Fig. 7.

WSCC 9-bus system clustered into three coherent zones.

Zone 1 in the clustered WSCC 9-bus system consists of a set of highly correlated buses like buses 2 and 7 and another set of buses (like buses 5 and 8) which are lesser correlated and linked to the highly correlated buses. Therefore, the first zone is divided into one perfect zone comprising the highly and perfectly correlated buses (buses 2 and 7) and two partial zones comprising the partially correlated buses (bus 5 and bus 8 respectively).

The clustered network and the coherent zones identified in this stage are informative and used in the last section of the algorithm to determine the optimal PMU location.

3.4. Optimal PMU placement rules

The PMU placement procedure in this stage is carried out based on simple proposed PMU placement rules to identify the most suitable buses for the PMU placement within each zone in the network.

There are some rules enhance the topological analysis [3, 4, 5, 10] illustrated as follow:

• •If the voltage and current phasors are known at any end of a line, then the voltage and current phasors at the other end are determinable.
• •If voltage phasors are known at both ends of a line, the current phasor through this line can be calculated.
• •Considering the zero injection bus (ZIB), i.e. the bus without any source or load, if the current phasors are known for all the lines linked to that ZIB, except one, the current phasor of the unknown line can be determined using KCL equations.

• According to the above-illustrated rules, a simple developed PMU placement rules are proposed and concluded as follow:

• 1.Each generator bus should be equipped with PMU

As the PMU placement is necessary to fully observe the power system network under fault condition, therefore each source feeding the fault should be monitored.

• 2.ZIB should not equipped with PMU

Considering the ability of the ZIB in obtaining the unknown current of one branch if the currents of other branches are known. It is not preferable to set the PMU at the ZIB.

• 3.Perfect Zones should be equipped with one PMU at least

The priority is to set the PMU at the generator buses involved within the perfect zone and in case of a couple normal buses are involved in the zone then set the PMU at the bus linked with more lines to cover more of the adjacent buses. If both buses are linked with the same number of lines then set the PMU at the both buses.

• 4.Partial zone buses should be equipped with PMU

The buses included in the partial zones should be equipped with PMU to cover all the zone lines.

After the PMUs placed on the suggested buses according to the placement rules, some of the PMUs may eliminated via checking the fault observability condition for each branch in the network i.e. the voltage at two ends of each line and the current at any end of the line are determinable.

The PMUs can be eliminated from any bus considering the priorities defined in the placement rules. The whole stages of the algorithm are summarized in the flowchart shown in Fig. 8.

Fig. 8.

Flowchart of the proposed algorithm.

4. Results & discussion

4.1. Simulation results

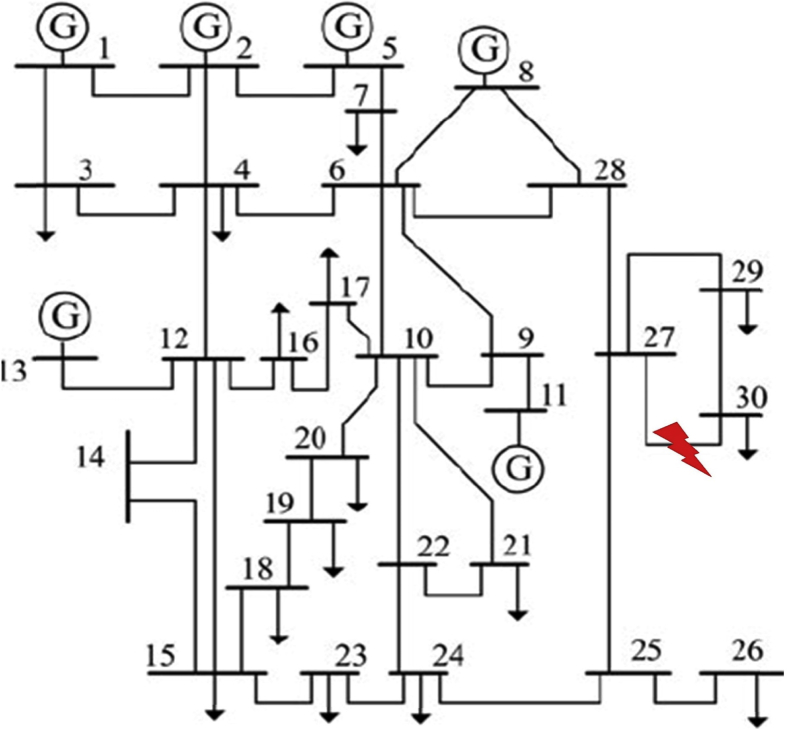
The methodology of the proposed algorithm is applied on a variety of the standard test systems to verify the simplicity and effectiveness of the algorithm. The algorithm implementation explained in details on the IEEE 30-bus test system shown in Fig. 9. The PSS/E program used to simulate the different fault types in the test systems. A three phase fault is simulated on the line (27–30) in the IEEE 30-bus test system in this example.

Fig. 9.

IEEE 30-bus system with fault on the line (27–30).

The FCM is formed based on the results of the change in voltage (ΔV) due to the fault condition of the IEEE 30-bus test system in this example. Then, the calculation procedures of the Hierarchical Clustering technique is processed using the statistics and machine learning toolbox in MATLAB software package.

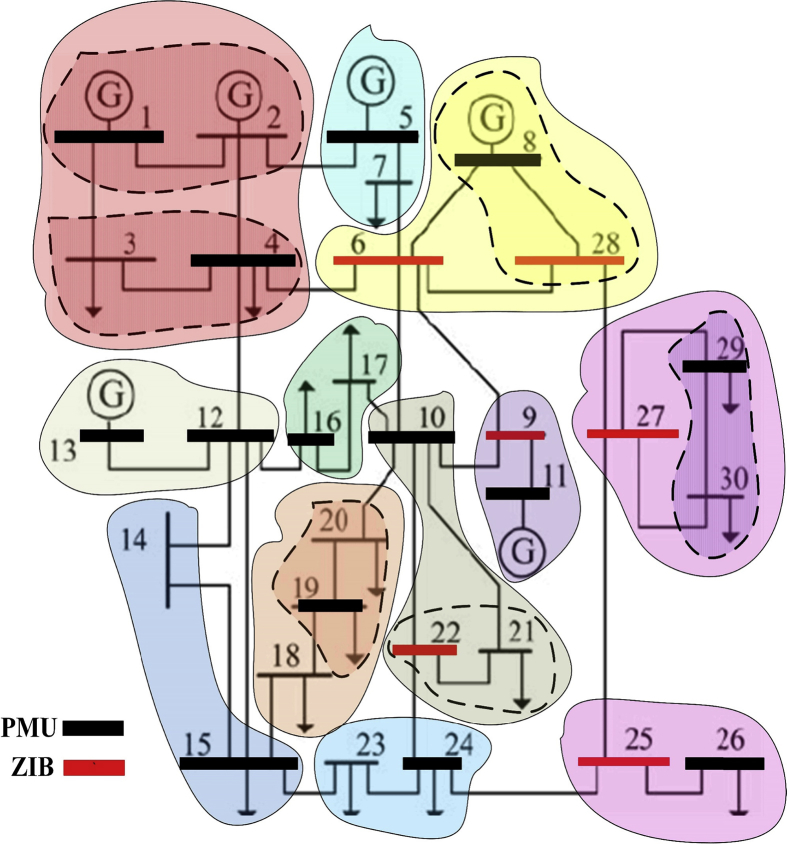
The Gap Statistic optimal results verified to cut off the hierarchical tree to obtain twelve groups of buses as shown in Fig. 10. The hierarchical tree is plotted with twelve different colors in the dendrogram plot in Fig. 11. The colored clusters in the dendrogram represent each coherent zone in the system. The IEEE 30-bus network is clustered according to the dendrogram as shown in Fig. 12.

Fig. 10.

Maximum Gap value marked at 12 as the optimal number of clusters.

Fig. 11.

Dendrogram plot marked with different colors for each zone (12 zones) due to the fault on the line (27–30) on the IEEE 30-bus system.

Fig. 12.

The clustered IEEE 30-bus system clarified with the PMU buses.

The PMU bus locations are selected within each coherent zone via applying the four proposed placement rules. The buses within each coherent zone and the selected buses for the PMU placement are clarified in Table 1. The details of the selection procedure are illustrated for each bus in the selection details column in Table 1.

Table 1.

Selected PMU buses according to the placement rules.

Coherent zone no.	Buses within each zone	Selected PMU bus location	Selection details
1	29, 30, 27	29, 30	Both buses 29 and 30 are selected because both buses are linked with the same number of lines in the perfect zone, while bus 27 is a ZIB so that it is abandoned according to the second placement rule.
2	1, 2, 3, 4	1, 2, 4	This zone comprised two perfect zones. In first perfect zone buses 1 and 2 are generator buses so both of them are selected according to first placement rule. In the second perfect zone buses 3 and 4. While bus 4 is linked with more lines than bus 3, so bus 4 is selected according to the third placement rule and bus 3 is abandoned.
3	5, 7	5	Bus 5 is a generator bus so it is selected according to first placement rule.
4	6, 8, 28	8	Bus 8 is selected because it generator bus, while both buses 8 and 28 are ZIBs so both are not selected.
5	9, 11	11	Bus 11 is selected because it generator bus, while bus 9 is a ZIB so that it is not selected.
6	10, 21, 22	10, 21	Buses 21 and 22 are included in the perfect zone. While bus 22 is a ZIB, so that it is not selected. Bus 10 is included in the partial zone so it is selected according to the fourth placement rule.
7	16, 17	16, 17	Both buses 16 and 17 are selected because both buses are linked with the same number of lines in the same perfect zone.
8	12, 13	12, 13	Bus 13 is selected because it a generator bus, while bus 12 is linked with more lines than bus 13 in the zone, so the both buses are selected according to the third placement rule.
9	14, 15	15	Bus 15 is linked with more lines than bus 14 in the same zone, so bus 15 is selected and bus 14 is abandoned.
10	18, 19, 20	18, 19, 20	Both buses 19 and 20 are selected because both of them are linked with the same number of lines in the perfect zone. Bus 18 is included in the partial zone so it selected according to the fourth placement rule.
11	23, 24	24	Bus 24 is linked with more lines than bus 23 in the same zone, so bus 24 is selected and bus 23 is abandoned.
12	25, 26	26	Bus 25 is a ZIB so it is not selected and bus 26 is selected according to the third placement rule.

The fault observability is checked for each branch in the network and some of the PMU locations can be eliminated from selection because there is no need for additional measurements in these buses.

Table 2 listed the eliminated PMU buses locations in each zone.

Table 2.

Eliminated PMU bus locations.

Zone no.	Selected PMU bus location	Eliminated PMU bus location
1	29, 30	30
2	1, 2, 4	2
3	5	-
4	8	-
5	11	-
6	10, 21	21
7	16, 17	17
8	12, 13	-
9	15	-
10	18, 19, 20	18, 20
11	24	-
12	26	-

The proposed algorithm is applied on different test systems. Table 3 concludes the algorithm test results on the WSCC 9-bus system, IEEE 14-bus, New England 39-bus and the 16-machine 68-bus test systems. The number of coherent zones for each test system and the optimal PMU bus locations are listed in Table 3.

Table 3.

Proposed algorithm results for different test systems.

Test system	Number of coherent zones	PMU bus location
WSCC 9-bus	3	1, 2, 3, 4, 7, 9
IEEE 14-bus	4	1, 2, 4, 6, 8, 9, 11, 13
New England IEEE 39-bus	9	3, 7, 12, 16, 19, 23, 26, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39
IEEE 68-bus	18	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 24, 26, 29, 37, 41, 42, 44, 45, 48, 49, 50, 53, 54, 55, 56, 58, 60, 61, 62, 64, 66, 67

4.2. Comparison with previous works

As mentioned early that the fault observability analysis has not extensively studied in literature work, However, there are few efforts made in [8, 9, 10, 11] as discussed in the introduction part. The proposed algorithm results compared with the previous works in this section.

The proposed algorithm provided minimal PMU numbers compared to the information theoretic approach in [8] for the IEEE 30-bus test system. Differential Evaluation method in [10] and the Semidefinite Programming in [11] provided the same number of PMUs compared to the proposed algorithm for the IEEE 14-bus and IEEE 30-bus systems. While the work presented in [9] failed to achieve the full network observability. Therefore, the results obtained from [9] are not considered in this comparison. Table 4 compares the number of PMUs of the proposed algorithm results with the results of the previous works for different test systems.

Table 4.

Number of PMUs comparison between the proposed algorithm and previous works.

Test system	Number of PMUs
	Proposed	Reference [8]	Reference [10]	Reference [11]
WSCC	6	Not reported	Not reported	Not reported
IEEE 14-bus	8	8	8	8
IEEE 30-bus	14	17	14	14
New England IEEE 39-bus	18	Not reported	Not reported	Not reported
IEEE 68-bus	38	Not reported	Not reported	Not reported

Unlike the majority of the literature, test results of the proposed algorithm implementation on a variety of standard test systems is presented in this paper. Moreover, the proposed algorithm can be easily implemented on any network especially large-scale networks with any configuration without complexity or sophisticated analysis.

5. Conclusion

A new algorithm is developed for optimal PMU placement achieving fault observability. The algorithm summarized in four stages. The Faulted Connectivity Matrix (FCM) is developed firstly to represent the topological structure of the network under fault condition. The correlation matrix is obtained in the second stage via applying the Pearson correlation coefficient to identify the system correlated buses and the degree of correlation among the buses. Based on the correlation matrix, the Hierarchical Clustering is processed in the third stage to classify the power system network into coherent zones. Each zone comprised the most correlated buses in the system and is represented graphically on the dendrogram plot. Four placement rules are proposed in the last stage to select the most suitable buses for PMU placement within each coherent zone.

The proposed algorithm avoided treating the PMU placement as an optimization problem and overcomes the difficulties of the optimization techniques such as;

• •The complexity in formulating the objective function.
• •The assumptions and the optimization technique factors that effect on the performance of the solutions.
• •Excessive iterations and significant computational burden of the optimization techniques.
• •Difficulty of implementation in case practical bulk networks.

The algorithm is implemented on a variety of the standard test systems to verify the simplicity and effectiveness of the algorithm on any network.

Including the effect of other system parameters like frequency and phase angle within the FCM and evaluating the proposed algorithm without considering the ZIB in the studied test system needed to be addressed in future studies. The limited measurement and communication channel of the PMUs are additional factors should be considered for future algorithm evaluation.

Declarations

Author contribution statement

Amr Kassem: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Moustafa Eissa: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.