Hitting the Target: Mathematical Attainment in Children Is Related to Interceptive-Timing Ability

Abstract

Interceptive timing is a fundamental ability underpinning numerous actions (e.g., ball catching), but its development and relationship with other cognitive functions remain poorly understood. Piaget suggested that children need to learn the physical rules that govern their environment before they can represent abstract concepts such as number and time. Thus, learning how objects move in space and time may underpin the development of related abstract representations (i.e., mathematics). To test this hypothesis, we captured objective measures of interceptive timing in 309 primary school children (5–11 years old), alongside scores for general motor skill and national standardized academic attainment. Bayesian estimation showed that interceptive timing (but not general motor capability) uniquely predicted mathematical ability even after we controlled for age, reading, and writing attainment. This finding demonstrates that interceptive timing is distinct from other motor skills with specificity in predicting childhood mathematical ability independently of other forms of attainment and motor capability.

Interceptive timing is a fundamental human sensorimotor ability that underpins actions in which the goal is to make contact with a target when the target and human are in relative motion (e.g., hitting a baseball). These tasks require both spatial and temporal accuracy, and proficiency in these tasks appears later in a child’s developmental history than skills with minimal temporal constraints, such as reaching to static objects (Sugden & Wade, 2013). Neurologically intact adult humans show exquisite precision in interceptive timing, with elite baseball batters able to swing their bat with a spatial accuracy of ±1.5 cm and a temporal accuracy of ±10 ms (Tresilian, 1999). The interceptive-timing skills of humans are a testimony to the incredible learning capacity of the sensorimotor system and its ability to overcome the challenges involved in controlling over 600 muscles with the inherent difficulties of nonlinearity, nonstationarity, information delays, and noise while operating within an uncertain world (Franklin & Wolpert, 2011). Temporal-processing delays are particularly problematic when performing interceptive-timing tasks, and so the individual will need to make predictions about where the object and the limb will be at the time of desired contact (Tresilian, 2012). These predictions require precise estimates of how the object will move over time, together with state estimates of the neuromuscular system.

It is widely believed that sensorimotor prediction relies on internal models within the sensorimotor system. Internal models allow for prediction of object motion through space and time (Merfeld, Zupan, & Peterka, 1999), with forward models being used to estimate the sensory consequences of motor commands (Flanagan & Wing, 1997; Wolpert, Miall, & Kawato, 1998). Thus, the development of these models is central to the ontogenetic acquisition of interceptive-timing skills. The deleterious impact of developmental delays in motor prediction can be readily imagined with regard to a child’s ability to engage in physical activity. But it is possible that sensorimotor impairments have consequences for a child’s cognitive capabilities (Cameron et al., 2012; Grissmer, Grimm, Aiyer, Murrah, & Steele, 2010; Roebers et al., 2014; Son & Meisels, 2006) in a manner that is not so readily appreciated by educational authorities. Such proposals are consistent with the view that the phylogenetic emergence of higher-order cognitive abilities were built on the evolutionary platform provided by the motor system (Barton, 2012), particularly with respect to estimating the future state of the environment and physical body (Desmurget & Grafton, 2000).

The idea that higher-order cognitive processes emerged from sensorimotor abilities is attractive (Wilson, 2002). It has been suggested that the fundamental importance of sensorimotor substrates to cognition extends to both the individual as well as the species, with Piaget (1955) suggesting that ontogeny recapitulates phylogeny in this regard. Thus, Piaget proposed that sensorimotor interactions with the environment underpin the development of cognitive representations, including our understanding of number. This idea has received a surge of support over the past decade, and evidence shows that abstract representations of number are grounded in early interactions with objects and an understanding of physical space (de Hevia & Spelke, 2010; Nieder & Dehaene, 2009). There is evidence to suggest that the basic spatial-processing abilities in infants (6–13 months old) are related to the mathematical capabilities developed at 4 years of age (Lauer & Lourenco, 2016). It also appears that number representations become spatially orientated (Fias, van Dijck, & Gevers, 2011), with representations of number and space sharing overlapping neural circuitry (Hubbard, Piazza, Pinel, & Dehaene, 2005).

Given that there appear to be close links between spatial and temporal representations (Bueti & Walsh, 2009; Burr, Ross, Binda, & Morrone, 2011; Chang, Tzeng, Hung, & Wu, 2011; Lourenco & Longo, 2010; Srinivasan & Carey, 2010; White & Diedrichsen, 2010; Wijdenes, Brenner, & Smeets, 2014), it is no great leap to hypothesize that representations of space, time, and number will all be processed by related systems. There is currently no direct evidence examining whether children’s skill performing interceptive timing is related to their ability in mathematics, but a robust test of this hypothesis would be to measure interceptive-timing skill and relate this to standardized school mathematical measures. A failure to find a relationship would allow us to reject the hypothesis, while a more general relationship between interceptive-timing skill and cognitive ability (e.g., in reading and writing) would suggest that there is no specific functional relationship between mathematics and interceptive timing over and above general academic achievement.

Thus, we developed an interceptive-timing task with 54 moving targets to test 309 primary school children (age = 5–11 years; see Fig. 1). Three target speeds and three target widths were presented (nine trial types) with a sufficient range to challenge older children while allowing younger children to also succeed. The number of targets hit (interceptive-timing score) was the primary measure of interest. In a separate task, the manual dexterity and postural control abilities of the children were measured to distinguish between general motor skill and interceptive-timing abilities. Mathematics ability was obtained from the children’s nationally standardized mathematics attainment scores (1–15 scale; see the Supplemental Material available online). These, along with reading and writing scores, were provided by the school.

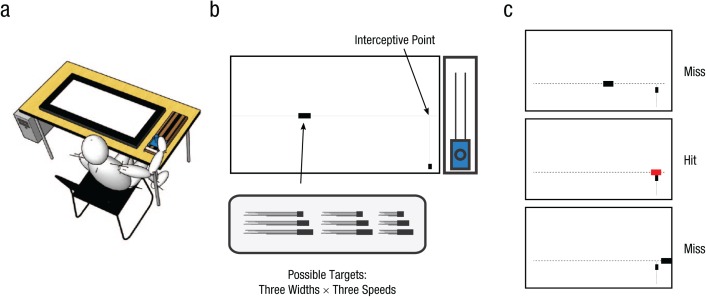
Fig. 1.

Experimental setup and design. Children viewed a horizontally oriented monitor (a) while controlling an on-screen “bat” with a 1-degree-of-freedom manipulandum (this example shows the experimental setup for a right-handed child, but the control was placed on the left of the display for left-handed participants with stimuli reversed). The schematic (b) shows the location of the target and bat on the experimental display as well as the manipulandum to the right of the display. Targets moved from left to right across the screen. Participants were instructed to hit the target from beneath with the bat. The possible outcomes are shown in (c). In the upper panel, the bat has arrived too early and missed the target. In the middle panel, the bat successfully hits the target on the underside. In the lower panel, the bat was too late and missed the target.

Method

Participants

Participants were recruited from a state primary school in Bradford, West Yorkshire, England. There were 368 children in UK School Years 1 to 6 (age range = 5–11 years) at the time of testing. All children were invited to take part in the study. The children completed two test sessions in which they completed a range of motor and cognitive tasks. All motor tasks took place in the first session. Ethical approval was obtained from the University of Leeds (School of Psychology) Ethics and Research committee.

From the 368 children at the school, 309 full data sets were included in the data analysis. Eleven children were removed from the 368 because they were classed as having special education needs by the school. Another 29 were excluded because the experimenter recorded that they did not complete one or more tasks, 14 were excluded because they did not provide data on the interception task, and 5 did not provide data on postural control.

Interceptive-timing task

Children completed a computer-based interception task in which they hit moving targets by controlling a custom-made 1-degree-of-freedom joystick (see Fig. 1). The joystick was placed next to a horizontally positioned BenQ (Taipei, Taiwan) XL2720Z LCD gaming display (resolution: 1,920 × 1,080 pixels, size: 598 × 336 mm, brightness: 300 cd/m², refresh rate: 144 Hz). The position of the joystick was represented on screen by a black rectangular “bat” (dimensions: 10 × 15 mm) that was always in line with the joystick (i.e., had the same position on the y-axis). All stimuli were generated using Python software (Version 2.7.9; Python Software Foundation, Beaverton, OR).

A “start box” appeared on screen at the beginning of every trial, and the participant was instructed to place the bat within it (coordinates [570 mm, 20 mm]; coordinate origin at bottom left of screen). A black target (height: 15 mm) then appeared at the left-hand side of the screen (coordinates [0 mm, 150 mm]; for left-handed participants, the apparatus and stimuli were reversed, with the manipulandum placed on the left side of the screen). After a delay drawn from a uniform distribution U (0.25, 3.0 s), the target moved from left to right at a constant speed. The center of the target passed in front of the center of the bat after moving 570 mm. The children were instructed to hit the target with the bat. The target was successfully hit if the upper edge of the bat collided with the lower edge of the target (see Fig. 1c). The target then stopped moving, turned red, and spun before disappearing, thereby providing motivating animated feedback for the children. If the bat passed in front of the target’s horizontal path, the target immediately stopped moving and then remained on screen for 1 s. Thus, participants could not simply move the bat in front of the target’s path and wait for the target. If the bat crossed the target’s path after the target had moved too far to be struck, then the target stopped and remained visible for 1 s. The position of the bat and target was time stamped and saved to computer memory at 144 Hz. The bat’s positional data were filtered using a low-pass second-order zero-lag Butterworth filter with a cutoff frequency of 10 Hz. Spline interpolation was used to estimate the time at which the bat reached the interception point. The total number of targets hit by each participant provided our measure of interceptive-timing ability.

Children performed 54 trials in which the target speed (250 mm/s, 400 mm/s, 550 mm/s) and target width (30 mm, 40 m, 50 mm) varied (9 trial types × 6). Each target type was presented in a block of three trials, with two blocks for each trial type. The blocks were pseudorandomly ordered with the constraint that two blocks of the same kind could not occur sequentially. All participants experienced an identical pseudorandom sequence of blocks.

Manual dexterity

To distinguish between general motor skills and interceptive-timing ability, we took measures of manual dexterity and postural ability. Manual dexterity was measured using the Kinematic Assessment Tool (Flatters, Hill, Williams, Barber, & Mon-Williams, 2014), which consists of three sensorimotor tasks that are presented on a tablet computer screen (Toshiba Portege M700-13p tablet; screen: 260 × 163 mm, 1,200 × 800 pixels resolution, 60 Hz refresh rate) and completed using a handheld stylus. The planar position of the stylus was recorded at 120 Hz and smoothed using a 10 Hz dual-pass Butterworth filter at the end of each testing session.

Steering task

The steering task required participants to trace a path displayed on the tablet (Fig. 2a). A box moved along the path every 5 s. Participants were told to trace the path as accurately as possible while ensuring they stayed within the moving box at all times. At each time point (120 Hz), the minimum two-dimensional distance between a reference path and the stylus was calculated. The arithmetic mean was calculated for these values across each trial, giving a measure of path accuracy. The ideal trial time if the participant remained within the moving box was 36 s. To normalize path accuracy for task time, we adjusted it by the percentage that the participant’s actual movement time deviated from the ideal 36-s value (adjusted path accuracy). Adjusted path accuracy, a measure that incorporated both timing and accuracy components, was used to determine performance on the steering task (with larger values indicating worse performance).

Fig. 2.

Examples from the steering, aiming, and tracking tasks. In the steering task (a), participants traced a spatial path (oriented in different ways) from the open to the closed black dot using the stylus, while staying within a moving box. In the aiming task (b), participants made movements to sequentially appearing targets (indicated here by the numbers, which were invisible to the participant) with a stylus. Open circles were not visible when moving between Dots 2 and 3. In the tracking task (c), participants followed a dot with the stylus. In the first trial, the dot followed the dashed path (invisible to participants). In the second trial, the guide track was visible. In each trial, the dot made three revolutions of the figure-eight pattern at each speed: fast, medium, and slow.

Aiming task

The aiming task (Fig. 2b) required participants to make 75 aiming movements to sequentially appearing circular targets (diameter: 5 mm). Once the participant successfully moved the stylus to the target dot, that target disappeared and the next target appeared (for details, see Flatters, Hill, et al., 2014). Movement time was the measure of interest and was defined as the time between arriving at one target location and arriving at the next. The mean movement time over the first 50 trials provided our measure of aiming performance (with longer trials indicating worse performance). The last 25 trials contained jump trials, in which the target dot moved position during the aiming movement, and which were not of interest in this study.

Tracking task (with and without spatial guide)

Participants completed two types of trial in the tracking task (Fig. 2c). In the first trial, they placed the stylus on a static dot (diameter: 10 mm) displayed on the center of the screen. After 1 s, the dot began to move across the screen in a figure-eight pattern. Participants were instructed to keep the tip of the stylus as close as possible to the dot’s center for the duration of the trial. The dot completed nine revolutions of the figure-eight pattern. The dot moved at a slow pace during the first three revolutions. In the next three revolutions, the dot moved at a medium pace, and in the last three, the dot moved at a fast pace (for details, see Flatters, Hill, et al., 2014). Participants then completed a second trial that was identical to the first except that a black 3-mm-wide guide line was displayed on the screen, indicating the path that the dot would follow.

The root-mean-square error (RMSE) provided a measure of the participant’s spatiotemporal accuracy, where the error was the straight-line distance in mm between the center of the target dot and the stylus. A separate RMSE score was calculated for each target speed within each trial. The median value of these was taken to provide an overall measure of performance on the tracking task (with larger values indicating worse performance).

Postural control task

Postural movements were measured using a custom rig (Flatters, Culmer, Holt, Wilkie, & Mon-Williams, 2014). Children stood with their feet shoulder-width apart on a Nintendo Wii Fit board, which recorded the participant’s center of pressure at 60 Hz. The data were filtered using a wavelet filter as described in Flatters, Culmer, et al. (2014). The two-dimensional path length subtended by the center of pressure (in mm) provided a measure of balance, first with eyes open and then with eyes closed. Larger values therefore indicated worse performance.

Academic attainment

Nationally standardized academic-attainment scores for mathematics, reading, and writing were provided by the school (https://www.gov.uk/national-curriculum/overview). Children were graded on a scale from 1 to 15, which maps to UK standardized scores (see the Supplemental Material).

Data analysis

Ordered probit regression was employed to model the data. This is appropriate when the dependent variable is ordinal, as is the case for the academic-attainment metrics. The model linearly combines predictor variables (interceptive timing, manual dexterity, posture, and age) to generate a latent academic-attainment score for the ith data point ($y_i^{*}$). This is done in exactly the same way as in linear regression:

$$y_i^{*}=N({\mathrm{\mu }}_i,\mathrm{\sigma })$$

$${\mathrm{\mu }}_i=X_i^T\mathrm{\beta },$$

where $X_i^T$ is a vector of predictors, β is a vector of re-gression coefficients, and µ_i is the expected latent attainment outcome for the ith participant (Equation 2). The latent attainment score ($y_i^{*}$) is then drawn from a normal distribution with mean µ_t and standard deviation σ (Equation 1). However, unlike in standard regression, $y_i^{*}$ is a latent score that is then mapped to the ordinal attainment variable (yi). This is done by slicing through the latent outcome scale with ordered thresholds C1, . . ., C_K–1, where K is the number of possible categorical outcomes. The ordered outcome y is then defined by which thresholds y * falls between (as illustrated in Fig. 3). This is known as the probit link function.

Fig. 3.

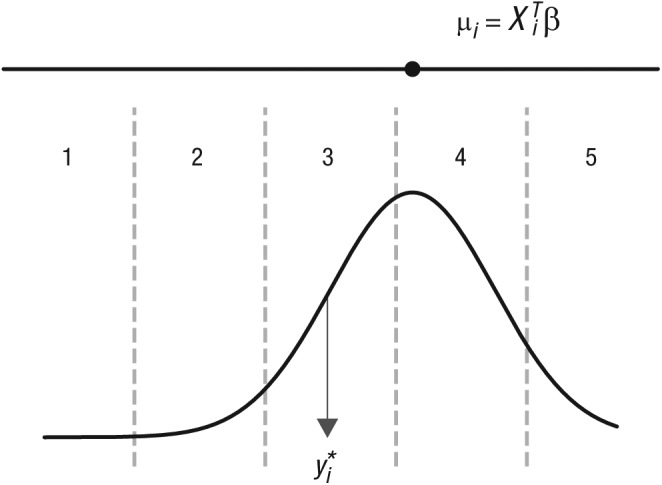
Illustration of an ordered probit model. The upper line represents a continuous latent attainment score. The expected latent attainment score for the ith participant is given by ${\mu }_i=X_i^T\beta$ and represented by the position of the black dot on the upper line. A latent attainment score $y_i^{*}$ is then sampled from a normal distribution (curved black line) with mean µ_i and standard deviation σ. The observed attainment score then depends on which of the thresholds C1, . . ., C_K–1 (gray dotted lines) $y_i^{*}$ falls between. Here, $y_i^{*}$ falls between the second and third thresholds, giving an observed attainment score of 3. Note that the threshold parameters will not necessarily be equally spaced.

As in standard regression, we wished to fit the model parameters (the regression coefficients, β, and standard deviation, σ) to the data. In addition, we also wanted to simultaneously fit the threshold parameters (C₁, . . ., C_K–1). While methods such as maximum likelihood can be used to fit the model, we employed Bayesian estimation techniques to yield a joint posterior distribution over all model parameters. Formally, we estimated the posterior distribution P(β, σ, C₁, . . ., C_K–1|y) using the No-U-Turn algorithm (Hoffman & Gelman, 2011) implemented in RStan software (Version 2.16.2). The posterior distribution was summarized using 95% highest-density intervals (HDIs), which provide an upper and lower bound for an interval that, according to the posterior, has a 95% probability of containing the true model parameter value, given the data, likelihood, and priors. The width of the HDI provides information about the estimate’s precision.

A model was fitted separately for each of the attainment outcomes (mathematics, reading, and writing). For each model, a representative sample was taken from the posterior distribution. Four chains of 10,000 samples were started at random locations of the joint posterior parameter space. Each chain first took 5,000 warm-up samples that were then discarded. Convergence was assessed by visually inspecting the chains and examining the Gelman-Rubin statistic ($\hat{R}$) (Gelman, 2014) and effective sample size of all parameters. All $\hat{R}$ values were close to 1, and the effective sample size was greater than 6,000 for all parameters.

Results

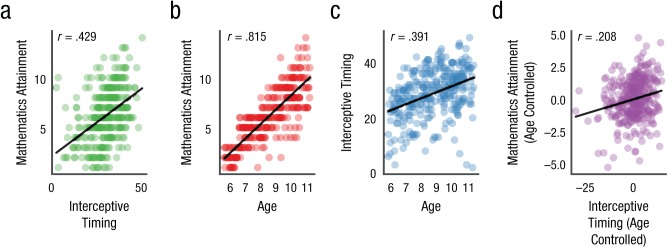
We were primarily interested in whether interceptive timing would be predictive of mathematics attainment after controlling for age and other motor skills. Figure 4a indicates that there is a relationship between mathematics attainment and interceptive timing but also between these variables and age (Figs. 4b and 4c). Figure 4d plots the correlation between interceptive timing and mathematics attainment after we controlled for age (r = .208).

Fig. 4.

Scatterplots (with least-squared regression lines) showing the correlation between (a) mathematics attainment and interceptive timing, (b) mathematics attainment and age, and (c) interceptive timing and age, and the partial correlation between (d) mathematics attainment and interceptive timing after controlling for age. Pearson’s correlation coefficients are given, but these values should be treated with caution because of the ordinal nature of attainment scores (hence reporting of the ordinal probit model elsewhere).

Although Figure 4 provides a useful illustration of the range of performance of children in the interceptive-timing task, the primary question of interest was whether interceptive timing would be predictive of mathematics attainment even after we controlled for age and general motor skills. Linear regression is not the most appropriate model for these data given that the attainment metrics used were ordinal in nature (thus the Pearson’s correlation coefficients given in Figure 4 should be interpreted with caution). To fully capture the relationships between the variables of interest, we utilized an ordered probit model to make inferences from the data. First, we fitted the model separately for each educational attainment outcome (mathematics, reading, and writing). We then examined the 95% HDI (thick horizontal black lines in Fig. 5) for each β coefficient to determine the region where the true parameter was likely to fall (with 95% confidence, given the likelihood, priors, and data). The β coefficient determines the amount by which a 1-unit change in the predictor variable will change the latent academic-attainment score (see Fig. 3).

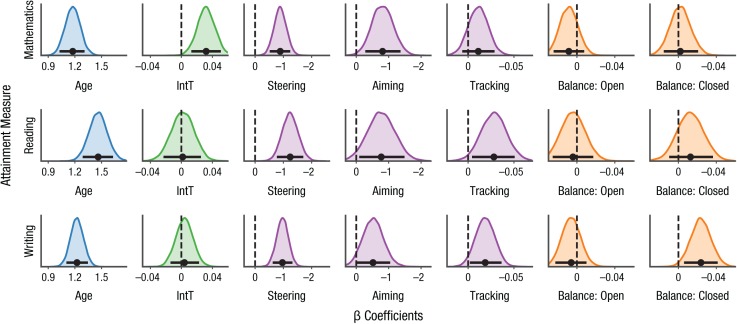
Fig. 5.

Marginal posterior distributions over coefficients (i.e., regression slopes) for the mathematics, reading, and writing models. For clarity, the x-axes for steering, aiming, tracking, and balance (eyes open and eyes closed) have been reversed because negative values for these measures indicate an increase in the latent attainment score. The x-axis scales are consistent within columns to allow comparisons between mathematics, reading, and writing models. The vertical dashed lines highlight the zero points where there would be no clear relationship, the filled circles represent the means, and the horizontal bars show the 95% highest density intervals. IntT = interceptive timing.

The β coefficient for interceptive timing (Fig. 5, green curves) was clearly nonzero for the mathematics-attainment model (Fig. 5, top row; 95% HDI excluded zero for interceptive timing), with a mean estimate of 0.03 (95% HDI = [0.01, 0.05]). This suggests that for every five additional targets hit, the model estimated an average increase of 0.15 on latent mathematics score for that individual. The link between interceptive timing and mathematics attainment can be contrasted with the reading and writing models (Fig. 5, green curves), where the 95% HDI of the interceptive-timing slopes contained zero and concentrated around comparatively smaller values, suggesting little or no relationship. Thus it appears that interceptive timing may have a specific relationship with mathematics but not educational attainment in general. This pattern contrasts with those of the other motor measures, none of which showed the same specificity for mathematics. Fine motor skills (Fig. 5, purple curves) showed a more general relationship with attainment measures: Steering had clear nonzero relationships with all three attainment scores, while aiming also showed a possible relationships with mathematics, reading, and writing. Tracking showed a nonzero relationship only with reading, while smaller coefficient values were more likely for mathematics and writing.

Balance measures of gross motor skills showed no clear relationship with mathematical- or reading-attainment scores, though there did seem to be a relationship between balance with eyes closed and writing attainment (Fig. 5, orange curves). This pattern highlights the importance of having a stable base when performing fine motor tasks such as writing (Flatters, Mushtaq, et al., 2014).

The modeling described in the previous paragraphs provides a method for describing the association between particular variables. However, the β coefficients are scale specific, and the observed coefficients may reflect small effects with little real-world significance. To allow for a meaningful examination of the size of these effects, we estimated how many months of age the typical range of scores on each sensorimotor task was worth, with respect to the associated increase in academic attainment. To perform this calculation, we defined the typical range as two times the standard deviation for each sensorimotor task after controlling for age (see the Supplemental Material for further details).

The effect size was calculated as follows:

$$\mathrm{equivalent\; age\; change}=\frac{2\times S{D}_j\times {\mathrm{\beta }}_j}{{\mathrm{\beta }}_{\mathrm{age}}}\times 12,$$

where SD_j is the estimated standard deviation for the jth sensorimotor measure (after controlling for age), β_j is the corresponding model coefficient, and β_age is the coefficient for age. We multiplied SD_j by 2 to give the typical range of scores and by 12 to convert the units from years to months. A detailed example of the effect-size calculation and how SD_j was calculated is provided in the Supplemental Material.

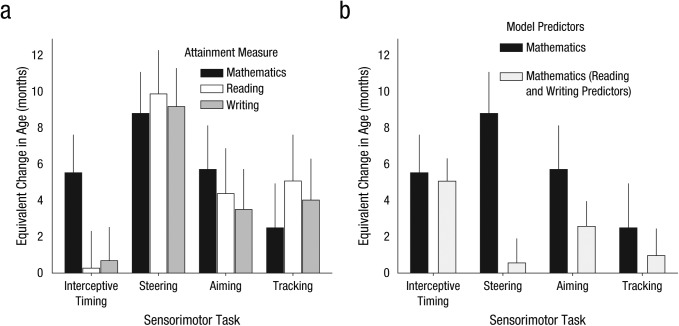
The metrics for equivalent change in age (Fig. 6a) highlight that the typical range of interceptive-timing scores for mathematics attainment was equivalent to approximately 5.5 months of age (i.e., for children of the same age with interceptive-timing scores differing by the typical range, we should expect a difference in latent mathematics attainment equivalent to 5.5 months). Steering actually had a larger effect size for mathematics attainment than interceptive timing (8.8 months), but steering also had similar large effects for reading and writing attainment (9.8 and 9.1 months, respectively), whereas interceptive timing has very little effect on these other attainment scores (0.3 and 0.7 months, respectively). The metric for equivalent change in age for aiming suggests that for mathematics attainment, aiming had a similar effect size as interceptive timing (5.7 months), but with values of 4.4 months and 3.4 months for reading and writing, respectively. Tracking had a value of 5 months for reading attainment and smaller values for mathematics and writing attainment (2.5 and 4 months).

Fig. 6.

Equivalent change in age as a function of sensorimotor task and (a) attainment measure and (b) model predictor. Adding reading and writing had little effect on the beta value for interceptive timing, but it did change beta values for steering, aiming, and tracking. The vertical error bars indicate the standard deviation of the posterior.

As with any observational study, there is always the possibility that omitted variables (e.g., general intelligence or handwriting ability) may be mediating the relationship between the sensorimotor measures and academic attainment (see Discussion). A reviewer noted that controlling for reading and writing scores (by including them as predictors in the mathematics model) may reduce the chances of an omitted variable bias and also provide a useful test of whether the relationship between interceptive timing and mathematics could be explained by a more general relationship between sensorimotor performance and academic ability. Thus, we carried out further (exploratory) analyses of the data by adding reading and writing to the mathematics model (see Fig. 6b). Adding the additional educational-attainment scores resulted in a substantial drop in the estimated equivalent-age effect-size estimate for general fine motor measures (steering, aiming, and tracking), but the effect size of interceptive timing was left largely unchanged.

Discussion

This study demonstrates for the first time that interceptive-timing ability can predict mathematical performance in primary school children. This finding is consistent with human sensorimotor systems and cognitive abilities being intrinsically linked. Correlational studies always raise questions about the direction of causality, but in this case it is difficult to see how enhanced mathematics ability could have improved performance on the interceptive-timing task given that the task involved subsecond sensorimotor processes (mean movement time = 340 ms, SD = 266). We probed the relationship in a variety of ways to determine whether it could be simply explained by generalized links between motor performance and educational attainment. We did indeed observe that some measures of fine motor skill had a general relationship with academic attainment: Notably, manual steering predicted academic attainment on reading, writing, and mathematics. However, interceptive timing reflected a more specialized relationship independent of general motor ability and also independent of academic-attainment scores for reading and writing.

It is worth considering whether there is an obvious unmeasured mediating variable that could explain this relationship. For example, imagine that the children who are better at mathematics are also those who spend longer playing computer games, and it is this exposure that leads to improved interceptive timing (rather than mathematics ability per se). While it is impossible to completely rule out such mediating variables, the specificity of the observed relationship makes it seem unlikely. In the computer game example, the games played would have to have no effect on general fine motor skills (steering, tracking, and aiming), nor on academic attainment for reading or writing. Thus, this explanation cannot rely on general exposure to computer games but would require specific training to ensure that children who are better at mathematics are selected to improve their interceptive-timing abilities (while leaving other general fine motor control unchanged). There was no evidence that games of such specificity were being deployed in this way within the school that took part in this study.

When considering why there is a relationship between sensorimotor interceptive-timing capability and the cognitive development of a child, one must also allow for the possibility that sensorimotor performance is a proxy measure of psychopathology, especially as populations with clinical motor control deficits sometimes exhibit poor mathematics ability (Pieters, Desoete, Van Waelvelde, Vanderswalmen, & Roeyers, 2012; Tinelli et al., 2015; Van Rooijen, Verhoeven, & Steenbergen, 2011). Indeed, fine motor skills can also predict measures of mathematics ability in healthy children (Carlson, Rowe, & Curby, 2013; Grissmer et al., 2010; Luo, Jose, Huntsinger, & Pigott, 2007; Pagani, Fitzpatrick, Archambault, & Janosz, 2010; Son & Meisels, 2006). While our data confirm these findings by showing a relationship between fine motor tasks (steering and aiming) and mathematics attainment, the relationship seemed to generalize to all the educational attainment measures (mathematics, reading, and writing). Furthermore, when we controlled for fine motor skills (steering, aiming, and tracing), we still found interceptive-timing scores were predictive of mathematics attainment (but not reading or writing attainment). These controls would seem to rule out simplistic explanations based on interceptive-timing skills acting as a proxy measure for psychopathology and also other potential mediating variables such as differences in parental involvement, access to technology, or social economic status (Ritchie & Bates, 2013).

These findings are consistent with the idea that number representations are linked with concepts of time and space, perhaps through a common representation of magnitude (Walsh, 2003). It is possible that children must first learn the physical rules that govern how objects move before they can form related abstract representations (Piaget, 1955). The ability to learn these physical rules is likely to vary between individuals, and our findings may reflect variance in the development of the neural structures that underpin predictive learning regarding how objects move in space and time. In this regard, our results are consistent with recent findings showing that basic spatial-processing abilities in infants relate to later mathematical ability (Lauer & Lourenco, 2016).

We should emphasize that we believe the relationship between interceptive-timing ability and mathematics is likely to be complex because it is a matter of common observation that not all elite sports people are excellent mathematicians, whereas many people with physical disability excel in mathematics. When evaluating the observed relationships between motor control performance and educational attainment outcomes, it is worth considering the magnitude of the observed effects. Once the change in attainment scores is transformed into equivalent-change-in-age units (Fig. 6; see also Fig. S1 in the Supplemental Material), it can be seen that the steering fine motor measure accounts for approximately 9 months of difference in reading, writing, and mathematics attainment. While this finding is noteworthy, it is likely that the relationship between steering and mathematics is fairly general because it disappears once reading and writing attainment have been taken into account. This may be due to general executive function acting as a mediating variable between some fine motor skills and attainment (Roebers et al., 2014). In contrast to the steering measure, interceptive timing had a smaller relationship with mathematics attainment (approximately 5.5 months), but this was independent of reading and writing attainment (Fig. 6). An important point to consider is whether an equivalent change in age of 5.5 months is actually important. From the perspective of a child with reduced academic attainment, this would be considered a substantial difference. However, because the mathematics-attainment scores themselves are fairly coarse, it actually takes quite a large change in mathematical ability to move between attainment brackets. It would, therefore, be unwise to use effects of this magnitude to try to persuade school teachers to redirect precious resources away from mathematics teaching to target training of interceptive timing. However, these effects do suggest that we should not neglect the importance of sensorimotor development in young children (given that the environment—broadly construed—is known to exert a large influence on sensorimotor ability). Indeed, the present work complements reports that physical activity can exert positive benefits on cognitive processing, even if the mechanisms remain opaque (Hill, Williams, Aucott, Thomson, & Mon-Williams, 2011). Thus, the quality of early sensorimotor interactions with the environment may have important implications for children’s education.