Tethered Particle Motion: an easy technique for probing DNA topology and transcription factor interactions

Abstract

Tethered Particle Motion (TPM) is a versatile in vitro technique for monitoring the conformations a linear macro-molecule, such as DNA, can exhibit. The technique involves monitoring the diffusive motion of a tracker particle anchored to a fixed point via the macro-molecule of interest, which acts as a tether. In this chapter, we provide an overview of TPM, review the fundamental principles that determine the accuracy with which effective tether lengths can be used to distinguish different tether conformations, present software tools that assist in capturing and analyzing TPM data, and provide a protocol which uses TPM to characterize lac repressor induced DNA looping. Critical to any TPM assay is understanding the timescale over which the diffusive motion of the tracker particle must be observed to accurately distinguish tether conformations. Approximating the tether as a Hookean spring, we show how to estimate the diffusion timescale, and discuss how it relates to the confidence with which tether conformations can be differentiated. Applying those estimates to a lac repressor titration assay, we describe how to perform a TPM experiment. Additionally, we also provide graphically driven software which can be used to speed up data collection and analysis. Lastly, we detail how TPM data from the titration assay can be used to calculate relevant molecular descriptors such as the DNA looping J factor and lac repressor – operator dissociation constants. While the included protocol is geared toward studying DNA looping, the technique, fundamental principles, and analytical methods are more general and can be adapted to a wide variety of molecular systems.

Introduction

Tethered Particle Motion (TPM) assays are simple but powerful tools for characterizing the effective length and behavior of various biomolecules. The basic idea behind TPM is to use a macromolecule of interest (such as DNA) to tether a submicron-sized, mobile reporter particle to an immobile point on a surface. Brownian motion randomly “kicks” the tethered particle, forcing the macromolecule to explore various conformations. By tracking the particle, the end-to-end distance of the molecule can be monitored and used to create length-vs-time recordings that can be interpreted in terms of molecular conformations. TPM has been used to measure kinesin-driven motion, transcription by RNA polymerases, protein synthesis, transcription factor-DNA binding, and to characterize transcription factor mediated DNA loop topology [1–14]. In this chapter we review the principles of TPM and detail how to employ it to study lac repressor-mediated DNA looping.

In E. coli the lac repressor (LacI) regulates the genes responsible for lactose metabolism. It represses transcription by binding the O₁ operator adjacent to the lacZ promoter of the lac operon. Two additional binding sites, O₂ and O₃, allow tetrameric LacI to form one of three possible large-scale looped structures. To simplify the looping topology, DNA sequences used in TPM experiments typically include only two operators. In addition to the wild-type operators, a palindromic operator, O_S, was engineered for which LacI has an affinity roughly 10 times that of O₁ [15, 16]. LacI concentration modulates the probability of LacI-induced looping; however, loop formation events occur due to fluctuations of the DNA molecule, which themselves are affected by physical factors including protein-DNA binding, distortions in the DNA molecule, and length of the DNA loop.

The mechanics of double-stranded DNA have been well studied, and at lengths longer than 150 bp it readily forms loops due to thermally induced fluctuations [17, 18]. The propensity of a DNA molecule to loop can be characterized using a quantity called the “J” factor [19]. The J factor is essentially a measurement of the effective, local concentration of one end of the looping segment relative to the other, and has units of molarity. The length of the loop segment greatly influences J factor values [20]. Over short lengths, the flexural stiffness of DNA prevents bending, which lowers the J factor. Intermediate lengths bend more easily and the ends meet often enough to spontaneously form loops. Long lengths also bend easily, but as the randomly coiled polymer extends through larger volumes, it becomes statistically unlikely that the two ends of a DNA molecule will meet, yielding a low J factor. The J factor versus length dependence has been measured in several experiments. For 400 bp length loops, such as those measured here, J is in the range 1-20 nM [19, 21].

In the protocol that follows, we use a DNA construct containing the O_S and O₁ operators. Since looping depends on one LacI tetramer binding simultaneously to two operators, the likelihood of forming such a loop has a modal dependence on LacI concentration. Below 1 pM, a LacI tetramer is unlikely to occupy either operator, and although random thermal fluctuations may bring the operators together, no repressor stabilizes this conformation. In the range up to 1 nM, the O_S operator is very likely to be occupied, given that the dissociation constant, K_D, of O_S is about 8-10 pM [13, 16]. This O_S - bound tetramer can stabilize a loop if the corresponding O₁ operator is unoccupied. As a result, looping probability depends primarily on the J factor of the DNA sequence and the degree of O₁ occupancy. At higher LacI concentrations (>100nM), separate tetramers occupy both operators, and reciprocally inhibit stabilization of a loop.

TPM experiments offer insight into the thermodynamics and kinetics of looping reactions. These reactions manifest as switching between distinct looped states, each of which have associated effective tether lengths. Longer tether states correspond to unlooped DNA, while looped tethers are shorter. The ratio of the time spent in looped conformations divided by the duration of the experiment is proportional to the free energy of the reaction and indicates the looping probability

$$p_{\mathit{loop}}\approx \frac{T_{\mathit{loop}}}{T_{\mathit{unloop}}+T_{\mathit{loop}}}.$$ Eq. 1

For Lacl concentrations between the K_D values of O_S and O₁, O_S will remain occupied while O₁ occupancy changes. In that range, one can expect an approximately linear relationship between the ratio of time spent in the looped and unlooped states and the LacI concentration [19, 20].

$$\frac{T_{\mathit{unloop}}}{T_{\mathit{loop}}}\approx \frac{2K_{D,O_1}}{J_{\mathit{loop}}}+\frac{2\left[\mathit{Lacl}\right]}{J_{\mathit{loop}}}.$$ Eq. 2

1.1. Parameters affecting TPM accuracy

Efforts to characterize the caveats and limitations of TPM include experimentation, numerical simulation, and analysis rooted in first-principles [8, 20, 22–26]. In this section, we summarize those caveats and highlight critical features of TPM experiments.

The customary readout of TPM experiments is the root mean square of excursions by the particle about the anchor point of the tether.

$${\rho }_{\mathit{RMS}}=\sqrt{\langle {\rho }^2\rangle }=\sqrt{\langle {(x-\stackrel{‒}{x})}^2+{(y-\stackrel{‒}{y})}^2\rangle }$$ Eq. 3

For linear macromolecules, such as DNA, the value of≈_RMS scales with tether length; however, the ρ_RMS precise functional relationship between the two depends on the physical characteristics of the molecule. At lengths greater than ~100 base pairs DNA is well described by a worm-like chain polymer model [27]. In the absence of boundary constraints (i.e. chamber wall and reporter particle), statistical-dynamics leads one to expect

$${\rho }_{\mathit{RMS}}\approx \sqrt{2l_p{L}_0},$$ Eq. 4

where l_p is the chain’s persistence length (about 50 nm for DNA in physiological salt conditions) and L₀ is the contour length (about 0.34 nm/base pair) [28]. In practice, however, steric effects of the chamber wall and reporter particle alter this scaling behavior [23]. While there is no analytical solution for the exact relationship between ρ_RMS and length, numerical simulations and corresponding experiments have been used to estimate the scaling law when a bead and wall are included [23, 24, 29].

When relating ρ_RMS to tether length, the time interval over which the excursion is averaged should be chosen carefully. The diffusive motion of the reporter particle is correlated over short time intervals such that the position of a particle at time t₀ + δt is related to the position at time t₀. Consequently, averaging over excessively short time intervals will underestimate the excursion (⟨ρ²⟩_Δt < ⟨ρ²⟩_∞). Approximating the tether as an entropic spring that pulls the reporter particle with a characteristic Hookean spring constant, K, illustrates this problem. In this case, the Smoluchowski equation describes the time evolution of the probability distribution of the location of the reporter particle. For Hookean-spring type systems the solution to that differential equation is

$$P(x,\mid x_0,t_0)\propto \mathit{exp}\left(-K\frac{{(x-x_0{e}^{-2(t-t_0)∕\tau })}^2}{2k_{B}T\cdot S(t,t_0)}\right),$$ Eq. 5

where

$$S(t,t_0)=1-\mathit{exp}\left(-\frac{4(t-t_0)}{\tau }\right),$$ Eq. 6

with time constant

$$\tau =\frac{2k_{B}T}{KD},$$ Eq. 7

and D is the diffusion constant given by the Stokes-Einstein equation [30]

$$D=\frac{k_{B}T}{6\pi \eta R}.$$ Eq. 8

In the limit t → ∞, the distribution decays to the steady-state

$$P\left(x\right)\propto e^{-\frac{K{x}^2}{2k_{B}T}},$$ Eq. 9

which yields a mean square excursion of ${\langle {\rho }^2\rangle }_{\infty }=\frac{2k_{B}T}{K}$. Equation 5 shows that the probability distribution for a particle localized at position x₀, P(x, t₀) = δ(x – x₀), will decay to the steady-state distribution with time-constant τ, the approximate temporal resolution for TPM. For short time scales Δt << τ, the tether has a negligible effect on the particle trajectory which exhibits apparently unrestricted diffusion. Consequently, to detect changes in the properties of the tether (such as length or effective spring constant) those changes must endure/be observed for longer than τ, the time required for the particle to diffuse such a distance that the work done on the tether approaches the scale of the available thermal energy (Eqn. 7).

In the low-force regime, DNA has an effective spring constant of $K\approx \frac{3k_{B}T}{2L_0{L}_p}$ [30]. For a 900 bp tether and a particle with radius R=160 nm Eq. 7 yields a time constant of τ ≈ 18 ms. In practice, this is only a lower estimate. Experimental measurements of τ produce values nearly twice as large as predicted [31]. One reason for the disparity is that the effective diffusion coefficient of a particle increases as it approaches a wall, increasing the time constant [22, 32].

For a series of independent measurements of a normally distributed quantity, we can establish with what confidence the variance of the distribution lies within the limits

$$\frac{(N-1)s^2}{{\chi }_{1-\frac{\alpha }{2},N-1}^2}<{\sigma }^2<\frac{(N-1)s^2}{{\chi }_{\frac{\alpha }{2},N-1}^2}$$ Eq. 10

where N is the number of samples, s² is the sample variance and χ² is the chi-square distribution for critical value α and N-1 degrees of freedom. For TPM, because particle positions are correlated over timescales shorter than τ, the relevant sample number N is the number of measurements made with frequency 1/τ [20], yielding

$$N\approx \frac{\Delta t}{\tau }.$$ Eq. 11

In summary, two main factors establish the utility of studying a given macromolecular system using TPM: the expected scale of changes in tether length, and the time scale of those changes. As a rough approximation, the length and stiffness of a molecule can be used to estimate the expected RMS-excursion (Eqn. 4). Similarly, the tether length and stiffness, along with the size of the reporter particle can be used to estimate the relevant time scale (Eq. 7) and confidence limits for a given measurement (equation 10-11).

The TPM protocol included in this chapter reveals the looping of a DNA segment due to the binding of lac repressor protein to flanking operator sites. Previous experiments have demonstrated that such loops persist for many seconds. The approximate lengths of the tether were 909 bp (~300 nm) before and 509 bp (~170 nm) after looping. Those lengths translate to expected RMS-excursions of approximately 180 nm and 130 nm respectively, with a time-constant τ≈20-40ms. When comparing the variance of two populations the ratio of variances follows the F-distribution with confidence limits given by (see Note 1)

$$\frac{s_1^2}{s_2^2}\left(\frac{1}{F_{\alpha \left(2\right),N_1-1,N_2-1}}\right)<\frac{{\sigma }_1^2}{{\sigma }_2^2}<\frac{s_1^2}{s_2^2}\left(F_{\alpha \left(2\right),N_1-1,N_2-1}\right).$$ Eq. 12

Additionally, the number of samples needed to resolve the two populations with a significance level α and power 1-β is given by

$$N\approx {\left[\frac{Z_{\alpha \left(2\right)}+Z_{\beta \left(1\right)}}{\text{ln}\frac{{\sigma }_1^2}{{\sigma }_2^2}}\right]}^2+2$$ Eq. 13

where Z is the inverse of the cumulative normal distribution. Using Eq. 13 with significance α = 0.05 and power 1-β = 0.9, and given our estimates for ρ_RMS, N=28 observations are required. Assuming a time constant of τ = 40 ms, that translates to an averaging interval of Δt = 1.12 seconds.

Materials

1.2. Instrumentation

1.2.1. Microscope & Camera

The technical requirements for TPM are relatively simple. See Note 2 for tips on microscope and camera selection. One implementation includes:

1. an upright DM LB2 Microscope (Leica Microsystems GmbH, Wetzlar, Germany)

2. a 100x 1.2-1.4 numerical aperture, oil-immersion objective (Leica)

3. a Dark-field condenser unit (Leica)

4. a jAi GigE CM-140GE Camera (JAI Inc., San Jose, CA)

5. a custom built PC running Windows 7 × 64, with an Intel i7 Quad-core 3.4 Ghz processor and 8 GB RAM.

6. MATLAB version R2014b or newer acquisition and analysis software

1.2.2. Particle Tracking Software

The protocol presented here featured custom software based on MATLAB and MicroManager (www.micro-manager.org). It includes a routine for real-time tracking of particles in dark field images based on a radial symmetry detection algorithm [33]. The algorithm used for tracking particles in DIC images calculates an intensity weighed center-point in a specified region of interest. Both routines are included with the control software (http://www.physics.emory.edu/faculty/finzi/research/code.shtml). For alternative particle-tracking routines see Note 3.

1.2.3. Installing TPM capture software

• 7.After downloading the TPM capture software and MicroManager, install MicroManager, and copy the TPM capture software to an accessible path.
• 8.Using MicroManager, setup and verify your camera is working (see instructions on micro-manager.org). Note the camera device module and device name.
• 9.Open MATLAB. Navigate to the TPM capture software folder. Open the “MM-Core” sub-folder and run MMsetup_javaclass.m. It should prompt you to navigate to the folder in which you installed MicroManager. This will import the interface for MicroManager into the MATLAB environment.
• 10.Restart MATLAB.
• 11.To run the TPM capture program simply navigate to the folder containing the script “CaptureTPM.m”. On the first run, it will ask you to specify the camera module and device names as well as the pixel scale. This can be measured using a calibration slide and the ImageJ “caliper.txt” macro included in the “Calibration Tools” directory with the TPM capture software.

1.3. Reagents

1.3.1. Stock Solutions

Unless otherwise noted, all reagents were purchased from Thermo Fisher Scientific and stored at 4°C. To minimize risk of contamination with nucleases, all stock solutions and reaction buffers should be prepared using nuclease free, Milli-Q water.

1. Nuclease-Free Milli-Q Water

2. 10x Phosphate Buffered Saline (PBS)

3. 3 M Potassium Chloride Solution

4. DMSO

5. 0.5 M EDTA Solution

6. 1 M Tris·HCl pH 7.4

7. 10 mM Tris·HCl pH 8.0

8. Ethanol 100%

9. 100 mM DTT. (Store at −20°C).

1.3.2. Buffers

1. Pre-wash buffer: 10 mM Tris·HCl pH 7.4, 0.1 mM EDTA, 0.5 mg/mL α-casein, 200 mM KCl

2. Experiment (“λ”) buffer: 10 mM Tris·HCl pH 7.4, 0.1 mM EDTA, 0.1 mg/mL α-casein, 200 mM KCl, 5% v/v DMSO, 0.2 mM DTT (See Note 4).

3. DNA binding buffer: 10 mM Tris·HCl pH 7.4, 200 mM KCl

1.3.3. Materials for the Preparation of DNA tethers

1. 1 μg/mL pYY-I1_400 plasmid DNA (see Note 5).

2. Forward Primer: 10 μM 5’-Biotin-(C6)-tgggaaggagaagataagatgg-3’ stored in 10 mM Tris·HCl pH8.0. Purchased from Eurofins MWG Operon LLC, Louisville, KY. See Note 6.

3. Reverse Primer: 10 μM 5’-Digoxigenin-cgttagggtcaatgcgggtc-3’ stored in 10 mM Tris·HCl pH8.0. Purchased from Eurofins MWG Operon LLC. See Note 6.

4. Taq polymerase with 10x Standard Taq Buffer (New England Biolabs, Ipswich, MA).

5. 10 mM dNTP mix (New England Biolabs).

6. QIAquick PCR Purification Kit (QIAGEN Inc., Valencia, CA)

7. Nuclease-free 200 μL PCR Tubes

8. Thermocycler

9. UV spectrophotometer (NanoDrop, Thermo Fisher Scientific)

1.3.4. Tethered Particles

1. 200 μg/mL polyclonal sheep anti-digoxigenin antibody in 1x PBS. (Sigma-Aldrich, St. Louis, MO)

2. 1% w/v Streptavidin-coated polystyrene microspheres 320 nm (Spherotech Inc., Lake Forest, IL)

3. Microcentrifuge

1.4. Flow Chambers

Note: Glass slides used to construct chambers were washed with 18 MΩ de-ionized water.

1. laboratory tissue

2. Alconox detergent

3. Parafilm spacer cut to form chamber pattern capable of holding 45-50 μL of fluid (See Note 7).

4. 75 × 25 mm standard microscope slide

5. 22 × 22 mm microscope coverslip

6. microscope slide staining rack (Electron Microscopy Sciences)

7. coverslip staining rack (Electron Microscopy Sciences)

8. hot plate

9. humid storage box: petri dish or empty pipette tip box with wet sponge placed at the bottom

10. bath sonicator or, alternatively, an orbital shaker

1.5. Lacl Titration

1. lac repressor was provided by Kathleen Matthews at Rice University.

Methods

1.6. Producing DNA Tethers Using PCR

1. Mix the following in a thin-walled PCR tube

   Reagent	Concentration	Volume (μL)
   Milli-Q Water		23.8
   Taq polymerase buffer	10x	3.0
   pYY-I1-400	100 ng/μL	0.1
   Taq Polymerase	5 U/μL	0.5
   dNTP Mix	10 mM	0.6
   forward primer	10 μM	1.0
   reverse primer	10 μM	1.0
   	Total (μL)	30.0

2. Set thermocycler to execute the following sequence. See Note 8.

   Step	Name	Time (min)	Temp (°C)
   1	Initial Denaturation	2:00	95
   2	Denaturation	0:15	95
   3	Annealing	0:30	51
   4	Elongation	0:45	68
   	Go To 2, (Repeat 30-40x)	--	--
   5	Final Elongation	1:00	72
   6	Final Annealing	5:00	37
   	Hold	--	4

3. Purify the amplicon using a QIAquick PCR cleanup kit following the manufacturer’s protocol. Elute DNA in 50 μL of 10 mM Tris·HCl pH8.0. Verify the 909 bp linear DNA amplicon by electrophoresis through a 1% agarose gel in TAE buffer.

4. Measure the concentration of DNA by UV absorption. See Note 9.

5. Dilute the DNA to a final concentration of 20 ng/μL (about 30 nM) in 10 mM Tris·HCl pH 8.0.

1.7. Flow Chamber Assembly

1.7.1. Prewashing

1. Rinse microscope slides and coverslips with de-ionized water to remove dust or other debris

2. Place slides and coverslips into staining racks and submerge in a jar filled with 0.5% w/v Alconox detergent in de-ionized water.

3. Sonicate slides for 15-30 min or agitate slides on an orbital shaker for 1-2 hrs.

4. Remove the slides from the Alconox solution and rinse thoroughly with tap water for 15 min.

5. Rinse the slides with de-ionized water by placing staining racks in a jar of fresh de-ionized water. Repeat 3-4 times.

6. Place the slide rack in ethanol and store sealed, at room temperature until you are ready to use the slides.

1.7.2. Assembly

1. With forceps remove a slide and coverslip from ethanol and carefully dry with N₂ or filtered compressed air. Be sure to inspect slides for streaks or water spots. Place in a closed container to shield from dust.

2. If using laser-cut Parafilm spacers, place a spacer in a beaker of ethanol to soften the paper backing. Once backing has softened, use a scalpel or razor to tease the edge until the backing can easily be removed.

3. Place the parafilm spacer between two tissues to remove ethanol droplets and allow it to dry for about a minute.

4. Next place parafilm spacer on glass slide and then cover with coverslip, leaving wells on either side exposed. See an assembled chamber in Figure 1.

5. Set a hot-plate to a low setting, 50°C. Place the glass chamber on the hot-plate surface to gently melt the Parafilm without sputtering or boiling. The Parafilm spacer becomes clear and tacky as it melts. Using a metal spatula or tweezer press the coverslip to seal the Parafilm to the glass surfaces and force any bubbles out of the melting Parafilm. Note that bubbles can cause leaks in the chamber.

6. Once the spacer has sealed to the glass surfaces, remove the chamber from the hot plate. The Parafilm should turn cloudy as it cools. See Figure 1.

Figure 1.

A TPM Chamber. The Parafilm spacer was cut using a laser cutter and melted between the microscope slide and coverslip. The exposed ends of the channel serve as reservoirs for depositing/removing fluid.

1.7.3. Anti-Digoxigenin Functionalization

1. Flush the chamber with PBS by pipetting 100-200 μL of solution into a well at one end (inlet) of the serpentine channel under the coverslip. Capillary force should draw the fluid into and fill the chamber.

2. Further rinse the chamber by adding more buffer to the inlet well and then touching a tissue to the solution emerging from the opposite end of the channel (outlet). As the solution wicks into the tissue at the outlet, additional fluid is drawn through the channel inlet. Gently draw the solution through the chamber without exhausting the supply of solution at the inlet to prevent bubbles from entering the chamber.

3. Dilute the anti-digoxigenin stock to produce 200 μL of a 4 μg/mL solution in PBS. Repeat the previous step, to exchange the buffer within the chamber with the antibody solution.

4. Place the chamber in a sealed, humid box and store at 4°C overnight or room temperature for approximately 1 hour.

1.8. Preparing Tethered Particles

1. Dilute 2.5 μL of 1%w/v 320 nm dia. Streptavidin-coated particles into 200 μL of 1x PBS. Be sure to vigorously mix the stock particle suspension before use as particles will settle during storage.

2. Centrifuge the diluted suspension at 17000 × g for 2 min. to form a pellet. Discard the supernatant and resuspend in PBS. Repeat once.

3. Centrifuge the diluted suspension again at 17000 × g for 2 min. to form a pellet and remove the supernatant. Resuspend the particles in DNA binding buffer and mix vigorously to break up bead aggregates.

4. Wash excess anti-digoxigenin out of the chamber by gently flushing ~200 μL of PBS through the chamber.

5. Gently flush the chamber with 150 μL of pre-wash buffer and incubate for 5-10 mins at room temperature.

6. Mix 1 μL of 20 ng/μL DNA stock with 100 μL of DNA binding buffer.

7. Gently draw 50 μL of the diluted DNA solution into the chamber and incubate at room temperature for 15 minutes.

8. Gently flush the chamber with 150 μL of pre-wash buffer. Then incubate for 5-10 minutes at room temperature.

9. Draw 50 μL of the bead suspension to the chamber and incubate at room temperature 10 minutes.

10. Gently flush the chamber with 100 μL of pre-wash buffer to remove un-bound beads. Store the chamber in the humidity box at 4°C for at most 1-3 days before starting an experiment.

11. To begin an experiment, gently flush the chamber with 100 μL of λ-Buffer, followed by 100 μL of λ-Buffer supplemented with the desired LacI concentration. To prevent evaporation during experiments, cover the wells at the inlet and outlet of the chamber with small pieces of tape. For the data presented here, LacI was titrated over a range of 150 pM to 20 nM.

1.9. Microscope Operation

1. Turn on the microscope and dark-field/bright-field lamp at least one hour before observing tethers to avoid drift during thermal equilibration. The chamber should also be at room temperature to avoid re-equilibration after placing it on the microscope.

2. Place the chamber on the microscope stage and observe using the oculars or the live video stream from the TPM capture program to bring the beads into focus using.

1.10. Data Collection

1. Launch MATLAB, navigate to the folder containing the TPM capture software, and “run” “CaptureTPM.m”.

2. If using DIC microscopy, select “DIC” in the algorithm selection drop-down on the “Tracking Controls” window, otherwise select “Radial Symmetry.”

3. Focus the microscope on the particles at the chamber surface. Adjust the camera gain and lamp intensity to minimize “speckle” noise, so that the particles are clearly visible.

4. If chamber is prepared correctly, many of the particles will jiggle and a few will be immobile. The jigglers are tethered by DNA molecules. The fixed particles are stuck to the coverglass.

5. From the menu bar in the “Tracking Controls” window select “Add Track”. A crosshair cursor will appear with which to draw a region of interest around a particle to begin tracking it.

6. Select 3-6 stuck particles to use as references for drift correction. Only one suffices but choosing several provides redundancy in case a bead detaches. Select as many moving beads as desired (Figure 2). With a modern, multi-core CPU, it is possible to track more than 30 particles without a loss in performance.

7. Next, select “Experiment->Record Live Data” from the program menu. This launches a dialog for the selection of a directory in which to save the tracking data. After choosing a directory, click “Run.” Data will be collected and automatically saved in the specified directory using a binary-file format. Saved data can be loaded into MatLab for analysis using the included TPManalysis Toolbox (next section).

Figure 2.

A screen shot from the microscope control program with regions of interest (boxes) superimposed on a dark field image of 320 nm, tethered particles. The cursors update continuously within the stationary boxes in the live image.

1.11. Analysis of tethered particle motion

As introduced in Section 1.1, the time-averaged, root-mean-square of particle excursions reflects the effective tether length. However, the excursion data recorded for tracked particles must first be corrected to eliminate drift (Figure 3), an artifact due to mechanical instability of the microscope. In addition, data corresponding to particles with multiple tethers must be culled from the ensemble. A package of MATLAB scripts for refining and manipulating TPM data can be found at http://www.physics.emory.edu/faculty/finzi/research/code.shtml

1. To use the scripts, navigate to directory containing LoadTPMdata.m, TPManalysis.m and the +TPManalysis package, or include this directory in the MATLAB path.

2. Run LoadTPMdata.m to load saved TPM data into the MatLab workspace. If the pixel scale was not specified during data acquisition, then change this value to reflect the correct scaling when given the option.

3. By default, LoadTPMdata.m will create a variable called “TPMdata”, but a different output variable name may be specified when executing LoadTPMdata.m (e.g YourVarName=LoadTPMdata();).

Figure 3.

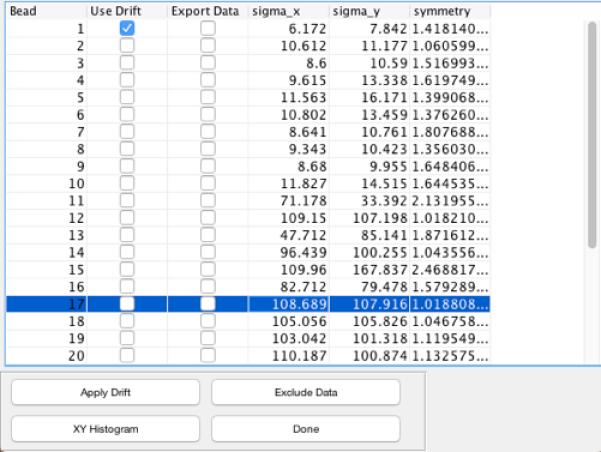
TPManalysis – Main Window. Particles are listed in the order of ROI origination along with the standard deviations along the X andY directions and symmetry values. Particle 1 is selected as a reference for drift correction. “Export Data” check-boxes can be toggled to mark data for analysis. The “symmetry” column lists values for $\sqrt{{\lambda }_1∕{\lambda }_1}$.

1.11.1. Drift Correction

The “TPMdata” variable data can be refined with TPManalysis.m, a toolbox for data selection and drift-correction.

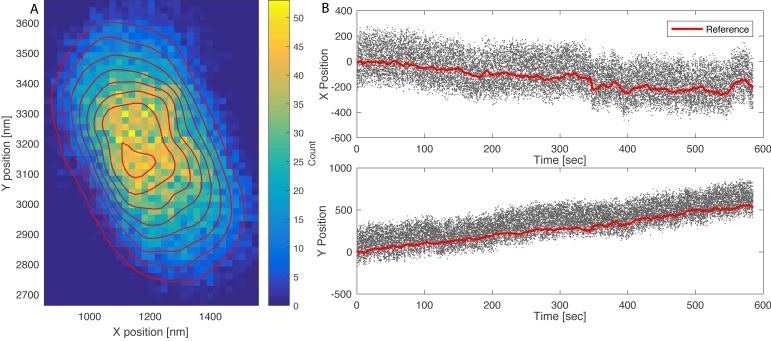
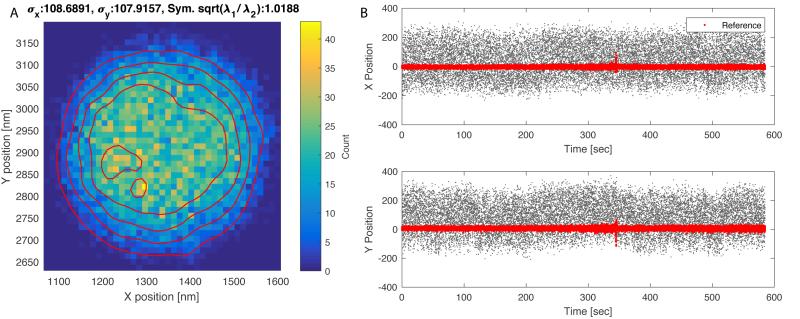
1. In the list of trajectories presented within TPManalysis.m (Figure 3), use the check-boxes under “Use Drift” to select the reference (stuck) particles and click “Apply Drift”. Drift is calculated by first applying a 1-second moving average to the trajectories for each selected reference particle, and then averaging the trajectories of all the reference particles, yielding a single drift-trajectory. The drift-trajectory is then subtracted from each of the particle trajectories, producing “drift free” traces. Figures 4 illustrates the trajectories of a tethered particle and an associated reference particle before drift correction. The two-dimensional histogram is elongated and plots of the X or Y positions show clear drift over time. After drift correction the two-dimensional histogram for the same particle becomes symmetrical and the average X and Y positions remain constant over time (Figure 5). The standard deviations along X and Y (σ_x, σ_y) are almost identical for this particle attached to a single tether, and can be used as rough estimates of tether length.

Figure 4.

The XY trajectory of a tethered particle before drift correction. (A) A two-dimensional histogram of particle positions. Shades indicate bin counts (colored online); contours delineate constant height profiles of the distribution. (B) X and Y positions vs. time trajectories for the tethered bead (dots); the thick lines (red online) correspond to the 1-second moving average of the trajectory of a single reference particle.

Figure 5.

The XY trajectory of the tethered particle shown in Figure 3 after drift correction. (A) Two-dimensional histogram of particle positions. Shades indicate bin counts (colored online); contours delineate constant height profiles of the distribution. The standard deviations along x and y (σ_x, σ_y) are almost identical for this particle attached to a single tether. The value of a symmetry indicator, $\sqrt{{\lambda }_1∕{\lambda }_1}$, near unity indicates highly symmetric excursions. (B) X and Y, positions vs. time trajectories for the tethered bead after drift subtraction (black dots); the thick dots (red online) indicate the (unaveraged) trajectory of a reference particle after subtracting drift.

1.11.2. Symmetry test

1. Particles tethered by multiple molecules often exhibit asymmetric XY motion. A simple symmetry metric identifies those that should be discarded from the analysis. For two-dimensional scatter plots, the distribution of excursions can is oriented along the Eigenvectors of the covariance matrix for X and Y positions. The Eigenvalues (λ₁, λ₂ in Figure 5) indicate the relative size of the distribution along their associated Eigenvectors [34]. In TPManalysis.m the square root of the ratio of the Eigenvalues, $\sqrt{{\lambda }_1∕{\lambda }_1}$, is used to gauge the symmetry of the excursions (“Symmetry” column in Figure 3) Particles with a root-ratio > 1.08 should be discarded as they likely correspond to a particle anchored by multiple DNA tethers [22].

2. Select the “Export Data” checkboxes for each particle that will be analyzed further. The checkbox sets a flag in each corresponding element of the TPMdata structure. After exiting TPManalysis, type “[TPMdata.Bead.UseForMeasurement]” on the command line to list the flags. Similarly, the command:

   TPMdata.Bead(###)

   will list all the data associated with the particle specified by ###.

1.11.3. Restricting data

During an experiment, a particle may transiently stick to the chamber surface, anomalously drift, or be obscured by a freely diffusing particle passing through the ROI. For analyses in which contiguous recording is not required, data corresponding to such interruptions may be excluded using the TPManalysis.m script.

1. To inspect and exclude data, highlight a particle and click “Exclude Data” to display a new window with buttons to exclude X or Y data (Figure 6).

2. Select either “Add Exclusion on X” or “Add Exclusion on Y” and draw rectangular selections on regions of the X or Y vs. time plots (respectively) to discard those segments of the data.

3. When finished with drift correction and data exclusion, click “Done” to export the edited data back to the MATLAB main workspace. If TPManalysis.m was called without an output argument, the data will be save to (or overwrite) a variable named “TPMdata” in the workspace.

4. Save the modified data using the standard “save” command (e.g. save(‘YourFileName.mat’,’TPMdata’); if using default variable names).

Figure 6.

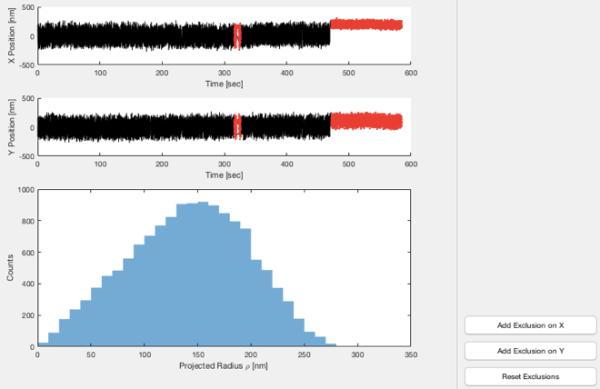
TPManalysis – Data exclusion. The upper panels show X and Y trajectories for a tethered particle. The lower panel shows a histogram of the magnitude of radial excursions about the average X and Y values for the entire segment. Adding exclusions by clicking “Add Exclusion on X” or “Add Exclusion on X” and extending rectangular selections across segments of the X or Y trajectories renders those segments in gray (red online).

1.12. Looping probability measurement

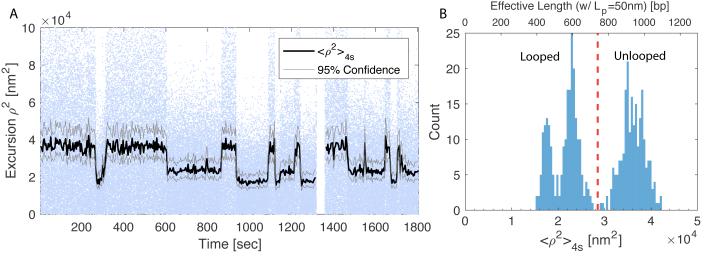
Looping and unlooping due to the binding and unbinding of lac repressor to operators manifests as switching between long and short RMS-excursions (Figure 7A). The square of the excursion was averaged using a moving window 4 seconds wide. (See Note 10.) 95% confidence limits determined using Equation 10 were based on a 50 Hz frame rate with exposures of 1 ms such that the window included 200 points. Due to parallel or anti-parallel DNA alignments and switching of the lac repressor between open and closed conformations, LacI-looped states exhibit a variety of topologies (see Figure 7B). For more details about loop topology see Note 11. Looping probability as defined in Equation 1, can be measured by calculating the fraction of time that a tether exhibits short RMS-excursions.

1. For each TPM particle trace, inspect the histogram of <ρ²>_4s values to identify ranges corresponding to unlooped and looped states. Choose a mean-squared excursion value as a threshold. Below the threshold, the tether is considered looped, while above the threshold it is unlooped. Note that due to differences in bead size, histograms of mean-squared-excursions are likely to shift slightly from particle to particle. Consequently, slightly different thresholds may be established for individual particles. In the case of the tether shown in Figure 7B, the threshold was 2.8×10⁴ nm².

2. The total time spent in each state is simply a sum of the number of samples above (unlooped) or below (looped) the threshold. Looping probability was calculated on a per-particle basis using Equation 1.

3. The looping probability of multiple particles at a given concentration can be averaged together using a total-duration weighted average:

   $$\overline{p_{\mathit{loop}}}=\frac{\sum _i{p}_i^{\mathit{loop}}\cdot T_i^{\mathit{total}}}{\sum _i{T}_i^{\mathit{total}}}.$$ Eq. 14

   The normal-approximation of the weighted sample variance can be calculated as

   $$s_W^2=\frac{\sum _i{T}_i^{\mathit{loop}}\cdot {(p_i^{\mathit{loop}}-\overline{p_{\mathit{loop}}})}^2}{\sum _i{T}_i^{\mathit{total}}}.$$ Eq. 15

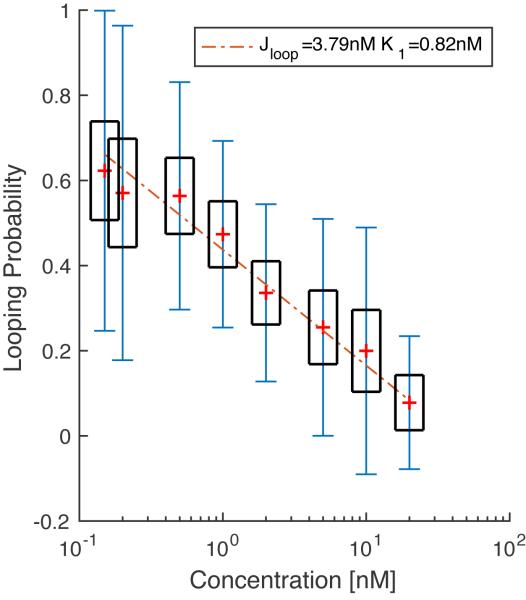
   The weighted standard error of the mean can be estimated as

   $${\mathit{SEM}}_w\approx \sqrt{s_W^2\cdot \frac{\sum _i{T}_i^{{\mathit{total}}^2}}{{\left(\sum _i{T}_i^{\mathit{total}}\right)}^2}}.$$ Eq. 16

4. After analyzing the data for each LacI concentration, a titration curve can be assembled and fit to Equation 2 assuming uninterrupted occupancy of O_S (Figure 8). The fit yields a K_D of 0.82±1.76 nM for LacI binding to O₁ and a J factor of 3.79±0.77 nM. These indicate that tethering LacI 400 bp away at the O_S site increases the effective concentration of LacI at the O₁ site four-fold with respect to the 1 nM concentration of the solution

Figure 7.

Tethered particle excursions in presence of 1 nM Lac-Repressor. (A) Squared-excursion vs. time. Dots indicate instantaneous excursions of the particle (Blue dots online). The black trace shows a 4s moving average of excursions. It switches between values of approximately 4×10⁴ nm², 2.3×10⁴ nm², and 1.7×10⁴ nm². The largest excursion corresponds to when the tether is unlooped. Lower values correspond to looped DNA with different topologies. 95% confidence intervals were calculated using Eq. 10. (B) A histogram of a 4s moving average of excursions exhibits three peaks. Squared-excursion can be roughly converted to effective DNA length (upper axis) using Eq. 4 with Lp = 50nm.

Figure 8.

LacI titration for a 400 bp O_S-O₁ loop. Markers (+, red online) indicate the average looping probability at each concentration. Black boxes indicate ±1.96*SEM_W confidence limits as determined using Eq. 16. Error bars (blue online) indicated weighted standard deviation defined by Eq 15. The dashed line corresponds to linear fit of data (Eq. 2) to estimate J_loop and K₁. A minimum of 27 tethers were measured at each concentration, with each particle being tracked for an average of 1400 sec.

Conclusion

This chapter is a description of the materials necessary to perform a typical TPM experiment and includes references to software for capturing and analyzing TPM data (Sections 2.1 and 3.6). While TPM is relatively simple to implement, care must be taken to ensure that the time-scales of a process of interest match the temporal resolution of the technique. To that end, approximating the tether as a Hookean spring yields a useful first-order approximation of the time-scales necessary to resolve different molecular conformations (Eq. 7-13).

As an example, this TPM protocol was used to quantitatively assess how lac repressor concentration regulates the stability of loops in a DNA sequence flanked by lac operators. For these experiments, the effective tether lengths of the various DNA conformations intermittently switched between approximately 400 and 900 bp. Distinguishing the TPM excursions associated with those looped and unlooped states required observations lasting 1-2 seconds (Eq. 13). lac-induced loop states typically persist for several seconds to minutes, so TPM is an ideal approach for this system. However, TPM experiments are somewhat tunable in that measuring even faster dynamics using shorter observation times would be possible for shorter tethers or molecules that have stiffer effective spring constants, both of which yield correspondingly lower TPM time constants (Eq. 7).

In this example, a lac titration was used to assess the effect of both looping energetics (characterized by the J factor) and operator occupancy via the approximation in Equation 2. An effective J factor of 3.79±0.77 nM and a dissociation constant K_D ≈ 0.82±1.76 nM for O₁ are commensurate with what has been reported previously [19]. Beyond simply distinguishing looped and unlooped states, TPM also reveals variation in DNA loop conformations, which manifest as distinct peaks in the histogram of particle excursions shown in Figure 7b. In fact, other authors have used TPM, combined with analysis methods based on Bayesian statistics and hidden Markov-models, to characterize looped conformations, revealing differences that would be otherwise unobservable [31, 35].

In summary, TPM is a versatile technique, useful for assessing protein-DNA interactions and capable of revealing protein-induced DNA loop conformations that would be difficult to detect with other techniques. Moreover, the discussion of the technical underpinnings of TPM presented here is not exclusive to DNA, but rather applies to any linear macromolecule. Consequently, both the technique and analytical methods presented in this chapter can be adapted to a wide variety of molecular systems.

Notes

1. For a Hookean spring potential, particle positions along X and Y are independent and are drawn from the distribution in Eq. 5. In the steady-state limit, Eq. 5 simplifies to a Gaussian with variance ${\sigma }^2=\frac{k_{B}T}{K}$. Assuming the spring constant is the same along both X and Y, a change of variable from the joint probabilit distribution $\sqrt{{(x-\stackrel{‒}{x})}^2+{(y-\stackrel{‒}{y})}^2)}$ yields a Rayleigh distribution

   $$P\left(\rho \right)=\frac{\rho }{{\sigma }^2}{e}^{-\frac{{\rho }^2}{2{\sigma }^2}}.$$ Eq. 17

   It is important to note that ⟨ρ²⟩_τ is not simply the variance $\left(\mathit{Var}\right(\rho )=\langle {(\rho -{\rho }^2)}^2\rangle )$. Rather, in the limit of τ → ∞, ⟨ρ²⟩ = 2σ². Consequently, although the ρ-distribution (Eq. 18) is non-normal, the Fisher test used in Eq. 12 still applies to ⟨ρ²⟩ since σ comes from the normal distributions of X and Y positions.

2. In most cases a standard research-grade microscope equipped with an objective with NA>1 is sufficient for observing tethered motion. Particles can be imaged with either dark-field or bright-field contrast. For bright-field, it is helpful to image using a contrast enhancement scheme such as DIC or phase-contrast microscopy. In this chapter we present methods for both dark-field and DIC imaging; in principle the particle tracking algorithms could also be adapted for phase-contrast microscopy.

   The choice of camera is slightly more specific. In selecting a camera one needs to consider the camera speed (frame rate), minimum exposure time, and effective pixel size when combined with the objective. Equation 7 provides an estimate of the minimum time interval required to assess Brownian (uncorrelated) motion of a particle. To maximize data-capture rates, roughly estimate the necessary frame rate with 1/τ. (Slower rates can be used in conjunction with longer measurement periods.) Care must also be taken to minimize exposure time. Excessive exposure time effectively blurs the image of the particle and shrinks the measured RMS-excursion [34]. For an exposure of δt, the measured RMS-excursion decreases by a factor of approximately

   $${\rho }_{\mathit{measured}}\approx \rho \frac{\tau }{\delta t}\left(1-e^{-\frac{\delta t}{\tau }}\right).$$ Eq. 18

   The experiments presented here were conducted with an exposure time of 1 ms. Using the estimate of τ given in eq. 7 this corresponds to a scale factor of 0.98; although, as noted in the introduction, near-wall drag effects tend to increase τ, meaning that the actual scaling effect is smaller.

   The effective resolution of the camera needs to be chosen to accurately localize the particle by at least an order of magnitude less than the expected RMS-excursion. In the presence of moderate noise, the tracking algorithms used here localize a particle centroid to within about 5-10% of a pixel, and improve with less noise. For our system, the combination of camera and 100x objective has a pixel size of about 65nm, yielding an accuracy of 3-6 nm, which is sufficient for discriminating between ρ_RMSunlooped = 180 nm and ρ_RMSlooped = 130 nm.

3. The wide-spread use of particle tracking techniques in various fields has led to the development of numerous packages implemented in various computer languages; see http://www.physics.emory.edu/faculty/weeks//idl/ for more software.

4. α-casein can be difficult to weigh and dissolve. Therefore, it is helpful to prepare a stock solution of 2% w/v in 1x Phosphate Buffered Saline and store at 4°C. Dried α-casein should be stored at −20°C per the manufacturer’s instructions.

5. Plasmid pYY_I1_400 (available upon request) was constructed using Gibson assembly (New England Biolabs, Ipswitch, MA) to simultaneously insert five synthetic fragments into the BsaI site of pBR322. The first fragment included the T7A1 promoter with CTP-dependent stall site at +37. Coupling to the other fragments positioned a proximal O_S operator site at +261, a distal O₁ operator site at +660, and a terminator at +1272. See supplementary info for the sequence.

6. Primers should have strong hybridization (GC-rich) at the 3’-end from which extension must proceed. Many researchers select primers with G and/or C as the final two bases. Primers should also be selected to minimize intramolecular hairpins and intermolecular pairing that would interfere with hybridization to the template strands. Oligo suppliers offer web pages with programs for predicting hybridization that might interfere, and they are useful for discarding undesirable base pairing. In practice, these predictions are not always accurate and several primer pairs for a given template sequence may need to be screened to optimize the yield.

7. Parafilm chamber spacers should be cut to form two 1 mm-wide channels that lead into a larger 5 mm × 10 mm channel that forms the central chamber. Parafilm spacers can be cut by hand using a straight-razor or scalpel using the template in Figure 9. Alternatively, a vector template is available for automated Laser cutting. See Supplementary Information. A 50 watt CO₂ laser cutter with the power set to 90% and pulse frequency of 500 PPI cuts Parafilm without excess melting or charring.

8. Thermocycling parameters may require adjustment to optimize PCR yield and specificity. See New England Biolabs website for tips on maximizing PCR product [36].

9. Most standard UV-Visible spectrophotometers can be used to measure absorption at 260 nm and 280 nm. A NanoDropLite Spectrophotometer from Thermo Fisher is convenient for determining DNA concentrations.

10. Based on the estimates in Section 1.1, 1.12 seconds should provide enough data to resolve the two populations with 95% significance; however, we chose 4 second long windows because that has is the range typically used in the TPM literature [20].

11. Due to the torsional flexibility of DNA over length scales larger than 100 bp, LacI binding between two operators can generate a number of different loop topologies [13, 19, 20]. Each results in a slightly different effective tether length. For the 909 bp sequence containing the O_S and O₁ operators separated by 400 bp, <ρ²>_4s is expected to switch between ≈ 3×10⁴ nm², corresponding to the unlooped state, and a looped states around <ρ²>_4s ≈ 2×10⁴ nm². Variation in effective loop lengths are due to the switching between alternate loop conformations. Figure 7B depicts a tether transitioning between what appear to be three distinct states. The largest corresponds to the unlooped state and the lower two correspond to looped topologies. Based on Monte-Carlo simulations and fitting TPM data to hidden Markov models, the larger of the two looped state likely corresponds to the DNA forming a crossed-loop, while the shortest state corresponds to the DNA have one of a few different uncrossed topologies [13, 19, 20].

Figure 9.

Parafilm Spacer Template.