Localization of Origins of Premature Ventricular Contraction by Means of Convolutional Neural Network from 12-lead ECG

Abstract

Objective

This paper proposes a novel method to localize origins of premature ventricular contractions (PVCs) from 12-lead electrocardiography (ECG) using convolutional neural network (CNN) and a realistic computer heart model.

Methods

The proposed method consists of two CNNs (Segment CNN and Epi-Endo CNN) to classify among ventricular sources from 25 segments and from epicardium (Epi) or endocardium (Endo). The inputs are the full time courses and the first half of QRS complexes of 12-lead ECG, respectively. After registering the ventricle computer model with an individual patient’s heart, the training datasets were generated by multiplying ventricular current dipoles derived from single pacing at various locations with patient-specific lead field. The origins of PVC are localized by calculating the weighted center of gravity of classification returned by the CNNs. A number of computer simulations were conducted to evaluate the proposed method under a variety of noise levels and heart registration errors. Furthermore, the proposed method was evaluated on 90 PVC beats from 9 human patients with PVCs and compared against ablation outcome in the same patients.

Results

The computer simulation evaluation returned relatively high accuracies for Segment CNN (~78%) and Epi-Endo CNN (~90%). Clinical testing in 9 PVC patients resulted an averaged localization error of 11 mm.

Conclusion

Our simulation and clinical evaluation results demonstrate the capability and merits of the proposed CNN-based method for localization of PVC.

Significance

This work suggests a new approach for cardiac source localization of origin of arrhythmias using only the 12-lead ECG by means of CNN, and may have important applications for future real-time monitoring and localizing origins of cardiac arrhythmias guiding ablation treatment.

I. Introduction

Since its invention, the 12-lead ECG has been widely used as a diagnostic test for cardiac arrhythmias and it can be recorded rapidly with portable equipment for a long time by using a Holter monitor. [1] A normal heart beat would produce four entities on the ECG: a P wave, a QRS complex, a T wave and a U wave. They represent different electrophysiological stages of the heart: atrial depolarization, ventricular depolarization, ventricular repolarization and papillary muscle repolarization. Among them, the QRS complex is of the most interest to cardiac electrophysiologists since a majority of ventricular arrhythmias are reflected by the changes of morphology on the QRS complex.

A premature ventricular contraction (PVC) is a type of ectopic beat, in which the heart beat is initiated by an ectopic pacemaker in the ventricles. It is one of the most common ventricular arrhythmias and its prevalence is associated with many factors. The prevalence of PVC is >6% among 15,792 adults (aged 45–65 years) from the US based on a 2-minute ECG in a large cross-sectional analysis. [2] If not treated in time, the condition of PVC may degenerate into other ventricular arrhythmias such as ventricular tachycardia (VT) and ventricular fibrillation (VF) and finally lead to sudden cardiac death. Radiofrequency catheter ablation [3] is a minimally invasive procedure that by delivering energy to the sections of the heart who are prone to producing arrhythmias, the arrhythmias are terminated and the patient is treated. To localize the site of ablation, pace-mapping is a predominant technique being used in clinical settings. [4] If the morphology of QRS complex by pacing at a site matches well with the VT or PVC observed on the 12-lead ECG, this site is considered to be a potential ablation site. Pace-mapping is done by stimulating at different endocardial sites, so it is invasive. Non-invasively, researchers have been investigating features of the QRS complex obtained from the 12-lead ECG to help identify ablation targets for PVC and VT. [5]–[7] Some typical characteristics of the QRS complex used for localization are QRS width, QRS axis, QRS patterns (qR, QS, RsR’ and so on), R wave amplitude and concordance.

Some characteristics of the QRS complex are easy to calculate automatically, however, for other features that involve pattern recognition, it is subjective to some degree and requires expertise obtained from a long-time training.

Neural network is well known for recognizing patterns and classification. [8]–[10] The accuracy can be higher than 90% given ample training samples. [11] The input to the neural network can be the original time course of the 12-lead ECG, [12] features extracted from time domain, [13] statistical features, [14], [15] features extracted from frequency domain, [16] components resulting from different transforms, [17]–[19] and outputs from some clustering algorithms. [20] The application of neural network can be the classification among ventricular arrhythmias, [12], [15], [16] classification between normal heart beat and arrhythmias [17], [21], [22] or among all types of arrhythmias. [20] Another important application is the discrimination between healthy subjects and patients, such as patients with myocardial infarction [23]–[25] and patients with coronary artery disease. [18] These applications of neural network are mostly concerned about the state of the heart, whether it is in arrhythmias or have cardiac diseases.

We propose to classify and localize origins of cardiac arrhythmias throughout the ventricles by applying neural networks to 12-lead ECG. The ventricles are divided into 25 segments based on standard myocardial segmentation of the left ventricle [26] and expanded it to the right ventricle. A realistic anisotropic ventricle computer model is used to generate QRS complexes of 12-lead ECG from pacing at all possible ventricular locations. The time course of QRS complexes generated are then fed to convolutional neural network (CNN) for classification and localization purpose.

Epicardial mapping and ablation have expanded considerably in the past few years. It was reported that 13% to 17% VT ablation procedures were epicardial mapping or ablation. [27], [28] On ECG, epicardial VT is reflected as a slow onset of the QRS because the initial part of the wave front progresses slowly until it reaches the Purkinje system at the subendocardium. [29] The intracardiac delay of electrical conduction produces a slurred initial part of the QRS complex (pseudo Δ wave) [30] So the initial part (first half) of the QRS is critical for the detection of an epicardial or endocardial focus. In this study, we use the first half of QRS complexes generated by the ventricle computer model as input to the CNN to classify between an epicardial ectopic beat and an endocardial ectopic beat.

Thus, our proposed method consists of two neural networks: Segment CNN with 25 classifications and Epi-Endo CNN with 2 classifications. The localization of origins of PVC is a function of probability distribution outputs of the two CNNs and the center of gravity of each segments in the ventricular model. Our proposed method was applied to the real 12-lead ECG collected from 9 PVC patients who underwent ablation treatment.

There are other studies to localize the origin of PVC from the 12-lead ECG. Van Dam et al. used myocardial activation imaging technique based on an equivalent double layer model to localize the PVC origin, [31]–[33] although positions of 12-lead ECG were unknown, thus the accuracy of results was reduced. Also, a quantitative measurement of localization error was lacking. In our study, electrodes’ positions were digitized and the average localization error was presented by calculating the spatial distance between the CNN predicted sites of origin of PVC and successful ablation sites recorded from EP study in the patient.

Recently, a patient specific model based intracardiac electrograms simulation was done to resemble clinical body surface signals. [34] Our study would be considered a step forward as the model-based noninvasive identification of ablation targets.

For a more accurate estimation of cardiac activation sequence to localize origins of PVC or VT, a noninvasive 3-dimensional cardiac electrical imaging technique was developed based on the body surface potential mapping. [35], [36] It was evaluated under a variety of animal studies [37]–[41], in pathological hearts [42], and applied to detect high-frequency drivers of atrial fibrillation. [43]

II. Method

The rationale behind this study is that we assume PVCs are generated by focal sources, and if we train CNN with all the possible 12-lead ECGs resulting from a single-site pacing covering the ventricular volume with a certain level of noise, the CNN will be able to identify which segment the origin of PVC lies in and whether it is an epicardial or endocardial source given a set of 12-lead ECGs. And depending on the probability distribution of CNN output, we could also give an estimation of source location based on the classification information.

A. Realistic Anisotropic Ventricle Computer Model

The ventricular excitation was simulated by a cellular automaton heart model. As described in the paper by He et al., [44] heart geometry was constructed from CT images of a human subject and discretized into around 38,000 cellular units with a side length of 1.5 mm. Then a generalized ventricle conduction anisotropy was incorporated into the model. The myocardial fiber orientations rotated counterclockwise over 120° from the outermost layer (epicardium, −60°) to the innermost layer (endocardium, +60°) with equivalent increment between the consecutive layers. The conduction velocity along the fiber was 0.6 m/s, and 0.2 m/s transverse to the fiber, respectively. Also the longitude intracellular conductivity was set as 0.3 S/m and the transverse intracellular conductivity was 0.075 S/m, respectively. The action potential and the vector of local fiber orientation were set individually over all the ventricular cellular units. The equivalent current-dipole density of each unit was computed as the product of the myocardial conductivity tensor and the spatial gradient of instantaneous transmembrane potential. Each dipole has three orthogonal components. Finally, cellular units were further grouped into 3,887 dipoles according to their segment number. The time resolution of electric potentials is 1 millisecond. This ventricle current-dipole model was used previously in the simulation study of a 3-dimensional cardiac imaging technique. [35], [36]

B. Segmentation of the Whole Ventricle and Extraction of Epicardium and Endocardium

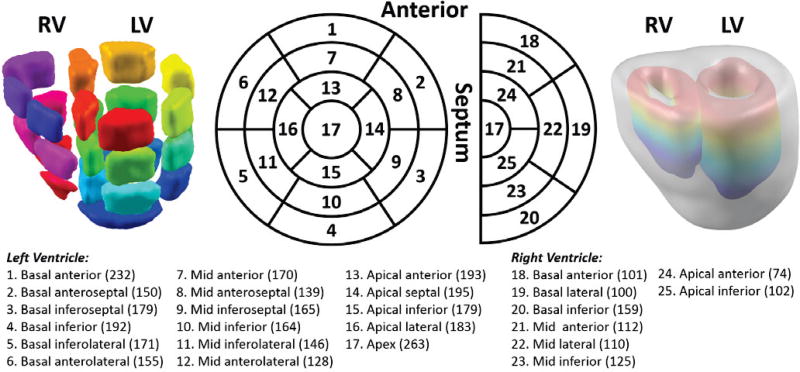
In the ventricle current-dipole model which consists of 3,887 cardiac dipoles, the left ventricle was segmented according to AHA standardized myocardial segmentation into 17 segments, [26] and the right ventricle was segmented in a similar way as the left ventricle into 8 segments. Thus, the whole ventricle was classified into 25 segments in total. The position and the number of each segment are shown in the middle column of Fig. 1. The number of cardiac dipoles each segment includes is in the parentheses on the bottom. The left column in Fig. 1 is a visualization of 25 segments. The dipoles lying on epicardium and endocardium were identified and labeled as 1 and 2 respectively, and all other dipoles were assigned 3 as transmural dipoles. Both the left side and the right side of the septum are considered as endocardium.

Figure 1.

Segmentation of the whole ventricles. Left ventricle segmentation follows the AHA standardized myocardial segmentation, and the right ventricle is segmented in a similar way developed by the authors. The most right column shows the colorful endo-surfaces of both ventricles and also the gray epicardium. The bottom panel lists all the segments in order, their physical position and the number of cardiac dipoles each segment contains in the ventricle current-dipole model. In total, there are 3,887 current dipoles in the model.

C. 12-lead ECG for Simulation

The torso and lungs were segmented from a high-resolution male torso MRI images (ViP V2.0 IT’IS Foundation, Zürich, Switzerland). Then the boundary element model of heart-torso was built using a commercial software (Curry 6.0, Neuraoscan, North Carolina, USA). 208 body surface electrodes were placed on the front and back of body surface. By multiplying the current-dipoles with the leadfield matrix between each dipole and each electrode, we could get body surface potentials. Among these signals, nine were chosen to generate 12-lead ECG. Three electrodes were selected to represent the electrodes placed on left leg, left arm, and right arm, respectively. So lead I, II III and lead aVL, aVR and aVF could be derived from the signals of these electrodes. Other six electrodes were selected as V1 to V6 according to their anatomical locations.

D. Training and Testing of Convolutional Neural Network

Convolutional neural network (CNN) is a type of deep, feed-forward artificial neural network. We used a deep learning toolbox in MATLAB developed by Rasmus Berg Palm [45] to setup, train and test CNN. It uses a sigmoid function as the activation function for feed forward propagation and a gradient descent projection method as the back propagation algorithm. Convolution and pooling were done in 2-dimension (2-D). The stride, namely the number of unit that convolutional kernel shifts each time, is equal to 1. There is no padding in convolutional layers. The 2-D convolutional kernel has an equal size along both directions. To ensure the applicability of the convolutional kernel, the input should also be in square shape. Thus, we added 4 more leads derived from three limb leads (LL for left leg, RA for right arm, LA for left arm): LL−RA−LA; LA−RA−LL; RA−LA−LL; (LL+RA+LA)/3. The last one corresponds to the Wilson central terminal. [46] Along the time dimension, we down-sampled the time courses of QRS (or first half of QRS) to 16 time points before adding noise in simulation. Therefore, each input set of ECGs is a 16 ×16 square matrix. This size results in the fast response of both CNNs.

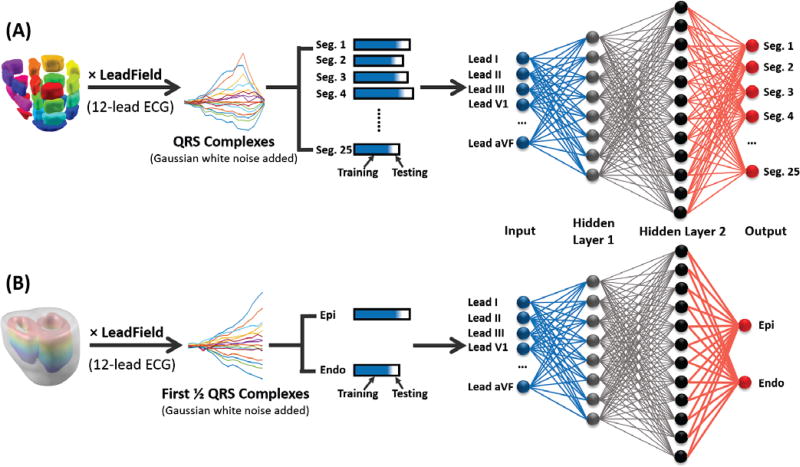
In order to localize the origins of PVCs, we utilized the classification information from two types of CNN: Segment CNN and Epi-Endo CNN. The study diagram of this section is shown in Fig. 2.

Figure 2.

Training and Testing study diagram. (A) Segment CNN. All cardiac dipoles are multiplied by the leadfield of 12-lead ECG to get the time courses of electric potentials. Then different levels of Gaussian white noise were added to the potentials. 90% of the QRS complexes (Blue in the bar) from 12-lead ECG were selected as the input to Segment CNN for training procedure. The other 10% (White in the bar) were used for testing. The output of Segment CNN is a probability distribution among 25 segments, the segment with the maximum probability is considered as the output segment. (B) Epi-Endo CNN. Cardiac dipoles located at epicardium and endocardium were selected and multiplied by the leadfield of 12-lead ECG. Different levels of Gaussian white noise were added and the first half of QRS complexes served as the input for Epi-Endo CNN. 90% of the data were for training and the other 10% were for testing. The output is a probability distribution among two output neurons, either neuron 1 (Epi) or neuron 2 (Endo) would have a larger probability.

Segment CNN

The cardiac dipole components resulted from pacing were multiplied by the lead field matrix to generate body surface electrical potentials. Thus, we would have 3,887 sets of 12-lead ECGs corresponding to pacing at 3,887 locations in the ventricular model. QRS complexes were extracted from each lead. A certain level of Gaussian white noise (20 dB, 10 dB or 5 dB) was added to all the leads 10 times to generate noise contaminated 12-lead QRS complexes. Adding a certain level of noise 10 times is for increasing the robustness of Segment CNN to this level of noise since we would have ample training samples representing different noise variations. In total, our data pool had 38,870 sets of noise-contaminated 12-lead QRS complexes. 10% of the whole data was used for testing, which means 3,887 sets were the testing data. In order to test the CNN without segment bias, within each segment, 155 (≈ 3,887/25) sets of 12-lead QRS complexes were randomly selected each time for testing. The remaining 90% data were used for training procedure. The Segment CNN consisted of 6 layers: Input layer (A set of 12-lead QRS complexes), Hidden layer 1 (convolutional layer with a kernel size of 5), Pooling layer 1 (sampling scale of 1), Hidden layer 2 (convolutional layer with a kernel size of 3), Pooling layer 2 (sampling scale of 2), and Output layer (25 neurons for 25 segments). The batch size was 23, alpha was 1 and the number of epochs was 10. After a ten-fold cross-validation, the accuracy and precision rate of each segment of Segment CNN were calculated.

Epi-Endo CNN

Similar to Segment CNN, 1,709 dipole sources located on epicardium and endocardium were identified and were used to generate single-site pacing 12-lead ECGs. QRS complexes were extracted and the first half of 12-lead QRS complexes was used. Gaussian white noise of a specific SNR was added 10 times. Thus for Epi-Endo CNN, we had 17,090 sets of first half of QRS complexes from 12 leads. 10% of this data was used for testing, which means 855 (≈1,709/2) sets were randomly selected from each category. The remaining 90% data were used for training. The Epi-Endo CNN consisted of 6 layers: Input layer (first half of QRS complexes from 12-lead ECGs), Hidden layer 1 (convolutional layer with a kernel size of 5), Pooling layer 1 (sampling scale of 2), Hidden layer 2 (convolutional layer with a kernel size of 3), Pooling layer 2 (sampling scale of 2), and Output layer (2 neurons corresponding to epicardium and enodcardium). Parameters were set as following: batch size = 25, alpha = 3 and number of epochs = 10. After a ten-fold cross-validation, the accuracy and precision rate of Epi or Endo were calculated.

E. Localization of Origins of PVCs

After training procedures, we tested the localization performance of these two CNNs by feeding a new set of data, which included 12-lead ECGs with a certain SNR resulting from pacing at all possible dipole locations. For each set of 12-lead ECGs, Segment CNN would assign a probability to each segment and Epi-Endo CNN would tell how possible it was from epicardium or endocardium. Based on these two probability distributions, the estimation of source location was calculated as following:

$$S=\sum _{i=1}^N{P}_i\times (\sum _{j=1}^2{P}_j\times {\mathit{\text{CoG}}}_{\mathit{\text{ij}}})$$ (1)

In (1), S is source location, P_i is the normalized probability of ith segment and its adjacent segments, the output of Segment CNN. N is the number of adjacent segments each segment has based on the ventricle segmentation in Fig. 1. P_j is the probability of Epi or Endo, the output of Epi-Endo CNN. And j is 1 for Epi; 2 for Endo. CoG_ij is the center of gravity of Epi or Endo dipole sources in ith segment.

The segment with the maximum probability from Segment CNN was considered as the output segment. Its adjacent segments (sharing boundaries with the output segment) were determined based on the ventricle segmentation in Fig. 1. The endocardial center of gravity and epicardial center of gravity in each segment were calculated. By multiplying spatial locations of epicardial and endocardial centers of gravity with the probabilities of epicardium and endocardium from Epi-Endo CNN, we obtained epi-endo-informed centers of gravity of the output segment and its adjacent segments. This process corresponds to the multiplication inside the parentheses in (1). Since some dipole sources locate near the boundary of two segments, it was probable that Segment CNN would assign it to its neighboring segment. This is why we took the adjacent segments of an output segment into consideration to decrease the localization error (LE). And it was done by first normalizing the output probabilities of Segment CNN only among the output segment and its adjacent segments, and then multiplying the normalized probability with each epi-endo-informed center of gravity. Adding all up, we estimated the source location.

F. Application to PVC Patients

We collected data from 9 PVC patients (Male = 3, Female = 6, average age = 48.3 ± 12.3 years old). The patient statistics were summarized in Table 1. None of them have undergone ablation procedure before and none of them have structural heart disease. Study protocols were approved by the Institutional Review Board of University of Minnesota and Shanghai Ruijin Hospital (affiliated with Shanghai Jiao Tong University School of Medicine, Shanghai, China). Written consent forms were obtained from all patients. For each patient, we had CT images of heart, lungs and torso. Then a boundary element model was built including lungs and torso by using a commercial software (Curry 6.0, Neuroscan, North Carolina, USA). After the segmentation of patient’s heart, we registered our ventricular model with it. Prior to the EP study, 208 Ag-AgCl carbon electrodes were placed on the front and back of body surface to record body surface electrical potentials with 2kHz sampling rate for about 10–30 minutes and positions of electrodes were digitized (Fastrak, Polhemus Inc., Colchester, VT, USA). During the recording, all of the patients have spontaneous PVCs recorded and 2 of them also have non-sustained VT detected. Nine electrodes were selected to form 12-lead ECGs later based on their anatomical positions. We registered the generic model with the patient’s heart based on the least sum of distances between the two. By using Curry 6.0, the leadfield between these nine electrodes and our generic ventricular model was generated. After the EP study, we also collected CARTO files, which contained spatial locations of successful ablation sites. And CARTO data were registered with the patient’s heart based on the landmarks of the geometry of ventricles recorded by the CARTO system. The successful ablation sites are considered as the origins of PVCs in this study.

Table 1.

Patient Statistics

Patient	Age	Gender	Diagnosis	Heart Rate (bpm)	Blood Pressure (mmHg)	Antiarrhythmic Medication	Medical History	PVCs/24 h	Ablation Outcome
1	41	F	PVC	74	116/77	None	Diabetes	15160	RVOT free wall
2	53	M	PVC, RBBB	70	105/63	Bisoprolol	Allergic to penicillin	25630	Left Anterior Fascicle
3	71	F	PVC, Nonsustained AT	70	117/61	Aspirin, Lipitor	Atherosclerosis of coronary artery and carotid artery, cervical disc herniation	21100	RVOT free wall
4	54	F	PVC	80	118/67	Moracizine	Allergic to cephalosporin	13441	RVOT free wall
5	37	M	PVC, Nonsustained VT	95	137/86	None	Sublingual gland excision	27161/23 h	RVOT free wall
6	42	F	PVC	78	115/75	None	None	26337	RVOT free wall
7	43	M	PVC	82	150/80	None	None	39476	RVOT septum
8	33	F	PVC	84	100/55	None	Cardiac arrhythmias, asthma	51226	RVOT free wall
9	61	F	PVC	82	129/79	Amiodarone, Moracizine, metoprolol	Paroxysmal palpitation	8470	RVOT septum

AT = atrial tachycardia; F = female; M = male; PVC = premature ventricular contraction; RBBB = right bundle branch block; RVOT = right ventricular outflow tract; VT = ventricular tachycardia.

QRS complexes of 10 PVCs were exported from body surface potential recordings of each patient. Body surface recordings were first filtered by a bandpass filter from 1 Hz to 30 Hz. After filtering, the QRS and the first half of QRS were down-sampled to 16 time points respectively to construct input for Segment CNN and Epi-Endo CNN. To estimate the SNR, signals of the same length as QRS complexes of PVCs between heart beats were also exported and were considered as noise. Average SNR is defined as the average of SNR of each channel. Then we trained and tested two CNNs using simulated 12-lead ECGs with the average SNR between QRS complexes and Gaussian white noise. Training and testing details are described in Section D. The only difference is that the leadfield used to generate 12-lead ECGs here is specific to each patient. Finally, 12-lead ECGs of 10 PVCs were fed into two trained CNNs to determine source locations.

G. Statistical Analysis

The accuracy of Segment CNN and Epi-Endo CNN were presented as mean ± SD. The localization error was defined as the spatial distance between the estimated source location and the location of the dipole source in the generic ventricular model that generates the 12-lead ECGs by pacing in simulation, and was defined as the spatial distance between the estimated source location and successful ablation sites in patients’ CARTO data.

III. Results

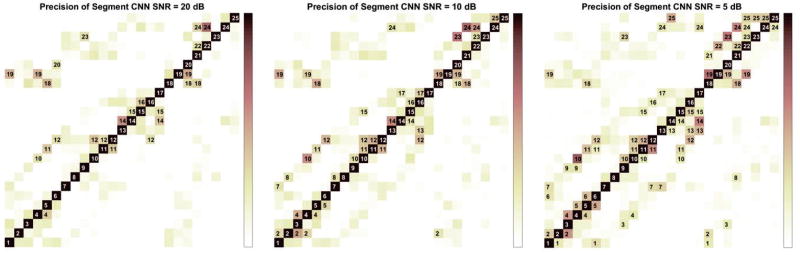
Table 2 shows the accuracy and precision of individual segment when Segment CNN was trained and tested on three different Gaussian white noise levels. Accuracy is defined as the percentage of dipole sources being correctly classified within each segment. Precision is defined as when Segment CNN predicts it is in one segment, how often it is correct. Fig. 3 shows the precision matrices of Segment CNN. Each column is the precision vector for this segment. When the probability of Segment CNN assigning this segment to other segments is higher than 5%, it is labeled in black in the figure. For example, when trained and tested on 20 dB, for segment 4, Segment CNN would have a relative higher probability of assigning segment 19 and segment 10 to segment 4 even though the precision for segment 4 is 74.1% from Table 2. Table 3 is the precision matrices of Epi-Endo CNN trained and tested on different noise levels.

Table 2.

Accuracy and precision rates for individual segments of Segment CNN trained and tested on 3 different SNR signals

	SNR=20 dB		SNR=10 dB		SNR=5 dB
Unit (%)	Accuracy	Precision	Accuracy	Precision	Accuracy	Precision
1	75.6	72.7	77.0	65.1	63.6	53.9
2	80.5	85.2	61.9	78.4	54.5	70.7
3	78.4	73.9	72.0	61.1	65.7	48.2
4	79.6	74.1	71.6	64.0	56.3	51.2
5	85.7	62.3	80.0	61.6	60.3	46.8
6	83.7	72.4	80.6	68.8	69.0	52.3
7	84.4	79.6	77.4	74.4	59.0	58.3
8	81.5	85.5	71.2	82.3	60.7	74.0
9	89.0	74.6	83.2	66.5	71.2	49.3
10	82.5	73.5	68.4	63.1	46.8	56.7
11	72.5	79.7	67.3	75.3	49.9	63.1
12	62.5	77.5	52.0	73.9	41.7	62.6
13	81.6	75.4	77.4	71.6	58.6	69.8
14	66.5	86.1	65.8	75.5	53.3	61.8
15	79.6	72.7	75.9	70.2	60.5	60.3
16	77.5	83.2	83.5	66.6	77.3	60.8
17	92.6	78.3	80.4	83.7	80.2	54.2
18	58.4	84.0	52.5	75.7	40.4	62.5
19	54.8	91.0	48.5	85.7	25.5	71.4
20	87.1	70.8	84.4	61.7	81.7	52.3
21	81.7	70.4	74.8	62.6	71.6	47.1
22	79.5	75.1	72.7	69.2	63.0	58.8
23	75.4	93.8	62.6	80.9	42.8	77.3
24	62.6	91.1	56.6	88.7	42.9	82.5
25	89.3	89.3	80.2	89.7	57.7	79.0

Figure 3.

Precision Matrix of Segment CNN trained and tested on 3 different SNR signals. Each column represents the precision of this segment over all the other segments. All the blocks with precision higher than 5% are labeled.

Table 3.

The Precision Matrix of Epi-Endo CNN trained and tested on 3 different SNR signals

	SNR=20 dB		SNR=10 dB		SNR=5 dB
Unit (%)	Epi	Endo	Epi	Endo	Epi	Endo
Epi	85.56	9.94	72.79	18.64	61.36	21.79
Endo	14.44	90.06	27.21	81.36	38.64	78.21

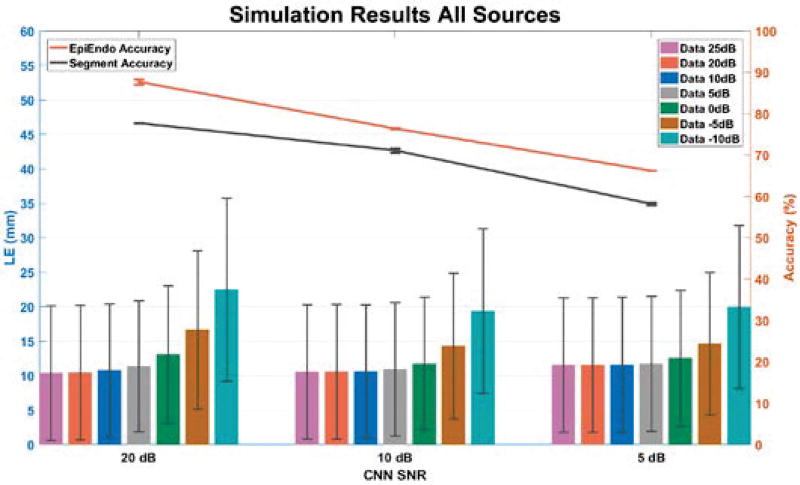
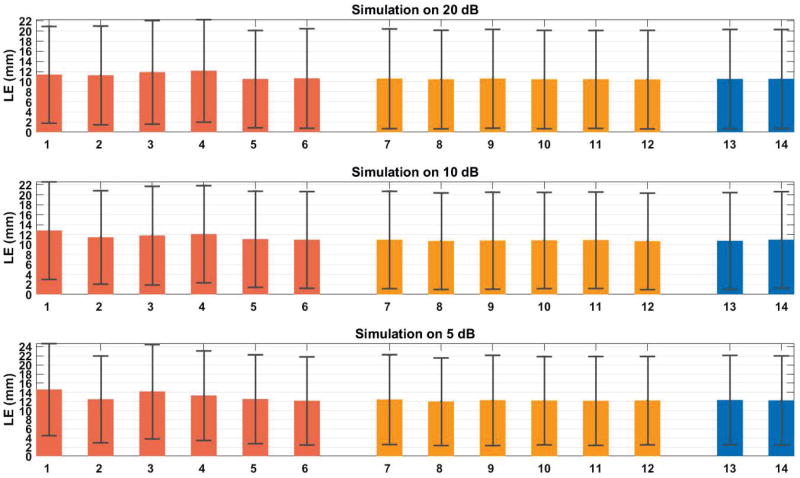
When we tested the localization performance of two CNNs, we tested them by feeding them 3,887 new sets of 12-lead ECGs by pacing at a single site with a variety of noise levels (25 dB, 20 dB, 10 dB, 5 dB, 0 dB, −5 dB and −10 dB). Fig. 4 presents the LEs along with average accuracies of Segment CNN and Epi-Endo CNN. The left part of the figure is the average LE when Segment CNN and Epi-Endo CNN were tested on 12-lead ECGs from all possible pacing sites in the ventricular model with different noise levels. And during the ten-fold cross validation, namely trained and tested on 20 dB 12-lead ECGs, the average accuracy of Epi-Endo CNN was 87.68 % and the average accuracy of Segment CNN was 77.71 %. The middle part and the right part are presented in a similar way as the left part. The exact numbers displayed on Fig. 4 are also included in Table 4.

Figure 4.

Simulation results of CNN. The top two lines are the average accuracy of Segment CNN and Epi-Endo CNN trained and tested on 3 different SNR signals. The bottom bars are the average localization errors when applying Segment CNN and Epi-Endo CNN together to data with different SNRs.

Table 4.

Accuracy of Segment CNN and Epi-Endo CNN (trained and tested on 3 different SNR signals) and localization errors of applying the CNNs under simulation

CNN SNR		20 dB	10 dB	5 dB
Segment Accuracy (%)		77.71±0.01	71.11±0.53	58.18±0.27
EpiEndo Accuracy (%)		87.68±0.61	76.40±0.07	66.20±0.01
Average LE(mm) of Different Data SNR	25 dB	10.37±9.74	10.56±9.73	11.55±9.74
	20 dB	10.43±9.77	10.58±9.74	11.55±9.75
	10 dB	10.76±9.65	10.61±9.64	11.56±9.82
	5 dB	11.38±9.51	10.94±9.68	11.73±9.80
	0 dB	13.09±9.97	11.73±9.65	12.54±9.80
	−5 dB	16.63±11.52	14.32±10.57	14.66±10.36
	−10 dB	22.47±13.28	19.36±11.94	19.96±11.85

IV. Discussion

This study shows the feasibility of utilizing convolutional neural network to localize origins of PVCs from 12-lead ECGs. We tested the method in both simulation data and clinical patients’ data, and obtained good localization errors in both situations.

A. Properties of Segment CNN and Epi-Endo CNN

The information in Fig. 3, Table 2 and Table 3 could be obtained when we train and test two CNNs on any patient-specific leadfield and under any noise level. It will guide us and give us a prior knowledge of how good two CNNs perform before we feed testing (or clinical) data to calculate the source location. From Fig. 3, we could see as SNR decreases, it is more likely for Segment CNN to assign dipole sources from other segments to one segment, which means the precision rates have dropped. The number of blocks labeled in the precision matrix increases as SNR decreases. Table 3 is the precision matrices of Epi-Endo CNN under different noise level. The common feature of these three precision matrices is that it is more likely for Epi-Endo CNN to assign sources on endocardial surfaces as epicardial sources. From Table 2, we could know the percentage of dipole sources in each segment that are correctly detected, namely the accuracy of each segment. And also how confident we are in the detection results if one dipole source is predicted to be from some segment.

B. Localization Errors of CNN

From Fig. 4 and Table 4, we could summarize the following trends of the performance of two CNNs: (1) as SNR drops, the accuracies of both CNNs decrease; (2) as SNR of input data drops, the average LE increases; (3) the average LE is the result of two factors, one is the SNR that two CNNs are trained and tested, the other is the similarity between input data and tested data. The accuracy of Segment CNN of 10 dB is only 6 % less than that of 20 dB. So when the SNR of input data is 10 dB and less than 10 dB, the average LEs of CNNs trained with 10 dB are all smaller than those of CNNs trained with 20 dB. This is when the similarity factor plays a dominant role. However, when the accuracy of Segment CNN drops to 58 %, which is 13 % less than that of 10 dB, the accuracy plays an important role in determining source locations. Because even though input data of 5 dB is more similar to CNNs trained with 5 dB, the average LE is larger than that of CNNs trained with 10 dB and input data of 5 dB. Actually, the average LEs of CNNs trained with 5 dB are all larger than those of CNNs trained with 10 dB. Finally, when we compare the performance between CNNs trained with 20 dB and trained with 5 dB, the average LEs of input data with 0 dB and less of CNNs trained with 5 dB are smaller than those of CNNs trained with 20 dB. This is because even with a much higher training accuracy, CNNs trained with 20 dB fail to classify 12-lead ECGs that are too unlike the training data.

A conclusion from the above simulation results is when the SNR of input data is very low, it is best to train and test CNNs with around 10 dB to minimize LEs, and when the SNR of input data is good, it is best to train and test CNNs with a noise level that is the same as the SNR of input data.

C. Localization Errors of CNN with Heart Registration Errors

Since we register our ventricle current-dipole model with patient’s heart and train and test CNNs using this model and finally use CNNs to localize origins of PVCs, it is necessary to investigate the influences of heart registration errors on the localization performance of CNNs. So Fig. 5 shows the average LE when we trained and tested CNNs with correct registration, and applied to localization when the input 12-lead ECGs were generated by the leadfield with heart registration errors. The SNR of training and testing data is the same as the SNR of input data for testing localization performance.

Figure 5.

Average localization errors of a variety of heart registration errors. 1=Heart move to the right 10 mm; 2=Heart move to the left 10 mm; 3=Heart move up 10 mm; 4=Heart move down 10 mm; 5=Heart move to the anterior 5 mm; 6=Heart move to the posterior 5 mm; 7=Heart rotate right 10°; 8=Heart rotate left 10°; 9=Heart rotate upwards 10°; 10=Heart rotate downwards 10°; 11=Heart rotate clockwise 10°; 12=Heart rotate counterclockwise 10°; 13= Heart inflated 10 mm; 14=Heart deflated 10 mm.

Three categories of heart registration errors were investigated: shift, rotation and scaling. Overall, all the average LEs are larger than those of correct registration. Within shift group, because heart is already very close to the front body surface, so we could only move heart forward by 5 mm. For comparison purpose, we also moved heart backwards by 5 mm. Heart moving to the right always generated a larger LE than moving to the left. Within rotation group, heart rotating to the right always generated a larger LE than rotating to the left. Within scaling group, there is no obvious trend. Among all the registration errors, we found that shift group gave higher LEs than the other two groups on average.

Based on the above analysis of the registration error results, we should pay attention when we need to shift the ventricular model for the registration with patient’s heart. And CNNs are generally robust to a variety of heart registration errors if we compare these LEs with those that are from correct registrations: 10.43 ± 9.77 mm (20 dB), 10.61 ± 9.64 mm (10 dB) and 11.73 ± 9.80 mm (5 dB). Generally, the above heart registration errors would increase average LE by 1 to 2 mm.

D. Application to PVC Patients

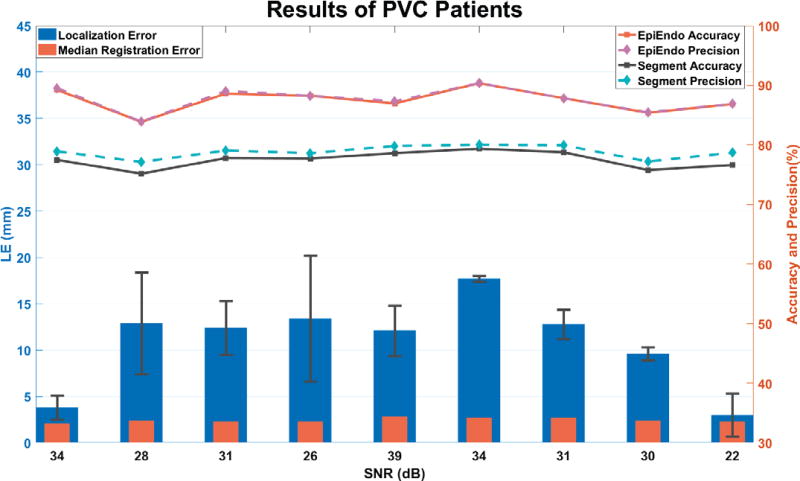
From the last column in Table 1, which is the ablation record from CARTO files, the origins of PVC lied in different regions in the ventricles, 1 patient had PVC originated from the left anterior fascicle, 6 patients were ablated at free-wall side of right ventricular outflow tract, and PVCs in the left 2 patients were detected in the septal side of right ventricular outflow tract. On average, the localization error of 9 patients is 10.9 ± 5.5 mm, which is good and reasonable considering the source location was estimated solely from 12-lead ECGs. The average median registration error is 2.4 ± 0.2 mm. Registration error is one factor that contributes to the final localization error. The present results demonstrated the feasibility of employing a generic anisotropic ventricle current-dipole model to mimic cardiac activities in a patient without structural heart disease. Generally, the more similar a patient’s heart is with the ventricular model, the more accurate the predictions will be. And this also shows the capability of our method to estimate origins of PVCs from different areas.

E. Merits and Limitations

Merits

This method can be applied to the localization of PVC and focal ventricular tachycardia (VT) since the training data is generated from single-site pacing. It is a stable method in the sense of two-fold: once CNNs are trained on a patient, they are applicable to all the other PVCs and focal VTs from the same patient; structures and parameters of both CNNs all remain the same across different subjects and noise levels. It is a robust method because average LEs under different noise levels and heart registration errors fluctuate in a range of 1 to 2 mm. Since a generic ventricle current-dipole model is used, this method does not require high-resolution contrast cardiac CT images. Anatomical CT images show the shape and orientation of ventricles are good enough for the registration purpose. Thus, we reduce patients’ burden by avoiding injecting contrast into the body. Training and testing of CNNs could be done off-line prior to the EP study and it generally takes about 20 minutes. The total analysis time including building the boundary element model, registration of the ventricular model, calculating the leadfield between electrodes and ventricular model, and training and testing CNNs would not be longer than 2 hours in a 64-bit operating system with 3.40 GHz Intel i7 processor. Once CNNs have been trained, it would take 0.2 s to calculate the source location given QRS complexes from 12-lead ECGs. Other than the previous methods which requires calculating statistical features from 12-lead ECGs, some expertise of recognizing patterns from 12-lead ECGs, and are usually limited in the types of ventricular arrhythmias, the method we present here is easy to implement, relieves the burden on electrophysiology specialists, and finally helps guide ablation procedure by providing potential source locations throughout the ventricles.

Limitations

Because it is a single-site pacing ventricle current-dipole model, this method is not applicable to multisite excitation activities and reentry VT. The sources of localization errors mainly come from two places: one is the registration between the ventricular model and patient’s heart, the other is the registration of 12-lead electrodes. While the latter can be reduced by digitizing more anatomical landmarks to help the registration of electrodes, the former is somehow unavoidable because we use a generic ventricular model. In the future, we could employ a personalized cardiac electrophysiology model as have been used in cardiac electrical imaging studies [36]-[43][47] to overcome the first source of localization errors.

V. Conclusion

We have proposed a novel method to localize the site of origin of premature ventricular contractions from 12-lead ECG using convolutional neural networks and a realistic anisotropic ventricle computer model. We have evaluated our method under various numerical experiments, and achieved good overall performance. By applying it to real data in a group of 9 PVC patients, we have shown the capability of our method to target the potential ablation site in premature ventricular contractions patients. This work suggests a new approach for cardiac source localization of origin of arrhythmias using only the 12-lead ECG by means of CNN, and may have important applications for future real-time monitoring and localizing origins of cardiac arrhythmias guiding ablation treatment.

Figure 6.

Results of 9 PVC patients. The right y axis represents the accuracy and average precision rate of the trained Segment CNN and Epi-Endo CNN. And the left y axis shows the average localization error of 10 PVCs from each of 9 patients (blue bars). The orange bars represent the median registration error between the general model and patient’s heart geometry. On the bottom, x axis is the noise level estimated from 12-lead ECGs and is also the noise level we trained and tested the CNNs by adding Gaussian white noise.