Modeling Keratinocyte Wound Healing Dynamics: Cell-cell Adhesion Promotes Sustained Collective Migration

Abstract

The in vitro migration of keratinocyte cell sheets displays behavioral and biochemical similarities to the in vivo wound healing response of keratinocytes in animal model systems. In both cases, ligand-dependent Epidermal Growth Factor Receptor (EGFR) activation is sufficient to elicit collective cell migration into the wound. Previous mathematical modeling studies of in vitro wound healing assays assume that physical connections between cells have a hindering effect on cell migration, but biological literature suggests a more complicated story. By combining mathematical modeling and experimental observations of collectively migrating sheets of keratinocytes, we investigate the role of cell-cell adhesion during in vitro keratinocyte wound healing assays. We develop and compare two nonlinear diffusion models of the wound healing process in which cell-cell adhesion either hinders or promotes migration. Both models can accurately fit the leading edge propagation of cell sheets during wound healing when using a time-dependent rate of cell-cell adhesion strength. The model that assumes a positive role of cell-cell adhesion on migration, however, is robust to changes in the leading edge definition and yields a qualitatively accurate density profile. Using RNAi for the critical adherens junction protein, α-catenin, we demonstrate that cell sheets with wild type cell-cell adhesion expression maintain migration into the wound longer than cell sheets with decreased cell-cell adhesion expression, which fail to exhibit collective migration. Our modeling and experimental data thus suggest that cell-cell adhesion promotes sustained migration as cells pull neighboring cells into the wound during wound healing.

1. Introduction

Collective cellular migration is a critical component of many biological processes, including embryo development[27], tissue repair [25], and tumorigenesis [1]. A group of cells is considered to be migrating collectively when neighboring cells adopt similar migration directions. In many cases of collective migration, neighboring cells are physically linked through some form of cell-cell junction [12]. The exact role of these cell-cell junctions has not been identified in this process, nor is it clear how temporal regulation of these junctions may influence the migration behavior of a collectively migrating group of cells. To date, cell-cell adhesion is believed to act as a component for cell-cell coupling during epithelial migration [17], but has also been shown experimentally to affect cell migration both positively [13, 15] and negatively [12, 15] in different situations. However, the majority of previous mathematical models of cell migration assume that cell-cell adhesion affects cell migration negatively [1, 2, 19]. In this study, we investigate the role of cell-cell adhesion during in vitro keratinocyte wound healing.

During the re-epithelialization phase of wound healing in mammalian skin, the migration of both fibroblasts and keratinocytes is required to reestablish the physically disrupted barrier between the organism and the surrounding environment [9]. In this process, collective migration of layers of keratinocytes that are physically linked through adherens junctions allows for the completion of wound healing and reformation of the epidermis [17]. Adherens junctions are composed of E-cadherin, α- and β- catenin, and are bound to the actin cytoskeleton through the adaptor protein vinculin, which binds α-catenin to filamentous actin [12, 14, 22]. Thus, adherens junctions serve as a bond between both the plasma membranes and actin cytoskeletons of adjacent cells.

Our experimental system of artificially constructed sheets of spontaneously immortalized human keratinocyte (HaCaT) cells (described previously in [7]) exhibits many similarities to in vivo keratinocyte behavior. These sheets of physically connected cells migrate into a wound area in response to epidermal growth factor (EGF) treatment in the same way that multiple layers of keratinocyte layers migrate during in vivo wound healing. Whereas fibroblasts secrete EGFR ligands in vivo [39], addition of exogenous EGF allows us to stimulate this keratinocyte migration into the wound. The stimulatory effect of EGF treatment on cell migration in this system is demonstrated in Figure 1.1, where we have displayed the leading edge propagation of untreated (denoted as mock) and EGF-treated keratinocyte sheets. The EGF-treated cell sheets migrate more than three times as far as the mock cell sheets after 35 hours.

Figure 1.1:

Mean leading edge propagation of mock (black dashed line in blue strip) and EGF (black line in red strip) experiments between 0 and 35 hours. Our leading edge computation finds where the normalized cell sheet profile reaches a certain value and is discussed in Section 2.3. The value used in this figure is 0.3. The total height of the colored strips correspond to two standard deviations of the leading edge data over time.

A plethora of recent quantitative studies have analyzed in vitro wounding assays to investigate aspects of collective cell migration for various cell types [3, 4, 6, 24, 32, 33, 34, 36]. For example, the continuum model developed in [3] investigated how wound area, shape, and aspect ratio influence gap wound healing as a means to improve predicted wound healing times in intestinal enterocyte cells [4]. In this current study, we investigate the role of cell-cell adhesion on collective cell migration during in vitro wound healing assays of keratinocyte cell sheets. To do so, we develop and compare two competing mathematical models to describe how cell sheets migrate into the wound. Both models are nonlinear diffusion equations based on assumptions of how cell-cell adhesion influences the space filling response of cells to a wound. Our first model (Model H) assumes cell-cell adhesion hinders migration into the wound through a drag force, while the other model (Model P) assumes cell-cell adhesion promotes this migration with a pulling force. We simulate both models with time-dependent rates of cell-cell adhesion to accurately fit the leading edge propagation of experiments from our model system. Model P is more robust than Model H to changes in the definition of the leading edge, so we determine it to be an appropriate model of keratinocyte migration during wound healing. We also show that it can reliably predict leading edge propagation from our experimental system.

Performing the same experimental protocol on cell sheets with decreased α-catenin expression demonstrates that cell sheets with weakened cell-cell junctions initially enter the wound area rapidly but do not display collective migration and are unable to maintain migration into the wound. Intact adherens junctions thus allow the cell sheet to sustain the wound healing response for long periods of time through collective migration. The agreement between sheet migration behavior in wild-type sheets and model P simulations, in addition to the inability of cell sheets with decreased α-catenin expression to maintain migration, leads us to conclude that cell pulling, which is mediated by cell-cell adhesion, promotes sustained collective migration during wound healing.

In Section 2, we present our two model derivations based on different assumptions for the role of cell-cell adhesion on cell migration. In Section 3, we demonstrate how both models can fit experimental leading edge propagation data, but that Model P is robust to changes in the leading edge dehnition. We then use keratinocyte sheets with decreased α-catenin expression to demonstrate that cell-cell adhesion is needed to maintain a sustained wound healing response. We discuss our conclusions in Section 4 and discuss the implications of these results as well as plans for future work in Section 5.

2. Model Development

To investigate the role of cell-cell adhesion on wound healing, we develop two contrasting models in Section 2.1. Model H assumes that cell drag hinders migration, while Model P assumes that cell pull promotes migration. In Section 2.2, we discuss the data collection procedure. In Section 2.3, we discuss our parameter estimation method.

2.1. Nonlinear Diffusion Models

Let u(t, x) denote the normalized cellular sheet density at location x and time t. We first discretize our solution domain with a uniform grid for both time and space, i.e., we set x_i = x_min + iΔx, i = 0,…,M − 1 and t_j = jΔt, j = 0,…,N − 1, where M and N denote the number of spatial and time points used, respectively. We simplify notation by writing the cell density at a fixed location over time as u_i = u(t, x_i).

Similar to [2], we first define discrete transition rates for our two models and then derive their continuum limits. The transition rate, denoted ${\tau }_i^{+}$, is the rate at which u_i (the cell density at location x_i) will move forward to the location x_i+1. Both models incorporate two terms in their transition rates that denote space-filling migration into the wound and the effect of cell-cell adhesion on this migration. For Model H, in which cell-cell adhesion hinders migration, we denote the transition rate ${\tau }_{i,H}^{+}$ as:

$${\tau }_{i,H}^{+}=\frac{D(1-u_{i+1})(1-\alpha u_{i-1})}{\Delta x^2}$$ (2.1)

where D denotes the rate of cell diffusion and the first term (1 − u_i+1) represents space-filling migration of the cell sheet (i.e., the cell density will migrate towards lower density areas). The parameter α denotes the rate of cell-cell adhesion, and thus the second term (1 – αu_i−1) in Equation (2.1) represents the neighboring density in the direction opposite migration decreasing the transition rate. In this scenario, strong physical connections to other cells will hinder cell migration, as the added weight of other cells provides a drag force that impedes migration into the wound. The transition rates ${\tau }_{i-1,H}^{+},{\tau }_{i,H}^{-}$, and ${\tau }_{i+1,H}^{-}$ are all defined analogously in Table E.6 in the appendix (${\tau }_i^{-}$ denotes the transition rate of u_i moving from position x_i to x_i−1).

We similarly define ${\tau }_{i+P}^{+}$ for model P, in which cell-cell adhesion promotes migration, as:

$${\tau }_{i,P}^{+}=\frac{D(1-u_{i+1})(1+\alpha u_{i+1})}{\Delta x^2}$$ (2.2)

where the first term again denotes space-filling migration, and the second term denotes cells located in the direction of migration increasing the transition rate. In this scenario, strong physical connections to other cells will promote migration as cells are pulled forward with the cells migrating in front of them. The transition rates ${\tau }_{i-1,P}^{+},{\tau }_{i,P}^{-}$, and ${\tau }_{i+1,P}^{-}$ are also given in Table E.6 in the appendix.

Given these transition probabilities, we derive the continuum limit by setting the time derivative of u_i equal to the flux into and out of x_i by:

$$\frac{d{u}_i}{dt}={\tau }_{i-1}^{+}{u}_{i-1}+{\tau }_{i+1}^{-}{u}_{i+1}-({\tau }_i^{+}+{\tau }_i^{-})u_i$$ (2.3)

and taking the limit as Δx → 0⁺. We follow the steps of [2] and derive the continuum limit for Model H as

$$u_t={\left(\left(D+3\gamma {\left(u-2/3\right)}^2-4/3\gamma \right)u_x\right)}_x$$ (2.4)

where γ = Dα represents our new rate of cell-cell adhesion. We note that backwards diffusion may occur with Equation (2.4) if 4γ > 3D and address this further in Section 2.3. In the appendix, we derive the continuum limit for Model P to be

$$u_t={\left(\left(D+\gamma u^2\right)u_x\right)}_x$$ (2.5)

where again γ = Dα. This diffusion term is always positive, so there is no potential for backwards diffusion to occur.

Adherens junctions change dynamically in response to a cell’s environmental cues, such as the presence of EGF and wound induction [12]. We will investigate time-dependent rates of cell-cell adhesion (denoted as Γ(t)) in response to EGF treatment, as previous studies have suggested using time-dependent parameters for modeling cell migration in response to EGF treatment [21]. Because the cell sheets transition from stationary to highly motile after wound induction and EGF treatment, we consider decreasing Γ(t) terms for Model H, as a decrease in cell drag should allow the cell sheet to increase its rate of migration. Similarly, we consider increasing Γ(t) terms for Model P. We write our final mathematical models as:

$$u_t={\left(\left(D+3\Gamma (t){\left(u-2/3\right)}^2-4/3\Gamma (t)\right)u_x\right)}_x(\text{Model\hspace{0.17em}H})$$ (2.6)

and

$$u_t={\left(\left(D+\Gamma (t)u^2\right)u_x\right)}_x,(\text{Model\hspace{0.17em}P})$$ (2.7)

and we will present the terms considered for Γ(t) in Section 3.1. We note that cell proliferation is negligible in our experimental system, as demonstrated in the appendix, so terms for proliferation have not been included in our model. We briefly review the two models, along with their terms and assumptions in Table 1. A list of all parameters used throughout this study is also given in Table 2.

Table 1:

Summary of equations and assumptions relating to Models H and P.

Model features	H		P
Cell-cell adhesion	Hinders migration		Promotes migration
Treatment	mock	EGF	mock	EGF
Γ(t)	γ1	γ1 + γ2 (1 − t/tfinal)	γ1	γ1 + γ2t\tfinal
Equation	(2.4)	(2.6)	(2.5)	(2.7)

Table 2:

List of parameters for the two models. Note that the fit values for different simulations are given in Tables 3 and 5.

Parameter	Description (units)
D	Baseline rate of diffusion (microns2/hr)
γ1	Baseline cell-cell adhesion rate between adjacent cells (microns2/hr)
γ2	Response of the rate of cell-cell adhesion to EGF treatment (microns2/hr2)

If w is the site of the wound, we use an indicator function for our initial condition that is set equal to 1 for x < w and 0 for x > w. This initial condition represents a high density behind the wound and no initial cell density in the wound area. Note that in experimental videos, we only observe a 3.24 mm × 3.24 mm field of view, whereas the experimental domain is actually 7 mm long and 5 mm wide. We accordingly use zero Neumann boundary conditions 4.86 mm behind and in front of the held of view to simulate no flux conditions at the walls of the well plate.

2.2. Description of experiments

In vitro wound healing experiments, as previously described in [7], begin with the growth of a confluent monolayer of cells to a density of about 4,000 cells/mm² in a well plate. After 24 hours, half of the cell population on one side of the well plate is manually removed with a pipette tip. EGF-treated populations are globally treated with a concentration of 100 nM of EGF. An ImageXpress MicroXL high throughput wide-field fluorescence microscope was used to image the cell populations every 20 minutes for 48 hours. We performed both mock and EGF experiments in triplicate¹. In Section 3.3, we perform the same protocol in triplicate on a cell line with decreased α-catenin expression using RNAi.

2.3. Parameter Estimation

In order to fit our model simulations to data on wound healing, we will use an inverse problem procedure to estimate the parameter vector $\overrightarrow{q}={[D,{\gamma }_1,{\gamma }_2]}^T$ for both models for mock and EGF data. We do so by comparing the locations of the leading edge for both the experimental data and model simulations, as has been done in previous quantitative wound healing studies [20, 21, 25, 37]. In the literature, there are many different definitions of the leading edge [7, 20, 25]. Similar to [25], we denote the leading edge as where the sheet profile reaches a certain value. In Figure 2.1, we have included some typical video snapshots along with their resulting data profile and leading edge designation. To calculate the data profile, we sum over the vertical axis for each image matrix and then normalize by the largest density in the population over each time step. We then calculate the leading edge by finding the location where the leading edge density is equal to some value, β, and denote its location over time as ${\mathcal{l}}_{data}^{\beta }(t)$. In Figure 2.1, we display this calculation for β = 0.3 but will consider β = 0.1, 0.2, 0.3 throughout this study. Note that the cell sheets move right as a coherent whole even through the leading edge is not completely vertical. Given a model simulation u(t,x), we calculate the leading edge for a relative density of β in a similar manner by approximating the location x̄ such that u(t, x̄) = β. We denote the leading edge of a model simulation resulting from a vector of parameter values $\overrightarrow{q}$ by ${\mathcal{l}}_{\mathrm{mod}el}^{\beta }(t,\overrightarrow{q})$.

Figure 2.1:

Experimental snap shots (top row) of the experiment at t = 0 and 20 hours and their resulting data profiles (bottom row), whose calculation is described in the text. The dashed lines against the snapshots denote the calculated leading edge location, and the thin lines denote one sample standard deviation. Note that there is no standard deviation at t = 0 because the leading edge for all experiments starts at 0. The dots depicted against the data profiles in the bottom row denote the calculated value for ${\mathcal{l}}_{data}^{0.3}(t)$.

As a means to estimate the true $\overrightarrow{q}$ using our models, we will implement an inverse problem in which we minimize a cost function between the model and data leading edge locations. In this work, we will use the cost function given by an ordinary least squares estimate:

$$J(\overrightarrow{q})={\displaystyle \sum }_{j=1}^N{\left|{\mathcal{l}}_{\mathrm{mod}el}^{\beta }(t_j,\overrightarrow{q})-{\mathcal{l}}_{data}^{\beta }(t_j)\right|}^2,$$

where ${\left\{t_j\right\}}_{j=1}^N$ are the time points sampled and N is the number of time points considered. Note that the experiment is performed for 48 hours, but we only compare the model to data between 10–35 hours for EGF experiments because there is an initial lag period before cell migration, and some leading edges run off the field of view after 35 hours. For mock experiments, we compare the models and data after t = 20 hours, because there is a longer initial lag period and cells do not run off the field of view. For example, in Figure 2.2 the blue rectangle depicts when we compare the model and data for the cost function. To find the $\widehat{q}$ estimate that minimizes the cost function, we use the Nelder-Mead algorithm as implemented in MATLAB’s fminsearch command. For Model H simulations, we use a barrier function to restrict 4D > 3(γ₁ + γ₂) to ensure that backwards diffusion does not occur (as mentioned in Section 2.1).

Figure 2.2:

Example of fitting the leading edge propagation of a model simulation (blue curve) to experimental leading edge propagation data (red dots) over time. Model P has been used here for illustration. The blue shaded region denotes where we compare the model to the data.

3. Results

We now investigate the performances of Models H and P in describing keratinocyte migration during wound healing. We determine the form of the time-dependent rate of cell-cell adhesion, Γ(t), for mock and EGF experiments in Section 3.1 and then fit ${\mathcal{l}}_{\mathrm{mod}el}^{\beta }(t,\overrightarrow{q})$ to ${\mathcal{l}}_{data}^{\beta }(t)$ for EGF experiments for β = 0.1, 0.2, 0.3 with Models H and P to investigate how the models respond to changes in β. Model P is more robust than Model H to changes in the leading edge definition, so we declare it a more appropriate model. We demonstrate the predictive capability of Model P in Section 3.2. Inspired by the results of Section 3.1, we perform the same experimental assay (as described in Section 2.2) on cell sheets with decreased α-catenin expression in Section 3.3 and observe that these sheets are unable to mediate a sustained wound healing response without intact adherens junctions.

3.1. Parameter estimation

Models H and P can both accurately ht ${\mathcal{l}}_{data}^{0.2}(t)$ for mock data with a constant rate of cell-cell adhesion (Γ(t) ≡ γ₁), as depicted in Figure 3.1. We used the parameter estimation method outlined in Section 2.3 to obtain the estimate values $\widehat{q}={[\widehat{D},{\widehat{\gamma }}_1]}^T$ for these simulations. The resulting estimate values for both models are depicted in Table 3. Note that the two models use very different simulations to achieve these similar leading edge locations: Model H uses large $\widehat{D}$ and ŷ₁ estimates while Model P uses a large ŷ₁ estimate and a very small $\widehat{D}$ estimate.

Figure 3.1:

Fitting the model leading edge propagation to mean experimental leading edge propagation data. The red region denotes a 95% confidence interval for the experimental data, the green dashed line denotes the leading edge propagation of Model H, and the solid blue line denotes the leading edge propagation of Model P. A constant rate of cell-cell adhesion is used in both model simulations shown.

Table 3:

Mock $\widehat{q}={[\widehat{D},{\widehat{\gamma }}_1]}^T$ estimate table when fitting ${\mathcal{l}}_{data}^{0.2}(t,\overrightarrow{q})$ to ${\mathcal{l}}_{data}^{0.2}(t)$ for Models H and P. Estimates are calculated by fitting the models to the mean leading edge distance traveled and the standard deviation is calculated from the standard deviation of the three estimates used to fit the individual data sets.

β	Model H parameters		Model P parameters
	D (μm2/hr)	γ1 (μm2/hr)	D (μm2/hr)	γ1 (μm2/hr)
0.2	32300 ± 600	21300 ± 400	10.8 ± 0.2	20000 ± 3300

Because adherens junctions are dynamically changing in response to their environment, we consider four simple terms for the rate of cell-cell adhesion over time in response to EGF treatment: constant, linear, quadratic, and square root. The exact forms for each are given in Table 4. Note that the Γ(t) terms we consider for model H decrease with time whereas the Γ(t) terms for model P increase with time, as these match the assumptions discussed in Section 2.1. Best-fit simulations for Models H and P to ${\mathcal{l}}_{data}^{0.2}(t)$ using these four different Γ(t) terms are depicted in Figure 3.2. As opposed to mock data, both models are unable to match the leading edge propagation data with a constant rate of cell-cell adhesion, as they overestimate the experimental leading edge location from t = 10 − 25 hours, and then underestimate the leading edge location afterwards. The linear term for Γ(t) appears to be a suitable candidate, as both model fits stay within the 95% confidence interval of the data for the majority of the experiment. This linear cell-cell adhesion term may be indicative of cells constantly increasing or decreasing their surface display of adherens junctions over time in response to EGF treatment. One of the two models fails to fit the experimental data well with the quadratic or square root terms, so we decide to further investigate the two models with a linear rate of cell-cell adhesion throughout the rest of this study.

Table 4:

Different terms considered for the time-dependent rate of cell-cell adhesion, Γ(t), when fitting Models H and P to experimental EGF data. The parameter γ₁ denotes a baseline rate of cell-cell adhesion, where γ₂ denotes the response of the rate of cell-cell adhesion to EGF treatment. Models H and P are fit to experimental EGF data using all four terms in Figure 3.2.

Γ(t)	Model H	Model P
constant	γ1	γ1
linear	γ1 + γ2 (1 − t/tfinal)	γ1 + γ2t/tfinal
quadratic	γ1 + γ2 (1 − t/tfinal)2	γ1 + γ2(t/tfinal)2
square root	γ1 + γ2 (1 − t/tfinal)1/2	γ1 + γ2(t/tfinal)1/2

Figure 3.2:

Determining a suitable form for the time-dependent rate of cell-cell adhesion, Γ(t), by fitting ${\mathcal{l}}_{model}^{0.2}(t,\overrightarrow{q})$ to ${\mathcal{l}}_{data}^{0.2}(t)$ We plot the best-fit simulations,${\mathcal{l}}_{model}^{0.2}(t,\widehat{q})$, for Models H and P with different rates of cell-cell adhesion in each frame. The four rates of cell-cell adhesion considered are constant (top left), linear (top right), square root (bottom left), and quadratic (bottom right). Each term is given in Table 4. The red region in each figure denotes a 95% confidence interval for the experimental data, the green dashed line denotes the leading edge propagation of Model H, and the solid blue line denotes the leading edge propagation of Model P.

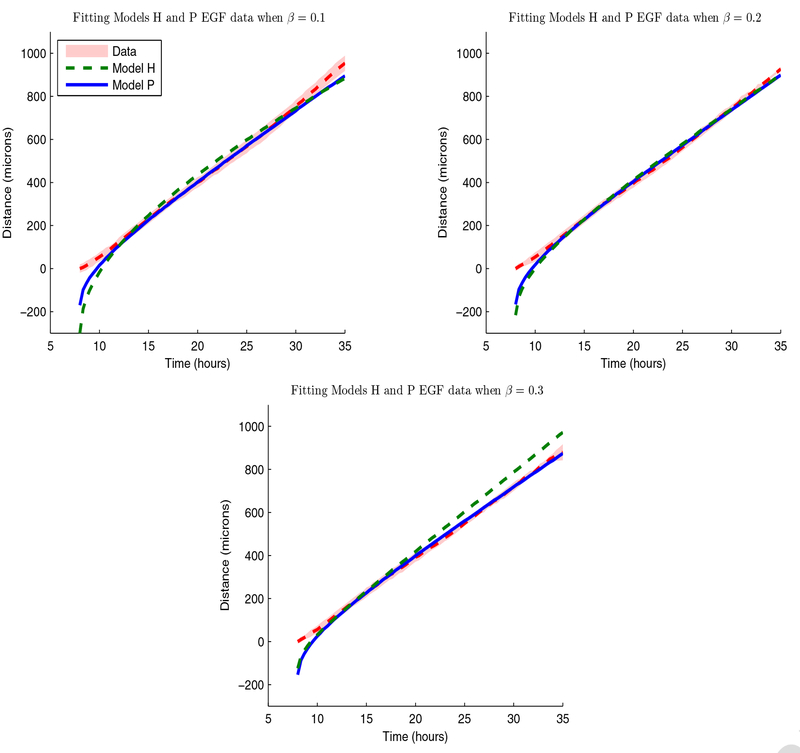
In Figure 3.3, we depict best-fit ${\mathcal{l}}_{model}^{\beta }(t,\widehat{q})$ simulations for Models H and P with a linear term for Γ(t) to mean leading edge propagation data, ${\mathcal{l}}_{data}^{\beta }(t)$ for β = 0.1, 0.2, and 0.3. While both models can fit ${\mathcal{l}}_{data}^{0.2}(t)$ very well, we observe that model H overestimates ${\mathcal{l}}_{data}^{0.1}(t)$ from t = 15 to 25 horns and fails to accurately match ${\mathcal{l}}_{data}^{0.3}(t)$ after t = 20 hours. Model P provides an excellent match to ${\mathcal{l}}_{data}^{0.3}(t)$ but underestimates ${\mathcal{l}}_{data}^{0.1}(t)$ after t = 30 hours. We present the best-fit parameter estimates $\widehat{q}={[\widehat{D},{\widehat{\gamma }}_1,{\widehat{\gamma }}_2]}^T$ when fitting to ${\mathcal{l}}_{data}^{\beta }(t)$ with a linear Γ(t) term in Table 5 for β = 0.1, 0.2, 0.3. We observe a wide range of $\widehat{q}$ estimates needed for Model H to fit ${\mathcal{l}}_{data}^{0.1}(t)$, ${\mathcal{l}}_{data}^{0.2}(t)$, and ${\mathcal{l}}_{data}^{0.3}(t)$ in comparison to Model P. For Model H, $\widehat{D}$ varies 347%, ${\widehat{\gamma }}_1$ varies 160%, and ${\widehat{\gamma }}_2$ varies 882%. For Model P, $\widehat{D}$ varies 146%, ${\widehat{\gamma }}_1$ varies 165%, and ${\widehat{\gamma }}_2$ varies 30%. Model H estimates thus appear more sensitive to changes in the leading edge definition than Model P estimates. We also note that both models use different types of simulations to fit the experimental data, as Model H yields large estimate values for $\widehat{D}$, ${\widehat{\gamma }}_1$, and ${\widehat{\gamma }}_2$ whereas Model P uses small estimate values for $\widehat{D}$ and ${\widehat{\gamma }}_1$ and large estimate values for ${\widehat{\gamma }}_2$. These differences in the parameter estimates prompted us to investigate the model profiles that led to these simulations.

Figure 3.3:

Best fits of ${\mathcal{l}}_{model}^{\beta }(t,\overrightarrow{q})$ to ${\mathcal{l}}_{data}^{\beta }(t)$ for β = 0.1 (top left), 0.2 (top right), and 0.3 (bottom left) when using a linear term for Γ(t) for Model H (green dashed line) and Model P (solid blue line). The red shaded region denotes a 95% confidence region for the experimental data.

Table 5:

EGF $\widehat{q}={[\widehat{D},{\widehat{\gamma }}_1,{\widehat{\gamma }}_2]}^T$ estimate table when fitting ${\mathcal{l}}_{model}^{\beta }(t,\overrightarrow{q})$ to ${\mathcal{l}}_{data}^{\beta }(t)$ for Models H and P for β = 0.1, 0.2, 0.3. Estimates are calculated by fitting the models to the mean leading edge distance traveled and the standard deviation is calculated from the sample standard deviation of the three estimates used to fit the individual data sets.

β	Model H			Model P
	$\widehat{D}$	${\widehat{\gamma }}_1$	${\widehat{\gamma }}_2$	$\widehat{D}$	${\widehat{\gamma }}_1$	${\widehat{\gamma }}_2$
0.1	32400 ± 1100	13100 ± 200	10300 ± 700	6·5 ± 13	40 ± 300	152600 ± 22500
0.2	73100 ± 2700	20500 ± 600	32900 ± 1500	16 ± 4	50 ± 1500	169900 ± 9400
0.3	144800 ± 9800	7900 ± 700	100700 ± 1100	13 ± 2	20 ± 400	198900 ± 12600
% change	347%	160%	882%	146%	165%	30%

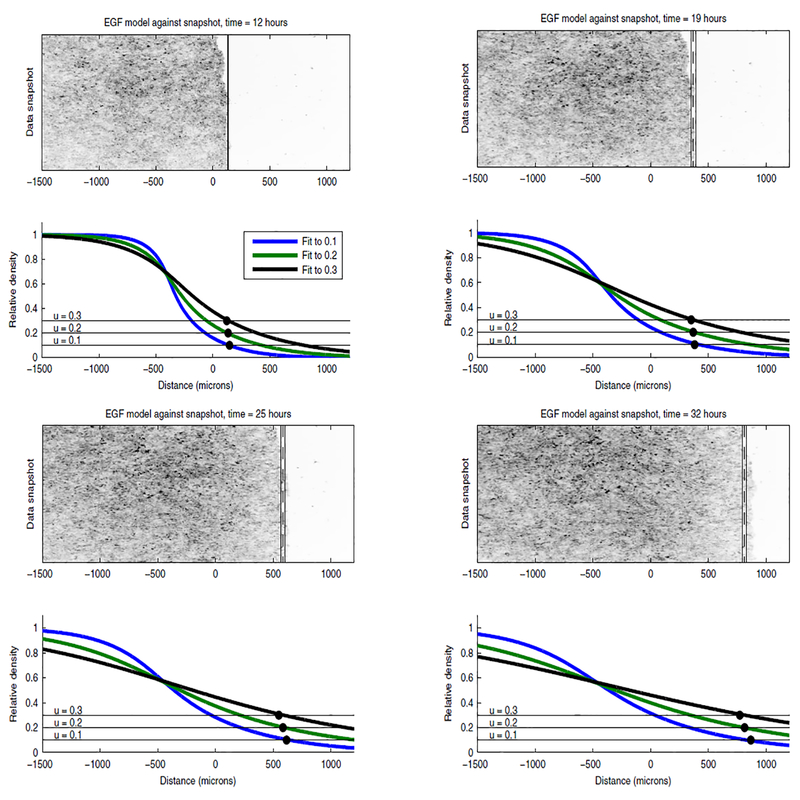
We depict the three model profiles that best fit ${\mathcal{l}}_{model}^{\beta }(t,\overrightarrow{q})$ to ${\mathcal{l}}_{data}^{\beta }(t)$ for β = 0.1, 0.2, 0.3 for Models H and P against experimental snapshots over time in Figures 3.4 and 3.5, respectively. Model H exhibits rapid expansion into the wound, which is likely due to its high $\widehat{D}$ estimate values. This rapid expansion causes Model H to predict a high cell density in areas that are empty in the experimental snapshot when fitting to ${\mathcal{l}}_{data}^{0.3}(t)$ (such as at x = 1000 microns when t = 25 hours) and to predict a low cell density in areas that appear confluent when fitting to ${\mathcal{l}}_{data}^{0.1}(t)$ (such as at x = 0 when t = 25 hours). Contrast Model H’s rapid expansion into the wound with the limited local expansion of Model P’s profile in Figure 3.5. Model P maintains a sharp front that propagates into the wound as a coherent unit over time. The sharp front allows Model P to qualitatively predict high and low density areas of the cell sheet well, and its profile simulations do not change significantly when fitting between ${\mathcal{l}}_{data}^{0.1}(t)$,${\mathcal{l}}_{data}^{0.2}(t)$or ${\mathcal{l}}_{data}^{0.3}(t)$.

Figure 3.4:

Model H simulations against experimental snapshots. The bottom frame depicts Profile plots of Model H that have been fit to ${\mathcal{l}}_{data}^{\beta }(t)$ for data set 3 when β = 0.1 (blue), 0.2 (green), 0.3 (black). The calculated value for ${\mathcal{l}}_{data}^{0.2}(t)$ depicted against the experimental snap shot with a dashed black line and the solid thin lines denote one standard deviation of the data. Against the model profile, we’ve depicted the lines u = 0.1, 0.2, 0.3 for easy identification of the model leading edge location. The black dots denote the experimental leading edge locations.

Figure 3.5:

Model P simulations against experimental snapshots. The bottom frames depicts Profile plots of Model P that have been fit to ${\mathcal{l}}_{data}^{\beta }(t)$ for data set 3 when β = 0.1 (blue), 0.2 (green), 0.3 (black). The calculated value for ${\mathcal{l}}_{data}^{0.2}(t)$ is depicted against the experimental snap shot with a dashed black line and the solid thin lines denote one standard deviation of the data. Against the model profile, we’ve depicted the lines u = 0.1, 0.2, 0.3 for easy identification of the model leading edge location. The black dots denote the experimental leading edge locations.

Due to Model P’s robustness to different leading edge definitions and its ability to qualitatively match experimental cell sheets, we suggest that Model P is a suitable model for keratinocyte migration during wound healing.

3.2. Fitting and predicting of individual data sets

We perform a type of cross validation as a means to demonstrate the predictive capacity of Model P. We do so by fitting ${\mathcal{l}}_{model}^{\beta }(t,\overrightarrow{q})$ from Model P simulations to ${\mathcal{l}}_{data}^{\beta }(t)$ for each data replicate and use these individual best-fit simulations to predict the other data replicate. The three leading edge replicates for ${\mathcal{l}}_{data}^{0.2}(t)$ are depicted in the top left frame of Figure 3.6. Because the data sets begin their wound healing response at different times, we predict a data set from a fit simulation by aligning their leading edge locations at t = 15 hours (after all data sets have started migrating).

Figure 3.6:

Using Model P fits to individual data sets to predict independent data sets. In the top left frame, we depicted experimental data for three replicates of wild type cell sheets in response to EGF treatment. In the top right frame, we fit Model P to data set 1. In two bottom frames, we use this Model P fit to predict the other two data sets by aligning the model simulation and data at t =15 hours. Leading edge computation here was done for β = 0.2. Examples for β = 0.1 and 0.3 are given in the appendix.

In the top right frame of Figure 3.6, we show the best-fit Model P simulation to ${\mathcal{l}}_{data}^{0.2}(t)$ for data set 1, and in the the bottom rows, we demonstrate how this simulation can accurately predict ${\mathcal{l}}_{data}^{0.2}(t)$ for data sets 2 and 3. We observe similar results after fitting to the other data sets and after fitting to and then predicting ${\mathcal{l}}_{data}^{0.1}(t)$ and ${\mathcal{l}}_{data}^{0.3}(t)$. Examples of fits and predictions to ${\mathcal{l}}_{data}^{0.1}(t)$ and ${\mathcal{l}}_{data}^{0.3}(t)$ are given in the appendix. We thus see that fit Model P simulations can reliably predict independent data sets given their leading edge location at t = 15 hours.

3.3. Decreasing cell-cell adhesion levels with RNA interference

We now investigate how wound healing is affected in a cell sheet with reduced cell-cell adhesion expression by performing RNA interference for α-catenin, a critical cell-cell adhesion protein [12, 14]. We denote these experiments as sh α-catenin cell sheets² and perform the same experimental protocol described in Section 2.2 in triplicate, in which a scratch wound is created with a pipette tip, and the sheet is treated with EGF to stimulate migration. We depict one sh α-catenin sheet against a wild type sheet in Video 1 of the supplementary material and observe that the leading edge of both experiments move at a similar rate. As another measure of wound healing, however, we consider an “area of cell invasion,” and define a wound healing ratio by:

$$\text{wound healing ratio}=\frac{\#\text{\hspace{0.17em}cells in area of cell invasion}}{\text{confluent cell count}}.$$ 3.1

The area of cell invasion is defined by the rectangle whose height spans from the initial leading edge location to 1200 μm into the wound and whose width is defined by the field of view. We count the number of cells that enter this area of invasion over time using imageJ’s FindMaxima function. To calculate the confluent cell count, we again use the FindMaxima function in a rectangle of the same size in the back of the sheet and use the largest cell count found in this region over the course of the experiment. This value does not change significantly between experiments. For an analogous wound healing ratio for model simulations, we calculate $\underset{0}{\overset{1200}{{\displaystyle \int }}}u(t,x)dx$ over time using Simpson’s rule, where x ∈ [0,1200] denotes a location in the area of invasion, and normalize this calculation by its final time point. This calculation measures the total cell mass in the area of invasion over time.

The experimental wound healing ratios over time are depicted for wild type and sh α-catenin cell sheets in Figure 3.7 with a 95% confidence interval of the wound closure ratio depicted in the blue and green shaded regions, respectively. The experimental sh α-catenin cell sheets initially migrate vigorously into the wound but are unable to maintain this response. The constantly-increasing wild type cell sheet wound healing ratio passes the sh α-catenin sheet wound healing ratio around t = 30 hours. We also depict the model wound healing ratio in the solid blue line in Figure 3.7 from the best-fit model P simulation to ${\mathcal{l}}_{data}^{0.2}(t)$, which recapitulates the constantly-increasing experimental wound healing ratio well. Note that both wild type ratios have an elbow around t = 35 hours, which we expect to see because cells at the leading edge begin moving past the area of invasion.

Figure 3.7:

Comparing wild type and sh α-catenin cell sheet wound healing. Top : We compare experimental wound closure ratios in the area of invasion (shaded regions) for wild type and sh α-catenin cell sheets using Equation 3.1. The mean experimental ratio values α-catenin sheets, respectively. The blue solid line denotes the wound healing ratio for the best-fit Model P simulation to ${\mathcal{l}}_{data}^{0.2}(t)$· Bottom: We use the Pathhnder software to display the individual cell trajectories of randomly picked cells in from experimental replicates after t = 35 hours. For each trajectory, an x indicates the cell’s initial location, and a triangle indicates the cell’s final location.

In Video 1 of the supplementary material, The sh α-catenin sheets appear to stop migrating into the wound around t = 35 hours, as demonstrated in the bottom frame of Figure 3.7, where we used the Pathfinder software to track individual cell trajectories after t = 35 hours in a thin slice of the area of invasion [8].The sh α-catenin sheets show only modest migration towards the wound, especially for cells located farther back in the cell sheet (between x = 0 and 300 microns). This lack of forward migration causes the wound healing ratio to decrease after t = 35 hours, as cells near the leading edge leave the area of invasion, but few cells in the back of the sheet migrate into the area of invasion. Compare this to the wild type sheets, which continue to migrate towards the wound for the entire 48 hours, even as cells move past the area of invasion. We thus observe that cell sheets with decreased α-catenin expression initially migrate into the wound efficiently but are unable to sustain a proper wound healing response.

4. Conclusions

In this study, we have developed two mathematical models for the migration of keratinocyte cell sheets during wound healing in response to EGF treatment. These two models are used to investigate the role of cell-cell adhesion on in vitro keratinocyte wound healing assays. Model H assumes that cell-cell adhesion hinders migration during wound healing due to a drag force, whereas Model P assumes that cell-cell adhesion promotes migration with a pulling force. Neither model is able to match experiment EGF-treated data with a constant rate of cell-cell adhesion, but adjusting the rate of cell-cell adhesion to be linear with time allows both models to fit the data well. In its best-fit simulations, Model H exhibits rapid initial expansion into the wound, whereas Model P has a sharp front that propagates into the wound. Model P maintains consistent $\widehat{q}={[\widehat{D},{\widehat{\gamma }}_1,{\widehat{\gamma }}_2]}^T$ estimates and profile shapes for different leading edge definitions, while Model H varies drastically in both of these aspects. We accordingly propose that Model P appropriately describes keratinocyte migration during wound healing assays, suggesting that keratinocytes use cell-cell adhesion to pull other cells forward during wound healing. The sharp profile front of Model P suggest that cell junctions may also hold cells together to limit drastic changes in density throughout the cell sheet.

We perform the same experimental protocol with HaCaT cell sheets with decreased α-catenin expression. These sheets display initially high migration into the wound, but this efficient migration response can not be maintained without intact adherens junctions. The experimental wild type cell sheets exhibit constant collective migration into the wound over the entire course of the experiment. We thus conclude that cell-cell adhesion acts to hold cells in close proximity to allow migrating cells to pull their neighboring cells into the wound during in vitro keratinocyte wound healing assays.

5. Future Work

The positive effect of EGF on wound repair is well documented [9, 10, 26], however, topical EGF treatment has had only moderate effects in clinical wound repair trials [5, 38]. Effective clinical treatment of chronic wounds (such as foot ulcers in diabetic patients) with EGF will require a thorough understanding of its role during wound healing [38]. The knowledge that cell-cell adhesions promote migration through cell pulling may guide future investigations in determining methods to increase the duration and speed of cell migration during wound repair. Such endeavors will aid in developing treatments to shorten the time needed for re-epithelialization to occur or cause chronic wounds to heal.

The simple nature of our first investigation into the effects of EGF treatment on wound healing in keratinocytes leaves ample opportunities for future studies. We note that all experiments considered in this study have the same high cell density (4000 cells/mm²) and EGF concentration treatment (10 nM). Recent studies have used various forms of Fisher’s equation (initially used to model the propagation of an advantageous gene [11]) to analyze the effects of cell density and EGF concentration on invasion of the prostate cancer PC-3 cell line [18, 21]. In [18], the authors found that a linear cell diffusion term in response to cell density was suitable for less sensitive parameter estimation than a constant diffusion term. Our assumptions on cell-cell adhesion for Model P led to a quadratic cell diffusion term that increases with cell density and yields consistent parameter estimates based on different leading edge definitions.

While this study provides insight into re-epithalialization, future work should also investigate other phases of wound healing such as inflammation and tissue remodeling. Inflammation is the body’s innate response to injury while tissue remodeling occurs mostly after re-epithelialization to restore dermal integrity [9]. Tissue remodeling involves the interaction of several different cell types, such as macrophages and fibroblasts, and various cytokines and chemokines [9]. Such studies would necessitate further work into the complicated interactions of fibroblasts with the extracellular matrix (ECM), as fibroblasts synthesize and deposit ECM during migration, but the ECM also affects fibroblast migration and ECM production [39]. There is a vast literature on continuum models of haptotaxis, chemotaxis, and mechanotaxis to inform and guide such studies [30, 31, 35].

From the accuracy of Model P, and the time-dependent rate of cell-cell adhesion needed to fit experimental data, we propose that cell-cell adhesion strength increases over time during keratinocyte wound healing. Future studies may also investigate the biochemical mechanisms that influence this time-dependent cell-cell adhesion strength. For example, the mitogen-activated protein kinase (MAPK) signaling cascade is downstream of EGFR and known to stimulate cell migration [7, 16]. In [32], the propagation of EGF ligand, reactive oxygen species, and EGF’s intracellular protease (which is directly linked to activation of the MAPK signaling cascade) was modeled in madine darby canine kidney cells, though cell migration was neglected. Some recent computational studies have modeled molecular signaling processes during inflammation with kinetic and agent based models and found macrophage flux to be a key regulator of the inflammatory response [28, 29, 40]. The cytokines tumor necrosis factor-α and transforming growth factor-β (both of whose receptors are upstream of MAPK) were determined to be reliable predictors of the the development of chronic inflammation. Incorporating our cell migration model with this signal propagation model and observations on inflammation may help elucidate the interaction between the MAPK signaling cascade and cell migration.

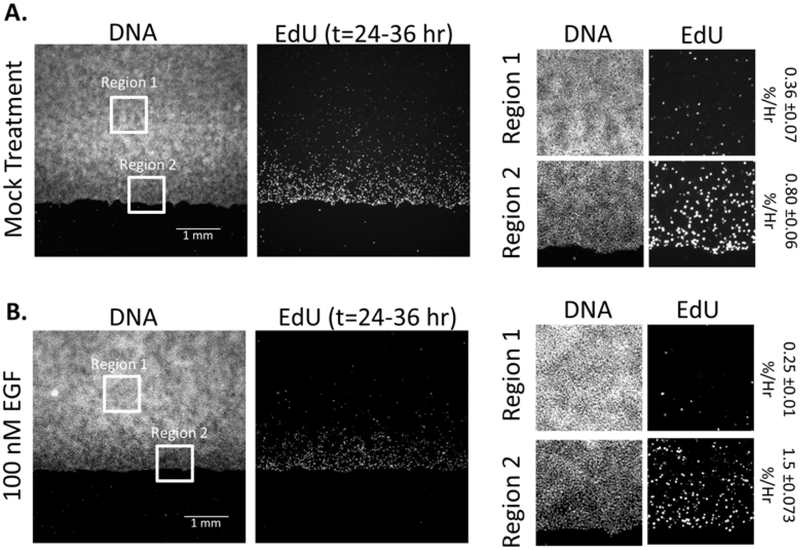
AppendixA. Cell sheets do not proliferate while migrating

In Figure A.1, we display our quantitative results of cellular proliferation during sheet migration. Sheets of HaCaT cells were labeled with Edu between t=24 and t=36 hrs post wound formation. Proliferating cells that incorporate EdU into their DNA were stained using the Click-IT EdU fluorescence labeling kit (ThermoFisher, Cl0337) and labeled and total cells were quantified by cell counting in selected regions using ImageJ. Although EGF is a potent stimulator of sheet migration between t=24 and 36 hrs, there is little difference between the quantified proliferation of Mock (A) and EGF (B) stimulated sheets, which display an average percent proliferation per hour below 1% of the population. We do note that there is a spatial distribution of proliferation in both cases, where a low level of proliferation is concentrated towards the region in close proximity to the wound.

Figure A.1:

AppendixB. Derivation of Model P

For our second model, we assume that cell-cell adhesions promote migration as leader cells pull the cells behind them forward and denote it as Model P. In this scenario, the upregulation of cell-cell adhesionpromotes migration. We now denote the forward transition rate ${\tau }_i^{+}$ of cell density u_i as

$${\tau }_{i,P}^{+}=\frac{D(1-u_{i+1})(1+\widehat{\alpha }{u}_{i+1})}{\Delta x^2},$$ (B.1)

where the first term again represent space filling, but >the second term in (Equation (B.1)) represents our second assumption in which cells located in the direction of migration (denoted u_i+1) >promote this space filling movement towards the wound by pulling on the cells behind them. We note again that >${\tau }_{i-1,P}^{+},{\tau }_{i,P}^{-}$, and ${\tau }_{i+1,P}^{-}$ are all defined analogously in Table E.6. Substituting the transition probability from (Equation (B.1)>) into Equation (2.3) yields

$$\begin{gathered} u_t=\frac{D(1-u_i)(1+\widehat{\alpha }{u}_i)u_{i-1}+D(1-u_i)(1+\widehat{\alpha }{u}_i)u_{i+1}-D((1-u_{i+1})(1+\widehat{\alpha }{u}_{i+1})+D(1-u_{i-1})(1+\widehat{\alpha }{u}_{i-1}))u_i}{\Delta x^2} \\ =\frac{D}{\Delta x^2}(u_{i-1}+\widehat{\alpha }{u}_{i-1}^2{u}_i-\widehat{\alpha }{u}_{i-1}{u}_i^2+u_{i+1}-2u_i-\widehat{\alpha }{u}_i^2{u}_{i+1}+\widehat{\alpha }{u}_i{u}_{i+1}^2) \\ =D\frac{u_{i-1}-2u_i+u_{i+1}}{\Delta x^2}+\alpha \frac{u_{i-1}^2{u}_i-u_{i-1}{u}_i^2-u_i^2{u}_{i+1}+u_i{u}_{i+1}^2}{\Delta x^2}, \end{gathered}$$ (B.2)

where we can recognize the first term on the right hand side as the standard central difference approximation to the second derivative and we have set $\alpha =D\widehat{\alpha }$. For the second term on the right hand side, we can simplify using Taylor series approximations as: $u_{i+1}\approx u_i+\Delta x\cdot {u^{\prime }}_i+\raisebox{1ex}{$\Delta x^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\cdot {u^{″}}_i,u_{i-1}\approx u_i-\Delta x\cdot {u^{\prime }}_i+\raisebox{1ex}{$\Delta x^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\cdot {u^{″}}_i$, where primes denote a spatial derivative term. Substituting these terms into the second term on the right hand side of Equation (B.2) reveals

$$\begin{gathered} u_t=D\frac{u_{i-1}-2u_i+u_{i+1}}{\Delta x^2}+\alpha \frac{2\Delta x^2{u}_i{({u^{\prime }}_i)}^2+u_i^2{u^{″}}_i\Delta x^2+\mathcal{O}(\Delta x^4)}{\Delta x^2} \\ =D{u^{″}}_i+\alpha (2u_i{({u^{\prime }}_i)}^2+u_i^2{u^{″}}_i)+\mathcal{O}(\Delta x^2) \\ =D{u^{″}}_i+\alpha (u_i^2{u^{\prime }}_i{)}^{\prime }+\mathcal{O}(\Delta x^2) \end{gathered}$$

resulting in the dimensionless continuum limit to be

$$u_t={((D+\gamma u^2)u_x)}_x,(\text{Model\hspace{0.17em}P})$$ (B.3)

where D and γ again denote the rates of cell diffusion and cell-cell adhesion, respectively.

AppendixC. Fitting and Predicting individual data sets

In Figures C.l and C.2, we depict the individual calculated experimental leading edges ${\mathcal{l}}_{data}^{0.1}(t)$ and ${\mathcal{l}}_{data}^{0.3}(t))$ for EGF experiments in the top left frames, along with the ability of both models to fit and predict this data using the parameter estimation method outlined in Section 3.2. In the top right of these figures, we demonstrate best-fit simulations of both models to one data set and in the the bottom rows, we demonstrate how this simulation can be used to accurately predict the leading edge locations of the other data sets. While we have only shown fits to one data set for both mock and EGF data, we see similar results after fitting to all three EGF data sets.

Figure C.1:

Figure C.2:

AppendixD. Numerical implementation

Note that for numerical implementation, we use a method of lines approach implemented with MATLAB’s odel5s command for time integration. For spatial discretization, we use the second order scheme for convection-diffusion equations (without convection in our case) from [23] given by

$${\dot{u}}_j(t)=\frac{P_{j+1/2}(t)-P_{j-1/2}(t)}{\Delta x}$$

where $P_{j+1/2}(t)$ is an approximation to the diffusive flux, given by

$$P_{j+1/2}(t)=\frac{1}{2}\left[Q\left(u_j(t),\frac{u_{j+1}(t)-u_j(t)}{\Delta x}\right)+Q\left(u_{j+1}(t),\frac{u_{j+1}(t)-u_j(t)}{\Delta x}\right)\right]$$

where Q(u, u_x) denotes the cellular diffusion rate.

AppendixE. Table of transition probabilities

Table E.6:

Table of transition probabilities, as discussed in Section 2.1 as a means to develop Models H and P. The transition rates for Model H denote cells in the direction opposite migration hindering migration through cell-cell adhesion, while the transition rates for Model P denote cells in the direction of migration promoting it through cell-cell adhesion.

	Model H	Model P
${\tau }_i^{+}$	$D(1-u_{i+1})(1-\alpha u_{i-1})/\Delta x^2$	$D(1-u_{i+1})(1+\alpha u_{i+1})/\Delta x^2$
${\tau }_i^{-}$	$D(1-u_{i-1})(1-\alpha u_{i+1})/\Delta x^2$	$D(1-u_{i-1})(1+\alpha u_{i-1})/\Delta x^2$
${\tau }_{i+1}^{+}$	$D(1-u_i)(1-\alpha u_{i-2})/\Delta x^2$	$D(1-u_i)(1+\alpha u_i)/\Delta x^2$
${\tau }_{i+1}^{-}$	$D(1-u_i)(1-\alpha u_{i+2})/\Delta x^2$	$D(1-u_i)(1+\alpha u_i)/\Delta x^2$