Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jul 17;122(31):17660–17667. doi: 10.1021/acs.jpcc.8b04013

Stabilizing Lead-Free All-Inorganic Tin Halide Perovskites by Ion Exchange

Junke Jiang †, Chidozie K Onwudinanti ‡, Ross A Hatton §, Peter A Bobbert †,∥, Shuxia Tao †,*
PMCID: PMC6089493  PMID: 30116464

Abstract

graphic file with name jp-2018-04013s_0005.jpg

Because of its thermal stability, lead-free composition, and nearly ideal optical and electronic properties, the orthorhombic CsSnI3 perovskite is considered promising as a light absorber for lead-free all-inorganic perovskite solar cells. However, the susceptibility of this three-dimensional perovskite toward oxidation in air has limited the development of solar cells based on this material. Here, we report the findings of a computational study which identifies promising RbyCs1–ySn(BrxI1–x)3 perovskites for solar cell applications, prepared by substituting cations (Rb for Cs) and anions (Br for I) in CsSnI3. We show the evolution of the material electronic structure as well as its thermal and structural stabilities upon gradual substitution. Importantly, we demonstrate how the unwanted yellow phase can be suppressed by substituting Br for I in CsSn(BrxI1–x)3 with x ≥ 1/3. We predict that substitution of Rb for Cs results in a highly homogeneous solid solution and therefore an improved film quality and applicability in solar cell devices.

Introduction

Organic–inorganic hybrid halide perovskite solar cells (PSCs) have attracted strong attention in the past few years and are becoming one of the most promising types of emerging thin-film solar cells.1−4 In less than a decade, the power conversion efficiency (PCE) of PSCs has increased from 3.8% in 2009 to 22.7% in 2017.5,6 Despite the high efficiency of PSCs, two challenges currently hinder their upscaling toward practical applications.7 One issue is the long-term instability of PSCs, which is mainly caused by the intrinsic thermal instability of hybrid perovskite materials.8−13 Encouragingly, it has been demonstrated recently that mixing the cations or replacing the organic cation with an inorganic cation can improve thermal stability and photostability (e.g., substituting FA for MA in MAPbI3, Rb for Cs in CsSnI3, and Cs for MA in MAPbI3; MA stands for CH3NH3, and FA stands for NH2CHNH2).7,14,15 The other concern is the well-documented toxicity of lead (Pb), which is particularly problematic because lead halide perovskites decompose into lead compounds that have significant solubility in water.16 Consequently, an intensive research effort focused on finding air-stable lead-free perovskites suitable as the light-harvesting semiconductor in PSCs is now underway.9,17−20

Among the various alternatives to lead, tin (Sn) is regarded as a promising substitute because Sn-based hybrid perovskites have been shown to exhibit outstanding electrical and optical properties, including high charge carrier mobilities, high absorption coefficients, and low exciton binding energies.21−23 Theoretical predictions by Even et al.24 and Chiarella et al.25 also confirmed the promising properties of Sn perovskites, such as suitable band gaps and favorable effective mass. However, Sn-based perovskites also have drawbacks, which have limited their application in efficient PSCs.1,23,26−29 The primary challenge is the susceptibility of tin toward oxidation from the +2 to the +4 oxidation state upon exposure to ambient air, which, in the case of CsSnI3, ultimately results in the formation of Cs2SnI6, whose relatively weak light absorption across the visible spectrum is undesirable for a photoabsorber.22,30−33 Consequently, to date, there has been much less research effort directed at the advancement of tin halide PSCs than their lead analogues, and their PCE has remained below 10%.27,28 Recently, a PCE as high as 9.0% in PSCs was achieved using single-crystalline FASnI3, made by mixing a small amount of two-dimensional (2D) Sn perovskites with three-dimensional (3D) FASnI3 in which the organic FA molecules are oriented randomly,34 an approach that promises further improvement.

As compared to hybrid organic–inorganic Sn perovskites, all-inorganic Sn perovskites could have the advantage of improved thermal stability while maintaining favorable optical and electronic properties for photovoltaic (PV) applications.35,36 For example, γ-CsSnI3 is a p-type semiconductor with a high hole mobility,21,37 a favorable band gap of ∼1.3 eV, a low exciton binding energy, and a high optical absorption coefficient.38,39 There have been a few attempts to fabricate solar cells using γ-CsSnI3 as a photoactive layer, but their maximum efficiency was still low. In 2012, Chen et al.40 first used CsSnI3 to fabricate a Schottky contact solar cell, which achieved a PCE of 0.9%. In 2014, Kumar et al.41 achieved a PCE of 2.02% by forming the perovskite from a solution under Sn-rich conditions, using SnF2 as the source of excess Sn, an approach that reduces the density of Sn vacancy defects. In 2016, Wang et al.19 achieved a PCE of 3.31%. By removing the electron-blocking layer in a simplified inverted solar cell architecture and using the additive SnCl2 instead of SnF2, Marshall et al.22 achieved the highest PCE to date of 3.56%, together with exceptional device stability under continuous illumination without device encapsulation. However, the PCE of γ-CsSnI3-based solar cells is still significantly lower than those of their hybrid organic–inorganic Sn and Pb perovskite counterparts, primarily because of the lower open-circuit voltage. The most important challenges are therefore to develop ways to increase the open-circuit voltage and to stabilize tin halide perovskites toward oxidation in air. The oxidation instability manifests as a phase transition from the photoactive black orthorhombic (γ) phase to a photoinactive 2D yellow (Y) phase upon exposure to water vapor, which spontaneously converts to the weakly absorbing one-dimensional Cs2SnI6,22 leading to difficulties in controlling the morphology and quality of the perovskite film.

In Pb halide perovskites, the strategy of mixing cations or anions has been widely used to improve the stability and PV performance of PSCs.12,42−47 In contrast, explorations of the mixing of cations and anions in all-inorganic Sn-based perovskites are scarce.7,48−50 Recently, the electronic structure variation of γ-CsSnI3 by mixing A-site cations (e.g., mixing Cs and Rb) has been investigated by Jung et al.7 However, the relative stability of the structures as compared to the Y phase was not investigated. To our knowledge, the amalgamated effect of exchange of both the A-site metal cation and the halide anion in completely inorganic tin perovskites has not been investigated.

In this paper, we present a theoretical study of the impact of cation and anion mixing (Rb/Cs cation exchange and Br/I anion exchange) in all-organic γ-CsSnI3 using the density functional theory (DFT)-1/2 method [the local density approximation (LDA)-1/2 version],51−54 taking into account the spin–orbit coupling (SOC) effect. We focus on the evolution of the electronic properties as well as the thermal and structural stabilities when substituting Br for I and Rb for Cs in γ-CsSnI3. We predict that 3D perovskites with the composition RbyCs1–ySn(BrxI1–x)3, where 0 ≤ x,y ≤ 1, are direct band gap semiconductors with band gaps in the range 1.3–2.0 eV. Importantly, our results indicate that substitution of Br for I in CsSnI3 can prevent the unwanted γ-to-Y phase transition, evidenced by the favorable formation energies of the γ phase over the Y phase. In addition, calculations of the free energy of mixing and the prediction of phase diagram demonstrate that further substitution of Rb for Cs in CsSn(BrxI1–x)3 can improve the mixing thermodynamics, which is expected to improve the film-forming properties. Our predicted trends in the thermodynamic stability and band gaps provide a guideline to develop more efficient and stable lead-free all-inorganic perovskites for PSCs.

Computational Methods and Structural Models

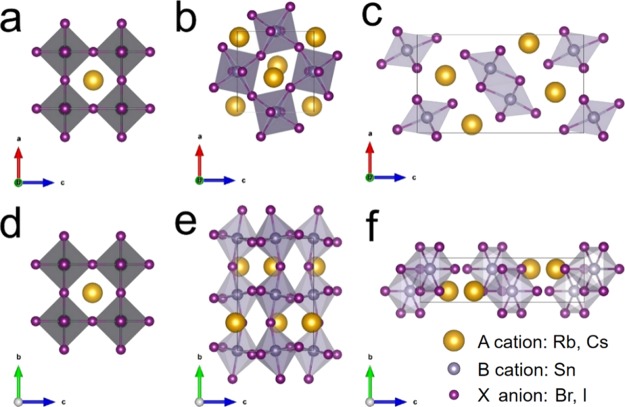
The initial structure optimizations are performed using DFT as implemented in the Vienna ab initio simulation package (VASP).55,56 The Perdew, Burke, and Ernzerhof (PBE) functional within the generalized gradient approximation is used.57 The outermost s, p, and d (in the case of Sn) electrons are treated as valence electrons, whose interactions with the remaining ions are modeled by pseudopotentials generated within the projector-augmented wave method.58,59Figure 1 shows the crystal structures and cells used in the DFT calculations. Unit cells with 20 atoms (four ASnX3 units) are used for all structures using a 1 × 1 × 1 cell for the γ and Y phases and 2 × 2 × 1 supercells for the α phase. In the structural optimization, the positions of the atoms as well as the cell volume and cell shape are all allowed to relax by setting ISIF = 3. An energy cutoff of 500 eV and 4 × 4 × 8, 6 × 4 × 6, and 4 × 10 × 2 k-point meshes (α, γ, and Y phase structures, respectively) are used to achieve an energy and force convergence of 0.1 meV and 2 meV/Å, respectively. The subsequent electronic structure calculations were performed using an efficient approximate quasi-particle DFT method, namely, the DFT-1/2 method. The DFT-1/2 method stems from Slater’s proposal of an approximation for the excitation energy, a transition-state method,60,61 to reduce the band gap inaccuracy by introducing a half-electron/half-hole occupation. Teles et al.51−54 extended the method to modern DFT and particularly to solid-state systems. Recently, we successfully applied this method in predicting accurate band gaps of metal halide perovskites.62 The computational effort is the same as for standard DFT, with a straightforward inclusion of SOC when coupled with VASP. In this work, we extend the use of the DFT-1/2 method with the same settings (CUT values of 2.30, 3.34, and 3.76 for Sn, I, and Br, respectively, with half-ionized p orbitals) to alloys of CsSnI3 when mixing Cs with Rb and I with Br. The physical insights of why Sn p and halide I or Br p orbitals are both half-ionized are demonstrated in Figure S1.

Figure 1.

Figure 1

Open in a new tab

Top (a–c) and side (d–f) views of the cubic (α, Pm3m), orthorhombic (γ, Pnma), and yellow phase (Y, Pnma) of ASnX3 (A = Cs and Rb and X = Br and I).

We calculated the free energy7,63 of mixing for each composition according to the expression

graphic file with name jp-2018-04013s_m001.jpg 1

where ΔU and ΔS are the internal energy and entropy of mixing, respectively, and T is the absolute temperature. The internal energy of mixing of RbxCs1–xSnX3 is then calculated via the formula

graphic file with name jp-2018-04013s_m002.jpg 2

where ERbxCs1–xSnX3, ERbSnX3, and ECsSnX3 are the total energies of RbxCs1–xSnX3, RbSnX3, and CsSnX3, respectively.

The internal energy of mixing of ASn(BrxI1–x)3 is calculated using the formula

graphic file with name jp-2018-04013s_m003.jpg 3

where EASn(BrxI1–x)3, EASnBr3, and EASnI3 are the total energies of ASn(BrxI1–x)3, ASnBr3, and ASnI3, respectively.

The entropy of mixing is calculated in the homogeneous limit according to the formula

graphic file with name jp-2018-04013s_m004.jpg 4

where kB is the Boltzmann constant.

We plot the phase diagram by using the generalized quasi-chemical approximation (GQCA)63,64 code developed by Walsh et al.63 to further investigate the thermodynamic properties of γ-ASnX3. The phase diagram offers insight into the critical temperature for mixing and into the stability of the solid solution for typical temperatures at which perovskites are synthesized.

On the basis of the size of the cells for calculations, we have considered seven (ASn(BrxI1–x)3, x = 0, 1/6, 1/3, 1/2, 2/3, 5/6, and 1) and five (RbyCs1–ySnX3, y = 0, 1/4, 1/2, 3/4, and 1) concentrations of A cations and X anions, respectively. For the γ phase structures, all possible configurations (2, 4, and 2 for y = 1/4, 1/2, and 3/4, respectively) of substituting Rb for Cs were considered. Owing to the large number of possible configurations of substituting Br for I (22, 139, 252, 139, and 22 possible configurations for x = 1/6, 1/3, 1/2, 2/3, and 5/6, respectively), we have considered only two possible configurations for each concentration of Br, namely, the two extreme cases with most negative and least negative ΔH. From Figure S2 and Table S1, the formation energy of configuration 3 is the most negative, whereas that of configuration 7 is the least negative. This indicates that the Br ions tend to sit as close as possible to each other and to form as many bonds as possible with Sn ions. We use this strategy to select two extreme configurations for all other Br–I alloys considered in this work.

Results and Discussion

Before studying the mixing of A cations and X anions in ASnX3, we first performed calculations for the four pure compounds: CsSnI3, CsSnBr3, RbSnI3, and RbSnBr3. The calculated lattice parameters of orthorhombic (γ) ASnX3 are shown in Table 1. Those of other polymorphs including cubic α, tetragonal β, and Y phase structures are listed in Table S2. The optimized lattice parameters are in good agreement with experiments, with a slight overestimation of lattice constants by about 1%, and with other theoretical results (differences within 0.1%).7,38,49,65−68 It should be noted here that the predicted lattice parameters of α-CsSnI3 and γ-CsSnI3 in our previous work are smaller because of the use of LDA, which slightly underestimates the lattice parameters.62 In this work, PBE is used, resulting in a slight overestimation of lattice parameters. Consequently, the predicted band gap of γ-CsSnI3 (1.36 eV) in this work (will be discussed in the next paragraph) is slightly higher compared to that of previous work (1.34 eV).62

Table 1. Lattice Constants (in Å) Obtained by DFT and Band Gap Energies Eg (in eV) Obtained with the DFT-1/2 Method Including SOC Compared to Experimental Data and Theoretical Predictions Based on Hybrid and GW Methods.

material lattice constants (this work) lattice constants (experimental) lattice constants (other theoretical work) Eg DFT-1/2 + SOC Eg (experimental) Eg + SOC
γ-CsSnI3 8.99, 12.52, 8.63 8.69, 12.38, 8.64a 8.94, 12.52, 8.69b 1.36 1.27c 1.34 (GW0)d
γ-RbSnI3 8.91, 12.28, 8.47   8.93, 12.28, 8.47b 1.55   1.13 (HSE06)b
γ-CsSnBr3 8.36, 11.79, 8.22     1.72   1.83 (GW0)d
γ-RbSnBr3 8.38, 11.55, 7.98     2.01    
Open in a new tab
a

Reference (38).

b

Reference (7).

c

Reference (49).

d

Reference (68).

The calculated band gaps of γ-CsSnI3 and γ-CsSnBr3 are 1.36 and 1.72 eV, respectively, in excellent agreement with reported experimental measurements49 (1.27 and 1.75 eV) and GW0 calculations68 (1.34 and 1.83 eV). There are no experimental reports known to us of the band gap of either RbSnI3 or RbSnBr3. Only theoretical results from HSE06 for γ-RbSnI3 and PBE for α-RbSnBr3 are found to be 1.41 and 0.57 eV, respectively.7,69 Our predicted band gap for γ-RbSnI3 is 1.55 eV. Substituting Br for I in γ-RbSnI3 further increases the band gap to 2.01 eV.

It is worth noting that although CsSnBr3 is reported to have the α structure at room temperature, the actual atomic arrangement at finite temperature (due to the dynamic disorder of the ions in the lattice)70 resembles that of the γ phase. Consequently, it is not surprising that predicted band gaps using α structures are always significantly smaller than those measured experimentally.7,24,71,72 Therefore, in this work, we always report band gaps calculated using γ phases. RbSnI3 has been reported to exist in a nonperovskite 2D Y phase structure owing to the small cationic size of Rb+.38,66 Nevertheless, for comparison with the alloys RbyCs1–ySnI3, the band gaps of RbSnI3 in a 3D γ phase are also predicted. In addition, all band gaps of α structures are also provided in the Supporting Information in Table S2 and Figure S3 for comparison. The calculated effective masses of the electrons and holes at the G point for γ-ASnX3 are given in Table S3.

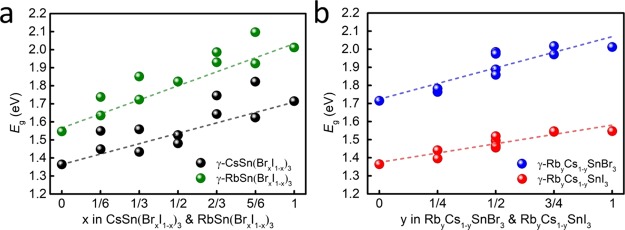
Figure 2 shows the computed band gaps for the γ phases of ASn(BrxI1–x)3 and RbyCs1–ySnX3 perovskites, whereas the band gaps of the other structures are shown in Figure S4. In general, the band gap increases with increasing percentage of Br in ASn(BrxI1–x)3 and Rb in RbyCs1–ySnX3. From Figure 2a and Table S4, generally, the band gaps change because of the variations in both volume and lattice distortion. However, the changes in cell volume have more pronounced effects on the band gaps than the changes in lattice distortion, that is, octahedral tilting. The reduction of the cell volume is responsible for the widening of the band gap in ASn(BrxI1–x)3 or RbyCs1–ySnX3 solid solutions with an increased Br or Rb percentage. For the band gap variations with the same Br or Rb percentage in ASn(BrxI1–x)3 or RbyCs1–ySnX3 solid solutions, there is no certain relationship found between the degree of lattice distortion (i.e., the degree of octahedral tilting, which is the tilting angle difference |Δθ̅|)4 and band gaps.

Figure 2.

Figure 2

Open in a new tab

Calculated band gaps of (a) γ-ASn(BrxI1–x)3 and (b) γ-RbyCs1–ySnX3 perovskites. The dashed lines are guides to the eye.

It is well-known that for single-junction and multijunction solar cells, the Shockley–Queisser limit suggests optimal band gap ranges of 0.9–1.6 and 1.6–2.0 eV, respectively, for achieving a maximum PCE.23,73 The band gaps of CsSn(BrxI1–x)3 are almost completely in the optimal range (1.30–1.55 eV) for single-junction PSCs. When substituting Rb for Cs in CsSn(BrxI1–x)3, the band gaps of RbSn(BrxI1–x)3 increase by 0.2–0.3 eV as compared to their Cs counterparts, making RbSn(BrxI1–x)3 (x > 1/3) ideal as a wide-band gap material for tandem solar cells in conjunction with narrow-band gap semiconductors such as Si or CsSn(BrxI1–x)3. The changes in band gap when mixing Rb and Cs cations are much smaller than those when mixing I and Br. This is true for all values 0 ≤ y ≤ 1 and also for different structures with a fixed y. The band gaps of RbyCs1–ySnBr3 (1.71–2.01 eV) and RbyCs1–ySnI3 (1.36–1.55 eV) are in the ideal range for tandem and single-junction solar cells, respectively.

In addition to the band gap, another key property for the application of mixed inorganic perovskites in PSCs is their structural stability. CsSnI3 has two coexisting polymorphs (the γ and Y phases) at room temperature, which both belong to the Pnma space group. Although both phases have similar free energies and stable phonon modes, a transition from the black γ phase to the yellow Y phase has been observed in ambient conditions.7,38,74 Oxidation of Sn2+ to Sn4+ spontaneously occurs after the transformation of the γ phase to the Y phase.75

Because of the different crystal structure and electronic properties of the Y phase (i.e., a 2D structure and an indirect band gap of 2.6 eV), the unwanted phase transition from γ to Y can considerably decrease the efficiency of a solar cell.14,22,75−77 In addition, the Y phase will spontaneously react with O2 when exposed to air, resulting in Cs2SnI6 with a face-centered cubic structure.30,32 Therefore, we focus here on the evolution of the stability of the γ and Y phases upon gradual substitution of Br for I and Rb for Cs. The results of our calculations for other structures are given in Figure S5.

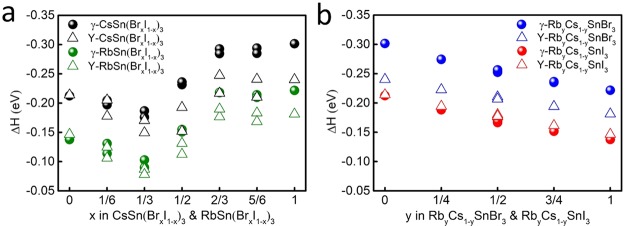
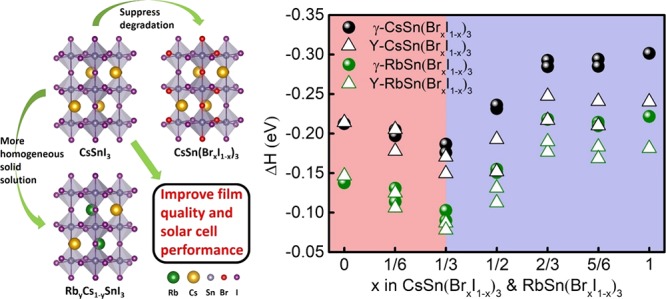
The formation energy of ASnX3 is defined as ΔH = EASnX3 – EAX – ESnX2, where EASnX3, EAX, and ESnX2 are the total energies of ASnX3, AX, and SnX2, respectively. Here, a negative value of ΔH represents favorable formation of ASnX3 perovskites. The more negative ΔH, the more stable the corresponding structure. It can be clearly seen in Figure 3 that all perovskites considered exhibit good thermal stability, with large negative ΔH values. Figure 3 also shows the effect of ion mixing on the stability of the γ phase with respect to the Y phase.

Figure 3.

Figure 3

Open in a new tab

Formation energy (ΔH) of (a) ASn(BrxI1–x)3 and (b) RbyCs1–ySnX3 perovskites for the γ and Y phases. Because of the large number of possible configurations for each substitution concentration x of Br in ASn(BrxI1–x)3, we only show in (a) the results for the two configurations with the most negative and least negative ΔH.

For CsSnI3, the formation energies of the γ and Y phases are the same. However, with the increase of Rb concentration, the structural instability of RbyCs1–ySnI3 becomes increasingly pronounced. Consequently, upon exposure to air, the rate at which the perovskite oxidizes is predicated to increase with an increasing Rb concentration.75 The substitution of Rb for Cs seems to facilitate the formation of the Y phase, as now evidenced by the more negative formation energy of the Y phase than the γ phase. It should be mentioned that the formation energies are both negative for RbSnI3 in both γ and Y phases. However, the formation energy of the Y phase is relatively more negative, indicating that the Y phase is more favorable than the γ phase. Indeed, the instability of the γ phase is in agreement with the experimental observation of RbSnI3 only existing in a 2D yellow phase.75 On the contrary, for CsSnBr3, the formation energy of the Y phase is much less negative than that of the γ phase (by 0.06 eV), indicating that the γ phase is more stable than the Y phase. The substitution of Rb for Cs results in a slight decrease (to 0.04 eV) in the energy differences between the two phases, with the γ phase still being favored.

The formation energies of mixing Cs and Rb in RbyCs1–ySnI3 or RbyCs1–ySnBr3 follow a perfect linear relation (Figure 3b), indicating favorable mixing thermodynamics. However, substitution of Br for I (Figure 3a) shows an unusual trend as a function of x: the curves show first a decrease and then an increase, with a valley point at x = 1/3 in both CsSn(BrxI1–x)3 and RbSn(BrxI1–x)3. When x < 1/3, the most negative ΔH of the γ phase for each concentration is relatively more positive than or nearly equal to the most negative ΔH of the Y phase, which indicates that the Y phase is favored over the γ phase. When x = 1/3, the most negative ΔH of the γ phase is clearly more negative than the most negative ΔH of the Y phase, whereas the least negative ΔH of the γ phase is almost equal to the most negative ΔH of the Y phase. When x > 1/3, all ΔH of the γ phase for each concentration are more negative than those of the Y phase, which means that the γ phase is stabilized. For RbyCs1–ySnI3 or RbyCs1–ySnBr3, mixing Cs and Rb does not change the stability of the γ phase with respect to the Y phase (Figure 3b). For RbyCs1–ySnI3, the Y phase is always favored when mixing Rb and Cs, whereas for RbyCs1–ySnBr3, the opposite is true. We conclude that the addition of Br to RbyCs1–ySnI3 tends to stabilize the favorable γ phase and suppress the transformation to the Y phase. The critical Br concentration is about one-third. This prediction calls for an experimental validation.

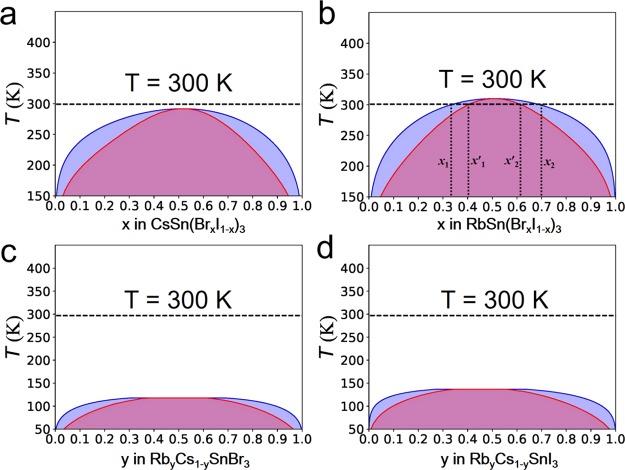
As shown in Figure 3, very different trends are observed for mixing of cations (Rb and Cs) and anions (I and Br) in γ-CsSnI3. For a deeper insight, we have investigated the different mixing thermodynamics by calculating the Helmholtz free energy of mixing. Details of the calculations can be found in the Computational Methods and Structural Models section. Results of these calculations are shown in Figure S6. On the basis of the Helmholtz free energies, we plot the phase diagram for γ-ASnX3 by using the GQCA63 code, as shown in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Predicted phase diagrams of (a) γ-CsSn(BrxI1–x)3, (b) γ-RbSn(BrxI1–x)3, (c) γ-RbyCs1–ySnBr3, and (d) γ-RbyCs1–ySnI3 solid solutions. The purple and pink lines are binodals and spinodals, respectively. The dashed horizontal lines indicate room temperature (300 K). In (b), the gap between the horizontal line and the critical miscibility temperature is the miscibility gap in γ-RbSn(BrxI1–x)3. A thermodynamically stable solid solution can be formed only in the white region.

For CsSn(BrxI1–x)3, the critical temperature is 291 K (see Figure 4a), indicating that the mixing of anions (I and Br) is favorable at room temperature (300 K). However, for RbSn(BrxI1–x)3 at 300 K, a miscibility gap is found in the composition region between x1 = 0.33 and x2 = 0.70 (see Figure 4b). The pure compounds RbSnI3 and RbSnBr3 are not miscible inside the miscibility gap under equilibrium conditions, leading to the formation of two phases with Br concentrations x1 and x2. Meanwhile, the alloy has spinodal points at the compositions x1′ = 0.40 and x2 = 0.62 at room temperature. Thus, in the intervals x1 < x < x1′ and x2 < x < x2, a metastable phase can occur, showing small fluctuations in composition. The predicted critical temperature (the temperature above which the solid solution is stable for any composition) is 312 K, which is significantly lower than the critical temperature of 343 K predicted for the MAPb(BrxI1–x)3 perovskite.63 This indicates that, although mixing of Br and I is not favored slightly below (for CsSn(BrxI1–x)3) or around (for RbSn(BrxI1–x)3) room temperature, the phase segregation in these alloys is less significant than that in MAPb(BrxI1–x)3 perovskites.

A uniform mixture can be synthesized either through control of the deposition kinetics or by annealing above the critical miscibility temperature. The uniform mixture tends to segregate below the critical temperature, but this segregation is a very slow process.63 The inclusion of smaller cations often provides an improvement, overcoming kinetic barriers and changing the local critical temperature. For example, smaller cations such as Cs and Rb were introduced in (FA/MA)Pb(I/Br)3 and were shown to have a positive effect on the structural and photostability of state-of-the-art PSCs.8,10,13,78 Indeed, we predict that mixing of Rb and Cs in RbyCs1–ySnX3 is very favorable at room temperature. For RbyCs1–ySnBr3 and RbyCs1–ySnI3, the phase diagrams show that mixing of cations (Rb and Cs) is favorable at temperatures above 118 and 137 K, respectively (see Figure 4c,d). Our prediction of the critical miscibility temperature of 137 K of RbyCs1–ySnI3 is in good agreement with the result of 140 K calculated by Jung et al.7 The slight difference of the predicted critical temperature could be caused by the small variation in energies per cell due to the differences in computational settings (energy cutoff value, k-point grid, version, and implementation of VASP codes) in DFT calculations. The critical temperatures of mixing of Rb and Cs in RbyCs1–ySnX3 are much lower than those of mixing of Br and I in ASn(BrxI1–x)3. Therefore, additional mixing of Cs and Rb in ASnIxBr1–x is predicted to bring down the critical temperature for mixing of Br and I below room temperature, suppressing phase segregation and resulting in better material quality for PV applications.

Conclusions

In summary, the effects of cation (Cs and Rb) and anion (I and Br) mixing in all-inorganic tin halide perovskites have been investigated with DFT-based calculations. Using standard DFT for structure optimization and the DFT-1/2 method with SOC for band structure calculations, we studied the evolution of the structural, thermodynamic, and electronic properties as a function of the extent of substitution of Rb for Cs and Br for I. We predict that CsyRb1–ySn(BrxI1–x)3 perovskites have direct band gaps in the range of 1.3–2.0 eV. The alloys with high I and Cs concentrations are well suited for highly efficient single-junction PSCs, whereas those with high Rb and Br concentrations are suitable as wide-band gap materials for tandem PSCs. Importantly, we found that substitution of Br for I can suppress the unwanted γ-to-Y phase transition. The critical concentration for stabilization of the γ phase with respect to the Y phase in CsyRb1–ySn(BrxI1–x)3 is x = 1/3. Furthermore, phase diagrams based on the free energy of mixing show that a solid solution of Br and I is thermodynamically possible around and slightly above room temperature for CsSn(BrxI1–x)3 and RbSn(BrxI1–x)3, respectively. Finally, substitution of Rb for Cs to ASn(BrxI1–x)3 is predicted to decrease the critical temperature to well below room temperature, enabling the formation of highly homogeneous solid solutions for improved solar cell performance. Our predictions regarding the stabilization of the γ phase and the use of five elements in RbyCs1–ySn(BrxI1–x)3 as an efficient and stable light absorber for PSCs call for experimental exploration.

Acknowledgments

S.T. and J.J. acknowledge the funding by the Computational Sciences for Energy Research (CSER) tenure track program of Shell, NWO, and FOM (Project number 15CST04-2). Dr. Peter Klaver is acknowledged for his technical support in the computational study in this work.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b04013.

  • Physical insights of why Sn p and halide I or Br p orbitals are both half-ionized; illustration of the selection strategy of ASn(BrxI1–x)3 to reduce computational effort; summary of lattice constants and band gaps (Eg) of polymorphs of ASnX3 (CsSnI3, RbSnI3, CsSnBr3, and RbSnBr3); band structures for CsSnI3, CsSnBr3, RbSnI3, and RbSnBr3 with the γ phase and the α phase; effective masses for γ-CsSnI3, γ-CsSnBr3, γ-RbSnI3, and γ-RbSnBr3; average tilting angles and cell volumes of γ-CsSn(BrxI1–x)3, γ-RbSn(BrxI1–x)3, γ-RbyCs1–ySnBr3, and γ-RbyCs1–ySnI3; band gaps and formation energies of ASn(BrxI1–x)3 and RbyCs1–ySnX3 perovskites, including the α phase; and Helmholtz free energy of mixing of α and γ polymorphs (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp8b04013_si_002.pdf (1.5MB, pdf)

References

  1. Yablonovitch E. Lead Halides Join the Top Optoelectronic League. Science 2016, 351, 1401. 10.1126/science.aaf4603. [DOI] [PubMed] [Google Scholar]
  2. Green M. A.; Ho-Baillie A.; Snaith H. J. The Emergence of Perovskite Solar Cells. Nat. Photonics 2014, 8, 506–514. 10.1038/nphoton.2014.134. [DOI] [Google Scholar]
  3. Kadro J. M.; Pellet N.; Giordano F.; Ulianov A.; Müntener O.; Maier J.; Grätzel M.; Hagfeldt A. Proof-of-Concept for Facile Perovskite Solar Cell Recycling. Energy Environ. Sci. 2016, 9, 3172–3179. 10.1039/c6ee02013e. [DOI] [Google Scholar]
  4. Pedesseau L.; Sapori D.; Traore B.; Robles R.; Fang H.-H.; Loi M. A.; Tsai H.; Nie W.; Blancon J.-C.; Neukirch A.; et al. Advances and Promises of Layered Halide Hybrid Perovskite Semiconductors. ACS Nano 2016, 10, 9776–9786. 10.1021/acsnano.6b05944. [DOI] [PubMed] [Google Scholar]
  5. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  6. National Renewable Energy Laboratory . Best Research-Cell Efficiencies. https://www.nrel.gov/pv/assets/images/efficiency-chart.png (accessed March 21, 2018).
  7. Jung Y.-K.; Lee J.-H.; Walsh A.; Soon A. Influence of Rb/Cs Cation-Exchange on Inorganic Sn Halide Perovskites: From Chemical Structure to Physical Properties. Chem. Mater. 2017, 29, 3181–3188. 10.1021/acs.chemmater.7b00260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Liang L.; Gao P. Lead-Free Hybrid Perovskite Absorbers for Viable Application: Can We Eat the Cake and Have It too?. Adv. Sci. 2017, 5, 1700331. 10.1002/advs.201700331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Wang A.; Guo Y.; Muhammad F.; Deng Z. Controlled Synthesis of Lead-Free Cesium Tin Halide Perovskite Cubic Nanocages with High Stability. Chem. Mater. 2017, 29, 6493–6501. 10.1021/acs.chemmater.7b02089. [DOI] [Google Scholar]
  10. Whalley L. D.; Frost J. M.; Jung Y.-K.; Walsh A. Perspective: Theory and Simulation of Hybrid Halide Perovskites. J. Chem. Phys. 2017, 146, 220901. 10.1063/1.4984964. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Sun Q.; Yin W.-J. Thermodynamic Stability Trend of Cubic Perovskites. J. Am. Chem. Soc. 2017, 139, 14905–14908. 10.1021/jacs.7b09379. [DOI] [PubMed] [Google Scholar]
  12. Gratia P.; Grancini G.; Audinot J.-N.; Jeanbourquin X.; Mosconi E.; Zimmermann I.; Dowsett D.; Lee Y.; Grätzel M.; De Angelis F.; et al. Intrinsic Halide Segregation at Nanometer Scale Determines the High Efficiency of Mixed Cation/Mixed Halide Perovskite Solar Cells. J. Am. Chem. Soc. 2016, 138, 15821–15824. 10.1021/jacs.6b10049. [DOI] [PubMed] [Google Scholar]
  13. Correa-Baena J.-P.; Abate A.; Saliba M.; Tress W.; Jesper Jacobsson T.; Grätzel M.; Hagfeldt A. The Rapid Evolution of Highly Efficient Perovskite Solar Cells. Energy Environ. Sci. 2017, 10, 710–727. 10.1039/c6ee03397k. [DOI] [Google Scholar]
  14. Yi C.; Luo J.; Meloni S.; Boziki A.; Ashari-Astani N.; Grätzel C.; Zakeeruddin S. M.; Röthlisberger U.; Grätzel M. Entropic stabilization of mixed A-cation ABX3 metal halide perovskites for high performance perovskite solar cells. Energy Environ. Sci. 2016, 9, 656–662. 10.1039/c5ee03255e. [DOI] [Google Scholar]
  15. Niemann R. G.; Gouda L.; Hu J.; Tirosh S.; Gottesman R.; Cameron P. J.; Zaban A. Cs+ incorporation into CH3NH3PbI3 perovskite: substitution limit and stability enhancement. J. Mater. Chem. A 2016, 4, 17819–17827. 10.1039/c6ta05869h. [DOI] [Google Scholar]
  16. Babayigit A.; Ethirajan A.; Muller M.; Conings B. Toxicity of Organometal Halide Perovskite Solar Cells. Nat. Mater. 2016, 15, 247–251. 10.1038/nmat4572. [DOI] [PubMed] [Google Scholar]
  17. Ju M.-G.; Chen M.; Zhou Y.; Garces H. F.; Dai J.; Ma L.; Padture N. P.; Zeng X. C. Earth-Abundant Nontoxic Titanium(IV)-based Vacancy-Ordered Double Perovskite Halides with Tunable 1.0 to 1.8 eV Bandgaps for Photovoltaic Applications. ACS Energy Lett. 2018, 3, 297–304. 10.1021/acsenergylett.7b01167. [DOI] [Google Scholar]
  18. Shi Z.; Guo J.; Chen Y.; Li Q.; Pan Y.; Zhang H.; Xia Y.; Huang W. Lead-Free Organic-Inorganic Hybrid Perovskites for Photovoltaic Applications: Recent Advances and Perspectives. Adv. Mater. 2017, 29, 1605005. 10.1002/adma.201605005. [DOI] [PubMed] [Google Scholar]
  19. Wang N.; Zhou Y.; Ju M.-G.; Garces H. F.; Ding T.; Pang S.; Zeng X. C.; Padture N. P.; Sun X. W. Heterojunction-Depleted Lead-Free Perovskite Solar Cells with Coarse-Grained B-γ-CsSnI3 Thin Films. Adv. Energy Mater. 2016, 6, 1601130. 10.1002/aenm.201601130. [DOI] [Google Scholar]
  20. Harikesh P. C.; Mulmudi H. K.; Ghosh B.; Goh T. W.; Teng Y. T.; Thirumal K.; Lockrey M.; Weber K.; Koh T. M.; Li S.; et al. Rb as an Alternative Cation for Templating Inorganic Lead-Free Perovskites for Solution Processed Photovoltaics. Chem. Mater. 2016, 28, 7496–7504. 10.1021/acs.chemmater.6b03310. [DOI] [Google Scholar]
  21. Chung I.; Lee B.; He J.; Chang R. P. H.; Kanatzidis M. G. All-Solid-State Dye-Sensitized Solar Cells with High Efficiency. Nature 2012, 485, 486–489. 10.1038/nature11067. [DOI] [PubMed] [Google Scholar]
  22. Marshall K. P.; Walker M.; Walton R. I.; Hatton R. A. Enhanced Stability and Efficiency in Hole-Transport-Layer-Free CsSnI3 Perovskite Photovoltaics. Nat. Energy 2016, 1, 16178. 10.1038/nenergy.2016.178. [DOI] [Google Scholar]
  23. Konstantakou M.; Stergiopoulos T. A Critical Review on Tin Halide Perovskite Solar Cells. J. Mater. Chem. A 2017, 5, 11518–11549. 10.1039/c7ta00929a. [DOI] [Google Scholar]
  24. Even J.; Pedesseau L.; Jancu J.-M.; Katan C. DFT and modelling of the phase transitions of lead and tin halide perovskites for photovoltaic cells. Phys. Status Solidi RRL 2014, 8, 31–35. 10.1002/pssr.201308183. [DOI] [Google Scholar]
  25. Chiarella F.; Zappettini A.; Licci F.; Borriello I.; Cantele G.; Ninno D.; Cassinese A.; Vaglio R. Combined Experimental and Theoretical Investigation of Optical, Structural, and Electronic Properties of CH3NH3SnX3 Thin Films (X= Cl, Br). Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 045129. 10.1103/physrevb.77.045129. [DOI] [Google Scholar]
  26. Abate A. Perovskite Solar Cells Go Lead Free. Joule 2017, 1, 659–664. 10.1016/j.joule.2017.09.007. [DOI] [Google Scholar]
  27. Noel N. K.; Stranks S. D.; Abate A.; Wehrenfennig C.; Guarnera S.; Haghighirad A.-A.; Sadhanala A.; Eperon G. E.; Pathak S. K.; Johnston M. B.; Petrozza A.; Herz L. M.; Snaith H. J. Lead-free organic-inorganic tin halide perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 3061–3068. 10.1039/c4ee01076k. [DOI] [Google Scholar]
  28. Hao F.; Stoumpos C. C.; Cao D. H.; Chang R. P. H.; Kanatzidis M. G. Lead-Free Solid-State Organic-Inorganic Halide Perovskite Solar Cells. Nat. Photonics 2014, 8, 489–494. 10.1038/nphoton.2014.82. [DOI] [Google Scholar]
  29. Sun Y.-Y.; Shi J.; Lian J.; Gao W.; Agiorgousis M. L.; Zhang P.; Zhang S. Discovering Lead-free Perovskite Solar Materials with a Split-Anion Approach. Nanoscale 2016, 8, 6284–6289. 10.1039/c5nr04310g. [DOI] [PubMed] [Google Scholar]
  30. Lee B.; Stoumpos C. C.; Zhou N.; Hao F.; Malliakas C.; Yeh C.-Y.; Marks T. J.; Kanatzidis M. G.; Chang R. P. H. Air-Stable Molecular Semiconducting Iodosalts for Solar Cell Applications: Cs2SnI6 as a Hole Conductor. J. Am. Chem. Soc. 2014, 136, 15379–15385. 10.1021/ja508464w. [DOI] [PubMed] [Google Scholar]
  31. Xiao Z.; Zhou Y.; Hosono H.; Kamiya T. Intrinsic defects in a photovoltaic perovskite variant Cs2SnI6. Phys. Chem. Chem. Phys. 2015, 17, 18900–18903. 10.1039/c5cp03102h. [DOI] [PubMed] [Google Scholar]
  32. Saparov B.; Sun J.-P.; Meng W.; Xiao Z.; Duan H.-S.; Gunawan O.; Shin D.; Hill I. G.; Yan Y.; Mitzi D. B. Thin-Film Deposition and Characterization of a Sn-Deficient Perovskite Derivative Cs2SnI6. Chem. Mater. 2016, 28, 2315–2322. 10.1021/acs.chemmater.6b00433. [DOI] [Google Scholar]
  33. Qiu X.; Cao B.; Yuan S.; Chen X.; Qiu Z.; Jiang Y.; Ye Q.; Wang H.; Zeng H.; Liu J.; et al. From unstable CsSnI3 to air-stable Cs2SnI6: A lead-free perovskite solar cell light absorber with bandgap of 1.48 eV and high absorption coefficient. Sol. Energy Mater. Sol. Cells 2017, 159, 227–234. 10.1016/j.solmat.2016.09.022. [DOI] [Google Scholar]
  34. Shao S.; Liu J.; Portale G.; Fang H.-H.; Blake G. R.; ten Brink G. H.; Koster L. J. A.; Loi M. A. Highly Reproducible Sn-Based Hybrid Perovskite Solar Cells with 9% Efficiency. Adv. Energy Mater. 2017, 8, 1702019. 10.1002/aenm.201702019. [DOI] [Google Scholar]
  35. Gupta S.; Bendikov T.; Hodes G.; Cahen D. CsSnBr3, A Lead-Free Halide Perovskite for Long-Term Solar Cell Application: Insights on SnF2 Addition. ACS Energy Lett. 2016, 1, 1028–1033. 10.1021/acsenergylett.6b00402. [DOI] [Google Scholar]
  36. Kontos A. G.; Kaltzoglou A.; Siranidi E.; Palles D.; Angeli G. K.; Arfanis M. K.; Psycharis V.; Raptis Y. S.; Kamitsos E. I.; Trikalitis P. N.; et al. Structural Stability, Vibrational Properties, and Photoluminescence in CsSnI3 Perovskite upon the Addition of SnF2. Inorg. Chem. 2017, 56, 84–91. 10.1021/acs.inorgchem.6b02318. [DOI] [PubMed] [Google Scholar]
  37. Xu P.; Chen S.; Xiang H.-J.; Gong X.-G.; Wei S.-H. Influence of Defects and Synthesis Conditions on the Photovoltaic Performance of Perovskite Semiconductor CsSnI3. Chem. Mater. 2014, 26, 6068–6072. 10.1021/cm503122j. [DOI] [Google Scholar]
  38. Chung I.; Song J.-H.; Im J.; Androulakis J.; Malliakas C. D.; Li H.; Freeman A. J.; Kenney J. T.; Kanatzidis M. G. CsSnI3: Semiconductor or Metal? High Electrical Conductivity and Strong Near-Infrared Photoluminescence from a Single Material. High Hole Mobility and Phase-Transitions. J. Am. Chem. Soc. 2012, 134, 8579–8587. 10.1021/ja301539s. [DOI] [PubMed] [Google Scholar]
  39. Huang L.-y.; Lambrecht W. R. L. Electronic Band Structure, Phonons, and Exciton Binding Energies of Halide Perovskites CsSnCl3, CsSnBr3, and CsSnI3. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 165203. 10.1103/physrevb.88.165203. [DOI] [Google Scholar]
  40. Chen Z.; Wang J. J.; Ren Y.; Yu C.; Shum K. Schottky solar cells based on CsSnI3 thin-films. Appl. Phys. Lett. 2012, 101, 093901. 10.1063/1.4748888. [DOI] [Google Scholar]
  41. Kumar M. H.; Dharani S.; Leong W. L.; Boix P. P.; Prabhakar R. R.; Baikie T.; Shi C.; Ding H.; Ramesh R.; Asta M.; Graetzel M.; Mhaisalkar S. G.; Mathews N. Lead-Free Halide Perovskite Solar Cells with High Photocurrents Realized Through Vacancy Modulation. Adv. Mater. 2014, 26, 7122–7127. 10.1002/adma.201401991. [DOI] [PubMed] [Google Scholar]
  42. Ono L. K.; Juarez-Perez E. J.; Qi Y. Progress on Perovskite Materials and Solar Cells with Mixed Cations and Halide Anions. ACS Appl. Mater. Interfaces 2017, 9, 30197–30246. 10.1021/acsami.7b06001. [DOI] [PubMed] [Google Scholar]
  43. Wang Z.; McMeekin D. P.; Sakai N.; van Reenen S.; Wojciechowski K.; Patel J. B.; Johnston M. B.; Snaith H. J. Efficient and Air-Stable Mixed-Cation Lead Mixed-Halide Perovskite Solar Cells with n-Doped Organic Electron Extraction Layers. Adv. Mater. 2017, 29, 1604186. 10.1002/adma.201604186. [DOI] [PubMed] [Google Scholar]
  44. Bi D.; Tress W.; Dar M. I.; Gao P.; Luo J.; Renevier C.; Schenk K.; Abate A.; Giordano F.; Correa Baena J.-P.; Decoppet J.-D.; Zakeeruddin S. M.; Nazeeruddin M. K.; Grätzel M.; Hagfeldt A. Efficient Luminescent Solar Cells Based on Tailored Mixed-Cation Perovskites. Sci. Adv. 2016, 2, e1501170 10.1126/sciadv.1501170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Pellet N.; Gao P.; Gregori G.; Yang T.-Y.; Nazeeruddin M. K.; Maier J.; Grätzel M. Mixed-Organic-Cation Perovskite Photovoltaics for Enhanced Solar-Light Harvesting. Angew. Chem., Int. Ed. 2014, 53, 3151–3157. 10.1002/anie.201309361. [DOI] [PubMed] [Google Scholar]
  46. Akkerman Q. A.; D’Innocenzo V.; Accornero S.; Scarpellini A.; Petrozza A.; Prato M.; Manna L. Tuning the Optical Properties of Cesium Lead Halide Perovskite Nanocrystals by Anion Exchange Reactions. J. Am. Chem. Soc. 2015, 137, 10276–10281. 10.1021/jacs.5b05602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. McMeekin D. P.; Sadoughi G.; Rehman W.; Eperon G. E.; Saliba M.; Horantner M. T.; Haghighirad A.; Sakai N.; Korte L.; Rech B.; Johnston M. B.; Herz L. M.; Snaith H. J. A Mixed-Cation Lead Mixed-Halide Perovskite Absorber for Tandem Solar Cells. Science 2016, 351, 151–155. 10.1126/science.aad5845. [DOI] [PubMed] [Google Scholar]
  48. Li W.; Li J.; Li J.; Fan J.; Mai Y.; Wang L. Addictive-assisted construction of all-inorganic CsSnIBr2 mesoscopic perovskite solar cells with superior thermal stability up to 473 K. J. Mater. Chem. A 2016, 4, 17104–17110. 10.1039/c6ta08332c. [DOI] [Google Scholar]
  49. Sabba D.; Mulmudi H. K.; Prabhakar R. R.; Krishnamoorthy T.; Baikie T.; Boix P. P.; Mhaisalkar S.; Mathews N. Impact of Anionic Br- Substitution on Open Circuit Voltage in Lead Free Perovskite (CsSnI3-xBrx) Solar Cells. J. Phys. Chem. C 2015, 119, 1763–1767. 10.1021/jp5126624. [DOI] [Google Scholar]
  50. Saliba M.; Matsui T.; Domanski K.; Seo J.-Y.; Ummadisingu A.; Zakeeruddin S. M.; Correa-Baena J.-P.; Tress W. R.; Abate A.; Hagfeldt A.; Gratzel M. Incorporation of Rubidium Cations into Perovskite Solar Cells Improves Photovoltaic Performance. Science 2016, 354, 206–209. 10.1126/science.aah5557. [DOI] [PubMed] [Google Scholar]
  51. Ferreira L. G.; Marques M.; Teles L. K. Approximation to Density Functional Theory for the Calculation of Band Gaps of Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 125116. 10.1103/physrevb.78.125116. [DOI] [Google Scholar]
  52. Pelá R. R.; Caetano C.; Marques M.; Ferreira L. G.; Furthmüller J.; Teles L. K. Accurate Band Gaps of AlGaN, InGaN, and AlInN Alloys Calculations Based on LDA-1/2 Approach. Appl. Phys. Lett. 2011, 98, 151907. 10.1063/1.3576570. [DOI] [Google Scholar]
  53. Ferreira L. G.; Marques M.; Teles L. K. Slater Half-Occupation Technique Revisited: the LDA-1/2 and GGA-1/2 Approaches for Atomic Ionization Energies and Band Gaps in Semiconductors. AIP Adv. 2011, 1, 032119. 10.1063/1.3624562. [DOI] [Google Scholar]
  54. Pela R. R.; Marques M.; Teles L. K. Comparing LDA-1/2, HSE03, HSE06 and G0W0 approaches for band gap calculations of alloys. J. Phys.: Condens. Matter 2015, 27, 505502. 10.1088/0953-8984/27/50/505502. [DOI] [PubMed] [Google Scholar]
  55. Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  56. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  57. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  58. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  59. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/physrevb.59.1758. [DOI] [Google Scholar]
  60. Slater J. C. Statistical Exchange-Correlation in the Self-Consistent Field. Adv. Quantum Chem. 1972, 6, 1–92. 10.1016/s0065-3276(08)60541-9. [DOI] [Google Scholar]
  61. Slater J. C.; Johnson K. H. Self-Consistent-Field X α Cluster Method for Polyatomic Molecules and Solids. Phys. Rev. B: Solid State 1972, 5, 844–853. 10.1103/physrevb.5.844. [DOI] [Google Scholar]
  62. Tao S. X.; Cao X.; Bobbert P. A. Accurate and Efficient Band Gap Predictions of Metal Halide Perovskites Using the DFT-1/2 Method: GW Accuracy with DFT Expense. Sci. Rep. 2017, 7, 14386. 10.1038/s41598-017-14435-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Brivio F.; Caetano C.; Walsh A. Thermodynamic Origin of Photoinstability in the CH3NH3Pb(I1-xBrx)3 Hybrid Halide Perovskite Alloy. J. Phys. Chem. Lett. 2016, 7, 1083–1087. 10.1021/acs.jpclett.6b00226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Sher A.; van Schilfgaarde M.; Chen A.-B.; Chen W. Quasichemical Approximation in Binary Alloys. Phys. Rev. B: Condens. Matter Mater. Phys. 1987, 36, 4279–4295. 10.1103/physrevb.36.4279. [DOI] [PubMed] [Google Scholar]
  65. Grote C.; Berger R. F. Strain Tuning of Tin-Halide and Lead-Halide Perovskites: A First-Principles Atomic and Electronic Structure Study. J. Phys. Chem. C 2015, 119, 22832–22837. 10.1021/acs.jpcc.5b07446. [DOI] [Google Scholar]
  66. Thiele G.; Serr B. Crystal Structure of Rubidium Triiodostannate (II), RbSnI3. Z. Kristallog.—Cryst. Mater. 1995, 210, 64. 10.1524/zkri.1995.210.1.64. [DOI] [Google Scholar]
  67. Scaife D. E.; Weller P. F.; Fisher W. G. Crystal preparation and properties of cesium tin(II) trihalides. J. Solid State Chem. 1974, 9, 308–314. 10.1016/0022-4596(74)90088-7. [DOI] [Google Scholar]
  68. Lang L.; Zhang Y.-Y.; Xu P.; Chen S.; Xiang H. J.; Gong X. G. Three-Step Approach for Computing Band Offsets and Its Application to Inorganic ABX3 Halide Perovskites. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 075102. 10.1103/physrevb.92.075102. [DOI] [Google Scholar]
  69. Krishnamoorthy T.; Ding H.; Yan C.; Leong W. L.; Baikie T.; Zhang Z.; Sherburne M.; Li S.; Asta M.; Mathews N.; et al. Lead-Free Germanium Iodide Perovskite Materials for Photovoltaic Applications. J. Mater. Chem. A 2015, 3, 23829–23832. 10.1039/c5ta05741h. [DOI] [Google Scholar]
  70. Carignano M. A.; Aravindh S. A.; Roqan I. S.; Even J.; Katan C. Critical Fluctuations and Anharmonicity in Lead Iodide Perovskites from Molecular Dynamics Supercell Simulations. J. Phys. Chem. C 2017, 121, 20729–20738. 10.1021/acs.jpcc.7b08220. [DOI] [Google Scholar]
  71. Zhou X.; Jankowska J.; Dong H.; Prezhdo O. V. Recent Theoretical Progress in the Development of Perovskite Photovoltaic Materials. J. Energy Chem. 2017, 27, 637. 10.1016/j.jechem.2017.10.010. [DOI] [Google Scholar]
  72. Ma C.-G.; Krasnenko V.; Brik M. G. First-principles calculations of different (001) surface terminations of three cubic perovskites CsCaBr3, CsGeBr3, and CsSnBr3. J. Phys. Chem. Solids 2018, 115, 289–299. 10.1016/j.jpcs.2017.12.052. [DOI] [Google Scholar]
  73. Ju M.-G.; Dai J.; Ma L.; Zeng X. C. Lead-Free Mixed Tin and Germanium Perovskites for Photovoltaic Application. J. Am. Chem. Soc. 2017, 139, 8038–8043. 10.1021/jacs.7b04219. [DOI] [PubMed] [Google Scholar]
  74. Da Silva E. L.; Skelton J. M.; Parker S. C.; Walsh A. Phase Stability and Transformations in the Halide Perovskite CsSnI3. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 144107. 10.1103/physrevb.91.144107. [DOI] [Google Scholar]
  75. Marshall K. P.; Tao S.; Walker M.; Cook D. S.; Lloyd-Hughes J.; Varagnolo S.; Wijesekara A.; Walker D.; Walton R. I.; Hatton R. A. Cs1–xRbxSnI3 Light Harvesting Semiconductors for Perovskite Photovoltaics. Mater. Chem. Front. 2018, 2, 1515–1522. 10.1039/c8qm00159f. [DOI] [Google Scholar]
  76. Saliba M.; Matsui T.; Seo J.-Y.; Domanski K.; Correa-Baena J.-P.; Nazeeruddin M. K.; Zakeeruddin S. M.; Tress W.; Abate A.; Hagfeldt A.; Grätzel M. Cesium-Containing Triple Cation Perovskite Solar Cells: Improved Stability, Reproducibility and High Efficiency. Energy Environ. Sci. 2016, 9, 1989–1997. 10.1039/c5ee03874j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Marshall K. P.; Walker M.; Walton R. I.; Hatton R. A. Elucidating the role of the hole-extracting electrode on the stability and efficiency of inverted CsSnI3/C60 perovskite photovoltaics. J. Mater. Chem. A 2017, 5, 21836–21845. 10.1039/c7ta05967a. [DOI] [Google Scholar]
  78. Unger E. L.; Kegelmann L.; Suchan K.; Sörell D.; Korte L.; Albrecht S. Roadmap and Roadblocks for the Band Gap Tunability of Metal Halide Perovskites. J. Mater. Chem. A 2017, 5, 11401–11409. 10.1039/c7ta00404d. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b04013_si_002.pdf (1.5MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES