Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jul 31;18(8):5324–5328. doi: 10.1021/acs.nanolett.8b02437

Ultrasensitive Displacement Noise Measurement of Carbon Nanotube Mechanical Resonators

S L de Bonis †, C Urgell †, W Yang †, C Samanta †, A Noury †, J Vergara-Cruz †, Q Dong ‡, Y Jin ‡, A Bachtold †,✉
PMCID: PMC6089494  PMID: 30062893

Abstract

graphic file with name nl-2018-02437n_0004.jpg

Mechanical resonators based on a single carbon nanotube are exceptional sensors of mass and force. The force sensitivity in these ultralight resonators is often limited by the noise in the detection of the vibrations. Here, we report on an ultrasensitive scheme based on a RLC resonator and a low-temperature amplifier to detect nanotube vibrations. We also show a new fabrication process of electromechanical nanotube resonators to reduce the separation between the suspended nanotube and the gate electrode down to ∼150 nm. These advances in detection and fabrication allow us to reach Inline graphic displacement sensitivity. Thermal vibrations cooled cryogenically at 300 mK are detected with a signal-to-noise ratio as high as 17 dB. We demonstrate Inline graphic force sensitivity, which is the best force sensitivity achieved thus far with a mechanical resonator. Our work is an important step toward imaging individual nuclear spins and studying the coupling between mechanical vibrations and electrons in different quantum electron transport regimes.

Keywords: Nanomechanical resonators, displacement sensitivity, force sensitivity, NEMS, carbon nanotube

The smallest operational mechanical resonators are based on low-dimensional materials, such as carbon nanotubes,1 graphene,2−4 semiconducting nanowires,5−8 and levitated particles.9,10 Such resonators are fantastic sensors of external forces11−14 and the adsorption of mass.15−17 They also provide a versatile platform for fundamental science, including the study of noise,18−20 nonlinear phenomena,21−24 electron–phonon coupling,25−29 and light–matter interaction.30,31 The greatest challenge with these tiny resonators is to transduce their mechanical vibrations into a measurable electrical or optical output signal. Novel detection methods have been continuously developed over the years.32−47 This effort has often been paid off with the improvement of sensing capabilities and the measurement of unexpected phenomena.

Care has to be taken to avoid heating when improving the detection of the motion. The transduction of the motion is achieved by applying some input power to the resonator. In the case of nanotube resonators, the input power is usually related to the oscillating voltage applied across the nanotube1 or the laser beam illuminating the nanotube.38,47 The displacement sensitivity becomes better when increasing the input power. However, the input power has to be kept low enough to avoid electrical Joule heating and optical adsorption heating. Heating is especially prominent in tiny objects, such as nanotubes, because of their small heat capacity. Heating is detrimental, because it deteriorates the force and the mass sensitivity and increases the number of quanta of vibrational energy.

Here, we report on a novel detection method that allows us to measure the mechanical vibrations of nanotube resonators with an unprecedented sensitivity. The detection consists in measuring the electrical signal with a RLC resonator and a high electron mobility transistor (HEMT) amplifier cooled at liquid-helium temperature. In order to further improve the detection, we developed a new fabrication process to enhance the capacitive coupling between the ultraclean carbon nanotube and the gate electrode. This allows us to achieve Inline graphic displacement sensitivity when the temperature of the measured eigenmode is 120 mK. At higher temperature, the resonator can be probed with larger input power, so that the sensitivity reaches Inline graphic at 300 mK.

We use a new fabrication process to grow ultraclean carbon nanotube resonators suspended over shallow trenches. Figure 1a shows an ∼1.3 μm long nanotube contacted electrically to two electrodes and separated from the local gate electrode by ∼150 nm. The electrodes made from platinum with a tungsten adhesion layer are evaporated on top of silicon dioxide grown by plasma-enhanced chemical vapor deposition. Nanotubes are grown by the “fast heating” chemical vapor deposition method in the last fabrication step.48 This method consists in rapidly sliding the quartz tube through the oven under a flow of methane, so that the sample moves from a position outside of the oven to the center of the oven, whose temperature is Tgrowth = 820 °C. This growth process has two assets compared to the usual growth of nanotube resonators.37 It allows us to suspend nanotubes over wide trenches. In addition, the electrodes are less prone to melt and change shape.

Figure 1.

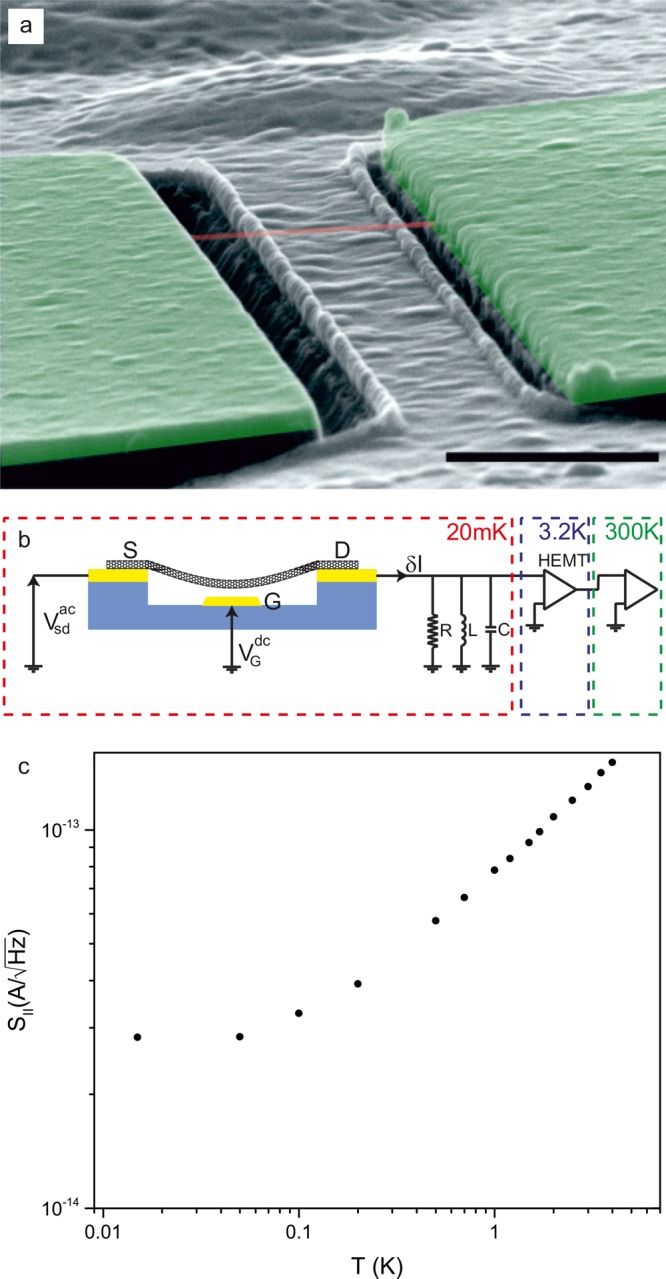
Figure 1

Open in a new tab

Nantotube resonator and electrical circuit for the detection of the vibrations. (a) False-color scanning electron microscopy image of a typical nanotube resonator fabricated with the “fast heating” chemical vapor deposition method. The ∼20 nm high ridges at the edges of the gate electrodes are attributed to resist residues. The scale bar is 1 μm. (b) Schematic of the measurement of the nanotube vibrations using the RLC resonator and the HEMT amplifier cooled at 3.2 K. The base temperature of the cryostat is ∼20 mK. An oscillating voltage with amplitude Vsdac is applied between electrodes S and D, and a constant voltage VG is applied to electrode G. (c) Temperature dependence of the current noise floor of the circuit measured at ωRLC.

Mechanical vibrations are detected electrically using a RLC resonator and a HEMT amplifier cooled at liquid–helium temperature (Figure 1b). Displacement modulation is transduced capacitively into current modulation by applying an input oscillating voltage Vsdac across the nanotube.1,12,37 The frequency ωsd/2π of the oscillating voltage is set to match ωsd = ω0 ± ωRLC, where ω0/2π is the resonance frequency of the nanotube resonator and ωRLC/2π = 1.25 MHz the resonance frequency of the RLC resonator. Driven vibrations are measured with the two-source method.1 Thermal vibrations are measured by recording the current noise at ∼ωRLC.12,37 These current noise measurements are similar to those recently carried out on quantum electron devices.49−51

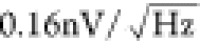The RLC resonator and the HEMT amplifier52 allow us to reduce the current noise floor at ∼ωRLC down to Inline graphic below ∼100 mK (Figure 1c). The current noise floor is temperature dependent above ∼100 mK because of the Johnson–Nyquist noise of the impedance of the RLC resonator. Below ∼100 mK, the Johnson–Nyquist noise becomes vanishingly small. The noise floor is then given by the current noise (Inline graphic) and the voltage noise (Inline graphic) of the HEMT amplifier and the voltage noise of the room-temperature amplifier. The gain of the HEMT amplifier is set at 5.6. The inductance of the circuit is given by the 66 μH inductance soldered onto a printed-circuit board (PCB). The 242 pF capacitance measured from the RLC resonance frequency comes from the capacitance of the radio frequency cables and the low-pass filter VLFX-80 between the device and the HEMT. The 7.52 kΩ resistance obtained from the 87 kHz line width of the RLC resonator is attributed to the 10 kΩ resistance soldered onto the PCB and the input impedance of the HEMT amplifier.

The lowest-lying flexural eigenmodes are identified by capacitively driving the resonator with an oscillating force and measuring the motion with the two-source method.1 The dependence of the resonance frequency as a function of the static voltage VGdc applied to the gate electrode demonstrates that the measured resonance is related to a mechanical eigenmode of the nanotube (Figure 2a). The amplitude of the lowest-frequency resonance is much larger than that of the second detected resonance (Figure 2b). We conclude that the detected eignmodes are polarized in the direction perpendicular to the surface of the gate electrode to a good approximation and that eigenmodes polarized in the parallel direction cannot be detected.

Figure 2.

Figure 2

Open in a new tab

Driven and thermal vibrations of the nanotube resonator. (a) Gate voltage dependence of the resonance frequency of the fundamental eigenmode. The small positive offset voltage Voff = 0.119 V due to the work function difference between the nanotube and the gate electrode is subtracted from the applied VGdc value. (b) Driven response of the two lowest-frequency detected mechanical eigenmodes as a function of the drive frequency measured with the two-source method. The resonances are indicated by two red arrows. (c) Spectrum of the displacement noise of the fundamental eigenmode measured at the base temperature of the cryostat when applying VG = −0.21 V and Vsdac = 40 μV. The resonance frequency f0 is given in the figure. (d) Variance of the displacement measured as a function of cryostat temperature.

The thermal vibrations are recorded at the base temperature of the dilution cryostat (Figure 2c). We switch off the driving force, and the displacement noise is recorded with the method described in refs.12,37 The quality factor is Q = 627,000 with the gate voltage set at VGdc = −0.21 V. We choose this gate voltage so that the electron transport is not in the Coulomb blockade regime. The Q-factor becomes lower at more negative gate voltages because of electrical losses53 and at positive gate voltages due to Coulomb blockade.25 We measure the dependence of the variance of the displacement ⟨δz2⟩ on the cryostat temperature T (Figure 2d). The linear dependence is in agreement with the equipartition theorem mω0⟨δz2⟩ = kbT, where m is the effective mass of the resonator. We obtain m = 8.6 ag from the slope, which is consistent with the mass expected for an ∼1.3 μm long nanotube. Below ∼120 mK, the eigenmode does not thermalize well with the cryostat (Figure 2d). Measurements on a second nanotube resonator show that the eigenmode reaches ∼50 mK (Supporting Information). The origin of this poor thermalization at low temperature may be related to a nonthermal force noise, such as the electrostatic force noise related to the voltage noise in the device.54

The force sensitivity derived from the noise spectrum in Figure 2c is Inline graphic. Because the thermal resonance is described by a Lorentzian line shape, the force sensitivity is quantified from the total displacement noise at resonance frequency using SFF = Szz(ω0)/|χ(ω0)|2 with the mechanical susceptibility |χ(ω0)| = Q/mω02. The force sensitivity is given to a large extent by the thermal force noise of the resonator Inline graphic, which is the fundamental limit of the force sensitivity set by the fluctuation–dissipation theorem. The noise of the imprecision in the detection contributes to the force sensitivity by a low amount. The error bar in the estimation of the force sensitivity originates essentially from the uncertainty in the nanotube diameter and the separation between the nanotube and the gate electrode. Table 1 shows that the force sensitivity measured in this work is better than what is reported with resonators microfabricated from bulk material55−57 and resonators based on nanotube,12 semiconducting nanowire,13,14,58 graphene,54 and levitating particles.18 In ref (37), the reported thermal force noise is lower but the cross-correlation noise measurement does not quantify the force noise due to the imprecision in the detection so that the total force noise cannot be quantified.

Table 1. Thermal Force Noise SFFth, Force Noise Due to the Imprecision of the Detection SFF, and Total Force Sensitivity SFF for Different Resonatorsa.

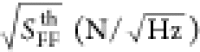Inline graphic Inline graphic Inline graphic description
4.0 × 10–21 1.6 × 10–21 4.3 × 10–21 nanotube (this work)
2.0 × 10–20 negligible 2.0 × 10–20 levitating particle18
2.7 × 10–19 2.7 × 10–19 3.9 × 10–19 graphene54
1.0 × 10–18 negligible 1.0 × 10–18 silicon nanowire58
5.0 × 10–18 negligible 5.0 × 10–18 GaAs/AlGaAs nanowire14
1.6 × 10–19 1.0 × 10–19 1.9 × 10–19 microfabricated ladder56
5.1 × 10–19 negligible 5.1 × 10–19 microfabricated beam55
2.0 × 10–17 negligible 2.0 × 10–17 microfabricated trampoline57
1.2 × 10–20 unknown unknown nanotube12
∼1 × 10–21 unknown unknown nanotube37
Open in a new tab
a

The three force noises are related by SFFth + SFF = SFF.

We now look at how the displacement noise is affected by the input power related to the oscillating voltage Vsdac (Figures 3a-d). The variance of the displacement increases abruptly above Vsd ≃ 80 μV when the cryostat is at base temperature (Figure 3c). This indicates the rise of the thermal vibration amplitude due to Joule heating. By contrast, the variance of the displacement remains constant over the whole range of Vsdac that we apply when the cryostat temperature is set at 300 mK (Figure 3d).

Figure 3.

Figure 3

Open in a new tab

Spectrum of the displacement noise modified by the oscillating voltage with amplitude Vsdac applied across the nanotube. (a) Spectrum of the displacement noise of the fundamental eigenmode measured at the base temperature of the cryostat when applying VG = −0.255 V and Vsdac = 70 μV. (b) Same as (a) but with the cryostat temperature set at 300 mK and Vsd = 400 μV. (c,d) Dependence of the variance of the displacement on Vsdac measured at the base temperature of the cryostat and 300 mK. (e,f) Dependence of the displacement sensitivity on Vsd measured at the base temperature of the cryostat and 300 mK.

Our detection scheme allows us to reach an excellent displacement sensitivity for input powers below the onset of Joule heating. The displacement sensitivity is given by the noise floor of the spectrum of thermal vibrations. The displacement sensitivity gets better when increasing Vsdac (Figures 3e,f). The displacement sensitivity at base temperature is Inline graphic at Vsd = 80 μV before that Joule heating starts to increase the variance of the displacement. When the cryostat temperature is set at 300 mK, the displacement sensitivity is Inline graphic at the largest Vsdac value that we apply. The corresponding signal-to-noise ratio in the spectrum of thermal vibrations is 17 dB (Figure 3b). The measured displacement sensitivity Szz scales as (1/Vsdac)2 (Figures 3e,f), indicating that Szz is limited by the noise of the detection circuit and not by the electron shot noise through the nanotube.59 The Q-factor in Figure 3 is lower than that in Figure 2c due to an unknown reason while cycling the cryostat through room temperature; the resonance frequency and the mass are not modified by the thermal cycling.

In conclusion, we report on a detection scheme of nanotube resonators with an unprecedented displacement sensitivity. It allows us to reach 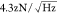Inline graphic force sensitivity, which surpasses what has been achieved with mechanical resonators to date. This high force sensitivity is an important step toward detecting individual nuclear spins with nuclear magnetic resonance measurements.60,61 The coupling between mechanical vibrations and spins can be achieved by applying a gradient of magnetic field that is generated with the current biased through the gate electrode in Figure 1a.58 In this context, the new fabrication process of nanotube resonators presented in this Letter is useful for increasing the gradient of the magnetic field, because it reduces the separation between the current-carrying electrode and the nanotube down to ∼150 nm. The device layout might also allow us to carry out magnetic resonance force microscopy (MRFM) measurements to image the location of individual nuclear spins adsorbed along the nanotube. Imaging can be done by periodically applying radio frequency pulses though the current-carrying electrode.62 Moreover, the advances in fabrication and detection described in this work offer new possibilities for studying the strong coupling between electrons and vibrations in nanoscale resonators.63−66 In the Coulomb blockade regime, the system has been predicted to feature a transition toward a mechanically bistable and blocked-current state.66−69 This hitherto unobserved transition is expected to occur at higher temperature for shorter separation between the nanotube and the gate electrode.66 The high quality displacement noise spectra reported here might allow us to study this transition in details66 as well as the different cooling schemes that have been proposed theoretically using different quantum electron transport regimes.70−74

Acknowledgments

This work is supported by the ERC advanced Grant 692876, the Foundation Cellex, the CERCA Programme, AGAUR, Severo Ochoa (SEV-2015-0522), the Grant FIS2015-69831-P of MINECO, and the Fondo Europeo de Desarrollo Regional (FEDER).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b02437.

  • Further information on the calibration of the displacement sensitivity and the force sensitivity; mechanical and electrical characterization of the device; displacement variance as a function of temperature of a second device (PDF)

Author Present Address

∥ (A.N.) Laboratoire Charles Coulomb (L2C), Univ Montpellier, CNRS, Montpellier, France.

Author Contributions

§ S.L.d.B. and C.U. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

nl8b02437_si_001.pdf (161.1KB, pdf)

References

  1. Sazonova V.; Yaish Y.; Ustunel H.; Roundy D.; Arias T. A.; McEuen P. L. Nature 2004, 431, 284. 10.1038/nature02905. [DOI] [PubMed] [Google Scholar]
  2. Bunch J. S.; van der Zande A. M.; Verbridge S. S.; Frank I. W.; Tanenbaum D. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Science 2007, 315, 490. 10.1126/science.1136836. [DOI] [PubMed] [Google Scholar]
  3. Singh V.; Sengupta S.; Solanki H. S.; Dhall R.; Allain A.; Dhara S.; Pant P.; Deshmukh M. M. Nanotechnology 2010, 21, 165204. 10.1088/0957-4484/21/16/165204. [DOI] [PubMed] [Google Scholar]
  4. Will M.; Hamer M.; Muller M.; Noury A.; Weber P.; Bachtold A.; Gorbachev R. V.; Stampfer C.; Guttinger J. Nano Lett. 2017, 17, 5950. 10.1021/acs.nanolett.7b01845. [DOI] [PubMed] [Google Scholar]
  5. Feng X. L.; He R.; Yang P.; Roukes M. L. Nano Lett. 2007, 7, 1953. 10.1021/nl0706695. [DOI] [Google Scholar]
  6. Gil-Santos E.; Ramos D.; Martinez J.; Fernandez-Regulez M.; Garcia R.; San Paulo A.; Calleja M.; Tamayo J. Nat. Nanotechnol. 2010, 5, 641. 10.1038/nnano.2010.151. [DOI] [PubMed] [Google Scholar]
  7. Sansa M.; Fernandez-Regulez M.; San Paulo A.; Perez-Murano F. Appl. Phys. Lett. 2012, 101, 243115. 10.1063/1.4771982. [DOI] [Google Scholar]
  8. Montinaro M.; Wust G.; Munsch M.; Fontana Y.; Russo-Averchi E.; Heiss M.; Fontcuberta i Morral A.; Warburton R. J.; Poggio M. Nano Lett. 2014, 14, 4454. 10.1021/nl501413t. [DOI] [PubMed] [Google Scholar]
  9. Gieseler J.; Deutsch B.; Quidant R.; Novotny L. Phys. Rev. Lett. 2012, 109, 103603. 10.1103/PhysRevLett.109.103603. [DOI] [PubMed] [Google Scholar]
  10. Kiesel N.; Blaser F.; Delic U.; Grass D.; Kaltenbaek R.; Aspelmeyer M. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 14180. 10.1073/pnas.1309167110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Nichol J. M.; Hemesath E. R.; Lauhon L. J.; Budakian R. Appl. Phys. Lett. 2008, 93, 193110. 10.1063/1.3025305. [DOI] [Google Scholar]
  12. Moser J.; Güttinger J.; Eichler A.; Esplandiu M. J.; Liu D. E.; Dykman M. I.; Bachtold A. Nat. Nanotechnol. 2013, 8, 493. 10.1038/nnano.2013.97. [DOI] [PubMed] [Google Scholar]
  13. de Lepinay L. M.; Pigeau B.; Besga B.; Vincent P.; Poncharal P.; Arcizet O. Nat. Nanotechnol. 2016, 12, 156. 10.1038/nnano.2016.193. [DOI] [PubMed] [Google Scholar]
  14. Rossi N.; Braakman F. R.; Cadeddu D.; Vasyukov D.; Tutuncuoglu G.; Fontcuberta i Morral A.; Poggio M. Nat. Nanotechnol. 2016, 12, 150. 10.1038/nnano.2016.189. [DOI] [PubMed] [Google Scholar]
  15. Chiu H.-Y.; Hung P.; Postma H. W. C.; Bockrath M. Nano Lett. 2008, 8, 4342. 10.1021/nl802181c. [DOI] [PubMed] [Google Scholar]
  16. Wang Z.; Wei J.; Morse P.; Dash J. G.; Vilches O. E.; Cobden D. H. Science 2010, 327, 552. 10.1126/science.1182507. [DOI] [PubMed] [Google Scholar]
  17. Chaste J.; Eichler A.; Moser J.; Ceballos G.; Rurali R.; Bachtold A. Nat. Nanotechnol. 2012, 7, 301. 10.1038/nnano.2012.42. [DOI] [PubMed] [Google Scholar]
  18. Gieseler J.; Novotny L.; Quidant R. Nat. Phys. 2013, 9, 806. 10.1038/nphys2798. [DOI] [Google Scholar]
  19. Zhang Y.; Moser J.; Güttinger J.; Bachtold A.; Dykman M. I. Phys. Rev. Lett. 2014, 113, 255502. 10.1103/PhysRevLett.113.255502. [DOI] [PubMed] [Google Scholar]
  20. Miao T. F.; Yeom S.; Wang P.; Standley B.; Bockrath M. Nano Lett. 2014, 14, 2982. 10.1021/nl403936a. [DOI] [PubMed] [Google Scholar]
  21. Eichler A.; Moser J.; Chaste J.; Zdrojek M.; Wilson-Rae I.; Bachtold A. Nat. Nanotechnol. 2011, 6, 339. 10.1038/nnano.2011.71. [DOI] [PubMed] [Google Scholar]
  22. Deng G.-W.; Zhu D.; Wang X.-H.; Zou C.-L.; Wang J.-T.; Li H.-O.; Cao G.; Liu D.; Li Y.; Xiao M.; Guo G.-C.; Jiang K.-L.; Dai X.-C.; Guo G.-P. Nano Lett. 2016, 16, 5456. 10.1021/acs.nanolett.6b01875. [DOI] [PubMed] [Google Scholar]
  23. De Alba R.; Massel F.; Storch I. R.; Abhilash T. S.; Hui A.; McEuen P. L.; Craighead H. G.; Parpia J. M. Nat. Nanotechnol. 2016, 11, 741. 10.1038/nnano.2016.86. [DOI] [PubMed] [Google Scholar]
  24. Mathew J. P.; Patel R. N.; Borah A.; Vijay R.; Deshmukh M. M. Nat. Nanotechnol. 2016, 11, 747. 10.1038/nnano.2016.94. [DOI] [PubMed] [Google Scholar]
  25. Lassagne B.; Tarakanov Y.; Kinaret J.; Garcia-Sanchez D.; Bachtold A. Science 2009, 325, 1107. 10.1126/science.1174290. [DOI] [PubMed] [Google Scholar]
  26. Steele G. A.; Huttel A. K.; Witkamp B.; Poot M.; Meerwaldt H. B.; Kouwenhoven L. P.; van der Zant H. S. J. Science 2009, 325, 1103. 10.1126/science.1176076. [DOI] [PubMed] [Google Scholar]
  27. Ganzhorn M.; Wernsdorfer W. Phys. Rev. Lett. 2012, 108, 175502. 10.1103/PhysRevLett.108.175502. [DOI] [PubMed] [Google Scholar]
  28. Benyamini A.; Hamo A.; Kusminskiy S. V.; von Oppen F.; Ilani S. Nat. Phys. 2014, 10, 151. 10.1038/nphys2842. [DOI] [Google Scholar]
  29. Ares N.; Pei T.; Mavalankar A.; Mergenthaler M.; Warner J. H.; Briggs G. A. D.; Laird E. A. Phys. Rev. Lett. 2016, 117, 170801. 10.1103/PhysRevLett.117.170801. [DOI] [PubMed] [Google Scholar]
  30. Gloppe A.; Verlot P.; Dupont-Ferrier E.; Siria A.; Poncharal P.; Bachelier G.; Vincent P.; Arcizet O. Nat. Nanotechnol. 2014, 9, 920. 10.1038/nnano.2014.189. [DOI] [PubMed] [Google Scholar]
  31. Reserbat-Plantey A.; Schadler K. G.; Gaudreau L.; Navickaite G.; Guttinger J.; Chang D.; Toninelli C.; Bachtold A.; Koppens F. H. L. Nat. Commun. 2016, 7, 10218. 10.1038/ncomms10218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Purcell S. T.; Vincent P.; Journet C.; Binh V. T. Phys. Rev. Lett. 2002, 89, 276103. 10.1103/PhysRevLett.89.276103. [DOI] [PubMed] [Google Scholar]
  33. Chen C.; Rosenblatt S.; Bolotin K. I.; Kalb W.; Kim P.; Kymissis I.; Stormer H. L.; Heinz T. F.; Hone J. Nat. Nanotechnol. 2009, 4, 861. 10.1038/nnano.2009.267. [DOI] [PubMed] [Google Scholar]
  34. Huttel A. K.; Steele G. A.; Witkamp B.; Poot M.; Kouwenhoven L. P.; van der Zant H. S. J. Nano Lett. 2009, 9, 2547. 10.1021/nl900612h. [DOI] [PubMed] [Google Scholar]
  35. Gouttenoire V.; Barois T.; Perisanu S.; Leclercq J. L.; Purcell S. T.; Vincent P.; Ayari A. Small 2010, 6, 1060. 10.1002/smll.200901984. [DOI] [PubMed] [Google Scholar]
  36. Arcizet O.; Jacques V.; Siria A.; Poncharal P.; Vincent P.; Seidelin S. Nat. Phys. 2011, 7, 879. 10.1038/nphys2070. [DOI] [Google Scholar]
  37. Moser J.; Eichler A.; Guttinger J.; Dykman M. I.; Bachtold A. Nat. Nanotechnol. 2014, 9, 1007. 10.1038/nnano.2014.234. [DOI] [PubMed] [Google Scholar]
  38. Stapfner S.; Ost L.; Hunger D.; Reichel J.; Favero I.; Weig E. M. Appl. Phys. Lett. 2013, 102, 151910. 10.1063/1.4802746. [DOI] [Google Scholar]
  39. Singh V.; Bosman S. J.; Schneider B. H.; Blanter Y. M.; Castellanos-Gomez A.; Steele G. A. Nat. Nanotechnol. 2014, 9, 820. 10.1038/nnano.2014.168. [DOI] [PubMed] [Google Scholar]
  40. Song X.; Oksanen M.; Li J.; Hakonen P. J.; Sillanpa M. A. Phys. Rev. Lett. 2014, 113, 027404. 10.1103/PhysRevLett.113.027404. [DOI] [PubMed] [Google Scholar]
  41. Weber P.; Güttinger J.; Tsioutsios I.; Chang D. E.; Bachtold A. Nano Lett. 2014, 14, 2854. 10.1021/nl500879k. [DOI] [PubMed] [Google Scholar]
  42. Schneider B. H.; Singh V.; Venstra W. J.; Meerwaldt H. B.; Steele G. A. Nat. Commun. 2014, 5, 5819. 10.1038/ncomms6819. [DOI] [PubMed] [Google Scholar]
  43. Nigues A.; Siria A.; Verlot P. Nat. Commun. 2015, 6, 8104. 10.1038/ncomms9104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Cole R. M.; Brawley G. A.; Adiga V. P.; De Alba R.; Parpia J. M.; Ilic B.; Craighead H. G.; Bowen W. P. Phys. Rev. Appl. 2015, 3, 024004. 10.1103/PhysRevApplied.3.024004. [DOI] [Google Scholar]
  45. Tsioutsios I.; Tavernarakis A.; Osmond J.; Verlot P.; Bachtold A. Nano Lett. 2017, 17, 1748. 10.1021/acs.nanolett.6b05065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Güttinger J.; Noury A.; Weber P.; Eriksson A. M.; Lagoin C.; Moser J.; Eichler C.; Wallraff A.; Isacsson A.; Bachtold A. Nat. Nanotechnol. 2017, 12, 631. 10.1038/nnano.2017.86. [DOI] [PubMed] [Google Scholar]
  47. Tavernarakis A.; Stavrinadis A.; Nowak A.; Tsioutsios I.; Bachtold A.; Verlot P. Nat. Commun. 2018, 9, 662. 10.1038/s41467-018-03097-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Huang S.; Woodson M.; Smalley R.; Liu J. Nano Lett. 2004, 4, 1025. 10.1021/nl049691d. [DOI] [Google Scholar]
  49. Jezouin S.; Parmentier F. D.; Anthore A.; Gennser U.; Cavanna A.; Jin Y.; Pierre F. Science 2013, 342, 601. 10.1126/science.1241912. [DOI] [PubMed] [Google Scholar]
  50. Bocquillon E.; Freulon V.; Berroir J.-M.; Degiovanni P.; Placais B.; Cavanna A.; Jin Y.; Feve G. Science 2013, 339, 1054. 10.1126/science.1232572. [DOI] [PubMed] [Google Scholar]
  51. Jullien T.; Roulleau P.; Roche B.; Cavanna A.; Jin Y.; Glattli D. C. Nature 2014, 514, 603. 10.1038/nature13821. [DOI] [PubMed] [Google Scholar]
  52. Dong Q.; Liang Y. X.; Ferry D.; Cavanna A.; Gennser U.; Couraud L.; Jin Y. Appl. Phys. Lett. 2014, 105, 013504. 10.1063/1.4887368. [DOI] [Google Scholar]
  53. Song X.; Oksanen M.; Sillanpa M. A.; Craighead H. G.; Parpia J. M.; Hakonen P. J. Nano Lett. 2012, 12, 198. 10.1021/nl203305q. [DOI] [PubMed] [Google Scholar]
  54. Weber P.; Guttinger J.; Noury A.; Vergara-Cruz J.; Bachtold A. Nat. Commun. 2016, 7, 12496. 10.1038/ncomms12496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Teufel J. D.; Donner T.; Castellanos-Beltran M. A.; Harlow J. W.; Lehnert K. W. Nat. Nanotechnol. 2009, 4, 820. 10.1038/nnano.2009.343. [DOI] [PubMed] [Google Scholar]
  56. Heritier M.; Eichler A.; Pan Y.; Grob U.; Shorubalko I.; Krass M. D.; Tao Y.; Degen C. L. Nano Lett. 2018, 18, 1814. 10.1021/acs.nanolett.7b05035. [DOI] [PubMed] [Google Scholar]
  57. Reinhardt C.; Muller T.; Bourassa A.; Sankey J. C. Phys. Rev. X 2016, 6, 021001. 10.1103/PhysRevX.6.021001. [DOI] [Google Scholar]
  58. Nichol J. M.; Hemesath E. R.; Lauhon L. J.; Budakian R. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 054414. 10.1103/PhysRevB.85.054414. [DOI] [Google Scholar]
  59. Wang Y.; Pistolesi F. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 035410. 10.1103/PhysRevB.95.035410. [DOI] [Google Scholar]
  60. Degen C. L.; Poggio M.; Mamin H. J.; Rettner C. T.; Rugar D. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 1313. 10.1073/pnas.0812068106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Mamin H. J.; Poggio M.; Degen C. L.; Rugar D. Nat. Nanotechnol. 2007, 2, 301. 10.1038/nnano.2007.105. [DOI] [PubMed] [Google Scholar]
  62. Nichol J. M.; Naibert T. R.; Hemesath E. R.; Lauhon L. J.; Budakian R. Phys. Rev. X 2013, 3, 031016. 10.1103/PhysRevX.3.049901. [DOI] [Google Scholar]
  63. Armour A. D.; Blencowe M. P.; Zhang Y. Phys. Rev. B: Condens. Matter Mater. Phys. 2004, 69, 125313. 10.1103/PhysRevB.69.125313. [DOI] [Google Scholar]
  64. Clerk A. A.; Bennett S. New J. Phys. 2005, 7, 238. 10.1088/1367-2630/7/1/238. [DOI] [Google Scholar]
  65. Naik A.; Buu O.; LaHaye M. D.; Armour A. D.; Clerk A. A.; Blencowe M. P.; Schwab K. C. Nature 2006, 443, 193. 10.1038/nature05027. [DOI] [PubMed] [Google Scholar]
  66. Micchi G.; Avriller R.; Pistolesi F. Phys. Rev. Lett. 2015, 115, 206802. 10.1103/PhysRevLett.115.206802. [DOI] [PubMed] [Google Scholar]
  67. Pistolesi F.; Labarthe S. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 165317. 10.1103/PhysRevB.76.165317. [DOI] [Google Scholar]
  68. Weick G.; von Oppen F.; Pistolesi F. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 035420. 10.1103/PhysRevB.83.035420. [DOI] [Google Scholar]
  69. Micchi G.; Avriller R.; Pistolesi F. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 125417. 10.1103/PhysRevB.94.125417. [DOI] [Google Scholar]
  70. Zippilli S.; Morigi G.; Bachtold A. Phys. Rev. Lett. 2009, 102, 096804. 10.1103/PhysRevLett.102.096804. [DOI] [PubMed] [Google Scholar]
  71. Santandrea F.; Gorelik L. Y.; Shekhter R. I.; Jonson M. Phys. Rev. Lett. 2011, 106, 186803. 10.1103/PhysRevLett.106.186803. [DOI] [PubMed] [Google Scholar]
  72. Stadler P.; Belzig W.; Rastelli G. Phys. Rev. Lett. 2014, 113, 047201. 10.1103/PhysRevLett.113.047201. [DOI] [PubMed] [Google Scholar]
  73. Arrachea L.; Bode N.; von Oppen F. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 125450. 10.1103/PhysRevB.90.125450. [DOI] [Google Scholar]
  74. Stadler P.; Belzig W.; Rastelli G. Phys. Rev. Lett. 2016, 117, 197202. 10.1103/PhysRevLett.117.197202. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl8b02437_si_001.pdf (161.1KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES