Primary Deuterium Kinetic Isotope Effects: A Probe for the Origin of the Rate Acceleration for Hydride Transfer Catalyzed by Glycerol-3-Phosphate Dehydrogenase

Abstract

Large primary deuterium kinetic isotope effects (1° DKIEs) on enzyme-catalyzed hydride transfer may be observed when the transferred hydride tunnels through the energy barrier. The following 1° DKIEs on k_cat/K_m and relative reaction driving force are reported for wild-type and mutant glycerol-3-phosphate dehydrogenase (GPDH)-catalyzed reactions of NADL (L = H, D): wild-type GPDH, ΔΔG^⧧ = 0 kcal/mol, 1° DKIE = 1.5; N270A, 5.6 kcal/mol, 3.1; R269A, 9.1 kcal/mol, 2.8; R269A + 1.0 M guanidine, 2.4 kcal/mol, 2.7; R269A/N270A, 11.5 kcal/mol, 2.4. Similar 1° DKIEs were observed on k_cat. The narrow range of 1° DKIEs (2.4–3.1) observed for a 9.1 kcal/mol change in reaction driving force provides strong evidence that these are intrinsic 1° DKIEs on rate-determining hydride transfer. Evidence is presented that the intrinsic DKIE on wild-type GPDH-catalyzed reduction of DHAP lies in this range. A similar range of 1° DKIEs (2.4–2.9) on (k_cat/K_GA, M^–1 s^–1) was reported for dianion-activated hydride transfer from NADL to glycolaldehyde (GA) [Reyes, A. C.; Amyes, T. L.; Richard, J. P. J. Am. Chem. Soc.2016, 138, 14526–14529]. These 1° DKIEs are much smaller than those observed for enzyme-catalyzed hydrogen transfer that occurs mainly by quantum mechanical tunneling. These results support the conclusion that the rate acceleration for GPDH-catalyzed reactions is due to the stabilization of the transition state for hydride transfer by interactions with the protein catalyst. The small 1° DKIEs reported for mutant GPDH-catalyzed and for wild-type dianion-activated reactions are inconsistent with a model where the dianion binding energy is utilized in the stabilization of a tunneling ready state.

We are interested in understanding the origin of the catalytic rate acceleration for the enzymatic catalysis of polar reactions, which include glycosyl transfer,¹⁻³ proton transfer,⁴⁻⁶ and decarboxylation reactions.^7,8 The activation barrier for nonenzymatic variants of these reactions is composed mainly of the thermodynamic barrier to the formation of unstable carbocation or carbanion reaction intermediates.^6,9,10 An important imperative for obtaining large rate accelerations is for the enzyme to stabilize the reaction intermediate relative to the substrate; this stabilization is expressed at late, intermediate-like transition states,¹¹ as is illustrated in Figure 1A for the triosephosphate isomerase-catalyzed deprotonation of the substrate to form an enediolate reaction intermediate.^4,12 We have also shown that interactions between orotidine 5′-monophosphate decarboxylase (OMPDC) and enzyme-bound uridine monophosphate induce a ≥10 unit decrease in the solution pK_a for the C6 uracil hydrogen.^7,13

Figure 1.

Free-energy reaction profiles that illustrate different strategies for enzymes to reduce the effective activation barrier. (A) The deprotonation of DHAP to form an enediolate phosphate intermediate catalyzed by triosephosphate isomerase.⁴ The activation barrier to the enzyme-catalyzed reaction is reduced by protein–ligand interactions that result in similar stabilization of the enediolate intermediate and the enediolate-like transition state relative to the bound substrate.¹² (B) A reaction coordinate profile for hydride transfer from NADH to the carbonyl group catalyzed by a representative dehydrogenase. The apparent activation barrier may be reduced below that for the formation of the transition state by quantum mechanical tunneling through the energy surface.

The imperatives for the catalysis of hydride transfer from NADH to the carbonyl group, for example, the reactions catalyzed by glycerol-3-phosphate dehydrogenase (GPDH, Scheme 1), are less clear. There is a requirement for the stabilization of the initial oxyanion product of hydride transfer. This may be accomplished through electrostatic and hydrogen bonding interactions with the protein¹⁴ and/or by the coordination of the oxyanion to a metal cation.¹⁵ Additionally, the effective kinetic reaction barrier may be reduced if passage over the transition state is avoided in a reaction that occurs primarily by quantum mechanical tunneling through the energy barrier.¹⁶ This is illustrated by the hypothetical reaction coordinate for hydride transfer (Figure 1B) where tunneling through the energy profile occurs at a position lower in energy than for that of the transition state.

Scheme 1. GPDH-Catalyzed Reduction of the Whole Substrate DHAP and the Dianion-Activated Reduction of Substrate Piece Glycolaldehyde.

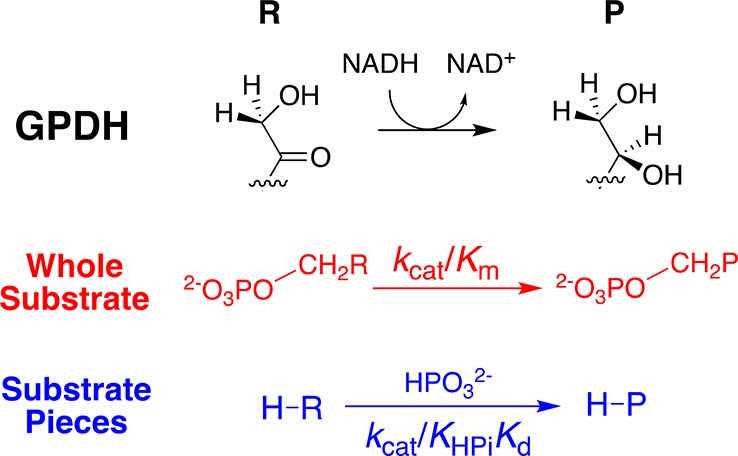
Recent discussions of the mechanism for enzyme-catalyzed hydride transfer are dominated by a consideration of the role of quantum mechanical tunneling.¹⁷⁻²⁰ We are interested in refocusing this discussion by treating tunneling and transition-state stabilization²¹ as two models for achieving enzymatic rate acceleration and examining which model provides the cleanest rationalization for experimental data. Our interest was prompted by results from studies of seemingly disparate enzymes: (i) orotidine 5′-monophosphate decarboxylase-catalyzed decarboxylation of OMP²²⁻²⁴ and triosephosphate isomerase-catalyzed isomerization of glyceraldehyde 3-phosphate through unstable carbanion reaction intermediates;^23,25,26 and (ii) glycerol-3-phosphate dehydrogenase-catalyzed hydride transfer from NADH to the carbonyl group of dihydroxyacetone phosphate (Scheme 1).^23,27 We have noted several striking similarities in the utilization of the binding energy of the substrate phosphodianion in the apparent stabilization of the transition states for these enzymatic reactions.

• (1)GPDH, OMPDC, and TIM each show a second-order rate constant of k_cat/K_m ≈ 0.1 M^–1 s^–1 for the catalysis of the reaction of a phosphodianion truncated substrate.^22,27,28 Appending the phosphodianion to the truncated substrates (e.g., Scheme 1) results in similar ca. 10⁹-fold increases in k_cat/K_m, corresponding to ca. 12 kcal/mol transition-state stabilizations from interactions between the enzyme and substrate phosphodianion.^22,25,28
• (2)GPDH, OMPDC, and TIM each show a third-order rate constant of [(k_cat/K_m)K_HPi] ≈ 10⁴ M^–2 s^–1 for the phosphite dianion activation of the reactions of a phosphodianion truncated substrate.²³ This activation by the phosphite dianion corresponds to a 6–8 kcal/mol stabilization of the respective enzymatic transition states by an interaction with the activator.²³
• (3)The active sites of GPDH, OMPDC, and TIM are divided into a catalytic domain that carries out the relevant chemistry and a dianion activation domain that utilizes the binding energy of the phosphite dianion to drive a conformational change, which activates these respective enzymes for the reaction at the catalytic site.^23,29−31
• (4)The dianion activation sites for GPDH, OMPDC, and TIM provide a similar relative transition-state stabilization from the utilization of the binding interactions from the following dianions: XYO₃^–2, FPO₃^–2, HPO₃^–2, OSO₃^–2, SSO₃^–2, and HOPO₃^–2.²³
• (5)There is a side-chain cation at the active site of each enzyme: Arg-269 for GPDH,²⁹ Arg-235 for OMPDC,³² and Lys-12 for TIM.³³ This side chain sits on the protein surface and forms an ion pair with the phosphodianion substrate, which is buried below the surface.^29,32,33
• (6)The mutation of these-side chain cations results in large increases in the barrier to formation of the respective rate-determining transition states: R269A for GPDH, 9.1 kcal/mol increase;²⁹ R235A for OMPDC, 5.6 kcal/mol increase;³² and K12G for TIM, 7.8 kcal/mol increase.³³
• (7)Small molecule analogues of the excised side chains provide efficient rescue of the activity of the mutant enzymes. The rescue represents the following transition-state stabilization by 1.0 M exogenous cation: K12G mutant of TIM, 3.4 kcal/mol stabilization by 1.0 M methylammonium cations;³⁴ R235A mutant of OMPDC, 3.0 kcal/mol stabilization by 1.0 M guanidine cation;³² and R269A mutant of GPDH, 6.7 kcal/mol stabilization by 1.0 M guanidine cation.²⁹

Our favored interpretation of these data is that GPDH, OMPDC, and TIM each utilize the phosphodianion binding energy from their respective substrates for the purpose of the stabilization of transition states for reactions that pass over an energy barrier.³⁵ However, we have not specifically addressed the question of whether GPDH utilizes the dianion binding energy to stabilize a Michaelis complex that favors efficient tunneling through the potential energy surface (Figure 1B).^19,36 This complex has been referred to as the tunneling-ready state. We report here the results of experiments designed to evaluate the role of tunneling in hydride-transfer reactions catalyzed by GPDH.

If the effective barrier to enzyme-catalyzed hydride transfer is reduced substantially by tunneling through the energy barrier, then the substantially longer quantum mechanical wavelength of −H compared with −D should give rise to more efficient tunneling for −H and a large 1° DKIE.³⁷ The 1° DKIE on wild-type GPDH-catalyzed reduction of DHAP by NADH is smaller than the intrinsic isotope effect because hydride transfer is only partly rate-determining for turnover.^38,39 We reported in a recent communication intrinsic 1° DKIEs of 2.7 ± 0.3 for the unactivated and dianion-activated human liver GPDH (hlGPDH)-catalyzed reduction of truncated substrate glycolaldehyde by NADL (Scheme 1).³⁹ These intrinsic 1° DKIEs are low, even for reactions that pass over an activation barrier, and much smaller than have been reported for hydrogen transfer that clearly proceeds with quantum mechanical tunneling through an energy barrier.⁴⁰⁻⁴²

We now report intrinsic 1° DKIEs on hydride transfer catalyzed by mutant forms of hlGPDH^29,43 and by an active complex of the R269A and guanidine cation pieces of hlGPDH.^23,44 These intrinsic 1° DKIEs on hlGPDH-catalyzed hydride transfer range from 2.3 to 3.1 and are independent of the activation barrier for enzyme-catalyzed hydride transfer. In all cases, the intrinsic isotope effects determined for reactions catalyzed by hlGPDH are smaller than those reported in earlier work for enzyme-catalyzed reactions that proceed with extensive tunneling beneath an energy barrier.⁴⁰⁻⁴²

Experimental Section

Materials

Q-Sepharose and Sephacryl S-200 were purchased from GE Healthcare. DEAE-Sephadex, Dowex 50WX4-200R (H⁺ form), nicotinamide adenine dinucleotide reduced form (NADH, disodium salt), NAD⁺ (free acid), dihydroxyacetone phosphate hemimagnesium salt, glycolaldehyde dimer, 2-(N-morpholino)ethanesulfonic acid sodium salt (MES, ≥99.5%), triethylamine (≥99.5%), triethanolamine hydrochloride (TEA·HCl, ≥99.5%), ampicillin, kanamycin sulfate, isopropyl β-d-thiogalactopyranoside (IPTG), and d,l-dithiothreitol (DTT) were purchased from Sigma-Aldrich. Protease inhibitor tablets (Complete) and bovine serum albumin, fraction V (BSA) were purchased from Roche. Ammonium sulfate (enzyme grade), guanidinium hydrochloride (electrophoresis grade, min. 99%), sodium hydroxide (1.0 N), and hydrochloric acid (1.0 N) were purchased from Fisher. Sodium phosphite (dibasic, pentahydrate) was purchased from Fluka. The water content of sodium phosphite was reduced to Na₂HPO₃·0.4H₂O as previously described.²⁵ Deuterium oxide (99.9% D) and [1-²H]-d-glucose (98%) were purchased from Cambridge Isotope Laboratories. Quikchange II site-directed mutagenesis kits were purchased from Agilent Technologies, and λDE3 lysogenization kits were purchased from Novagen. Water was purified using a Milli-Q purification system. All other chemicals were reagent grade or better and were used without further purification.

The solution pH was determined at 25 °C using an Orion model 720A pH meter equipped with a Radiometer pHC4006-9 combination electrode that was standardized at pH 4.00, 7.00, and 10.00 at 25 °C. TEA and MES buffers were prepared by the addition of 1 N NaOH or 1 N HCl and solid NaCl to give the desired pH and final ionic strength. A stock solution of triethylammonium bicarbonate buffer at pH 7.5 was prepared by saturating a 1 M triethylamine solution with carbon dioxide at 4 °C for 3–4 h until the desired pH was reached. The resulting buffered solution was stored at 4 °C. A stock solution of sodium bicarbonate was prepared by dissolving the solid salt in water and adjusting the pH to 7.5.

The disodium salt of 4S-[4-²H]-NADH (NADD) was prepared by a literature procedure, with minor modifications.^39,45 Stock solutions of NADH and NADD, prepared separately by dissolving the disodium form of the coenzyme in water, were stored at 4 °C. The concentration of NADH and NADD in aqueous solutions was determined from the absorbance at 340 nm using a value of ε = 6220 M^–1 cm^–1. Stock solutions of DHAP were prepared, starting with the hemimagnesium salt, and stirred over Dowex 50WX4-200R (H⁺ form) in water for 5–10 min at 25 °C to give the free acid. Dowex was removed by filtration, the pH of the resulting solution was adjusted from ∼2.0 to 7.5 using 1 M NaOH, and the solution was stored at −20 °C. The concentration of DHAP was determined spectrophotometrically at 340 nm, as the concentration of NADH oxidized upon quantitative conversion to glycerol 3-phosphate catalyzed by GPDH. Stock solutions of glycolaldehyde (200 mM) were prepared by the spontaneous breakdown of the dimer over a period of 3 days at room temperature.²⁵ Stock solutions of guanidinium hydrochloride were prepared by dissolving the solid salt in water and adjusting the pH to 7.5 with 1 N HCl.

The wild-type and mutant (R269A, N270A, and R269A/N270A) forms of hlGPDH were expressed and purified by published procedures.^23,29,43 Stock solutions (10–20 mg/mL) of wild-type and mutant hlGPDH were dialyzed exhaustively against 20 mM TEA at 4 °C. More dilute stock solutions were then prepared in 20 mM TEA buffer (pH 7.5) that contains 5–10 mM DTT and 0.1 mg/mL BSA. The enzyme concentration was determined from the absorbance at 280 nm, using the extinction coefficient of 18 450 M^–1 cm^–1 and a subunit molecular weight of 37 500 Da.⁴⁶⁻⁴⁸

Enzyme Assays

All enzyme assays were conducted at 25 °C and an ionic strength of I = 0.12 (NaCl) in a volume of 1.0 mL. hlGPDH was assayed by monitoring the oxidation of NADL by DHAP. BSA was included in assays where the substrate is DHAP, in order to minimize the absorption of hlGPDH onto the quartz cuvettes. A Cary 300-Bio UV–vis spectrophotometer was used for initial velocity (v_i) measurements. Initial velocities of the oxidation of NADL (≤5% reaction) by either DHAP or truncated substrate glycolaldehyde (GA) were calculated from the change in absorbance at 340 nm using an ε of 6220 M^–1c m^–1. The standard assay mixture contained 100 mM TEA (pH 7.5), 1 mM DHAP, 0.20 mM NADL, 0.1 mg/mL BSA, 50 μM DTT, and ca. 0.67 nM hlGPDH at I = 0.12 (NaCl).

Mutant hlGPDH-Catalyzed Reaction of DHAP

Assay mixtures contained 20 mM TEA (pH 7.5), 0.1 mg/mL BSA, 0–15 mM DHAP, and 100–200 μM NADL at I = 0.12 (NaCl) with the following mutant enzyme concentrations: 10 μM, R269A; 0.17 μM, N270A; and 20 μM, R269A/N270A. Assay mixtures for the R269A mutant hlGPDH-catalyzed reduction of DHAP by NADL in the presence of the guanidine cation contained 20 mM TEA buffer (pH 7.5), 0.1 mg/mL BSA, 50 μM DTT, 200 μM NADL, 0.050–1.2 mM DHAP, 2–80 mM guanidinium hydrochloride, and ca. 0.12–1.2 μM R269A hlGPDH at I = 0.12 (NaCl). The change in absorbance at 340 nm was monitored, and the initial velocities for reactions catalyzed by mutant hlGPDHs were determined over 5–10 min (N270A) and 15–30 min (R269A and R269A/N270A) reaction times. The primary deuterium kinetic isotope effects (1° DKIEs) were determined using initial reaction velocities from parallel experiments using NADD and NADH. The kinetic parameters and 1° DKIEs for the hlGPDH-catalyzed reduction of DHAP by NADL were determined from the global fits of initial reaction velocities to the appropriate kinetic scheme, using the fitting software provided by the Prism (GraphPad) or SigmaPlot 12.5 (Systat) graphing program. The values of K_m (≈ K_d) for the reactive carbonyl form of DHAP were calculated from the observed K_d and a value of f_car = 0.55 for the fraction of DHAP present in the free carbonyl form.⁴⁹

N270A hlGPDH-Catalyzed Reaction of Glycolaldehyde

Assay mixtures contained 10 mM TEA (pH 7.5), 5–60 mM GA, 200 μM NADL, 8 μM N270A and hlGPDH at I = 0.12 (NaCl). The change in absorbance at 340 nm was monitored, and the initial reaction velocities were determined over a 10–30 min reaction time. The 1° DKIEs were determined using initial reaction velocities determined in parallel experiments using NADD and NADH. The kinetic parameters and 1° DKIEs for the N270A hlGPDH-catalyzed reduction of the carbonyl form of GA (f_car = 0.06)²⁵ by NADH were determined from the global fits of kinetic data to the appropriate kinetic scheme using the fitting software provided by the Prism (GraphPad) or SigmaPlot 12.5 (Systat) graphing program.

Results

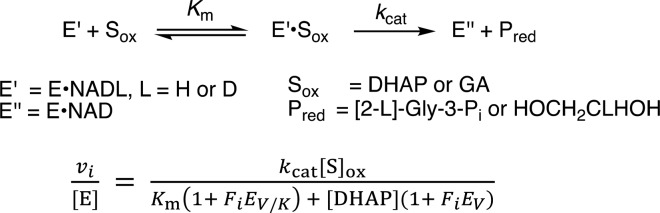
The GPDH-catalyzed reduction of DHAP follows an ordered kinetic mechanism with the NADL cofactor binding first to the enzyme.⁵⁰Figure 2A–C shows plots of the dependence of v/[E] (s^–1) on [DHAP] for the reduction of DHAP by 0.2 mM ≫ K_m NADH (F_i = 0)^29,43 or NADD (F_i = 1.0) catalyzed by R269A, N270A, and R269A/N270A mutants of hlGPDH. These data were fit to eq 1, derived for Scheme 2 [S_ox = DHAP] where E_V/K and E_V are equal to (1° DKIE – 1), and 1° DKIE is the primary deuterium kinetic isotope effect ^D(k_cat/K_m) or ^Dk_cat.^51,52 The kinetic parameters and primary deuterium isotope effects determined from the fits of the correlations from Figure 2 are reported in Table 1.

Figure 2.

Dependence of v/[E] (s^–1) on [DHAP] for the mutant hlGPDH-catalyzed reduction of DHAP by NADH or NADD (0.2 mM) at pH 7.5, 25 °C, and I = 0.12 (NaCl): (A) R269A mutant, (B) N270A mutant, (C) R269A/N270A mutant.

Scheme 2. Minimal Kinetic Mechanism for GPDH-Catalyzed Reactions.

Table 1. Kinetic Parameters and Primary Deuterium KIEs for Wild-type and Mutant hlGPDH-Catalyzed Hydride-Transfer Reactions^a.

hlGPDH	substrate	kcat (s–1)b	Dkcatb	kcat/Kmb	ΔΔG⧧ (kcal/mol)c	D(kcat/Km)b
WTd	DHAP	240 ± 10	1.5 ± 0.1	(4.6 ± 0.3) × 106	0	1.5 ± 0.1
	GA	(3.1 ± 0.3) × 10–4	2.4 ± 0.4	0.050 ± 0.006	10.8h	2.4 ± 0.2
	GA + FPO32–	6.4 ± 0.3e	2.8 ± 0.2	75 000 ± 6000f	2.4i	2.8 ± 0.1
	GA + HPO32–	5.5 ± 0.3e	2.8 ± 0.1	16 000 ± 1300f	3.3i	2.5 ± 0.1
	GA + SO42–	0.36 ± 0.04e	3.2 ± 0.3	1100 ± 100f	4.9i	2.8 ± 0.2
	GA + HOPO32	0.032 ± 0.001e	3.1 ± 0.2	200 ± 20f	5.9i	2.5 ± 0.1
	GA + S2O32–	0.019 ± 0.002e	3.0 ± 0.2	35 ± 5f	7.0i	2.9 ± 0.1
R269A	DHAP	(5.9 ± 0.4) × 10–3	2.7 ± 0.4	1.0 ± 0.1	9.1j	2.8 ± 0.3
	DHAP + Gua+			(8.0 ± 0.5) × 104 g	2.4k	2.7 ± 0.2m
N270A	DHAP	9.0 ± 0.5	3.0 ± 0.2	360 ± 35	5.6j	3.1 ± 0.1
	GA	(1.0 ± 0.1) × 10–2	2.7 ± 0.3	2.0 ± 0.2	8.7l	3.1 ± 0.4
R269A/N270A	DHAP	(2.8 ± 0.1) × 10–4	2.3 ± 0.3	(1.7 ± 0.1) × 10–2	11.5j	2.4 ± 0.2

^aFor reactions at pH 7.5 (20 mM TEA, DHAP, or 10 mM TEA for GA), 25 °C, 0.2 mM NADH or NADD, and I = 0.12 (NaCl).

^bThe uncertainty in the kinetic parameters is the standard error from the global fitting of the kinetic data. Units are M^–1 s^–1 unless noted otherwise.

^cThe difference [(ΔG^‡)_WT – (ΔG^‡)_X] between the activation barrier (ΔG^‡)_WT for the wild-type hlGPDH-catalyzed reduction of DHAP and the barriers (ΔG^‡)_X to a second reaction.

^dData from refs (23) and (39).

^eReaction in the presence of a saturating concentration of GA and dianion activator (Scheme 4, ref (39)).

^fThe value of [(k_cat)_X/K_XK_GA, M^–2 s^–1] for the dianion-activated reactions in the presence of a saturating concentration of NADL (Scheme 4, ref (39)).

^gThe product of the third-order rate constant [(k_cat/K_m)/K_Gua] in M^–2 s^–1 for the activation of the R269A mutant hlGPDH-catalyzed reduction of DHAP in the presence of 1.0 M guanidine activator (ref (29)).

^h(ΔG^⧧)_WT – (ΔG^⧧)_X, where (ΔG^⧧)_X is the activation barrier for the wild-type hlGPDH-catalyzed reduction of GA.

ⁱ(ΔG^⧧)_WT – (ΔG^⧧)_X, where (ΔG^⧧)_X is the activation barrier for the wild-type hlGPDH-catalyzed reduction of GA in the presence of 1.0 M dianion activator.

^j(ΔG^⧧)_WT – (ΔG^⧧)_X, where (ΔG^⧧)_X is the activation barrier for the mutant hlGPDH-catalyzed reduction of DHAP.

^k(ΔG^⧧)_WT – (ΔG^⧧)_X, where (ΔG^⧧)_X is the activation barrier for the R269A mutant hlGPDH-catalyzed reduction of DHAP in the presence of 1.0 M guanidine activator.

^l(ΔG^⧧)_WT – (ΔG^⧧)_X, where (ΔG^⧧)_X is the activation barrier for the N270A mutant hlGPDH-catalyzed reduction of GA.

^mThe 1° DKIE ^D[(k_cat/K_m)/K_Gua] determined from data from Figure 5, as described in the text.

Figure 3 shows a plot of the dependence of v/[E] (s^–1) on [GA] for the reduction of GA by 0.2 mM NADL (F_i = 0) or NADD (F_i = 1.0) catalyzed by the N270A mutants of hlGPDH. These data were fit to eq 1 derived for Scheme 2 [S_ox = GA] where E_V/K and E_V are equal to (1°DKIE – 1), and 1° DKIE is the primary deuterium kinetic isotope effect ^D(k_cat/K_m) or ^Dk_cat.^51,52 The kinetic parameters and primary deuterium isotope effects determined from the fits of the correlation from Figure 3 are reported in Table 1.

Figure 3.

Dependence of v/[E] (s^–1) on [GA] for the N270A mutant hlGPDH-catalyzed reduction of DHAP by NADH or NADD (0.2 mM) at pH 7.5, 25 °C, and I = 0.12 (NaCl).

Figure 4 shows the effect of increasing [DHAP] on v/[E] (s^–1) for the R269A mutant hlGPDH-catalyzed reduction of DHAP by NADH or NADD in the presence of increasing fixed concentrations of Gua⁺.²³ The slopes of these correlations are equal to the apparent second-order rate constants (k_cat/K_m)_obs for the hlGPDH-catalyzed reduction of DHAP. Figure 5 shows the effect of increasing [Gua⁺] on the values of (k_cat/K_m)_obs. The slope of the linear correlation for reactions of NADL, reported in Table 1, is equal to the third-order rate constant [(k_cat/K_m)/K_Gua] for the activation of the R269A mutant by the guanidine cation (Scheme 3).²³ The value of the kinetic isotope effect for the Gua⁺-activated reduction of DHAP catalyzed by R269A hlGPDH, calculated as the ratio of the third-order rate constants [(k_cat/K_m)/K_Gua] for the reduction of DHAP by NADH and NADD (^D[(k_cat/K_m)/K_Gua]), is reported in Table 1.

Figure 4.

Effect of the guanidine cation on the R269A mutant hlGPDH-catalyzed reduction of DHAP by NADH or NADD for reactions at pH 7.5 (20 mM TEA buffer), 25 °C, 0.2 mM NADL, and I = 0.12 (NaCl): (⧫) 2 mM Gua⁺, (▼) 5 mM Gua⁺, (▲) 10 mM Gua⁺, (●) 15 mM Gua⁺, and (○) 20 mM Gua⁺.

Figure 5.

Effect of increasing [Gua⁺] on the values of (k_cat/K_m)_obs determined as the slopes of correlations from Figure 4 for the R269A mutant hlGPDH-catalyzed reduction of DHAP by NADH and NADD at pH 7.5 (20 mM TEA buffer), 25 °C, 0.2 mM NADL, and I = 0.12 (NaCl).

Scheme 3. Activation of the R269A Mutant hlGPDH-Catalyzed Reduction of S = DHAP by NADL.

The following kinetic parameters for the wild-type hlGPDH-catalyzed reduction of DHAP or GA in the presence of saturating [NADL] = 0.2 mM, that were determined in earlier work,^23,39 are also reported in Table 1.

• (1)Values of k_cat and k_cat/K_m for the hlGPDH-catalyzed reduction of DHAP and GA.²³
• (2)Values of the kinetic parameters for the dianion-activated hlGPDH-catalyzed reduction of GA (Scheme 4)³⁹ where k_cat = (k_cat)_X for reactions at saturating concentrations of GA and dianion and [(k_cat)_X/K_XK_GA, M^–2 s^–1] for dianion-activated reactions in the presence of a saturating concentration of NADL (Scheme 4).³⁹

Scheme 4. Kinetic Mechanism for the hlGPDH-Catalyzed Reduction of GA at Saturating Concentrations of NADH or NADD.

Discussion

GPDH follows an ordered kinetic mechanism; NADL (L = H, D) binds first, with K_NADL = 7 μM,⁵³ followed by DHAP.^50,53 We reported a value of 1.5 for ^Dk_cat and ^D(k_cat/K_m) (Table 1),³⁹ and the 1° DKIEs on the reduction of DHAP was catalyzed by the binary E·NADL complex of wild-type hlGPDH at a saturating concentration of 0.2 mM NADL. These 1° DKIEs are smaller than the true intrinsic kinetic isotope effects because the hydride-transfer step is not fully rate-determining for reactions at low [DHAP], where the velocity is governed by kinetic parameter k_cat/K_m, or for reactions at high [DHAP], where the velocity is governed by k_cat.³⁸ Larger 1° DKIEs are observed for the reactions of hlGPDH crippled by site-directed mutations or by the truncation of the phosphodianion from the substrate DHAP (Table 1). We note that the larger uncertainties are in the 1° DKIEs on k_cat (^Dk_cat) compared with those for k_cat/K_m (^D(k_cat/K_m), Table 1). This reflects the weak affinity of wild-type hlGPDH for dianion activators or the mutant hlGPDH for DHAP (Figure 2 and Table 1); it is only possible to work at concentrations of the varied reagents that approach K_d but which are below saturation.³⁹ The observation of similar KIEs on these two kinetic parameters is consistent with identical rate-determining steps for reactions at low and high concentrations of the varied reagent.

Mutant hlGPDH-Catalyzed Reactions

The following effects of mutations of the side chains of Arg-269 and Asn-270 have been accounted for by a consideration of the interactions of these side chains with the transition state for the hlGPDH-catalyzed reduction of DHAP. We consider in a later section the possibility that the interactions of these side chains are utilized in the stabilization of a tunneling-ready state.³⁶

• (1)The R269A mutation results in a 9.1 kcal/mol increase in the activation barrier for the conversion of DHAP in water to the rate-determining transition state for enzyme-catalyzed hydride transfer (Table 1).⁴³ The effect of this mutation has been partitioned into a 2.8 kcal/mol effect on the formation of the Michaelis complex to DHAP and a 6.3 kcal/mol effect on the conversion of the Michaelis complex to the transition state for enzyme-catalyzed hydride transfer. The former effect provides an estimate for the direct stabilization of the Michaelis complex by the interaction between the side-chain cation of Arg-269 and the substrate phosphodianion. The additional 6.3 kcal/mol effect on k_cat reflects the strengthening of these electrostatic interactions associated with the increase in formal charge at the carbonyl oxygen from 0 at the Michaelis complex to ≤|−1| at the transition state for hydride transfer.
• (2)The binding of the guanidine cation to R269A mutant hlGPDH results in the efficient rescue of enzyme activity, which corresponds to a 6.7 kcal/mol decrease in the activation barrier for the reduction of DHAP by NADH at a standard state of the 1 M guanidine cation (Scheme 3 and Table 1).²⁹ The connection between the R269A mutant of hlGPDH and the piece of guanidine cation provides a (9.1 – 6.7 =) 2.4 kcal/mol stabilization of the transition state for the hlGPDH-catalyzed reaction of DHAP.^29,44
• (3)The amide side chain of N270 interacts with the phosphodianion of DHAP (Figure 6); however, the 5.6 kcal/mol effect of the N270A mutation on the barrier to conversion of DHAP to the transition state for hlGPDH-catalyzed hydride transfer is larger than expected for the loss of interaction between the neutral amide side chain and the anionic transition state. The (5.6 + 5.9 =) 11.5 kcal/mol total effect of the R269A/N270A double mutation on the activation barrier for hydride transfer catalyzed by wild-type hlGPDH is 3.2 kcal/mol smaller than the sum (9.1 + 5.6 kcal/mol) of the effects of the single mutations, so the effect of R269A and N270A single mutations to give the R269A/N270A double mutant is only 5.9 and 2.4 kcal/mol, respectively (Scheme 5). We proposed that Asn-270 serves the additional role of locking the phosphodianion into a position that provides for optimal interactions with the side chain of Arg-269 and that the 5.6 kcal/mol effect of the single N270A mutation is the sum of the effects of the loss of the 2.4 kcal/mol interaction between the phosphodianion and the amide side chain and a 3.2 kcal/mol weakening of the interaction between the transition state and the side chain of R269 (Scheme 5).⁴³

Figure 6.

Representation of the X-ray crystal structure of the nonproductive ternary complex between hlGPDH, DHAP, and NAD⁺ (PDB entry 1WPQ) showing the side chains for Arg-269 and Asn-270 that interact with the substrate phosphodianion. Also shown are loop residues 292–297 (green) that fold over DHAP and the hydrogen-bonded side chains [Asn-270, Thr-264, Asn-205, Lys-204, Asp-260, and Lys-120] that connect the catalytic and dianion activation sites.

Scheme 5. Cycle That Shows the Effect of Consecutive R269A and N270A Mutations on the Activation Barrier ΔG_DHAP^⧧ for the Wild-Type hlGPDH-Catalyzed Reduction of DHAP by NADH.

The N270A mutation results in a surprising 2.1 kcal/mol stabilization of the transition state for the wild-type hlGPDH-catalyzed reduction of GA by NADH. This mutation apparently results in structural changes at the enzyme active site which favor the binding of GA in a conformation that shows enhanced reactivity toward the hlGPDH-catalyzed reduction by NADH.⁴³

Structure–Reactivity Effects on hlGPDH-Catalyzed Hydride Transfer

The increase in the suppressed 1° DKIEs for the wild-type hlGPDH-catalyzed reduction of DHAP by NADL to a value of ca. 3 (Table 1) reflects the following changes in the barriers to the reactions with rate constants (k_–d)_S and (k_–d)_P, which favor rate-determining hydride transfer (k_chem) for hlGPDH-catalyzed reactions, and the observation of an intrinsic 1° DKIE (Figure 7).

• (1)An increase in the rate constants (k_–d)_S and (k_–d)_P for the release of reactant S_ox and product P_red, respectively, from hlGPDH, which corresponds to decreases in the activation barriers for these reactions. Changes in the barrier for ligand dissociation result from (A) cutting substrate DHAP into glycolaldehyde and phosphite dianion pieces (Scheme 4), where the weaker interactions between hlGPDH and the individual pieces compared with the combined interactions with the whole substrate favor fast ligand disassociation. (B) The elimination of binding interactions between hlGPDH and DHAP, which is reflected by the large increases in K_m determined for the reduction of DHAP catalyzed by the R269A, N270A, and R269A/N270A mutants.^29,43
• (2)An increase in the activation barrier to k_chem for the reduction of the enzyme-bound substrate. The R269A, N270A and R269A/N270A mutations each result in large decreases in k_cat for the hlGPDH-catalyzed reduction of DHAP, which correspond to increases in the chemical barrier (k_chem) for the reactions catalyzed by these mutant enzymes.

Figure 7.

Hypothetical reaction coordinates which show the barriers for the microscopic rate constants that control the rate-determining step for the hlGPDH-catalyzed reduction of S_ox = GA or DHAP: (k_–d)_S for the release of substrate S_ox; k_chem for hydride transfer; and (k_–d)_P for the release of product P_red. Hydride transfer is only partially rate-determining for the reaction catalyzed by wild-type hlGPDH (black lines). The observation of intrinsic kinetic isotope effects on the hlGPDH-catalyzed reactions of the substrate in pieces or the mutant hlGPDH-catalyzed reactions reflects the decreasing barriers to (k_–d)_S and (k_–d)_P and the increasing barrier to k_chem (blue lines), as described in the text.

1° DKIEs on hlGPDH-Catalyzed Hydride Transfer

These experiments were carried out to examine whether quantum mechanical tunneling results in a large decrease in the barrier of the hlGPDH-catalyzed hydride transfer reaction⁵⁴ compared to the reaction that passes through a semiclassical transition state. The probes for tunneling in enzyme-catalyzed hydride transfer include (1) 1° DKIEs,^40−42,55 (2) the temperature dependence of 1° DKIEs,²⁰ (3) and the determination of whether the ratio of deuterium and tritium isotope effects shows deviations from the Swain–Schaad relationship that are consistent with tunneling.^19,56−58 While each of these protocols has been designed to detect the existence of tunneling during hydride transfer, the interpretation of the experimental data is difficult and sometimes controversial.³⁷

For example, Arrhenius plots of ln(k_H/k_D) against 1/T for reactions of hydrogen- and deuterium-labeled substrates are predicted to show a y intercept = 0 ((k_H/k_D) = 1.0) for hydron transfer over a reaction barrier when hydron transfer is cleanly rate-determining,^20,59 but deviations from this ideal behavior may be observed when hydron transfer is only partly rate-determining.⁵⁹ Reactions that proceed with tunneling may show y intercepts for Arrhenius plots of >0, =0, or <0 depending upon whether there are changes in the contribution of tunneling over the temperature range examined.²⁰ These experiments are useful when there is a high degree of confidence that hydron transfer proceeds with tunneling because the DKIE is much larger than the semiclassical limit k_H/k_D ≈ 10. They are much more difficult to interpret when the DKIE falls inside this semiclassical limit because of the possibility that a temperature-dependent change in the rate-determining step for the enzymatic reaction contributes to the change in DKIE.

In order to minimize controversy, we accept the results of computational studies that support the existence of tunneling during enzyme-catalyzed hydride transfer reactions⁶⁰⁻⁶² and assume the following in the interpretation of the 1° DKIE determined in this work (Table 1).

• (1)The simplest explanation for the observation of an intrinsic 1° DKIE on enzyme-catalyzed hydride transfer in the range of 2–7 is that the isotope effect reflects the difference in zero-point energy lost for −H and −D on proceeding from the reactant to the transition state for hydride transfer.
• (2)The observation of intrinsic 1° DKIEs in the range of ca. 2–7 does not exclude the possibility of the tunneling of hydride through the reaction barrier at a point close to the top of the barrier. For example, the results of computational studies on hydride transfer catalyzed by lactate dehydrogenase give a calculated 1° DKIE of 3.6 and require a tunnel correction consistent with a “dominant tunneling energy at a point 0.40 kcal/mol below the effective barrier top”.⁶⁰
• (3)Quantum mechanical tunneling will result only in a substantial reduction in the barrier for the reaction that passes over an energy maximum when the reaction proceeds essentially exclusively by tunneling at a point significantly lower on the energy surface than that of the transition state (Figure 1B). A large 1° DKIE is required in this case because the tunneling of −H compared to −D through the energy barrier will be strongly favored by the longer QM wavelength for the former.

Intrinsic 1° DKIEs on hlGPDH-Catalyzed Hydride-Transfer Reactions

The very large 1° DKIEs of ^D(k_cat/K_m) of 60–100 reported for the hydrogen atom transfer reactions catalyzed by lipoxygenases^40−42,55 are greater than that of the classical limit of 7 for reactions in which the transferred hydron passes over an energy barrier.⁶³ This result provides solid evidence that these enzyme-catalyzed hydrogen transfer reactions proceed with tunneling of the hydron through the reaction barrier and that the relative reaction rates of substrates labeled with −H and −D are controlled by the longer QM wavelength of H.

The suppressed 1° DKIE of 1.5 for the wild-type hlGPDH-catalyzed reduction of DHAP by NADL will increase to the intrinsic 1° DKIE as the activation barrier to hydride transfer becomes large and rate-determining (Figure 7) and then will remain roughly constant with further changes in this barrier.³⁸ Three approaches for effecting an increase in the barrier to hydride transfer were adopted; each approach gave a value of 3 for the intrinsic isotope effect on hlGPDH-catalyzed hydride transfer (Table 1).

• (1)Variations in the structure of the substrate (DHAP or GA) or hlGPDH (R269A, N270A, and R269A/N270A mutants of hlGPDH) result in 2.4–11.5 kcal/mol increases in the activation barrier for the wild-type hlGPDH-catalyzed reaction of physiological substrate DHAP. These give rise to the narrow range of 1° DKIEs (2.3–3.1) reported in Table 1.
• (2)There is no systematic change in the 1° DKIEs (2.8–3.1) for dianion-activated hlGPDH-catalyzed reductions of GA by NADL (Scheme 4) as the reaction barrier is increased by 7.0 kcal/mol by variations in the structure of the dianion activator (Table 1).³⁹
• (3)There is no change in the 1° DKIE of 2.7 for the reduction of DHAP catalyzed by the R269A mutant of hlGPDH as the reaction barrier is lowered by the addition of the guanidine cation rescue reagent (Table 1).

These observations of 1° DKIEs on hlGPDH-catalyzed hydride transfer that are essentially independent of the overall reaction activation barrier provide strong evidence that these 1° DKIEs are intrinsic isotope effects. We conclude that there is no large effect of the difference in the quantum mechanical wavelength of −H and −D on the rate of the reduction of DHAP catalyzed by crippled forms of the hlGPDH and no effect and on the rate of the dianion-activated wild-type hlGPDH-catalyzed reduction of truncated substrate glycolaldehyde. The simplest explanation for the intrinsic 1° DKIEs of ca. 3 on these hlGPDH-catalyzed reactions is that they reflect the larger zero-point energy (zpe) for the C–H compared with that of the C–D bond of NADL and the requirement for the partial loss of zero-point energy on proceeding from reactants to the transition state for the enzyme-catalyzed hydride transfer reaction.⁶³⁻⁶⁵

The intrinsic 1° DKIEs from Table 1 are similar to the isotope effects (k_cat/K_m) for the reduction of ring-substituted benzaldehydes by NADL catalyzed by alcohol dehydrogenase (ADH): substituent X, ^D(k_cat/K_m); H, 3.7; 4-Br, 3.7; 4-Cl, 4.2; 4-Me, 3.5; and 4-MeO, 2.9.⁶⁶ These appear to represent intrinsic kinetic isotope effects on ADH-catalyzed reactions because they show no simple dependence on substrate reactivity. The small magnitude of these isotope effects on ADH-catalyzed reactions (<7) provides evidence that there is no large reduction in the activation barrier for enzyme-catalyzed hydride transfer from quantum tunneling through the energy barrier (Figure 1B).

Wild-Type hlGPDH-Catalyzed Hydride Transfer

Our results are consistent with an intrinsic 1° DKIE of 3, similar to the other intrinsic 1° DKIEs from Table 1, for the wild-type hlGPDH-catalyzed reduction of DHAP. An alternative possibility is a sharp increase in the 1° DKIE due to an increase in the contribution of QM tunneling to the hydride transfer reaction. This would require a driving force to promote hydride transfer by tunneling through the reaction coordinate. The following observations show that there can be no large rate acceleration from tunneling for wild-type hlGPDH-catalyzed hydride transfer compared to that of other reactions with intrinsic 1° DKIEs of 3.

• (1)The rate advantage for the reaction of whole substrate DHAP compared with the reaction of GA⁺ phosphite dianion pieces is 3.3 kcal/mol (Table 1).⁴⁴ Most or all of this represents the entropic advantage for the reaction of the single whole substrate rather than an advantage from tunneling through the reaction coordinate since related connections of substrate pieces result in similar, or larger,⁴⁴ purely entropic rate advantages for enzymatic reactions in cases where there is no possibility that the connection favors tunneling.
• (2)The rate advantage for catalysis by the whole wild-type enzyme compared with catalysis by R269A and guanidine cation pieces is 2.4 kcal/mol (Table 1).²³ Most or all of this rate advantage represents the entropic advantage for the reaction of the single whole enzyme rather than an advantage from tunneling because related connections of enzyme pieces result in similar, or larger, purely entropic rate advantages for enzymatic reactions where there is no possibility that the connection favors tunneling.^29,32,34,44

There is also no evidence that protein–ligand interactions are utilized in the stabilization of a tunneling ready state, which enables the efficient tunneling of hydride through the reaction barrier.³⁶ This change to a reaction that proceeds by tunneling should result in an increase in the intrinsic 1° DKIE for hydride transfer. However, Table 1 shows that changing the apparent magnitude of protein transition-state interactions causes no systematic change in the observed 1° DKIEs for hlGPDH-catalyzed reactions, except for in the case of the reaction catalyzed by wild-type hlGPDH where a minimum 1° DKIE is observed. The simple and clear rationalization for these experimental results is that the reduced 1° DKIE determined for hydride transfer catalyzed by wild-type hlGPDH (Table 1) is the consequence of the change in the rate-determining step for the hlGPDH-catalyzed reaction from hydride transfer over a reaction barrier to substrate binding or product release (Figure 7).

Summary and Conclusions

An approximate 7 × 10¹⁰-fold rate acceleration for the hlGPDH-catalyzed reduction of the carbonyl group of DHAP can be estimated as the ratio of second-order rate constants k_cat/K_m = (4.6 ± 0.3) × 10⁶ M^–1 s^–1 for the reduction of DHAP by the binary E·NADH complex (Table 1) and (6.7 ± 0.3) × 10^–5 M^–1 s^–1 for the nonenzymatic reduction of a benzaldehyde-type carbonyl group tethered to RNA by exogenous NADH.⁶⁷ This rate acceleration is remarkably similar to the 3 × 10¹⁰-fold rate acceleration for the TIM-catalyzed isomerization of GAP,⁶⁸ given that hlGPDH and TIM catalyze reactions of the same DHAP substrate and that each enzyme has evolved to provide 11–12 kcal/mol (see Introduction) transition-state stabilization from interactions with the substrate phosphodianion.^27,28 This similarity is consistent with the notion that the intrinsic binding energy of DHAP is sufficient to enable the catalysis of both deprotonation of the substrate α-carbonyl carbon and reduction of the carbonyl group by NADH.

The 1° DKIEs of 2.3–3.1 for wild-type hlGPDH-catalyzed hydride transfer to substrate piece GA or for hydride transfer to DHAP catalyzed by crippled forms of hlGPDH are well below the classical limit of 7 (Table 1). This shows that the longer quantum mechanical wavelength of H compared that of with D has little or no effect on the rate of hydride transfer from the enzyme-bound cofactor to the substrate carbonyl group. We are not aware of models that allow for tunneling rate constants that are nearly independent of the wavelength of the transferred atom, and we therefore conclude that there is minimal tunneling for these enzymatic reactions. The results of previous studies on GPDH can be fully rationalized by the classical Pauling model, where the rate acceleration is obtained by the stabilization of the transition state by interactions with the protein catalyst.⁶⁹

The binding energy of the phosphodianion of DHAP is utilized to drive a change in protein conformation, which locks the substrate in a protein cage and activates hlGPDH for the catalysis of hydride transfer.³¹ The binding of the NAD cofactor to the horse liver alcohol dehydrogenase–alcohol binary complex likewise induces a global conformational change that results in the folding of the active site over the ternary enzyme–substrate complex.⁷⁰⁻⁷² We suggest that the conformational changes of hlGPDH and horse liver alcohol dehydrogenase serve a similar function of activating these enzymes for the catalysis of hydride transfer.^31,73 In the case of hlGPDH, the conformational change is driven largely by the utilization of the binding energy from the phosphodianion of DHAP. By contrast, the binding energy available from minimal substrate acetaldehyde is insufficient to drive an activating conformational change of ADH, so this enzyme recruits additional binding energy from the nicotinamide cofactor for this purpose.

We appreciate the difficulties in providing rigorous proof for negatives, such as for the absence of tunneling through the reaction barrier during catalysis by hlGPDH or that there are no effects of coupling protein and substrate motions on the rate of this enzyme-catalyzed hydride transfer.¹⁷ On the other hand, we find no evidence that these phenomena contribute to the rate acceleration for catalysis by hlGPDH and that Pauling’s model provides a self-consistent explanation for our experimental results.³⁵ We suggest that transition-state stabilization according to the classical Pauling model may also provide a satisfactory rationalization for the rate accelerations observed for other dehydrogenases.⁶⁹

Glossary

Abbreviations

OMPDC

orotidine 5′-monophosphate decarboxylase

TIM

triosephosphate isomerase

GPDH

glycerol-3-phosphate dehydrogenase

hlGPDH

glycerol-3-phosphate dehydrogenase from human liver

DHAP

dihydroxyacetone phosphate

GA

glycolaldehyde

NADH

nicotinamide adenine dinucleotide, reduced form

NAD

nicotinamide adenine dinucleotide, oxidized form

MES

2-(N-morpholino)ethanesulfonic acid

TEA

triethanolamine

Gua⁺

guanidine cation

1° DKIE

primary deuterium kinetic isotope effect

This work was generously supported by the following grants from the U.S. National Institutes of Health: GM116921 and GM039754.

The authors declare no competing financial interest.