Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Aug 22.
Published in final edited form as: J Biomech. 2018 Jul 25;77:223–227. doi: 10.1016/j.jbiomech.2018.07.009

Variogram-based evaluations of DXA correlate with vertebral strength, but do not enhance the prediction compared to aBMD alone

Xuanliang Neil Dong 1, Yongtao Lu 2,3, Matthias Krause 4, Gerd Huber 3, Yan Chevalier 5, Huijie Leng 6, Ghislain Maquer 7
PMCID: PMC6091628  NIHMSID: NIHMS1500128  PMID: 30055841

Abstract

Ancillary evaluation of spinal Dual-energy X-ray Absorptiometry (DXA) via variogram-based texture evaluation (e.g., Trabecular Bone Score) is used for improving the fracture risk assessment, despite no proven relationship with vertebral strength. The purpose of this study was thus to determine whether classical variogram-based parameters (sill variance and correlation length) evaluated from simulated DXA scans could help predicting the in vitro vertebral strength.

Experimental data of thirteen human full vertebrae (i.e., with posterior elements) and twelve vertebral bodies were obtained from two existing studies. Areal bone mineral density (aBMD) was calculated from 2D projection images of the 3D HR-pQCT scan of the specimens mimicking clinical DXA scans. Stochastic predictors, sill variance and correlation length, were calculated from their experimental variogram. Vertebral strength was measured as the maximum failure load of human vertebrae and vertebral bodies from mechanical tests.

Vertebral strength correlated significantly with sill variance (r=0.727) and correlation length (r=0.727) for the vertebral bodies, and with correlation length (r=0.593) for full vertebrae. However, the stochastic predictors improved the strength prediction made by aBMD alone by only 11 percent for the vertebral bodies while no improvement was observed for the full vertebrae.

Despite a correlation, classical variogram parameters such as sill variance and correlation length do not enhance the prediction of in vitro vertebral strength beyond aBMD. It remains unclear why some variogram-based evaluations of DXA improve fracture prediction without a proven relationship with vertebral strength.

Keywords: Bone mineral density (BMD), dual-energy X-ray absorptiometry (DXA), osteoporosis, experimental variogram, human vertebrae

1. Introduction

Areal bone mineral density (aBMD) measured from lumbar dual-energy X-ray absorptiometry (DXA) is the gold standard for assessing the risk of vertebral fractures (WHO, 2003). However, aBMD measures cannot account for other factors associated with fracture risks, such as architecture, turnover, damage accumulation and mineralization (NIH, 2000). Consequently, overlaps among BMD have been observed for subjects with and without osteoporotic fractures (Hui et al., 1988; Schuit et al., 2004). Therefore, it is necessary to develop techniques that are complementary to aBMD to predict bone fragility.

Texture parameters from DXA images may help distinguishing subjects with and without osteoporotic fractures. Indeed, several clinical studies demonstrated the effectiveness of the trabecular bone score (TBS), one of these textural indices, in improving the prediction of bone fractures (Martineau and Leslie, 2017). However, the foundation of TBS in assessing bone strength has not been well established as only a few ex vivo and in vivo studies are available in the literature (Pothuaud et al., 2008; Pothuaud et al., 2009; Roux et al., 2013; Winzenrieth et al., 2013). Inconsistent results have been reported for the relationship between the TBS and microarchitecture of trabecular bone (Bousson et al., 2012; Bousson et al., 2015). In particular, trabecular thickness is not associated with the TBS. Additionally, no significant correlation was observed between the lumbar TBS and vertebral strength measured from mechanical testing although the significant correlation between TBS and vertebral stiffness was observed (Roux et al., 2013). On the other hand, a recent study has presented significant correlation (r=0.63, p<0.001) between TBS and vertebral strength on 35 human vertebrae from 13 human subjects (Tran et al., 2017). Furthermore, the “initial slope of the variogram”, foundation of TBS, is not associated with vertebral strength (Maquer et al., 2016).

Stochastic predictors such as sill variance (c) and correlation length (L) are also texture parameters derived from the experimental variogram of DXA scans (Dong et al., 2010; Dong et al., 2013; Dong et al., 2015; Dong et al., 2015). In a previous study, sill variance and correlation length were used to assess the inhomogeneity of BMD from lumbar DXA scans (Dong et al., 2015) and were shown to correlate significantly with trabecular microarchitecture parameters determined from 3D Micro-CT scans of human vertebrae. Consequently, the objective of this study was: 1) to examine the relationship between stochastic predictors from simulated DXA scans and vertebral strength measured from mechanical testing; 2) to investigate whether a combination of aBMD and stochastic predictors would enhance the prediction of vertebral strength than using aBMD alone.

2. Materials and Methods

2.1 Specimen preparation, imaging, and mechanical testing

Experimental data of human whole vertebrae with intact posterior elements (i.e., human vertebrae) and vertebral bodies without posterior elements were obtained from two existing studies (Chevalier et al., 2008; Lu et al., 2014).

The first data set consisted of thirteen human vertebrae (T12) from thirteen female donors (age: 80.1± 7.6 years old, range: 65-95 years) (Lu et al., 2014). Human vertebrae (Fig.1a) were scanned with an HR-pQCT system (XtremeCT, Scanco Medical, Zurich, Switzerland) with a voxel size of 82 μm. The specimens were stripped from all soft tissues but the intervertebral discs and fixed to a servo-hydraulic testing machine (Bionix 858.2, MTS Systems, Eden Prairie, MN, USA). After preconditioning, a quasi-static uniaxial compression (6 mm/min) was applied on each spinal segment with a 4° angle until anterior failure of the human vertebrae (Fig.1b). The vertebral strength of human vertebrae was calculated as the maximum force (Fmax) sustained by human vertebrae before failure (Lu et al., 2014).

Figure 1.

Figure 1

Open in a new tab

3D images of human vertebrae (a) and vertebral bodies (e) were acquired from HR-pQCT; Mechanical testing of human vertebrae (b) and vertebral bodies (f); Simulated DXA scans were generated by projecting the HR-pQCT images along the posterior-anterior axis of human vertebrae (c) and vertebral bodies (g); Stochastic predictors, correlation length and sill variance, were obtained by fitting an exponential model to the experimental variograms of the simulated DXA scans from human vertebrae (d) and vertebral bodies (h).

The second data set included twelve cadaveric lumbar vertebral bodies acquired from four male donors (age: 66.5±14.9 years old; range: 47-83 years old) (Chevalier et al., 2008). After intervertebral discs and soft tissues were removed, the vertebral bodies were embedded with 10-mm-thick polymethylmethacrylate (PMMA) with 4 mm thickness above their superior and inferior endplates (Chevalier et al., 2008). Then, the vertebral bodies were scanned at 82 μm resolution with the HR-pQCT system (Fig.1e). Compressive tests were conducted on the vertebral bodies with a servo-hydraulic testing system (5560 Table Model, Instron, Norwood, MA, USA) under a constant displacement rate of 5 mm/min (Fig.1f). The vertebral strength was defined as the maximum force (Fmax) sustained by vertebral bodies before failure (Chevalier et al., 2008).

2.2 Simulated DXA scans and stochastic predictors

The three-dimensional HR-pQCT images were used to create two-dimensional projection images of human vertebrae (Fig.1c) and vertebral bodies (Fig.1g), mimicking clinical DXA scans in the posterior-anterior direction with a resolution of 0.901 mm × 1.008 mm (Burghardt et al., 2009; Dall’Ara et al., 2012; Maquer et al., 2016). Areal bone mineral density (aBMD) was obtained for each specimen by averaging the projected BMD values of simulated DXAs (Burghardt et al., 2009; Maquer et al., 2016).

Furthermore, the spatial heterogeneity of simulated DXA scans was described by experimental variograms from human vertebrae (Fig.1d) and vertebral bodies (Fig.1h), which indicated how the variation of intensity between pixels located at various separation distances varied. Stochastic predictors (sill variance and correlation length) were calculated by fitting an exponential model to the experimental variograms (Fig.1d and Fig.1h). Details regarding the stochastic predictors of 2D projection images (e.g., DXA scans) are available from previous publications (Dong et al., 2010; Dong et al., 2013; Dong et al., 2015; Dong et al., 2015). Briefly, the sill variance (c) is the a priori variance of the random field, towards which the variogram is converging. The correlation length (L) describes the local changes of spatial variation. The larger the correlation length, the smoother the local variations.

2.3 Statistical analysis

Pearson correlation analyses were performed to examine the relationship among aBMD, the stochastic predictors from simulated DXA scans and the vertebral strength (Fmax) from mechanical testing. Then, simple linear regression analyses were conducted to determine the association between Fmax and aBMD alone. Furthermore, multiple linear regression analyses were used to examine the dependency of Fmax on aBMD, c and L. Finally, partial correlation analyses were performed to examine the relationship between stochastic predictors and vertebral strength after adjusting by aBMD. Statistical analyses were performed with SPSS (Version 24, IBM, Armonk, NY) with a significance level at p < 0.05.

3. Results

The descriptive statistics of the vertebral strength, aBMD measurements and stochastic predictors from simulated DXA scans were summarized for both human vertebrae and vertebral bodies (Table 1). Shapiro-Wilk tests revealed that normal distributions were observed for these variables.

Table 1.

Mean and standard deviation of vertebral strength (Fmax), aBMD, correlation length (L) and sill variance (c) of human vertebrae with intact posterir elements (i.e., human verterbae) and without posterir elements (vertebral bodies).

Fmax (kN) aBMD (mg/cm2) L (mm) c (gray value2)
Human verterbrae 2.1±0.5 1141.8±161.1 5.3±1.3 26.2±0.1
Vertebral bodies 5.5±2.1 395.9±72.4 5.955±1.564 3.1±1.6
Open in a new tab

For human full vertebrae, Pearson correlation analysis (Table 2) indicated that vertebral strength was significantly correlated with aBMD (r=0.711, p=0.006) and correlation length (r=0.593, p=0.031, Fig.2a). A statistically non-significant positive correlation was observed between vertebral strength and sill variance (r=0.513, p=0.073, Fig.2b). aBMD was also significantly correlated with correlation length (r=0.558, p=0.048) and sill variance (r=0.736, p=0.004) for human vertebrae (Table 2). Correlation length also had a significantly positive correlation (r=0.900, p=0.001) with sill variance (Table 2).

Table 2.

Pearson correlations coefficients (r) among aBMD, correlation length (L) and sill variance (c) and vertebral stength (Fmax) for human verterbrae.

aBMD (mg/cm2) Fmax (kN) L (mm)
Fmax (kN) r=0.711
p=0.006
L (mm) r=0.558
p=0.048 		r=0.593
p=0.031
c (gray value2) r=0.736
p=0.004 		r=0.513
p=0.073		 r=0.629
p=0.021
Open in a new tab

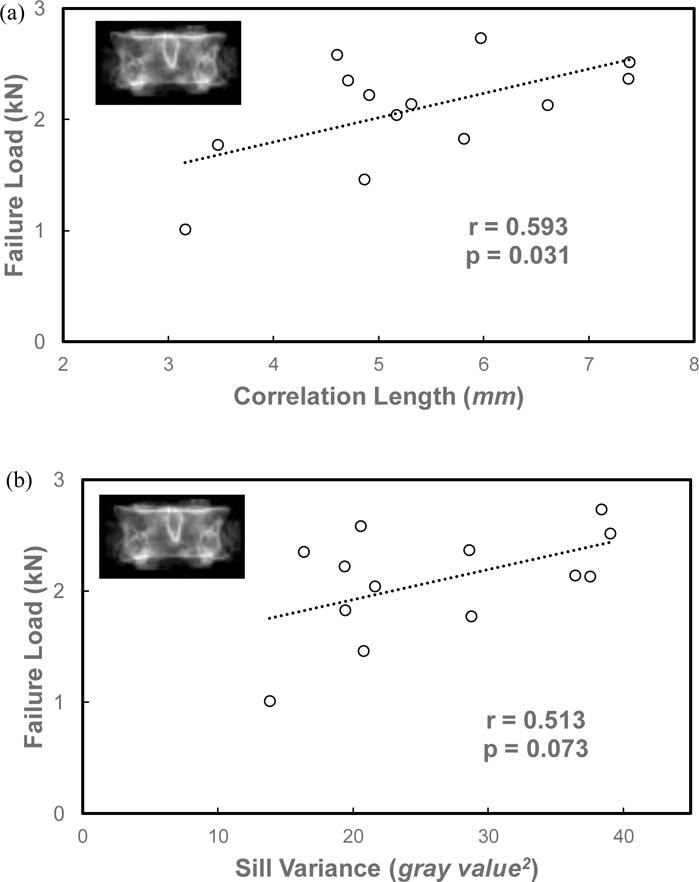
Figure 2.

Figure 2

Open in a new tab

Relationships between vertebral strength and the stochastic predictors, correlation length (a) and sill variance (b), from the simulated DXA images of human vertebrae.

In addition, simple linear regression indicated a significantly linear relationship between vertebral strength and aBMD for human vertebrae (R2=0.505, adjusted R2=0.460, p=0.001). Multiple linear regression analysis (Table 3) also indicated a significant relationship (R2=0.577, adjusted R2=0.436, p=0.001) between vertebral strength and a combination of aBMD and stochastic predictors. Collinearity was observed among independent variables, showing that the VIFs (Variance Inflation Factors) for aBMD, correlation length and sill were 2.256, 1.709 and 2.570, respectively. Partial correlation analysis indicated that the correlation between vertebral strength and correlation length was 0.344 (p=0.274) after adjusting for aBMD. Similarly, the correlation between vertebral strength and sill variance was −0.020 (p=0.950) after adjusting for aBMD.

Table 3.

Multiple regression analysis between vertebral strength (Fmax) and aBMD, correlation length (L) and sill variance (c) for human verterbae. The regresssion model is Fmax = β0+β1*aBMD + β2*L+β3*c. The R-squared value and the adjusted R-squared value for the regression was 0.577 and 0.436, respectively. The p-value from the F-test in the ANOVA table of the regression analysis was 0.043.

Predictors Coef. Std.error t p-value
(constant) −0.553 0.839 −0.659 0.527
aBMD (mg/cm2) 0.002 0.001 2.007 0.076
L (mm) 0.129 0.104 1.238 0.247
c (gray value2) −0.010 0.018 −0.541 0.601
Open in a new tab

For vertebral bodies, Pearson correlation analysis indicated that the vertebral strength was significantly correlated with aBMD (r=0.887, p=0.001), correlation length (r=0.727, p=0.007, Fig.3a) and sill variance (r=0.727, p=0.007, Fig.3b). Significantly positive correlations were also found among aBMD, correlation and sill variance for vertebral bodies (Table 4).

Figure 3.

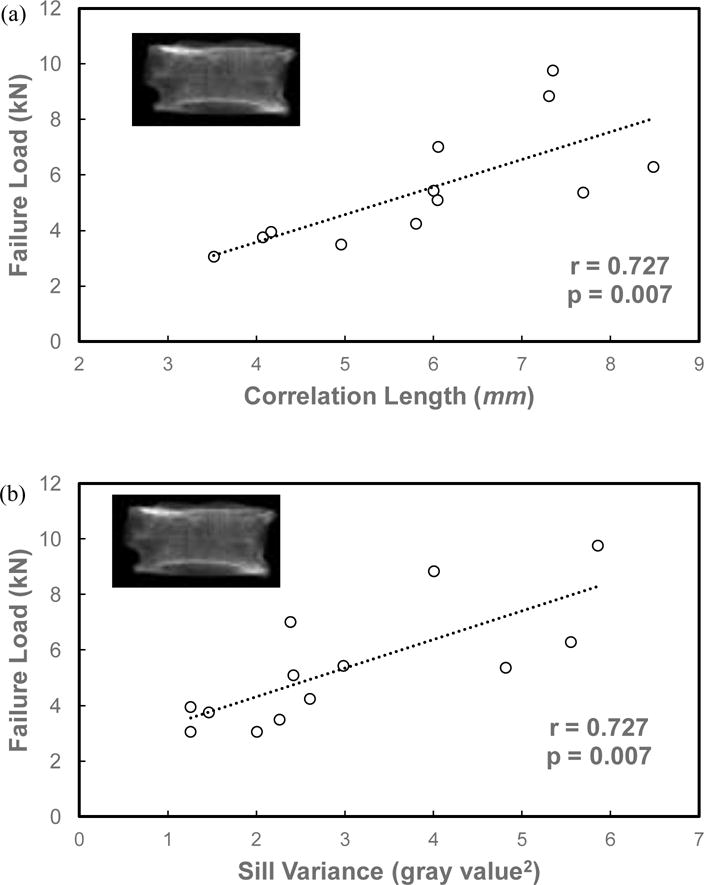
Figure 3

Open in a new tab

Relationships between vertebral strength and the stochastic predictors, correlation length (a) and sill variance (b), from the simulated DXA images of vertebral bodies.

Table 4.

Pearson correlations coefficients (r) among aBMD, correlation length (L) and sill variance (c) and vertebral stength (Fmax) for vertebral bodies

aBMD (mg/cm2) Fmax (kN) L (mm)
Fmax (kN) r=0.887
p=0.001
L (mm) r=0.651
p=0.022 		r=0.727
p=0.007
c (gray value2) r=0.803
p=0.007 		r=0.727
p=0.007 		r=0.900
p=0.001
Open in a new tab

Additionally, simple linear regression showed a significantly linear relationship between aBMD and vertebral strength for vertebral bodies (R2=0.787, adjusted R2=0.766, p=0.001). Multiple regression analysis from vertebral bodies indicated that a combination of aBMD and stochastic predictors from simulated DXA scans incrementally (R2=0.890, adjusted R2=0.849, p=0.001, Table 5) improved the prediction of vertebral strength compared to aBMD alone. Collinearity was examined and VIFs for aBMD, correlation length and sill variance were 3.045, 5.707 and 9.251, respectively. Partial correlation analysis indicated that the correlation between vertebral strength and correlation length was 0.428 (p=0.189) after adjusting for aBMD. Similarly, the correlation between vertebral strength and sill variance was 0.055 (p=0.873) after adjusting for aBMD.

Table 5.

Multiple regression analysis between vertebral strength and aBMD, correlation length (L) and sill variance (c) for verterbal bodies. The regresssion model is Fmax = β0+β1*aBMD + β2*L+β3*c. The R-squared value and the adjusted R-squared value for the regression was 0.890 and 0.849, respectively. The p-value from the F-test in the ANOVA table of the regression analysis was 0.001.

Predictors Coef. Std.error t p-value
(constant) −9.032 2.364 −3.921 0.005
aBMD (mg/cm2) 0.029 0.006 4.923 0.001
L (mm) 1.036 0.380 2.728 0.026
c (gray value2) −1.049 0.486 −2.157 0.063
Open in a new tab

4. Discussion

This study demonstrates that the stochastic predictors from simulated DXA scans of human vertebrae and vertebral bodies are positively correlated with the vertebral strength. However, a combination of stochastic predictors and aBMD does not substantially enhance the prediction of vertebral strength than using aBMD alone.

Vertebral strength featured significantly positive correlations with the sill variance and correlation length of simulated DXA scans for vertebral bodies, and correlation length for human vertebrae. A previous study (Dong et al., 2013) also showed that the sill variance of 2D projection images from the trabecular bone specimens of proximal human tibia was positively associated with its strength and elastic modulus. In another study (Dong et al., 2015), it was observed that the sill variance of DXA scans of human vertebrae was correlated with the microarchitecture of trabecular bone within human vertebrae. In particular, sill variance was positively correlated with trabecular thickness, trabecular number, connectivity density and bone volume fraction. It is not a surprise that the vertebral strength, being partially determined from its microarchitecture, is also positively correlated with the stochastic predictors.

Areal bone mineral density (aBMD) of both human vertebrae and vertebral bodies also demonstrated significantly positive correlations with vertebral strength. The correlation between aBMD and vertebral strength was higher with the vertebral bodies (r=0.887) than with the full vertebrae (r=0.711) in this study. Such observation is consistent with the literature (Ebbesen et al., 1999; Perilli et al., 2012) and the consequence of the moderate contribution of the posterior elements to the load bearing capability of the vertebra despite increasing drastically the aBMD value in frontal DXA.

No substantial improvement of vertebral strength prediction could be demonstrated when the stochastic predictors are combined to aBMD. For the vertebral bodies, the improvement due to sill variance and correlation length was only of about 11 percent changes of adjusted R-squared values. Multiple regression analysis (Table 5) indeed indicated an adjusted R-squared value of 0.766 for a simple linear regression with aBMD alone and 0.849 for a combination of stochastic predictors and aBMD. For the full vertebrae, the addition of the stochastic predictors to aBMD did not increase the power in predicting vertebral strength. A decrease of about 5 percent in adjusted R-squared values was even observed from simple linear regression (R2=0.460) to multiple linear regression (R2=0.436).

The lack of improvement by the stochastic predictors in predicting vertebral strength over aBMD may be a result of the collinearity. Strong correlations between aBMD, sill variance and correlation length were indeed observed for both full vertebrae (Table 2) and vertebral bodies (Table 4). Partial correlation analyses demonstrated that the correlations between vertebral strength and stochastic predictors of simulated DXA scans were not statistically significant after adjusting for aBMD. The vanishing of statistical significance could be due to strong correlations between aBMD and stochastic predictors.

This study relies on DXA scans simulated from 3D images of HR-pQCT, but aBMD values obtained from simulated and genuine DXAs are almost equivalent (Maquer et al., 2016). Despite this limitation, sill variance and correlation length appear to have positive correlations with vertebrae strength with and without intact posterior elements, but that they do not improve vertebral strength predictions compared to aBMD alone. Together, sill variance, correlation length, and “initial slope of the variogram” (Maquer et al., 2016) are enough to describe the entire variogram (i.e., the heterogeneity of the DXA). The effectiveness of variogram-based evaluation of spinal DXAs in improving the prediction of fractures made by aBMD remain therefore surprising.

Acknowledgments

This study was partly supported by the NIAMS of the NIH under Award number R15AR061740 and by the National Natural Science Foundation of China (Grants 11472017). The authors acknowledge Prof. Philippe Zysset (University of Bern, Switzerland) for sharing the imaging and experimental data.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of Interest Statement

Each author in this manuscript does not have and will not receive benefits in any form from a commercial party related directly or indirectly to the content in this manuscript.

The authors declare that they have no competing financial interests.

References

  1. Bousson V, Bergot C, Sutter B, Levitz P, Cortet B. Trabecular bone score (TBS): available knowledge, clinical relevance, and future prospects. Osteoporos Int. 2012;23:1489–501. doi: 10.1007/s00198-011-1824-6. [DOI] [PubMed] [Google Scholar]
  2. Bousson V, Bergot C, Sutter B, Thomas T, Bendavid S, Benhamou CL, Blain H, Brazier M, Breuil V, Briot K, Chapurlat R, Chapuis L, Cohen Solal M, Fardellone P, Feron JM, Gauvain JB, Laroche M, Legrand E, Lespessailles E, Linglart A, Marcelli C, Roux C, Souberbielle JC, Tremollieres F, Weryha G, Cortet B, Groupe de Recherche et d’Information sur les, O. Trabecular Bone Score: Where are we now? Joint Bone Spine. 2015;82:320–5. doi: 10.1016/j.jbspin.2015.02.005. [DOI] [PubMed] [Google Scholar]
  3. Burghardt AJ, Kazakia GJ, Link TM, Majumdar S. Automated simulation of areal bone mineral density assessment in the distal radius from high-resolution peripheral quantitative computed tomography. Osteoporos Int. 2009;20:2017–24. doi: 10.1007/s00198-009-0907-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chevalier Y, Charlebois M, Pahra D, Varga P, Heini P, Schneider E, Zysset P. A patient-specific finite element methodology to predict damage accumulation in vertebral bodies under axial compression, sagittal flexion and combined loads. Comput Methods Biomech Biomed Engin. 2008;11:477–87. doi: 10.1080/10255840802078022. [DOI] [PubMed] [Google Scholar]
  5. Dall’Ara E, Pahr D, Varga P, Kainberger F, Zysset P. QCT-based finite element models predict human vertebral strength in vitro significantly better than simulated DEXA. Osteoporos Int. 2012;23:563–72. doi: 10.1007/s00198-011-1568-3. [DOI] [PubMed] [Google Scholar]
  6. Dong XN, Luo Q, Sparkman DM, Millwater HR, Wang X. Random field assessment of nanoscopic inhomogeneity of bone. Bone. 2010;47:1080–4. doi: 10.1016/j.bone.2010.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dong XN, Pinninti R, Lowe T, Cussen P, Ballard JE, Di Paolo D, Shirvaikar M. Random field assessment of inhomogeneous bone mineral density from DXA scans can enhance the differentiation between postmenopausal women with and without hip fractures. J Biomech. 2015;48:1043–51. doi: 10.1016/j.jbiomech.2015.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Dong XN, Pinninti R, Tvinnereim A, Lowe T, Di Paolo D, Shirvaikar M. Stochastic predictors from the DXA scans of human lumbar vertebrae are correlated with the microarchitecture parameters of trabecular bone. J Biomech. 2015;48:2968–2975. doi: 10.1016/j.jbiomech.2015.07.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dong XN, Shirvaikar M, Wang X. Biomechanical properties and microarchitecture parameters of trabecular bone are correlated with stochastic measures of 2D projection images. Bone. 2013;56:327–36. doi: 10.1016/j.bone.2013.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ebbesen EN, Thomsen JS, Beck-Nielsen H, Nepper-Rasmussen HJ, Mosekilde L. Lumbar vertebral body compressive strength evaluated by dual-energy X-ray absorptiometry, quantitative computed tomography, and ashing. Bone. 1999;25:713–24. doi: 10.1016/s8756-3282(99)00216-1. [DOI] [PubMed] [Google Scholar]
  11. Hui SL, Slemenda CW, Johnston CC., Jr Age and bone mass as predictors of fracture in a prospective study. J Clin Invest. 1988;81:1804–9. doi: 10.1172/JCI113523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lu Y, Maquer G, Museyko O, Puschel K, Engelke K, Zysset P, Morlock M, Huber G. Finite element analyses of human vertebral bodies embedded in polymethylmethalcrylate or loaded via the hyperelastic intervertebral disc models provide equivalent predictions of experimental strength. J Biomech. 2014;47:2512–6. doi: 10.1016/j.jbiomech.2014.04.015. [DOI] [PubMed] [Google Scholar]
  13. Maquer G, Lu Y, Dall’Ara E, Chevalier Y, Krause M, Yang L, Eastell R, Lippuner K, Zysset PK. The Initial Slope of the Variogram, Foundation of the Trabecular Bone Score, Is Not or Is Poorly Associated With Vertebral Strength. J Bone Miner Res. 2016;31:341–6. doi: 10.1002/jbmr.2610. [DOI] [PubMed] [Google Scholar]
  14. Martineau P, Leslie WD. Trabecular bone score (TBS): Method and applications. Bone. 2017;104:66–72. doi: 10.1016/j.bone.2017.01.035. [DOI] [PubMed] [Google Scholar]
  15. NIH. Osteoporosis prevention, diagnosis, and therapy. NIH Consens Statement. 2000;17:1–45. [PubMed] [Google Scholar]
  16. Perilli E, Briggs AM, Kantor S, Codrington J, Wark JD, Parkinson IH, Fazzalari NL. Failure strength of human vertebrae: Prediction using bone mineral density measured by DXA and bone volume by micro-CT. Bone. 2012;50:1416–25. doi: 10.1016/j.bone.2012.03.002. [DOI] [PubMed] [Google Scholar]
  17. Pothuaud L, Barthe N, Krieg MA, Mehsen N, Carceller P, Hans D. Evaluation of the potential use of trabecular bone score to complement bone mineral density in the diagnosis of osteoporosis: a preliminary spine BMD-matched, case-control study. J Clin Densitom. 2009;12:170–6. doi: 10.1016/j.jocd.2008.11.006. [DOI] [PubMed] [Google Scholar]
  18. Pothuaud L, Carceller P, Hans D. Correlations between grey-level variations in 2D projection images (TBS) and 3D microarchitecture: applications in the study of human trabecular bone microarchitecture. Bone. 2008;42:775–87. doi: 10.1016/j.bone.2007.11.018. [DOI] [PubMed] [Google Scholar]
  19. Roux JP, Wegrzyn J, Boutroy S, Bouxsein ML, Hans D, Chapurlat R. The predictive value of trabecular bone score (TBS) on whole lumbar vertebrae mechanics: an ex vivo study. Osteoporos Int. 2013;24:2455–60. doi: 10.1007/s00198-013-2316-7. [DOI] [PubMed] [Google Scholar]
  20. Schuit SC, van der Klift M, Weel AE, de Laet CE, Burger H, Seeman E, Hofman A, Uitterlinden AG, van Leeuwen JP, Pols HA. Fracture incidence and association with bone mineral density in elderly men and women: the Rotterdam Study. Bone. 2004;34:195–202. doi: 10.1016/j.bone.2003.10.001. [DOI] [PubMed] [Google Scholar]
  21. Tran D, Michelet F, Lelong C, Hans D. TBS is associated with biomechanical properties of human vertebrae, ex-vivo. ASBMR 2017 Annual Meeting; Denver, Colorado. 2017. [Google Scholar]
  22. WHO. Prevention and management of osteoporosis. World Health Organ Tech Rep Ser. 2003;921:1–164. [PubMed] [Google Scholar]
  23. Winzenrieth R, Michelet F, Hans D. Three-dimensional (3D) microarchitecture correlations with 2D projection image gray-level variations assessed by trabecular bone score using high-resolution computed tomographic acquisitions: effects of resolution and noise. J Clin Densitom. 2013;16:287–96. doi: 10.1016/j.jocd.2012.05.001. [DOI] [PubMed] [Google Scholar]

RESOURCES