Different levels of category abstraction by different dynamics in different prefrontal areas

SUMMARY

Categories can be grouped by shared sensory attributes (i.e. cats) or by a more abstract rule (i.e. animals). We explored the neural basis of abstraction by recording from multi-electrode arrays in prefrontal cortex (PFC) while monkeys performed a dot-pattern categorization task. Category abstraction was varied by the degree of exemplar distortion from the prototype pattern. Different dynamics in different PFC regions processed different levels of category abstraction. Bottom-up dynamics (stimulus-locked gamma power and spiking) in ventral PFC processed more low-level abstractions whereas top-down dynamics (beta power and beta spike-LFP coherence) in dorsal PFC processed more high-level abstractions. Our results suggest a two-stage, rhythm-based model for abstracting categories.

eTOC Blurb

Wutz et al. show that different levels of category abstraction engage different oscillatory dynamics in different prefrontal cortex (PFC) areas. This suggests a functional specialization within PFC for low-level, stimulus-based categories (e.g. cats) and high-level, rule-based categories (e.g. animals).

INTRODUCTION

Categorization is the capacity to organize items based on shared characteristics. Those characteristics can vary by level of abstraction. Sometimes they are more feature-based with members looking physically similar (e.g., housecats). Other times they are more conceptual (e.g., animal) with members looking different (e.g., cats and elephants). There is little known about how the brain achieves different levels of abstraction. Does higher-level abstraction simply engage more of the same mechanisms and networks as lower-level, feature-based categorization? Or do they engage different mechanisms and/or areas?

We used a dot-pattern categorization task (Posner and Keele, 1968; Knowlton and Squire, 1993; Vogels et al., 2002) that varied abstraction by the degree of spatial distortion of each exemplar from its category prototype. Low distortion exemplars look alike. High distortion exemplars require greater abstraction of the category’s “essence” (Figure 1A and B). Monkeys learned two new categories in each session. Local field potentials and multi-unit spiking activity were recorded in dorsolateral and ventrolateral prefrontal cortex (dlPFC, vlPFC; Figure 1C).

Figure 1. Dot-pattern category stimuli, task and recording locations.

(A) Two dot-pattern categories under low and high distortion. (B) Summed Euclidean distance in degrees visual angle (DVA) between exemplars and prototypes (distance to same category (distortion) in yellow; distance to other category (distance between categories) in green). (C) Array locations in dlPFC and vlPFC. AS = arcuate sulcus, PS = principal sulcus. (D) Trial sequence of the delayed match-to-category paradigm.

Neural correlates of categorization have been reported in many cortical and sub-cortical brain areas (Merchant et al., 1997; Kreiman et al., 2000; Sigala and Logothetis, 2002; Hampson et al., 2004; Ashby and O’Brien, 2005; Seger, 2008; Poldrack and Foerde, 2008). For high-level abstraction, however, the prefrontal cortex (PFC) may play a central role (Wallis et al., 2001; Fabre-Thorpe, 2003; Freedman et al., 2003; Badre and D’esposito, 2009; Christoff et al., 2009; Cromer et al., 2010; Goodwin et al., 2012). Likewise, different oscillatory dynamics may subserve different functions for category processing. There is growing evidence that beta (~20 Hz) vs gamma (>40 Hz) oscillations are involved in top-down vs bottom-up cortical processing, respectively (Jensen et al., 2007; Buschman and Miller, 2007; Engel and Fries, 2010). Thus, different oscillatory dynamics might reflect different functional roles for categorization based on bottom-up features or more abstract concepts (top-down). We found abstraction organized by PFC area and oscillatory rhythm. vlPFC-gamma oscillations were more engaged for lower-level abstraction and dlPFC-beta oscillations for higher abstraction.

RESULTS

Two monkeys were trained in a delayed-match-to-category task (Figure 1D). First, a sample exemplar from one of the two categories appeared for 1s. After a memory delay period (0.85 s plus a jitter of max. 0.4s), two test exemplars appeared on the right and left. One of the exemplars was the same category as the sample (match); the other was from the other category (non-match). The monkeys free-viewed the test exemplars and were rewarded for maintaining fixation (0.7s) on the match. Each session was organized into a set of training blocks, each of which contained an increasing number of category exemplars. To move on to the next block, animals had to perform at or above 70% correct. We used correct trials from training blocks five and above (minimum of 64 exemplars per category). Level of abstraction was varied by the degree of exemplar distortion from the category prototype (summed Euclidean distance median ± IQR = 0.95 ± 0.2 degrees visual angle (DVA), Figure 1B). A complete description of the methods and analyses can be found in the STAR methods section.

Prefrontal cortex was organized into beta (dlPFC) and gamma (vlPFC) regions

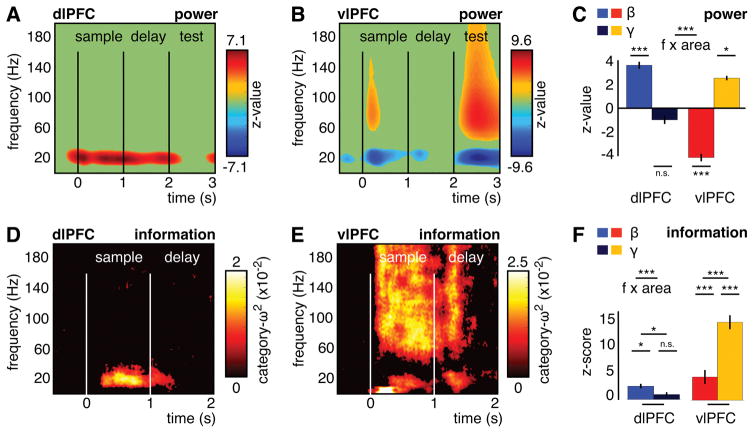
Local field potentials (LFPs) were recorded from chronic multi-electrode arrays in dorsolateral and ventrolateral PFC (dlPFC, vlPFC; Figure 1C). There was a task-related increase in LFP oscillatory power in different frequency bands in dlPFC vs vlPFC (Wilcoxon sign-rank z-value relative to −1 to −.75 s before sample onset, see STAR methods). In dlPFC, it was mainly in the beta band (Figures 2A and S1; significant for 13–30 Hz for 0–1s (sample) and 13–28 Hz for 1–2 s (delay), 52% channels, Bonferroni corrected). In vlPFC, gamma power increased and beta decreased during sample and test stimulus presentation (Figures 2B and S1; gamma: 63–110 Hz for 0.1–0.3 s, 46–172 Hz for 2.5–2.7 s, 20% channels; beta: 13–33 Hz for 0.1–0.3 s, 11–33 Hz for 2.5–2.7 s, 69% channels). vlPFC gamma power to sample onset (0.1–0.3 s) was maximal between 80–120 Hz and then decreased with increasing frequency (tested between four adjacent gamma sub-bands: (1) 41–80 Hz vs. 81–120 Hz, z= −4.8, p< 1.9×10⁻⁶; (2) 81–120 Hz vs. 121–160 Hz, z= 4.8, p< 1.7×10⁻⁶; (3) 121–160 Hz vs. 161–200 Hz, z= 4.8, p< 1.9×10⁻⁶; Figure S1). If gamma power simply reflected a spike-bleed through effect, one would expect a monotonic increase with increasing frequency. Thus, this suggests that the gamma effects were a true oscillatory event in a circumscribed frequency and not spiking activity bleeding into the gamma frequencies (see also the multi-unit spiking analysis below). Over time (0–3 s), beta (10–35 Hz) and gamma power (60–160 Hz) were negatively correlated within each area (dlPFC mean r ± SD: −0.3 ± 0.39, Wilcoxon test vs. 0 z= −3.1, p< .002; vlPFC −0.83 ± 0.13, z= −4.8, p< 1.7×10⁻⁶) and across areas (dlPFC-beta with vlPFC-gamma −0.64 ± 0.17, z= −4.8, p< 1.9×10⁻⁶). Due to the opposite changes in power in beta vs gamma between dlPFC and vlPFC, there was a highly significant interaction between frequency bands and PFC areas for oscillatory power (F(1,29)= 365, p< 1.1×10⁻¹⁶; Figure 2C).

Figure 2. LFP-power and its category information.

(A, B) Power change (Wilcoxon z-value) relative to baseline in dlPFC (A) and vlPFC (B). z-values with p< .001 are shown. These effects appeared in a large proportion of channels (see Figure S1). (C) Power change (Wilcoxon z-value) for beta and gamma power in dlPFC and vlPFC. Error bars show +/−1 SE. Asterisks indicate the significance level vs baseline and for the interaction between frequency bands and areas (with n.s. = not significant, * p< .05, *** p< .001). (D, E) Category information (ω²) in dlPFC (D) and vlPFC (E) averaged over significant channels for beta or gamma power (see Figure S1). ω² with p< .001 are shown. (F) Information z-scores vs. random permutations for beta and gamma power in dlPFC and vlPFC. Error bars show +/−1 SE. Asterisks indicate the significance level for each z-score, between the z-scores per frequency in each area and for the interaction between frequency bands and areas (with n.s. = not significant, * p< .05, *** p< .001).

The dominant frequency in each PFC area carried more category information

We computed the category information in the LFP power of each area (ω²-statistic, see STAR methods). This metric quantifies the percentage explained variance in the neural activity by the category membership of an exemplar. The ω²-statistic results in a zero-mean statistic when there is no category information (see baseline interval from −0.5 to 0 s in Figure 2D, E) and its maximal value would be 1 indicating 100% explained variance. To simultaneously capture category information across the sample and delay epochs, we averaged power in beta (10–35 Hz) and gamma (60–160 Hz) from 0.5 to 1.5 s after sample onset. Power and information don’t have to be co-modulated (i.e. there can be significant information when power is not elevated). Figures 2D and E plot category information for significant channels (ω²-statistic with p< .001, permutation test; see STAR methods) in either the beta or gamma band (Figure S1; dlPFC: 25% channels for beta, none for gamma; vlPFC: 49% for beta, 71% for gamma). Black colors indicate no category information and warm colors (red-white) indicate significant information (p< .001). There was significant information in dlPFC-beta power (Figures 2D and S1, 10–42 Hz for 0–1s and 14–27 Hz for 1–2 s). In vlPFC, information was found in low and high frequencies (Figures 2E and S1, 1–25 & 35–200 Hz for 0–1s and 12–200 Hz for 1–2 s) but it was maximal between 80–120 Hz (for 0–1 s: (1) 41–80 Hz vs. 81–120 Hz, z= −2.2, p< .026; (2) 81–120 Hz vs. 121–160 Hz, z= 2.2, p< .029; (3) 121–160 Hz vs. 161–200 Hz, z= 2.7, p< .008; Figure S1). Overall, we found a highly significant interaction for category information between PFC areas and frequency bands (F(1,29)= 31.8, p< 4.3×10⁻⁶). There was more category information for the dominant frequencies in each area (dlPFC: beta > gamma, z= 2.1, p< .039; vlPFC: gamma > beta, z= −4.6, p< 3.5×10⁻⁶; Figure 2F).

Category information in bottom-up inputs to vlPFC and in top-down dynamics in dlPFC

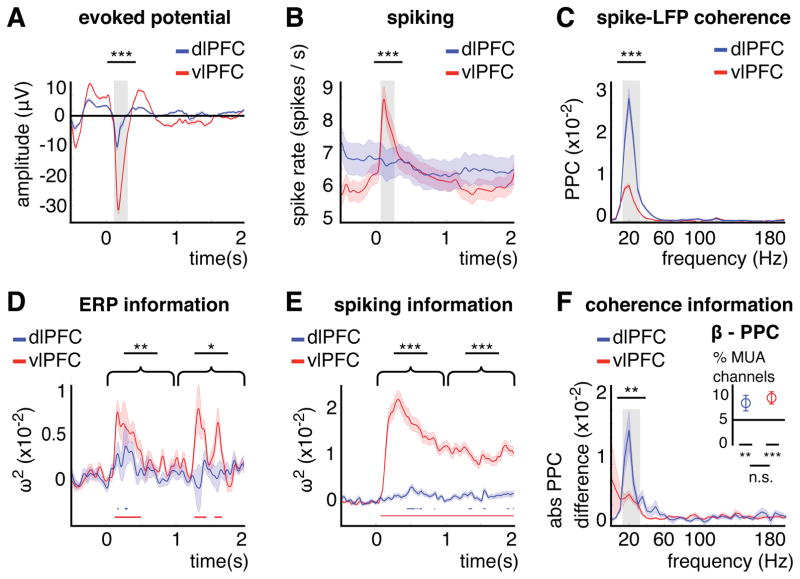
Gamma oscillations (which were stronger in vlPFC) have been associated with processing of bottom-up sensory inputs. Indeed, in vlPFC there was nearly a 3-fold stronger stimulus-evoked potential (ERP, vs dlPFC, z= 4.8, p< 1.9×10⁻⁶, Figure 3A). Moreover, multi-unit spiking activity (MUA, average spike rate/s for 0–2 s > 1) was present on more vlPFC channels across recording days (608 channels (34%) vs. 335 (19%) in dlPFC, z= 4.4, p< 1.2×10⁻⁵; Figure S1). In vlPFC, spiking was strongly time-locked to sample onset (0.1–0.3 s vs dlPFC, z=4, p< 6.3×10⁻⁵; Figure 3B). By contrast, the average spike rate in dlPFC remained largely constant throughout the trial. This was not caused by increased/decreased firing over MUA channels canceling each other out because the spike rate variance remained constant as well (Figure 3B). One would predict different amounts of variance at different times in a trial if the average rate would be calculated from increasing/decreasing, rather than constant, spike rates. Moreover, there was no difference between the variances in vlPFC and dlPFC (Levene-Test for variance homogeneity for 0.1–0.3 s, p= .91). The time series (between 0–3 s) of the evoked potential and of multi-unit spike rates (in spikes/s) in vlPFC correlated positively with the time series of gamma (ERP mean r ± SD: 0.21 ± 0.17, z= 4.3, p< 1.8×10⁻⁵; MUA 0.5 ± 0.37, z= 19.3, p< 6.6×10⁻⁸³) and negatively with beta power (ERP mean r ± SD −0.19 ± 0.13, z= −4.3, p< 1.8×10⁻⁵; MUA −0.28 ± 0.4, z= −14.1, p< 2.4×10⁻⁴⁵).

Figure 3. Evoked activity, spiking and spike-LFP coherence and its category information.

(A) Evoked potential averaged over all dlPFC and vlPFC channels. (B) Spike rate (spikes/s) averaged over all dlPFC and vlPFC MUA channels (MUA channel = average spike rate between 0–2 s > 1; see Figure S1). (C) Spike-LFP coherence (pairwise phase consistency (PPC) between 0–2 s) averaged over all dlPFC and vlPFC MUA channels with significant beta coherence (Rayleigh test, p< .001). The spike-LFP coherence results between areas and over time are shown in Figure S2. For (A–C), shaded areas show +/−1 SE. Asterisks indicate the significance level for the difference between areas for intervals (0.1–0.3 s)/frequencies (10–35 Hz) of interest (gray area; with *** p< .001). (D) Category information in evoked activity in dlPFC and vlPFC. (E) Category information in spiking activity in dlPFC and vlPFC. For (D, E), shaded areas show +/−1 SE. Asterisks indicate the significance level for the difference between areas for sample (0–1 s) and delay epochs (1–2 s, with * p< .05, ** p< .01, *** p< .001). (F) Absolute PPC difference between categories over frequency averaged over all significant MUA channels per area in the beta band (gray area). The median absolute PPC difference from each category-shuffled permutation distribution was subtracted from the observed absolute PPC difference per MUA channel. Inset plot: % MUA channels with a significant beta PPC difference (p< .05, permutation test). Asterisks indicate the significance level for the PPC difference between areas and against chance (at 5%) for the proportions (with n.s. = not significant, ** p< .01, *** p< .001). Error bars and shaded areas show +/−1 SE.

By contrast in dlPFC, there was no significant correlation between beta power and evoked activity (mean r ± SD −0.007 ± .18, z= 0.6, p= .54; Fisher’s r-to-z test vs. vlPFC-beta z= −2.2, p< .028) and the MUA spike rates correlated less with power than in vlPFC (beta: mean r ± SD −0.07 ± 0.41; vs. vlPFC z= −2.6, p< .011; gamma: 0.24 ± 0.35, vs. vlPFC z= 3.6, p< 3.8×10⁻⁴). Instead, dlPFC-spiking was more coupled to oscillatory beta phase as shown by stronger spike-LFP coherence (pairwise phase consistency metric (PPC), Vinck et al., 2010; see STAR methods). For both areas, spike-LFP coherence (spikes and LFPs within the same area but across different channels) between 0–2 s was greatest in the beta band (averaged over all LFP channels per area; Rayleigh test p< .001 for 27.5% MUA channels in vlPFC, 32.5% in dlPFC; Figure S2). This beta coherence was stronger in dlPFC vs vlPFC (z= −4.6, p< 4.9×10⁻⁶; Figures 3C and S2).

These different dynamics between PFC areas were also reflected in category information. Evoked activity in vlPFC carried significantly more category information than in dlPFC (sample, 0–1 s: z= 2.8, p< .006; delay, 1–2 s: z= 2.3, p< .02; Figure 3D, see also transient low-frequency information in Figure 2E). Likewise, there was significantly more category information in vlPFC spiking (vs dlPFC, sample, 0–1 s: z=14.7, p< 3.5×10⁻⁴⁹; delay, 1–2 s: z=12.6, p< 1.8×10⁻³⁶; Figure 3E). In vlPFC, 40% of the 608 spike-recording MUA channels contained category information (p< .001 between 0–2 s), whereas in dlPFC it was only 4% of the 335 MUA channels (Figure S1).

Category selectivity in spike-LFP coherence was tested for the 10% most informative LFP-channels for power per PFC area (Figure S1; beta in dlPFC, gamma in vlPFC; see Figure S2 for beta in vlPFC). It was assessed by the difference in PPC between categories for each MUA channel (permutation test p< .05, frequency-cluster corrected). In dlPFC, 11.6% of MUA channels and in vlPFC 9.7% of MUA channels showed category selectivity in their coherence spectrum (from 1–200 Hz). The strongest category-selectivity was in the beta band (Figure 3F). In both PFC areas, there were higher proportions of MUA channels than chance (at 5%) with significant beta PPC differences between categories (averaged between 10–35 Hz; inset plot in Figure 3F; 8.4% MUA channels in dlPFC, Binomial test vs. 5% p< .006; 9.4% in vlPFC, p< 5.710⁻⁶). These ×proportions were not different between areas (χ²= 0.3, p= .6). However, the absolute beta PPC difference between categories on these category-selective MUA channels was significantly greater in dlPFC (vs. vlPFC-gamma LFP z=−2.8, p< .006; vs. vlPFC-beta LFP z=−2.2, p< .028, Figure S2). We subtracted the median absolute PPC difference from each category-shuffled permutation distribution from the observed absolute PPC difference per MUA channel, in order to partial out between-area differences due to an overall different PPC level (as shown in Figure 3C) and to ensure that the between-area differences were due to differences in category-selectivity. In sum, in vlPFC most category information was found in the spike rates, whereas in dlPFC there was more category information in beta spike-LFP coherence. This suggests that vlPFC was more driven by bottom-up inputs (sample onset), whereas dlPFC was more in sync with its beta oscillatory/top-down dynamics.

Power in the dominant frequency per PFC area correlated with category preference in behavior

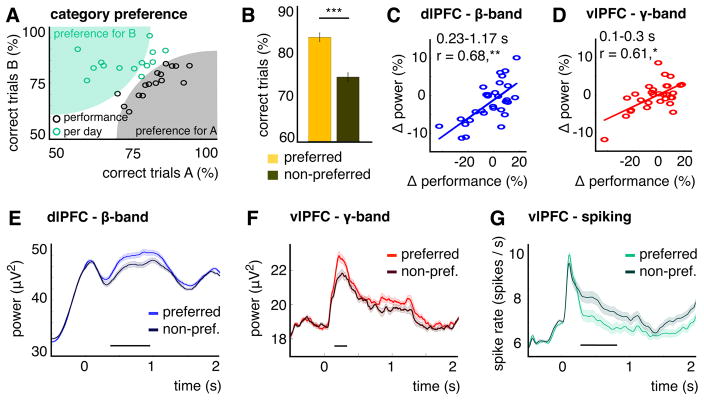
Monkeys learned new categories each day and often performed better on one (“preferred”). In 2/3 of sessions, there was a difference by more than 5 % (correct trials) between categories (Figure 4A). Pooling performance over preferred and non-preferred categories across recording days revealed a highly significant difference (t(29)= 7, p< 1.1×10⁻⁷; Figure 4B). This behavioral preference was reflected in each region’s dominant frequency.

Figure 4. Category preference in behavior, LFP-power and spiking.

(A) Performance (% correct trials) per category for each recording day (circles). Data points away from the main diagonal indicate a behavioral preference for a particular category on that day (A in black or B in green). (B) Performance for preferred and non-preferred categories. Error bars show +/−1 SE. Asterisks indicate the significance level (with *** p< .001). (C, D) dlPFC-beta power (C) and vlPFC-gamma power (D) difference between categories, averaged over significant time intervals (0.23–1.17 s for (C), 0.1–0.3 s for (D), see Figure S3), plotted against performance difference. Asterisks indicate the significance level (with * p< .05, ** p< .01). (E–G) dlPFC-beta power (E), vlPFC-gamma power (F) and vlPFC-spiking (G) for preferred/non-preferred categories (averaged over channels with a significant correlation ((E, F), see Figure S3) or all MUA channels with category information (G). Shaded areas show +/−1 SE. Horizontal lines show significant time intervals (p< .05, time-cluster corrected).

For each session, we arbitrarily subtracted the performance and power for one category from the other: Differences in performance ranged from about −20 to +20% and in power from −10% to +10% (normalized to overall performance/power, see STAR methods). In dlPFC, there was a positive correlation across recording days between the performance differences and the beta power differences (significant between 0.23 – 1.17 s with p< .002, time-cluster corrected, Figures 4C and S3). On average 61 % of the dlPFC channels were significant during this time period (channel-cluster corrected, Figure S3). There was no significant correlation between dlPFC-gamma power and performance differences (Figure S3). Conversely in vlPFC, gamma power differences correlated positively with performance differences (0.1 – 0.3 s with p< .02, 28% channels, Figures 4D and S3). A further contrast with dlPFC was that vlPFC-beta power differences were negatively correlated with category preference (1.13–1.52 s with p< .016, Figure S3). When averaging over all channels with a significant correlation, we found stronger power for the preferred category for beta in dlPFC (p< .006, time-cluster corrected, Figure 4E) and for gamma in vlPFC (p< .024, Figure 4F),.

The gamma power effects in vlPFC contrasted with the effects for spiking activity. At first, the peak spiking response was transiently stronger for the preferred category (0.09–0.14 s, p< .042, uncorrected). The more prominent pattern, however, was a sustained period with less spiking for the preferred vs. non-preferred category (0.275–0.81 s, p< .02, time-cluster corrected; Figure 4G). Thus, although gamma power and spiking were correlated in their time course (see analysis above and Figure 4F, G) and were anatomically co-located in vlPFC (Figure S1), the two signals were not the same. They showed opposite effects with respect to category preference. This was confirmed by a two-way ANOVA for gamma power/spiking (averaged between 0–2 s and normalized to overall spiking/power, see STAR methods) and for preferred/non-preferred categories over all MUA channels with category information (Figure S3). We found a significant interaction between gamma power/spiking and category preference (F(1,241)= 5.8, p< .018). To sum, preferred categories elicited less spiking activity in vlPFC and stronger power in the dominant frequency in each area (beta in dlPFC, gamma in vlPFC).

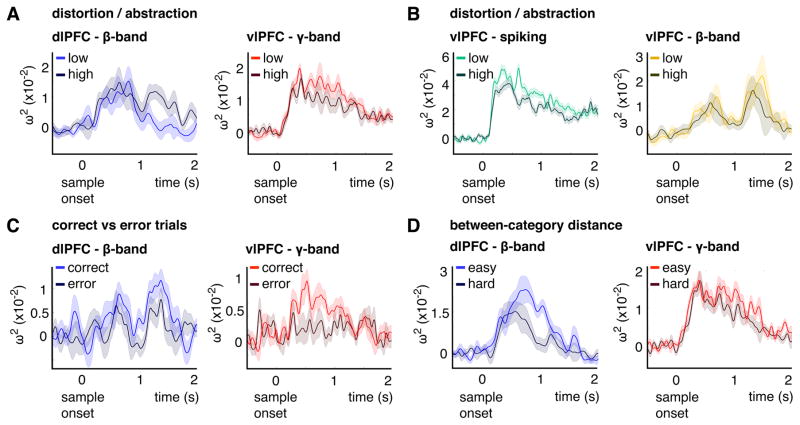
dlPFC-beta carried more information for higher, and vlPFC-gamma for lower abstractness

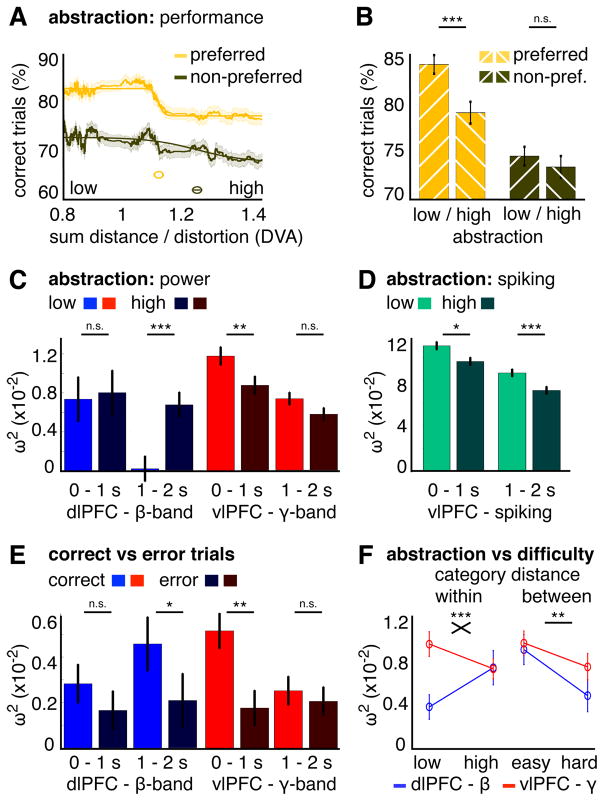
We found stronger behavioral effects of abstraction for behaviorally preferred categories. Preferred category performance as a function of dot pattern distortion was best fit with a decreasing sigmoid function with a sharp inflection point (R²= 0.87, inflection ± CI at 1.1 ± 0.0004 DVA; steepness ± CI = 144 ± 7.7 % correct trials/DVA, Figure 5A). This was less so for the non-preferred category (R²= 0.5, inflection at 1.2 ± 0.008 DVA; steepness ± CI = 15 ± 1.1 %/DVA). We used the preferred-category inflection point to separate exemplars into high vs low abstractness. This revealed a main effect for abstractness on performance (low vs high, F(1,29)= 17.7, p< 2.2×10⁻⁴) and a significant interaction of abstractness with preference (F(1,29)= 4.6, p< .042). The performance difference between low and high abstractness was significant for the preferred category (t(29)= 4.2, p< 2.5×10⁻⁴) but not for the non-preferred category (t(29)= 1, p< 0.33; Figure 5B).

Figure 5. Category abstraction in behavior, LFP-power and spiking.

(A) Performance (% correct trials) as a function of exemplar distortion for preferred and non-preferred categories. Shaded areas show +/−1 SE. Lines show the sigmoid fit and inset circles show its inflection point. (B) Performance for low and high distortion separately for preferred and non-preferred categories. (C, D) Category information (ω²) for low and high distortion separately for sample (0–1 s) and delay epochs (1–2 s) for dlPFC-beta power, for vlPFC-gamma power (C) and for vlPFC-spking (D). (E) Category information (ω²) for correct and error trials separately for sample (0–1 s) and delay epochs (1–2 s) for dlPFC-beta power and vlPFC-gamma power. (F) Category information (ω²) for dlPFC-beta power and vlPFC-gamma power between 0–2 s for low/high distortion (left) and median split by between-category distance (right; easy = above median, hard = below median). For (B–F), error bars show +/−1 SE. Asterisks indicate the significance level (with n.s. = not significant, * p< .05, ** p< .01, *** p< .001). Additional analyses for time course stability are shown in Figure S4.

Category information (ω²-statistic) in power was compared between low and high abstractness levels for the 10% channels per PFC area with the most category information (Figure S1) separately for sample (0–1 s) and delay epochs (1–2 s; see Figure 6 for the time series data). In dlPFC, category information in beta power was significant (permutation test p< .001) for both abstractness levels during the sample epoch (low vs. high z= −0.6, p= .54). During the delay epoch, however, it only remained significant for high abstractness and it was significantly greater than that for low abstractness (z= −3.5, p< 5.3×10⁻⁴; Figure 5C and 6A). Because category information was exclusive for high abstractness during the delay, there was reduced information during that epoch when calculated over all trials (low and high together as shown in Figure 2D). By contrast, vlPFC-gamma power showed significantly more category information for low vs. high abstractness during the sample epoch (z= 2.9, p< .005; Figure 5C and 6A) but not during the delay (z= 1.5, p= .15). There was no significant difference for category information in beta power in vlPFC (sample: z= 0.4, p= .72, delay: z= −0.2, p= .83; Figure 6B). The sample/delay epoch differences between low vs. high abstractness were also tested with non-parametric permutation tests for (1) the maximum/minimum statistic per task epoch (max. gamma-sample p< .027; min. beta-delay p< .01, one-sided) and (2) over time with a cluster-based method for multiple comparison correction (gamma p< .038; beta p< .01). The time courses were aligned to the first time point with significant category information for each recording day (with p< .05, permutation test) for the time-cluster tests. The alignment accounts for variability in the latency of category information due to different categories and exemplars on different recording days (Figure S4).

Figure 6. Time-series data for category information.

(A) Category information (ω²) as a function of time from sample onset for low (light hue) and high distortion (dark hue) for dlPFC-beta power (blue) and vlPFC-gamma power (red) averaged over the 10% most informative electrodes per area (see Figure S1). (B) Category information (ω²) as a function of time from sample onset for low (light hue) and high distortion (dark hue) for vlPFC-spiking (green) averaged over all channels that contained significant category information for spiking (242 MUA channels) and vlPFC-beta power (yellow) averaged over the 10% most informative electrodes per area (see Figure S1). (C) Category information (ω²) as a function of time from sample onset for correct (light hue) and error trials (dark hue) for dlPFC-beta power (blue) and vlPFC-gamma power (red) averaged over the 10% most informative electrodes per area (see Figure S1). (D) Category information (ω²) as a function of time from sample onset for above Median (easy) between-category distance (light hue) and below Median (hard) between-category distance for dlPFC-beta power (blue) and vlPFC-gamma power (red) averaged over the 10% most informative electrodes per area (see Figure S1). For (A–D), shaded areas show +/−1 SE. See also Figure S4.

The pattern of category selectivity in power on different abstractness levels was further supported by spiking and spike-LFP beta coherence. As shown above, for the spike rates we found the strongest category signals in vlPFC and almost no information in dlPFC. By contrast for beta spike-LFP coherence, dlPFC showed stronger category effects compared to vlPFC. Thus, we expected the strongest differences in category information between different abstractness levels for spiking in vlPFC and for beta spike-LFP coherence in dlPFC. Indeed, vlPFC-spiking contained more information for low vs. high abstractness (sample: z= 2.5, p< .013; delay: z= 3.8, p< 1.5×10⁻⁴; Figure 5D). Overall there was more category information in spiking compared to LFP power. This might be explained by the fact that spiking reflects the behavior of only a few, well-isolated neurons, whereas LFP signals reflect the collective activity of many cells, of which only a subset might contain information.

In contrast to vlPFC-spiking, spike-LFP beta coherence in dlPFC showed stronger category selectivity for high vs. low abstractness. Table 1 shows the proportions of MUA channels in dlPFC with a significant difference in beta PPC between categories (permutation test, p< .05) for each abstractness level and task epoch. Importantly in dlPFC, there was a higher proportion of category-selective MUA channels for high abstractness during the sample epoch (9.3% for high, vs. chance p< .002; 4.8 % for low, vs. chance p= .51; low vs. high p< .039). There was no category selectivity in dlPFC during the delay. Conversely in vlPFC (Table 2), there were significant proportions of category-selective MUA channels for both abstractness levels during both epochs but no difference between them.

Table 1.

Category selectivity in beta spike-LFP coherence in dlPFC for different distortion levels

Contingency tables for % MUA channels with a significant difference in beta PPC between categories (p< .05, permutation test) on low and high distortion levels for dlPFC during sample (0–1 s) and delay epochs (1–2 s). Asterisks indicate the significance level for the proportions for each condition vs. chance (5%, binomial test) and against each other (McNemar test, with n.s. = not significant, * p< .05, ** p< .01).

		high			epoch	category info
	% MUA	p < .05	p > .05	total		low	high	low vs high
	p < .05	0.6	4.2	4.8
low	p > .05	8.7	86.5	95.2	sample	n.s.	**	*
	total	9.3	90.7	100
	p < .05	0.3	4.5	4.8
low	p > .05	4.8	90.4	95.2	delay	n.s.	n.s.	n.s.
	total	5.1	94.9	100

Table 2.

Category selectivity in beta spike-LFP coherence in vlPFC for different distortion levels

Contingency tables for % MUA channels with a significant difference in beta PPC between categories (p< .05, permutation test) on low and high distortion levels separately for vlPFC during sample (0–1 s) and delay epochs (1–2 s). Asterisks indicate the significance level for the proportions for each condition vs. chance (5%, binomial test) and against each other (McNemar test, with n.s. = not significant, * p< .05, ** p< .01, *** p< .001).

	% MUA	high			epoch	category info
		p < .05	p > .05	total		low	high	low vs high
	p < .05	1.4	6.9	8.3
low	p > .05	6.3	85.4	91.7	sample	***	**	n.s.
	total	7.7	92.3	100
	p < .05	1.1	6.3	7.4
low	p > .05	5.9	86.7	92.6	delay	**	*	n.s.
	total	7	93	100

Functional significance of category abstraction effects

The functional relevance of the abstraction results was supported by a correct vs. error trials analysis. For both PFC areas, there was more category information on correct trials. For dlPFC-beta the difference was significant during the delay epoch (z= 2.4, p< .019), while for vlPFC-gamma it was significant during the sample epoch (z= 3, p< .003; Figures 5E and 6C). There was no significant difference in the other respective task epochs (dlPFC-beta sample z= 0.9, p= .38; vlPFC-gamma delay z= 1.2, p= .21).

Moreover, the abstraction/distortion results were not merely due to a more generic effect of task difficulty or attention. This was shown by a control analysis that varied task difficulty while holding distortion constant. The trials were re-grouped by whether the sample exemplar was below vs. above the median distance to the second category prototype (median= 4.3 ± 0.02 DVA, by contrast for distortion/abstractness the trials were sorted by the distance to the same category prototype; see Figure 1A, B). Because exemplars above this median split are farther away from the other category prototype, they are easier to categorize (above: 78.8% correct trials vs. below: 77.5%, t(29)= 2.1, p< .046). Critically, there was no difference in exemplar distortion between the median distance split trial subsets (t(29)= 0.65, p= .52). For category information in power (between 0–2 s), there was a significant main effect with less information below the median distance for both frequencies (F(1,29)= 9.6, p< .005; no interaction F(1,29)= 1.3, p= .27; Figures 5F and 6D). By contrast for distortion/abstractness, we found a significant interaction between frequencies and abstractness levels (F(1,29)= 13.3, p< .001, no main effect of distortion F(1,29)= 0.35, p= .56; Figure 5F and 6A). Thus, greater difficulty (lesser distance between categories) reduced category information for both frequencies, whereas distortion/abstractness had opposite effects on them. vlPFC-gamma power had more category information for low abstractness, whereas dlPFC-beta power had more information for high abstractness.

DISCUSSION

We found a dissociation between PFC sub-region (vlPFC, dlPFC), oscillatory frequency (gamma vs beta) and level of category abstraction. Gamma power increased in vlPFC and beta in dlPFC. The frequency bands were anticorrelated between and within areas, which might reflect a general principle of working memory in PFC (Lundqvist et al., 2016). Gamma rhythms have been associated with bottom-up, and beta with top-down processing. For example, learned rules are expressed in beta oscillations (Engel and Fries, 2010; Buschman et al., 2012; Antzoulatos and Miller, 2014). Gamma oscillations are involved in encoding bottom-up information in working memory (Buschman and Miller, 2007; Jensen et al., 2007; Jutras et al., 2009). Correspondingly, we found stronger evoked potentials and stronger stimulus-locked spiking in vlPFC. There, gamma power and spiking carried more information at low abstractness. In line with previous results (e.g. Jia et al., 2013; Lundqvist et al., 2016), we found that gamma power and spiking were tightly associated. But gamma power did not simply index spiking. For (behaviorally) preferred vs. non-preferred categories, we found less spiking but more power for the preferred category. Thus, the two signals are not the same and they contribute differently to category information in vlPFC. Whereas vlPFC was more driven by bottom-up inputs (sample onset), dlPFC was more in sync with its oscillatory/top-down dynamics. Beta oscillations were predominant in power and spike-LFP coherence in dlPFC; and carried more information at high abstractness. This suggests a two-stage, rhythm-based model for category abstraction in different PFC regions. Lower-level categories are first extracted from bottom-up inputs to vlPFC reflected in stimulus-locked gamma power and spiking. Then, beta network interactions in dlPFC encode more abstract levels that transcend appearance and depend more on top-down processing.

This anatomical distinction between PFC regions by level of abstraction might result from their differential connectivity to posterior cortex. vlPFC may be more governed by bottom-up processing, because it receives direct inputs from inferior temporal cortex (IT) via the ventral stream (“the what”) and may, thus, continue the functional properties of IT neurons into PFC. Therefore, category processing in vlPFC can be viewed as an object recognition problem based on bottom-up/stimulus-based principles. By contrast, dlPFC has stronger connectivity to parietal cortex via the dorsal stream (“the where/how”) and thus may identify more complex relationships to objects that optimize behavior (O’Reilly, 2010). Categorization in dlPFC may therefore extend beyond object recognition to less stimulus-based, more rule-based, top-down and abstract processing. This fits with the framework that gamma rhythms support the feedforward flow of cortical information, while beta rhythms support feedback (Jensen et al., 2015; Bastos et al., 2015).

Category information in vlPFC-gamma was stronger for low abstractness during the sample epoch, whereas for dlPFC-beta it was stronger for high abstractness during the delay. This temporal pattern further supports the bottom-up/top-down distinction. Low-distortion exemplars can be judged on their physical appearance using bottom-up processing, because they look like their prototypes. Thus, the category judgment for low-distortions can be made more quickly during the influx of sensory information. Consequently, gamma power showed more information for low distortions during stimulus presentation (sample epoch). By contrast, beta power and information was less tied to stimulus onset, it was equally strong for low and high abstractness during the sample epoch and for high abstractness this selectivity was maintained into the delay. In this view, the category signal in dlPFC-beta was more robust against abstractness, such that it remained at a constant level in face of increasing amounts of distortion. Another interpretation might be that higher distortions require more abstraction (and thus more top-down processing) because the defining characteristics of the category, the unseen prototype, are less obvious. They don’t “look alike” like the lower distortions and thus rely more on rule-based categorization. Thus, information in beta power might remain significant during the delay for high distortions (while it declines for low distortions) because the higher degree of abstraction requires more thought and thus longer top-down processing extending after the bottom-up sensory input has ceased. This pattern suggests that category information in dlPFC is not just passively robust against increasing degrees of abstractness. Instead, dlPFC-beta oscillations might reflect a specialized top-down mechanism for high abstractness levels.

The functional relevance of category abstraction in PFC was supported by the data in three different ways. First, there was more category information on correct trials for vlPFC-gamma in the sample epoch and for dlPFC-beta in the delay. Beyond buttressing its functional importance in the task, this pattern mirrors the effects seen for distortion/abstraction (i.e., gamma during sample, beta during delay), which, in turn, is in line with the bottom-up vs. top-down distinction. Second, the distortion/abstraction effects were not merely due to more generic effects of task difficulty or attention. Greater difficulty reduced information for both frequencies, while abstractness had opposite effects on them (more information for low in vlPFC-gamma and for high in dlPFC-beta). Third, the category preference observed in behavior was directly reflected in the neural dynamics in PFC. Categorization can be based on dividing exemplars in two categories (“A vs. B”) or by a strategy with one dominant category, against which all exemplars are judged (“A vs not-A”, analogous to a figure-ground distinction). Our results suggest the latter. Behaviorally, one category was often preferred (“A”) and, on this category, performance differed between low and high abstractness levels. In the neural effects, category preference was observed in lower spike rates and higher power in the dominant frequency per PFC area (dlPFC-beta, vlPFC-gamma) for the preferred category. This resulted in positive correlation between power differences and behavioral performance differences between categories. The negative correlation for vlPFC-beta power is in line with the antagonistic relationship between beta and gamma in each PFC subdivision. In line with recent findings and computational models, stronger gamma power co-occurs with weaker beta power and vice versa (Lundqvist et al, 2011; 2016). Thus, the negative correlation with performance of vlPFC-beta power (which signals higher relative power for the “non-preferred” category) could have resulted from a stronger suppression effect for the “preferred” category.

Disorders like autism are marked by a decreased capacity to categorize and schizophrenia by a confusion between bottom-up and top-down signaling (Gastgeb et al., 2012; Uhlhaas and Singer, 2010). Our results support an anatomically distinct, rhythm-based model for category abstraction in the PFC. They might guide the way to new insights into the underlying pathology and therapy of psychiatric disorders and into the creation of abstractions by the brain.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Earl K. Miller (ekmiller@mit.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Two, middle-aged monkeys (macaca mulatta) were used in this study: one male (9–10 years old), and one female (8–9 years old). The male weighed about 13 kg and was treated with cyclosporine daily, and the female weighed 9 kg. They were both experimentally naïve, pair-housed, on a 12-hr day/night cycle, and in a temperature controlled environment (80 degrees Fahrenheit). The animals were handled in accord with National Institutes of Health guidelines and approved by the Massachusetts Institute of Technology Committee on Animal Care.

METHOD DETAILS

Prototype and exemplar generation

The visual stimuli were composed of 7 randomly located dots on a black background. To generate the categories, we followed previously published procedures (Posner and Keele, 1968; Knowlton and Squire, 1993; Vogels et al., 2002; Antzoulatos and Miller, 2011). Figure 1A shows two example categories. Every day, two novel prototypes were created at random. These prototypes (as would be the exemplars) were generated as 7 arbitrarily positioned, 0.35 DVA dots on a grid of 7 by 7 DVA. In order to control for difficulty, these arbitrarily constructed prototypes had to obey a number of rules: (1) They had no dot centers that fell within 0.7 DVA of one another. (2) The average position of the prototype was at the center of the grid. (3) No dots from each exemplar fell within a 0.5 DVA margin around the grid edges. And, (4) the maximum Euclidean distance (summed across all pairs of dots) between each exemplar and each prototype was 10 DVA.

In order to generate the exemplars, the prototype dot patterns were distorted according to a procedure first established by Posner and colleagues (Posner and Keele, 1968). We first defined 5 concentric annular regions around each dot, which were spaced apart radially by 0.35 DVA. Region 1 refers to the annulus immediately surrounding the dot center, 1 dot-diameter away, and region 5 refers to the annulus 5 dot-diameters away. Next, each dot was shifted away from its prototypical location by at least 1 region. Whether any particular dot was moved to regions 2 through 5 depended on the distortion level desired. Posner et al. defined different levels of distortion based on the probability of a dot-shift to each concentric region. Distortion level 1 was used in this task. At distortion level 1, 88% of dots were shifted to region 1, 10% to region 2, 1.5% to region 3, 0.4% to region 4, and 0.2% to region 5. To ensure that each exemplar was unique no more than 2 dots from each exemplar could be less than 0.5 DVA away from any other exemplar’s dots. Across all trials used here, the median Euclidean distance summed over all pairs of dots between each exemplar and its corresponding prototype (distortion) was 0.95 DVA, the minimum and maximum distance was 0.81 and 2.17 DVA, respectively. The median Euclidean distance summed over all pairs of dots between each exemplar and the nearest dots in the other prototype (distance between categories) was 4.28 DVA, the minimum and maximum was 3.1 and 5.94 DVA, respectively. Figure 1B shows the distributions of all available trials as a function of distance between the presented exemplar and its own category prototype (distortion, yellow) and to the other category prototype (between-category distance, green).

Overall, the use of these visual stimuli provided us with a number of advantages: (1) The categories were not imbued with any overt meaning to the animal, for they held no apparent relationship to objects seen in daily life. (2) The categories could not be distinguished by any simple rule. (3) The perceptual distance between categories was controlled over sessions and exemplars from different categories were different enough to ensure above chance performance. (4) The exemplars from each category, which could in fact look distinctively different from one another, were always perceptually related and averaged out to the original prototype. And (5), the stimuli provided parametric control over the similarity of sensory features between each exemplar and its prototype (distortion) and thus allowed us to vary the level of required abstraction.

Task

In each session, animals had to classify numerous category exemplars into their respective categories (delayed match-to-category paradigm, Figure 1D). To initiate each trial, each animal had to fixate within 2.5 (DVA) of a centrally located, red dot (0.2 DVA in diameter) for 0.5 s. After this fixation, an exemplar of one of the two categories was presented at the center of the screen (7 by 7 DVA) for 1s. If the animal continued to fixate through this sample epoch, and a subsequent delay of at minimum 0.85 s (plus an additional jitter of max. 0.4s), then the central fixation dot disappeared and two new exemplars from either category (match vs. non-match) were presented on the left and right side of the screen (9 from the center of the screen). Once the test exemplars appeared, the animal had the opportunity to freely view both of the exemplars presented, and make the choice. The animal indicated its choice by fixating for 0.7s on one of the two peripherally presented exemplars. Neither category was tied to any particular location. If the animal made the correct choice, the white dots of the chosen exemplar turned green and the animal received juice. If the animal made the wrong choice, the chosen exemplar turned red and no juice was given. Depending on the animal, the length of timeout incurred on error trials varied from 5–16 s. For the analysis, we focused on the sample and delay epochs in this paradigm (when the animals’ eyes were fixating the screen center), because the neural signals during the test epoch might also reflect eye-movement related activity.

Block Design

To facilitate category learning, each session was organized into blocks. The blocks were defined by a progressively growing pool of available exemplars. In block 1, there were two exemplars per category. The pool of available exemplars grew by accretion; “new” exemplars were added to a bank of “familiar” ones, so that the total number of available exemplars for each category was equal to 2^block. The terms novel and familiar are not an indication for how familiar any exemplar was to an animal, but simply a reflection of when it became available in the pool of potentially usable exemplars. As the blocks progressed, the chances for only seeing novel exemplars increased substantially, and above chance performance on these novel exemplars suggested successful categorization. In fact, block transition was not possible without successful categorization, and the overlap of available exemplars between blocks favored a smooth learning process. In order to pass from one block to another, each animal had to successfully complete 70% of the previous 10 trials for each potential condition (Category A – on left, Category A – on right, Category B – on left, and Category B – on right). This behavioral criterion ensured that the animals were able to categorize stimuli from an increasing pool of different exemplars and supposedly learned the underlying category rule by the end of the training blocks. We only used correct trials above training block 5 with a minimum of 64 different exemplars per category for the analysis of neurophysiological data presented here. In addition, the behavioral criterion limited idiosyncratic biases of the animals for either choosing a particular location and/or a particular category. Because of these behavioral criteria, not all available exemplars were presented in each block (see Bias correction below). An additional restraint was imposed on the pool of available exemplars presented in block 1. Because both animals struggled to pass block one, in which two exemplars from each category were presented, the two exemplars from each category had to have a summed Euclidean distance of less than 1 DVA apart. This constraint reduced the difficulty of the first block, promoted rapid block passage, and ultimately favored category abstraction. Following block one, there was no limitation on the presented exemplars.

Bias Correction

As stated above, each of the animals attempted suboptimal strategies (i.e. exhibited biased behavioral choices) and, if left to their own devices, they would fail to learn to categorize stimuli. To avoid these aberrant behaviors, we detected the animals’ biases, and scaled the probability that any particular condition was shown to counteract these “easier,” inefficient strategies. In order to assess bias in any one of the four conditions enumerated above, we compared performance in each of the four conditions to one another, and computed a Mann Whitney U test statistic for each comparison. From this test statistic, we obtained the area under the curve, subtracted 0.5 to obtain a bias measure, and remapped this bias measure to a value between [0–1] by dividing it by 0.5. We then used this measure to scale the probability that any particular condition would be seen (i.e. we forced more choices for the non-preferred condition by showing it more often). We only implemented this bias correction algorithm after 20 trials were performed in each block. The bias correction ensured that the animals’ performance was above chance for exemplars from both categories. Despite this bias correction, the animals still maintained preferences for a particular category in each session.

Recordings

Stimulus presentation and reward delivery were controlled by custom software written in Matlab (The MathWorks, Natick, MA) using PsychToolbox (Brainard, 1997; Pelli, 1997). All stimuli were presented on an LCD screen at 144 Hz (ViewSonic VG2401mh 24″ Gaming Monitor). Eye movements and pupil size were monitored using EyeLink II at 1000 Hz sampling. Two 8×8 channel Blackrock Cereport arrays with 1mm long electrodes were placed within dorosolateral prefrontal cortex (dlPFC), and ventrolateral prefrontal cortex (vlPFC) of each monkey. Both monkeys also had two more arrays chronically implanted in the frontal and supplementary eye-fields regions (FEF, SEF). Only data from the PFC arrays was analyzed for this paper. Each electrode was separated by 400 μm. vlPFC and dlPFC were defined by anatomical landmarks following a large craniotomy. 3D MRI brain reconstructions and plastic models were used to guide the surgical implants of the array. The vlPFC array was placed 1 mm ventral to the principal sulcus and was centered at 9–12 mm anterior to the genu of the arcuate sulcus. In contrast, the dlPFC array was positioned slightly more rostral, 12–15 mm anterior to the genu of the arcuate and 1 mm dorsal to the principal sulcus. Figure 1C shows the approximate anatomical locations. Signals were recorded through a headstage (Blackrock Cereplex M and Cereplex E), sampled at 30 kHz, band-passed between 0.3 Hz and 7.5 kHz (1st order Butterworth high-pass and 3rd order Butterworth low-pass), and digitized at a 16-bit, 250 nV/bit. Summed over all 30 recording days, there were in total 608 channels in vlPFC and 335 channels in dlPFC with spikes. A channel was defined as recording spikes (multi-unit activity (MUA) channel) when its spike count per second averaged over trials and over sample and delay epochs (0–2 s) was greater than one. Figure S1 shows the array topographies for the percentages over recording days that a given channel recorded spikes for each animal. The details about the multi-unit spiking activity (MUA) analysis are reported below. Local field potentials (LFPs) were recorded with a sampling frequency of 1 kHz, referenced to ground and AC-coupled.

Data from 15 recording days were analyzed from each of the two monkeys for the LFP analysis. There were two data sets less for monkey G for the MUA analysis. For the analysis of neurophysiological data, we used equal proportions of trials from the two categories in each session (by drawing a random sub-sample of trials equal to the minimum trial number across categories). Further, we used only correct trials above training block 5 (see section Block design). The only exception from this procedure was the correct vs. error trial analysis. Across sessions, on average 269 trials were used from monkey P (min= 94, max= 520) and 293 trials for monkey G (min= 140, max= 572). For the analysis on category information across different levels of distortion, median split by between-category distance and for correct vs. error trials, we equated the trial numbers per condition for each session (see below for details). This reduced the number of available trials for the distortion analysis (monkey P: 185 trials, min= 48, max= 364; monkey G: 200 trials, min= 80, max= 360) and the correct vs. error analysis (monkey P: 142 trials, min= 36, max= 284; monkey G: 111 trials, min= 24, max= 244).

QUANTIFICATION AND STATISTICAL ANALYSIS

Behavioral data

Behavioral and neurophysiological results were very similar between monkeys and therefore pooled across animals. All analytic measures for behavioral and LFP data were calculated for each recording session separately (unit of observation n= 30 sessions, unless otherwise indicated). For MUA analysis, all measures were calculated for each channel that recorded spiking activity (MUA channel). For behavior and LFPs, this yielded repeated measures between the tested conditions in each session and, thus, the statistical contrasts were calculated for a dependent-samples design across sessions. For MUA, this yielded repeated measures between conditions in the same area (same MUA channels) and independent measures for between-area contrasts (different MUA channels). For the dependent-samples case, the error bars and shaded error regions show the standard error of the mean for repeated measures. The mean between conditions in each session was subtracted from the data in each condition before calculating the standard error. The resulting error estimate was bias corrected by the number of conditions (M, multiplied by √ (M/(M−1)), as described in Morey, 2008).

Behavioral performance (percent correct trials) was well above chance (50 %) in every session (mean ± SD: 78 ± 6 %, t-value vs. 50 %: t(29)= 27, p< 5.3×10⁻²², Figure 4A). Performance was analyzed as a function of distortion level, median split by between-category distance (difficulty) and for preferred and non-preferred categories. Category preference was based on the proportion of correct trials for each category on any given recording day. The better-performed category was defined as “preferred”. Performance was then pooled over preferred and non-preferred categories across recording days. For the effect of exemplar distortion on behavioral performance, we sorted all trials across all recording days by the summed Euclidean distance of the shown exemplar to its category prototype (distortion, see Prototype and exemplar generation above). Performance curves as a function of exemplar distortion were calculated by convolving the distortion-sorted performance vectors with a sliding-average window, encompassing 10% of the trials (width for preferred categories: 1243 trials; non-preferred categories: 1403 trials). Performance remained largely unchanged across a wide range of distortion levels but then decreased sharply at a critical distance from the prototype. Generalization across different exemplars and sharp distinctions with increasing category distance are hallmarks of categorization. Performance curves were fitted with a generalized logistic function (sigmoid S, Eqn. 1) with four free parameters (A = lower asymptote, B = upper – lower asymptote, C = steepness, x0 = mid-point) to estimate the inflection point (x0; see Figure 5A).

$$\mathrm{S}=\mathrm{A}+\mathrm{B}/(1+{\mathrm{e}}^{(\mathrm{C}\ast (\mathrm{x}-\mathrm{x}0))})$$ Eqn. 1

The coefficient of determination (R²) was used to determine the goodness of the fit, and the 95%-confidence intervals of the parameter estimates were calculated. In order to directly compare performance between low and high distortion levels, we split the data sets for each session at the estimated inflection point for preferred category trials (1.1 DVA). For the difficulty analysis, the data sets per session were split at the median distance between exemplars and the second category prototype (on average 4.3 DVA). The effects of category preference and exemplar distortion (low vs. high split at the inflection point) or difficulty (median split) across sessions on behavioral accuracy (% correct trials) were then tested with a two-way, repeated-measures analysis of variance (ANOVA). Interaction effects were explored with post-hoc dependent-samples t-tests (Figure 5B, F). The difference in exemplar distortion between the median split trial subsets for between-category distance was tested with a dependent-samples t-test across sessions.

LFP pre-processing

Data was analyzed using custom Matlab code (The MathWorks, Natick, MA) and the Fieldtrip toolbox (Oostenveld et al., 2011). The continuous local field potential (LFP) for each of the 64 electrodes on each recording array (vlPFC, dlPFC) was cut into trials between −2 s to 4 s around the sample onset. For the evoked response analysis, the LFP signal from each area was referenced to the same common reference (ground) and band-pass filtered between 1 and 15 Hz with a zero-phase Butterworth filter (4th order) applied in the forward and reverse direction. Before filtering, each trial was zero-padded to a length of 10 s to avoid edge artifacts. Stimulus-evoked activity was derived by averaging the LFP signal at each electrode across trials and baseline correcting it to the pre-trial interval between −1 to −0.75 s relative to sample onset. For the analysis of oscillatory power, LFPs were re-referenced to the array average, subtracting out the common signal components across all electrodes. LFPs were then band-pass filtered between 1 and 250 Hz and band-stop filtered around line noise frequencies (60, 120, 180, 240 ± 1 Hz, same filter settings as above). In order to obtain induced activity without the contribution from stimulus-evoked LFP components, the trial-average was subtracted from each single trial.

Time-frequency representations were calculated using a Fourier transform applied to short sliding time windows in steps of 10 ms in the time interval between −1 to 3 s relative to sample onset and in the frequency range between 1 to 200 Hz. Fourier estimates were computed by means of a multi-taper transformation (discrete prolate spheroidal sequences (dpss), 3 tapers) applied to single trial data. The squared absolute value of the Fourier estimate gave the LFP signal power for each electrode across different frequencies and time points. For time-frequency representations and frequency spectra, we used a fixed 200 ms window width with a fixed amount of spectral smoothing (±10 Hz for frequencies between 1–200 Hz in steps of 1 Hz). This procedure yielded a good resolution in the frequency domain (see Figures 2 and S1). For the power time courses, we opted for a better temporal resolution (especially for higher frequencies) and used a frequency-dependent window width (5 cycles per frequency between 1–59 Hz in 1 Hz steps, between 60–99 Hz in 5 Hz steps, between 100–200 Hz in 10 Hz steps) and smoothing (0.4 times the frequency of interest). Subsequently, we averaged over the respective frequency bands to derive the time course of beta (10–35 Hz) and gamma power (60–160 Hz) and information (see Figures 4, S3 and 6). The two methods yielded very similar results apart from the described trade-off between spectral and temporal resolution.

Task-related changes in LFP power

LFP signal power during the sample presentation (0–1 s), the memory delay epoch (on average 1–2 s, jittered between 1 to 1.85–2.25 s) and at the test epoch (>2.25 s) was compared to the pre-trial baseline epoch (−1 to −0.75 s relative to sample onset) by means of a Wilcoxon signed-rank test. This time epoch was chosen as baseline because it was free from stimulus-evoked and eye-movement related activity by the onset of the fixation dot and the associated saccade. Baseline activity for each trial was calculated by averaging power between −1 to −0.75 s for every frequency bin on each electrode. Single-trial baseline values were then compared to each time-frequency bin during the task epoch. The sum of the signed rank difference across trials (Wilcoxon test statistic) was converted into a z-value for a standard normal distribution. The resulting time-frequency z-value maps for each electrode were averaged over sessions.

For Figures 2A and B, the time-frequency z-value maps were averaged over all electrodes in each area and masked at a conservative threshold of z = ± 3.29 (corresponding to p< .001, two-sided). For the array topographies (Figure S1) the z-value maps were averaged over the time interval between 0–3 s and either the beta (10–35 Hz) or the gamma band (60–160 HZ). For the power spectra (Figure S1) the z-value maps were averaged over all electrodes in each area and over the time intervals between 0–1 s/1–2 s for dlPFC and 0.1–0.3 s/2.5–2.7 s for vlPFC. Both z-value power spectra and topographies were Bonferroni corrected for multiple comparisons (200 frequency bins, 64 electrodes). The locus of maximal power changes in vlPFC was explored by separating the broadband gamma spectrum into four equally spaced frequency ranges between 40 and 200 Hz (41–80 Hz, 81–120 Hz, 121–160 Hz, 161–200 Hz). The average z-value over each of these frequency ranges was then tested between adjacent sub-bands with a Wilcoxon sign-rank test. In order to obtain a single value representing the power modulations relative to baseline in each session, as shown in Figure 2C, we averaged the z-values over each frequency band, the time epoch from 0–3 s and all electrodes per area. This power modulation value was used to explore the interaction between the frequency bands across areas with a two-way, repeated-measures ANOVA.

The degree of correlation between the beta and gamma power time-courses within and across areas was tested by averaging power changes over all electrodes per area and in the respective frequency band (beta: 10–35 Hz, gamma: 60–160 Hz) and calculating the Pearson-correlation over the time interval between 0–3 s after sample onset. The resulting r-coefficients over sessions were compared against 0 with a Wilcoxon sign-rank test.

Category information in LFP power

We assessed category selectivity in LFP power in vlPFC and dlPFC using a percentage of explained variance statistic (ω²-statistic). The ω²-statistic reflects how much variance in the LFP signal can be explained by the category membership of a particular presented exemplar in each trial (Eqn. 2, where SS_between is the sum of squared residuals between categories SS_between = Σ_category N_category * (mean_category – mean_total)², SS_total is the total sum of squared residuals across all trials SS_total = Σ_trials (x_exemplar - mean_total)², df₁ is the degrees of freedom between categories (i.e: 1, number of categories – 1), MSE is the mean squared error MSE = 1/df₂ * Σ_trials (x_exemplar - mean_category)², where df₂ is the degrees of freedom of the error (i.e: number of trials – number of categories).

$${\mathrm{\omega }}^2=({\text{SS}}_{\text{between}}-{\text{df}}_1\ast \text{MSE)}/({\text{SS}}_{\text{total}}+\text{MSE})$$ Eqn. 2

ω² is an unbiased measure of explained variance (Olejnik and Algina, 2003). It results in a zero-mean statistic when there is no category information (see baseline interval from −0.5 to 0 s in Figure 2D, E) and its upper limit would be 1 indicating 100 % explained variance. Note that slightly negative ω² - values can occur due to the bias-correction of the statistic for small sample sizes (i.e. subtracting the MSE in Eqn. 2).

Category information expressed in the ω²-statistic was calculated for each recording session, in each of which a new set of categories was presented, and then averaged over sessions. A permutation test was used to determine significant category information (ω²) in the LFP-signal. To this end, the association between neural activity and category membership was broken up by randomly shuffling the category labels across trials. The ω²-statistic was recorded after each permutation run, generating a reference distribution of ω²-statistics under the null hypothesis of no category information in the LFP signal (approximated with a Monte Carlo procedure of 1000 permutations). Akin to the analysis of the observed data, the reference distributions were generated for each session separately and subsequently averaged over sessions. The observed ω²-statistic was then compared with this null distribution. A given electrode, time- or frequency sample was defined as carrying category information, if its associated, observed ω²-statistic exceeded the 99.9% - quantile of the corresponding reference distribution (p< .001). For example, we determined the percentage of category-informative electrodes (see Figure S1) in each area (vlPFC, dlPFC) for each frequency band (beta: 10–35 Hz; gamma: 60–160 Hz). To this end we averaged power across the respective frequency band and the time interval between 0.5 to 1.5 s after sample onset and calculated for each electrode the ω²-statistic (and its corresponding null-distribution). An electrode was then defined as carrying category information, if its associated, observed ω²-statistic exceeded the 99.9% - quantile of the corresponding reference distribution.

Figures 2D and E show the time-frequency maps averaged over all category-informative electrodes in either frequency band in each area and masked at a conservative threshold of p< .001. In Figure S1, we show category information as a function of frequency averaged over all category-informative electrodes and either the sample (0–1 s) or delay epoch (1–2 s). Significant frequency ranges were defined for observed ω²-statistics with p< .001. The locus of maximal category information in vlPFC was explored by separating the broadband gamma spectrum into four equally spaced frequency ranges between 40 and 200 Hz (41–80 Hz, 81–120 Hz, 121–160 Hz, 161–200 Hz). The average ω²-statistic over each of these frequency ranges was then tested between adjacent sub-bands with a Wilcoxon sign-rank test. For each array (vlPFC, dlPFC), we calculated a single value representing the category information in each frequency band (beta, gamma, averaged between 0.5–1.5 s, see above). We averaged the ω²-statistics for each frequency band across all electrodes per area and converted it into a z-score for each session relative to the session’s permutation distribution (i.e. subtracting the mean of the distribution and dividing by its standard deviation, see Figure 2F). This category information value was used a) to assess the amount of category information per frequency band and cortical area and b) to explore their interaction with a two-way, repeated-measures ANOVA and Wilcoxon sign-rank tests.

Evoked activity

The evoked potential was calculated as the trial-average LFP signal between 1–15 Hz (see above). The evoked potentials for each electrode were baseline corrected for the average amplitude in the baseline epoch (−1 to −0.75 s before sample onset) and then averaged over all electrodes per area. The absolute amplitude time-locked to sample onset (averaged between 0.1 to 0.3 s after sample onset) was compared between areas (vlPFC, dlPFC) with a Wilcoxon sign-rank test (Figure 3A). Category information in the evoked activity (ω²-statistic) in each area was calculated for the band-bass filtered single trial data (averaged over all electrodes) and its statistical significance assessed with a permutation test (as described above for LFP power). The information time courses were smoothed with a Gaussian filter (width: 100 ms, sigma: 25 ms) for better illustration (Figure 3D). The results were identical between raw and smoothed time courses. Significant differences in information between areas were tested independently for the sample (0–1 s) and memory delay epoch (1–2 s) with a Wilcoxon sign-rank test for the average ω²-statistic over the respective time interval.

Multi-unit spiking activity

Multi-unit activity (MUA) was derived from the 30 kHz-sampled raw signals (see Recordings). Each channel was re-referenced to the array average, subtracting out the common signal components across all electrodes. The signals were then high-pass filtered at 300 Hz (6th order Butterworth, zero-phase), rectified and thresholded at five times above each channel’s noise level (Eqn. 3).

$$\text{thr}=5\ast \text{median}(\text{abs}(\text{signal})/0.6745)$$ Eqn. 3

This noise estimate improves on the estimation based on a channel’s standard deviation because it remains largely constant across different firing rate regimes and spike amplitudes (Quiroga et al., 2004). We chose a conservative threshold (5 times above the channel’s noise level), in order to capture only very few neurons near an electrode. Because nearby neurons tend to show similar properties, this local MUA activity is nearly identical to single-unit activity. Spike time stamps were extracted for each threshold crossing between −1 s before to 3 s after sample onset on each trial with a minimal time interval of 1 ms (30 samples) between successive time stamps. All channels with an average spike rate (spikes/s) between 0–2 s > 1 were defined as containing multi-unit spiking activity (MUA channel). Given the inter-electrode distance (400 μm), the same neuron cannot contribute to MUA activity on multiple channels. Thus, each MUA channel was treated as an independent unit of observation (n= 608 channels in vlPFC, n= 335 channels in dlPFC).

Category information for each MUA channel was calculated with the ω²-statistic for the summed spike counts between 0–2 s and its statistical significance assessed with a permutation test (as described above for LFP power). The ω²-statistic accounts for category information for both increased and reduced firing rates for one or the other category (i.e. category A > category B and category B > category A contribute equally to information in the ω² – statistic). Figure S1 shows the array topographies for the percentage over recording days that a given channel recorded spikes and that it contained category information (p< .001). The spike rates over time (spikes/s) were calculated by convolution with a Gaussian filter (width: 100 ms, sigma: 25 ms) and then down-sampled to 1000 Hz. Category information over time was calculated by the ω²-statistic for each time bin. The difference in the average spike rates between 0.1–0.3 s and in the average category information during sample (0–1 s) and delay epochs (1–2 s) between PFC areas was tested with a Mann-Whitney U-test across all MUA channels per area. The Pearson-correlation between the power time-courses and spike rates was calculated over the time interval between 0–3 s after sample onset for each MUA channel. The resulting r-coefficients were compared against 0 with a Wilcoxon sign-rank test. The average r-coefficients were compared between PFC areas with Fisher’s r to z test.

Spike-LFP coherence

The LFP-phase in the frequency range between 1 to 200 Hz was computed locally around the spike time stamps (± 0.1 s; spike-triggered spectrum) using a Fourier transform (Hanning taper). To exclude the possibility of spike bleed-through artifacts, we linearly interpolated the LFP traces in the interval ±2 ms around the spike time stamps. Spike-LFP phase coherence was calculated for each MUA channel averaged over all LFP channels per area (within- and between PFC areas) except for the spike-recording MUA channel. Each LFP channel was normalized for its power prior to averaging across channels. We used the pair-wise phase consistency metric (PPC, Vinck et al., 2010) to assess the degree of spike-LFP coherence. PPC is an unbiased measure of phase coherence with respect to sample size (i.e. its mean is independent of the number of observations). Thus, PPC yields similar results for different spike counts (i.e. when many or few LFP phases are compared). However, the variance of PPC does depend on the number of observations (Vinck et al., 2010). Thus, PPC estimates based on less than 30 spikes were discarded (i.e. replaced with NaN). PPC spectra were calculated for all spikes between 0–2 s. The time-frequency PPC representations were generated using short sliding time windows (width 0.2 s) in steps of 10 ms in the time interval between −0.5 to 2 s relative to sample onset. We used a Rayleigh test to assess significance for spike-LFP coherence across each MUA channel’s entire spectrum (p<. 05, Bonferroni corrected for 1–200 Hz) and averaged in the beta band (10–35 Hz, p<. 001). The difference in beta PPC between PFC areas was tested with a Mann-Whitney U test across all MUA channels per area with significant PPC in the beta band (vlPFC n= 167, dlPFC n= 109). The same test was used for the PPC time-frequency representations and the resulting statistical map was masked at p< .001.

For category information in spike-LFP coherence, we restricted our analyses to LFP channels that carried most category information in power (10% most informative channels per area and frequency band, see green dots in Figure S1). Category selectivity for each MUA channel was tested with a non-parametric permutation approach for the PPC difference between categories either averaged in the beta band or frequency-cluster corrected for the entire spectrum (p< .05; similar to the description in Maris et al., 2007). The reference distribution was approximated by a Monte Carlo procedure based on 500 permutations, each time shuffling the category labels across trials, splitting the trial-shuffled data into two equal sets and re-calculating the PPC difference between categories. Cluster-level statistics were calculated by summing over supra-threshold PPC differences when they were adjacent in frequency space. The threshold for clustering was defined non-parametrically for each frequency sample in both the observed spectrum and each random permutation based on all other permutations (p< .05). The maximum cluster level statistic was recorded after each permutation run, generating a reference distribution of cluster-level statistics. A given MUA channel was category selective when its observed PPC difference between categories exceeded the 2.5% and 97.5%-quantiles of its corresponding reference distribution (averaged in beta or on the cluster-level). The absolute difference between categories in beta band PPC was compared between PFC areas by means of a Mann Whitney U test across all MUA channels per area with significant beta PPC differences (vlPFC gamma-LFP n= 57, vlPFC beta-LFP n= 54, dlPFC n= 28). We subtracted the median absolute PPC difference from each category-shuffled permutation distribution from the observed absolute PPC difference per MUA channel, in order to partial out between-area differences due to an overall different PPC level and to ensure that the between-area differences were due to differences in category-selectivity.

Category selectivity in beta spike-LFP coherence for different distortion levels was assessed with a non-parametric permutation approach (as described above) separately for spikes in the sample (0–1 s) and delay epochs (1–2 s). The proportions of category-selective MUA channels (for all trials and per distortion level) were tested against a chance level of 5% with a binomial test and between PFC areas with a χ²-test for independence. We used a McNemar test to assess the difference in the proportions of category-selective MUA channels between low and high distortion levels. It takes the condition pairing across MUA channels into account (i.e. each MUA channel was tested twice for category selectivity, once for low and high distortion). The p-value for the McNemar statistic (the number of discordant pairs) was derived from a binomial distribution with p=0.5.

Correlation between behavioral category performance and LFP power changes

We tested the relationship between the behavioral preference for a particular category in a given session with the task-related change in LFP power in the beta and gamma bands. To this end, we computed an index of behavioral category preference as the difference in the proportion of correct trials (pcor) between the two categories divided by the overall proportion of correct trials per session (Eqn. 4). Likewise, the LFP power differences between categories in the beta (averaged between 10–35 Hz) and gamma band (60–160 Hz) were quantified by the difference in the average LFP power (pow) between the two categories divided by the overall LFP power in that band per session (Eqn. 5).

$$({\text{pcor}}_{\mathrm{A}}-{\text{pcor}}_{\mathrm{B}})/{\text{pcor}}_{\text{all}}$$ Eqn. 4

$$({\text{pow}}_{\mathrm{A}}-{\text{pow}}_{\mathrm{B}})/{\text{pow}}_{\text{all}}$$ Eqn. 5

The performance and power differences were divided by overall performance/power, in order to bring the magnitude of the behavioral and neural effects onto the same scale. The LFP power differences were averaged over all electrodes for each array (vlPFC, dlPFC) and the Pearson-correlation (Pearson-r_sessions) between behavioral and power differences per frequency band was calculated for each time point between 0–2 s.

In order to correct for multiple comparisons at multiple time samples, we used a nonparametric cluster-based permutation test (Maris and Oostenveld, 2007). First, clusters of temporally adjacent supra-threshold correlation (Pearson-correlation exceeding p < .05, two-sided) were identified. Within one cluster, r coefficients were summed up to obtain a cluster-level test statistic. Then, random permutations of the data were drawn by exchanging the session labels and therefore breaking up the relationship between behavioral category preference and LFP power change between categories in each session. The maximum cluster level statistic was recorded after each permutation run, generating a reference distribution of cluster-level statistics (approximated with a Monte Carlo procedure of 1000 permutations). Cluster-level p-values were then estimated as the proportion of values in the corresponding reference distribution exceeding the cluster-level statistic obtained in the actual data. The cluster-level statistic represents the significant correlation over a time interval, which is effectively controlled for multiple comparisons at multiple time samples (see Figure S3).

Figures 4C and D show the power differences between categories, averaged over these significant time intervals, plotted against behavioral differences. We estimated the percentage of electrodes in each array with a significant correlation during those significant time intervals. To this end, the LFP power change was averaged within the time intervals of interest (0.23–1.17 s for dlPFC beta; 0.1–0.3 s for vlPFC gamma) and the Pearson-correlation with behavioral differences was calculated for each electrode. The cluster-based permutation procedure (see above) was used for multiple comparison correction at multiple electrodes (Figure S3). In order to form sensor clusters, the electrode neighborhood on the array was defined by Delaunay triangulation. We tested the difference in power between preferred and non-preferred categories per session (defined based on behavior, see Behavioral data above) for the average power across the strongest connected cluster of electrodes with a significant correlation (see Figure S3). For spiking in vlPFC, we tested the difference in the spike rates (spikes/s) for preferred vs. non-preferred categories across all MUA channels that contained category information (n = 242 MUA channels). Dependent-samples t-statistics were calculated for the power or spiking difference between preferred and non-preferred categories for the time course between 0–2 s and the cluster-based permutation test (see above) was used for multiple comparison correction at multiple time samples (Figure 4E–G).

For vlPFC-gamma power, we repeated the same analysis averaged over all MUA channels that contained category information (like for the spiking analysis), instead of averaging over recording sessions, in order to directly compare the gamma power and spiking effects on the same electrodes (Figure S3 H). We used a two-way, repeated-measures ANOVA with the factors category preference (preferred/non-preferred) and neural measure (gamma power/spiking) to contrast the average activity between 0–2 s. The neural measures (power and spiking) were transformed into a relative change to its mean activity (subtracted and divided by the mean power/spike rate over all MUA channels and preferred/non-preferred categories), in order to bring the magnitude of the spiking and power effects onto the same scale.

Category information as a function of exemplar distortion, correct vs. error trials and difficulty

In order to compare category information across different levels of exemplar distortion, we split the data sets for each recording day at the critical distortion level (1.1 DVA, based on the inflection point for behavioral performance on the preferred category, see Behavioral data). For the difficulty analysis, the data sets per session were split at the median distance between exemplars and the second category prototype (on average 4.3 DVA). Likewise, we compared category information between correct and error trials. We calculated the ω²-statistic separately for each trial subset. Although the mean of ω² is unbiased (around zero when there is no information), the distribution of observed values still varies with the number of observations (the skew of the distribution). Therefore, the data sub-sets were balanced in trial numbers for each session (by drawing a random sub-sample of trials equal to the minimum trial number across conditions, see section Recordings above).

For power, we restricted our analyses to electrodes that carried most category information between 0.5 to 1.5 s after sample onset (see green dots in Figure S1). Category information (ω²-statistic) was averaged between the balanced trial subsets and then the 10% most informative electrodes in each area and each frequency band were selected. This ensured that we simultaneously captured effects in the sample and delay epoch on those informative electrodes without any bias to either trial subset. Significant differences in information were tested independently for the sample (0–1 s) and memory delay epoch (1–2 s) with a Wilcoxon sign-rank test for the average ω²-statistic over the respective task epoch. For spiking in vlPFC, we tested the differences between low and high distortion in the ω²-statistic calculated for the summed spike counts per epoch and for all MUA channels that contained category information (n = 242 MUA channels). For the distortion and difficulty analyses, we used a two-way repeated-measures ANOVA with the factors frequency (gamma/beta) and trial subset (either low/high distortion or above/below median distance) for the average category information between 0–2 s. The time courses of category information shown in Figures 6 and S4 were smoothed with a Gaussian filter (width: 100 ms, sigma: 25 ms) for better illustration.

The sample/delay epoch differences between low vs. high abstractness were also tested (1) with a non-parametric permutation tests for the maximum/minimum statistic per task epoch and (2) over time with a cluster-based method for multiple comparison correction (see above; Figure S4). For (1), the empirically observed maximum/minimum statistic over the respective task epoch (max. for gamma in sample (0–1 s), min. for beta in delay (1–2 s)) for the Wilcoxon test statistic between low and high distortions was compared to the 95%-quantile of random permutations. The reference distributions were generated by shuffling the condition labels across sessions (but keeping the session-pairing between conditions), calculating the Wilcoxon test-statistic and recording the maximum/minimum statistics over the respective epoch (approximated with a Monte Carlo procedure of 1000 permutations). For (2), the time courses were first aligned to the first time point with significant category information for each recording day (with p< .05, permutation test). In case there was no time point with p< .05 (which happened in dlPFC-beta for 2/30 recording days), we aligned to the time point with maximal information. The alignment accounts for variability in the latency of category information due to different categories and exemplars on different recording days. For dlPFC-beta, the first time point with information was on average at 0.532 s ± 0.375 s SD. For vlPFC-gamma, this time point was on average at 0.186 s ± 0.162 s SD. We tested across all time points that were consistently available across all recording days from the first significant time point per day up to the test exemplar onset (sample and delay epoch) with a Wilcoxon test-statistic and a cluster-based permutation approach for multiple comparison correction (0–1 s for vlPFC-gamma, 0–0.6 s for dlPFC-beta; 1000 permutations).

DATA AND SOFTWARE AVAILABILITY

Custom code for analyses will be provided upon request to the Lead Contact.

Highlights.

• Category abstraction was organized by oscillatory dynamics and PFC sub-region.

• Gamma oscillations in ventrolateral PFC signaled low-level category abstraction.

• Beta oscillations in dorsolateral PFC signaled high-level category abstraction.