Controlling load-dependent kinetics of β-cardiac myosin at the single molecule level

Abstract

Concepts in molecular tension sensing in biology are growing and have their origins in studies of muscle contraction. In the heart muscle, a key parameter of contractility is the detachment rate from actin of myosin, which determines the time that myosin is bound to actin in a force-producing state and, importantly, depends on the load (force) against which myosin works. Here, we measure the detachment rate of single molecules of human β-cardiac myosin and its load dependence. We find that both can be modulated by both small molecule compounds and cardiomyopathy-causing mutations. Furthermore, effects of mutations can be reversed by introducing appropriate compounds. Our results suggest that activating vs. inhibitory perturbations of cardiac myosin are discriminated by the aggregate result on duty ratio, average force, and ultimately average power output and that cardiac contractility can be controlled by tuning the load-dependent kinetics of single myosin molecules.

Main.

The ability to sense and respond to force is a fundamental feature observed across all scales of biology, from tissues^1,2, to cells^3,4, and to individual molecules^5–8. Muscle contraction is a classic example in which tension sensing of the tissue ⁹ has its roots in the individual molecular motors working in every muscle cell – the myosin molecule.

Detachment rate is a key kinetic parameter describing myosin’s actin-activated ATPase cycle because it determines the time myosin is bound to actin in a force-producing state. Importantly, this rate depends on the force (load) against which myosin works as demonstrated in single molecule optical trap experiments with cardiac ^10,11, skeletal ¹², smooth ¹³, and non-muscle myosins ^14–16. The load-dependent detachment rate (k_det(F)) is a fundamental characteristic of every individual myosin molecule. As such, it determines whether a non-muscle myosin is a force sensor (myosin Ib) or a transporter (myosins V, Ic), while for muscle myosins, it defines the identity of the particular muscle (skeletal, cardiac, smooth). Even within a particular muscle type, different isoforms have different load-dependent kinetics adapted to their specific function^17–19. For instance, the beta isoform of cardiac muscle myosin is slower but has higher load-bearing ability than the alpha isoform ²⁰, consistent with its dominant presence in the ventricles rather than the atria of the heart ²¹. The cardiac myosin identity is so specifically tuned such that the relative composition of the alpha and beta isoforms changes in the failing heart ²¹. Furthermore, replacement of one by the other had a detrimental effect in transgenic mice subjected to cardiovascular stress ²².

Thus, it is apparent that significant differences in the amino acid sequences of different myosin types dramatically change k_det(F) to accommodate their molecular functions. However, it is not known whether small perturbations such as disease-causing mutations and small molecule drugs can control and alter the k_det(F) in any specific myosin. Here, we address this question by measuring the effects of various small perturbations on the load-dependent kinetics of human β-cardiac myosin. Measurement of k_det(F) of single striated muscle myosin molecules under physiological (~2 mM) ATP conditions is challenging due to their short binding lifetime. Existing techniques, while able to measure k_det(F), require fast feedback and/or are not efficient at obtaining a large number of events. In contrast, Harmonic Force Spectroscopy (HFS) presented a simple and efficient solution without the need for feedback ¹¹. In the present study, we first demonstrate the robustness of the HFS method by measuring k_det(F) for a population (N=36) of single molecules of a truncated recombinant human β-cardiac subfragment-1 (short S1 or sS1, residues 1–808) (Supplementary Fig. 1), the motor domain of the myosin responsible for force production in the ventricles of the heart (hereafter referred to as myosin). The efficiency of this method allowed us to tackle the aforementioned question: how is myosin’s load-dependent kinetics controlled and affected by various biologically-relevant perturbations? We tested the extent to which small molecule compounds affect k_det(F). These compounds include both allosteric activators and an inhibitor of cardiac myosin, including the potential heart failure drug omecamtiv mecarbil (OM) ²³, and the potential active-site therapeutic 2-deoxy-ATP (dATP) ^24,25. Next, we introduced mutations into β-cardiac sS1 that cause hypertrophic (HCM: D239N and H251N) or dilated (DCM: A223T, R237W and S532P) cardiomyopathies and measured their effects on k_det(F). We show that the effects of mutations can be reversed by adding the appropriate small molecule compounds. In addition, we further investigated the mechanism of one of the compounds, OM, by measuring its dose-dependent effect on the detachment kinetics of myosin. Finally, our findings provide a new single molecule-level understanding of cardiac myosin’s power production under these various perturbations.

Harmonic Force Spectroscopy enables simple and efficient measurement of load-dependent kinetics on single molecules of human β-cardiac myosin

In Harmonic Force Spectroscopy (HFS) optical trap experiments, the lifetimes of binding events between a single myosin motor and actin under various loads can be directly measured in saturating (2 mM) ATP conditions ¹¹. The sample stage oscillates so that when myosin binds to actin, it experiences a sinusoidally varying load with a certain mean value (Fig. 1a). Unlike other methods which require feedback to apply a load ^10,12,13,26, HFS does not. Oscillation serves two essential purposes: 1) A range of mean loads, both positive and negative, is automatically applied over the course of many events by virtue of the randomness of where myosin initially attaches to actin (Fig. 1a) (see also Supplementary Note). 2) Oscillation allows for the detection of short binding events of cardiac myosin to actin, which were previously more difficult to detect than longer events. In the unattached state, the dumbbell oscillates π/2 ahead of the stage due to fluid motion, and in the attached state the dumbbell oscillates in phase and with a larger amplitude due to stronger association with the oscillating stage (Fig. 1b). Therefore, events are detected automatically based on a simultaneous increase in oscillation amplitude above a threshold and a decrease in phase below a threshold (Fig. 1b). In this way, HFS enables detection of short binding events (>5 ms, one period of stage oscillation) under load regardless of the length of an event.

Figure 1: Load-dependent kinetics of single molecules of human β-cardiac myosin measured by harmonic force spectroscopy (HFS).

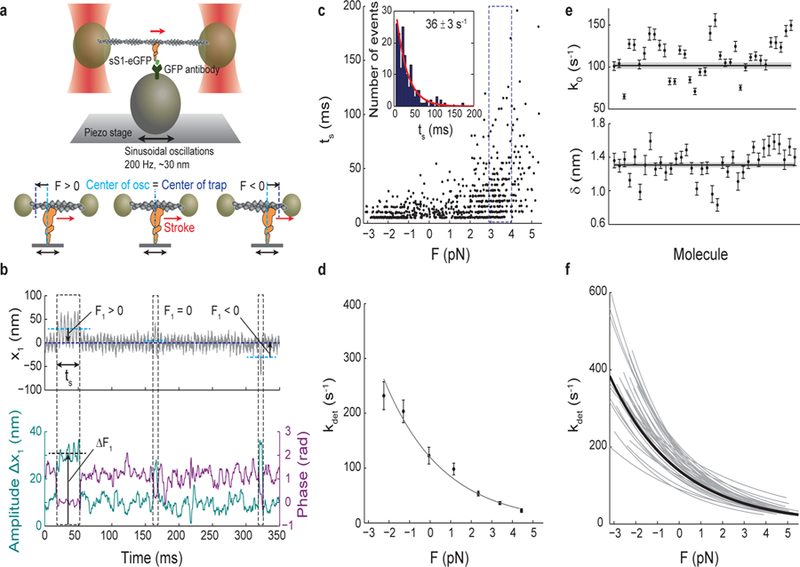
a, Oscillations of the piezo stage on which myosin is attached in the three-bead optical trap system (top) apply a sinusoidal load (force) to myosin upon attachment to actin (bottom). b, Example trace of the position of one trapped bead, x₁ (top). An increase in the amplitude of oscillation and a simultaneous decrease in the phase between the trapped bead and piezo stage (bottom) are the two criteria used in the automated detection of an event. Over the course of many individual events, a range of forces with mean F₁ (calculated as x₁ multiplied by the trap stiffness) is automatically applied as myosin attaches randomly along actin to experience both positive (resistive) or negative (assistive) loads ¹¹. Three events are outlined: F₁ > 0, F₁ ~ 0, and F₁ < 0. Each event experiences the oscillatory force with mean F₁ and amplitude ΔF₁, calculated as the amplitude Δx₁ multiplied by the trap stiffness. Force F in Eqn. 1 is calculated as the sum of F₁ and F₂ from the second trapped bead, and the force amplitude ΔF is calculated as the sum of ΔF₁ and ΔF₂ (~3–4 pN). c, All events (N=729) for one example molecule. Duration of event (t_s) is plotted against force. Events binned by force (dashed outline) have exponentially-distributed binding times from which the detachment rate at that force is determined by maximum likelihood estimation (MLE) (inset). The error on the rate is calculated from the variance of the MLE as the inverse Fisher information. d, The Arrhenius equation with harmonic force correction (Eqn. 1) is fitted to the detachment rates at each force to yield the load-dependent kinetics curve for one molecule. For this molecule, k₀ = 84 ± 4 s⁻¹, the rate at zero load, and 𝛿 = 1.31 ± 0.03 nm, the distance to the transition state, which is a measure of force sensitivity. Errors on k₀ and 𝛿 are from the covariance matrix (inverse Fisher information matrix) for the parameters. e, k₀ and 𝛿 for all molecules measured (N=36). Their weighted means, k₀ = 102 ± 4 s⁻¹, 𝛿 = 1.31 ± 0.03 nm, are shown as horizontal lines with s.e.m. in gray. f, Load-dependent kinetics curves for all molecules measured (gray), each described by a (k₀, 𝛿) pair in (e). Individual data points as in (d) are not shown for clarity. The curve corresponding to the weighted means of k₀ and 𝛿 is shown in black. All experiments were done at saturating (2 mM) ATP.

In the analysis of time trace data for a single myosin molecule, binding events are first detected, each defined by the duration t_s and mean force F (Fig. 1c). Events are then binned in force increments of ~1 pN so that the detachment rate for each bin k_det(F) can be calculated by a maximum likelihood estimation (MLE) on the exponentially-distributed bound times (Fig. 1c inset). Since the load experienced by myosin during an event is sinusoidal with amplitude ΔF and mean F, the dependence of the detachment rate k_det on force is given by the Arrhenius equation with a harmonic force correction:

$$k_{det}\left(F, \Delta F\right)=k_0{I}_o\left(\frac{\Delta F\delta }{k_{B}T}\right)\text{exp}\left(-\frac{F\delta }{k_{B}T}\right)$$ Eqn. 1

where k₀ is the rate at zero load, 𝛿 is the distance to the transition state of the rate limiting step in the bound state (a measure of sensitivity to force), k_B is the Boltzmann constant, T is temperature, and I₀ is the zeroth-order modified Bessel function of the first kind (to correct for the harmonic force). This equation is fitted to the detachment rates k_det(F) with the parameters k₀ and 𝛿 to obtain the loaded curve for a single myosin molecule (Fig. 1d).

Measurements of a population (N=36) of single molecules of human β-cardiac myosin yielded the mean values k₀ = 102 ± 4 s⁻¹ and 𝛿 = 1.31 ± 0.03 nm (standard error of mean, s.e.m.) (Fig. 1e-f), consistent with previous studies ^10,11. The HFS method produces a load-dependent curve for each molecule rather than one from events aggregated across multiple molecules, therefore providing the distribution of the population and revealing inherent molecule-to-molecule differences (Fig. 1e-f).

Allosteric effectors of human β-cardiac myosin slow down ensemble actin-sliding velocity

We investigated four allosteric activators (A2876 (1), C2981 (2), D3390 (3), OM), one allosteric inhibitor (F3345 (4)), and the active-site substrate dATP as small molecule effectors of cardiac myosin (Fig. 2a). dATP, a potential heart failure therapeutic ²⁴, acts in place of ATP and has been shown to enhance cardiac myosin’s ATPase activity ²⁵. A2876 (1), C2981 (2), and D3390 (3) were derived from hits discovered from an ATPase screen using bovine cardiac subfragment-1 and regulated thin filaments (purified bovine actin, tropomyosin, and troponins C, I, and T), and F3345 (4) was derived from a hit discovered from an ATPase screen using bovine myofibrils, all by MyoKardia, Inc. OM, an investigational drug in phase III clinical trials for heart failure ^23,27 (GALACTIC-HF, www.clinicaltrials.gov NCT02929329), has been proposed to increase ensemble force by increasing myosin’s duty ratio, the fraction of time spent in the strongly-bound, force producing state ^20,28–30. The rate of ADP release normally determines the strongly-bound state time, but surprisingly, OM was found to delay the power stroke ³⁰ without affecting this rate ^23,28–30. To clarify OM’s mechanism of action, we used HFS to directly measure whether the drug causes a single cardiac myosin molecule to stay bound longer to actin.

Figure 2: Dose-dependent effects of small molecule compounds on the actin-sliding velocity of β-cardiac myosin in unloaded in vitro motility.

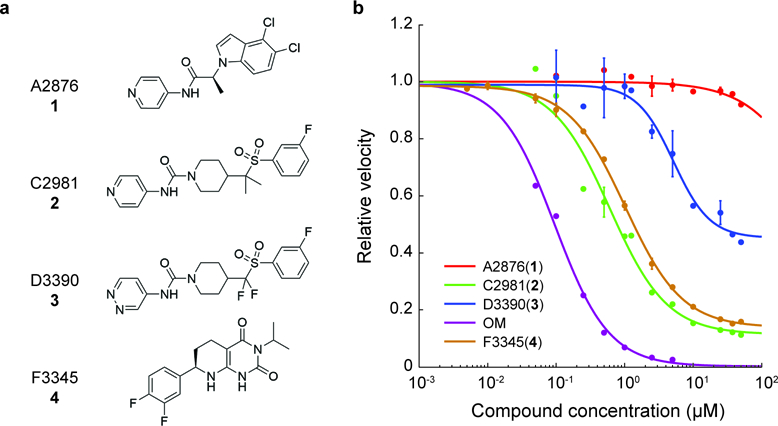
a, Structures of the compounds used in this study. The structure of omecamtiv mecarbil (OM) is reported in Malik et al. ²³. b, Dose-dependent effects of the compounds on the actin-sliding velocity of human β-cardiac myosin. Velocities are normalized to the value at zero compound concentration. Note that some data points have error bars smaller than the displayed point. Error bars represent s.e.m. between two experiments, each tracking ~400 to ~1900 actin filament movements. Curves are 4-parameter logistic fits.

To determine the effects of the compounds when a single myosin molecule has a compound bound, a saturating concentration of compound was required. To determine this concentration, we measured the dose-dependent effects of the compounds on the actin-sliding velocities of human β-cardiac myosin in an in vitro motility assay ^20,31. Surprisingly, both activators and inhibitors slowed down velocities (Fig. 2b). OM had the most dramatic effect with a median effective concentration (EC₅₀) ~0.1 µM, in close agreement with previous measurements ^20,28,29. Activator A2876 (1) had no effect on the velocity beyond that from DMSO alone (see methods).

Guided by the motility measurements, we performed subsequent single-molecule experiments that involve allosteric effectors at a concentration of 25 µM in 2% DMSO.

Small molecule compounds modulate the load-dependent kinetics of single molecules of human β-cardiac myosin

We measured the effects of the small molecule compounds on the load-dependent detachment rates of single molecules of human β-cardiac myosin using HFS (Fig. 3). For clarity, we present only the average load-dependent kinetics curve for each condition in Fig. 3b (for curves of the individual molecules, see Supplementary Figs. 2, 3, and 4). Values of k₀ and 𝛿 are summarized in Table 1 and Supplementary Table 1. When dATP was used instead of ATP, the rate k₀ increased (dATP: k₀ = 168 ± 7 s⁻¹ vs ATP: 102 ± 4 s⁻¹) while 𝛿 did not change significantly (dATP: 𝛿 = 1.5 ± 0.1 nm vs ATP: 𝛿 = 1.31± 0.03 nm, p = 0.13), in close agreement with experiments performed using bovine cardiac heavy meromyosin (HMM) (Tomasic I., Liu C., Rodriguez H., Spudich J.A., Bartholomew Ingle S.R., manuscript in preparation). Compound A2876 (1) had no effect beyond that from DMSO. This result is consistent with observations that A2876 (1) has no effect on the actin-activated ATPase of purified bovine cardiac myosin and actin, but only activates myosin’s ATPase activity in the presence of regulated thin filaments, suggesting possible interactions with the tropomyosin-troponin complex (R. Anderson, MyoKardia Inc. unpublished results). The activators C2981 (2), D3390 (3), and OM decreased k₀ dramatically (C2981 (2): k₀ = 23 ± 1 s⁻¹, D3390 (3): k₀ = 55 ± 3 s⁻¹, OM: k₀ = 12 ± 1 s⁻¹) while also decreasing 𝛿 (C2981 (2): 𝛿 = 0.79 ± 0.05 nm, D3390 (3): 𝛿 = 0.93 ± 0.03 nm, OM: 𝛿 =0.26 ± 0.05 nm) (Fig. 3a), resulting in much lower and flatter curves that are less sensitive to force (Fig. 3b). These three activators probably interact directly with myosin, and lowering of both k₀ and 𝛿 may be a general characteristic of myosin-associated activators. In contrast, the inhibitor F3345 (4) decreased the detachment rate (k₀ = 36 ± 2 s⁻¹) without changing the force sensitivity (𝛿 = 1.27 ± 0.06 nm), suggesting a possible mechanism of action distinct from the activators. Taken together, we found that small molecule effectors can modulate the detachment rate and load sensitivity of cardiac myosin to various degrees.

Figure 3: Effects of small molecule compounds on the load-dependent kinetics of single molecules of β-cardiac myosin.

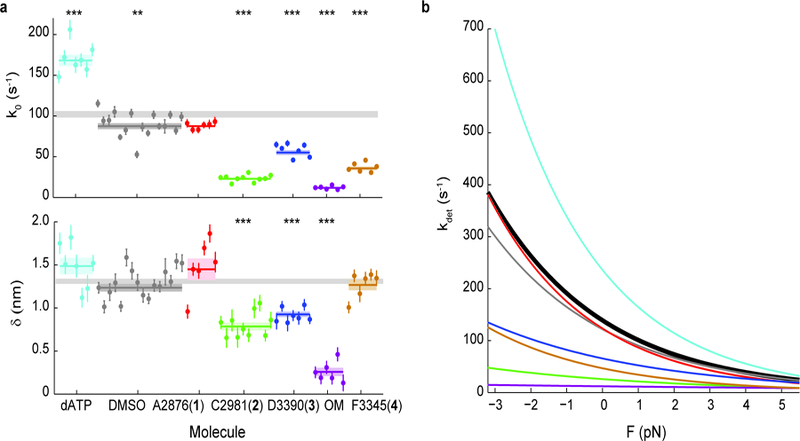
a, k₀ and 𝛿 for all molecules measured. Note that some molecules have error bars smaller than the displayed data point. Weighted means ± s.e.m. are shown as horizontal lines and shaded areas, with those of untreated myosin shown as gray bars (replicated from Fig. 1) across the plots. In the case of 2-deoxy-ATP (dATP), 2 mM dATP was used in place of ATP. All other conditions used 2 mM ATP, 2% DMSO, and 25 µM compound concentration. 2-tailed unequal variances t-test was performed on dATP vs ATP, DMSO vs WT, and compounds vs DMSO. **p<0.001, ***p<0.0001. For detailed values, see Table 1 and Supplementary Table 1. b, The exponential dependence of detachment rate k_det on force for every compound. Curves correspond to the weighted means of k₀ and 𝛿 (see Supplementary Figs. 2, 3, and 4 for curves of individual molecules). Myosin without treatment is shown in black.

Table 1. Summary of single molecule detachment kinetics (k₀, 𝛿) and actin-activated ATPase (k_cat) data for human β-cardiac myosin with effects of small molecule compounds and cardiomyopathy-causing mutations.

Values are mean ± s.e.m. The attachment rate k_attach is calculated by Eqn. 3, with propagated error. k_cat of mutants are obtained from other studies ^20,32,44. For dATP, 2 mM dATP was used in place of ATP. All other conditions used 2 mM ATP, 2% DMSO, and 25 µM compound concentration. 2-tailed unequal variances (for k₀ and 𝛿) and paired (for k_cat) (see Methods) t-test performed on dATP vs ATP, DMSO vs WT, compounds + DMSO vs DMSO alone, and mutants vs WT. For values and number of molecules of all conditions measured, see Supplementary Table 1. Mean and s.e.m. of k_cat’s are from two protein preparations with 5–7 replicates for each condition (see Supplementary Fig. 10 and Methods).

	k0 (s−1)	δ (nm)	kcat (s−1)	kattach (s−1)
WT	102 ± 4	1.31 ± 0.03	4.5 ± 0.4	4.7 ± 0.5
+dATP	168 ± 7 ***	1.49 ± 0.10	5.2 ± 0.4 *	5.4 ± 0.4
+DMSO	87 ± 4 **	1.24 ± 0.04	3.8 ± 0.1	4.0 ± 0.1
+A2876 (1)	87 ± 2	1.45 ± 0.13	3.7 ± 0.1	3.8 ± 0.1
+C2981 (2)	23 ± 1 ***	0.79 ± 0.05 ***	4.6 ± 0.1 *	5.7 ± 0.2
+D3390 (3)	55 ± 3 ***	0.93 ± 0.03 ***	5.1 ± 0.1 *	5.6 ± 0.1
+OM	12 ± 1 ***	0.26 ± 0.05 ***	1.6 ± 0.1 *	1.9 ± 0.1
+F3345 (4)	36 ± 2 ***	1.27 ± 0.06	1.7 ± 0.1 *	1.8 ± 0.1
D239N	140 ± 3 ***	1.40 ± 0.03 *	6.7 ± 0.5 *	7.0 ± 0.5
H251N	152 ± 7 **	1.53 ± 0.08 *	5.6 ± 0.4 *	5.8 ± 0.4
A223T	104 ± 4	1.48 ± 0.09	3.2 ± 0.2 *	3.3 ± 0.3
R237W	155 ± 15 *	1.25 ± 0.06	2.2 ± 0.4 *	2.2 ± 0.4
S532P	80 ± 8 *	1.37 ± 0.06	1.4 ± 0.1 *	1.4 ± 0.1

^*p < 0.05

^**p < 0.001

^***p < 0.0001

Cardiomyopathy-causing mutations alter the load-dependent kinetics of single molecules of human β-cardiac myosin

We next measured the effects of various cardiomyopathy-causing mutations on the load-dependent detachment rates of single molecules of human β-cardiac myosin using HFS (Fig. 4 and Supplementary Figs. 3 and 5, Table 1 and Supplementary Table 1). Two early-onset HCM mutations (D239N and H251N) were previously found to cause myosin to have higher actin sliding velocities in the in vitro motility assay ³². Consistent with their hyperactivities, these two HCM mutants exhibited faster detachment rates than the wild-type (WT) protein at the single-molecule level (D239N: k₀ = 140 ± 3 s⁻¹, p = 0.04; H251N: 152 ± 7 s⁻¹, p = 0.02) and had minimal effects on force sensitivity (D239N: 𝛿 = 1.40 ± 0.03 nm, p = 0.04; H251N: 𝛿 = 1.53 ± 0.08 nm, p = 0.02). Of the three DCM mutations we studied, A223T did not change the detachment kinetics compared to WT (k₀ = 104 ± 4 s⁻¹, p = 0.17; 𝛿 = 1.48 ± 0.09 nm, p = 0.13), R237W increased the rate without changing force sensitivity (k₀ = 155 ± 15 s⁻¹, p = 0.004; 𝛿 = 1.25 ± 0.06 nm, p = 0.43), and S532P decreased the rate slightly without changing force sensitivity (k₀ = 80 ± 8 s⁻¹, p = 0.02; 𝛿 = 1.37 ± 0.06 nm, p = 0.57). Thus, point mutations that cause disease can indeed alter the load-dependent kinetics of cardiac myosin to various degrees, but whether the mutation is clinically HCM or DCM does not dictate the direction of the change (Supplementary Fig. 6). Interestingly, the DCM mutants R237W and S532P both had greater molecule-to-molecule variabilities in k₀ compared to WT and other mutants (Fig. 4a and Supplementary Fig. 5), suggesting that these mutations may cause a disruption in protein folding that affects individual myosin molecules in a population to different extents.

Figure 4: Effects of cardiomyopathy-causing mutations on the load-dependent kinetics of single molecules of β-cardiac myosin, and their reversal by small molecule compounds.

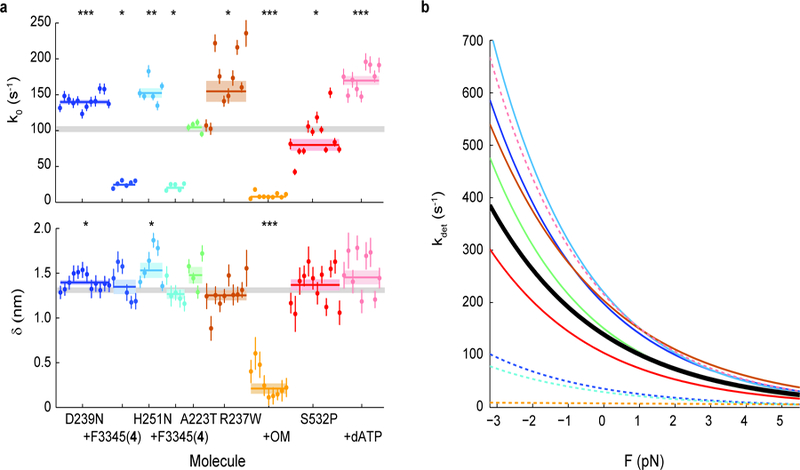
a, k₀ and 𝛿 for all molecules measured. Note that some molecules have error bars smaller than the displayed data point. Weighted means ± s.e.m. are shown as horizontal lines and shaded areas, with those of untreated WT myosin shown as gray bars (replicated from Fig. 1) across the plots. Addition of allosteric compounds (F3345(4) to D239N and H251N; OM to R237W) were in presence of 2% DMSO. 2-tailed unequal variances t-test was performed on mutants vs WT and mutants + compounds + DMSO vs mutants + DMSO, or S532P + ATP vs S532P + dATP. *p<0.05, **p<0.001, ***p<0.0001. For detailed values, see Table 1 and Supplementary Table 1. b, The exponential dependence of detachment rate k_det on force for every mutant. Curves correspond to the weighted means of k₀ and 𝛿 (see Supplementary Figs. 3 and 5 for curves of individual molecules). WT is shown in black. Dashed lines are mutants with treatment.

The effects of cardiomyopathy-causing mutations can be reversed by appropriate small molecule compounds

If an effect of a disease-causing mutation is to alter the detachment rate, then we hypothesized that a small molecule compound with the opposite effect on WT myosin will reverse the alteration caused by the mutation, provided the mutation does not interfere with the action of the compound. To test our hypothesis, we first measured the effects of the inhibitor F3345 (4) on the load-dependent kinetics of each of the two HCM mutants. As expected, we observed a dramatic decrease in the detachment rates of both (D239N + F3345 (4): k₀ = 24 ± 2 s⁻¹, H251N + F3345 (4): 20 ± 2 s⁻¹) without a significant change in force sensitivity (D239N + F3345 (4): 𝛿 = 1.35 ± 0.08 nm, p = 0.71; H251N + F3345 (4): 1.27 ± 0.05 nm, p = 0.17) (Fig. 4 and Supplementary Fig. 5, Supplementary Table 1). Next, since the DCM mutant R237W has a faster detachment rate than WT, we applied the activator OM and found a similarly dramatic reversal (k₀ = 8 ± 1 s⁻¹), this time with a much lower force sensitivity (𝛿 = 0.21 ± 0.06 nm) as expected from the effects of OM (Fig. 4 and Supplementary Fig. 5, Supplementary Table 1). Finally, since S532P had a slower detachment rate than WT, we found that replacement of ATP with dATP reversed the mutation’s effect (k₀ = 170 ± 6 s⁻¹). Since saturating compound concentrations (25 µM allosteric effectors or 2 mM dATP) reversed the effects of mutations beyond WT levels (Fig. 4), we expect that appropriate lower concentrations can adjust the detachment kinetics of mutants to match that of WT myosin if desired.

To this end, we then investigated the dose-dependent effects of OM on single cardiac myosin molecules’ detachment kinetics.

Dose-dependent effects of omecamtiv mecarbil on single myosins’ detachment kinetics

Plasma concentrations of OM in patients in clinical trials are ~500 nM²⁷. Therefore, we used HFS to measure the bound times of myosin in the presence of 30 nM to 25 µM OM. We found that with OM, the bound times within a force bin follow a double exponential distribution (Fig 5ab) instead of a single exponential distribution as observed under all other conditions (Fig. 1c, Supplementary Fig. 7). The presence of two populations suggests that for each event, myosin either has or does not have OM bound; the kinetics of OM binding and unbinding myosin are slow such that a single exponential distribution with an average rate is not observed³³. This data is consistent with two possible models (Fig 5d). In both models, a fraction A of events do not have OM bound to myosin and thus undergo detachment from actin via rate k₁, presumably the same rate k_det(F) measured for myosin in the absence of compounds. The fraction 1-A of events which do have OM bound undergo detachment from actin via one (Model 1) or two (Model 2) steps. In Model 1, the OM-bound myosin detaches from actin at rate k₂. In Model 2, OM must first unbind myosin at rate k₂ before the rest of the actin-bound state (powerstroke, ADP release, ATP binding) proceeds at rate k₁.

Figure 5: Dosage analysis of OM’s effect on the load-dependent detachment kinetics of single molecules of β-cardiac myosin.

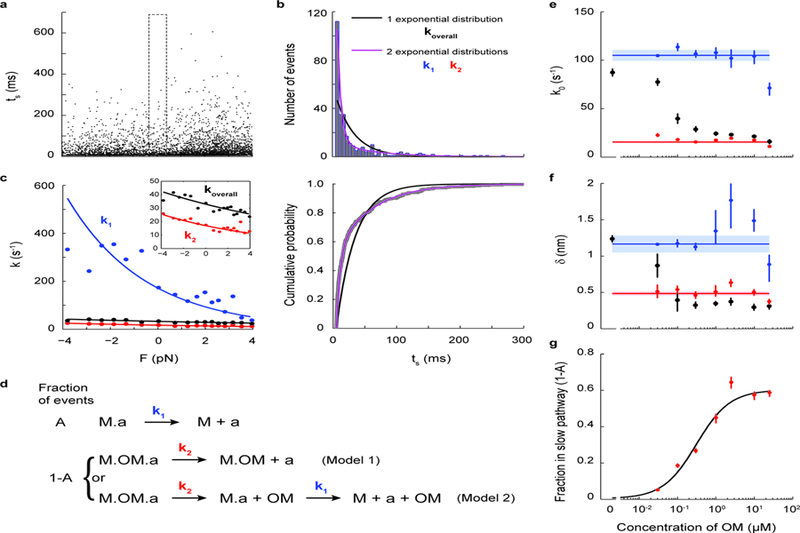
a, Lifetimes of all events (N=5424) from 7 myosin molecules measured at 300 nM OM. b, Within each force bin (the F=0 force bin is shown, as outlined in a), the binding times follow a double exponential distribution (purple) in which the fast k₁ and slow k₂ rates describe the kinetics of steps illustrated in d. The comparison between single vs. double exponential fits are shown as distribution (top) and cumulative probability (bottom). c, Rate as a function of force (Eqn. 1) as determined from all events of the 300 nM OM dataset. The overall rate (black) was obtained by fitting a single exponential distribution. When the double exponential distribution is used, the two fitted rates k₁ (blue) and k₂ (red) each follow Eqn. 1. The curves were obtained from a MLE on all events without binning by force. Independently, the rates at each force were obtained by a MLE on events binned by force (as in b) and plotted as data points. Inset shows a zoomed-in view. See Methods for details. d, Kinetic models of OM’s action on single myosin molecules. The fraction A of events in which OM is not bound to myosin (“M”) undergo detachment from actin (“a”) at rate k₁, the load-dependent detachment rate of myosin as measured earlier in this work (top). In the fraction 1-A of events in which OM is bound to myosin, either OM-bound myosin detaches from actin at rate k₂ (Model 1), or myosin releases OM first at rate k₁ and then detaches from actin at rate k₁ (Model 2). e-f, k₀ and 𝛿 at different concentrations of OM for the overall detachment (black) and its fast (blue) and slow (red) components, obtained by MLE on all events from 6–9 molecules for each concentration of OM (as in c). Weighted means ± s.e.m. are shown as horizontal lines and shaded areas. Their values are: k₀₁ = 105 ± 6 s⁻¹, 𝛿₁ = 1.2 ± 0.1 nm, k₀₂ = 16 ± 1 s⁻¹, 𝛿₂ = 0.48 ± 0.03 nm. g, The fraction 1-A of events with OM bound at different concentrations of OM. A fit to the Michaelis-Menton equation gives an apparent K_d = 0.31 ± 0.05 µM and max(1-A) = 0.60 ± 0.03. Individual error bars in e-g are the 68% confidence interval from bootstrapping 1000 iterations.

Event lifetimes are MLE-fitted using MEMLET³⁴ to a double exponential distribution whose two characteristic rates k₁ and k₂ follow Eqn. 1 independently (see Methods). The fitted variables are k₀₁, 𝛿₁, k₀₂, 𝛿₂, and A. The analysis process is illustrated for the 300 nM OM case in Fig. 5a-c. As expected, whereas the overall rate k_overall from fitting to a single exponential distribution has k₀ and 𝛿 that decrease as OM concentration increases (black in Fig. 5e-f), the parameters describing each population (k₀₁, 𝛿₁, k₀₂, and 𝛿₂) are independent of OM concentration (Fig. 5e-f). The values of k₀₁ and 𝛿₁ (k₀₁ = 105 ± 6 s⁻¹, 𝛿₁ = 1.2 ± 0.1 nm) are consistent with the detachment kinetics of WT myosin from actin (Fig. 1e, Table 1). The interpretation of k₀₂ and 𝛿₂ (k₀₂ = 16 ± 1 s⁻¹, 𝛿₂ = 0.48 ± 0.03 nm) differ between the two models. In Model 1, they are interpreted as the slow and slightly load-dependent detachment kinetics of OM-bound myosin from actin. In Model 2, they are interpreted as the detachment kinetics of OM from myosin. In the latter case, the non-zero positive 𝛿₂ suggests that the unbinding of OM is also slightly force-sensitive: a force in the direction of the powerstroke likely destabilizes OM’s binding pocket³⁵, speeding up its release.

The fraction of OM-bound events (1-A) increases with OM concentration (Fig. 5g). A fit to the Michaelis-Menton equation gives an apparent K_d = 0.31 ± 0.05 µM, in perfect agreement with the affinity of OM to myosin’s pre-powerstroke state measured by isothermal titration calorimetry³⁵. Interestingly, this fraction (1-A) does not reach 1 even at saturating OM concentrations; ~40% of events are able to escape the slow pathway involving OM (Fig. 5g and Supplementary Fig. 7). This result suggests that there must be a state in which myosin either does not bind the drug or binds it in a different manner such that its release is fast.

The above dosage analysis reveals OM’s mechanism of modulating cardiac myosin’s detachment kinetics at both high and low, clinically-relevant concentrations. Taken together, we have found that both small molecule effectors and disease-causing mutations in human β-cardiac myosin can independently and in combination modulate the behavior of single myosin molecules under load. This allows one to have a fine-tuned control over the fundamental load-dependent kinetics curve that defines cardiac myosin.

Single molecule load-dependent kinetics is the basis of the ensemble force-velocity relationship in β-cardiac myosin

In ensemble motility, the sliding velocity of an actin filament is limited by how fast the attached myosin molecule can let go of it, i.e., the detachment rate of myosin³⁶. Given enough heads on the surface and a relatively short tether, as is the case in our motility assays with cardiac sS1, velocities are detachment-limited rather than attachment-limited³⁷. Therefore, as expected here, ensemble velocities measured by the in vitro motility assay were linearly related to the single molecule detachment rate k₀ with a slope of 8.9 nm and R² = 0.81 (Fig. 6a). In contrast, linear regression of velocity vs. attachment rate k_attach (see Discussion for calculation of k_attach) gave R² = 0.35 (Supplementary Fig. 8). In simplest terms, since unloaded velocity v = d/t_s = d*k₀, where d = step size and t_s = strongly bound state time, the slope obtained from the linear fit can be interpreted as the effective step size of myosin in the ensemble. This effective step size (8.9 nm) is greater than the value from direct step size measurements on single cardiac myosin molecules (~7 nm) ^10,38,39 because the non-zero load-dependence (𝛿) of cardiac myosin results in faster detachment rates in the ensemble ⁴⁰. Interestingly, the activators and HCM mutants lie on or above the fitted line while the inhibitor F3345 (4) and DCM mutants lie below it (Fig. 6a) (see also Supplementary Note). This presents a possible distinction between the two groups in which activating perturbations produce greater coordinated movement in the ensemble than predicted by single molecule detachment rates while inhibitory perturbations result in less enhancement.

Figure 6: Single molecule load-dependent kinetics as the basis of the ensemble force-velocity relationship in β-cardiac myosin.

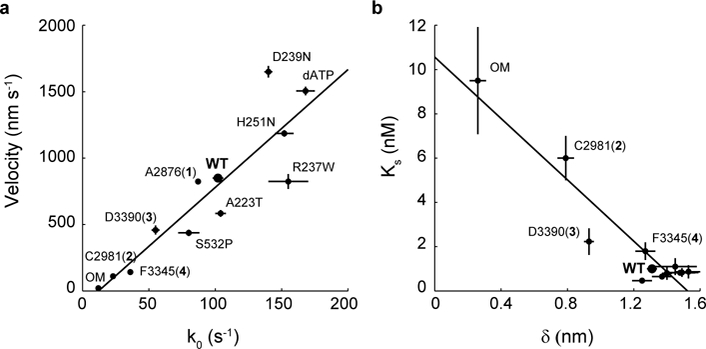
a, Unloaded actin sliding velocity measured by in vitro motility assay vs. k₀, the detachment rate at zero load for a single myosin molecule, for the compounds and mutations studied. Linear regression gives a slope of 8.9 nm and R² = 0.81. Note that some points have error bars smaller than the dot. b, The parameter K_s from the loaded motility assay is a measure of load-bearing ability at the ensemble level, while 𝛿 is the load-sensitivity parameter determined at the single molecule level. Pearson correlation −0.94. For clarity, the cluster of data points at the lower right corner are not individually labeled. Motility velocity and K_s values of mutants and dATP are obtained from other studies ^20,25,32,44 (Tomasic I., Liu C., Rodriguez H., Spudich J.A., Bartholomew Ingle S.R., manuscript in preparation). Error bars represent s.e.m.

In addition to k₀, our data revealed differences in force sensitivity (𝛿) under different perturbations to cardiac myosin at the single molecule level (Figs. 3a, 4a). Therefore, we asked whether changes to force sensitivity of single molecules result in similar findings on the ensemble level. We measured ensemble force sensitivity by a loaded in vitro motility assay ²⁰. In this assay, utrophin on the surface binds to actin to provide the load against which myosin must overcome in moving actin filaments. Increasing concentrations of utrophin increase load and thus decreases actin sliding velocity. This gives an ensemble force-velocity curve (Supplementary Fig. 9). The concentration of utrophin K_s required to reduce velocity by half is therefore a measure of force sensitivity. As expected, we found that K_s is inversely proportional to 𝛿 (Pearson correlation coefficient = −0.94) (Fig. 6b and Supplementary Fig. 9). As single myosin molecules become insensitive to load (smaller 𝛿), such as in the presence of the activators OM, C2981 (2), and D3390 (3), higher concentrations of utrophin are required to reduce the ensemble velocities by a half.

In conclusion, we have found that the load-dependent kinetics inherent to each single molecule of cardiac myosin can be modulated by various small molecule compounds and mutations. This single molecule characteristic underlies the force-velocity relationship exhibited in ensemble.

Discussion

Different types of myosin have dramatically different scales of the load-dependent detachment rate. Myosin I ^15,16, V ¹⁴, smooth ¹³, and β-cardiac ^10,11 isoforms have distinct rates and force sensitivities ranging from k₀ ~ 1 to 100 s⁻¹, and 𝛿 ~ 1 to 12 nm. Here, armed with the efficient HFS method, we explored whether changes to the detachment kinetics can be made via small perturbations in the form of small molecule compounds and cardiomyopathy-causing single missense mutations in human β-cardiac myosin. The results lie across the spectrum: not all perturbations changed the single molecule load-dependent detachment rates (activator A2876 (1), DCM mutant A223T), while the rest modulated the curve to various extents (Figs. 3, 4, and Supplementary Fig. 6). Modulation was seen in the rate at zero load k₀ (~ 10 to 170 s⁻¹) and/or the force sensitivity 𝛿 (~ 0.2 to 1.5 nm). Furthermore, the effects of mutations could be reversed by an appropriate compound (Fig. 4). Thus we have observed fine tuning of the load-dependent kinetics on single molecules of cardiac myosin. In oversimplified terms, we can control cardiac contractility at the single molecule level.

Perturbations to myosin change its load-dependent detachment rates through different steps in the ATPase cycle

Any step in the strongly-bound state may be affected by the compounds and mutations. ADP release is the canonical rate-limiting step of the strongly bound state for WT cardiac myosin. This is likely the acted-upon step for dATP, inhibitor F3345 (4), and mutations since the transition state distance (𝛿) for those conditions remained close to that of unperturbed WT myosin (Figs. 3a, 4a, and Table 1). Furthermore, it has been measured by stopped flow experiments of bovine cardiac HMM that the faster nucleotide release rate when dATP is used in place of ATP matches the detachment rate measured on single molecules (Tomasic I., Liu C., Rodriguez H., Spudich J.A., Bartholomew Ingle S.R., manuscript in preparation). For the activators C2981 (2), D3390 (3), and OM, the significantly smaller 𝛿’s (Fig. 3a and Table 1) suggest a new rate limiting step. Future kinetic studies can illuminate the precise steps at which they act.

For OM, it has been shown that the drug stabilizes the pre-powerstroke state in which myosin is ready to bind to actin ³⁵, accelerates phosphate release ^23,28,30, then delays the power stroke while myosin is in the actin-bound state ³⁰. Structural data shows that the OM binding pocket is incompatible with the post-stroke state, which suggests that OM unbinds before the stroke ³⁵, thus leaving the ADP release rate unaffected ^23,28–30. In our study, we measured a large increase in the lifetime (1/k_det) of the bound state^41,42, consistent with the previously observed delay in powerstroke. We determined that this delay can be attributed to the off rate of OM-bound myosin from actin (one-step model) or the off rate of OM from myosin (two-steps model) for events in which myosin has the drug bound at the start (see also Supplementary Note). Our data is consistent with and cannot distinguish between the two models. But while this paper was in revision ⁴¹, new data has been presented which lends support to the one-step model ⁴².

Unlike an ultrafast feedback trap¹², HFS cannot, so far, measure the powerstroke. Thus, in OM’s case, we cannot observe the exact proposed sequence of events from myosin binding to actin, delay, stroke or no stroke (depending on the model), and finally detachment from actin. Despite the limitations of HFS in distinguishing different phases of the bound state, it can be argued that wherever in this state an effector acts, the same result is achieved: the overall bound time is changed, and it is this overall bound time that limits ensemble velocity and determines force production.

Indeed, we found a strong linear relationship between single molecule detachment rate k₀ and ensemble velocity (Fig. 6a). A linear relationship had also been observed between the ADP release rate, which limits detachment, and the unloaded shortening velocity of skeletal muscle fibers^17,18. In addition, changes to the force sensitivity δ of individual molecules are mirrored at the ensemble level (Fig. 6b). Thus, different mechanisms of changing the detachment rate and its force dependence inherent to a single molecule can lead to the same ensemble force-velocity behavior.

We have found that activating and inhibitory perturbations can increase, decrease, or not affect the detachment rates (Figs. 3, 4, and Supplementary Fig. 6). While this may be expected since compounds and mutations can act via different mechanisms, the question remains: what distinguishes one group from the other? A heart containing an HCM mutation (eg. H251N) undoubtedly is hyper-contractile ⁴³ compared to one bearing a DCM mutation (eg. R237W) despite both having faster detachment rates. Given knowledge of their load-dependent kinetics, we believe that the answer lies in an assessment of the resulting duty ratio, average force, and power output.

Implications of single-molecule load-dependent kinetics on power production by β-cardiac myosin

The duty ratio is the fraction of time that myosin spends in the strongly bound, force producing state. It is a function of load force F (see Methods):

$$r\left(F\right)=\frac{k_{attach}}{k_{attach}+k_{det}\left(F\right)}$$ Eqn. 2

where k_attach describes the lifetime of the unbound state. k_attach can be calculated by

$$k_{attach}={\left(\frac{1}{k_{cat}}-\frac{1}{k_0}\right)}^{-1}$$ Eqn. 3

where k_cat is the overall cycle rate measured by steady state ATPase. The average force a single molecule produces can then be calculated given the duty ratio:

$$F_{av}\left(F\right)=F r\left(F\right)$$ Eqn. 4

The values of all variables in these equations are known (Table 1): k_det(F) given by Eqn. 1 is measured by HFS in this study, k_cat is measured in an actin activated ATPase assay in this study (Table 1 and Supplementary Fig. 10) and others ^20,32,44. Consistent with physiological expectations^{28–30,35,45}, we find that the duty ratios of the activators and HCM mutations are in general greater than those of the inhibitor and DCM mutations (Fig. 7a). Higher duty ratios lead to higher average forces (Fig. 7b). OM increases the duty ratio and average force of cardiac myosin at low forces, confirming previous studies’ proposal that it causes myosin to spend a much greater fraction of time in the strongly bound state ^28–30,35. At high forces, its duty ratio does not increase as much as that of others due to its low force sensitivity (𝛿) (Fig. 3). Surprisingly, two of the activators (C2981 (2) and D3390 (3)) increased the duty ratio and force even more dramatically than OM.

Figure 7: The effects of small molecule compounds and cardiomyopathy-causing mutations on the power produced by single molecules of β-cardiac myosin.

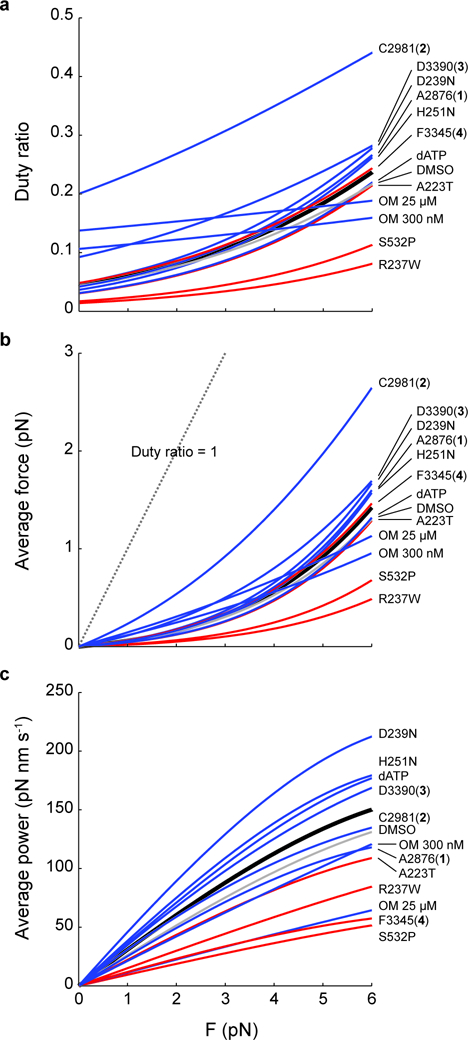
a, Duty ratio, b, average force, and c, average power as a function of the load force F, calculated by Eqns. 2–5. All curves are calculated using values of detachment rate kinetics (k₀, 𝛿), k_cat, and k_attach given in Table 1. Black: WT. Gray: DMSO. Blue: HCM or activators. Red: DCM or inhibitor.

Finally, we calculate the average power produced by a single myosin:

$$P_{av}\left(F\right)=F d k_{det}\left(F\right) r\left(F\right)$$ Eqn. 5

where step size d is taken to be 7 nm (see Supplementary Note and Methods). Here again, HCM and activators segregate from DCM mutations and inhibitors (Fig. 7c). The activator OM is the notable exception: at 25 µM, it causes decreased power despite a higher average force because of its much slower kinetics; at 300 nM, while the dramatic power reduction is alleviated, its power is still on the lower end of the group of activators. This helps explain the effects of OM observed at the organ level: the predicted higher average force is consistent with an increase in peak time-dependent elastance of the left ventricle (a measure of LV contractility) and stroke volume, while the slower kinetics is consistent with a longer time to maximum pressure and a longer time in systole ^23,27.

Our dosage analysis of OM revealed that a common molecular mechanism underlies the drug’s effect across a large range of concentrations, including clinically relevant doses (~500 nM)²⁷ (Fig. 5). At the same time, the sensitivity of myosin’s power production to the concentration of OM (Fig. 7c) illustrates the importance of the therapeutic window: a careful balance of OM’s slow kinetics with its activating function to increase the duty ratio must be and is considered in clinical trials. Finding the optimal degree of alteration in myosin function is critical in modulating ventricular function as a whole.

The k_cat term in the above equations encapsulates the term N_a, the number of available heads. The myosin “mesa” is a relatively flat surface on the motor domain that is involved in the interaction of folded back heads with the proximal tail, forming the so-called interacting heads motif (IHM), and which harbors many HCM mutations.⁴⁶ Mutations on the mesa and compounds which regulate IHM may change N_a, thus changing k_cat ^47–51. While the current study did not assess changes to k_cat through N_a because the sS1 construct lacks the tail domain, future studies will do so using HMM. In addition, other factors that build a more complex, comprehensive system (eg. regulated thin filament, myosin binding protein C) can also change k_cat through modulation of IHM.

Given the above considerations, we propose a model in which activating vs inhibitory perturbations of cardiac myosin are discriminated by the effect on duty ratio, average force, and ultimately, average power (Fig. 8). Neither the detachment rate nor the overall cycle rate can distinguish by themselves the two types of perturbations. When both are taken into account by the duty ratio, force, and power, then we see the physiologically expected outcome: activating perturbations are hyper-contractile, inhibitory ones are hypo-contractile. To build a comprehensive understanding of the molecular mechanism underlying muscle contraction, these calculations take into consideration all the parameters of power production: load force F, load-dependent detachment rate k_det(F), overall cycle rate k_cat, number of functionally available heads N_a (included in k_cat), and step size d.

Figure 8: Predictions of the effects of small molecule compounds and cardiomyopathy-causing mutations on the contractility of β-cardiac myosin at the single molecule level.

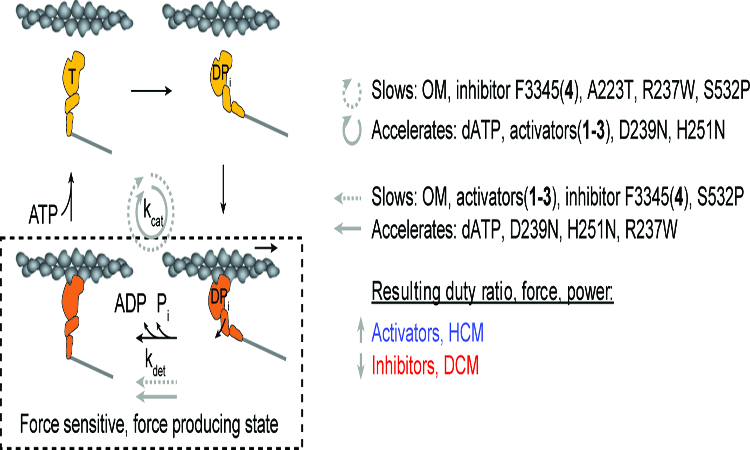
Both the overall cycle (k_cat) and the strongly bound state (k_det) can be slowed or accelerated by activators, inhibitors, HCM, and DCM mutations. It is the aggregate effects on the parameters of power production which discriminates activating (activators, HCM mutations) from inhibitory perturbations (inhibitors, DCM mutations).

Recent studies of the HCM mutations R453C ³⁸, R403Q ³⁹, and three in the converter domain ⁵² found variable changes to parameters of force production (without k_det(F) measurements) which do not clearly point to a hyper-contractile phenotype. Armed with the efficiency of the HFS method, future studies measuring k_det(F) for these mutants and others will determine whether molecular hyper-contractility and hypo-contractility are indeed the respective underlying effects of HCM and DCM.

Methods.

Small molecule compounds

were a generous gift from MyoKardia Inc. (South San Francisco). They are stored at 10 mM in DMSO at 4 °C.

Protein preparation

Construction, expression and purification of the WT and mutated recombinant human β-cardiac myosin sS1s are described in detail elsewhere ^32,38. Briefly, a truncated version of MYH7 (residues 1 – 808), corresponding to sS1, with either a C-terminal enhanced green fluorescent protein (eGFP) or a C-terminal eight-residue (RGSIDTWV) PDZ-binding peptide was co-expressed with myosin light chain 3 (MYL3) encoding human ventricular essential light chain (ELC) and containing an N-terminal FLAG tag (DYKDDDDK) and tobacco etch virus (TEV) protease site in mouse myoblast C2C12 cells using the AdEasy Vector System (Obiogene Inc.). The myosin heavy chain with its associated FLAG-tagged ELC was first purified from clarified lysate with anti-FLAG resin (Sigma). After cleaving off the FLAG tag with TEV protease, the human β-cardiac sS1 was further purified using anion exchange chromatography on a 1 mL HiTrap Q HP column (GE Healthcare). Peak fractions were eluted with column buffer (10 mM Imidazole, pH 7.5, ~200 mM NaCl, 4 mM MgCl₂, 1 mM DTT, 2 mM ATP and 10% sucrose) and concentrated by centrifugation in Amicon Ultra-0.5 10 kDa cutoff spin filters (EMD Millipore) before being stored at −80°C. The purity of the protein was confirmed using SDS-PAGE (Supplementary Fig. 1). Frozen proteins exhibited similar activities in the motility, single-molecule, and ATPase assays compared to their fresh counterparts, as seen in previous work ⁵².

Deadheading myosin

Myosin protein used for motility and trap experiments was further subjected to a “deadheading” procedure to remove inactive heads. Myosin was mixed with 10x excess of unlabeled F-actin on ice for 5 min, followed by addition of 2 mM ATP for 3 min, then centrifuged at 95K rpm in a TLA-100 rotor (Beckman Coulter) at 4 °C for 20 min. The supernatant was collected to be used in the motility and trap experiments. Myosin used in the ATPase assay was not subjected to deadheading.

Actin-activated ATPase

Purified bovine cardiac G-actin provided by MyoKardia Inc. was freshly cycled to F-actin by extensive (4 times over 4 days) dialysis in ATPase buffer (10 mM Imidazole, pH 7.5, 5 mM KCl, 3 mM MgCl₂ and 1 mM DTT) to remove any residual ATP up to a week before each experiment. The monomeric concentration of F-actin was determined by measuring the absorbance of a serial dilution of the actin in 6 M guanidine hydrochloride both at 290 nm with an extinction coefficient of 26,600 M⁻¹ cm⁻¹ and at 280 nm with an extinction coefficient of 45,840 M⁻¹ cm⁻¹ in a spectrophotometer (NanoDrop). Full-length human gelsolin was added to actin at a ratio of 1:1000 to reduce the viscosity of the actin and thereby decrease pipetting error at higher actin concentrations without affecting the ATPase activity ³⁸. The steady-state actin-activated ATPase activities of freshly prepared human β-cardiac sS1-eGFP were determined using a colorimetric readout of phosphate production ⁵³. In this assay, reactions containing sS1 at a final concentration of 0.01 mg mL⁻¹, 2 mM ATP or dATP, and actin at concentrations ranging from 2 to 100 μM were performed at 23°C with plate shaking using a microplate spectrophotometer (Thermo Scientific Multiskan GO). Prior to the start of each reaction, sS1s were incubated on ice with 25 μM of the indicated type of small molecule compound in 2% DMSO for 5 min. ATP or dATP was added at t = 0, and four additional time points up to 30 min were measured subsequently for each actin concentration. The rate of sS1 activity was obtained by linear fitting the phosphate signal as a function of time and converted to activity units using a phosphate standard.

A set of experiments measuring all conditions (dATP and compounds) on WT sS1-eGFP were performed on the same day that myosin was purified to ensure that conditions can be directly compared to each other without variation due to different protein preparations. Each experiment of each condition was performed in duplicates or triplicates. The error on each data point (ATPase activity at a certain actin concentration) represents the s.e.m. of the replicates. The Michaelis-Menten equation was fitted to determine the maximal activity (k_cat) and the actin concentration at half-maximum (apparent K_m for actin). Data from one day is shown in Supplementary Fig. 10a. The k_cat values from each day’s experiment are averaged and presented in Table 1 along with their s.e.m.’s. Here we performed two sets of experiments using two protein preparations and a total of 5–7 replicates. Since each set of experiments measured all conditions on the same day using the same protein prep, we used the paired t-test to test for significance (Table 1). We also performed a Michaelis-Menten fit to the aggregated data from both days (Supplementary Fig. 10b).

In vitro motility

The basic method followed our previously described motility assay with some modifications ^31,39,52. Dose-dependent change in unloaded velocity was observed by measuring actin velocity at 8–12 different concentration of each compound. Four different concentrations of a compound were tested on each motility slide, and 2–3 slides were simultaneously analyzed in each set of experiment to obtain full dose-titration curve. Normalization of velocity was done using the velocity of the WT control from the same set of experiments. For loaded in vitro motility assays, 2–4 different concentrations for each compound (including baseline control) were chosen according to the dose-titration curve of unloaded velocity. For each compound concentration, the force-velocity curve was obtained by measuring actin velocity at 8–12 different concentrations of utrophin. Four different concentrations of utrophin were tested on each motility slide, and 2–3 slides were simultaneously analyzed in each set of experiments to obtain full force-velocity curves. Movies were analyzed using FAST (Fast Automated Spud Trekker), software that automates tracking of actin filaments for in vitro motility assays and analyzes the velocity of each filament in high throughput²⁰. Velocities reported are mean velocity (MVEL) with 20% tolerance, as described previously ²⁰. Each experiment tracked ~400 to ~1900 actin filament movements, and the same condition was repeated. For unloaded velocity, mean +/− standard error of mean from the two experiments are plotted against compound concentration (Fig. 2). After myosin was attached to the motility surface and washed with BSA-containing assay buffer, a final solution that contained fluorescently-labeled bovine actin, 2 mM ATP, an oxygen-scavenging system (0.4% glucose, 0.11 mg ml⁻¹ glucose oxidase, and 0.018 mg ml⁻¹ catalase), an ATP regeneration system [1 mM phosphocreatine (PCR), 0.1 mg/mL creatine phosphokinase (CPK)], and a designated concentration of compound in 0.5% DMSO was added. The myosin was incubated in the final solution containing compound for at least 5 minutes before movies were taken. The amount of time the final solution was incubated in the chamber before movies were taken did not affect the velocity (data not shown). DMSO had minimal effect on velocity (2% DMSO had a 10% reduction in velocity). All experiments were performed at 23 °C.

Single molecule measurements of load-dependent detachment rates

Measurements were performed using the Harmonic force spectroscopy (HFS) method in a dual beam optical trap ¹¹.

Sample chamber preparation.

The sample chamber was built on a glass coverslip spin-coated first with 1.6 µm-diameter silica beads (Bang Laboratories) as platforms and then with a solution of 0.1% nitrocellulose 0.1% collodion in amyl acetate. The flow channel was constructed by two double-sided tapes between a glass slide and the coverslip. Experiments were performed at 23 °C. GFP antibody (Abcam ab1218) at a final concentration of ~1 nM diluted in assay buffer (AB) (25 mM imidazole pH 7.5, 25 mM KCl, 4 mM MgCl₂, 1 mM EGTA, and 10 mM DTT) was flowed into the channel to bind the surface for 5 min, followed by washing and blocking with 1 mg ml⁻¹ BSA in AB (ABBSA) for 5 min. Dead-headed human β-cardiac myosin sS1-eGFP diluted to a final concentration of ~10–50 nM in ABBSA was flowed in next and allowed to saturate GFP antibody binding sites for 5 min. Then unbound myosin was washed out with ABBSA. Lastly, the final solution was flowed in consisting of 2 mM ATP, 1 nM TMR-phalloidin-labelled biotinylated actin (Cytoskeleton, ~1 biotin per monomer) filaments, an oxygen-scavenging system (0.4% glucose, 0.11 mg ml⁻¹ glucose oxidase, and 0.018 mg ml⁻¹ catalase), and 1 µm-diameter neutravidin-coated polystyrene beads (ThermoFisher) diluted in ABBSA. The chamber was sealed with vacuum grease. For experiments with 2-deoxy-ATP, 2 mM 2-deoxy-ATP was used in place of ATP. For experiments with other small molecule compounds, ABBSA contained 2% DMSO and specified concentration of compound.

HFS experiment.

Details of the technique have been presented elsewhere ¹¹. Two neutravidin beads were trapped in two trap beams. The beads were moved in ~57 nm steps in a 9×9 raster scan using acousto-optic deflectors while their displacements were recorded both in brightfield (in nm) and with quadrant photodiode (QPD) detectors (in voltage) to produce a voltage-to-nm calibration. The stiffness of each trap beam was calculated by the equipartition method and was typically ~0.07 pN nm⁻¹ (right) and 0.09 pN nm⁻¹ (left) in these experiments. After this calibration, an actin filament was stretched to ~5 pN pre-tension between the two trapped beads to form a “dumbbell.” We sinusoidally oscillated the piezoelectric stage at 200 Hz with amplitude set at 50 nm. While the amplitude was set to 50 nm, the stage actually oscillated at ~30 nm due to the response of the stage at 200 Hz. The dumbbell was lowered near a platform bead to check for binding to a potential myosin on the platform, as indicated by large, brief increases in the position amplitudes of the trapped beads (“robust interactions”) due to stronger association with the oscillating stage. Due to compliance, the dumbbell oscillates with amplitude ~15–25 nm during a binding event, which corresponds to a total force dF ~3–4 pN from the two traps. We typically explored ~5–10 platform beads before robust interactions were observed, suggesting that the GFP antibody and myosin concentrations used in this study resulted in sufficiently low number of properly-oriented molecules on the surface such that events observed were likely due to a single myosin. Control experiments with GFP antibody only (without myosin) revealed that any interactions between the antibody and the dumbbell are not “robust” as defined above; their amplitudes are small, and the durations are very short such that they would not pass the analysis’s detection criteria as detailed below. The positions of the trapped beads and the piezoelectric stage were recorded at 50 kHz sampling frequency. We recorded data on each molecule for ~10 min and used each slide for 1.5–2 hr. We did not observe slowing down of motor during the 10-min recording for one molecule nor for multiple molecules on one slide during a 2 hr experiment, suggesting that the 2 mM ATP was not significantly depleted despite our foregoing an ATP regeneration system.

HFS data analysis.

The theory of the HFS method and the data processing details have been presented elsewhere ¹¹. In summary, in the unattached state, the dumbbell oscillates π/2 ahead of the stage due to the fluid motion while in the attached state the dumbbell oscillates in phase and with a larger amplitude due to stronger association with the stage. Therefore, events are detected based on a simultaneous increase in oscillation amplitude above a threshold (~15 nm) and a decrease in phase below a threshold (~0.5 rad) for at least one full stage oscillation period. Several additional filtering of events are applied to minimize false positives. The final number of events for each molecule ranged from ~300–1000. For each event, the mean force due to each trap is calculated as the bead position averaged over the duration of binding multiplied by the trap stiffness. The total mean force on myosin is the sum of the two mean forces. A range of forces, both positive and negative, is automatically applied to myosin because binding can occur anywhere in the cycle of oscillation. Through this event detection algorithm, the mean force, amplitude of oscillation, and duration (F, ΔF, t_s) of each event are obtained.

For each molecule, events are binned by force in ~1 pN increments, and a maximum likelihood estimation (MLE) of the geometric distribution (the discrete version of the exponential distribution) of bound times, with dead-time correction (5 ms), is performed for each bin to obtain the detachment rate for the mean force of the bin, k_det(F). The error on k_det(F) is calculated from the variance of the MLE as the inverse Fisher information. This results in a plot of k_det(F) vs. F to which we perform a weighted least-squares fit of Eqn. 1 using k₀ and 𝛿 as fitting parameters. Theoretical errors on the estimates for k₀ and 𝛿 are calculated from the inverse Fisher information matrix. Thus we have k₀ and 𝛿 and their errors for each molecule. Then, values of k₀ and 𝛿 from each molecule are averaged weighted by their errors (variance) to obtain mean values for each condition. The errors on these mean values are calculated as the s.e.m.

We have also used MEMLET³⁴ to analyze a few molecules to compare the two analysis methods. The input data to MEMLET is the same (F, ΔF, t_s) produced by the HFS analysis program. MEMLET does not require binning events in force. Instead, it produces the fitted variables k₀ and δ from a MLE fit of all events of one molecule to the geometric distribution in which the rate parameter of the distribution is given by Eqn. 1. In the molecules we tested, MEMLET gave nearly identical k₀ and δ values. MEMLET uses bootstrapping to obtain the uncertainties of the fitted variables. The 68% confidence intervals obtained by MEMLET bootstrapping were very similar to the errors calculated by the inverse Fisher information matrix. The excellent agreement between these two analysis methods, one which bins in force and the other which does not, is expected because the large number of events available through the HFS method minimizes the negative effects of binning³⁴. Note, however, that bootstrapping 1000 iterations requires several minutes (or even ~1 hr for more complex distribution functions such as ones used in the OM dosage analysis below), while calculation of errors from the Fisher information matrix uses < 1 sec.

Analysis of single molecule OM dosage data.

According to Model 1 in Fig. 5d, the distribution of bound times is given by

$$f\left(t; k_{01},{\delta }_1,k_{02}, {\delta }_2,A\right)=A{k}_1{e}^{-k_{1}t}+\left(1-A\right)k_2{e}^{-k_{2}t}$$

According to Model 2, the distribution is given by

$$f\left(t; k_{01},{\delta }_1,k_{02}, {\delta }_2,A\right)=A{k}_1{e}^{-k_{1}t}+\left(1-A\right)\frac{k_1{k}_2}{k_1-k_2}\left(e^{-k_{2}t}-e^{-k_{1}t}\right)$$

where

$$k_1\left(F,\Delta F\right)=k_{01}{I}_0\left(\frac{\Delta F{\delta }_1}{k_{B}T}\right)\text{exp}\left(-\frac{F{\delta }_1}{k_{B}T}\right)$$

$$k_2\left(F,\Delta F\right)=k_{02}{I}_0\left(\frac{\Delta F{\delta }_2}{k_{B}T}\right)\text{exp}\left(-\frac{F{\delta }_2}{k_{B}T}\right)$$

Model 2’s distribution is still a sum of two exponentials, as seen more clearly by redefining the coefficients:

$$f\left(t; k_{01},{\delta }_1,k_{02}, {\delta }_2,A\right)=\alpha k_1{e}^{-k_{1}t}+\left(1-\alpha \right)k_2{e}^{-k_{2}t}$$

where

$$\alpha =A-\left(1-A\right)\frac{k_2}{k_1-k_2}$$

In MLE fitting, the actual function used is the discrete geometric rather than the continuous exponential distribution due to the requirements of HFS to bin durations in an integer number of periods of stage oscillation¹¹. In addition, the minimum detectable time (5 ms) is taken into account by a dead time correction.

MEMLET uses the above probability distribution function to fit to the (F, ΔF, t_s) data, producing the 5 fitted parameters: k₀₁, δ₁, k₀₂, δ₂, A. Here, the advantage of fitting without binning by force can be appreciated: the larger number of fit parameters gives rise to variability when fitting a subset of data in one force bin. For this same reason and for simplicity of analysis, rather than performing separate analyses on individual molecules (as we have done with all other compound and mutation conditions), we aggregated events from all molecules for each OM concentration before performing the MLE. Note that the slow and fast population of events were observed for every single molecule; thus it is not the case that some molecules simply do not bind OM. The curves in Fig. 5c and all data in Fig. 5e-g use values of the 5 parameters from fitting without binning by force. Independent from the MLE without binning by force, the rates k₁ and k₂ at each force were obtained by a 2-exponential MLE on events binned by force (as in Fig. 5b) and plotted as data points in Fig. 5c. The later analysis method validates the existence of the two underlying force-dependent rates since it does not assume the Arrhenius equation, yet the resulting data points do indeed follow the equation (Fig. 5c).

Fitting to Model 1 or Model 2 gave very similar results for (k₀₁, δ₁, k₀₂, δ₂, A) (Supplementary Table 2). Since log-likelihoods were almost identical from the two models, our data is consistent with both and cannot distinguish between them. Fig. 5e-g displays values from Model 1. Error bars in Fig. 5e-g are from bootstrapping 1000 iterations using MEMLET.

To test the significance of the non-zero δ₂, a likelihood ratio (LR) test was performed comparing fitting with fixed δ₂ = 0 vs free δ₂. In both models and across different concentrations of OM, LR tests gave p-value’s < 1e-16, rejecting the null hypothesis of δ₂ = 0. Furthermore, force binned fitting two rates and an amplitude clearly shows a non-flat curve for the slower rate k₂ (red data points in Fig. 5c). Similarly, LR test of non-zero δ in the single exponential fitting (black data points in Fig. 5) also gave p-values < 1e-16.

At 30 nM OM, the number of events from the slow population is not sufficiently large for an accurate fitting. Therefore, for the 30 nM OM data point only (Fig. 5e-g), we fixed k₀₁ = 105 s⁻¹ and δ₁ =1.16 nm (the weighted means of the rest of the OM concentrations data) and performed the MLE to obtain k₀₂, δ₂, and A. Indeed, the fit produced A = 0.95, confirming that there were very few events in the slow population.

Calculations of duty ratio, average force, and average power

The duty ratio is the time myosin spends in the strongly bound state t_s divided by its entire cycle t_c. The entire cycle is made up of time in the strong and weak states, t_s and t_w, respectively. The duty ratio as a function of load force F can be expressed as

$$\begin{gathered} r(F)=\frac{t_s}{t_c} \\ =\frac{t_s}{t_s+t_w} \\ =\frac{1/k_{\det }(F)}{1/k_{\det }(F)+1/k_{attach}} \\ =\frac{k_{attach}}{k_{attach}+k_{\det }(F)} \end{gathered}$$

where k_attach describes the lifetime of the weak binding state and is assumed to be independent of force since myosin cannot yet sense any load on actin when unbound. k_attach cannot be determined by directly measuring the lifetimes of the unbound state in the optical trap because there, the rate of attachment is sensitive to the positions of the actin dumbbell and myosin. However, k_attach can be calculated by

$$\begin{gathered} k_{attach}={\left(\frac{1}{k_{cat}}-\frac{1}{k_{\det }(F=0)}\right)}^{-1} \\ ={\left(\frac{1}{k_{cat}}-\frac{1}{k_0}\right)}^{-1} \end{gathered}$$

where k_cat is the overall cycle rate measured by steady state ATPase.

Myosin produces an equal and opposite force against the load force F up to the isometric force. Thus, average force is the load force multiplied by the duty ratio (Eqn. 4) (Fig. 7b). The maximum value of the x-axis in Fig. 7 is the isometric force, taken to be 6 pN ¹².

In the calculation of average power (Eqn. 5), a constant step size d may be a simplification as some perturbations may alter it (see Supplementary Note). Nevertheless, it is illustrative to calculate the power produced by single myosins to understand the effects of changes to the detachment rate.

Calculations are given by Eqn. 2–5 using values in Table 1. Values and errors referenced from other studies are normalized by each of their corresponding WT protein controls. Errors in k_attach are calculated as propagated errors derived from Eqn. 3.

Normalization of in vitro motility results

The range of WT velocities from different protein preparations was 600–1100 nm/s, and this variability has also been observed previously ⁵². Because of this, velocities and K_s of different conditions (compounds and mutations) were normalize-adjusted by each of their WT controls. For example, if condition x had a velocity of v_x, and its corresponding WT control had a velocity of v_{x_control}, then the adjusted velocity was v_{x_adjusted} = v_x*v_WT/v_{x_control} where v_WT is the velocity of the WT measured in this study against which everything else is compared.

Code availability

FAST program code use to analyze motility data is available for download at http://spudlab.stanford.edu/fast-for-automatic-motility-measurements/ as described in a previous publication²⁰. Custom code used to analyze HFS data is available upon request.

Data availability

All data supporting the findings of this study are available within the paper and in the Supplementary data set.