Dynamic Scaling of Exosome Sizes

Abstract

A model is proposed for characterizing exosome size distributions based on dynamic scaling of domain growth on the limiting membrane of multivesicular bodies in the established exosome biogenesis pathway. The scaling exponent in this model captures the asymmetry of exosome size distributions, which are notably right-skewed to larger vesicles, independent of the minimum detectable vesicle size. Analyses of exosome size distributions obtained by cryogenic transmission electron microscopy imaging and nanoparticle tracking show, respectively, that the scaling exponent is sensitive to the state of the cell source for exosomes in cell culture supernatants and can distinguish exosome size distributions in serum samples taken from cancer patients relative to those from healthy donors. Finally, we comment on mechanistic differences between our dynamic scaling model and random fragmentation models used to describe size distributions of synthetic vesicles.

Graphical Abstract

INTRODUCTION

The discovery of functional RNAs encapsulated in and/or associated with vesicles actively released by almost all cell types has generated widespread interest in extracellular vesicles (EVs), and specifically the exosome subpopulation of EVs, for their diagnostic potential as biomarkers accessible using minimally invasive sampling procedures,^1,2 and their therapeutic potential as natural delivery vehicles for proteins and nucleic acids.^3,4 Nonetheless, the characterization of exosomes as a nanometer-sized EV subpopulation distinct from shedding vesicles, apoptotic bodies, RNA-binding protein complexes, and high-density lipoprotein particles, which also contain extracellular RNA, remains a formidable challenge.^5–9 No single exosome-specific biomarker has been identified that can uniquely detect this EV subpopulation.^10,11 Instead, a combination of biochemical and biophysical characteristics related to the biogenesis pathway of exosomes is applied: average vesicle size and/or size distribution; spherical, unilamellar morphology; enrichment of specific membrane proteins, including tetraspanins; and vesicle cargo.^5–7,12,13 Although this combinatorial approach circumvents the lack of a unique, unequivocal exosome biomarker, it is limited to an extent by the semiquantitative nature of the exosome-defining criteria now applied to the individual biomarkers. For example, the vesicle size distribution typically associated with exosomes is 30–100 nm in diameter based largely on their distinctive, but artificial cup-shaped morphology seen in transmission electron microscopy images.^5–7 However, much broader size distributions have been reported,^14,15 and spherical vesicles with the morphological properties of exosomes and diameters up to ~200 nm have been observed directly in cryogenic transmission electron microscopy (cryo-TEM) images.^13,14,16 Moreover, exosome size distributions are notably right-skewed to larger vesicles, a characteristic that is not captured by specifying either an average vesicle diameter or a range of diameters as a defining criterion for the exosome subpopulation of EVs.

In this work, we propose a dynamic scaling model for the size distribution of exosomes based on the established biogenesis pathway for exosome formation described below. We show that the scaling exponent in this model captures the characteristic asymmetry of exosome size distributions, independent of the minimum detectable vesicle size intrinsic to different measurements. We also show that this scaling exponent is sensitive to different signaling pathway inhibitor treatments of the cell source and can distinguish exosome size distributions in serum samples from cancer patients relative to those from healthy donors. Finally, we point out mechanistic differences between our dynamic scaling model and random fragmentation models used to describe the size distribution of nanometer-sized synthetic vesicles formed using conventional preparation methods.

RESULTS AND DISCUSSION

Exosomes form via the reorganization of membrane proteins into tetraspanin-rich domains on the limiting membrane of multivesicular bodies (MVBs) and are subsequently released from cells by exocytosis in response to specific stimuli.^6,17 The process involves nucleation of small domains on the MVB limiting membrane, followed by the growth of domains above a certain critical size by coarsening and coalescence. Invagination of domains large enough to deform leads to the formation of intraluminal vesicles (ILVs), which then detach from the MVB limiting membrane to become internalized vesicles or exosomes.^17,18 We assume the exosome diameter is fixed at this point; therefore, the experimentally observed size distribution of exosomes released into the extracellular environment is related to the size distribution of domains that grow and subsequently invaginate and detach from the MVB limiting membrane.

We model domain growth as a competition between two driving forces: classical phase separation in which the increase in the characteristic length scale of a domain over time, l(t), exhibits power-law scaling,¹⁹

$$l(t)\propto t^{\xi }\xi >0$$ (1)

and a countervailing driving force that suppresses phase separation; for example, the inhibition of domain growth by coalescence when membrane curvature is coupled locally to the composition of the phase-separating constituents.^20–22 Domain growth under the influence of these competing driving forces reaches a steady state characterized by a length scale that follows power-law scaling of the form,

$$l_{\mathrm{D}}\propto {\lambda }^{-\xi }$$ (2)

where λ is the rate associated with the countervailing driving force. We take λ to be the rate at which domains on the MVB membrane undergo budding, invaginate, and detach to form ILVs/exosomes with diameter, D ∝ l_D. Dynamic scaling described by eq 2 was originally reported for reaction-controlled domain (pattern) formation in phase-separating mixtures,^23,24 and thereafter, for the reaction-controlled interconversion of membrane components coupled to membrane curvature,^25,26 and domain formation in which phase separation competes with lipid recycling.^27–29 The scaling exponents for model systems fall within the range of ξ = 1/3 (small λ/strong segregation) and ξ = 1/4 (large λ/weak segregation),^24–26 although positive values of ξ that are smaller in magnitude have also been reported.^20,30 We note that eq 2 with ξ > 0 predicts that larger domains persist longer in agreement with experimental observations.²⁹

We consider ILV/exosome formation to be a Poisson process for which the probability of observing n discrete formation events during the time interval, τ, is given by the probability density distribution function,

$$p(n\mid \lambda ,\tau )=\frac{{(\lambda \tau )}^n}{n!}{\mathrm{e}}^{-\lambda \tau }$$ (3)

where λ ≡ 〈n〉/τ is the mean rate of ILV/exosome formation with 〈n〉 the average value of n and also the variance, σ_n² = 〈n〉. When 〈n〉 is computed over long times, λ is a constant. However, as the observation or averaging time becomes shorter, the observed rate of formation will deviate from the mean due to random variations in the time interval between successive events, or equivalently, random variations in the number of events within the defined time interval.³¹ This behavior, which is illustrated in Figure 1, can be described by considering the variance in the observed event rate, n/τ, around the mean, given by

Figure 1.

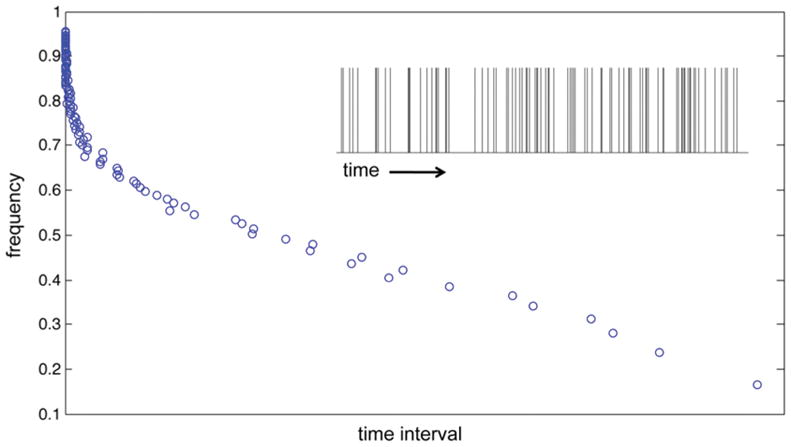
Distribution of the time intervals (scaled by ξ = 1/3) between successive exosome formation events simulated as a Poisson process (eq 3). A portion of the time sequence of events is shown in the inset.

$${{\sigma }_{\lambda }}^2=\frac{{{\sigma }_n}^2}{{\tau }^2}=\frac{\lambda }{\tau }$$ (4)

As τ → ∞, the expected variance in the observed rate → 0 and λ is a constant (=〈n〉/τ). If we now divide τ into a large number of disjoint subintervals, δτ, the distribution of the number of events within these subintervals will be described by eq 3, and the variance in the observed event rate around the mean in the subintervals will be described by eq 4 with τ → δτ. Thus, as δτ becomes shorter, the variance in the observed event rate increases. We can expect, therefore, a distribution of rates of ILV/exosome formation as a consequence of finite (short) time intervals, τ.

The probability of observing a certain rate of ILV/exosome formation given n events over τ is obtained from the Poisson distribution eq 3 by applying Bayes theorem and enforcing normalization,³²

$$p(\lambda \mid n,\tau )=\tau \frac{{(\lambda \tau )}^n}{n!}{\mathrm{e}}^{-\lambda \tau }$$ (5)

Setting n = 0 then gives the probability of observing the rate at which a domain on the MVB membrane forms an ILV/exosome conditioned on the formation of no ILVs/exosomes over the time interval, τ,

$$p(\lambda \mid n=0,\tau )=\tau {\mathrm{e}}^{-\lambda \tau }$$ (6)

Assuming an average time interval, τ̄, over which ILV/exosome formation on the MVB membrane does not occur,

$$p(\lambda )={\int }_0^{\infty }p(\lambda \mid n=0,\tau )\delta (\tau -\overline{\tau })\mathrm{d}\tau$$ (7)

from which we obtain the probability density distribution of exosome diameters,

$$\begin{gathered} p(D)=p(\lambda )\left|\frac{\mathrm{d}\lambda }{\mathrm{d}D}\right| \\ =\frac{\overline{\tau }}{\xi }{D}^{-1+\xi /\xi }exp[-\overline{\tau }{D}^{-1/\xi }] \end{gathered}$$ (8)

where the proportionality constant implied by eq 2 is determined by normalization,

$${\int }_0^{\infty }p(D)\mathrm{d}D=1$$ (9)

The mean exosome diameter obtained from eq 8 is

$$\langle D\rangle ={\overline{\tau }}^{\xi }\mathrm{\Gamma }(1-\xi )$$ (10)

where Γ(…) is the gamma function for noninteger arguments. For ξ > 0, the exponential factor in the probability density distribution function eq 8 rapidly approaches unity with increasing exosome diameter for D > 〈D〉, and the distribution function exhibits a power-law dependence on the exosome diameter. This power-law dependence with the scaling exponent, ξ, thus captures the characteristic asymmetry of exosome size distributions, which are right-skewed to larger vesicles. Equation 10 can be used to define the average time interval, τ̄, in terms of the experimentally derived mean exosome diameter, 〈D〉, which is substituted into the probability density distribution function eq 8. Thus, the experimental exosome size distributions are fit using effectively one adjustable parameter, the scaling exponent ξ, with the mean exosome diameter computed independently from the experiments.

As a test of our model, we apply the probability density distribution function eq 8 to describe the size distributions of exosomes derived from untreated TPC1 thyroid cancer cells and TPC1 cells treated with the signaling pathway inhibitors: LY294002 (PI3K-AKT pathway) and U0126 (MAPK pathway). ^16,33 These size distributions were obtained from cryo-TEM images and measured independently by asymmetric flow field-flow fractionation/multiangle light scattering (A4F/MALS).¹⁶ The cryo-TEM and A4F/MALS size distributions for exosomes derived from untreated TPC1 cells are compared in Figure 2. As a consequence of the lower resolution of A4F/MALS for smaller vesicles, the A4F/MALS distributions are shifted to larger vesicle diameters relative to the cryo-TEM distributions.¹⁶ Equation 8 suggests that the difference in resolution between the two measurements can be taken into account by normalizing the exosome diameters by 〈D〉. The extended tails of the two distributions plotted using this normalization are in good agreement, indicating that the scaling exponent is insensitive to the difference in the minimum detectable vesicle size for the two methods. Differences in the minimum detectable vesicle size, and as such, different vesicle size distributions have also been reported for nanoparticle tracking (NTA), resistive pulse sensing, and flow cytometry.³⁴ The results in Figure 2 suggest the scaling exponent as a parameter independent of this lower detection limit makes possible quantitative comparisons of exosome size distributions obtained from multiple detection methods. We also note that the upper limit of vesicle diameters that can be observed by cryo-TEM, which is determined by the sample thickness, is ~250 nm.^35,36 This limit corresponds to D/〈D〉 ≈ 5 in Figure 2 and is not a factor here.

Figure 2.

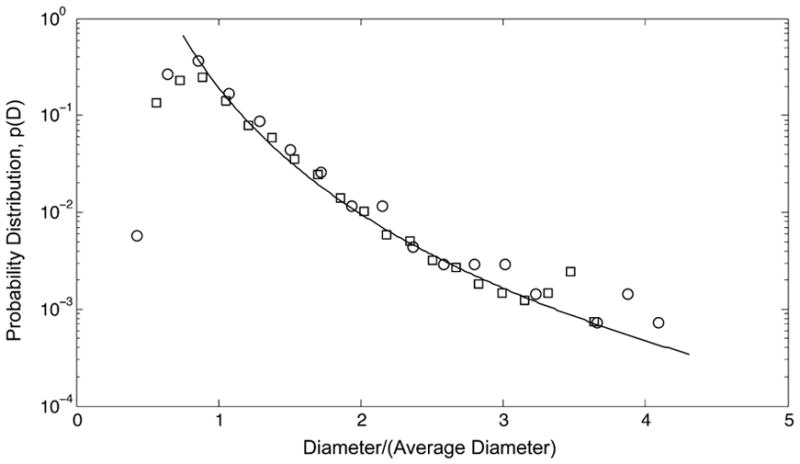
Probability distribution, p(D), of vesicle diameters from cryo-TEM images (circles) and independently from A4F/MALS measurements (squares) for exosomes released from untreated TPC1 thyroid cancer cells¹⁶ plotted as a function of reduced diameter, D/〈D〉, where 〈D〉 = 46.6 nm (cryo-TEM, n = 1387) and 〈D〉 = 61.9 nm (A4F/MALS). The line corresponding to the extended tail of the distributions is provided to guide the eye.

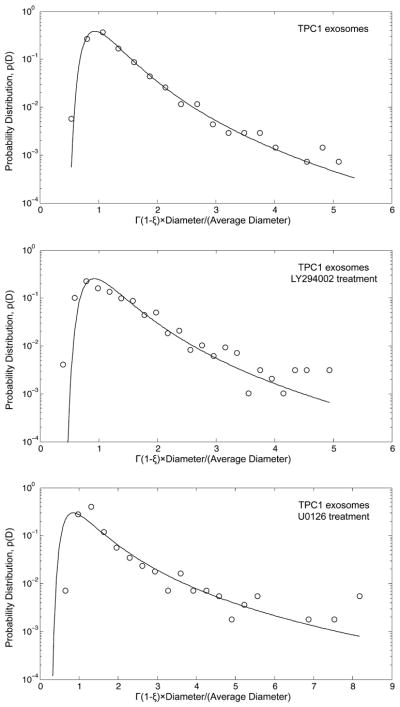
Focusing on the cryo-TEM data, we determine scaling exponents characterizing the size distributions of exosomes from treated and untreated TPC1 cells using the method of maximum likelihood, which is described in detail elsewhere.³⁷ This method requires defining the lower bound or minimum exosome diameter, D_min, of the power-law regime for each distribution. To this end, we choose the value of D_min that minimizes the maximum distance between the cumulative distribution function (cdf) derived from the data and the cdf obtained from the power-law model that best fits the data for D > D_min [Kolmogorov–Smirnov (KS) statistic]. The second parameter in the probability density distribution function eq 8, the mean exosome diameter 〈D〉, is calculated directly from the experimental data. Comparing experimental and calculated distribution functions in Figure 3 shows that the asymmetry of each size distribution is accurately captured by the power-law behavior imbedded in eq 8. In addition, the peak in the size distribution for exosomes from untreated TPC1 cells is accurately described by eq 8, and reasonably well described for exosomes from the treated TPC1 cells. For diameters less than 〈D〉, the exosome size distribution is shifted slightly to larger vesicle diameters for the LY294002 treatment and to smaller vesicle diameters for the U0126 treatment. The mean diameters of exosomes from untreated TPC1 cells and the U0126-treated cells are essentially identical, whereas the mean diameter of exosomes from the LY294002-treated cells is larger, but within one standard deviation of the other two (Table 1). The scaling exponents, on the other hand, are notably different with larger values corresponding to the inhibitor treatments of the TPC1 cell source (Table 1). These larger values of ξ indicate that the power-law behavior in eq 8 extends further into the tail of those exosome size distributions—i.e., larger exosomes are present in higher fractions. For the size distributions of exosomes from the untreated TPC1 cells and the LY294002-treated cells, the scaling exponents fall within the expected range of ξ = 1/3 (small λ/strong segregation) and ξ = 1/4 (large λ/weak segregation) noted above for model membrane systems. However, the scaling exponent that characterizes the exosome size distribution for the U0126-treated cells falls outside this expected range. We note the much smaller number of cryo-TEM images in Table 1 for exosomes from the U0126-treated cells, which is less than half the number for the untreated cells, although the number of images in the power-law region is comparable to that for the LY294002-treated cells.

Figure 3.

Probability distribution, p(D), of vesicle diameters from cryo-TEM images (circles) for exosomes released from untreated TPC1 cells, LY294002-treated cells, and U0126-treated cells¹⁶ plotted as a function of reduced diameter, Γ(1 − ξ)D/〈D〉, where Γ(…) is the gamma function for noninteger arguments (see eq 10). The solid lines are calculated using the probability density distribution function eq 8. See Table 1 for all parameter values.

Table 1.

Number of Cryo-TEM Images, n, Mean Exosome Diameter, 〈D〉, Scaling Exponent, ξ, Minimum Exosome Diameter, D_min, for Power-Law Behavior, Number of Cryo-TEM Images in the Power-Law Region, n_tail, and the KS Test Result for the Plausibility of the Power-Law Characterization of the Tail of the Exosome Size Distribution as a Function of the Inhibitor Treatment of the TPC1 Cells^a

exosome cell source	n	〈D〉	ξ	Dmin	ntail	KS test
untreated TPC1 cells	1387	46.6 ± 18.8	0.2650	57	258	0.40
LY294002-treated TPC1 cells	974	65.8 ± 35.1	0.3009	88	177	0.49
U0126-treated TPC1 cells	556	48.8 ± 31.1	0.4436	46	159	0.34

^aDiameters are in units of nanometers. Uncertainties for the mean diameters correspond to one standard deviation.

We tested the plausibility of our power-law characterization of the extended tail of the exosome size distributions using a semiparametric bootstrap approach.³⁷ Specifically, we generated 15 000 synthetic size distributions for each case with an extended tail that obeys the power-law behavior in eq 8 with ξ and D_min obtained from our analyses of the cryo-TEM distributions (Table 1). Diameters less than D_min were selected randomly from the experimental data. The extended tail of each synthetic distribution was then individually fit to the power-law model and the corresponding KS statistic calculated as described above. The fraction of synthetic data sets for which the resulting KS statistic is greater than that for the cryo-TEM data represents the likelihood that deviations from the hypothesized power-law behavior are greater for the synthetic size distributions relative to the cryo-TEM distributions. If this fraction is large, then the difference between the extended tails of the cryo-TEM distributions and our power-law characterization based on eq 8 can be attributed to statistical fluctuations. As suggested elsewhere,³⁷ we accept our power-law characterization as plausible if this fraction is greater than 0.10. The results of this KS test are given in Table 1. In each case, the fraction is much greater than 0.10. Thus, we conclude that the power-law behavior imbedded in eq 8 gives a plausible characterization of the tail of these exosome size distributions.

We now turn to assessing the effectiveness of our scaling exponent as a characteristic parameter that can distinguish the size distributions of exosomes isolated from different human serum samples. To this end, we use an extension of the maximum likelihood method described above to binned experimental data³⁸ to analyze NTA measurements of the exosome size distributions in serum samples taken from a cohort of four patients diagnosed with early-stage squamous cell carcinoma (SCC) and from a cohort of five healthy donors.³⁹ The results are summarized in Table 2. We find that the scaling exponents, which characterize the size distributions of exosomes from the cancer patients (SCC exosomes), are on average significantly greater (p-value < 0.001) than the scaling exponents, which characterize the size distributions of exosomes from the healthy donors (HS exosomes). In contrast, the difference in 〈D〉 between the two cohorts is on average not statistically significant (Table 2). That the scaling exponent is more effective than the mean diameter in distinguishing these exosome size distributions is not surprising. The characteristic asymmetry of the distributions captured by ξ reflects the presence of larger exosomes in much greater numbers than would be expected from a normal or Gaussian distribution. Thus, the exosome size distributions are not well characterized by their mean values.

Table 2.

Scaling Exponents and Mean Exosome Diameters Obtained from Eq 10 that Characterize the Size Distribution of Exosomes in Serum Samples from Four Patients Diagnosed with Early-Stage SCC (SCC-EX) and from Five Healthy Donors (HS-EX) Measured by NTA^39a

serum sample	scaling exponent, ξ	mean diameter, 〈D〉
SCC-EX1	0.3643	135.1
SCC-EX2	0.3802	116.1
SCC-EX3	0.3984	99.8
SCC-EX4	0.3377	93.4
average	0.3702 ± 0.0257	111.1 ± 18.6
HS-EX1	0.2253	107.6
HS-EX2	0.2800	100.6
HS-EX3	0.3007	112.4
HS-EX4	0.2484	109.0
HS-EX5	0.2238	97.6
average	0.2556 ± 0.0340	105.4 ± 6.1
p-value	<0.001	>0.5

^aMean diameters are in units of nanometers.

As noted above for the TPC1 cell-derived exosomes, the larger values of ξ obtained for the serum exosome size distributions from the cancer patients indicate the power-law behavior in eq 8 extends further into the tails of those distributions. This extended power-law behavior does not imply, however, the presence of larger vesicles produced by an entirely different biogenesis pathway–e.g., shedding vesicles.^5–7 As shown in Figure 4, a single value of the scaling exponent accurately describes the tail of the SSC-EX1 exosome size distribution, which extends well beyond that for the HS-EX3 exosomes. We would not expect this power-law behavior with the same scaling exponent to apply to the larger vesicles if these vesicles originated from an entirely different biogenesis pathway. In the context of our dynamic scaling model, the larger values of ξ reflect slower rates of domain budding, invagination, and/or scission—i.e., slower rates of ILV/exosome formation—that inhibit domain growth by coalescence on the MVB membrane. If we consider the inhibition of domain growth to be a consequence of the local coupling of membrane curvature to composition, then we might expect changes in ξ to correlate with changes in membrane composition and possibly the cargo of the exosomes. The suggestion that changes in the scaling exponent reflect changes in the membrane composition of exosomes is supported by recent work that points to high levels of phosphatidylserine-expressing exosomes in patient blood as a potential diagnostic for cancer.⁴⁰

Figure 4.

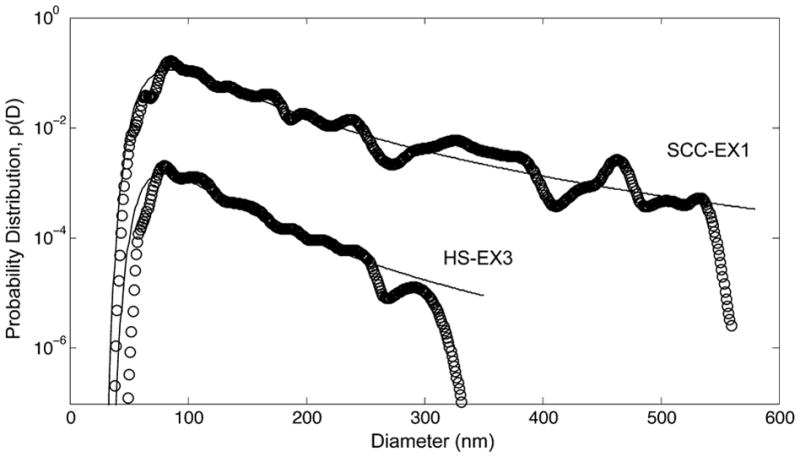
Probability distribution, p(D), of exosome diameters measured by NTA for exosomes isolated from serum samples taken from a patient diagnosed with early-stage SCC (SCC-EX1) and a healthy donor (HS-EX3). Open circles are the NTA data; solid lines are calculated using the probability density distribution function eq 8 with scaling exponents and average exosome diameters given in Table 2. Distributions are shifted up (SCC-EX1) and down (HS-EX3) by a factor of 10 for visual clarity.

The proposition of dynamic scaling (eq 2) of the length scale of ILV/exosome-forming membrane domains in our model of exosome size distributions defines a scaling exponent that is opposite in sign from the scaling exponent in the Weibull extreme value distribution (EVD) function that has been used to describe size distributions of vesicles prepared by sonication, extrusion, or detergent dialysis, although the size range of spherical vesicles formed in these preparations is comparable to that for exosomes.⁴¹ The Weibull EVD description is based on a random fragmentation model in which an upper limit to the vesicle diameter is defined.^42,43 The power-law behavior defined by eq 2 with ξ > 0 leads to a distribution function that can be derived from the Fréchet EVD in which a minimum vesicle diameter is defined.⁴⁴ The Fréchet EVD was identified previously by us as the EVD function that best represents TPC1 cell-derived exosome size distributions when fitting the measured distributions to the probability density function for the generalized EVD.¹⁶ We note that fitting exosome size distributions using the Weibull distribution can give a negative and therefore unphysical minimum vesicle diameter for the distribution.³⁴

CONCLUSIONS

The model proposed herein for characterizing exosome size distributions is based on a dynamic scaling ansatz that relates exosome diameters to the characteristic length scale of ILV-forming domains on the MVB limiting membrane. This dynamic scaling model contains two parameters: the mean exosome diameter and a scaling exponent that captures the characteristic asymmetry of exosome size distributions that are right-skewed to larger vesicle sizes. The mean exosome diameter is obtained directly from experiments as an average of the measured diameters. Thus, the scaling exponent alone is fit to the experimental exosome size distributions. We show that the scaling exponents so obtained are sensitive to the state of the exosome cell source and insensitive to the minimum detectable vesicle size intrinsic to different detection methods. Importantly, we also find statistically significant differences in the scaling exponents that characterize the exosome size distributions in serum samples taken from cancer patients relative to those from healthy donors. Conversely, statistically significant differences in the mean exosome diameters are not obtained. Our analysis further suggests that there is no need to invoke alternative biogenesis pathways to explain the presence of large vesicles in exosome size distributions. Collectively, these results establish the potential of dynamic scaling of exosome sizes, in general, and the scaling exponent specifically as a quantitative biophysical parameter for identifying and characterizing the exosome subpopulation of EVs. Finally, we speculate that changes in the scaling exponent may reflect changes in the membrane composition of exosomes. In this regard, we can consider the scaling exponent to be a biophysical biomarker for exosomes comparable and complementary to biochemical exosome biomarkers, notably specific membrane proteins, such as tetraspanins.