Abstract
Purpose
To investigate the sensitivity of diffusion‐MR signal to microstructural change in muscle tissue associated with pathology, and recommend optimal acquisition parameters.
Methods
We employ Monte‐Carlo simulation of diffusing spins in hierarchical tissue to generate synthetic diffusion‐weighted signal curves over a wide range of scan parameters. Curves are analyzed using entropy—a measure of curve complexity. Entropy change between a baseline and various microstructural scenarios is investigated. We find acquisitions that optimize entropy difference in each scenario.
Results
Permeability changes have a large effect on the diffusion‐weighted signal curve. Muscle fiber atrophy is also important, although differentiating between mechanisms is challenging. Several acquisitions over a range of diffusion times is optimal for imaging microstructural change in muscle tissue. Sensitivity to permeability is optimized for high gradient strengths, but sensitivity to other scenarios is optimal at other values.
Conclusions
The diffusion‐attenuated signal is sensitive to the microstructural changes, but the changes are subtle. Taking full advantage of the changes to the overall curve requires a set of acquisitions over a range of diffusion times. Permeability causes the largest changes, but even the very subtle changes associated with fiber radius distribution change the curves more than noise alone. Magn Reson Med 78:1187–1198, 2017. © 2016 The Authors Magnetic Resonance in Medicine published by Wiley Periodicals, Inc. on behalf of International Society for Magnetic Resonance in Medicine. This is an open access article under the terms of the Creative Commons Attribution‐NonCommercial‐NoDerivs License, which permits use and distribution in any medium, provided the original work is properly cited, the use is non‐commercial and no modifications or adaptations are made.
Keywords: diffusion MRI, Monte‐Carlo simulation, muscle, pathology modeling, Duchenne muscular dystrophy, entropy
INTRODUCTION
Diffusion MRI is known to have a degree of sensitivity to changes to the microstructural properties of tissue. Techniques such as diffusion tensor imaging (DTI) 1 and spherical deconvolution 2 have allowed estimation of the orientation of brain tissue in vivo, and a large body of research literature has developed around inferring more detailed microstructural information such as axon fiber radius distribution 3, 4. Application of advanced methods in brain benefits from the favorable relaxation properties of the tissue to allow MR measurements with sufficient signal‐to‐noise ratio (SNR), to provide informative parameter estimates.
Application to muscle tissue has historically been more challenging. T2 of skeletal muscle is shorter than in brain (5 gives 50 ± 4 ms in skeletal muscle at 3 Tesla (T) versus 99 ± 7 ms in gray matter and 69 ± 3 ms in white matter), making pulse sequence design more challenging, particularly for diffusion MRI. Recently, however, scanner hardware has improved to the point where muscle imaging is feasible on advanced clinical systems. 3T systems and improved gradient hardware enable diffusion‐weighted images of muscle tissue to be acquired with short, clinically practical acquisition times.
There have been a number of applications of advanced diffusion methodology to muscle. DTI and tractography have been applied to image fibers in the myocardium 6, and HARDI has been applied to resolve crossing fibers ex vivo in the bovine esophagus 7. More recently, Sigmund et al. derived properties such as surface area to volume ratio from skeletal muscle 8.
A number of pathologies affect muscle tissue structure. Duchenne muscular dystrophy (DMD), for example, is a progressive, genetic muscle‐wasting pathology. The development of novel drug therapies is hampered by the lack of quantitative measures of disease progression. The gold standard is biopsy, which is both invasive and highly localized 9.
Image‐based biomarkers offer the potential to measure pathological changes in tissue noninvasively and in a way that covers entire muscle groups rather than specific locations in tissue. Previous applications of MRI to DMD typically provide images that quantify tissue fat‐fraction 10, but the replacement of muscle tissue with fat is a late stage of the pathological process and there is a need for imaging that can resolve earlier changes. Diffusion MRI is a candidate but it is not clear a priori how sensitive the signal is to muscle microstructure or how the pathology alters diffusion‐weighted measurements.
One challenge is the structure of muscle tissue itself. Most of the modeling literature in diffusion MRI was developed for application in brain, particularly in white matter. Here, tissue can be approximated by oriented structures such as parallel cylinders, which can be captured both in simulation and simpler models suitable for fitting to in vivo data 11. White‐matter fibers have typical radii on the order of 1–5 microns 12, which is compatible with diffusion times accessible in pulse gradient spin‐echo (PGSE) or oscillating gradient spin‐echo (OGSE) sequences. Muscle fibers are considerably larger: typically 20–90 microns 13, requiring longer diffusion times to probe. Perhaps more importantly, the tissue is hierarchical. It consists of bundle fibers that are in turn bundles of smaller fibers 14. This form of structure restricts diffusion across a wide range of length scales from the macroscopic down to the nanoscale.
Constructing an explicit model of diffusion in a multiscale structure is very challenging. Such a model would require smoothing on multiple hierarchical levels, which would lead to a model that is not only complicated and difficult to fit, but also degenerate with many other curves. Here we adopt an approach based on the curve entropy, which requires no explicit description of tissue and no model‐fitting step while still quantifying the difference between different decay curves. We use this approach to explore the sensitivity of synthetic diffusion‐weighted MRI data. We quantify the diffusion‐weighted signal curve across a range of gradient strengths and diffusion times by considering the information‐theoretic entropy of the signal 15.
We construct a Monte‐Carlo simulation of diffusion in muscle tissue, and synthesize diffusion‐weighted measurements across a wide range of gradient strengths and diffusion times. We consider a baseline tissue model derived from histology of healthy tissue and compare those data with several scenarios that capture microstructural changes that result from DMD pathology.
There has been a considerable research effort in modeling the diffusion signal in brain (see 4 for a review). Monte‐Carlo simulation was first employed in diffusion MRI research by Szafer et al. 16. Since that time it has become a vital part of the diffusion imaging methods development process. It has been used, for example, as a validation tool 17 and to aid the development of novel analyses 3. The current work uses the Camino Monte‐Carlo simulation framework 17, 18, employing a new model of muscle tissue and extending the framework to increase numerical efficiency.
Changes in the form of the diffusion signal curve are quantified using entropy, which measures how much information is encoded in a curve. Changes to curve shape cause changes in curve entropy, and the magnitude of entropy change provides a convenient measure of the change in curve shape.
Entropy in this context was originally proposed by Shannon 15 in 1948. It is common in signal processing and has been used in genetics 19 and finance 20. In diffusion MRI, Ingo et al. 21 considered the entropy of a model fitted to diffusion‐weighted MR data, but in principle there is no requirement for model fitting. An entropy can be calculated directly from diffusion‐weighted data. We obtain entropies directly from synthetic measurements from simulation to investigate sensitivity in the data without intermediate models. This removes bias caused by the sensitivity of the model to particular change in the underlying data.
We investigate the effect on the diffusion signal resulting from several microstructural scenarios:
Permeability changes. All barriers to diffusion are given a finite probability of allowing spins to diffuse through them;
Atrophy of internal muscle fibers. Fibers inside bundles are reduced in radius by a constant factor (Figs. 2b and 2d);
Fiber radius distribution. Distribution of fiber sizes is fitted to a mouse disease model of DMD (Fig. 2e); and
Removal of fibers from the substrate (Fig. 2f).
Figure 2.
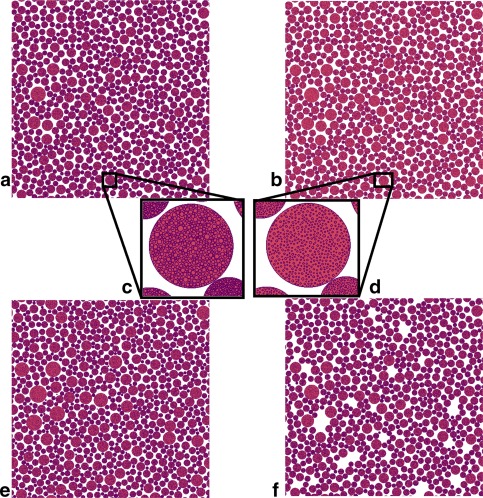
Cross sections of substrates used in different microstructural scenarios. Space outside cylinders is colored white, space inside cylinders is red, and cell membranes are purple. (a) Baseline substrate. Outer cylinders have radii drawn from a gamma distribution fitted to histology of healthy, wild‐type mouse forelimb tissue. Each cylinder on the substrate contains regularly packed internal cylinders (c). (b) Effect of atrophy scenario 1, in which all internal cylinders are reduced in radius by a fixed factor. (d) The same cylinder as (c) with internal cylinders reduced in radius. Positions are unchanged. (e) A substrate with cylinder radii drawn from a different distribution, fitted to histology of an Mdx mouse model of DMD. Close inspection reveals that these cylinders have a wider range of radii than those in (a), but the packing fractions achieved are similar. Internal structure in (e) is similar to that in (a). (f) Atrophy scenario 2. Here, complete nested cylinders are removed from the baseline arrangement at random. In this example, 10% have been removed. The permeability scenario is not shown, as it is visually identical to the baseline.
Each scenario is simulated using different degrees of parameter change. Differences between each set of synthetic measurements and a baseline scenario (Fig. 2a and 2c) are quantified using the percentage entropy change. For comparison, we also obtain entropy changes as a result of Rician noise at SNR = 20. We then employ an optimization procedure that finds subsets of acquisitions, which maximizes the change in entropy. Magnitude of parameter changes are chosen to assess the sensitivity of the signal to the effect.
METHODS
Monte‐Carlo Simulation
Skeletal muscle tissue structure is hierarchical 14. Length scales of these structures ranges over several orders of magnitude. We model muscle tissue as an environment consisting of nested cylinders (cylinders that contain other, smaller cylinders).
Data are synthesized using the Camino Monte‐Carlo simulation framework 17, 18. Permeability is modeled using a fixed probability of a spin stepping through a barrier using the implementation of 22. Parallel cylinders are arranged in reverse order of size using a dynamic spatial map 23. Cylinder placement is top‐down: Larger structures are placed first, then the internal structure is added to each cylinder. Internal cylinders are parallel to the enclosing cylinder, randomly packed, nonoverlapping, have gamma distributed radii, and do not intersect the boundary of the outer cylinder.
The most numerically expensive step in Monte‐Carlo simulations is checking intersections: Cylinders must be placed such that they do not overlap, and steps in the spins' random walks must be checked for intersections with tissue structure. An efficient intersection‐checking algorithm can provide an orders‐of‐magnitude improvement over brute force methods. Previously, the Camino Monte‐Carlo simulation has employed a regular spatial subdivision procedure, which is efficient when the size of the objects is unimodal and they are approximately evenly distributed in space.
Here we employ a hierarchical intersection checking procedure that is better suited to hierarchical structures. Maps of cylinder positions to spatial regions are assembled during tissue model construction, and then used during dynamics simulation.
Hierarchical Intersection Checking
The method of intersection checking is an extension of uniform spatial subdivision 23, 24. Maps are constructed of spatial subregions to sets of objects that intersect them (Fig. 1a). In uniform spatial subdivision intersection checking, a regular grid is imposed on the tissue substrate and a map created from objects to the grid elements they intersect. Because it is simple to construct a list of grid elements surrounding a test object, explicit checks need only be performed on a list of candidates that intersect these elements.
Figure 1.
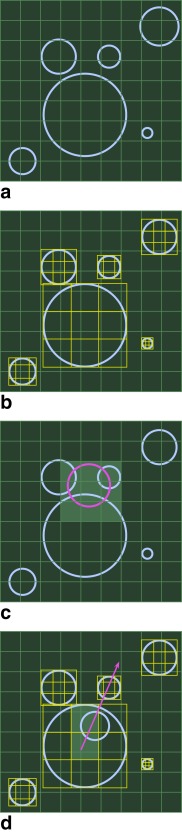
Hierarchical spatial intersection checking. Substrate is uniformly subdivided (a). Each nested structure has its own uniform subgrid (b). The regular subgrid makes intersection checking in the extracellular space more numerically efficient (c). Each local subgrid facilitates efficient intersection checking against internal structure (d).
The hierarchical scheme attaches an additional grid to each nested object (Fig. 1b). A map is assembled from elements of the local grid to the elements of the nested cylinder's structure. When an explicit check for intersection with the nested cylinder is required, the local grid is used to assemble a list of candidates to perform explicit checks (Fig. 1c). This scheme can be applied to any level of nest depth.
Tissue Model Construction
Tissue substrates are constructed by arranging a specified number of parallel cylinders in a region with periodic boundaries. Cylinders have radii drawn from a gamma distribution with specified shape and scale parameters (k and θ, respectively). Cylinders that intersect the boundaries on the simulated region are copied on the opposite side of the substrate to ensure periodicity 23.
Once all cylinders have been placed on the substrate, each cylinder then has an internal structure added. Internal cylinders are parallel to the outer cylinder, and have radii drawn from a gamma distribution with the same shape parameter as the outer cylinder distribution, but scale parameter multiplied by the area fraction of the outer cylinder on the substrate.
Internal cylinders are also nonintersecting. Each cylinder has circular cross section and is infinitely long; therefore, we only need to pick a trial location in the cross‐sectional disk. Uniform sampling is achieved by picking coordinates using a relation that preserves the volume element of the unit disk:
| (1) |
where is the radial coordinate on the disk. Cartesian coordinates uniformly distributed on the disk are obtained using
| (2) |
| (3) |
Note that this transformation is required for uniform sampling density on the disk 25. Trial coordinates on the unit disk are generated by sampling uniformly in and uniformly in . The coordinates are then scaled and translated from the unit disk at the origin to the cylinder of radius at position
| (4) |
| (5) |
where is the radius of the cylinder being placed.
Intersection checking is performed using the hierarchical method outlined previously. Once a position for the new cylinder is found that does not intersect with any others, it is added to the local map and the process repeats. The complete map is reused during dynamics simulation (Fig. 1d).
Diffusion Dynamics and Intersection Checking
Diffusing spins execute random walks in three dimensions (3D). Each step in a spin's trajectory must be checked for intersection with the tissue substrate. As with the tissue substrate construction phase, the efficiency of this check has a significant effect on the simulation performance.
For each step in a spin's trajectory, a set of intersecting cells is generated using Breshenham's algorithm 24, 26. The step is tested against objects that intersect these grid elements. For internal intersection checks, the step is projected into the local map, and parametric clipping 24, 27 is employed to exclude portions of the step that fall outside it.
Tissue Models
This section describes tissue models designed to investigate microstructural change as well as a baseline model of healthy muscle tissue.
Baseline
The baseline scenario is used as a basis for comparison for microstructural changes. We employ microstructural parameters from a histological study of healthy mouse forelimb muscle tissue 13. We use maximum likelihood estimation to obtain gamma distribution parameters from histograms of muscle fiber diameter (shape = 13.5, scale = 3.02 × 10−6 m, 3 sig. figs.) and construct tissue substrates containing 750 parallel cylinders. The size of the substrate was chosen to maximize intracellular volume fraction. A substrate size of m gives intracellular volumes fractions of 70% or greater. Each cylinder contains 525 internal cylinders.
Atrophy as a Result of Fiber Diameter Shrinkage
Atrophy is modeled as change in the radii of internal cylinders. The radius of each internal cylinder is reduced by a specified factor. Positions of cylinders are unchanged. This increases the space between fibers and reduces restriction inside top‐level cylinders. Substrates in which the atrophy ratio is set to 5, 10, and 20% (ie, cylinder radii are 95, 90, or 80% of the equivalent in the baseline) are investigated. Figures 2b and 2d illustrate the internal fiber atrophy.
Fiber Removal
Atrophy is modeled as the loss of a fixed proportion of cylinders on the substrate. After constructing the baseline substrate, cylinders are removed with a fixed probability, resulting in gaps between neighboring cylinders (see Fig. 2f). Cylinders are removed with 2, 5, and 10% probability.
Permeability
We introduce a finite probability for spins to step through barriers rather than be reflected by them, but all other microstructural parameters as the baseline. Permeabilities are set to 0.5, 1, and 2%. Permeability scenario substrates are visually identical to the baseline.
Fiber Radius Distribution
We fit gamma distribution parameters to histological data from 13 (shape = 6.01; scale = 6.16 × 10−6 m; 3 sig. figs.). We pack 850 cylinders, each containing 590 internals, into the substrate (see Fig. 2e). Numbers of cylinders and substrate size were chosen empirically to obtain as good agreement as possible between intracellular volume fractions between this and the baseline.
Figures 2a and 2e are visually quite similar, however Figure 2e exhibits a wider range of radii and a greater proportion of larger cylinders than Figure 2a. The visual similarity between this and the baseline illustrates the subtlety of changes we aim to resolve in diffusion signals.
Noise Only
Rician noise is introduced to the baseline signal at SNR = 20 (defined on the unweighted image) by adding Gaussian noise to the real and imaginary components and taking the magnitude 28.
Entropy
We use nonnormalized entropy 21 given by
| (6) |
where = 205 is the number of measurements (one per scan parameter combination in Supporting Table S1) and is the th normalized diffusion‐weighted measurement.
The magnitude of the entropy of each set of synthetic measurements is of less importance than the changes in the value of the entropy between each pathological scenario and the baseline. We report percentage changes in entropy between each scenario and the baseline.
Experiments
Monte‐Carlo Simulation
Thirty simulations were run for each of the microstructural scenarios described in the Methods section. Care was taken to ensure that the step lengths in spins' random walks were sufficiently smaller than the smallest cylinders on the substrate. The number of updates was chosen such that the step length in all simulations was smaller than half the radius of the smallest cylinder. Simulation duration was fixed by the pulse sequences considered. Once the number of updates were chosen, we simulated as many spins as were computationally feasible.
Simulations have 10000 spins and 100000 updates, giving a step length of 8.3 × 10−7 m. Simulations in each ensemble differ only in the seed of the random number generator.
Simulations were run on a Dell Precision T7610 PC running Ubuntu Linux 14.04, with dual 8‐core Intel Xeon processors and 128 GB RAM running a Java 7 SE Runtime Environment Hotspot 64‐bit Server VM in mixed mode. Typical execution time for each simulation was 4 to 5 h, requiring 12–16 GB of RAM, depending on scenario.
Synthetic diffusion‐weighted signals were obtained from each simulation for the gradient strength ranging from 0.01–0.12 Tm−1 and diffusion times ranging from 40–200 ms. In all cases, the gradient duration was 20 ms and gradients were applied perpendicular to cylinder axes. We calculated a mean and standard deviation for each diffusion‐weighted signal across each ensemble.
The range of diffusion times and gradient strengths chosen was designed to cover and exceed the range accessible on a modern state‐of‐the‐art clinical system, which might include maximum gradient strengths of 0.08 Tm−1. The range of diffusion times considered greatly exceeded what was feasible for a PGSE sequence, but is accessible using a diffusion‐weighted STimulated Echo Acquisition Mode (STEAM) sequence.
Acquisition Subset Optimization
Optimization searches were performed for a subset of M combinations of gradient strength and diffusion time that maximize the entropy difference between the baseline and each microstructural scenario. We tested each combination of size M from the global set, excluding repetitions and re‐orderings.
The optimization proceeded as follows:
-
For all combinations of M indices
-
1.1
Calculate the entropy of the baseline signal from the subset
-
1.2
For each microstructural scenario
-
1.2.1
Calculate the entropy of the microstructural scenario using only those acquisitions in the subset
-
1.2.2
Calculate the percentage change in entropy between scenario and baseline
-
1.2.3
Record the largest change
-
1.2.1
-
1.1
Report the subsets and entropy changes for all scenarios
We optimized subsets of sizes M = 5 and 6 from a total set of 205.
Optimization code was written in C+ + 11 and run on the same computing setup as the previous section.
RESULTS
Monte‐Carlo Simulations
Figures 3, 4, 5, 6 show the synthetic diffusion‐weighted signals as a function of gradient strength and diffusion time. Solid lines represent the ensemble mean, and error bars show ±1 standard deviation.
Figure 3.
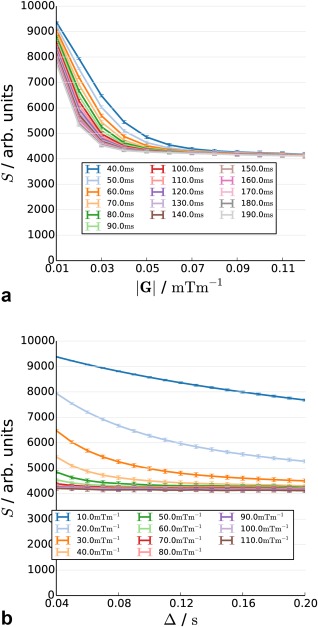
Synthetic diffusion attenuated decay curve from the baseline scenario as a function of diffusion time (a) and gradient strength (b).
Figure 4.
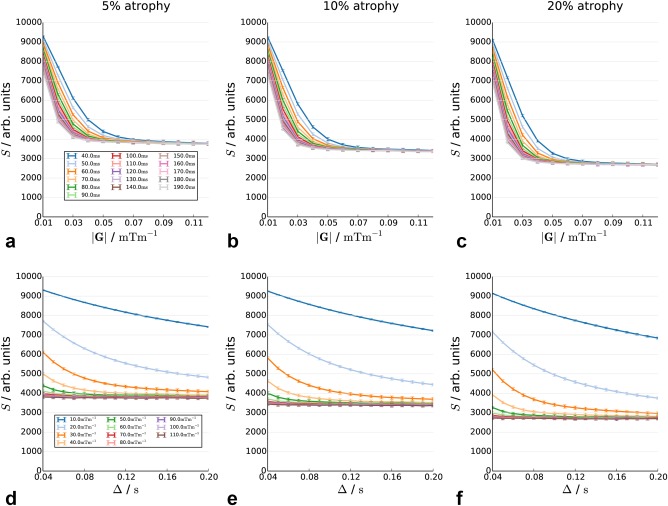
Decay curves in substrates with 5, 10, and 20% atrophy in the internal cylinder radius, as a function of diffusion time (top row) and gradient strength (bottom row).
Figure 5.
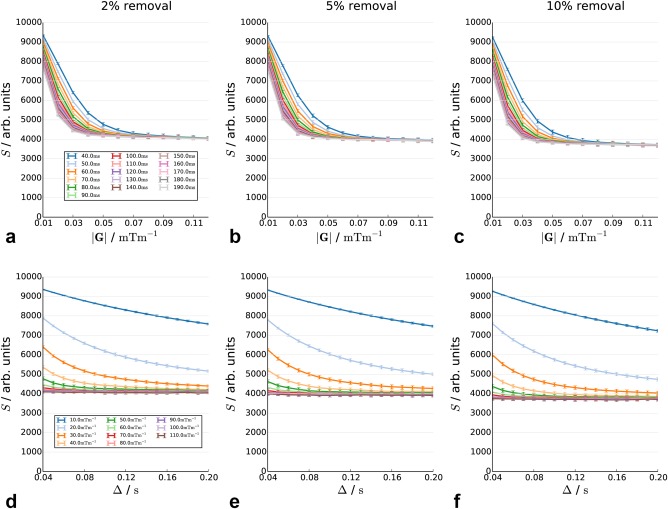
Decay curve in substrate with 2, 5, and 10% of fibers removed. The positions of the remaining cylinders are the same as in the baseline scenario. The signal is plotted as a function of diffusion time (top row) and gradient strength (bottom row).
Figure 6.
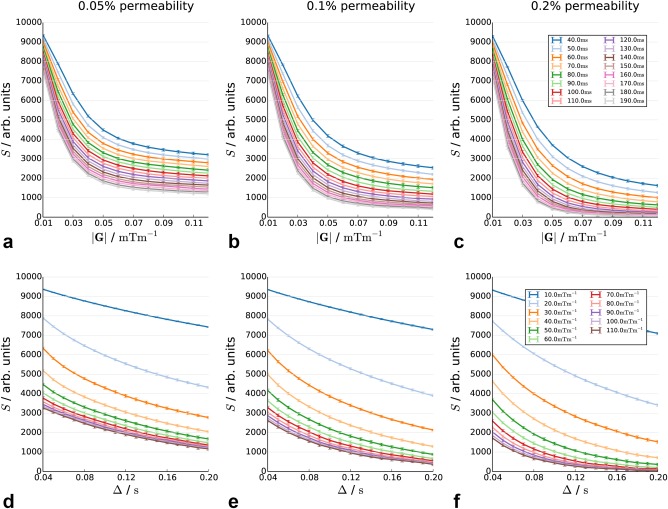
Decay curves in substrates with 0.05, 0.1, and 0.2% permeability in restricting membranes, as a function of diffusion time (top row) and gradient strength (bottom row).
The baseline (Figs. 3a and 3b, Supporting Fig. S3) shows rapidly increasing diffusion attenuation at lower gradient strengths and shorter diffusion times, with a plateau at higher diffusion weightings. The plateau itself is not completely flat; a small decrease is observed with increasing diffusion time.
Figures 4a–4f show the effect of atrophy of inner fibers by 5, 10, and 20%. Increasing atrophy acts primarily to lower the plateau in the signal. The 5, 10, and 20% atrophy scenarios give changes of 9.4, 18.64, and 34.7% in the signal, respectively.
Figures 5a–5f show the effect of the removal of a fixed proportion of fibers. The overall pattern is similar to Figure 4, although the change in the height of the plateau is less marked. Extreme values on the plateaus are 4027, 3903, and 3707 for 2, 5, and 10% changes, respectively.
Figures 6a–6f show the effect of permeabilities of 0.005, 0.01, and 0.02%. The addition of permeability strongly changes the form of the curve. Plateauing is not present, with the curve continuing to decrease with increasing diffusion time and gradient strength.
Figures 7a and 7c show the synthetic diffusion‐weighted signal with fiber‐distribution parameters fitted to Mdx mouse model tissue histology. Changes in the curve are subtler than in previous scenarios and are difficult to distinguish visually. We therefore plot the ratio of each signal from the scenario to the equivalent in the baseline. The baseline scenario measurements are generally of higher magnitude than in the baseline. The difference between the two signals is largest for diffusion times above 40 ms, and there is a small increase with gradient strength, although this is very weak.
Figure 7.
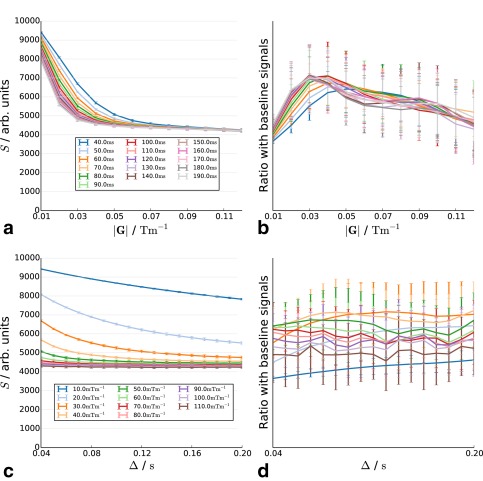
Decay curves in substrates with cylinder radius distribution parameters fitted to Mdx mouse model tissue as a function of diffusion time (a) and gradient strength (c). (b) and (d) show the ratio of the signal with the baseline scenario curve.
Entropy Changes between Microstructural Scenarios
Figure 8 shows the signed percentage changes in entropy between each scenario and the baseline. The largest entropy changes are the result of changes in permeability, on the order of 40–60%.
Figure 8.
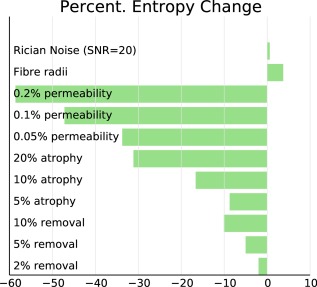
Percent change in entropy of synthesized curves in each microstructural scenario from the baseline.
Atrophy as a result of shrinkage also leads to large changes in entropy. The changes are less pronounced than those observed for changes in permeability, but we observe changes of 30–45%. Atrophy as a result of loss of fibers shows entropy changes of 4–10%.
Changes in fiber radius distribution are more subtle than those observed for the other scenarios, with entropy changes on the order of 4–5%. These changes are still considerably greater than those observed for noise alone, which results in a mean entropy change of 0.6%.
Change in entropy as a result of fiber radius distribution has the opposite sign to that of the other scenarios, indicating that the signal curve becomes more complex, rather than less. The sign of the noise change is also positive, but the standard deviation of the noise entropy change is 0.8% and hence not significantly different from zero.
Acquisition Subset Optimization
Sensitivity is optimized to each microstructural scenario. Optimal subsets of sizes 5 and 6 are given in Table 1 for the smallest parameter change in each scenario. Acquisitions selected in the M = 6 subsets, which are not present in M = 5, are in bold. In each case, the overlap between the sets is maximal.
Table 1.
Optimal Acquisition Subsets
| Atrophy | (inner) | Atrophy | (removal) | Permeability | Radii | ||
|---|---|---|---|---|---|---|---|
| |G|/Tm−1 | Δ/ms | |G|/Tm−1 | Δ/ms | |G|/Tm−1 | Δ/ms | |G|/Tm−1 | Δ/ms |
| 5 acquisitions | |||||||
| 0.030 | 90 | 0.100 | 40 | 0.100 | 190 | 0.030 | 80 |
| 0.040 | 90 | 0.110 | 40 | 0.110 | 190 | 0.030 | 90 |
| 0.030 | 100 | 0.040 | 180 | 0.090 | 200 | 0.020 | 130 |
| 0.060 | 130 | 0.050 | 180 | 0.100 | 200 | 0.020 | 140 |
| 0.040 | 180 | 0.060 | 180 | 0.110 | 200 | 0.030 | 200 |
| 6 acquisitions | |||||||
| 0.030 | 90 | 0.100 | 40 | 0.100 | 190 | 0.030 | 80 |
| 0.040 | 90 | 0.110 | 40 | 0.110 | 190 | 0.030 | 90 |
| 0.030 | 100 | 0.060 | 170 | 0.090 | 200 | 0.020 | 120 |
| 0.060 | 120 | 0.040 | 180 | 0.100 | 200 | 0.020 | 130 |
| 0.060 | 130 | 0.050 | 180 | 0.110 | 200 | 0.020 | 140 |
| 0.040 | 180 | 0.060 | 180 | 0.120 | 200 | 0.030 | 200 |
Parameter ranges optimizing entropy change is highly dependent on the scenario. Permeability scenarios are optimized for the longest diffusion times (180–200 ms) and highest gradient strengths (0.090–0.120 Tm−1) considered. Internal fiber atrophy sensitivity is optimized for parameter ranges that are dependent on the degree of atrophy: the 5% scenario is optimized for diffusion times between 90 and 180 ms, the 10% scenario 130–150 ms, and the 20% scenario 120–170 ms, reflecting the change in typical length scales. Notably, these diffusion time ranges are well defined in each scenario. Optimal gradient strengths tend to be repeated in each set. The fiber radius distribution scenario is optimally sensitive over a very wide range of diffusion times: from 80–200 ms, but with quite moderate gradient strengths of 0.020–0.030 Tm−1.
DISCUSSION AND CONCLUSIONS
We constructed Monte‐Carlo simulations of diffusion in hierarchical muscle tissue and investigated the effect of changes to tissue microstructure on synthetic diffusion‐weighted measurements. The nested structure of muscle tissue is fundamentally different from that experienced by spins diffusing in brain tissue, and this affects the diffusion dynamics. To quantify changes in diffusion signal, we employ an approach based on entropy, which estimates the information content of the curve. Changes in entropy can be used to assess sensitivity of the signal to microstructural change.
Entropy changes observed suggest there is a measurable effect on signal in all microstructural scenarios considered. The signal is more sensitive to changes in permeability than any of the other effects, even though the change in the underlying parameter is an order of magnitude smaller.
Plateaus in attenuation are observed in all scenarios except permeability. These are the result of hard limits on diffusion caused by restriction. In the long run, restriction puts a limit on diffusion displacement. This is not present for hindered compartments, which eventually attenuate away completely. Permeability acts to reduce the overall amount of restriction present in the system and removes hard limits on net displacement for spins inside fibers, making the dynamics look more like free diffusion than in the completely restricted case. This removes the plateau otherwise observed in the signal curve.
Acquisition optimization results show that sensitivity to the difference scenarios is optimized at different parameter ranges. Changes in signal as a result of permeability increase with increasing diffusion sensitivity; hence, the optimization process picks the highest weightings available. Changes as a result of atrophy and fiber removal act to change the height of the plateau, possibly because of changes in porosity (Supporting Table S2); hence, the optimal set of acquisition parameters sample the plateau. Changes to the curve as a result of reduction in the size of internal radii shows a similar pattern, but over a different range of diffusion times, reflecting the shorter internal length scales. The optimization therefore selects a range of diffusion times associated with these length scales, and specific gradient strengths that optimize the change in plateau height.
The current work treats each microstructural change separately. In practice we would expect to encounter all these effects together, and measure an overall diffusion curve. Based on these simulated results, small changes in permeability cause large differences in the signal. The fact that no previous study has established a link between permeability change and Apparent Diffusion Coefficient (ADC) places bounds on the amount of permeability and permeability change in the tissue. The effect of the two atrophy scenarios, although differing in magnitude, is quite similar in terms of the actual changes to the curve, and differentiating between them is not currently possible. Additionally, changes in plateau height would appear difficult to resolve in the presence of increased permeability, which removes the plateauing behavior. This further suggests that the absence of a plateau in diffusion decay curves at long diffusion times is an indication that permeability is present in the tissue.
We have chosen to model muscles using parallel cylinders. Although muscle tissue is known to consist of highly parallel fibers, dispersion is known to be an important effect from modeling work in brain tissue. The current results show the effect of each microstructural scenario separately to the effect of dispersion, which is necessary so that effects not the result of fiber dispersion can be separated out.
Measuring changes to underlying fiber radius distribution has received a lot of interest in the diffusion MR modeling literature for the brain. Although some techniques have succeeded in estimating distribution parameters there 3, 29, the resulting maps are frequently noisy and the estimates are biased. The very small changes in curve entropy observed here suggest that, at least for the level of difference in radius distribution considered, measuring fiber radius distribution parameters in muscle tissue directly is challenging, especially if permeability is not taken into account. We do observe, however, that changes to the signal as a result of fiber radius distribution differences are measurable across the entire curve. For clinical purposes, it may be more profitable to concentrate on classifying the overall decay curve, such as by calculating an entropy for each voxel directly from the scan data, as we have done here for simulated data.
An important question regarding the current results is how we can be sure that the simulations are giving the correct results, given that there are no analytical models available to test against. Validation of the current simulation is indeed challenging, but the current implementation is able to make use of a large body of previous work. Camino employs a robust object‐oriented design that enables code to be reused. The code that simulates each individual cylinder in the simulation has been extensively validated 11, 17, as have the code that generates diffusion‐weighted phase shifts, the code used to generate radius samples 17, and the implementation of permeable barriers 22.
The novel aspects of the simulation employed here are the recursive cylinder positioning and hierarchical intersection checking. These were tested by constructing test cases of increasing complexity, whose results could be verified by a separate calculation. These tests covered intersection‐checking inside and outside nested cylinders and at different levels of cylinder hierarchy. The code passes all test cases to the limits of floating point accuracy. A sanity check is provided by the generation of substrate cross‐section images, in which pixels are colored according to the results of checking the intersection. Accordingly, the images in Figure 2 provide an additional assurance that the code is working correctly.
Throughout this work we have assumed gamma distributions for fiber radii. This choice is motivated by the observation that radius histograms are skewed and nonnegative. The gamma distribution is a common choice in the brain literature. There has been recent criticism of the use of gamma distributions in modeling white matter, specifically that they put too much weight in the tail. As we have seen, changes to the signal due to changes in fiber distribution are subtle, so we would not expect the choice of distribution to have a strong effect on these results. Experiments with Gaussian distributions of radii reveal the choice to have an effect on the magnitude of changes observed here, but the overall pattern of results remain the same (Supporting Fig. S2).
The entropy we use here is conceptually related to the more familiar thermodynamic entropy. The precise relationship between the two quantities has been long‐debated 30, but for current purposes it is enough to say that the two qualities differ mostly in their interpretation of the underlying quantity. Information theory concerns itself with the probability of a given set of received data, whereas thermodynamic entropy considers the probabilities attached to sets of states in a microcanonical ensemble. Both are a measure of the complexity of the system. Additionally, non‐thermodynamic entropies are not bound by the second law of thermodynamics, and may increase or decrease with changes to the system, as indeed we observed in this study.
Changes in entropy reflect the curve shape, and these changes may or may not be reflected in ADCs fitted to the data (Supporting Fig. S1). The analysis presented here can be adapted to consider ADC and which scan parameters maximize ADC difference, but some care is required to investigate how value, number, and ranges of gradient strengths affect ADC and its sensitivity. Further work is required to investigate this fully, but the current results do show a difference between the time dependence of ADC in permeable and impermeable scenarios.
The substrate construction method has a proscribed termination depth. Internal cylinders may also have an internal structure of their own. The choice made here is motivated by the range of length scales of interest in the tissue, and constrained ultimately by the memory available on the system. Other than memory restrictions, there is no reason why this approach could not be used to construct models with deeper recursion, although an appropriately short step length would be necessary to minimize bias in the resulting signal.
Our optimization results suggest that individual effects may be difficult to disentangle unambiguously from the diffusion signal, but that the overall change to the diffusion as a result of microstructural changes is measurable over a specific parameter ranges. This suggests that acquisitions can be tuned to individual changes or applied in a more “broadband” sense.
Clinically, if we wish to image the net effect of all scenarios, a broad range of several diffusion times is preferred, covering the entire range considered here so as to capture changes to fiber radius at 80 ms, atrophy scenarios at 90–180 ms, and permeability at 180–200 ms. Although in all cases we have used a gradient duration of 20 ms, there may be scope for further improvement by changing this.
The simulation code, including all novel additions described here, is available open‐source as part of the Camino diffusion MR framework (http://www.camino.org.uk) 18. Scripts used to generate all results and figures are available upon request.
Simulation of water diffusion in a hierarchical system such as muscle suggests that different ranges of diffusion time should be used depending on whether the prevalent feature of the pathology to be detected is a change in permeability, loss of external or internal fibers, or net reduction in fiber diameter. However, assuming these factors do not change and that there is only change in the fiber radius distribution (a possible scenario arising from DMD histopathology), then changes of this nature can be captured using diffusion times spanning 80 to 200 ms and gradient strengths of 0.02 to 0.03 Tm−1. Overall, however, it may be desirable to acquire a broader range of diffusion times to include sensitivity to all microstructural scenarios.
Supporting information
Fig. S1. ADC as a function of diffusion time on lin‐lin (left) and log‐log (right).
Fig. S2. Entropy changes in each scenario using Gaussian‐distributed cylinder radii.
Fig. S3. Lin‐log (a and b) and log‐log (c and d) plots of baseline signal decay. Non‐monoexponential decay is clearly evident.
Table S1. Combinations of gradient strength and diffusion time used to generate synthetic measurements.
Table S2. Porosities in the atrophy scenario are unchanged at the top level of structure and instead affect the volume fractions of cylinders nested inside the outermost layer. In this case the porosity change is predictable from the square of the atrophy factor. 2, 5, and 10% gives porosity changes of 3.96, 9.75, and 10.90%, respectively. Baseline mean porosity inside cylinders is 0.35, placing the overall change in the same range as for the removal scenario.
This work was supported by the European Union NMD‐Bioimage project. Seventh framework (FP7/2007‐2013) under grant 602485 Bioimage‐NMD project.
REFERENCES
- 1. Basser PJ, Mattello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 1994;66:259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Tournier J‐D, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non‐negativity constrained super‐resolved spherical deconvolution. NeuroImage 2008;35:1459–1472. [DOI] [PubMed] [Google Scholar]
- 3. Dyrby TB, Søgaard LV, Hall MG, Ptito M, Alexander DC. Contrast and stability of the axon diameter index from microstructure imaging with diffusion MRI. Magn Reson Med 2012;70:711–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Nilsson M, vanWesten D, Stahlberg F, Sundgren PC, Latt J. The role of tissue micrrostructure and water exchange in biophysical modelling of diffusion in white matter. Magn Reson Phys Biol Med 2013;26:345–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman M. T1, T2 relaxation and magnetisation transfer in tissue at 3T. Magn Reson Med 2005;54:507–512. [DOI] [PubMed] [Google Scholar]
- 6. Mekkaoui C, Reese TG, Jackowski MP, Bhat H, Sosnovik DE. Diffusion MRI in the heart. NMR Biomed 2017;30(3). doi: 10.1002/nbm.3426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Magnusson L, Gilbert RJ, Napadow VJ, Wang R, Crespigny AD, Reese TG, Benner T, Wedeen VJ. Complex fiber architecture of the tongue and esophagus revealed by MRI diffusion spectrum tractography. Proc Intl Soc Magn Reson Med 2005;13:575. [Google Scholar]
- 8. Sigmund EE, Novikov DS, Sui D, Ukpebor O, Baete S, Babb JS, Liu K, Feiweie T, Kwon J, McGorty K, Bencardino J, Fieremans E. Time‐dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients. NMR Biomed 2014;27:519–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Bushby K, Finkel R, Birnkrant DJ, Case LE, Clemens PR, Cripe L, Kaul A, Kinnett K, McDonald C, Pandya S, Poysky J, Shapiro F, Tomezsko J, Constantin C. Diagnosis and management of Duchenne muscular dystrophy. Part 1: diagnosis, and pharmacological and psychosocial management. Lancet Neurol 2010;9:77–93. [DOI] [PubMed] [Google Scholar]
- 10. Gaeta M, Messina S, Mileto A, Vita G, Ascenti G, Vinci S, Bottari A, Vita G, Settineri N, Bruschetta D, Racchiusa S, Minutoli F. Muscle fat‐fraction and mapping in Duchenne muscular dystrophy: evaluation of disease distribution and correlation with clinical assessments. Preliminary experience. Skeletal Radiol 2012;41:955–961. [DOI] [PubMed] [Google Scholar]
- 11. Alexander DC, Hubbard PL, Hall MG, Moore EA, Ptito M, Parker GJ, Dyrby TB. Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage 2010;52:1374–1389. [DOI] [PubMed] [Google Scholar]
- 12. Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res 1992;598:143–153. [DOI] [PubMed] [Google Scholar]
- 13. Hooijmans MT, Damon BM, Froeling M, Versluis MJ, Burakiewicz J, Verschuuren JJGM, Niks EH, Webb AG, Kan HE. Evaluation of skeletal muscle DTI in patients with duchenne muscular dystrophy. NMR Biomed 2015;28:1589–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Saladin KS. Anatomy and Physiology, 3rd Ed. New York: Watnik, 2010. p 405–406. [Google Scholar]
- 15. Shannon CE. A mathematical theory of communication. Bell Sys Tech J 1948;27:379–423. [Google Scholar]
- 16. Szafer A, Zhong J, Gore JC. Theoretical model for water diffusion in tissues. Magn Reson Med 1995;33:697–712. [DOI] [PubMed] [Google Scholar]
- 17. Hall MG, Alexander DC. Convergence and parameter choice for Monte‐Carlo simulations of diffusion MRI. IEEE Trans Med Imaging 2009;28:1354–1364. [DOI] [PubMed] [Google Scholar]
- 18. Cook PA, Bai Y, Nedjati‐Gilani S, Seunarine KK, Hall MG, Parker GJ, Alexander DC. Camino: open‐source diffusion‐MRI reconstruction and processing. Proc Intl Soc Magn Reson Med 2006;2759. [Google Scholar]
- 19. deAndrade M, Wang X. Entropy based genetic association tests and gene‐gene interaction tests. Stat Appl Genet Mol Biol 2011;10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Ormos M, Zibriczky D. Entropy‐based financial asset pricing. PLoS One 2014;9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Ingo C, Magin RL, Colon‐Perez L, Triplett W, Mareci TH. On random walks and entropy in diffusion‐weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med 2013;71:617–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Nedjati‐Gilani GL, Schneider T, Hall MG, Wheeler‐Kingshott CA, Alexander DC. Machine learning based compartment models with permeability for white matter microstructure imaging. Med Image Comput Comput Assist Interv 2014;17:257–264. [DOI] [PubMed] [Google Scholar]
- 23. Hall MG, Nedjati‐Gilani G, Alexander DC. Monte‐Carlo simulation of diffusion MRI with realistic voxel sizes. Proc Intl Soc Magn Reson Med 2014;2463. [Google Scholar]
- 24. Slater M, Steed A, Chrysanthou Y. Computer Graphics and Virtual Environments: From Realism to Real‐Time. Upper Saddle River, NJ: Pearson Education/Addison‐Wesley, 2002. [Google Scholar]
- 25. Weisstein EW. CRC Concise Encyclopedia of Mathematics, 2nd Ed. New York: Chapman and Hall/CRC, 2002. [Google Scholar]
- 26. Bresenham JE. Algorithm for computer control of a digital plotter. IBM Sys J 1965;4:25–30. [Google Scholar]
- 27. Liang Y, Barsky B. A new concept and method for line clipping. ACM TOG 1984;3:1–22. [Google Scholar]
- 28. Sijbers J, den Decker A, Van Audekerke J, Verhoye M, Van Dyke D. Estimation of the noise in magnitude MR images. Magn Reson Imaging 1998;16:87–90. [DOI] [PubMed] [Google Scholar]
- 29. Assaf Y, Blumenfeld‐Katzir T, Yovel Y, Basser P. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med 2008;59:1347–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Parrondo JMR, Horowitz JM, Sagawa T. Thermodynamics of information. Nature Phys 2015;11:131–139. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1. ADC as a function of diffusion time on lin‐lin (left) and log‐log (right).
Fig. S2. Entropy changes in each scenario using Gaussian‐distributed cylinder radii.
Fig. S3. Lin‐log (a and b) and log‐log (c and d) plots of baseline signal decay. Non‐monoexponential decay is clearly evident.
Table S1. Combinations of gradient strength and diffusion time used to generate synthetic measurements.
Table S2. Porosities in the atrophy scenario are unchanged at the top level of structure and instead affect the volume fractions of cylinders nested inside the outermost layer. In this case the porosity change is predictable from the square of the atrophy factor. 2, 5, and 10% gives porosity changes of 3.96, 9.75, and 10.90%, respectively. Baseline mean porosity inside cylinders is 0.35, placing the overall change in the same range as for the removal scenario.


