Distinct Beta-band Oscillatory Circuits Underlie Corticospinal Gain Modulation

Abstract

Rhythmic synchronization of neurons is known to affect neuronal interactions. In the motor system, oscillatory power fluctuations modulate corticospinal excitability. However, previous research addressing phase-specific gain modulation in the motor system has resulted in contradictory findings. It remains unclear how many time windows of increased responsiveness each oscillatory cycle provides. Moreover, we still lack conclusive evidence as to whether the motor cortex entails an intrinsic response modulation along the rhythm cycle, as shown for spinal neurons. We investigated this question with single-pulse transcranial magnetic stimulation over the primary motor cortex at rest. Application of near-motor threshold stimuli revealed a frequency- and phase-specific gain modulation at both cortical and spinal level, independent of the spontaneous oscillatory power fluctuations at each level. We detected bilateral sensorimotor circuits in the lower beta-band (14–17 Hz) and unilateral corticospinal circuits in the upper beta-band (20–24 Hz). These findings provide novel evidence that intrinsic activity in the human motor cortex modulates input gain along the beta oscillatory cycle within distinct circuits. In accordance with periodic alternations of synchronous hyper- and depolarization, increased neuronal responsiveness occurred once per oscillatory beta cycle. This information may lead to new brain state-dependent and circuit-specific interventions for targeted neuromodulation.

Introduction

Oscillatory neuronal activity occurs in distinct frequency bands and mediates the information flow between distant brain regions (Buzsáki 2006). These neurons have a greater influence on each other when their temporal interaction windows open simultaneously, that is, when the rhythmic synchronization within the groups is also synchronized between them (Womelsdorf et al. 2007). When the strength of such a neuronal interaction is dynamically modulated, it is referred to as gain modulation of neuronal connections (Salinas and Thier 2000). It has been proposed that the synchronization of high-frequency bands determines this neuronal interaction strength (Fries 2005). In the motor system, synchronized beta-band activity of spinal neurons during isometric contraction modulates the efficacy of synaptic input into this neuronal group along the rhythm cycle (van Elswijk et al. 2010). This spinal phase-dependent gain modulation revealed 1 peak of corticospinal excitability (CSE) per oscillatory cycle; minimum CSE occurred with a 180° phase shift. However, no response modulation was found in phase with the intrinsic oscillatory rhythm of the motor cortex. This was unexpected since the neuronal input in this study was mediated via transcranial magnetic stimulation (TMS) to the primary motor cortex (M1). Another study, performed during mild tonic contraction to keep the hand still, reported a phase-dependent CSE modulation in the oscillatory beta-band of both cortical and spinal activity (Keil et al. 2014). Surprisingly, however, this work described 2 CSE maxima in 1 cycle with a 180° phase shift, that is, at both the peak and trough of the same oscillatory cycle. This contradicts the observations of van Elswijk and colleagues (2010) at spinal level and the known alternations of hyper- and depolarization within 1 beta oscillatory cycle (Baker 2007; Fries et al. 2007; Lacey et al. 2014).

In a parallel line of research, where M1 rhythmic activity was artificially modulated, the findings were different. Specifically, when rhythmic activity in the beta-band was exogenously imposed on M1 by electrical (Pogosyan et al. 2009) or magnetic stimulation (Romei et al. 2016), corticomuscular coherence (CMC) increased in the stimulation frequency. Importantly, the entrainment effects depended on the precision with which the input was synchronized to the intrinsic cortical beta-rhythm (Romei et al. 2016). The technique of combining alternating current stimulation in the beta frequency band with concurrently applied and temporally targeted single-pulse TMS (Guerra et al. 2016; Nakazono et al. 2016; Raco et al. 2016) made it possible to detect the phase- and frequency-dependent characteristics of the different interneuronal populations in M1 (Guerra et al. 2016). Notably, these studies were performed when the subjects were at rest, thereby avoiding task-related modulations that might have altered the oscillatory characteristics of cortical interneuronal populations (Murthy and Fetz 1996). However, conclusive evidence as to whether the intrinsic oscillations of the motor cortex entail a similar phase-specific response modulation independent of exogenously imposed rhythms is still lacking.

When searching for a phase-specific response modulation of M1 independent of exogenously imposed rhythms, task-related changes of interneuronal oscillatory characteristics are to be avoided, that is, the study should be conducted at rest. Furthermore, to target distinct neuronal circuitries, the corticospinal pathway needs to be activated with different TMS intensities (Devanne et al. 1997; Di Lazzaro et al. 1998, 2001; Ziemann and Rothwell 2000; Garry and Thomson 2009). Moreover, a recent study confirmed earlier suggestions (Kiers et al. 1993; Devanne et al. 1997; Capaday et al. 1999) that the variability of motor-evoked potentials (MEPs) at rest was inversely related to the stimulation intensity and described by a logarithmic fit (Klein-Fluegge et al. 2013). This finding, in turn, may imply that a potential phase- and frequency-dependent gain modulation of intrinsic oscillations can be detected by applying near-threshold TMS intensities when maximizing the response variability.

In the light of these considerations, the present study provides novel evidence for frequency- and phase-specific gain modulation along the beta-rhythm cycle at both cortical and spinal level, independent of the spontaneous oscillatory power fluctuations at each level. Increased neuronal responsiveness occurred once per oscillatory cycle and was mediated by spectrally and spatially distinct neuronal networks.

Material and Method

Experimental Design

Subjects

Sixty-one healthy, right-handed subjects (mean age, 24.32 ± 3.4 years, range 18–36 years, 38 female), with no contraindications to TMS (Rossi et al. 2009) and no history of a psychiatric or neurological disease, were recruited for this study. Edinburgh handedness inventory (Oldfield 1971) was used to confirm right-handedness. All subjects gave their written informed consent before participation in the study, which had been approved by the ethics committee of the Medical Faculty of the University of Tuebingen. This study conformed to the standards set by the latest version of the Declaration of Helsinki. Data acquisition was performed as recently described by our group and is cited here when performed in the same way (Royter and Gharabaghi 2016; Kraus, Naros, Bauer, Khademi et al. 2016):

Data Acquisition

Electromyography (EMG) / electroencephalography (EEG) data were recorded at a sampling rate of 5 kHz after band-pass filtering (using an antialiasing filter) with cutoff frequencies at 0.16 Hz and 1 kHz. In a next step, data were downsampled to 1.1 kHz by the BrainAmp Amplifier (Royter and Gharabaghi 2016; Kraus, Naros, Bauer, Khademi et al. 2016). The high-pass filter was first-order (6 dB/Octave), and the low-pass filter was fifth-order Butterworth (30 dB/Octave). Ag/AgCI AmbuNeuroline 720 wet gel surface electrodes (Ambu GmbH, Bad Nauheim, Germany) were used to record EMG activity from the left Extensor Carpi Radialis (ECR) muscle. Two electrodes were placed 2 cm apart from each other on the muscle belly. Even though EMG does not exclusively reflect spinal activity, we refer to the corresponding findings as “at the spinal level” to remain consistent with previous work on the same topic (van Elswijk et al. 2010; Keil et al. 2014).

Ag/AgCl electrodes (BrainCap for TMS, Brain Products GmbH, Gilching, Germany) were used to record electroencephalography (EEG) at 64 channels (Fp1, Fp2, AF7, AF3, AF4, AF8, F7, F5, F3, F1, Fz, F2, F4, F6, F8, FT9, FT7, FC5, FC3, FC1, FCz, FC2, FC4, FC6, FT8, FT10, T7, C5, C3, C1, Cz, C2, C4, C6, T8, TP9, TP7, CP5, CP3, CP1, CPz, CP2, CP4, CP6, TP8, TP10, P7, P5, P3, P1, Pz, P2, P4, P6, P8, PO7, PO3, POz, PO4, PO8, O1, Oz, O2, and Iz with FCz as reference).Impedances at all electrodes were kept below 10 kΩ. Ambient noise was reduced and the decrease of 50 Hz line noise was verified online (Royter and Gharabaghi 2016; Kraus, Naros, Bauer, Khademi et al. 2016).

TMS Protocol

We used a TMS stimulator (MagPro-R30+MagOption, MagVenture, Willich, Germany) with a biphasic current waveform connected to a figure-8 MCF-B70coil (97 mm outer diameter, Mathew et al. 2016). Coil navigation was based on frameless stereotaxy (TMS Navigator, Localite GmbH, SanktAugustin, Germany) with a standard MNI dataset (MNI ICBM152 non-linear symmetric T1 Average Brain). Subjects sat relaxed in a reclining chair throughout the TMS measurements.

Hotspot detection

The TMS hotspot of their left forearm muscles was determined in the right hemisphere according to the following procedure. Stimulation was initiated over C4 with a coil orientation perpendicular to the scalp and in the posterior-anterior direction with a stimulation intensity of 40% of the maximum stimulator output (MSO). Stimulation was manually triggered, and the coil was moved gradually around the initial position (Kraus and Gharabaghi 2015, 2016). If the search did not elicit any discernable MEP, the intensity was increased in 5% steps, and the search was repeated. Once a candidate location, that is, the region that resulted in the largest MEP amplitude was detected, we step-wise decreased the stimulator intensity to focus on the hotspot area (Kraus and Gharabaghi 2015; Raco et al. 2017). We then determined the resting motor threshold (RMT) using the relative frequency method, that is, by detecting the minimum stimulus intensity (in steps of 2% of MSO) that resulted in MEPs > 50 μV in the peak-to-peak amplitude in at least 5 out of 10 consecutive trials (Groppa et al. 2012).

Stimulation intensities

Earlier research suggested that phase-dependency of TMS effects might be found for specific TMS intensities only (Raco et al. 2017). Our study design therefore assessed different TMS intensities. To avoid a bias due to day-to-day variability, we examined several intensities within 1 session. Considering that cumulative effects have been described already after 200 single TMS pulses (Pellicciari et al. 2016), we restricted the number of stimuli per intensity to avoid carry-over effects. We chose to minimize the absolute number of pulses applied, while still covering a broad range of different stimulation intensities. The experiment consisted therefore of 1 session with 8 blocks. Within each block, 10 TMS pulses were applied at 90%, 100%, 110%, 120%, 130%, 140%, 145%, and 150% RMT (Fig. 1A). The blocks were obtained in systematic order starting with the lowest TMS intensity. There was a ~1 min break between blocks. In all, 80 stimuli were applied during ~10 min for each subject (Royter and Gharabaghi 2016). Due to this relatively small number of stimuli per condition, pooling data was mandatory to enable us to compare the effects of different intensities. Potential issues with regard to pooling data are addressed in the statistics section (see below).

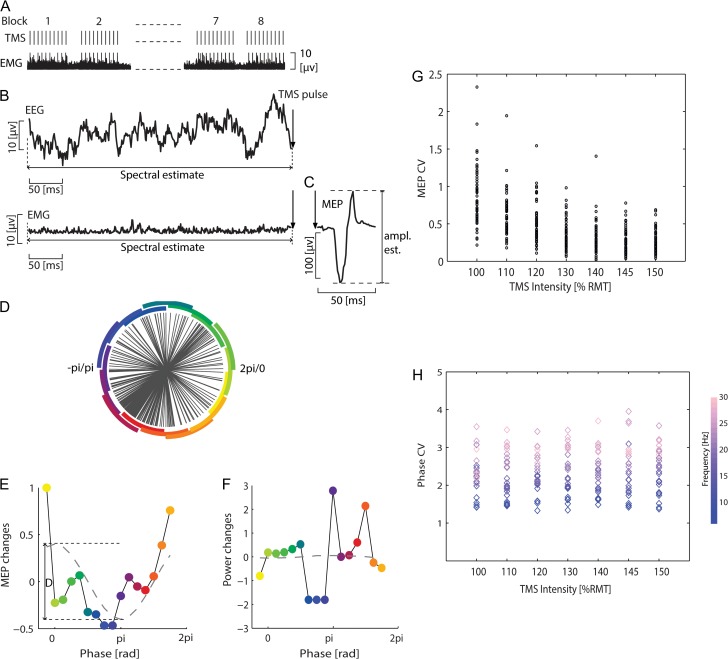
Figure 1.

Experimental design, example data of pre-TMS oscillatory activity (EEG/EMG) and MEP. (A) Experiment consisted of 8 blocks; 10 TMS pulses were applied within each block, with intervals of ~2 s between consecutive pulses, and ~ 1 min breaks between blocks. (B) Example of pre-TMS EEG/EMG signals. (C) Response was quantified by the peak-to-peak amplitude of the TMS-evoked motor potential (MEP). (D) Group data of the distribution of the phase after Fourier decomposition of the EEG (C4 channel, 17 Hz; near-threshold intensity). Circle segments illustrate the phase binning, and the colors signify phase in the same way as in E and F. (E) Mean peak-to-peak MEP amplitudes as a function of the pre-TMS phase of the EEG. The dashed line is a least-squares fitted cosine function. The MEP (as a function of phase) modulation was quantified by the fitted cosine function called modulation depth (denoted by the symbol D). (F) Same as (E) but for average EEG power. (G) Coefficient of variation of the MEP amplitude (y-axis) was estimated for each subject (represented by a circle) and intensity (x-axis). (H) Same as G but for EEG phase; each diamond represents 1 frequency (between 6 to 30 Hz).

Data Analysis

EEG/EMG analysis was performed as described by van Elswijk and colleagues (2010) and is cited here when performed in the same way:

Electrophysiological Signal Preprocessing

Data were analyzed offline using custom-written code and FieldTrip (Oostenveld et al. 2011) in MATLAB (The MathWorks, Inc., Natick, MA, United States). The analysis of EEG/ EMG phase and power was performed as described by vvan Elswijk and colleagues (2010). We were interested in the frequency range 6–30 Hz, resolved in steps of 1 Hz for all electrophysiological analyses (i.e., EMG, EEG and CMC estimation). Description and justification of the selected analyses are specified in the following paragraphs.

Preprocessing

The raw EEG and EMG signals were cut into epochs of ±1 s around the TMS pulse and linearly detrended. The signal from 5 ms before to 15 ms after the TMS pulse was blanked to remove the stimulation artifact. We subsequently rejected trials based on visual inspection (eye movement, eye blinking, and muscle artifacts), and excluded trials with MEP < 50μV.Including artifact rejection, this yielded an average of 348 ± 119 (SD) artifact-free trials per TMS intensity across all subjects (an average of 6 ± 3 trials per subject). Since most of the trials from the stimulation block at 90% RMT had to be rejected due to MEP < 50μV removal, this block was not used for further analysis. To confirm the findings for the 100% RMT condition above the threshold of 50 μV, we adapted our approach and evaluated MEPs above the thresholds of 40 μV, 30 μV, and 20 μV, respectively, as well. The pre-TMS EMG was subsequently rectified to estimate the EMG amplitude.

Assessing MEP amplitude

The post-TMS EMG signal was required for determining the MEP amplitude (van Elswijk et al. 2010) and was not rectified. We estimated the MEP amplitude using the peak-to-peak amplitude, that is, the difference between the lowest and highest value within 15–60 ms following the TMS pulse (Fig. 1C).

Assessing pre-TMS EEG/EMG power

The power spectrum was estimated using Fourier transformation with zero-padding. Epochs were given a length of 360 ms before the TMS onset (5 ms before the onset of the TMS artifact) to ensure that they included at least 2 cycles of the respective frequency between 6–30 Hz. In detail, we chose a fixed time (Gross et al. 2013) window with sufficient window length to cover 2 cycles of the minimum frequency of interest (i.e., 6 Hz). In our setup, which had a sampling rate of 1100 Hz, this required a minimum of 367 samples. We therefore selected 400 samples, that is, 360 ms, for our analysis. We chose this time window instead of a longer one (e.g., 1000 ms) to capture the effect of EEG oscillations close to the onset of the TMS pulse on the subsequent MEP.

Assessing pre-TMS EEG/EMG phase

The phase of the EEG/EMG rhythm was estimated in 1 Hz intervals preceding the TMS pulse for all frequencies between 6 and 30 Hz. Epochs had a length of 2 cycles at the respective frequency and ended prior to the TMS artifact. They were Fourier transformed to determine the phase at the respective frequency (van Elswijk et al. 2010).

Normalization before pooling

Since EEG/EMG power may differ across subjects, the absolute values of the latter cannot be directly compared. Normalization is thus necessary prior to group analysis. We therefore normalized the pre-TMS EEG/EMG power and MEP amplitude for each subject individually before group analysis. The MEP amplitude (and pre-TMS power accordingly)of each epoch was normalized for each subject with respect to the maximum MEP amplitude (power)across all epochs. We thereby acquired a relative measure of the maximum and minimum MEP amplitude and the corresponding pre-TMS EEG/EMG power. For the subsequent analysis of this study we quantified the effect of pre-TMS phase and power on the peak-to-peak MEP amplitude. The phase values were pooled without normalization across subjects, since the phase progression of a sinusoidal oscillator at a specific frequency is subject-independent with values ranging between −π and +π.

Assessing the Relationship Between Pre-TMS EEG/EMG Phase and Post-TMS MEP Amplitude

Phase binning EEG/EMG

In accordance with the procedure of van Elswijk and colleagues (2010), a frequency-wise estimation of the pre-TMS EEG/EMG phase was used to bin the epochs. Specifically, we defined 16 phase bins on the unit circle, with centers equally spaced between −π and +π. For the binning procedure, we assigned the epochs in which the pre-TMS EEG/EMG phases were closest to the center phase of the bin. The MEP amplitudes were averaged for each group of bins to obtain the mean MEP amplitude. In addition, the pre-TMS EEG/EMG phase was averaged for each group of bins. This approach resulted in an average of 22 trials per phase bin and provided us with 16 pairs (1 per phase bin) of pre-TMS EEG/EMG phase and MEP amplitude per frequency.

Evaluation of phase binning

To ensure that the binned phases resembled sufficiently a uniform distribution, and to ensure that there was no difference in this distribution across intensities and frequencies, we calculated the coefficient of variation (CV) on the distance between nearest phase epochs. In general, the CV is not suitable for circular data because it would remain constant in the case of uniform as well as clustered data. We calculated, however, the CV of the differences between adjacent samples. With this approach, the CV increases towards infinity if phases are clustered and remains constant if phases are uniformly distributed. CV thereby allowed assessing the degree of uniformity on the unit circle for each frequency and TMS intensity (Fig. 1D). CV between stimulation intensities were tested with a 1-way ANOVA.

Despite normalization, averaging MEP amplitudes within bins may cause the variance across bins to differ between intensities and frequencies, resulting in a bias of the subsequent analysis of modulation. Specifically, a high variance may bias towards high modulation even if no modulation was present. Therefore, an F-test was performed to test whether MEP amplitude variance had an influence on the results. MEP amplitude variance across phase bins did not differ significantly with regard to stimulation intensity and EEG/EMG frequency. The minimum and maximum P-values for the corresponding analysis were 0.07 and 1, respectively. In line with this, the minimum and maximum F-statistic values were 0.32 and 3.15, respectively. Furthermore, the MEP amplitude was divided by its SD, which was estimated by a jackknife procedure (Efron and Tibshirani 1993; van Elswijk et al. 2010).

Cosine fitting

To quantify the relationship between the pre-TMS EEG/EMG phase and MEP amplitude, a cosine (least-squares) function was fitted to the MEP amplitudes as a function of the EEG/EMG phases (van Elswijk et al. 2010). Subsequently, we measured the magnitude of the cosine by estimating the difference between its minimum and maximum. This measure indicates the strength of phase-dependent modulation. We estimated the goodness of fit with a non-linear fitting model (NonLinearModel.fit function available in Matlab) by comparing the fitted model versus zero model.

In case of no relationship between phase and amplitude, the distribution of amplitudes over phases would be uniform, resembling a flat line with zero magnitude. With increasing modulation, the amplitudes would vary over phase. Since even noise would increase variance, only a variation resembling a cosine would indicate the modulation to be phase-dependent. In that regard, the magnitude of a cosine fit can be considered a direct measure of phase-dependent modulation.

Assessing the Relationship Between Pre-TMS EEG/EMG Power and Post-TMS MEP Amplitude

Previous work indicates that the MEP amplitude correlates positively with EMG activity (Di Lazzaro et al. 1998; Mitchell et al. 2007) and inversely with sensorimotor rhythms in the EEG (Takemi et al. 2013; Schulz et al. 2014). We therefore also computed the linear relationship between pre-TMS EEG/EMG power and MEP amplitude to estimate frequency wise the Spearman’s rank correlation coefficient between the pre-TMS EEG/EMG power and MEP amplitude for each EEG and EMG channel.

Since EEG power might influence the estimate of EEG phase, we averaged the power for each phase bin, and performed a cosine fit, as described above. When EEG phase and power were confounded, we would expect a cosine-shaped fitting curve (with the phase-lag of π) for their relationship. Absence of such a cosine modulation, however, would indicate power and phase to be independent predictors of MEP amplitude.

Assessing the Pre-TMS EEG and EMG Coherence

We investigated the synchronous oscillatory activity between the signal of the brain and the forearm muscle by analyzing the corticomuscular coherence (CMC).The epochs used for pre-TMS power estimation (i.e., 360 ms time window before TMS artifact, see above) were also used to assess the CMC between EEG and EMG. We calculated the CMC by estimating the cross-spectral density matrix per frequency between EEG channels and EMG channels (Schulz et al. 2014). The cross-spectral density matrix was calculated frequency wise by the multi-taper method (5 tapers) and normalized by the magnitudes of the summed cross-spectral density matrix for each frequency by the corresponding power values at that frequency (Schulz et al. 2014). This approach leads to values between 0 and 1, with 0 indicating no coherence and 1 indicating maximum coherence of the signals.

Assessing the Relationship of Pre-TMS CMC and MEP Amplitude

To investigate the influence of the pre-TMS CMC on the MEP amplitude, we used the 16 bins described earlier in the methods section. We then estimated the CMC for each bin. The magnitude of the coherence is a function of the sample size (Maris et al. 2007), which can induce a bias. Normalization can account for the difference in sample sizes. We therefore transformed the CMC values to z-values in each bin. This entailed using the number of degrees of freedom (d.f.) of the sample coherence. When CMC values were above 0.4 and the d.f. greater than 20, the latter represented the variance of the sample coherence and the CMC values could then be transformed to z-values (Enochson and Goodman 1965; Maris et al. 2007). When the CMC values were below 0.4, we used d.f. as the standard deviation. This led to a z-value transformation and coherence statistics comparable to the method proposed by Rosenberg and colleagues (1989). We used the following transformation:

$$Z\left(f\right)=\frac{{\tanh }^{-1}\left(C\left(f\right)\right)-{\left(2/\left(d.f.-2\right)\right)}^2}{\left(2/\left(d.f.-2\right)\right)},$$

where C(f) is the coherence at the frequency f and d.f. the degrees of freedom. A non-parametric test (Maris et al. 2007) was then used to test the linear relation between CMC and MEP. The average of the z-values from the EEG channels of interest was estimated, yielding 1 z-value for each group of bins. The average of the peak-to-peak MEP amplitude of each group of bins was now used as the MEP amplitude for correlation with the corresponding bin. This procedure resulted in16 pairs of bias-corrected CMC and MEP amplitudes.

Statistical Analysis

Pooling

Pooling data from different subjects was mandatory in our study design. This approach may, however, introduce a bias by single subjects and inflate the degrees of freedom. To reduce these pooling issues, we applied the following precautions. First, we investigated a fairly large cohort of more than 60 subjects to reduce the relative contribution of single individuals. Second, all measures that could introduce a subject-dependent bias (e.g., power and MEP amplitudes) were normalized within subjects. Third, we used a stricter than usual alpha-threshold of 0.01, which was furthermore Bonferroni-corrected, to address the possibly inflated degrees of freedom. Finally, we limited ourselves to non-parametric measures for relationships (e.g., Spearman’s rank correlation coefficient) and distribution-free statistical tests (e.g., boot-strapping, randomization) since these approaches are less sensitive to outliers, assumptions and a possible bias introduced by pooling.

Testing the Coefficient of Variation for MEP and Phase

By dividing the estimated standard deviation (SD) by the mean of the same population for each subject and TMS intensity, we calculated their coefficient of variation (CV) which we then used to assess the MEP and phase-lag variability (Klein-Fluegge et al. 2013). CV differences between stimulation intensities were tested with a 1-way ANOVA.

Testing Significance of EEG and EMG Power-dependent MEP Amplitudes

We used a Spearman’s rank correlation coefficient to assess the relationship between the pre-TMS power and MEP amplitude. To test the significance of the estimated effect, we applied the randomization approach. Our null hypothesis was that the pre-TMS power and MEP were not correlated. A cluster-based randomization test with 10 000 repetitions was therefore performed at each electrode (i.e., 1-dimensional clustering for the frequency) for multiple frequency bins by shuffling the pre-TMS EEG/EMG amplitudes (independent variable) versus MEP amplitudes (dependent variable).

Testing Significance of EEG and EMG Phase-dependent MEP Amplitudes

Our analysis showed that the relationship between pre-TMS EEG/EMG phase and MEP amplitude was cosine-shaped (Fig. 1E for the pre-TMS EEG). We therefore quantified this relationship by (least-squares) fitting a cosine function with the unconstrained phase (dashed line in Fig. 1E).The modulation depth (peak-to-peak difference) of the fitted cosine was used as an estimate of the strength of the relationship between pre-TMS EEG/EMG phase and MEP amplitude. Since the cosine was fitted with the unconstrained phases, it had an amplitude with a positive bias (van Elswijk et al. 2010). We estimated this bias by randomly shuffling (100 repetitions)pre-TMS phase (independent variable) versus MEP amplitudes (dependent variable). At each randomization, we fitted the cosine function and estimated the modulation depth. After 100 repetitions, we averaged the modulation depth. The analysis described above was performed per frequency so that, by the end of the procedure, we had 2 spectra per intensity: 1 spectrum of the effect and 1 of the bias estimate (van Elswijk et al. 2010). To determine whether the estimated effect was significantly greater than the estimated bias, we designed a randomization test by randomly shuffling the pre-TMS phases (independent variable) versus MEP amplitudes (dependent variable). The null hypothesis was that the effect spectrum was no greater than the bias spectrum (van Elswijk et al. 2010).

Cluster-based Randomization Test

For the cluster-based randomization test (see above) we calculated the test statistic (Spearman’s rank correlation coefficient for power; the modulation depth for phase) for each frequency bin and clustered adjacent frequency bins in the same set when the test statistic exceeded the threshold of P < 0.001. We then calculated the cluster-level statistics by taking the sum of the test statistics for each cluster. This led to broad frequencies clusters. The maximum of the cluster-level statistics was applied later for comparisons if multiple clusters were observed. The P-value to reject the null hypothesis was the proportion of cluster-based randomizations that resulted in larger test statistics than observed here (without randomization).

Testing Significance of Corticomuscular Coherence

For absolute CMC, the significance level was calculated according to the procedure proposed by Rosenberg and colleagues (1989):

$$C_{\alpha }^{\lim }=1-{\left(1-\alpha /100\right)}^{1/(n-1)}.$$

where α is the confidence probability and n the number of epochs in which n-1 is the d.f. In our case, d.f. was 2* number of epochs (n)* number of tapers (k) (Maris et al. 2007). We therefore calculated as follows:

$$C_{\alpha }^{\lim }=1-{\left(1-\alpha /100\right)}^{1/(2\ast n\ast k-1)}.$$

A confidence probability of α = 0.999% (P = 0.001) was chosen. The resulting confidence limit provided us with the significance level. The CMCs from the frequency bins above the significance level were considered as significant.

Testing Significant Correlation of CMC and MEP

We used a randomization test with 10 000 repetitions for the null hypothesis that the relationship between pre-TMS CMC and MEP was random. We shuffled pre-TMS CMC (independent variable) and MEP amplitude (dependent variable). At each randomization step, Spearman’s rank correlation coefficient was used to estimate the test statistics. The proportion of the randomizations test that led to larger test statistics than observed here (without randomization) was used to reject the null hypothesis.

Testing Significant Differences Between the Lower and the Upper Beta

The differences between distributions of the modulation depths in the lower and upper beta-band were estimated by using the bootstrap method (1000 repetitions). The null hypothesis was that the distributions of both lower and upper beta were not significantly different. The P-value to reject the null hypothesis was calculated after bootstrap estimation by counting the values of 1 frequency band that were greater (smaller) than the mean value of the other frequency band. We then took the mean of the 2 resulting P-values, that is, 1 P-value for each frequency band (Mooney and Duval 1993).

Results

The variability of corticospinal excitability (CSE), that is, the coefficient of variation for MEP (CV_MEP), increased with lower stimulation intensities and was at its highest at near-threshold intensity. CV_MEP increased from 0.25 ± 0.15 at 150% RMT to 0.85 ± 0.37 at 100% RMT (Fig. 1G). One-way ANOVA showed that CV_MEP differed significantly between intensities (F(6 460) = 51.49, P < 0.00001, ANOVA); the post hoc test revealed a significant difference between CV_MEP at 100% RMT and at all other stimulation intensities (t(120) = 3.76;, 110% RMT; t(120) = 5.98,; 120% RMT; t(120) = 8.88,;130% RMT; t(120) = 10.09; 140% RMT; t(120) = 11.32; 145% RMT; and t(120) = 11.66 150% RMT, unpaired t-tests, all P < 0.00001, significant for Bonferroni-corrected threshold at P = 0.0014).

The phases’ distribution on the unit circle (Fig. 1D, at the time of stimulation) did not differ significantly between the various intensities (Fig. 1H), that is, the coefficient of variation for phase (CV_phase) remained unchanged across different stimulation intensities (average CV_phaseof 2.33 ± 0.59), with no statistically significant difference of CV_phase between intensities (F(6 168) = 0.33, P = 0.92, ANOVA, Fig. 1H). Together, these findings suggest that the stimulation intensity-dependent findings were not biased by a potentially different distribution of phases at the time of stimulation. Further analysis revealed that robust predictions of CSE were possible only when stimuli were applied at near-threshold intensity (Figs. 2 and 3).

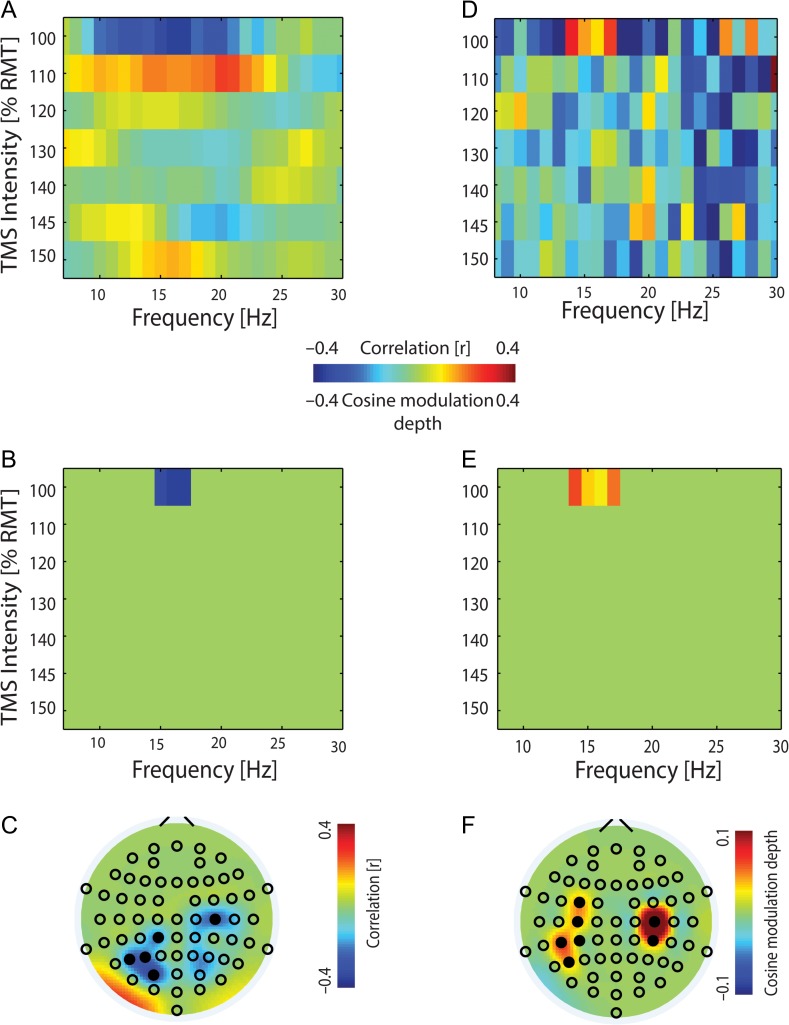
Figure 2.

Pre-TMS EEG power and phase predict corticospinal excitability (CSE). (A) Spearman’s rank correlation between pre-TMS EEG power at the site of stimulation, i.e., C4 electrode, and MEP amplitude (group data, right sensorimotor cortex was the site of stimulation). (B) Same as (A) but with statistically significant frequency bands (P ≤ 0.0001). (C) Topographical distribution of the significant frequency band (15–17 Hz) of (B) at near-threshold TMS intensity (100% RMT). (D) Modulation of MEP by pre-TMS EEG phase with the bias for the cosine-fitted function subtracted (group data). (E) Same as (D) but with significant modulation depth (P ≤ 0.001) with respect to the positive bias of the cosine fit. (F) Topographical distribution of the significant frequency band (14–17 Hz) of (E) at near-threshold TMS intensity (100% RMT).

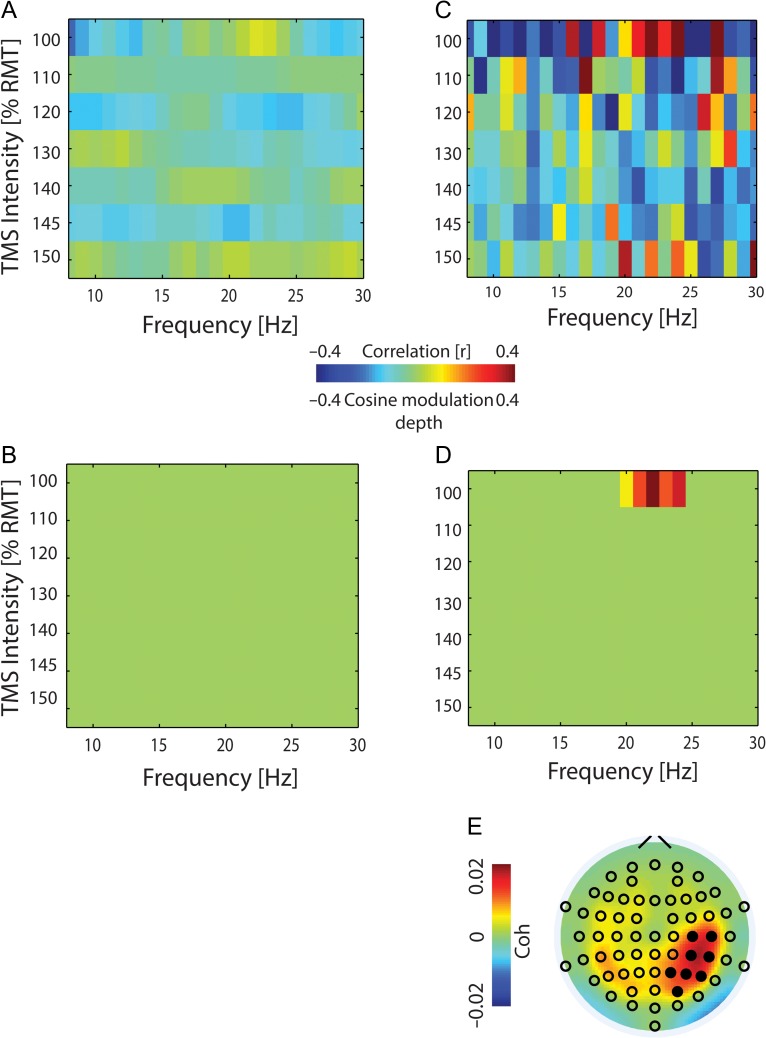
Figure 3.

Pre-TMS EMG phase (but not power) predicts CSE. (A) Spearman’s rank correlation between pre-TMS EMG power and MEP amplitude. (B) Same as (A) but with no statistically significant frequency band (P > 0.16). (C) Modulation of MEP by pre-TMS EMG phase with the bias for the cosine-fitted function subtracted (group data). (D) Same as (C) but with significant modulation depth (P ≤ 0.001). (E) The CMC topographical distribution of the significant frequency band (20–24 Hz) of (D) at near-threshold TMS intensity (100% RMT).

At the cortical level, power (15–17 Hz; P = 0.0001, randomization test (10 000 repetitions)) and phase (14–17 Hz; P = 0.001) in the lower beta-band predicted CSE in a frequency-specific way (Fig. 2B, E) and revealed a stable topographical pattern (Fig. 2C, F). This pattern showed that CSE could be predicted at the site of stimulation (C4) and in a more distributed cortical network: specifically, by the oscillatory beta phase recorded at sensors projecting to the sensorimotor cortex ipsilateral (C4, CP4) and contralateral (C3, CP3) to the site of stimulation, and at contralateral FC3, CP5 and P5 (Fig. 2F); and by the beta-power recorded at sensors projecting to the ipsilateral motor cortex (C2) and contralateral CP1, P5, P3, and PO3 (Fig. 2C).

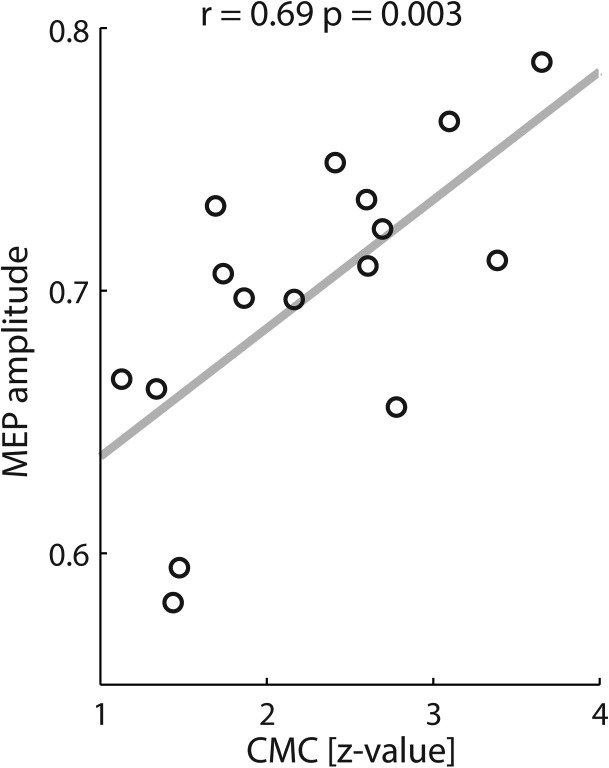
At the spinal level, CSE was predicted in a frequency-specific way by the phase in the upper beta-band (20–24 Hz, Fig. 3D; P = 0.001,), but not by power (Fig. 3B; P > 0.16,). CMC coherence in this frequency band projected to the sensorimotor (C4, C6, CP4, CP6) and parietal cortex (P2, P4, P6, PO4) in the stimulated hemisphere (Fig. 3E; d.f. = 690, P = 0.001). This pre-TMS CMC predicted post-TMS CSE (Fig. 4; r = 0.63, P = 0.0031, Spearman’s rank correlation).

Figure 4.

Pre-TMS CMC predicts CSE. Spearman’s rank correlation (r = 0.63, P = 0.0031) between CMC in the 20–24 Hz band and MEP amplitude with the regression line in gray. Each circle represents 1 phase bin.

When the bins were sorted into 16 overlapping bins (Fig. 1D) according to the beta phase immediately preceding the neuronal input (TMS pulse), and the response modulation (MEP amplitude) was determined separately for each phase bin (Fig. 1E), the CSE resulted in a cosine-shaped function of pre-stimulus beta phase (Fig. 1E). This pattern occurred at both the cortical (EEG) and spinal (EMG) level in the lower (14–17 Hz) and upper (20–24 Hz) beta-band, respectively. Specifically, CSE was at its highest when stimuli arrived at the rising phase of cortical oscillations in the lower beta-band (Fig. 5A; r-squared = 0.108; F-statistic vs. zero model: 7.87; P = 0.0066) or spinal oscillations in the upper beta-band (Fig. 5B; r-squared = 0.246; F-statistic vs. zero model; 16.30; P < 0.0001), but at its lowest when stimuli arrived at the falling phase of cortical oscillations in the lower beta-band (Fig. 5C; r-squared = 0.094; F-statistic vs. zero model: 6.76; P = 0.0115) or spinal oscillations (Fig. 5D; r-squared = 0.162; F-statistic vs. zero model; 9.66; P = 0.0031) in the upper beta-band (Fig. 5).

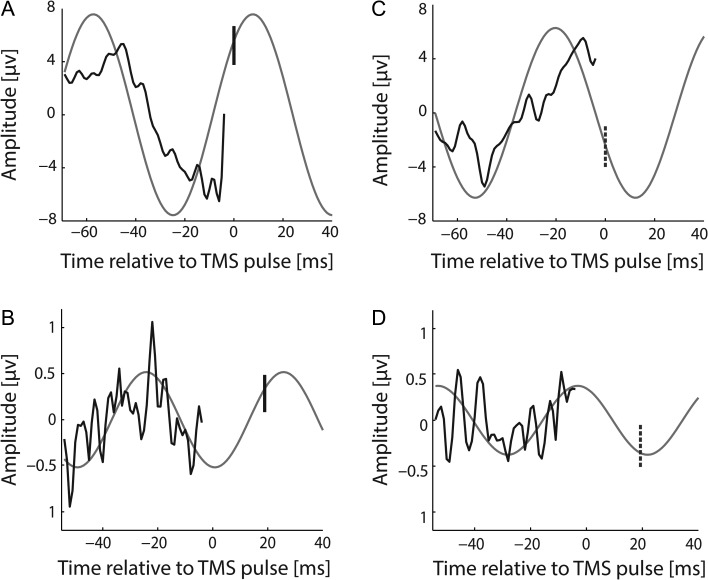
Figure 5.

Synaptic input is most effective when it arrives at the rising phase of the cortical and spinal beta-rhythm. (A) and (C) Average of the pre-TMS EEG epochs at 17 Hz preceding (A) maximum (vertical solid line) and (C) minimum (vertical dashed line) MEP amplitudes. (B) and (D) Average of the pre-TMS EMG epochs at 22 Hz preceding (B) maximum (vertical solid line) and (D) minimum (vertical dashed line) MEP amplitudes. In all figures, the light gray curve is the fitted cosine continued to the moment of TMS-induced synaptic input (vertical line) to the cortex (A) and (C) or spinal cord (B) and (D) to estimate the phase of the respective beta-rhythm.

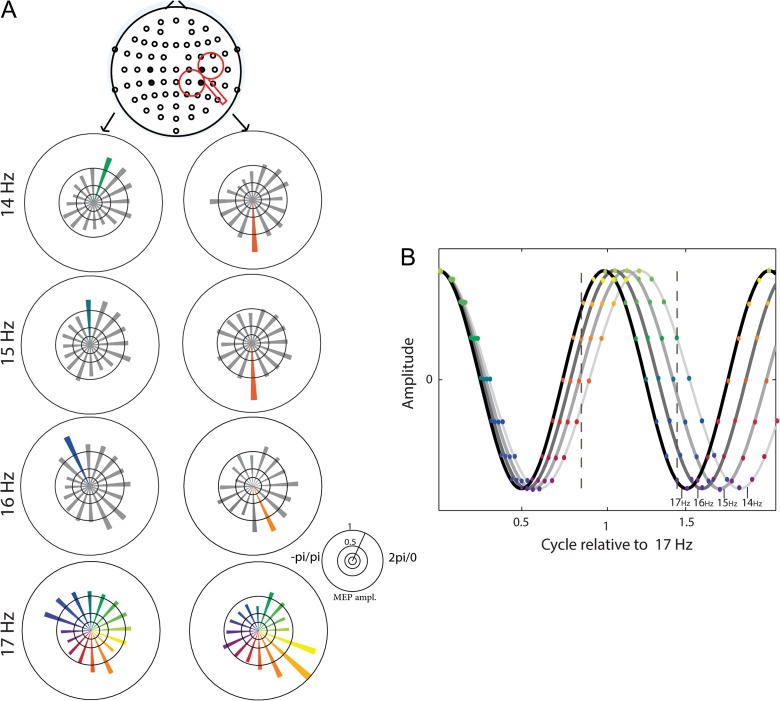
Notably, the phase of ipsilateral (C4, CP4) and contralateral (C3, CP3) sensorimotor beta-rhythms, which predicted CSE, was shifted by ~π radian (Fig. 6A). Moreover, the phase-dependent modulation of CSE was consistent across frequencies (14–17 Hz) and within each hemisphere, that is, the maximum MEP mapped onto the corresponding spot in the rising phase of the oscillatory cycle for each of the frequencies that predicted CSE (Fig. 6A). Furthermore, the phase-dependent modulation of CSE remained stable during modification of the threshold of included MEPs (Fig. 7).

Figure 6.

The phase bin preceding maximum MEP amplitude was shifted by ~π radian between the left and right hemisphere. (A) Peak-to-peak amplitudes of MEPs (group data) as a function of the pre-TMS phase of the EEG for C3 and CP3 (left) and C4 and CP4 (right). (B) Simulation of the phase-lag from 14 Hz to 17 Hz oscillations starting with a zero phase-lag. The color-coded dots represent the phases according to (A). The spot of maximal MEP (vertical dashed lines) moves along the oscillatory cycle with increasing frequency, for the stimulated (left dashed line) and not stimulated (right dashed line) hemispheres, respectively.

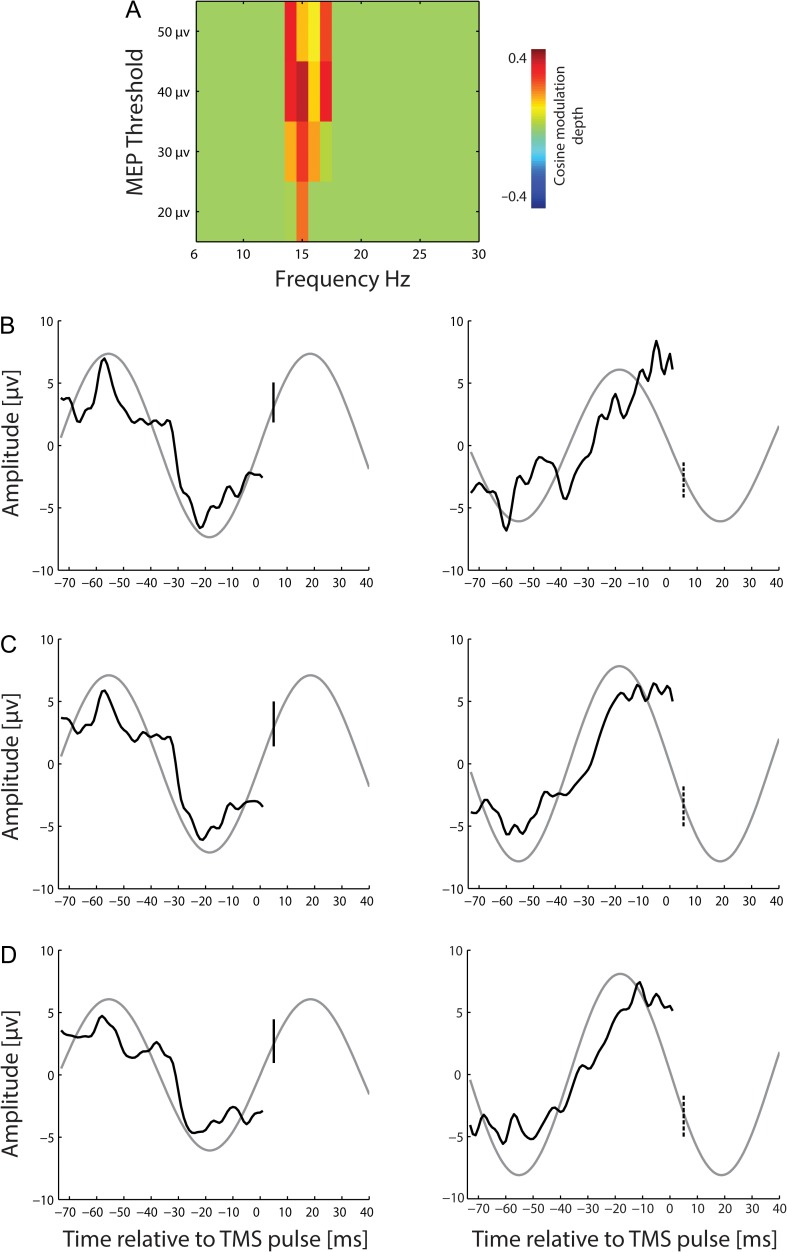
Figure 7.

Pre-TMS EEG phase predicts corticospinal excitability for different MEP thresholds. (A) Modulation of MEP by pre-TMS EEG phase (with significant modulation depth (P ≤ 0.001) with respect to the positive bias of the cosine fit) for different MEP thresholds, i.e., 50 μV, 40 μV, 30 μV, and 20 μV. (B–D) Average of the pre-TMS EEG (at 15 Hz) preceding the maximum (left; solid line) and minimum (right; dashed line) MEP amplitude at different MEP thresholds, respectively. A light gray curve is the fitted cosine continued to the time of TMS-induced synaptic input (vertical line) to the cortex.

Importantly, the phase-dependent CSE modulation at the cortical and spinal level was not confounded by the respective power fluctuation in the EEG and EMG. Specifically, EMG power did not predict CSE at all, whereas EEG power showed a significant inverse correlation with CSE in frequency bins (15–17 Hz) that overlapped with those showing the phase-dependent modulation (14–17 Hz). Pre-TMS phases preceding “high” MEPs might, therefore, be confounded by “low” beta-power which preceded “high” MEPs as well, and vice versa. However, a cosine fitting to the average power of each of the 16 bins that led to the cosine-shaped function of pre-stimulus beta phase resulted in a flat curve (Fig. 1F, dashed line), that is, the phase modulation of CSE was not confounded by power fluctuations in the same frequency band.

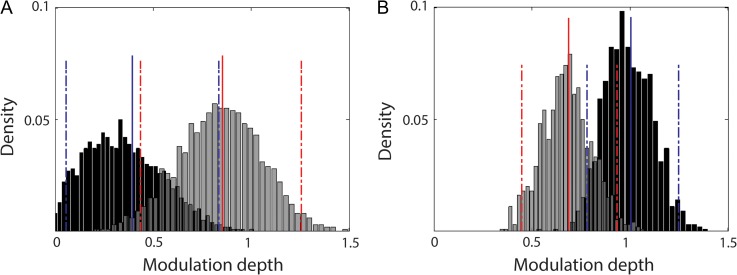
Histograms of the distribution of modulation depths for 14–17 Hz and 20–24 indicate significant differences between the lower and the upper beta frequency band at both cortical (P = 0.008) and spinal (P = 0.005) levels. Specifically, the phase-dependency of MEP amplitudes was more prominent at cortical and spinal levels for 14–17 Hz and 20–24 Hz activities, respectively (Fig. 8).

Figure 8.

Frequency-specific differences of cortical and spinal modulation depths. Estimation of the modulation depth (x-axis) of 14–17 Hz (gray color) and 20–24 Hz activities (black color) and the relative frequency of occurrence (y-axis) for both EEG (A) and EMG (B) signals by using the boot-strapping method (1000 repetitions). In the histograms, solid and dashed lines represent the mean of the respective distributions and the lower/upper limits of the confidence intervals (estimated according to the 95% percentile method), respectively.

Discussion

This study has demonstrated that the intrinsic beta-rhythm of the motor cortex entails rhythmical gain changes. This frequency- and phase-specific response modulation, mediated by spectrally and spatially distinct neuronal networks, occurred independent of spontaneous oscillatory power fluctuations at cortical and spinal levels.

Methodological Consideration

That rhythmic activity can be recorded in the EEG and EMG (sufficient for stereotyped phase patterns to be determined) implies that there is some degree of rhythmic synchronization in the underlying neuronal populations. The underlying neuronal population must therefore be engaged in a weak (mostly subthreshold) set of alternating up and down states. For this to then influence the response to probe stimulation, the latter must be weak, for if it is supra-threshold every-time it will trigger responses regardless of whether neurons are in relative up or down states. Therefore, the gain modulation was revealed only when stimuli were applied at near-threshold intensity, that is, at 100% RMT. This might be due to the larger variability of the evoked MEP amplitudes compared to those elicited at higher stimulation intensities (Klein-Fluegge et al. 2013) or to the activation of distinct neuronal circuitries (Di Lazzaro et al. 1998). Specifically, TMS intensities below 110% RMT induce MEPs by recruiting indirect circuits in the motor cortex, that is, the early presynaptic activation of the corticospinal pathway (Di Lazzaro et al. 2001; Garry and Thomson 2009). Alternatively, the gain modulation of intrinsic oscillations might have been detected due to the maximized response variability during the application of near-threshold TMS intensities (Fig. 1E). Since the phenomenon of gain modulation at near-threshold stimulation intensities was observed at both cortical (Fig. 2E) and spinal (Fig. 3D) level, the latter explanation appears more plausible in the light of the findings of the present study. The various stimulation intensities were, however, examined in a predefined order in this study, that is, incrementally increasing the TMS intensity from block to block. This might have prevented us from detecting gain modulation at higher TMS intensities, that is, in later blocks within 1 session, since even these single TMS pulses can induce a systematic modulation of corticospinal excitability over time (Pellicciari et al. 2016). To minimize undesirable order effects, future studies investigating the influence of stimulation intensity on corticospinal gain modulation should therefore examine different intensities in a randomized order.

Power-related Gain Modulation

At the cortical and spinal level, spontaneous oscillatory power fluctuations played a different role in predicting CSE in this study. Specifically, EMG power did not predict CSE, which might be most parsimoniously explained by the fact that the experiment was performed in resting state. Albeit the observation that beta corticomuscular coherence could predict CSE may appear surprising in this context, Romei and colleagues (2016) recently proposed that, even while at rest, low-level tonic firing from spontaneous spiking in spinal motor neurons (Blankenship and Kuno 1968) may occur in some motor units. Corticomuscular beta coherence could then ensue from increased temporal structuring at beta frequencies of this spontaneous spiking activity (Romei et al. 2016). This work provides evidence that such a “temporal structuring” occurs along the rhythm cycle of synchronized beta activity of spinal neurons even in the resting state, that is, without overt movement.

Unlike the EMG power, the EEG power in the lower beta-band (15–17 Hz) predicted CSE even at rest. This was not surprising, given that sensorimotor oscillations are modulated by thalamo-cortical and cortico-cortical interactions (Thut and Miniussi 2009; Jensen and Mazaheri 2010) and reflect the current brain state (Salinas and Thier 2000; Chance et al. 2002), that is, high and low oscillatory power indicate the inhibitory and excitatory state, respectively. Intrinsic fluctuations of oscillatory activity may thus determine the brain’s responsiveness to external stimuli and at least partly account for the variability of CSE in this study.

The state of the motor system, that is, rest or movement, and the influence of concurrent muscle activity might be responsible for the ambiguous results of previous studies on the oscillatory power-related gain modulation of the sensorimotor cortex. In particular, studies in which single TMS pulses were applied during rest revealed an inverse correlation between CSE and pre-stimulus power. There was, however, some ambiguity with regard to the frequency bands and cortical sites involved, that is, ipsilateral sensorimotor cortex for the alpha- (Zarkowski et al. 2006; Sauseng et al. 2009) or beta-band (Lepage et al. 2008; Mäki and Ilmoniemi 2010), and the posterior parietal cortex contralateral to the stimulation site in the beta-band (Keil et al. 2014). These diverse findings are probably related to the large variability of spontaneous oscillatory activity in the human sensorimotor cortex captured in relatively small sample sizes. Notably, studies that applied the same stimulation during movement tasks showed a correlation of the CSE with the pre-stimulus EMG activity in the beta-band (Mitchell et al. 2007; van Elswijk et al. 2010) or the corticomuscular coherence in the alpha-band (Schulz et al. 2014) but not with the oscillatory power in stimulated sensorimotor cortex (Mitchell et al. 2007; van Elswijk et al. 2010). When the CSE correlated with cortical power, it tended to be located in a more distant fronto-parietal beta-network (Schulz et al. 2014). This ambiguity is probably related to the respective task designs, that is, isometric contraction (Mitchell et al. 2007; van Elswijk et al. 2010) versus post-movement beta-rebound (Schulz et al. 2014). Specifically, the task-related periods of increased cortical beta-power, that is, reduced cortical excitability, were paralleled by elevated EMG power in the alpha- and beta-band during the isometric contraction task (Kilner et al. 2000), which, in turn, correlated significantly with CSE. This suggests a more complex interaction between the oscillatory state of the peripheral and central motor system with respect to the stimulation-induced MEP, that is, between the EMG activity immediately before the stimulus and the cortical excitability at the moment of stimulation (Mitchell et al. 2007).

In the present work, we reduced this complexity by studying the cortical gain modulation at rest by minimizing confounding EMG activity and by avoiding task-related modulations that can alter the oscillatory characteristics of cortical interneuronal populations (Murthy and Fetz 1996). Furthermore, the robustness of the findings was ensured by the statistical approach chosen—the application of a randomization test with 10 000 repetitions to the frequency spectrum between 6 and 30 Hz in a rather large group of subjects.

Moreover, the spectrum and topography of the beta-power, which correlated inversely with CSE, overlapped at least partially with the spectrum and topography of the phase-dependent modulation (see below), thereby underlining the consistency of the findings. Importantly, both power- and phase-dependency of CSE in the present study converged at the M1 site of stimulation (i.e., at the C4 sensor), while previous studies showed rather distributed cortical patterns (Keil et al. 2014; Schulz et al. 2014).

Phase-related Gain Modulation

Previous discrepancies with regard to the CSE phase-dependency might be related to methodological differences of data processing and phase estimation, for example, broad-band filtering with Fast Fourier Transform (van Elswijk et al. 2010) versus narrow-band filtering with Hilbert Transform (Keil et al. 2014). In particular, Keil and colleagues (2014) did not show a phase-dependency along the beta oscillatory cycle, whereas van Elswijk and colleagues (2010) fitted a cosine function to the MEP amplitudes. Instead, Keil and colleagues (2014) estimated an angular-linear correlation which showed 2 MEP peaks within 1 cycle for the very same 18 Hz frequency for which van Elswijk et al. (2010) had already demonstrated 1 MEP peak.

In the present work, we applied the data analysis proposed by van Elswijk and colleagues (2010), but removed the task-related muscle activity following the observations in the study of Keil and colleagues (2014). By fitting a cosine function to the MEP amplitudes, we observed a frequency-specific response modulation in-phase with the intrinsic oscillatory rhythm, that is, along the beta-rhythm cycle at both the cortical and spinal level. At the cortical level, the phase in the lower (14–17 Hz) beta-band predicted CSE (Fig. 2E). At the spinal level, CSE was predicted by the phase in the upper (20–24 Hz) beta-band (Fig. 3D). CMC coherence in this latter frequency band also predicted the post-TMS amplitude (Fig. 4). The phenomenon of CMC is predicated on coupled phase effects at similar frequencies. We indeed detected CMC peaks in both the lower and the upper beta-band. However, only the later CMC peak (i.e., 20–24 Hz) correlated significantly with the MEP amplitude. We speculate this difference between the cortical and CMC phase at 14–17 Hz—that is, with regard to correlation with the MEP amplitude—to be related to attenuation of lower frequencies by recurrent inhibition from spinal Renshaw cells (Williams et al. 2010). In line with this interpretation, a direct comparison between 14–17 Hz and 20–24 Hz activities revealed the phase-dependency of MEP amplitudes to be more prominent at cortical and spinal levels, respectively (Fig. 8).

Notably, CSE was highest when stimuli arrived at the rising phase of cortical or spinal beta oscillations (Fig. 6), thereby reflecting the responsiveness of the respective neuronal pools to a synaptic input. This was already known to be the case for spinal beta-rhythms during movement (van Elswijk et al. 2010) and has now been extended to the resting state and the cortical level, suggesting a more general mechanism. This phase-dependent input gain is therefore probably attributable to the rhythmic inhibition after population spikes, depending systematically on the delay from the last population spike (Burchell et al. 1998; van Elswijk et al. 2010).

Distinct Beta-band Oscillatory Circuits

Such frequency-specific findings suggest a response modulation of CSE in 2 distinct neuronal circuitries: a cortical oscillatory circuit in the lower, and a corticospinal circuit in the upper beta-band. These 2 networks could also be distinguished on the basis of their topographical patterns. While the cortical network was characterized by a bilateral topography of homologous sensorimotor sensors (Fig. 2F), the corticospinal connectivity projected to a broader unilateral area of the sensorimotor and parietal cortex in the stimulated hemisphere (Fig. 3E).

Accordingly, previous pharmacological studies functionally dissociated the power of cortical beta oscillations (Baker and Baker 2003) from the magnitude of corticomuscular beta coherence (Riddle et al. 2004). Specifically, carbamazepine was shown to significantly increase beta CMC without affecting the power or frequency of cortical oscillations (Riddle et al. 2004). The same group also showed that diazepam could double the power of cortical beta oscillations without altering the magnitude of CMC (Baker and Baker 2003). Our work complements these findings by proposing that the effective information flow within these distinct beta circuits is mediated in a frequency- and phase-dependent way.

The network showing a significant inverse correlation of beta-power (15–17 Hz) with CSE overlapped at least partly with the spectrum (14–17 Hz) and topography (specifically at the C4 sensor, i.e., at the site of stimulation) of the network revealing a phase-dependent modulation. This suggests that different motor system circuits converge (Fig. 2) prior to signal propagation to downstream spinal motor neurons. Importantly, however, the phase modulation of CSE was not confounded by power fluctuations in the same frequency band (Fig. 1F).

We acknowledge, however, that our approach of investigating state-dependency across 16 phase bins and different stimulation intensities necessitated each subject to contribute rather few trials. The statistical evaluation was therefore directly performed on data compiled from all subjects, and not on data derived in individual subjects and then averaged before group analysis. This means that the degrees of freedom were potentially higher than with more standard analyses. To address this limitation and ensure the robustness of our findings, we used a stricter alpha-level threshold of P < 0.01, which was further Bonferroni-corrected to P < 0.0014. Furthermore, we applied only non-parametric tests for our statistical analysis, which are less affected by the degrees of freedom (Mooney and Ducal 1993). Based on our findings, future studies will be able to investigate specific phase bins and stimulation intensities with more trials per subject than in the present study.

Conclusion

These findings provide novel evidence that intrinsic activity in the human motor cortex modulates phase- and frequency-specific input gain along the beta oscillatory cycle. In accordance with periodic alternations of synchronous hyper- and depolarization, increased neuronal responsiveness occurred once per oscillatory beta cycle. These findings may lead to novel brain state-dependent and circuit-specific interventions (Naros et al. 2016; Kraus, Naros, Bauer, Khademi et al. 2016; Kraus, Naros, Bauer, Leão et al. 2016; Kraus et al. 2018) for addressing neurorehabilitation of motor function after stroke (Belardinelli et al. 2017; Naros and Gharabaghi 2017).

Authors’ Contributions

A.G. designed research; V.R. performed research; F.K. and A.G. analyzed data; F.K. and A.G. wrote the manuscript.

Funding

F.K. and V.R. were supported by the Graduate Training Centre of Neuroscience & International Max Planck Research School, Graduate School of Neural Information Processing (F.K.) and Graduate School of Neural and Behavioral Sciences (V.R.), Tuebingen, Germany. A.G. was supported by grants from the Baden-Wuerttemberg Foundation [NEU005, NEMOPLAST] and the German Federal Ministry of Education and Research [BMBF 13GW0119B, IMONAS; 13GW0214B, INSPIRATION].