Abstract
An objective of commercial beef cattle crossbreeding programs is to simultaneously optimize use of additive (breed differences) and non-additive (heterosis) effects. A total of 6,794 multibreed and crossbred beef cattle with phenotype and Illumina BovineSNP50 genotype data were used to predict genomic heterosis for growth and carcass traits by applying two methods assumed to be linearly proportional to heterosis. The methods were as follows: 1) retained heterozygosity predicted from genomic breed fractions (HET1) and 2) deviation of adjusted crossbred phenotype from midparent value (HET2). Comparison of methods was based on prediction accuracy from cross-validation. Here, a mutually exclusive random sampling of all crossbred animals (n = 5,327) was performed to form five groups replicated five times with approximately 1,065 animals per group. In each run within a replicate, one group was assigned as a validation set, while the remaining four groups were combined to form the reference set. The phenotype of the animals in the validation set was assumed to be unknown; thus, it resulted in every animal having heterosis values that were predicted without using its own phenotype, allowing their adjusted phenotype to be used for validation. The same approach was used to test the impact of predicted heterosis on accuracy of genomic breeding values (GBV). The results showed positive heterotic effects for growth traits but not for carcass traits that reflect the importance of heterosis for growth traits in beef cattle. Heterosis predicted by HET1 method resulted in less variable estimates that were mostly within the range of estimates generated by HET2. Prediction accuracy was greater for HET2 (0.37–0.98) than HET1 (0.34–0.43). Proper consideration of heterosis in genomic evaluation models has debatable effects on accuracy of EBV predictions. However, opportunity exists for predicting heterosis, improving accuracy of genomic selection, and consequently optimizing crossbreeding programs in beef cattle.
Keywords: beef cattle, dominance, genomics, growth and carcass traits, heterozygosity, hybrid vigour
INTRODUCTION
George H. Shull (1914, 1948) coined the term “heterosis” (Syn. hybrid vigour) to describe a phenomenon where crossbred organisms have increased growth, productivity, fertility, and vigour over their purebred parents. Heterosis has immense economic value in plant and animal agriculture and has been exploited in many production systems (Lippman and Zamir, 2007; Krishnan et al., 2013). Although, the genetic basis of heterosis is still a subject of investigation, the hypotheses are based on the evidence of increased heterozygosity in crossbreds relative to straightbreds and is maximized in F1 hybrids (Falconer and Mackay, 1996). Retention of heterosis in crossbreds past the F1 generation is predictable based on a dominance model and is assumed proportional to heterozygosity retained (Dickerson, 1973).
In practice, identification of superior parents to be used for crossbreeding and testing the performance of different crosses under field conditions can be expensive and time consuming. Attempts have been made using genomic tools to estimate the proportion of phenotypic variation attributable to non-additive SNP effects for traits that express heterosis (Su et al., 2012; Bolormaa et al., 2015). Working with poultry, Amuzu-Aweh et al. (2013) predicted heterosis with accuracy up to 50% using the genome-wide average squared difference in allele frequency (SDAF). Developing a reliable method of predicting heterosis for crossbred beef cattle could improve the efficiency of crossbreeding and improve the accuracy of estimated breeding values (EBV) by accounting for non- additive genetic effects in the genomic evaluation model.
The aim of the present study was to predict genomic heterosis for growth and carcass traits in beef cattle using two methods assumed to be linearly proportional to heterosis, to compare methods based on prediction accuracy from cross- validation, and to test the impact of predicted heterosis on the accuracy of genomic breeding values (GBV).
MATERIALS AND METHODS
All management and procedures involving live animals, where applicable, conformed to the guidelines outlined by the Canadian Council on Animal Care (1993); otherwise, existing data sets from the various Canadian research herds were used.
Animals, Phenotypes, and Genotypes
A total of 6,796 straightbred, multibreed composite and crossbred beef cattle with phenotypes and 50K genotypes were used for this study. Data were collated from various projects and research herds across Canada, including 3,692 from the Phenomic Gap Project based at Lacombe Research Centre, Lacombe, AB; 2,350 from the University of Alberta’s Roy Berg Kinsella Research Ranch, Kinsella, AB; and 754 from the University of Guelph’s Elora Beef Cattle Research Station, Elora, ON. The population structure, breeds, and animal management were previously described in detail by Lu et al. (2016). Briefly, the whole data set consisted of 968 Angus, 572 Charolais, 316 Hereford, 17 Simmental, 17 Limousine, 1,225 Angus-Hereford crossbred, 484 Angus-Simmental crossbred, 353 Charolais-Red Angus crossbred, 1,178 Kinsella composite, 1,105 Beefbooster TX composite, and 561 animals of other breed combinations. Kinsella composite is a beef–dairy hybrid heavily influenced by Hereford and Angus breeds with infusion of Holstein (Wang et al., 2006). Beefbooster TX composite is predominantly Charolais based with infusion of Holstein, Maine Anjou, and Chianina (http://www.beefbooster.com).
Phenotypic records were birth weight (BWT), actual weaning weight (WWT), 205-d weaning weight (W205D), pre-weaning daily gain (PDG), average daily gain on feedlot (ADG), yearling weight (YWT), hot carcass weight (HCW), back fat thickness (BFT), rib eye area (REA), marbling score (MBS), lean meat yield (LMY), and calculated yield grade (CYG). Yield grade was calculated according to USDA specification (Holland and Loveday, 2013). The data was edited to remove records > or <3 SD from the mean after correcting for systematic effects of sex, age of dam, herd, and year of birth. Pedigree extending to purebred ancestors was known, assumed accurate, and available for all animals used in the study. The pedigree records consisted of 11,905 individuals including 873 sires and 4,483 dams over five generations.
Marker genotypes were obtained using BovineSNP50 BeadChip (50K; Illumina, San Diego, California, USA) from Delta Genomics, Edmonton, Alberta, Canada. Quality control was performed to remove SNPs with minor allele frequency < 0.01 and call rate < 0.90 (Lu et al., 2016). Missing genotypes were imputed using FImpute v2.0 (Sargolzaei et al., 2014). In addition, two animals with call rate less than 90% were also removed, and only autosomal SNPs with known genome position according to the UMD_3.1 bovine assembly map (Zimin et al., 2009) were used. After editing, 42,610 SNPs and 6,794 animals were used for this study.
Prediction of Genomic Breed Fractions
Genomic breed fractions were predicted for all individuals (n = 6,794) using the ADMIXTURE software (Alexander et al., 2009). A 10-fold cross- validation procedure available in ADMIXTURE was performed to find the best possible K value with the lowest cross-validation error (Alexander et al., 2009). The resulting breed fractions at K = 6 were selected from the ADMIXTURE analysis and aligned with the known sire breed information to identify the various breed ancestries existing in the dataset. Six breed ancestors were uniquely identified and defined as Angus, Hereford, Charolais, Crosses, Kinsella Composite, and Beefbooster TX Composite. The Crosses represented two or more way crossbreds involving Angus, Hereford, Charolais, Simmental, Gelbvieh, Limousin, and Piedmontese. The genomic breed fraction was used to designate animals as purebred Angus, Hereford, or Charolais based on having greater than 80% of the represented major breeds, while another set of animals were grouped as Angus-based, Hereford-based, and Charolais-based crossbreds based on having 50%–80% of the leading breed fraction. Also, the breed fractions were fitted as covariates in the various statistical models defined below to correct for population stratification and breed effects.
Model Definitions and Statistical Analysis
As a first step, assuming heterosis is due to dominance and overdominance, variance component analyses were carried out to estimate the contribution of additive and non-additive genetic effects to the total phenotypic variation of the studied traits using four linear mixed effect models and all dataset (n = 6,794). Each model differed based on the source of relationship matrix used in the analysis.
| (1) |
| (2) |
| (3) |
| (4) |
where y is a vector of phenotypic observations; µ is the population mean and 1 is a vector of ones; depending on the trait analyzed, X is the design matrix that relates the fixed effects to the observation while b is an unknown vector of fixed effects (contemporary groups formed based on herd, year, sex, and management groups; data source, covariates of dam age, weaning age, start age for feedlot test, slaughter age, and breed fractions); a and g are vectors of random additive genetic effects; w and d are vectors of random dominance effects; e is a vector of random residual effects; Z1, Z2, Z3, and Z4 are incidence matrices that relate effects to phenotypes; a, w, g, d, and e are normally distributed as: a ~ N(0,σ2aA), w ~ N(0,σ2wW), g ~ N(0,σ2gG), d ~ N(0,σ2dD) and e ~ N(0,σ2eI), respectively.
The matrix A is the numerator relationship constructed from pedigree, I is an identity matrix, and W is the dominance relationship based on pedigree which was extracted from a gametic relationship matrix constructed by the method described by Schaeffer et al. (1989). The gametic relationship is defined as the matrix of probabilities that two alleles are identical by descent and has the order 2n for n individuals assuming two alleles at a locus (e.g., individual A has alleles A1 and A2). Therefore, W between two animals, A and B, in the absence of inbreeding was derived from a gametic relationship matrix as ([A1, B1]*[A2, B2] + [A1, B2]*[A2, B1]), where A1 and A2 are the alleles of individual A, and B1 and B2 are the alleles of individual B. The genomic additive relationship matrix G was constructed from genotype information according to the method described in detail by VanRaden (2008) as follows: G = ZZʹ/ 2 Σ (pj) (1–pj). The matrix Z is of the order n × m (i.e., the number of individuals by the number of SNPs). The elements in Z are equal to −2pj, 1−2pj, and 2−2pj for genotypes AA, AB, and BB, while pj is the allele frequency of the B allele at the jth SNP. The genomic dominance relationship matrix D was constructed from genotype information following the method described by Vitezica et al. (2013) as follows: D = HHʹ/2Σ(pjqj). Depending on the genotype at jth SNP, the elements of H matrix were −2qj2, 2pjqj, and −2pj2 for AA, AB, and BB genotypes, while pj and qj are the allele frequencies.
In constructing G and D for these multibreed and crossbred dataset, breed-specific allele frequencies were not applied because Ibánẽz-Escriche et al. (2009) noted that models that fit breed-specific SNP allele effects for crossbred population may not be necessary if high density markers are utilized to trace ancestor alleles with precision. More so, across-breed genomic predictions were performed successfully in previous studies using samples of the current dataset without assuming breed-specific allele frequencies for the G matrix (Lu et al., 2016; Akanno et al., 2017). In addition, phenotypes will be adjusted for breed effects using the predicted genomic breed fractions, which accounts for any potential confounding due to breed. Because there were 1,492 dams with two or more progeny with records, random maternal genetic effects and maternal permanent environmental effects were included in the model for analysis of pre-weaning traits. See Table 1 for details of model definition for each trait. Genomic prediction was carried out using the genomic best linear unbiased prediction (GBLUP). In the GBLUP analyses, pedigree was used to account for random maternal effects for pre-weaning traits because most dams were not genotyped.
Table 1.
Model definitions for growth and carcass traits of beef cattle
| Factors | Fixed or random | Traits | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BWT | WWTa | PDG | ADG | YWT | HCW | BFT | REA | MBS | LMY | CYG | ||
| Contemporary group | Fixed | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Age of dam | Covariate | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Weaning age | Covariate | √ | √ | |||||||||
| Start age of feedlot test | Covariate | √ | √ | |||||||||
| Slaughter age | Covariate | √ | √ | √ | √ | √ | √ | |||||
| Breed fractions | Covariate | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Maternal genetic | Random | √ | √ | √ | ||||||||
| Maternal permanent effect | Random | √ | √ | √ | ||||||||
| Direct additive | Random | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Direct dominance | Random | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
aThe model used for WWT is similar to the one used for W205D except that weaning age was not included.
Prediction of Genomic Heterotic Effects
Genomic heterotic effects were predicted by two methods: 1) Heterosis was assumed to be linearly proportional to retained breed heterozygosity (HET1). First, genomic retained heterozygosity (RH) was calculated for all individuals following the formula of Dickerson (1973):
where is the genomic breed fractions of each of the s contributing breeds. To test the significance of RH for predicting heterosis, crossbred phenotypes were regressed on calculated RH values by extending model 1 as follows:
| (5) |
where y is a vector of the observed phenotypes for crossbreds, 1, µ, X, b, Z1,a, and e were as defined for model 1 above, is the estimated linear coefficient of the regression of crossbred phenotypes on . Predicted heterosis was then derived as the product of estimated for each trait and values. This approach is similar to the method applied by Amuzu-Aweh et al. (2013) using SDAF. Later, calculated RH values were averaged across all the breed groups described previously and expressed in percentage by multiplying by 100. 2) Heterosis was predicted as the deviation of adjusted crossbred phenotypes from the midparent value (MPV) termed HET2.
| (6) |
where y is a vector of crossbred phenotypes; µ is the population mean; X is the design matrix while is the coefficients of all fixed effects in model 1 but excluding genomic breed fractions; y* is the adjusted crossbred phenotype; ABF is the average genomic breed fractions of parents across s contributing breed ancestors and is the breed effect of breed i on studied traits. Here, was estimated from another run of model 1 that includes genomic breed fractions as fixed covariate. Producing y* this way allows MPV to account for breed effects when predicting heterosis, elsewhere adjusted phenotypes were produced by adjusting all systematic effects including breed fractions.
Accuracy of Predicted Heterosis
To evaluate the accuracy of predicted heterosis, another form of adjusted phenotype (y#) was first obtained for all crossbred individuals as where was estimated from model 1 that fits all fixed effects associated with each trait including genomic breed fractions. This adjusted phenotype (y#) was treated as observed heterosis and assigned for validation purpose following the approach described by Amuzu-Aweh et al. (2013). Subsequently, a mutually exclusive random sampling of all crossbred animals (n = 5,327) was performed to form five groups replicated five times with approximately 1,065 animals per group. In each run within a replicate, one group was assigned as the validation set, while the remaining four groups were combined to form the reference set used for estimation of or depending on the method of heterosis prediction. Thus, genomic heterosis was predicted for every crossbred animal without using its own observation and the correlation between the observed heterosis and the predicted heterosis was taken as the accuracy of heterosis prediction. Note that for predicting and validating HET2, y* ≠ y#. That is, model 1 was applied to generate y* in the validation animals excluding breed fractions in the model followed by estimating in the training set using full model 1, while y# was obtained for all crossbred individuals using full model 1.
Improving Accuracy of Genomic Prediction of Breeding Values
A scenario for improving prediction accuracy of GBV by accounting for predicted heterosis in the genomic evaluation model for crossbreds was studied. The following three models were tested:
| (7) |
| (8) |
| (9) |
where HET1 and HET2 are heterosis predicted for every crossbred animal according to the two methods described above. The rest of the terms in the models were as previously defined. A cross- validation approach was applied and genetic correlation was used to compare all models for GBV prediction accuracy. All analyses were conducted in R statistical software using default programs where applicable (Ihaka and Gentleman, 1996) and linked to ASReml software (Gilmour et al., 2015) for variance component estimation and genomic prediction.
RESULTS AND DISCUSSION
Descriptive Statistics and Variance Components Estimation
The number of records used, mean performance, and coefficient of variation for all traits studied in purebreds and crossbred beef cattle populations are summarized in Table 2. Mean phenotypic performance across traits were typical of commercial beef cattle and showed considerable variation in purebreds and crossbreds. Traits that typically express heterosis had slightly greater coefficient of variation in crossbreds than in purebreds. Table 3 shows the proportions of total phenotypic variance explained by all genetic effects for growth and carcass traits in beef cattle derived from four models that utilized a pedigree-based or genome-based relationship. Random maternal genetic and maternal permanent environmental effects were included in all models for evaluating pre-weaning traits (e.g., BWT, WWT, W205D, and PDG). This was achieved by using pedigree relationship to account for maternal effects in both pedigree-based and genome-based models because dams with more than one progeny in the dataset frequently were not genotyped.
Table 2.
Number of animals with record (N), mean and standard deviation (SD) and coefficient of variation (CV; %) for growth and carcass traits of purebred and crossbred beef cattlea
| Traits | N | Mean | SD | Purebreds (CV%) | Crossbreds (CV%) |
|---|---|---|---|---|---|
| Birth weight, kg | 5,481 | 41.87 | 6.69 | 16.84 | 15.58 |
| Actual weaning weight, kg | 6,261 | 239.33 | 44.60 | 14.23 | 19.61 |
| 205-d weaning weight, kg | 5,258 | 232.47 | 35.75 | 16.03 | 15.16 |
| Pre-weaning daily gain, kg/d | 5,255 | 1.13 | 0.17 | 15.75 | 15.10 |
| Average daily gain, kg/d | 6,772 | 1.45 | 0.39 | 19.98 | 27.98 |
| Yearling weight, kg | 6,019 | 366.91 | 66.92 | 19.57 | 17.77 |
| Hot carcass weight, kg | 4,071 | 335.87 | 34.26 | 9.25 | 10.48 |
| Back fat thickness, mm | 4,002 | 11.19 | 4.50 | 38.00 | 38.25 |
| Rib eye area, cm2 | 4,054 | 85.61 | 11.18 | 13.68 | 12.75 |
| Marbling score | 4,054 | 406.19 | 94.55 | 25.49 | 21.06 |
| Lean meat yield, % | 4,062 | 58.37 | 4.57 | 9.55 | 6.82 |
| Calculated yield grade | 4,008 | 2.66 | 0.81 | 30.27 | 29.13 |
| Age at weaning | 6,153 | 181.35 | 26.72 | 11.63 | 15.52 |
| Age at start of feedlot test | 6,794 | 300.58 | 51.52 | 12.65 | 18.18 |
| Slaughter age | 4,126 | 443.38 | 48.76 | 4.73 | 12.22 |
aPurebred individuals have >80% of Angus, Hereford and Charolais; Crossbred individuals included Kinsella composite, Beefbooster TX composite (www.beefbooster.com) and two and more way crosses involving Angus, Hereford, Charolais, Gelbvieh, Simmental, Limousin, and Piedmontese.
Table 3.
Variance component estimates for growth and carcass traits of beef cattle using pedigree-based relationships (Models 1 and 2) and genome-based relationships (Models 3 and 4)
| Models | Sources | BWT | WWT | W205D | PDG | ADG | YWT | HCW | BFT | REA | MBS | LMY | CYG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | h2dir | 0.64 ± 0.05 | 0.47 ± 0.05 | 0.45 ± 0.05 | 0.44 ± 0.05 | 0.37 ± 0.04 | 0.63 ± 0.04 | 0.44 ± 0.05 | 0.28 ± 0.05 | 0.45 ± 0.05 | 0.35 ± 0.05 | 0.40 ± 0.05 | 0.42 ± 0.05 |
| h2mat | 0.04 ± 0.06 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | – | – | – | – | – | – | – | – | |
| Mpe | 0.02 ± 0.05 | 0.22 ± 0.03 | 0.21 ± 0.03 | 0.23 ± 0.03 | – | – | – | – | – | – | – | – | |
| rmat,dir | −0.66 | −0.45 | −0.64 | −0.52 | – | – | – | – | – | – | – | – | |
| 2 | h2dir | 0.64 ± 0.05 | 0.47 ± 0.05 | 0.45 ± 0.05 | 0.44 ± 0.05 | 0.37 ± 0.04 | 0.63 ± 0.04 | 0.44 ± 0.05 | 0.28 ± 0.05 | 0.45 ± 0.05 | 0.35 ± 0.05 | 0.40 ± 0.05 | 0.42 ± 0.05 |
| d2 | 0.28 ± 0.21 | 0.20 ± 0.20 | 0.22 ± 0.21 | 0.29 ± 0.21 | 0.00 ± 0.00 | 0.15 ± 0.24 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.15 ± 0.44 | 0.00 ± 0.00 | 0.00 ± 0.00 | |
| h2mat | 0.04 ± 0.06 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | – | – | – | – | – | – | – | – | |
| mpe | 0.02 ± 0.05 | 0.22 ± 0.09 | 0.22 ± 0.02 | 0.23 ± 0.02 | – | – | – | – | – | – | – | – | |
| rmat,dir | −0.65 | −0.44 | −0.64 | −0.53 | – | – | – | – | – | – | – | – | |
| 3 | h2dir | 0.54 ± 0.02 | 0.40 ± 0.02 | 0.38 ± 0.03 | 0.38 ± 0.03 | 0.30 ± 0.02 | 0.48 ± 0.02 | 0.41 ± 0.03 | 0.28 ± 0.03 | 0.40 ± 0.03 | 0.26 ± 0.03 | 0.34 ± 0.03 | 0.35 ± 0.03 |
| h2mat | 0.03 ± 0.05 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | – | – | – | – | – | – | – | – | |
| mpe | 0.02 ± 0.05 | 0.22 ± 0.02 | 0.20 ± 0.09 | 0.23 ± 0.02 | – | – | – | – | – | – | – | – | |
| 4 | h2dir | 0.53 ± 0.02 | 0.39 ± 0.02 | 0.37 ± 0.03 | 0.37 ± 0.03 | 0.31 ± 0.02 | 0.48 ± 0.02 | 0.41 ± 0.03 | 0.28 ± 0.03 | 0.40 ± 0.03 | 0.27 ± 0.03 | 0.33 ± 0.03 | 0.34 ± 0.03 |
| d2 | 0.09 ± 0.03 | 0.07 ± 0.03 | 0.09 ± 0.03 | 0.09 ± 0.03 | 0.02 ± 0.03 | 0.08 ± 0.03 | 0.00 ± 0.04 | 0.02 ± 0.04 | 0.00 ± 0.04 | 0.00 ± 0.04 | 0.06 ± 0.04 | 0.05 ± 0.04 | |
| h2mat | 0.03 ± 0.05 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | – | – | – | – | – | – | – | – | |
| mpe | 0.02 ± 0.05 | 0.22 ± 0.02 | 0.20 ± 0.09 | 0.23 ± 0.02 | – | – | – | – | – | – | – | – | |
| 2 vs. 4 | Diffs. h2dir | 0.11 | 0.08 | 0.08 | 0.07 | 0.06 | 0.15 | 0.03 | 0 | 0.05 | 0.08 | 0.07 | 0.08 |
| Diffs. d2 | 0.19 | 0.13 | 0.13 | 0.20 | −0.02 | 0.07 | 0.00 | −0.02 | 0 | 0.15 | −0.06 | −0.05 |
h2dir = direct heritability; d2 = ratio of dominance to total phenotypic variance; h2mat = maternal heritability; mpe = maternal permanent environment; rmat,dir = correlation between direct and maternal effect; Diffs. h2dir = Differences between heritability estimates from models 2 and 4; Diffs. d2 = Differences between estimates of dominance proportion from models 2 and 4.
Narrow-sense heritability estimates from models 1 and 2 that used a pedigree relationship were similar for each trait evaluated (Table 3). Similarly, heritability estimates from models 3 and 4 that utilized a genomic relationship were also similar for each of the studied traits. This similarity in heritability estimates between models utilizing the same type of relationship matrix has been previously observed in a study with pigs (Lopes et al., 2015). However, estimates of heritability from a genome-based model were generally lower than the estimates from pedigree-based models (Table 3). This reduction in heritability estimates from a genome-based model as opposed to a pedigree-based model has also been observed before (Lopes et al., 2015; Akanno et al., 2017) and has been referred to as missing heritability (Lee et al., 2011). This is because the heritability from the genome-based model includes only the contribution of causal variants in linkage disequilibrium with the SNP markers and not the contribution of all causal variants as in the pedigree-based model.
The estimates of heritability for growth traits in our population using all four models were moderate to highly heritable ranging from 0.30 to 0.64 (Table 3), which is slightly greater than values of 0.22 to 0.55 previously reported for growth traits in North American beef cattle populations (Schenkel et al., 2004; Schiermiester et al., 2015). On the other hand, heritability estimates for carcass traits across all models ranged from 0.26 to 0.45, which agrees with the range of values reported by Miar et al. (2014) for a Canadian dataset (0.22 to 0.38) and those reported (0.15 to 0.97) in a review by Rios Utrera and Van Vleck (2004) for beef cattle in general. Heritability estimates from the current study are based on multiple breeds and crossbred dataset, which is likely to be greater compared with estimates from a single breed as in previous studies.
Accounting for dominance effects in both pedigree- and genome-based models for across breed genetic evaluation of growth traits (BWT, WWT, W205D, PDG and YWT) improved the predictability of the models based on likelihood ratio test (P < 0.01) but not for carcass traits. The estimates of the proportion of phenotypic variance explained by dominance deviation from a pedigree-based model were generally large with large standard errors (SE) and ranged from 0 to 0.29 for growth traits and 0 to 0.15 for carcass traits, while estimates from a genome-based model ranged from 0.02 to 0.09 for growth traits and 0 to 0.06 for carcass traits (Table 3). The large proportion of dominance variance from a pedigree-based model may indicate potential confounding of dominance deviation with other genetic and non-genetic factors like maternal and maternal permanent environmental effects especially for those traits where maternal effects are important.
Here, maternal heritability estimates observed for pre-weaning traits were zero or near zero across all models evaluated, while estimates of maternal permanent environmental effects ranged from 0.02 for BWT to 0.23 for PDG, on average (Table 3). The correlation between direct and maternal genetic effects were large and negative ranging from −0.44 (WWT) to −0.66 (BWT). Several studies have shown that estimates of maternal effects on pre-weaning traits largely depends on data structure and a negative correlation between direct and maternal genetic effects can be influenced by data structure, actual genetic antagonism, or due to sire by year interaction (Meyer, 1992; Konstantinov and Brien, 2003; Maniatis and Pollott, 2003). As there were 1,492 dams out of 4,483 with two or more progeny and only a five generation pedigree, the current data structure may not allow for proper estimation of maternal genetic and permanent environmental effects for growth traits when using pedigree relationship. Thus, the contribution of dominance deviation to phenotypic variation may be inflated and may be the reason for the large SE reported for dominance ratio from pedigree-based models.
However, the fact that dominance was identified for growth traits using pedigree-based models corroborates results from genome-based models and indicates that dominance is important for growth traits in beef cattle. The rather low estimates of dominance ratio from a genome-based model may be related to lack of power for estimating these effects when using SNP panel of limited density. Increasing the density of markers used for computing the dominance relationship among animals may lead to more accurate estimation of dominance effects for a multibreed and crossbred dataset. For example, while working with this data, Lu et al. (2016) observed stability in accuracy of genomic prediction for crossbreds using an imputed high density SNP panel, which suggest potential for higher density SNP panels to improve across breed genomic predictions.
In addition, the magnitude of dominance ratios reported for growth traits using genome-based models were within the range of values observed previously for beef cattle (0.07–0.47; Misztal et al., 1998; Roso et al., 2005; Chen et al., 2014; Bolormaa et al., 2015) and for other species (0.04–0.44; Dufrasne et al., 2014; Moghaddar and van der Werf, 2014). Generally, growth traits are moderately heritable with a documented evidence of non-additive genetic effects and heterosis (Williams et al., 2010; Schiermiester et al., 2015). Further, significant dominance effects were not detected in carcass traits (0.02–0.06) using the genomic model indicating that dominance effects may be less important for these traits. Chen et al. (2014), however, observed dominance ratios in the range of 0.05–0.14 for carcass traits of Angus steers sampled from the data used in this study. Similarly, Bolormaa et al. (2015) reported dominance ratio of 0.10 and 0.18 for carcass fat and carcass yield, respectively.
In order to help understand the extent of contribution of genomic-based dominance effects on the variation of growth and carcass traits in beef cattle, the potential for confounding of these effects due to population stratification was investigated by splitting the entire dataset into purebred and crossbred samples based on their predicted genomic breed fractions (Figure 1). The results showed that the best estimates of proportion of total phenotypic variance explained by dominance effects were obtained for purebreds, which are largely made up of over 70% Angus breed (Table 4). Our hypothesis was that the dominance effects would be larger in the crossbreds than in the purebreds reflecting greater heterosis. Surprisingly, we were generally unable to detect differences in the proportion of dominance variance between purebreds and crossbreds. This lack of significant difference in the estimates of dominance proportions between purebred and crossbred groups and across the array of studied traits may have several possible reasons including a limitation in the current dataset, which lacked the structure for proper estimation of these effects as previously discussed and could also be a consequence of ignoring breed-specific allele frequencies when constructing relationship matrix. Because the dataset used in this study consisted of multibreed and crossbred population with differing base populations, assuming a common base allele frequency in the construction of genomic relationship matrix may bias the estimation of genetic variances and (co)variance between breeds. Recently, Chen et al. (2013) and Wientjes et al. (2017) provided methods that consider population-specific allele frequencies in the construction of genomic relationship matrix of multipopulations for unbiased estimation of genetic variance and better genomic prediction. The results of the current study, however, indicated a potential for non-additive genetic effects for growth traits in beef cattle. Breeders can continue to exploit these additional effects when planning a genetic improvement program for beef cattle.
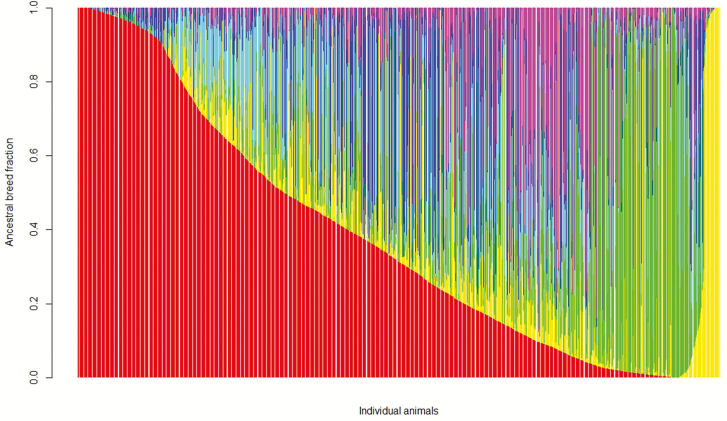
Figure 1.
Distribution of estimated genomic breed fractions of commercial beef cattle population (n = 6,794). Angus is red, Hereford is yellow, Charolais is green, Crosses is cyan, Kinsella composite is blue, and Beefbooster TX composite is purple. See online version for figure in colour.
Table 4.
Proportions of phenotypic variance explained by additive and dominance effects in purebreds, crossbreds, and overall populationsa using genomic relationship and model 4
| Traits | Purebreds (n = 1,467) | Crossbreds (n = 5,327) | Overall (n = 6,794) | |||
|---|---|---|---|---|---|---|
| Additive | Dominance | Additive | Dominance | Additive | Dominance | |
| Birth weight, kg | 0.61 ± 0.05 | 0.08 ± 0.09 | 0.56 ± 0.03 | 0.11 ± 0.04 | 0.53 ± 0.02 | 0.09 ± 0.03 |
| Actual weaning weight, kg | 0.46 ± 0.06 | 0.14 ± 0.10 | 0.43 ± 0.03 | 0.04 ± 0.03 | 0.39 ± 0.02 | 0.07 ± 0.03 |
| 205-d weaning weight, kg | 0.38 ± 0.07 | 0.23 ± 0.10 | 0.41 ± 0.03 | 0.06 ± 0.04 | 0.37 ± 0.03 | 0.09 ± 0.03 |
| Pre-weaning daily gain, kg/d | 0.37 ± 0.07 | 0.22 ± 0.10 | 0.42 ± 0.03 | 0.06 ± 0.04 | 0.37 ± 0.03 | 0.09 ± 0.03 |
| Average daily gain, kg/d | 0.33 ± 0.06 | 0.07 ± 0.10 | 0.33 ± 0.03 | 0.00 ± 0.03 | 0.31 ± 0.02 | 0.02 ± 0.03 |
| Yearling weight, kg | 0.57 ± 0.06 | 0.00 ± 0.09 | 0.52 ± 0.03 | 0.09 ± 0.03 | 0.48 ± 0.02 | 0.08 ± 0.03 |
| Hot carcass weight, kg | 0.43 ± 0.08 | 0.03 ± 0.14 | 0.42 ± 0.04 | 0.00 ± 0.06 | 0.41 ± 0.03 | 0.00 ± 0.04 |
| Back fat thickness, mm | 0.48 ± 0.08 | 0.00 ± 0.15 | 0.23 ± 0.03 | 0.04 ± 0.06 | 0.28 ± 0.03 | 0.02 ± 0.04 |
| Rib eye area, cm2 | 0.46 ± 0.08 | 0.00 ± 0.15 | 0.38 ± 0.03 | 0.00 ± 0.06 | 0.40 ± 0.03 | 0.00 ± 0.04 |
| Marbling score | 0.29 ± 0.07 | 0.00 ± 0.15 | 0.33 ± 0.04 | 0.10 ± 0.06 | 0.27 ± 0.03 | 0.00 ± 0.04 |
| Lean meat yield, % | 0.50 ± 0.07 | 0.05 ± 0.15 | 0.31 ± 0.04 | 0.05 ± 0.06 | 0.33 ± 0.03 | 0.06 ± 0.04 |
| Calculated yield grade | 0.50 ± 0.07 | 0.07 ± 0.15 | 0.33 ± 0.04 | 0.05 ± 0.06 | 0.34 ± 0.03 | 0.05 ± 0.04 |
aPurebred individuals have >80% of Angus, Hereford and Charolais; Crossbred individuals included Kinsella composite, Beefbooster TX composite (www.beefbooster.com) and two and more way crosses involving Angus, Hereford, Charolais, Gelbvieh, Simmental, Limousin, and Piedmontese.
Predictions of Genomic Retained Heterozygosity
Knowledge of breed composition can be used for assessment of admixture level, correction of population stratification in genetic analysis, and planning crossbreeding programs that will exploit heterosis and breed complementarity. Here, SNP markers were used to trace the breed ancestry of a multibreed and crossbred beef cattle population to six founding genetic groups, which corresponded closely to Angus, Hereford, Charolais, Beefbooster TX composite, Kinsella composite, and a sixth group that represents a mixture of different crosses based on known sire breed information (Figure 1). In most commercial crossbreeding systems, it may be infeasible to track ancestries of crossbred animals or the founder breeds may be wrongly assigned. In such a situation, genotypes of the crossbred individuals may be used to estimate the ancestries directly (Akanno et al., 2017). Rapid prediction of breed composition using genomics in beef cattle populations may also be beneficial for checking the integrity of pedigree recording for seed stock.
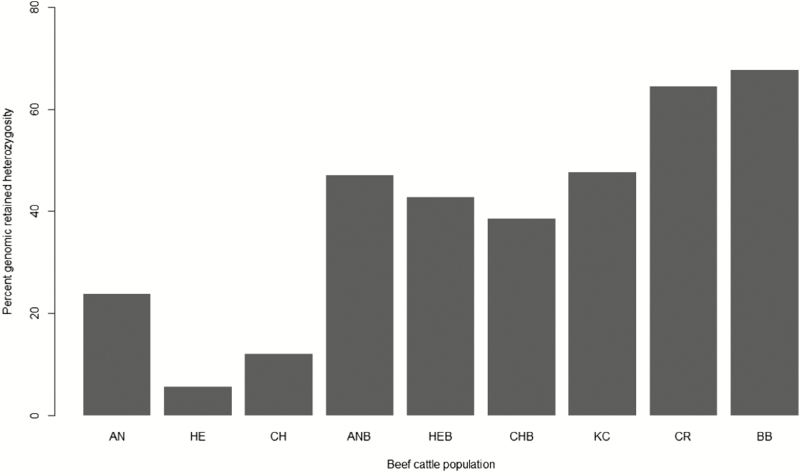
In a crossbreeding program, the amount of heterosis retained per generation is proportional to the breed heterozygosity retained, which also depends on the number and proportions of component breeds involved in the crosses (Dickerson, 1973). Genomic retained heterozygosity was predicted for all individuals according to the formula of Dickerson (1973) and using the predicted genomic breed fractions as inputs. The percentage of individual genomic retained heterozygosity predicted for purebreds, for different crosses, and composite populations are shown in Figure 2. Among purebreds, the Angus breed had the highest level of retained heterozygosity followed by Charolais and Hereford. A low level of genomic retained heterozygosity as observed in Hereford breed suggests a high inbreeding level. In a genetic diversity study by Abo-Ismail et al. (2016), the highest level of genomic inbreeding was observed for Hereford breed compared with other North American beef cattle breeds. Similarly, Cleveland et al. (2005) reported increases in pedigree inbreeding level in American Hereford cattle population over many decades, which can happen in any closed population.
Figure 2.
Percentage of individual breed heterozygosity retained in purebreds (>80% of Angus (AN), Hereford (HE), or Charolais (CH) breed fractions), Angus-based crossbreds (ANB; 50%–80% of Angus fractions in crosses), Hereford-based crossbreds (HEB; 50%–80% of Hereford fractions in crosses), Charolais-based crossbreds (CHB; 50%–80% of Charolais fractions in crosses), Kinsella composite (KC; beef–dairy hybrid heavily influenced by Hereford and Angus breeds with infusion of Holstein), Crosses (CR; Two or more way crosses involving Angus, Hereford, Charolais, Gelbvieh, Simmental, Limousin, and Piedmontese), and Beefbooster TX composite (BB; Charolais based with infusion of Holstein, Maine Anjou, and Chianina ; http://www.beefbooster.com).
When the Angus breed fraction dominated in two or more way crossbreeding, the percentage of retained heterozygosity was greatest followed by Hereford- and Charolais-based crosses. The Beefbooster TX composite, which was developed from Continental breeds (Charolais, Chianina, Maine-Anjou) and Holstein, had greater genomic retained heterozygosity than the Kinsella composite that was developed from British breeds (Hereford and Angus) plus Holstein. The remaining crossbred group had a slightly less retained heterozygosity compared with Beefbooster TX composites. This group was assumed to represent the outcome of crosses involving British and Continental cattle breeds such as Angus, Hereford, Charolais, Gelbvieh, Simmental, Limousin, and Piedmontese. As British and Continental cattle breeds are distantly diverged (Kuehn et al., 2011), crossbreeding them is expected to maximize breed heterozygosity and heterosis. Previous studies have shown greater heterosis benefits for crosses involving British and Continental cattle breeds in North American environment (Williams et al., 2010; Schiermiester et al. 2015).
Effects of Genomic RH and Breed
A summary of breed and RH effect solutions and their associated SE for all traits studied are listed in Table 5. Among the growth traits, the effect of RH was positive for BWT, WWT, and PDG but negative for ADG and YWT. Except for ADG, the RH effects on growth traits were not significantly different from zero (P > 0.05). For carcass traits, RH effects were positive for BFT and LMY but negative for the rest of the traits. The RH effects on HCW and MBS were significant (P < 0.05). A positive effect of RH means that the interactions between paternal and maternal alleles of different breeds yielded a value that was greater than the interactions between paternal and maternal alleles of the same breed. On the other hand, a negative effect of RH means that the interactions between paternal and maternal alleles of different breeds yielded a value that was lower than the interactions between paternal and maternal alleles of the same breed, which is akin to negative heterosis. The range of positive effects of RH on BWT and WWT (0.55 to 4.26) were within the range of heterosis (0.47–8.65) reported by Williams et al. (2010) and Schiermiester et al. (2015) for crosses involving British and Continental cattle breeds. For carcass traits, the magnitude and direction of effects of RH from this study were different from those reported for heterosis in a review by Williams et al. (2010). Most carcass traits are highly heritable with limited contribution of heterosis to the expression of the traits.
Table 5.
Effects of RHa and representative breed effectsb as deviations from Kinsella composite for the studied traits
| Traits | RH | AN | HE | CH | CR | BB |
|---|---|---|---|---|---|---|
| Birth weight, kg | 0.55 ± 0.79 | 3.34 ± 1.39* | 5.76 ± 1.67*** | 13.58 ± 1.68*** | 4.40 ± 2.03* | 12.65 ± 1.95*** |
| Actual weaning weight, kg | 0.82 ± 3.47 | 8.62 ± 6.53 | 8.40 ± 7.74 | 25.75 ± 7.58*** | 30.19 ± 8.71*** | 25.75 ± 8.49** |
| 205-d Weaning weight, kg | 4.26 ± 4.02 | −4.74 ± 7.24 | −4.04 ± 8.65 | 13.46 ± 8.67 | 18.83 ± 10.61 | 18.77 ± 10.00 |
| Pre-weaning daily gain, kg/d | 0.02 ± 0.02 | −0.01 ± 0.03 | −0.02 ± 0.04 | 0.06 ± 0.04 | 0.10 ± 0.05* | 0.07 ± 0.05 |
| Average daily gain, kg/d | −0.08 ± 0.03* | 0.19 ± 0.06*** | 0.150.07* | 0.19 ± 0.07** | 0.12 ± 0.07 | 0.15 ± 0.08 |
| Yearling weight, kg | −2.89 ± 4.88 | 17.60 ± 8.78* | −1.42 ± 10.42 | 26.03 ± 10.23* | 39.77 ± 12.10** | 54.81 ± 11.60*** |
| Hot carcass weight, kg | −21.70 ± 4.99*** | 34.25 ± 8.03*** | 19.91 ± 9.80* | 47.26 ± 8.87*** | 49.86 ± 10.51*** | 52.60 ± 10.26*** |
| Back fat thickness, mm | 0.09 ± 0.62 | 1.03 ± 0.97 | 0.35 ± 1.18 | −5.95 ± 1.06*** | −5.54 ± 1.29*** | −4.21 ± 1.23*** |
| Rib eye area, cm2 | −1.62 ± 1.63 | −0.73 ± 2.62 | −5.32 ± 3.19 | 17.06 ± 2.89*** | 16.01 ± 3.42*** | 15.18 ± 3.35*** |
| Marbling score | −28.82 ± 12.26* | 5.04 ± 19.54 | −52.32 ± 23.81* | −101.5 ± 21.43*** | −46.55 ± 25.62 | −75.26 ± 25.06** |
| Lean meat yield, % | 0.18 ± 0.61 | −2.20 ± 0.97* | −1.99 ± 1.19 | 6.60 ± 1.08*** | 5.92 ± 1.28*** | 4.73 ± 1.25*** |
| Calculated yield grade | −0.07 ± 0.11 | 0.47 ± 0.18** | 0.47 ± 0.22* | −1.09 ± 0.20*** | −1.00 ± 0.23*** | −0.78 ± 0.23*** |
1RH was fitted as fixed covariates in model 3 to estimate effects.
bEstimated in model 3 using all data (n = 6,794); AN = Angus, HE = Hereford, CH = Charolais, CR = two and more way crosses, BB = Beefbooster TX composite (www.beefbooster.com).
*P < 0.05; **P < 0.01; ***P < 0.001.
The breed effects refer to the influence of individual genomic breed fractions on the traits of interest. Overall, the larger framed Continental breeds (Charolais and Beefbooster TX) had effects that were mostly positive (P < 0.05) across studied traits, whereas the smaller framed British breeds (Angus and Hereford) had effects that were mostly near zero (P > 0.05). A similar relationship has been previously observed (Arango et al., 2002). These estimates were reported as deviations from Kinsella composite. Because previous studies (Rodriguez-Almeida et al., 1997; Arango et al., 2002; Williams et al., 2010) reported breed comparisons as deviations from a different breed, it is not possible to make trait-based comparison to the results from the current study; however, there is similarity in the trends when comparing association in British and Continental cattle breeds.
Predicted Genomic Heterosis
Predicted genomic heterosis for growth and carcass traits in different crosses of beef cattle validation groups are shown in Figures 3 and 4. In general, heterosis predicted by HET1 method resulted in less variable estimates than HET2. However, heterosis predictions from HET1 method were mostly within the range of estimates generated by HET2. Further, heterosis predicted by HET1 methods were mostly positive for growth traits (Figure 3) but were largely negative for most of the carcass traits (Figure 4). This suggests greater importance of heterosis for growth traits. Williams et al. (2010) and Schiermiester et al. (2015) reported positive heterosis effects for growth traits including BWT, WWT, and YWT. Also, positive heterosis effects were reported for carcass traits including HCW, LMY, BFT, and MBS in crosses involving British and Continental cattle breeds (Williams et al., 2010). For all traits evaluated, the trend in predicted heterosis tended to increase slightly, on average, as one moves from a two-way cross that utilizes British breeds to composites developed from British and Continental cattle breeds (Figures 3 and 4). This is expected because British and Continental cattle breeds are genetically divergent from each other (Kuehn et al., 2011), and thus, heterosis is expected to be maximized in the direction of increased divergence of breeds.
Figure 3.
Individual genomic heterosis for growth traits predicted in the crossbred validation group of beef cattle using two prediction methods (Red = heterosis predicted as retained heterozygosity (HET1), Black = heterosis predicted as deviation of adjusted crossbred phenotype from MPV (HET2)). ANB = Angus-based crosses (50%–80% Angus proportion in crossbreds), HEB = Hereford-based crosses (50%–80% Hereford proportion in crossbreds), CHB = Charolais-based crosses (50%–80% Charolais proportion in crossbreds), CR = Two or more way crosses involving Angus, Hereford, Charolais, Gelbvieh, Simmental, Limousin, and Piedmontese, KC = Kinsella composite, and BB = Beefbooster TX composite (www.beefbooster.com).
Figure 4.
Individual genomic heterosis for carcass traits predicted in the crossbred validation group of beef cattle using two prediction methods (Red = heterosis predicted as retained heterozygosity (HET1), Black = heterosis predicted as deviation of adjusted crossbred phenotype from MPV (HET2)). ANB = Angus-based crosses (50%–80% Angus proportion in crossbreds), HEB = Hereford-based crosses (50%–80% Hereford proportion in crossbreds), CHB = Charolais-based crosses (50%–80% Charolais proportion in crossbreds), CR = Two or more way crosses involving Angus, Hereford, Charolais, Gelbvieh, Simmental, Limousin, and Piedmontese, KC = Kinsella composite, and BB = Beefbooster TX composite (www.beefbooster.com).
Here, genomic tools were applied to investigate the contribution of heterosis to phenotypic expression of beef cattle production traits. The assumption was that heterosis is due to events of dominance and over-dominance at the molecular genetic level, which means that the presence of heterosis implies presence of dominance and overdominance effects. However, the presence of dominance and overdominance effects does not directly translate to the presence of heterosis unless dominance and overdominance effects are directional. Although, the genetic basis of heterosis is still a subject of scientific investigation, a few studies have shown that dominance is an important factor contributing to heterosis in beef cattle (Su et al., 2012; Bolormaa et al., 2015; Akanno et al., 2017), while epistatic effects have also been observed (Bolormaa et al., 2015). We investigated epistasis by performing a joint genome-wide association that models epistatic effects for a set of previously identified additive and dominant SNPs. The results showed negligible effects of epistasis on phenotypic variation of beef cattle traits in our dataset (unpublished data). Therefore, further investigation is warranted. Moreover, previous studies have investigated the relationship between production traits and genomic heterozygosity, which is similar to heterosis predicted by HET1 method, and have concluded that a strong relationship between genomic heterozygosity and heterosis does exist, which will be useful for predicting hybrid performance (Xiao et al., 1995; Tambasco-Talhari et al., 2005). In the presence of dominance and overdominance, superior performance of heterozygotes could be described as a manifestation of physiological differences between heterozygotes and parental homozygotes, which cause variations in observed characters.
In crossbreeding systems, the identification of crosses with superior performance is usually the major focus. This identification requires testing the performance of different crosses under field conditions, which can be expensive and time consuming. To address this question, we predicted genomic heterosis by a cross-validation approach, where the two measures of heterosis were predicted from crossbred data that excludes validation animals in the training set (Figures 3 and 4). This allows us to use the validation animals for testing the performance of the different crosses and hybrids. Note that observed heterosis was generated for all crossbred individuals by adjusting their phenotype using the default model 1 and following the approach reported by Amuzu-Aweh et al. (2013). Thus, both predicted heterosis and observed heterosis was available for each individual. This gives the opportunity to evaluate the expected heterosis for different crosses and composite populations using two measures of heterosis prediction and to test the accuracy of prediction.
Accuracy of Genomic Heterosis Predictions
Table 6 shows the average accuracy of genomic heterosis predictions using a cross- validation approach for two prediction methods. The accuracy was assessed as correlation between observed and predicted heterosis (Amuzu-Aweh et al., 2013). For growth traits, the average accuracy ranged from 0.34 for WWT to 0.43 for ADG using HET1 method and from 0.37 for BWT to 0.98 for ADG using HET2 method, respectively. For carcass traits, the average accuracy ranged from 0.38 for HCW to 0.41 for BFT using HET1 method and from 0.57 for LMY to 0.87 for HCW using HET2 method, respectively. Across traits, accuracy of genomic predictions tended to be greater using the HET2 method than HET1. This is probably because heterosis predicted by HET2 captured most of the non- genetic effects that were not explained by the model used in estimating the adjusted crossbred phenotypes. However, the HET1 method is convenient and straight forward for heterosis prediction when genomic data are utilized because the retained heterozygosity applied in this method can be explicitly predicted from genomic breed fractions. In a preliminary study of heterosis prediction using a subset of data from this study, we found that the correlation between heterosis predicted by HET1 method and retained heterosis predicted from pedigree-based breed fractions was about 0.96 and we concluded in that study that the HET1 method was a good predictor of heterosis (Akanno et al., 2017). More so, the HET1 method depends on the assumption that heterosis is linearly proportional to expected breed heterozygosity, and the average prediction accuracy across traits (0.38) was close to ~0.50 reported by Amuzu-Aweh et al. (2013) for egg production traits using the method of SDAF. Prediction accuracy was better for growth traits than for carcass traits using the two methods, which suggests that breeders can explore this extra benefit of heterosis when planning genetic improvement for growth traits in beef cattle.
Table 6.
Average accuracy (±SE) of genomic heterosis and GBVs for growth and carcass traits of beef cattle using a cross-validation approach
| Traits | Accuracy of genomic heterosis | Accuracy of GBVsa | |||
|---|---|---|---|---|---|
| HET1 | HET2 | A only | A + HET1 | A + HET2 | |
| Birth weight, kg | 0.35 ± 0.01 | 0.37 ± 0.02 | 0.49 ± 0.001 | 0.49 ± 0.001 | 0.53 ± 0.001 |
| Actual weaning weight, kg | 0.34 ± 0.01 | 0.76 ± 0.01 | 0.47 ± 0.001 | 0.47 ± 0.002 | 0.54 ± 0.003 |
| 205-d weaning weight, kg | 0.36 ± 0.01 | 0.79 ± 0.01 | 0.44 ± 0.001 | 0.44 ± 0.001 | 0.53 ± 0.002 |
| Pre-weaning daily gain, kg/d | 0.36 ± 0.01 | 0.87 ± 0.01 | 0.44 ± 0.002 | 0.44 ± 0.001 | 0.53 ± 0.003 |
| Average daily gain, kg/d | 0.43 ± 0.01 | 0.98 ± 0.01 | 0.52 ± 0.009 | 0.52 ± 0.009 | 0.66 ± 0.001 |
| Yearling weight, kg | 0.36 ± 0.01 | 0.76 ± 0.01 | 0.44 ± 0.002 | 0.44 ± 0.002 | 0.51 ± 0.002 |
| Hot carcass weight, kg | 0.38 ± 0.02 | 0.87 ± 0.01 | 0.45 ± 0.002 | 0.45 ± 0.001 | 0.59 ± 0.002 |
| Back fat thickness, mm | 0.41 ± 0.01 | 0.74 ± 0.01 | 0.39 ± 0.001 | 0.39 ± 0.001 | 0.57 ± 0.002 |
| Rib eye area, cm2 | 0.40 ± 0.01 | 0.66 ± 0.01 | 0.44 ± 0.001 | 0.44 ± 0.001 | 0.59 ± 0.002 |
| Marbling score | 0.40 ± 0.01 | 0.80 ± 0.01 | 0.38 ± 0.001 | 0.38 ± 0.001 | 0.52 ± 0.002 |
| Lean meat yield, % | 0.40 ± 0.02 | 0.57 ± 0.01 | 0.42 ± 0.001 | 0.42 ± 0.001 | 0.56 ± 0.002 |
| Calculated yield grade | 0.40 ± 0.01 | 0.57 ± 0.01 | 0.42 ± 0.001 | 0.42 ± 0.001 | 0.56 ± 0.002 |
HET1 = Heterosis predicted from retained heterozygosity; HET2 = Heterosis predicted from deviation of adjusted crossbred phenotype from MPV
aAccounting for genomic heterosis in the genomic evaluation models: A = Additive model only; A+HET1 = Model including additive (A) plus heterosis predicted from retained heterozygosity (HET1); A+HET2 = Model including additive (A) plus heterosis predicted as deviation of adjusted crossbred phenotype from mid-parent value (HET2)
Improving Accuracy of GBVs Prediction
This study also evaluated a scenario for improving prediction accuracy of GBV by accounting for non-additive genetic effects and heterosis in the genomic evaluation models (Table 6). Surprisingly, no changes in prediction accuracy of GBV were observed when including heterosis predicted by the HET1 method in the genetic evaluation models for each trait. Thus, accounting for retained heterozygosity in the genomic evaluation model did not improve prediction accuracy. This finding is consistent with the results of previous studies (Moghaddar and van der Werf, 2014; Bolormaa et al., 2015), which showed that accounting for non-additive genetic effects in genomic evaluation models does not improve accuracy of GBV predictions. However, the likelihood ratio test used to compare models with and without heterosis predicted by HET1 methods were significantly different (P < 0.01), which suggests that including heterosis predicted by HET1 method in genomic evaluation of multibreed and crossbred beef cattle population can improve model predictability and unbiasedness of genomic predictions (Su et al., 2012). Earlier research by Misztal et al. (1998) also demonstrated the benefit of incorporating non-additive genetic effects in genetic evaluations of swine, dairy, and beef cattle. Moreover, application of heterosis model in selection and mating programs creates opportunity for predicting hybrid performance through the exploitation of specific combining ability to maximize growth potentials (Dufrasne et al., 2014).
An interesting observation from this study was that including predicted heterosis from the HET2 method in the genomic evaluation model improved accuracy of GBV prediction up to 20% for some traits. Although, it is not very clear why this result occurred, it is most likely that the predicted heterosis accounted for some of the unknown sources of variation in a typical genomic evaluation model for crossbreds. Nevertheless, this study shows that opportunity exists for improving accuracy of GBV prediction for multibreed and crossbred beef cattle populations based on currently available 50K genotypes; thus, further research is warranted to validate this finding.
CONCLUSIONS
This study utilized genomic tools to develop and evaluate methods for predicting heterosis in beef cattle and to ascertain if dominance, overdominance, and breed heterozygosity can be assessed at the molecular genetic level. Positive associations of non-additive genetic effects were observed especially for growth traits, which reflect the importance of heterosis for these traits. The HET2 method was more effective in explaining phenotypic variation attributable to heterosis than HET1. Proper consideration of heterosis in genomic evaluation models has debatable effects on accuracy of EBV predictions. However, opportunity exists for predicting heterosis, and improving accuracy of genomic selection, and consequently optimizing crossbreeding programs in beef cattle.
Footnotes
The authors gratefully acknowledge funding support from Alberta Livestock and Meat Agency Ltd., Alberta Innovates Bio Solutions, and Alberta Agriculture and Forestry (AF) and in-kind contribution in animals, facilities and people received from Agriculture and Agri-Food Canada, Lacombe Research and Development Centre, with special thanks to Cletus Sehn, Ken Grimson, and their staff for animal care and management. Special thanks are also extended to Cathy Bryant and Sheldon Johnston of AF and Lisa McKeown (Livestock Gentec) for project coordination, data collection and database management.
LITERATURE CITED
- Abo-Ismail M. K., Akanno E. C., Khorshidi R., Crowley J., Chen L., Karisa B. K., Li X., Wang Z., Basarab J., Li C.,. et al. 2016. 0310 Assessing genetic diversity in Canadian beef cattle populations using Illumina BovineSNP50 chip. J. Anim. Sci. 94(Suppl. 5):148–149. doi:10.2527/jam2016-0310 [Google Scholar]
- Akanno E. C., Chen L., Abo-Ismail M. K., Crowley J. J., Wang Z., Li C., Basarab J. A., MacNeil M., and Plastow G. S.. 2017. Genomic prediction of breed composition and heterosis effects in Angus, Charolais and Hereford crosses using 50K genotypes. Can. J. Anim. Sci. 97:431–438, doi: 10.1139/cjas-2016-0124 [Google Scholar]
- Alexander D. H., Novembre J., and Lange K.. 2009. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 19:1655–1664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amuzu-Aweh E. N., Bijma P., Kinghorn B. P., Vereijken A., Visscher J., van Arendonk J. A. M., and Bovenhuis H.. 2013. Prediction of heterosis using genome-wide SNP-marker data: application to egg production traits in white Leghorn crosses. Heredity 111:530–538, doi:10.1038/hdy.2013.77 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arango J. A., Cundiff L. V., and Van Vleck L. D.. 2002. Comparisons of angus-, braunvieh-, chianina-, hereford-, gelbvieh-, maine anjou-, and red poll-sired cows for weight, weight adjusted for body condition score, height, and body condition score. J. Anim. Sci. 80:3133–3141. doi:10.2527/2002.80123133 [DOI] [PubMed] [Google Scholar]
- Bolormaa S., Pryce J. E., Zhang Y., Reverter A., Barendse W., Hayes B. J., and Goddard M. E.. 2015. Non-additive genetic variation in growth, carcass and fertility traits of beef cattle. Gen. Sel. Evo. 47:26. doi.10.1186/s12711-015-0114-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canadian Council on Animal Care 1993. In: Olfert E.D., Cross B.M., and McWilliams A.A., editors. Guide to the care and use of experimental animals. Vol. 1 Ottawa (ON): Canadian Council on Animal Care. [Google Scholar]
- Cleveland M. A., Blackburn H. D., Enns R. M., and Garrick D. J.. 2005. Changes in inbreeding of U.S. Herefords during the twentieth century. J. Anim. Sci. 83:992–1001. [DOI] [PubMed] [Google Scholar]
- Chen L., Schenkel F., Vinsky M., Crews D., and Li C.. 2013. Accuracy of predicting genomic breeding values for residual feed intake in angus and charolais beef cattle. J. Anim. Sci. 91:4669–4678. [DOI] [PubMed] [Google Scholar]
- Chen L., Plastow G., and Li C.. 2014. Estimating variance components for growth, feed efficiency and carcass merit traits in angus steers using additive and dominance genomic relationship matrices. In: Proceedings, 10th World Congress of Genetics Applied to Livestock Production., Vancouver, BC, Canada: https://asas.org/docs/defaultsource/wcgalp-posters/461_paper_8508_manuscript_144_0.pdf?sfvrsn=2 (Accessed 20 April 2017). [Google Scholar]
- Dickerson G. E. 1973. Inbreeding and heterosis in animals. In: Proceedings of the Animal Breeding and Genetics Symposium in Honor of Dr. J. L. Lush. Champaign (IL): American Society of Animal Science and American Dairy Science Association, pp. 54–77. [Google Scholar]
- Dufrasne M., Faux P., Piedboeuf M., Wavreille J., and Gengler N.. 2014. Estimation of dominance variance for live body weight in a crossbred population of pigs. J. Anim. Sci. 92:4313–4318. doi:10.2527/jas.2014–7833 [DOI] [PubMed] [Google Scholar]
- Falconer D. S. and Mackay T. F. C.. 1996. Introduction to quantitative genetics. 4th ed England: Longman Group limited. [Google Scholar]
- Gilmour A. R., Gogel B. J., Cullis B. R., Welham S. J., and Thompson R.. 2015. ASReml user guide release 4.1 www.vsni.co.uk. Hemel Hempstead, HP1 1ES, UK: VSN International Ltd. [Google Scholar]
- Holland R., and D., Loveday 2013. Understanding yield grades and quality grades for value-added beef producers and marketers. Knoxville, TN, USA:Extension SP 755 University of Tennessee Institute of Agriculture. [Google Scholar]
- Ibánẽz-Escriche N., Fernando R. L., Toosi A., and Dekkers J. C. M.. 2009. Genomic selection of purebreds for crossbred performance. Gen. Sel. Evo. 41(1):12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ihaka R., and R. Gentleman. 1996. R: a language for data analysis and graphics. J. Comp. Graph. Stat. 5:299–314. [Google Scholar]
- Konstantinov K. V., and F. D., Brien 2003. Influence of sire by year interactions on the direct-maternal genetic correlation for weaning weight of Western Australian Merino sheep. Aust. J. Agric. Res. 54:723–729. [Google Scholar]
- Krishnan G. S., Singh A. K., Waters D. L. E., and Henry R. J.. 2013. Molecular markers for harnessing heterosis.. In: Henry R. J, Molecular markers in Plants. 1st ed Ames, IA, USA:John Wiley & Sons, Inc. [Google Scholar]
- Kuehn L. A., Keele J. W., Bennett G. L., McDaneld T. G., Smith T. P. L., Snelling W. M., Sonstegard T. S., and Thallman R. M.. 2011. Predicting breed composition using breed frequencies of 50,000 markers from the US meat animal research Center 2,000 Bull Project. J. Anim. Sci. 89:1742–1750. [DOI] [PubMed] [Google Scholar]
- Lippman Z. B., and D., Zamir 2007. Heterosis: revisiting the magic, trends in Genetics, 23(2):60–66, doi.10.1016/j.tig.2006.12.006 [DOI] [PubMed] [Google Scholar]
- Lu D., Akanno E. C., Crowley J. J., Schenkel F., Li H., De Pauw M., Moore S. S., Wang Z., Li C., Stothard P.,. et al. 2016. Accuracy of genomic predictions for feed efficiency traits of beef cattle using 50K and imputed HD genotypes. J. Anim. Sci. 94(4):1342–1353. [DOI] [PubMed] [Google Scholar]
- Lee S. H., Wray N. R., Goddard M. E., and Visscher P. M.. 2011. Estimating missing heritability for disease from genome-wide association studies. American J. Human Genet. 88(3)294–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes M. S., Bastiaansen J. W. M., Janss L., Knol E. F., and Bovenhuis H.. 2015. Estimation of additive, dominance, and imprinting genetic variance using genomic data. G3 (Bethesda). 5:2629–2637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maniatis N., and G. E., Pollott 2003. The impact of data structure on genetic (co)variance components of early growth in sheep, estimated using an animal model with maternal effects. J. Anim. Sci. 81:101–109. [DOI] [PubMed] [Google Scholar]
- Meyer K. 1992Variance components due to direct and maternal effects for growth traits of Australian beef cattle. Livest. Prod. Sci. 31:179–204. [Google Scholar]
- Misztal I., Varona L., Culbertson M., Bertrand J. K., Mabry J., Lawlor T. J., Van Tassel C. P., and Gengler N.. 1998. Studies on the value of incorporating the effect of dominance in genetic evaluations of dairy cattle, beef cattle and swine. Biotechnol. Agron. Soc. Environ. 2:227–233. [Google Scholar]
- Miar Y., Plastow G. S., Moore S. S., Manafiazar G., Charagu P., Kemp R. A., Van Haandel B., Huisman A. E., Zhang C. Y., McKay R. M.,. et al. 2014. Genetic and phenotypic parameters for carcass and meat quality traits in commercial crossbred pigs. J. Anim. Sci. 92:2869–2884. doi:10.2527/jas.2014–7685 [DOI] [PubMed] [Google Scholar]
- Moghaddar N., and J. H. J., van der Werf 2014. Genomic estimation of additive and dominance genetic variance and their effect on the accuracy of genomic prediction of sheep. In: Proceedings of the 10th World Congress on Genetics Applied to Livestock Production. Vancouver, BC, Canada: https://asas.org/docs/defaultsource/wcgalp-posters/461_paper_8508_manuscript_144_0.pdf?sfvrsn=2 (Accessed 20 March 2017). [Google Scholar]
- Sargolzaei M., Chesnais J. P., and Schenkel F. S.. 2014. A new approach for efficient genotype imputation using information from relatives. BMC Genomics, 15:478. doi:10.1186/1471-2164-15-478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaeffer L. R B. W. Kennedy, and Gibson J. P.. 1989. The inverse of the gametic relationship matrix. J. Dairy Sci. 72:1266–1272. [Google Scholar]
- Schenkel F. S., Miller S. P., and Wilton J. W.. 2004. Genetic parameters and breed differences for feed efficiency, growth and body composition traits of young beef bulls. Can. J. Anim. Sci. 84:177–185. [Google Scholar]
- Schiermiester L. N., Thallman R. M., Kuehn L. A., Kachman S. D., and Spangler M. L.. 2015. Estimation of breed-specific heterosis effects for birth, weaning, and yearling weight in cattle. J. Anim. Sci. 93:46–52, doi:10.2527/jas2014-8493 [DOI] [PubMed] [Google Scholar]
- Shull G. H. 1914. Duplicate genes for capsule form in bursa bursa-pastoris. Z.I.A.V. 12: 97–149 [Google Scholar]
- Shull G. H. 1948. What is heterosis?Genetics 33:439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su G., Christensen O. F., Ostersen T., Henryon M., and Lund M. S.. 2012. Estimating additive and non-additive genetic variances and predicting genetic merits using genome-wide dense single nucleotide polymorphism markers. PLoS ONE 7(9): e45293. doi.10.1371/journal.pone.0045293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tambasco-Talhari D., de Alencar M. M., Paro de Paz C. C., da Cruz G. M., Rodrigues A. A., Packer I. U., Coutinho L. L., and de Almeida Regitano L. C.. 2005. Molecular marker heterozygosities and genetic distances as correlates of production traits in F1 bovine crosses. Genet. Mol. Biol. 28 (2):218–224 [Google Scholar]
- Rios Utrera A., and Van Vleck L. D.. 2004. Heritability estimates for carcass traits of cattle: a review. Genet. Mol. Res. 3:380–394. [PubMed] [Google Scholar]
- Rodriguez-Almeida F. A., Van Vleck L. D., and Gregory K. E.. 1997. Estimation of direct and maternal breed effects for prediction of expected progeny differences for birth and weaning weights in three multi-breed populations. J. Anim. Sci. 75:1203–1212. [DOI] [PubMed] [Google Scholar]
- Roso V. M., Schenkel F. S., Miller S. P., and Wilton J. W.. 2005. Additive, dominance, and epistatic loss effects on pre-weaning weight gain of crossbred beef cattle from different Bos taurus breeds1. J. Anim. Sci. 83:1780–1787. [DOI] [PubMed] [Google Scholar]
- Vitezica Z. G., Varona L., and Legarra A.. 2013. On the additive and dominance variance and covariance of individuals within the genomic selection scope. Genetics, 195:1223–1230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanRaden P. M. 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91:4414–4423. [DOI] [PubMed] [Google Scholar]
- Wang Z., Nkrumah J. D., Li C., Basarab J. A., Goonewardene L. A., Okine E. K., Crews D. H. Jr., and Moore S. S.. 2006. Test duration for growth, feed intake, and feed efficiency in beef cattle using the growsafe system. J. Anim. Sci. 84:2289–2298. [DOI] [PubMed] [Google Scholar]
- Wientjes Y., Bijma P., Vandenplas J., and Calus M. P. L.. 2017. Multi-population genomic relationships for estimating current genetic variances within and genetic correlations between populations. Genetics. doi.10.1534/genetics.117.300152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams J. L., Aguilar I., Rekaya R., and Bertrand J. K.. 2010. Estimation of breed and heterosis effects for growth and carcass traits in cattle using published crossbreeding studies. J. Anim. Sci. 88:460–466. doi:10.2527/jas.2008-1628 [DOI] [PubMed] [Google Scholar]
- Xiao J. H., Li J. M., Yuan L. P., and Tanksley S. D.. 1995. Dominance is the major genetic-basis of heterosis in rice as revealed by QTL analysis using molecular markers. Genetics 140:745–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimin A. V., Delcher A. L., Florea L.,. et al. 2009. A whole-genome assembly of the domestic cow, Bos taurus. Genome Biol. 10: R42. [DOI] [PMC free article] [PubMed] [Google Scholar]