Dynamic resting state fMRI analysis in mice reveals a set of Quasi-Periodic Patterns and illustrates their relationship with the global signal

Abstract

Time-resolved ‘dynamic’ over whole-period ‘static’ analysis of low frequency (LF) blood-oxygen level dependent (BOLD) fluctuations provides many additional insights into the macroscale organization and dynamics of neural activity. Although there has been considerable advancement in the development of mouse resting state fMRI (rsfMRI), very little remains known about its dynamic repertoire. Here, we report for the first time the detection of a set of recurring spatiotemporal Quasi-Periodic Patterns (QPPs) in mice, which show spatial similarity with known resting state networks. Furthermore, we establish a close relationship between several of these patterns and the global signal. We acquired high temporal rsfMRI scans under conditions of low (LA) and high (HA) medetomidine-isoflurane anesthesia. We then employed the algorithm developed by Majeed et al. (2011), previously applied in rats and humans, which detects and averages recurring spatiotemporal patterns in the LF BOLD signal. One type of observed patterns in mice was highly similar to those originally observed in rats, displaying propagation from lateral to medial cortical regions, which suggestively pertain to a mouse Task-Positive like network (TPN) and Default Mode like network (DMN). Other QPPs showed more widespread or striatal involvement and were no longer detected after global signal regression (GSR). This was further supported by diminished detection of subcortical dynamics after GSR, with cortical dynamics predominating. Observed QPPs were both qualitatively and quantitatively determined to be consistent across both anesthesia conditions, with GSR producing the same outcome. Under LA, QPPs were consistently detected at both group and single subject level. Under HA, consistency and pattern occurrence rate decreased, whilst cortical contribution to the patterns diminished. These findings confirm the robustness of QPPs across species and demonstrate a new approach to study mouse LF BOLD spatiotemporal dynamics and mechanisms underlying functional connectivity. The observed impact of GSR on QPPs might help better comprehend its controversial role in conventional resting state studies. Finally, consistent detection of QPPs at single subject level under LA promises a step forward towards more reliable mouse rsfMRI and further confirms the importance of selecting an optimal anesthesia regime.

Introduction

Resting state functional magnetic resonance imaging (rsfMRI) can be used to investigate functional connectivity (FC) between different brain regions by calculating temporal coherence between their spontaneous low frequency (LF) blood-oxygen level dependent (BOLD) fluctuations (Biswal et al., 1995; van den Heuvel and Hulshoff Pol, 2010; Damoiseaux et al., 2006). In humans, this allows identification of several resting state networks (RSNs) (Biswal et al., 1995; Cordes et al., 2000; Fox et al., 2006; Zhang et al., 2008), including two wide-scale anti-correlated RSNs, termed the ‘default mode network’ (DMN), containing regions active during rest, and the ‘task-positive network’ (TPN), containing regions that become activated during task performance (Fox et al., 2005; Greicius et al., 2003). By investigating FC changes in these RSNs, rsfMRI enables the clinical investigation of multiple neurological disorders (Greicius, 2008; Lee et al., 2013; Zhang and Raichle, 2010).

Recently, rsfMRI has been performed in mice, allowing reliable detection of RSNs similar to those found in humans and primates (Liska et al., 2015; Gozzi and Schwarz, 2015; Grandjean et al., 2014; Zerbi et al., 2015; Sforazzini et al., 2014; Jonckers et al., 2011; Nasrallah et al., 2014a,b). Initial applications in disease models demonstrate its usefulness to track down and disentangle underlying disease mechanisms (Shah et al., 2013, 2016a,b; Liska and Gozzi, 2016; Sforazzini et al., 2016; Stafford et al., 2014). With strict control over genetic and environmental conditions available in mice, mouse rsfMRI shows great promise as a pre-clinical tool to study FC changes in neurological disorders and enable fundamental research into mechanisms underlying LF BOLD (Keilholz et al., 2016).

RsfMRI studies are generally performed with an experimental and methodological paradigm that either assumes or imposes static FC, meaning that statistical interdependence of LF BOLD signals between different brain regions stays the same over the length of the entire scan (Biswal et al., 1995). During the last decade, studies in several species have demonstrated that this is not the case and that dynamic analysis of rsfMRI FC provides many additional insights into the macroscale organization and dynamics of neural activity (Calhoun et al., 2014; Deco et al., 2011; Hansen et al., 2015; Hutchison et al., 2013; Keilholz, 2014). Only just recently, Grandjean et al. (2017a) showed for the first time that dynamic FC could be investigated in mice and allowed identification of several highly reproducible dynamic functional states. These states display complex inter- and intra-modular organization and shed new light on information processing in the mouse brain. Dynamic rsfMRI (drsfMRI) can also be applied to investigate pathology, better explaining observed FC differences in RSNs and improving distinction between disease and control groups (Sakoglu et al., 2010; Jones et al., 2012; Damaraju et al., 2014; Rashid et al., 2014; Grandjean et al., 2017a).

Most commonly, drsfMRI is based on the sliding-window analysis (SWA) approach, where a FC metric of interest is investigated within short time windows that are incrementally shifted along the image series of the scan (Chang and Glover, 2010; Hutchison et al., 2013; Keilholz et al., 2013). For all windows, region-to-region FC matrices are obtained, which can be clustered to identify stable neural ‘states’ (Allen et al., 2014; Damaraju et al., 2014; Gonzalez-Castillo et al., 2015, 2014). SWA has shown great potential, even just recently in mice (Grandjean et al., 2017a), yet there is a lot of controversy regarding its use. The approach further suffers from the dependence on user-defined window lengths and limitations of signal-to-noise ratio that can spuriously induce FC changes (Hindriks et al., 2015; Hutchison et al., 2013; Preti et al., 2016; Shakil et al., 2016). Given these limitations and the fact that FC is inherently an indirect readout of spontaneous LF BOLD coherences, recent approaches attempted to track down instantaneous single volume BOLD configurations that underlie the observed FC (Liu and Duyn, 2013; Preti et al., 2016; Tagliazucchi et al., 2012; Wu et al., 2013). This spurred the discovery of co-activation patterns (CAPs), which resemble known RSNs and help to better comprehend dynamic changes in SWA FC (Karahanoğlu and Van De Ville, 2015).

An interesting alternative to the CAP approach is the detection of recurring consecutive sequences of ‘instantaneous’ BOLD volumes, or so-called spatiotemporal patterns, which can better capture the temporal evolution of RSNs. Such patterns were first observed in the anesthetized rat by Majeed et al. (2009), using a high temporal resolution resting state scan, and consist of bilateral intensity waves propagating from lateral somatosensory to medial cortical areas. Majeed et al. further developed an automated algorithm to track down these spatiotemporal patterns, reproducing their results in rats and discovering similar patterns in humans, where they alternatingly involve brain regions which are part of the DMN and TPN (Majeed et al., 2011). Due to their repeated occurrence and cyclical behavior, they were termed Quasi-Periodic Patterns (QPPs) (Garth John Thompson et al., 2014b). A prominent finding is that QPPs can be observed across species and are consistently detected at the single subject level with high occurrences, making them promising candidates to contribute to both static and dynamic FC. Preliminary data in humans with major depressive disorder supports this hypothesis (Wang et al., 2016). In rats, QPPs were also detected using cerebral blood volume (CBV)-weighted resting state scans (Magnuson et al., 2010), confirming their contribution to LF BOLD haemodynamics. Furthermore, they seem to have a neural precedent through correlation with infraslow local field potentials (Thompson et al., 2014a,b; Thompson et al., 2015; Pan et al., 2013). Altogether, QPPs open up a new perspective on studying FC and dynamics of LF BOLD.

In the current study, we thus investigated whether QPPs can be detected in mouse rsfMRI. If similar patterns could be observed, this would further validate the relevance of QPPs as a mechanism contributing to spontaneous BOLD coherences, and at the same time it would help to validate mouse rsfMRI as a pre-clinical tool by confirming interspecies preservation of resting state dynamics. Single subject detection of QPPs would constitute a step forward in more reliable mouse rsfMRI analysis, provide new perspectives on studying mechanisms underlying FC, and mark the development of a potential new biomarker for neurological disorders. Given the controversy on the impact of anesthesia on FC readouts in mice, we compare a low anesthesia regime of mede-tomidine and isoflurane, illustrated to allow optimal FC preservation (Grandjean et al., 2014), with an analogous higher anesthesia regime. Finally, due to the hypothesized large-scale nature of QPPs, we investigate how their behavior and detection is affected by global signal regression.

Materials and methods

Animals, preparation and anesthesia

All procedures were performed in strict accordance with the European Directive 2010/63/EU on the protection of animals used for scientific purposes. The protocols were approved by the Committee on Animal Care and Use at the University of Antwerp, Belgium (permit number 2014–04), and all efforts were made to minimize animal suffering.

Eleven male C57BL/6 J mice (Charles River) between 22 and 24 weeks old were studied. Animals were initially anesthetized with 3.5% isoflurane and maintained at 2% during handling. The animals’ heads were positioned with incisors secured over a bite bar and fixed with ear bars. Ophthalmic ointment was applied to the eyes and a rectal temperature probe was used to monitor animal temperature, which was kept stable at 37 °C via a hot air supply (MR-compatible Small Animal Heating System, SA Instruments, Inc.). Physiological parameters were measured via a pressure sensitive pad, to assess breathing rate, and a fiber-optic pulse oximeter placed over the tail, to assess heart rate and O₂ saturation (MR-compatible Small Animal Monitoring and Gating system, SA Instruments, Inc.). The respective signals were sampled at 15.895 Hz for the low anesthesia animal group (Signal breakout module, SA Instruments, Inc.). Using Short-Time Fourier Transform (window size 19.994s; intersperse 0.503s), followed by DC-component filtering, respiration and cardiac rate were determined as the frequencies corresponding to max power intensities for each time point.

Following preparation, animals received a bolus injection of medetomidine (Domitor, Pfizer, Karlsruhe, Germany), after which isoflurane was gradually lowered to 0.4% over the course of 15min and maintained at this level for the remainder of the imaging procedures. A subcutaneous catheter was inserted to allow continuous infusion of medetomidine starting at 15min post-bolus. Animals were scanned under a high anesthesia regime (HA; bolus 0.3 mg/kg & infusion 0.6 mg/kg/h; n 11) and two weeks later under a low anesthesia regime (LA; bolus 0.05 mg/kg & infusion 0.1 mg/kg/h; n = 11), to assess the impact of anesthesia on spatiotemporal dynamics in LF BOLD. Two animals from the HA group were excluded from the presented analysis, due to acquisition with offset imaging parameters (flip angle 90° instead of 55°). High temporal resolution functional resting state scans under HA and LA were acquired respectively 30min post-bolus, lasting 20min, and 40min post-bolus, lasting 10min. Conventional lower temporal resolution functional resting state scans were acquired in the LA group 30min post-bolus, lasting 5min. These scans were acquired to compare conventional ‘static’ rsfMRI analysis across both scan types in the same session, so that QPPs could be related to whole-brain dynamics. Both conventional and spatiotemporal analysis did not show any significant differences in the first or last 10min of the HA group (data not shown). Great care was taken to keep procedures and conditions identical across animals, with preparatory handling never exceeding 10min.

RsfMRI acquisition

MRI procedures were performed using a Bruker Biospec 9.4T system (Bruker Biospin MRI, Ettlingen, Germany), with a four-element receive-only phase array coil (RAPID MR international, Ohio, USA) and a volume resonator for transmission. Anatomical images were acquired in the sagittal, coronal and axial plane to allow exact and reproducible positioning of axial slices (0.4 mm thickness, 0.1 mm inter-slice). Slices were positioned to allow optimal targeting of cingulate and somatosensory areas, centered 0.1 mm caudally of bregma according to a stereotaxic mouse brain atlas (Paxinos and Franklin, 2007). The anatomical reference scan was acquired with a spin echo Turbo-RARE sequence: field of view (FOV) (20 × 20)mm², matrix dimensions (MD) [256 × 256], repetition time (TR) 3000 ms, effective echo time (TE) 33 ms, and RARE factor 8. B0 field maps were acquired to allow shimming in the target area of interest. High temporal resolution rsfMRI scans were positioned according to the anatomical reference scans and were acquired using a gradient-echo echo-planar imaging (EPI) sequence: FOV (20×20)mm², MD [128×64], slices 3, flip angle 55°, bandwidth 400 kHz, TR 500 ms, and TE 16 ms. The shorter TR enables an imaging sampling frequency of 2 Hz, necessary to investigate spatiotemporal dynamics at short time scales. Conventional temporal resolution rsfMRI scans with matching slice positions were also acquired for the LA group, using a gradient-echo EPI sequence: FOV (20×20)mm², MD [128×64], slices 16, flip angle 90°, bandwidth 400 kHz, TR 2000 ms, and TE 16 ms.

Preprocessing

All analyses were performed using MATLAB2015a (Mathworks, Natick, MA). Motion parameters for rsfMRI images were computed using 3 rigid body parameters for the high temporal resolution low slice count datasets, which retains all 3 slices for single subject analysis, and 6 rigid body parameters for the conventional high slice count dataset. RsfMRI images were then realigned, normalized to a user-defined reference subject, smoothed (σ = 2 pixels), and motion vectors were regressed out of the image series. These preprocessing steps were performed using Statistical Parametric Mapping (SPM12) software (Wellcome Department of Cognitive Neurology, London, UK). Afterwards, image series were band-pass filtered with a FIR filter between 0.01 and 0.2 Hz, quadratic detrended and normalized to unit variance. Before and after filtering, transient time points at the start and end of the image series were removed. Consecutive group-level analysis of the high temporal resolution low slice count datasets was performed solely on the center slice, given that the first and last slices were lost during the normalization process. For detection of spatiotemporal patterns, images were investigated with and without global signal regression, and a brain mask was employed that excludes the ventricles to avoid their contribution to spatiotemporal pattern detection.

Conventional resting state fMRI analysis

Group independent component analysis (ICA) was performed using the GIFT toolbox (v4.0a) (Calhoun et al., 2004) on data that was not motion regressed. For the high temporal resolution data, where only the single center slice was investigated, we tested several different numbers of independent components (IC). When more than six ICs were used, this caused the observation of unilateral components, while when six ICs were used, this preserved the integrity of bilateral BOLD signals matching known neuroanatomical regions. Using these criteria, 6 ICs were empirically determined appropriate for single-slice analysis. For the conventional 16-slice lower temporal resolution dataset, we employed 15 ICs, based on preceding literature (Shah et al., 2015, 2016a; Sforazzini et al., 2014). All ICA analysis was run on variance-normalized data, filtered between 0.01 and 0.2 Hz, and using the Infomax algorithm with no auto-filling of data reduction values. A brain mask was used to remove signals exterior to the brain. Stability analysis was performed using the ICASSO algorithm, rerunning the ICA 50 times with a minimal cluster size of 30 and maximal of 50. All other default parameters of GIFT were left unaltered.

For conventional ‘static’ functional connectivity (FC) analysis, regions of interest (ROI), measuring 6 voxels, were selected matching both a stereotaxic mouse brain atlas (Paxinos and Franklin, 2007) and overlapping with maximal intensities in ICs determined with ICA. ROIs were subsequently used to construct ROI-based FC matrices and seed-based FC maps. FC values were Fisher Z-transformed. For within group statistical analysis of ICs and seed-based FC maps, one sample T-tests (two-tailed, p < 0.05) were performed with false discovered rate (FDR) correction. For between group statistical analysis of the ROI-based FC matric, a paired T-test (two-tailed, p < 0.05, FDR-correction) was used. All statistical analyses were performed using SPM12 software.

Spatiotemporal pattern-finding algorithm and k-means clustering

To track down putative recurring spatiotemporal patterns, we employed the algorithm from the group of Shella Keilholz that was previously used to identify Quasi-Periodic Patterns (QPP) in humans and rats (Majeed et al., 2011) (The respective MATLAB code is available upon request via contact with the corresponding author). The algorithm uses a data-driven correlation approach that identifies spatiotemporally similar subsections in the functional (BOLD) image series. It essentially increases the signal-to-noise ratio of repetitive spatiotemporal blocks, allowing averaging and preservation of temporal information. In brief, the algorithm works by first isolating a random seed section, consisting of a series of consecutive images at a random starting time point. The length of the spatiotemporal template (i.e. the window size or number of images) is defined by the user. The template is then incrementally shifted (a single TR) along the image series and a Pearson correlation value is calculated at every time point (movie 1). A Sliding Template Correlation (STC) time series is derived which identifies when the template is similar to the image series. Peak correlation values, exceeding an arbitrary threshold, are used to select and average the associated image series at related time points into a new updated template, which can then be used to extract correlations in the same way. This process is iteratively repeated until the template no longer changes, i.e. the cross-correlation (cc) of templates of two consecutive iteration steps > 0.9999. At this point, the QPP is established and correlation peaks in the STC exceeding the threshold reflect moments of pattern occurrences. A more detailed description can be found in the original article (Majeed et al., 2011). In the current study, we employed the same correlation thresholds.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.075.

Because the starting time point of the initial random seed template can affect the final outcome, the entire process described above is repeated several times to derive a set of QPPs for a respective window size under investigation. To identify a single representative QPP from this set, each of the obtained QPPs is transformed into its vector form, which measures the total amount of voxels comprised in the image mask multiplied by the amount of image frames within the QPP (i.e. vectors from each masked image frame are concatenated). These vectors are then clustered via k-means clustering, using correlation as a distance metric. The optimal QPP is determined by tracking down the QPP, which presents the maximal silhouette value within the cluster with the highest average silhouette values. A silhouette value indicates how similar an object is to its own cluster and how much it differs from other clusters. K-means clustering has been employed previously in rsfMRI literature to cluster functional images (Anderson et al., 2010; Liu and Duyn, 2013). The way k-means is employed in this study, without prior phasing of QPPs, essentially tracks down the QPP that was most robustly detected while being at a specific phase.

The procedures described above were performed for all investigated template window sizes. Data presented in this work was either analyzed at group level, through concatenation of normalized image series, which allowed pattern identification in a single center slice, or at individual subject level, which allowed pattern identification in all three slices. We employed respectively 500 (group) and 200 (subject) random starting time points.

Spatial and temporal cross-correlation

QPPs were compared with each other via two basic ways. The STCs of individual QPPs describe their similarity and timing with respect to the image series. By performing cc between STCs, one can establish a measure of QPP similarity, and identify their temporal offsets from one another. The latter information is used to display QPPs at their appropriate timing (e.g. Fig. 3A) and to phase-align them (e.g. Fig. 2). Another option to identify QPP similarity is via circular cc of their spatiotemporal images. Each single QPP is transformed into its vector form, which measures the total amount of voxels comprised in the image mask multiplied by the amount of image frames within the QPP. The resultant vector can be circularly shifted (using the MATLAB ‘circshift’ function), with increments measuring the length of indices in the image mask (i.e. a single frame), to calculate the cc.

Fig. 3. Spatiotemporal patterns detected at the group level.

A) Illustration of the Sliding Template Correlation (STC) time series associated with QPPs observed at different window sizes. Upper panel. Single STC excerpt at a window size of 12s. Red line indicates the threshold for pattern detection, with QPP occurrences indicated by black triangles. Lower Panel. Close-up of several STCs at different window sizes, illustrating phase offsets between detected patterns. Red indicates anti-phasic detections, versus similar phase detections in blue. B) Cross-correlation (cc) matrix of STCs at different window sizes. Lower triangle indicates max cc values, while upper triangle shows phase offsets (seconds) between detected patterns. Note the high cc from window size 12s upwards. C) Rows present QPPs determined for different window sizes of analysis (vertical axis), while their temporal unfolding is shown across the columns (horizontal axis; images interspersed by 1.5s). Images display normalized BOLD signals. QPPs are phased using the time delays of their STC cc (left panel). The resultant alignment can be visually appreciated. Note that the figure suggests that several types of QPPs could be observed (e.g. at 7.5s, 10.5s & 12s). At 12s we observed a full non-redundant pattern, displaying bilateral S2 towards medial Cg intensity propagation, followed by a low intensity wave (green square). Red square indicates redundancy or repeating parts of the cycle.

Fig. 2. Additional whole-brain resting state networks.

This figure is complimentary to Fig. 1E and displays the remaining ICA-derived RSNs, obtained from the whole-brain low temporal resolution data. Note the observation of bilateral RSNs that display similarity with preceding mouse rsfMRI literature. Maps display thresholded T-values (one-sample T-test, p < 0.05 FDR-corrected).

Data-driven identification of pattern optimal window size

The ideal window size of putative mouse rsfMRI QPPs is unknown. Previous strategies used visual inspection and pattern speed as a reference (Majeed et al. 2009, 2011; Thompson et al., 2014b). Here, we developed an automated processing tool to determine optimal window sizes in a data-driven fashion, termed fractional average correlation (FA).

In a set of QPPs of the same pattern type, where each QPP is determined at a different window size and at the same phase, each individual pattern is subdivided into all possible consecutive fractions of a fixed length specified by the smallest window size investigated. To illustrate, in the presented analysis the smallest window size is set at 6 TRs (3s), meaning that a pattern of e.g. 24 TRs long will be divided into 19 fractions of 6 consecutive images, each shifted by 1 TR (Fig. S1A). Each individual fraction from a QPP at a specific window size is then treated as a reference, and the maximal cc value is calculated with respect to the complete ‘target’ QPP at another window size (Fig. S1A-B). The average of the resultant cc values represents a measure of how many fractions the reference and target QPP have in common, i.e. the FA. The FA value is calculated for all possible combinations of window sizes, constructing an n × n correlation matrix, where n represents the number of different window-sized QPPs and each column represents the FA values for a specific reference QPP with each respective QPP in the set (Fig. S1C). By averaging the FA matrix across its columns, the set-wise FA value for each QPP is determined.

The power of this approach lies in the notion that target QPPs at smaller window sizes than the reference QPP under investigation have less fractions in common, given that they only represent a subpart. Comparing larger reference QPPs with non-matching subparts in short target QPPs decreases the FA value. Long target QPPs, however, are likely to contain the full pattern and will therefore show a high FA. The tipping point of increasing FA, before a plateau is reached, reflects the optimal window size.

Data-driven pattern classification using hierarchical clustering

Within a set of patterns, determined at a given window size for the group wide analysis, multiple types of spatiotemporal patterns could be visually distinguished. To validate visual classification, set-wise n × n cc matrices are constructed via either spatial or STC cc, where n is the number of QPPs compared (n = 500). The columns of these symmetrical matrices are used to perform hierarchical clustering, using correlation as a distance metric. Cc scopes QPP similarity with one another and consecutive clustering of set-wise cc values for each QPP further accentuates their overall relationship. Opposed to the employed strategy for k-means clustering, cc inherently aligns QPP phase during the clustering process. Hierarchical clustering is an unsupervised approach, thus removing potential bias from cluster number pre-selection. Visual observation of sorted block designs and inspection of their content then serves to validate pattern subtype separation.

Phase sorting of spatiotemporal patterns

After global signal regression (GSR), opposite phase detections of QPPs dominated hierarchical clustering off cc matrices. To illustrate that only a single QPP was detected at opposite phases, QPPs can first be sorted based on their phase, prior to performing clustering. The Cingulate (Cg) component was present in both LA and HA groups, as determined with ICA and observed in all established QPPs. Masks were therefore constructed from the Cg independent component thresholded T-maps, which were subsequently used to calculate the average Cg intensity across each image frame of the QPPs. This establishes a time series of the Cg region that can be used to phase sort QPPs based on either displaying first high or low Cg activity.

Global co-activation patterns

To more closely investigate the shape of the global signal, an analysis methodology is employed that was inspired by the CAP approach (Liu and Duyn, 2013). Briefly, in the latter, supra-threshold crossings of signal in chosen neuroanatomical seed locations are used to extract fMRI frames to be averaged or further processed by clustering. This allows the detection of instantaneous fMRI volumes that contribute to FC and known RSNs. The same strategy is adapted for the current study, but using the global signal as a seed region, and increasing the extent of averaged fMRI frames to a window centered on peak intensity time points. Essentially, all peaks in the global signal of the concatenated group image series are identified and out of these, the subset highest peaks are chosen. The latter is determined by matching the amount of chosen peaks to the average occurrences of QPPs (at their ideal window length) that we hypothesize to be related to the global signal (pattern 2 & 3 for LA; pattern 2 & 4 for HA; cfr. Results). Given the resultant set of peak time points T = {T₁, T₂, …, T_P}, with P being the number of peaks, a 3D matrix Y = [X_Ti-WL/2, X_Ti-WL/2+1, …, X_Ti+WL/2] is constructed, with X_Ti being the image frame at time T_i and WL the chosen window length for frames to be averaged. The matrix Y is averaged across the third dimension to produce the global CAP.

Results

We acquired high temporal resolution rsfMRI scans in a set of 11 C57BL/6 J mice. Subjects were scanned under a high anesthesia regime (HA, 0.3 mg/kg bolus & 0.6 mg/kg/h infusion of medetomidine) and were rescanned two weeks later under a low anesthesia regime (LA, 0.05 mg/kg bolus & 0.1 mg/kg/h medetomidine). Two subjects of the HA group were not included in the presented analysis due to acquisition with offset parameters. We focus on the outcome of the LA group, while results under HA are more briefly addressed at the end of each section and related figures are presented in the supplementary data. A direct comparison is made in sections Spectral information and resting state network functional connectivity and Quantitative comparison of Quasi-Periodic patterns between high and low anesthesia, before and after global signal regression.

Spectral information and resting state network functional connectivity

Conventional rsfMRI analysis in rodents typically employs a TR between 1 and 2s and investigates LF BOLD fluctuations filtered in ranges between 0.01 and 0.1 Hz or 0.01–0.3 Hz (Gozzi and Schwarz, 2015; Grandjean et al., 2014; Jonckers et al., 2015; Liska et al., 2015). To enable detection of propagating spatiotemporal patterns, we acquired scans with a TR of 500 ms, providing a spectrum with a wider range (up to 1 Hz) and higher temporal resolution. Visual inspection of group-average power spectra revealed that under LA the highest spectral information content was confined to the range below 0.2 Hz, while power in the HA group was in general lower (Fig. 1A). The spectra of both groups displayed a high peak below ~0.015 Hz, consistent with literature suggesting band-pass filtering above 0.01 Hz to remove baseline drift (Bianciardi et al., 2009; Yan et al., 2009).

Fig. 1. Spectral range and resting state networks.

All ICA and FC maps display thresholded T-values (one-sample T-test, p < 0.05 FDR-corrected). A-D) Single-slice high temporal resolution data. A) Group average multitaper power spectral density of the center brain slice for the low (LA, blue) and high (HA, red) anesthesia groups. Patches indicate standard deviations. Note the higher power under LA. The frequency range displays the highest spectral content, with the full range shown on top. Based on this observation, all data were filtered between 0.01 and 0.2 Hz. B) LA (top) and HA (bottom) RSNs determined with ICA. Top row text indicates similarity with resting state networks, lower row indicates overlap with anatomical parcellations (Paxinos and Franklin, 2007). C) ROI-based zFC matrix for LA (top right) and HA (bottom left). Significant differences are indicated with ‘S’ (two-sample T-test, FDR p < 0.05). ROIs are indicated on a representative EPI image. D) LA (top) and HA (bottom) seed-based FC maps, using left ROIs (C). Note for HA, the loss of FC, and for LA, the similarity with ICA-derived RSNs (B). E-F) Whole-brain low temporal resolution data. The matching slice, investigated in the high temporal resolution data, is indicated in blue. E) LA whole brain RSNs matching those shown in (B). Note the speculative mouse TPN and DMN, matching single slice lateral and cingulate ctx networks. Only two whole-brain striatal networks were observed, and two S1 networks instead of one. F) LA Seed-based FC maps illustrate similarity with RSNs (E). A third striatal network is now again observed. Abbreviations. LA, low anesthesia; HA, high anesthesia; ctx, cortex; Cg, Cingulate; S1, somatosensory area 1; FL, forelimb; HL, hindlimb; BF, barrel field; S2, somatosensory area 2; Cpu, caudate putamen; d, dorsal; vl, ventro-lateral; VP, ventral pallidum; Pir, piriform ctx; I, insular ctx; En; enthorhinal ctx; Tea, temporal association ctx; HC, hippocampus; TH, thalamus; DMN, default mode network; TPN, task positive network; RSN, resting state network.

Group-level analysis was restricted to a single slice, due to image normalization. After 0.01–0.2 Hz band-pass filtering, group ICA of the LA data revealed the presence of six meaningful bilateral RSNs, overlapping with neuroanatomical locations (Fig. 1B): Ventral Pallidum (VP), ventro-lateral Caudate Putamen (Cpu vl), dorsal Caudate Putamen (Cpu d), Somatosensory area 1 (S1) forelimb and hindlimb (HL/FL), Somatosensory area 2 (S2), and Cingulate cortex (Cg). These six RSNs appeared to match known mouse RSNs (Zerbi et al., 2015; Grandjean et al., 2017b; Liska et al., 2015; Sforazzini et al., 2014). To validate if single-slice RSNs in short TR (0.5s) data match with those in conventional whole-brain lower TR (2s) data, 16-slice rsfMRI scans were acquired during the same LA sessions. ICA of this data indeed revealed the same RSNs (Fig. 1E). However, in this data we observed only a single Cpu component and two somatosensory components, of which the S1 HL/FL component partially overlapped with S1 barrel field (BF).

When LA RSNs of the short and long TR data were compared, it became apparent that S2 and Cg components, determined in the short TR data, overlapped respectively with the large-scale lateral cortical network and the Default Mode like network (DMN) in the long TR data. The lateral cortical network has been suggested to represent a potential mouse Task-Positive like network (TPN) (Gozzi and Schwarz, 2015; Liska et al., 2015). These findings suggested that short TR single-slice RSNs pertain to whole-brain networks. This supported the conceptual paradigm that a well-positioned single-slice investigation allows a view into whole-brain dynamics. Under HA, ICA of the short TR data revealed similar single-slice RSNs as under LA, but with a less pronounced bilateral extent (Fig. 1B), suggesting compromised FC.

Finally, we also directly investigated FC. Left and right ROIs, matching with both the RSN peak intensities and a mouse stereotaxic brain atlas (Paxinos and Franklin, 2007), were used to construct a FC matrix in which HA and LA groups were compared (Fig. 1C). S2, Cg, and Cpu d showed significantly decreased bilateral FC in the HA group (two-smaple T-test, two-tailed, p < 0.05 FDR-corrected). Cpu d – Cg, VP – Cg, S1FL – S2, and Cpu vl – S2 also showed significantly lowered FC under HA. Seed-based FC analysis of the short TR LA data resulted in FC maps that were highly similar to the respective RSNs (Fig. 1B&D). For the HA short TR data, no FC was apparent after significance thresholding. Seed-based FC analysis of the long 2s TR data similarly reproduced whole brain RSNs and additionally allowed the detection of both Cpu d and Cpu vl components (Fig. 1F).

Lastly, it should be noted that, while all observed RSNs matched generally with known mouse RSNs, some inconsistencies in homotopic representation and functional coupling were apparent (study limitations in dicussion). Therefore, to provide full transparency into our findings, we additionally present the remaining ICA-derived RSNs that were observed in the LA whole-brain 2s-TR data (Fig. 2). These RSNs displayed bilateral coupling similar to what has been observed in other mouse rsfMRI studies (Grandjean et al., 2014; Liska et al., 2015).

Exploring group wide spatiotemporal dynamics

Without a clear a priori knowledge of the time span of putative QPPs, we investigated a series of different window sizes. This was achieved by running the spatiotemporal pattern finding algorithm on the center slice image series of all subjects.

We observed consistent and well-defined bilateral spatiotemporal patterns for all investigated window sizes ranging from 3 to 18s (Fig. 3C). To interpret the findings across different window sizes, three major factors need to be considered: (1) the algorithm is to some extent insensitive to phase, meaning that patterns can be detected at different start times; (2) small window sizes inherently only scope part of a larger pattern; (3) different window sizes can skew detection towards different patterns. In a first approach, we addressed this by making use of each observed pattern’s correlation time series, determined via sliding window correlation with the image series, which we refer to as the Sliding Template Correlation (STC) (movie 1 & Fig. 3A). By calculating the cc of different patterns’ STCs at different window sizes, we can establish their temporal overlap and adjust their phase so that the patterns align (Fig. 3B). Using visual inspection, this initial exploration of the data revealed a non-redundant full-size QPP at 12s. Phasing to the STC of this QPP allowed a meaningful alignment of all observed QPPs (Fig. 3C), facilitating comparison and interpretation.

Starting from a window size of 12s and upward, we observed high and consistent STC cc and QPP spatial cc, with average values of respectively (0.96 ± 0.03) and (0.94 ± 0.01). STC cc from shorter window sizes with the STC at 12s were however considerably lower and less consistent (0.66 ± 0.10), while QPP cc was less diminished (0.81 ± 0.04). This discrepancy in STC cc between shorter and longer window sizes suggested the detection of different spatiotemporal patterns, which was also hinted by visual inspection of Fig. 2C.

The same analysis was performed for the HA group (Fig. S2), where an optimal window size was visually determined at 7.5s. STC cc (0.84 ± 0.09) and QPP cc (0.89 ± 0.05) were high sizes. across all window This initially suggested the observation of only one single spatiotemporal pattern.

Multiple Quasi-Periodic Patterns

The group wide QPPs displayed in Fig. 2C were derived from iteratively running the algorithm 500 times per window size and selecting the optimal one via k-means clustering and silhouette classification. We repeated this analysis at each window size with 100 iterations, but now visually inspected all individual QPPs to determine the full repertoire. We consistently observed a set of 3 different QPPs (Fig. 4A–B & movie 2), which could be detected at almost all window sizes (Fig. 4D). Pattern identification was supported by their high spatial similarity with known RSNs in mice (Fig. 1B&D). For the purpose of consistent classification, we employed a set of selection criteria that describes their behavior (Fig. 4B). Pattern 1 (PAT1) first displays high intensity in lateral cortices centered on S2, and subsequently also involves S1 areas, Cpu vl, and to some extent the enthorhinal (En) and insular (I) cortices. The pattern further spreads with lower intensity along Cpu d, towards medial cortical areas centered on Cg. Regional contrasting high and low intensities are marked by a positive and negative cycle, followed by a prolonged more global negative intensity. PAT2 displays simultaneous high intensity in the Cpu d and Cg. PAT3 starts similar to PAT1 with lateral high intensity, which now becomes more widespread involving a larger area of Cpu, S1, En and Cg. Both PAT2 and PAT3 display a negative wave to complete the cycle.

Fig. 4. Detection of multiple Quasi-Periodic Patterns based on window size and visual inspection.

A) Three different types of QPPs could be identified and are displayed at their respective ideal window sizes, after phase-alignment (1s intersperse). PAT1 is marked by contributions in cortical regions with opposing intensities. PAT2 and PAT3 display stronger involvement of Caudate Putamen, which are co-active with medial cortical regions. PAT2 does not display lateral cortical high intensities. Both PAT2 and PAT3 high intensities coincide with the S2-Cg intensity switch of PAT1”, instead of “coincide with PAT1’s S2-Cg intensity switch. B) Schematic illustration of the spatiotemporal flow of the three patterns. Circles indicate key regions that were used to visually classify patterns, while activity propagation is indicated by arrows. Red indicates high and blue low intensities. All involved brain regions are indicated in green on the middle illustration. C) STC cc matrices across all window sizes, for each pattern. PAT1 was more reliably detected at longer window sizes, PAT2 more at shorter ones. PAT3 appeared similarly correlated across most window sizes. D) Detection rate of each pattern, as determined by visual classification of a 100 patterns per window size. Note the bell-shape curve of PAT2 and PAT3 at shorter window sizes, and the U-curve for PAT1, which takes over after 12s (red circle). These curves illustrate skewed pattern detection dependent on window size. E) Fractional average correlation per window size. Red circles indicate the start of a plateau, representing the ideal window size. F) Occurrence rate across window sizes. Note the higher occurrence rates for PAT2 and PAT3 at shorter window sizes. G) Illustration of the overlap between non-phase-corrected STCs, determined for each pattern’s ideal window size. Although there is variation in peak timing and temporal correlation, individual patterns display coincident behavior with one another.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.075.

Classification of QPPs allowed us to estimate the detection rate across window sizes (Fig. 4D). PAT2 and PAT3 displayed a bell-shaped curve, with detection rates exceeding that of PAT1 at window sizes between 7.5 and 10.5s. PAT1 displayed a U-shaped curve, with higher detection rates at the smallest and largest window sizes. Especially interesting is the take-over at 12s and upward, exceeding PAT2 and PAT3 detection rates. The observed distributions of detection rates were strongly in line with QPPs determined in the general analysis using k-means clustering and silhouette detection (Fig. 3C). To validate if QPPs in the latter were representative, the k-means algorithm was iterated 10 times and the outcomes were visually inspected. Below 9s, pattern detection was highly consistent, always finding the same QPPs, at 9s a mixture of PAT2 and PAT3 was found, at 10.5s a mixture of PAT1 and PAT3, and above 12s a mixture of PAT1 and PAT3 with PAT1 dominating (74%). These findings were in line with presented results and illustrate how k-means clustering becomes less reliable towards longer window sizes.

To further investigate this skewed detection, we isolated QPPs and their associated STCs for each type of pattern at every window size. STC cc was high and consistent at window sizes of 10.5–18s for PAT1 (0.93 ± 0.02) and 6–13.5s for PAT2 (0.94 ± 0.03), while PAT3 seemed less confined to a specific range (6–16.5s; 0.88 ± 0.06) (Fig. 4C). QPP cc was high across all window sizes: PAT1 (0.94 ± 0.04), PAT2 (0.87 ± 0.10) & PAT3 (0.92 ± 0.06). PAT2 QPP cc was higher at window sizes of 6–13.5s (0.94 ± 0.02). Further, PAT2 and PAT3 displayed higher occurrence rates (i.e. the amount of correlation peak threshold crossings in the STC) at window sizes below 10.5s (Fig. 4F), but became equal with PAT1 afterwards.

After establishing the presence and behavior of 3 individual patterns, we used visual inspection, QPP detection rate (Fig. 4D), and FA (Fig. 4E) to determine optimal window sizes for each: PAT1 12s, PAT2 9s and PAT3 9s. These optimal sizes seem in line with the skewed detection rates across window sizes. All three patterns were observed throughout the different subjects, with PAT1 and PAT3 displaying higher variability (Table 1). An overlay of each pattern’s STC, determined for its respective ideal length, illustrated their overall coincident behavior (Fig. 4G). Although there was variation in timings and temporal correlation strength, patterns appeared to often be co-active, but could nonetheless be separated by the spatiotemporal pattern-finding algorithm. Specifically, PAT2 & PAT3 appeared to lag behind PAT1, causing their high intensity phase to fall in between the S2-Cg switch of PAT1 (Fig. 4A).

Table 1.

Pattern occurrence rate per subject.

	Pattern occurrence rate (counts/min)
	Sub1	Sub2	Sub3	Sub4	Sub5	Sub6	Sub7	Sub8	Sub9	Sub10	Sub11	Mean
PAT1 - 12s	2.0	0.8	0.5	1.1	0.8	1.9	0.6	1.9	1.6	0.7	2.8	1.3 ± 0.7
PAT2 - 9s	1.0	1.4	1.2	1.4	1.4	1.8	1.6	2.2	1.3	1.7	1.8	1.5 ± 0.3
PAT3 - 9s	2.0	1.2	1.4	1.4	0.7	2.2	1.1	2.3	1.3	2.2	2.5	1.7 ± 0.6
GSR - 9s	1.8	1.4	1.0	1.3	1.0	2.9	0.7	1.9	2.2	1.4	3.1	1.7 ± 0.8
Cortex - 9s	4.0	3.0	2.4	2.9	2.2	4.0	2.0	3.7	3.7	3.4	4.0	3.2 ± 0.7
Cp - 9s	2.5	2.3	3.7	1.8	1.2	2.8	1.8	3.2	2.5	1.7	2.8	2.4 ± 0.7

Half cycle times, defined as the time to change from maximal to minimal intensity of a brain region within the QPP, were similar across all three patterns and different window sizes, averaging to approximately 4.6s (Table 2). Propagation time, defined as the time delay of maximal intensity occurring in one brain region within the QPP after maximal intensity detection in another region, from lateral (S2 or Cpu) to medial regions were different between the patterns, being shorter for PAT2 and PAT3.

Table 2.

Pattern half cycle time and propagation time from lateral to medial, averaged across relevant window sizes.

	Half cycle time (max to min)					Propagation speed
	Lateral left	Lateral right	Medial	Cp left	Cp right	Lateral Left to Medial	Lateral right to Medial	Cp left to Medial	Cp right to Medial
PAT1	4.5 ± 0.4s	4.8 ± 0.5s	4.2 ± 0.4s	4.7 ± 0.9s	3.9 ± 0.4s	4.4 ± 0.6s	4.6 ± 0.7s	3.3 ± 1.4s	4.3 ± 0.8s
PAT2	4.4 ± 0.6s	5.2 ± 1.0s	4.6 ± 0.3s	4.2 ± 0.3s	4.6 ± 0.6s	1.7 ± 0.4s	2.0 ± 0.7s	0.6 ± 0.2s	0.7 ± 0.3s
PAT3	4.5 ± 0.4s	4.7 ± 0.5s	4.7 ± 0.6s	4.4 ± 0.5s	4.3 ± 0.4s	1.2 ± 0.7s	1.1 ± 0.6s	0.4 ± 0.3s	0.8 ± 0.4s
GSR	4.5 ± 0.5s	4.3 ± 0.4s	4.5 ± 0.3s	8.4 ± 4.8s	4.7 ± 2.4s	4.8 ± 0.4s	4.7 ± 0.4s	5.5 ± 1.5s	1.8 ± 1.5s
Cortex	4.4 ± 0.7s	4.3 ± 0.4s	4.2 ± 0.4s	5.6 ± 1.6s	4.5 ± 0.8s	3.8 ± 0.4s	3.8 ± 0.4s	3.5 ± 0.6s	2.2 ± 1.3s
Cp	5.2 ± 1.5s	4.5 ± 1.0s	4.5 ± 0.6s	3.8 ± 0.5s	3.7 ± 0.3s	1.4 ± 0.5s	1.4 ± 0.3s	0.6 ± 0.4s	0.5 ± 0.4s

Classification analysis was also performed on the HA group, which originally displayed only one type of pattern (Fig. S2A) that appeared highly similar to PAT2. Further inspection revealed detections of patterns similar to PAT1 and a fourth type (Fig. S3A & movie 3). The latter appeared similar to PAT2, but with more widespread and ventral involvement of Cpu, and less contribution of the medial cortex. QPPs further tended to display more unilateral behavior or bilateral delays.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.075.

Under HA, PAT2 detection rate seemed to be dominant across all window sizes (Fig. S3C), in line with the QPPs observed in the general analysis. Repeating the k-means algorithm for the HA group similarly revealed that mostly PAT2 was detected. STC cc revealed that PAT1 (0.73 ± 0.09) could now only be consistently detected up to a window size of 7.5s, while PAT2 (0.84 ± 0.09) and PAT4 (0.73 ± 0.10) were similar across all window sizes (Fig. S3B). Overall cc values were lower for HA than for LA, illustrating increased difficulty of consistent observations. Occurrence rate was similar across all three patterns, averaging ±0.8 occurrences/min (approx. half that of under LA: ±1.5 occurrences/min), and they were detected in all subjects (Table S1). Ideal window sizes for all types of HA patterns were observed at 7.5s (Fig. S3D), while half cycle times averaged to ±3.7s. Consistent with the respective spatiotemporal shape, and as was observed in the LA group, propagation time from lateral to medial was shorter in PAT2 and PAT4 than in PAT1 (Table S2).

Data-driven validation confirms multiple Quasi-Periodic Patterns

Visual classification might suffer from user bias, leading to a potentially wrongful identification of three separate patterns under LA. To validate our findings, we employed a novel approach to cluster spatiotemporal patterns, utilizing hierarchical sorting of pattern cc matrices. Individual patterns at respective window sizes (7.5–13.5s) were clustered using either their spatial structure (Fig. 5A) or their STC (Fig. 5B). In both cases clustering was most successful at shorter window sizes, clearly indicating the presence of three separate clusters. Visual inspection of their content revealed that clusters predominantly contained a single type of pattern, confirming the existence of three patterns types. Similarly, the sorted average cc of all individual patterns with every other pattern revealed stepwise transitions, confirming clear pattern distinction.

Fig. 5. Hierarchical clustering confirms three Quasi-Periodic Patterns.

All 500 individual QPPs, determined at each displayed window size, were hierarchically clustered using a maximal cross-correlation (cc) matrix based on: A) QPP spatial similarity. B) QPP temporal occurrence similarity, i.e. STC cc. Columns indicate the respective window size under investigation. Upper row panels show clustered cc matrices of the QPPs. Clusters were visually inspected and their content marked above the panels (MIX = mixture of all pattern subtypes). Note the clear presence of three clusters at shorter window sizes, especially via STC cc, confirming the prior visual classification. Lower row panels show the average sorted cc of each QPP with all other QPPs (black trace, STD indicated by grey patch). This serves as an indicator of overall QPP (dis)similarity, supporting the notion of different subtypes. Blue curves indicate the 10% fraction of QPPs that displayed the highest cc plateaus. Note the sharp transitions at shorter window sizes, indicating clear distinction between different pattern subtypes.

With increasing window size clustering became more difficult and pattern separation less clear. This was similar to the observations made for k-means clustering and was to be expected given the increasing dimensionality of data to be clustered. Towards longer window sizes PAT1 detection rate increased, which matched preceding results (Fig. 4). PAT2 and PAT3 ideal window sizes had been determined at 9s, thus increasing the window size under investigation forces the detection algorithm to find longer patterns that contain more noise or overlap with other patterns, potentially contributing to less efficient clustering at higher window sizes. The proposed clustering method at this point seemed not to be sufficiently reliable to replace visual classification, but did serve valuable to illustrate the existence of three different patterns.

Under HA, hierarchical clustering similarly allowed separation of PAT1, PAT2 and PAT4 at short window sizes (Fig. S4). However PAT2 and PAT4 were less clearly separable, suggesting some potential overlap. At longer window sizes pattern cc was very low and only minor clustering could be observed.

Global signal regression accentuates pattern 1 while removing spatiotemporal dynamics closely related to the global signal

After GSR, using the k-means algorithm and silhouette scoring, only a single QPP could be observed across all window sizes (Fig. S5A). Repeating k-means clustering 10 times consistently reproduced this finding. GSR QPPs were highly consistent across window sizes (STC cc 0.96 ± 0.02 & QPP cc 0.96 ± 0.04) (Fig. S5B), with their ideal length judged at 9s by taking into account FA. GSR QPPs were highly similar to PAT1 (QPP cc 0.88), displaying the same lateral to medial cortical propagation (Fig. 6A & movie 4). The spatiotemporal profile after GSR was marked by a sharper contrast between positive and negative intensities and a loss of the prolonged negative intensity observed in PAT1.

Fig. 6. Global signal regression removes detection of PAT2 and PAT3, while preserving only PAT1. PAT2 and PAT3 display high similarity with the global signal.

A) QPPs observed after GSR. The three displayed patterns are the same, but due to differences in phase detection, the starts and ends display higher intensities. P1 and P2 respectively refer to high and low intensities in the Cg. GSR P1 and P2 are shown phase-aligned to PAT GSR. A global CAP is shown below to illustrate its timing as falling between the S2-Cg switch. B) To illustrate the detection of only one pattern after GSR, hierarchical clustering was employed, but patterns were first sorted based on their temporal intensities in the Cg. Respective average Cg time series are displayed in red and blue, while black lines indicate unsorted patterns (center phase). A comparison is shown on the left under conditions of no GSR. Clusters were visually inspected and their content marked in red or blue to indicate relationship to Cg phase. C) Upper panel. Illustration of the overlap between non-phase-corrected STCs for PAT1-3 and PAT GSR. Note the high STC overlap and similarity between PAT1 and PAT GSR. Lower panel. All three apparent GSR patterns are displayed at the same timing as the above panel. Note their clear anti-phasic behavior, indicating they are the same. D) Left panel. STC cc between PAT1-3 and PAT GSR. Note the clear and low cc of PAT GSR with PAT2-3, suggesting that GSR removes their occurrences. Right panel. STC cc with the global signal. Note higher cc values for PAT2-3. Abbreviations. GSR, global signal regression; CAP, co-activation pattern.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.075.

Visual inspection off all GSR QPPs indicated that PAT2 and PAT3 detection was abolished. Hierarchical clustering appeared to produce separate clusters, which would suggest the detection of different patterns (Fig. 6B). However, inspection of these clusters revealed they were composed of a single type of QPP, with some patterns displaying either high (GSR P1) or low (GSR P2) intensity in the medial Cg component (and vice versa the lateral S2 component) (Fig. 6A). This indicated that the phase at which a pattern was detected, became a dominant factor in the clustering after GSR. Phase sorting of QPPs prior to hierarchical clustering, based on their intensity time series in the Cg, confirmed the detection of a single GSR QPP (Fig. 6B). An overlay of STCs of the QPPs after GSR further confirmed their detection at opposite phases (Fig. 6C).

An STC overlay of PAT1-3 and the GSR PAT clearly illustrated matching of PAT1 with the GSR PAT (Fig. 6C). This was further confirmed by STC cc at each window size, which showed strongly decreased cc of the GSR PAT with PAT2-3 and high cc with PAT1 (Fig. 6D, left panel). Direct cc of PAT1-3 with the global signal further demonstrated its close relationship with PAT2-3, but less so with PAT1 (Fig. 6D, right panel). Using the CAP approach, we identified the spatiotemporal shape associated with global signal and displayed it with its respective timing to the GSR PAT (Fig. 6A). This illustrated that the global signal falls on the Cg-S2 intensity switch. PAT2-3 displayed a similar timing and spatiotemporal shape (Fig. 4A), suggesting at least partial overlap with the global signal.

Under HA, GSR had very similar effects (Fig. S6). PAT2 and PAT4 were no longer observable, while the GSR pattern displayed similarity with PAT1 (STC cc 0.83 and QPP cc 0.71) (Fig. S3A & movie 3). STC cc across window sizes was however slightly diminished (0.70 ± 0.13), not displaying the high consistency as observed under LA (Fig. S3B). PAT2 and PAT4 displayed a close relationship with the global signal (Fig. S6D, right panel). The global CAP displayed a similar timing as described under LA and its spatiotemporal shape showed consistency with PAT2 and PAT4 (Fig. S6A).

Cortex and caudate putamen differentially contribute to Quasi-Periodic patterns. Global signal regression diminishes subcortical dynamics

Under LA, PAT2 and PAT3 showed a higher detection rate at window sizes of 6–10.5s. Both displayed a spatiotemporal pattern that more strongly involves Cpu, while PAT1 was marked most by lateral to medial cortical propagation and window sizes above 10.5s. To further investigate this ‘skewed’ detection of patterns involving different brain regions, we performed the same general analysis as presented in Fig. 2, now with masks comprising either only cortical or Cpu regions. This allowed, for the cortical mask, observation of a pattern highly similar to PAT1 (QPP cc 0.92), and for the Cpu mask, observation of a pattern similar to PAT2 (QPP cc 0.70), consisting of bilateral alternating high and low intensities in the full Cpu and Cg (Fig. 7A & movie 4). Interestingly, when the Cpu mask was employed, the algorithm didn’t use information of the cortex to select whole brain images to be averaged, yet a pattern including the Cg was still determined, indicating partially preserved coupling with the cortex. A similar outcome was also observed in rats (Majeed et al., 2011). Timing of the Cpu pattern indicated it as falling in between the PAT1 S2-Cg switch, similar to PAT2-3 (Fig. 4).

Fig. 7. Relationship with cortex, Caudate Putamen and global signal regression.

A) QPPs observed without GSR, after GSR, with a cortical mask, and a Cpu mask. Patterns are shown phase-aligned with each other. Note the high similarity between GSR and cortical QPPs, lacking a clear Cpu contribution. With a Cpu-mask, a bilateral alternating high and low intensity could be observed in Cpu, with preserved coupling to the Cg area. Note the timing of the Cpu pattern between the GSR pattern’s S2-Cg switch. B) STCs of the patterns described in (A). Note the overlap between all STCs, except for that of the Cpu pattern, which synchronized and dephased through time. This illustrates how subcortical patterns could behave independently of cortical patterns, but still couple at specific time points, potentially contributing to the observation of patterns like PAT2 and PAT3. C) STC cc between patterns illustrated in (A - 3 lower panels) and whole brain patterns observed in Fig. 3C. Note the high cc with Cpu-masked QPPs at shorter window sizes and the high cc with cortical-masked QPPs at longer window sizes. GSR strongly lowered the cc at shorter window sizes, suggesting it diminished Cpu spatiotemporal dynamics. D) FA-values indicated the ideal window size for each QPP. Grey patch indicates the range of interest for the different patterns. E) Occurrence rates at all window sizes.

STC cc with whole brain QPPs obtained via k-means clustering (Fig. 3) confirmed a high overlap with Cpu spatiotemporal dynamics at shorter window sizes (0.76 ± 0.02), while at high window sizes QPPs were highly consistent with cortical only dynamics (0.94 ± 0.03) (Fig. 7C). Visual inspection of the STCs displayed how the Cpu QPP both synchronizes and falls out of phase with the cortical QPP and whole brain PAT1 (Fig. 7B). This illustrated a potential common relationship between the two, which visually disappeared due to differential averaging (e.g. with a cortical mask in- and out-of phase Cpu occurrences could average to zero, or vice versa).

Ideal window sizes for Cpu and cortical QPPs were determined at 9s (visual inspection + FA, Fig. 7D). The cortical-mask QPP still displayed the prolonged negative intensity, but less clearly. Therefore the ideal window size was determined by taking into account FA. Half cycle times for Cpu QPPs appeared shorter in the Cpu (±0.6s) compared to PAT2, while propagation time in cortical QPPs appeared faster than in PAT1 (±0.7s) (Table 2). These differences served to illustrate different temporal dynamics across brain regions, which likely contributed to the observation of different patterns. Both Cpu and cortical QPPs were observed across all subjects and occurrence rates were higher across all window sizes versus whole brain QPPs (Fig. 7E & Table 1).

We showed earlier that GSR abolished PAT2-3 detection, leaving only a pattern highly similar to PAT1. Cortical QPP spatiotemporal dynamics were found to be highly similar to GSR QPPs (QPP cc 0.88) (Fig. 7A). They further produced a similar STC cc profile as described for the cortical QPPs, displaying respectively diminished and preserved cc with whole brain QPPs at lower and higher window sizes (Fig. 7C). These results indicated that GSR diminished the detection of subcortical dynamics and the related PAT2/PAT3.

Under HA, similar outcomes were observed. The Cpu mask led to the detection of a pattern highly similar to PAT4 (QPP cc 0.89), while with the cortical mask a pattern similar to PAT1 was found, which displayed diminished intensities in the lateral cortical S2 component (Fig. S7). The Cpu QPP displayed a similar timing with respect to PAT1 and PAT GSR, as described for LA. Detection rates are shown in Table S1.

Quantitative comparison of Quasi-Periodic patterns between high and low anesthesia, before and after global signal regression

After patterns were determined at their ideal window length, based off the image series of a specific group (LA – no GSR, LA – GSR, HA – no GSR, HA GSR), they could be compared to those of other groups via sliding template correlation. This allowed patterns that were hypothesized to be the same across groups to be compared in terms of how similar they correlate with the respective time series: e.g. PAT1 determined under LA was used to derive the STC with the HA image series (STC PAT1 LA- > HA), to then be compared with the original STC of PAT1 determined under HA. STC LA- > HA cc was determined to be 0.87 for PAT1, 0.89 for PAT2, and 0.89 for PAT GSR. These high cc values suggested that visually classified common patterns displayed a highly similar interaction with the respective image series and thus pertained to the same spatiotemporal dynamics across anesthesia groups.

In a similar way as described above, reference- > target STCs were used to compare detection rates of patterns before and after GSR in the respective anesthesia groups (Fig. 8). This showed a clear suppression of PAT2-4 and Cpu QPP detections after GSR in both groups, with only the Cpu QPP showing some preservation in the LA group. On the other hand, PAT1, PAT GSR and the cortical QPP showed consistent detection rates before and after GSR, whilst cortical QPP detections under HA increased after GSR. PAT3 and PAT4 were not clearly visually discerned in respectively the HA and LA group, but could be compared for their potential presence via this strategy. Both displayed the lowest occurrence rate in the alternate anesthesia group.

Fig. 8. Pattern occurrence rate before and after global signal regression.

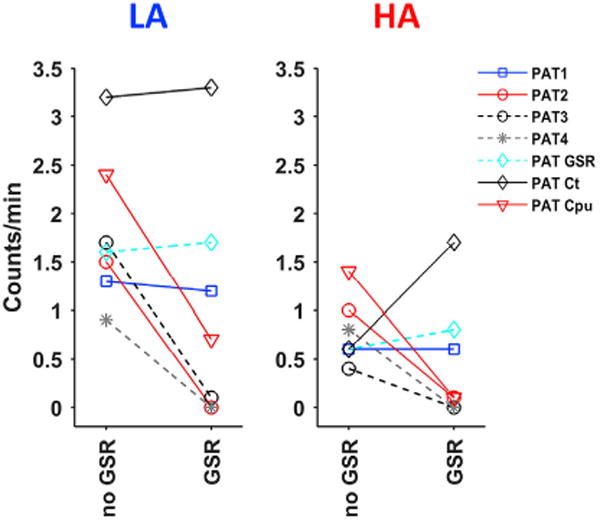
All described QPPs were determined from the image series of 4 groups: LA – no GSR, LA – GSR, HA – no GSR, HA GSR. QPPs of one group were compared with the image series of others via sliding template correlation, to quantify occurrence rates across conditions. Panels display the occurrence rates of patterns before and after GSR, in their respective anesthesia groups. Both clearly indicate that PAT2-4 were no longer detected after GSR. Cpu QPP detections were lowered in the LA group and no longer seen in the HA group. PAT3 and PAT4, which were not visually identified in respectively the HA and LA group, were compared with the other anesthesia group in which they displayed the overall lowest occurrence rates. Abbreviations. LA, low anesthesia; HA, high anesthesia; GSR, global signal regression.

Single subject Quasi-Periodic Pattern detection and consistency with group-level analysis

Once we established the repertoire and behavior of QPPs at the group level, we further investigated whether patterns could be detected at the single subject level. The algorithm was run on each subject for window sizes of 3–15s, with and without GSR. We investigated cc between the STC of the subject individually and the STC of the same subject, derived from the group-level analysis. For single-subject data there was no need for image normalization, allowing all three slices to be included in the analysis. Pattern similarity was therefore visually confirmed.

We present results from three example subjects, displaying QPPs with and without GSR (Fig. 9). Subjects were chosen to illustrate, respectively, high PAT1 contribution in subject 11 (Fig. 9A), high PAT1 and PAT2 contribution in subject 8 (Fig. 9B), high PAT2 contribution in subject 4 (Fig. 9C). The two patterns could clearly be visually observed throughout all three slices, with a high similarity and timing. Below each illustration, a 200s excerpt is shown from the STCs at single subject and group level after phasing via cc. Subject 11 and 8 presented a very high degree of overlap for their respective patterns, while subject 4 showed partial overlap and sporadic aphasic behavior. These graphs illustrate the high consistency between group and single subject analysis.

Fig. 9. Single subject detection of Quasi-Periodic Patterns and the relationship with group analysis.

Illustrations of QPPs detected for single subject three-slice images, with (left) and without (right) GSR: A) subject 11, high PAT1 contribution B) subject 8, high PAT1 & PAT2 contribution C) subject 4, high PAT2 contribution. Below each panel an excerpt of the subject’s STC and its STC, derived from the group-level analysis, are shown. The middle lowest panel shows the overlay of single subject STCs with and without GSR. A-B) Note the consistent high overlap for subject 11 and 8 across all panels. These subjects displayed strong cortical contributions in their QPPs. C) Subject 4’s QPP, without GSR, was dominated by Cpu intensities and showed less STC overlap. After GSR, a cortical component could be observed in the QPP and the STCs nicely overlapped. The subject’s STC after GSR overlapped with PAT1 at the group level, indicating removal of PAT2 and the Cpu contribution.

After GSR, subject 11’s QPP stayed highly similar, while in subject 8 the Cpu contribution seemed slightly reduced. In subject 4, where no lateral cortical contribution could be observed earlier, a lateral to medial cortical wave similar to PAT1 could afterwards be appreciated. STCs for group and subject data with GSR are shown below the figures on the right. In all three subjects a high overlap could be observed, indicating that GSR allowed reproducible QPP detection.

In the lowest middle graph below each subject, an overlay is shown between single subject STC with GSR and without GSR. Subject 11 and 8 respectively showed high overlap, while subject 4 showed very little overlap. When however for subject 4 the group level STC of PAT1 was additionally plotted, a high similarity could be observed. This supported the notion that GSR removed contribution of the Cpu and PAT2, which involved more pronounced subcortical dynamics. A similar illustration for PAT3 can be appreciated in subject 9 (movie 5&6). Speculatively, in subjects 11 and 8 the cortical contribution, consistent with PAT1, was already high to start with so the STCs after GSR stayed similar.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.075.

We observed similar trends over all subjects, with individual subjects displaying differences in which patterns seemed to be dominantly present (movie 5&6). To illustrate this, we present a visual overview of STC cc of each subject, per window size, with the group-level patterns before and after GSR (Fig. S8). Some subjects showed lower pattern detection (e.g. subject 7) and QPPs could not be detected for all window sizes. This was especially the case after GSR.

Under HA, single subject detection of QPPs was much more challenging and visual assessment of pattern type was often not possible (Fig. S9 & movie 7). After GSR, this slightly improved, but patterns remained challenging to discern and tended to display lateralization (movie 8). STC overlap of group and single subject data further illustrated substantial difficulty to find reliable matching.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.075.

Discussion

Overview

Often, the assumption is made that BOLD FC is stationary, but recent studies indicate that dynamic analysis of FC better captures the interaction between different brain regions and resting state networks (RSNs), providing additional insights into the macroscale organization and dynamics of neural activity (Calhoun et al., 2014; Deco et al., 2011; Hutchison et al., 2013; Keilholz, 2014). Only just recently, Grandjean et al. (2017a) applied sliding window analysis (SWA) and dictionary learning to identify for the first time several highly reproducible dynamic functional states in mice. Other dynamic rsfMRI techniques focus directly on the LF BOLD fluctuations, tracking down instantaneous single volume BOLD configurations that underlie observed FC and RSNs, e.g. the CAP approach (Liu and Duyn, 2013; Preti et al., 2016), and in an alternative extension their recurring spatiotemporal evolution (Majeed et al., 2011). It has been speculated that SWA and spatiotemporal dynamics both scope different aspects of the neural basis underlying dynamic rsfMRI (Keilholz, 2014). Being able to apply and compare both techniques in mice would thus represent an important step forward.

We investigated such spatiotemporal dynamics by acquiring high temporal rsfMRI scans in mice under an analogous HA and LA condition. Using the pattern detection algorithm developed by Majeed et al. (2011), we report the detection of a set of group-level QPPs, which appear to capture the spatiotemporal occurrence of BOLD configurations resembling known RSNs. We present an initial framework for the interpretation of observed QPPs, illustrating the influence of analysis window size on skewing detection towards either more cortical (PAT1) or widespread and subcortical (PAT2-4) spatiotemporal dynamics. PAT1-2 and the pattern after GSR were both visually and quantitatively determined to be the same across both anesthesia conditions, where they display different occurrence rates and lower lateral cortical intensities under HA. PAT3 and PAT4 were identified separately under respectively LA and HA, and both displayed a similar spatiotemporal shape to the global CAP. We went on to illustrate the relationship between observed patterns and the global signal, showing how GSR removed detection of PAT2-4 and diminished the detection of subcortical spatiotemporal dynamics. This resulted in the dominant detection of PAT1. To aid interpretation, we developed a novel data-driven approach to guide identification of optimal window sizes, we proposed a clustering approach to confirm different pattern subtypes, we added an extension of the CAP approach to investigate the global signal spatiotemporal pattern, and provided a means of quantitatively comparing patterns across groups. Interestingly, our findings suggest that QPPs and their interaction with the global signal were consistent across anesthesia conditions, but that their detection rates were diminished under higher anesthesia levels.

PAT1 is highly similar to the QPPs detected in preceding rat studies, displaying a propagating intensity from lateral S2 towards medial Cg cortical areas, with almost the same propagation time and half cycle length (Magnuson et al., 2010; Majeed et al., 2011, 2009) (movie 2). This interspecies consistency supports that QPPs are a robust phenomenon and further validates mouse rsfMRI as a pre-clinical tool. In the current study, QPPs could only be investigated in a single slice. By utilizing conventional resting state analysis on both low and high temporal resolution datasets, acquired in the same LA session, we illustrate how single slice investigations allow a view into brain-wide BOLD dynamics. We suggest that the S2 and Cg components of PAT1 pertain to anti-correlated interaction between the mouse DMN-like and lateral cortical networks. We further speculate that the lateral cortical network might represent a mouse TPN-like network. These networks have been conjectured to be present in mice (Liska et al., 2015), and match a similar DMN-TPN anti-correlation (Fox et al., 2005) and quasi-periodicity in humans (Majeed et al., 2011; Yousefi et al., 2017). Although the exact subcortical patterns shown in the current study were not reported in rats, Majeed et al. (2011) did indicate the presence of a pattern including Cpu. The latter similarly locked in-and-out of phase with the rat whole-brain pattern and displayed shorter cycle lengths, consistent with our findings.

Comparison of group-level QPPs with single subject multi-slice QPPs, by means of STC cc, allowed us to investigate detection reliability at the subject-level. The latter seemed consistent under conditions of LA and was improved by GSR. At group-level, subjects displayed occurrences of all patterns, but contributions were skewed towards one or multiple subtypes. Visual inspection and STC cc of single-subject with group-wide QPPs confirmed this observation. The variability in QPP contribution and occurrence across subjects might be related to the commonly observed inter-subject variability in rodent rsfMRI, which knows numerous origins (Keilholz et al., 2016). It is interesting to speculate that different contributions of QPPs might contribute to inter-subject differences in FC readouts. In humans it was already indicated that QPPs contribute to FC (Wang et al., 2016). Single subject investigation of QPPs promises a step forward towards more reliable resting state fMRI.

Anesthesia and resting state network resemblance

Anesthesia type and dosage are known to alter neurovascular coupling, haemodynamics and BOLD FC patterns (Grandjean et al., 2014; Jonckers et al., 2014; Keilholz et al., 2016; Masamoto and Kanno, 2012; Schlegel et al., 2015; Schroeter et al., 2014; Williams et al., 2010). Several rodent rsfMRI studies point at a combination of low dosage medetomidine and isoflurane (MedIso) as a potential optimal anesthesia regime that preserves vascular reactivity, preserves FC within and between cortical and subcortical structures, and allows high retention of local activity measured via regional homogeneity (Bukhari et al., 2017; Fukuda et al., 2013; Grandjean et al., 2014; Wu et al., 2017). We therefore scanned animals with a similar regime (LA – low anesthesia) and also under a higher dosage (HA) for comparison. Our results confirm the importance of choosing optimal anesthesia and are in line with the outcomes of several studies.

BOLD configurations of the observed QPPs match well with several RSNs described in (Grandjean et al., 2014) and those in a follow-up study of the same lab (Zerbi et al., 2015). The lateral cortical components of PAT1 and PAT3 match the bilateral sensory cortical map obtained with a seed-based analysis in (Grandjean et al., 2014), which displays involvement of somatosensory areas (S1 & S2), a ventral part of the Cpu, and partially extends to enthorinal and insular cortices. After GSR, this FC map displays anti-correlation between S1BF/S2 and Cg, similar to the contrast observed in PAT1. A seed in the dorsal Cpu further indicates a bilateral striatal network that we observe throughout all patterns. Zerbi et al. (2015) used ICA to identify bilateral RSNs, which also match with QPPs. The configuration with co-active dorsal Cpu and Cg was not shown, yet a high correlation was determined between their time series. Furthermore, in a recent study employing MedIso anesthesia, this configuration could be observed and it was even correlated to underlying monosynaptic structural connectivity (Grandjean et al., 2017b). It was also observed as a part of the DMN module and with CBV-weighted rsfMRI, when halothane was used as an optimal anesthesia regime (Liska et al., 2015; Sforazzini et al., 2014). In these two studies, similar RSN topologies as described above were identified.

Under HA, we observe diminished cortical contribution to the QPPs, while spatiotemporal dynamics displaying bilateral striatal co-activation predominate. This is in line with diminished cortico-cortical and preserved striatal connectivity observed at higher dosages of medetomidine (Grandjean et al., 2014; Nasrallah et al., 2014a,b). Medetomidine is a potent vasoconstrictor (Ganjoo et al., 1998), exerting its effect via interaction with α2-adrenorecptors (Lakhlani et al., 1997; Lukasik and Gillies, 2003), which have different expression densities throughout the brain (Nasrallah et al., 2012). Cortical expression is higher than in striatum, leading to local diminished vascular reactivity, which supports observations in our study and that of (Grandjean et al., 2014).

Haemodynamics

QPP half cycle times across different pattern subtypes under LA were consistent, averaging to 4.6s across relevant window sizes. Interestingly, for QPPs derived with a cortical and subcortical mask, these values average respectively to 4.4s and 3.8s. Although the temporal resolution in the current experimental setup is limited to 0.5s, this difference was determined to be significant (T-test, p < 0.01) across window sizes, supporting our hypothesis that subcortical and cortical spatiotemporal dynamics differ. The latter might skew detection of pattern subtypes, depending on the window size under investigation. As described above, differences in haemodynamics due to regional expression variation in anesthetic-binding receptors could contribute to this phenomenon. Regional differences in haemodynamics were indicated before in rats (Devonshire et al., 2012; Sloan et al., 2010), and more recently also in mice (Schlegel et al., 2015; Schroeter et al., 2014). Visual inspection of the mouse S1 haemodynamic response function (HRF), determined under medetomidine in (Schlegel et al., 2015), suggests a similar cycle time (9–10s) as we observe for mouse QPPs. On the other hand, for a subcortical structure (thalamus) the HRF was determined to be shorter, which is in line with our observed shorter subcortical dynamics. The authors suggested that this could be attributed to regional differences in vascular structure and blood supply.

It thus becomes interesting to speculate that QPPs reflect spontaneous haemodynamic events. It has already been suggested that haemodynamics in the mouse somatosensory cortex, due to spontaneous neural activity, resemble stimulus-evoked haemodynamics (Bruyns-Haylett et al., 2013). Further support comes from other multimodal imaging modalities. Particularly, two studies in mice employed wide-field optical imaging to visualize calcium and intrinsic optical signals, to investigate and relate respectively neuronal activity with haemodynamics (Ma et al., 2016; Matsui et al., 2016). It was shown how in the resting state, spontaneous symmetrical events in cortical synchronized neural activity translate into similar patterns of haemodynamics, which may reflect the basis of RSNs as detected by rsfMRI. Matsui et al. (2016) went on to show global waves of neural activity propagating across the cortex, with functionally connected cortical regions co-activating at different time points along the wave. These events could be translated into spatially similar haemodynamic co-activations. In both studies, haemodynamics under anesthesia were on the order of ~10s and illustrated the existence of transiently co-activating large-scale patterns. Although speculative, there seems to be a consistency with the currently detected QPPs, which were also on the order of ~10s. Future studies applying the pattern detection algorithm of (Majeed et al., 2011) on these types of data, or multimodal experiments combining rsfMRI with neuronal recordings in mice, might answer this hypothesis.

Impact of physiology, motion, spectral range and processing

A critique to the above statement is that QPPs might be confounded by contributions of physiological noise or could arise from imaging/processing artifacts. However, phase randomization of the respective BOLD data and analysis of data acquired in a dead rat does not allow detection of QPPs, addressing the latter concern (Majeed et al., 2011) (Fig. S10). In the original study in rats (Majeed et al., 2009), in which a highly similar QPP was detected to the one we observe in mice (PAT1 & GSR), rsfMRI was acquired with a TR of 100 ms to prevent aliasing of cardiac and respiratory noise into the lower frequencies under investigation. With short TRs, the BOLD signal becomes more weighted to cerebral blood flow (CBF), which then might predominantly underlie QPPs, but a subsequent study with CBV-weighted BOLD imaging also allowed detection of similar QPPs (Magnuson et al., 2010). The consistent regional FC and observation of QPPs between ‘CBF-‘ and CBV-weighted rsfMRI in this study further confirms a relationship with neurovascular coupling and suggests that both readouts are primarily reflective of vascular fluctuations.

Spurious repeating patterns, captured by the spatiotemporal pattern detection algorithm, might reflect sporadic or respiratory/cardiac-induced motion. To ensure that motion was not causative to QPP events, we calculated frame-wise displacement (FD), based on the backwards looking temporal derivatives of the motion time series (Power et al., 2012), and cross-correlated the resultant FD time series with the STCs of the 3 main patterns found under LA. This was done for both raw motion time series and motion time series pre-processed in the same way as the functional data (filtering, detrending and normalization to unit variance). In both cases cross-correlation was minimal across all subjects, never exceeding 0.11 (Fig. S11), suggesting there is no influence of motion on detected QPPs. Mean FD across subjects was low (0.0066 ± 0.0005 mm). Illustrative motion time series, FD time series and lack of overlap with STCs can be appreciated in Fig. S12A-C for individual subjects, matching those described in Fig. 9.

Several studies investigating QPPs in rats employed medetomidine as an anesthetic, which revealed power spectra peaking close towards 0.2 Hz and containing most of the spectral information below this point (Magnuson et al., 2010, 2014; Majeed et al., 2011). Similar power spectra under medetomidine have been observed in mice (Grandjean et al., 2014), and also in the current study. In rats, QPPs were variably investigated in frequency ranges higher than those in conventional rsfMRI (0.05 > f < 0.3 Hz; cfr. respective articles), while for the currently presented mice data we chose 0.01–0.2 Hz. Majeed et al. (2009, 2011) split these spectral confines into a lower and higher frequency range, concluding that the range of 0.08–0.2 Hz was most appropriate to investigate rat spatiotemporal dynamics. Although we also observed some differences between lower and higher frequencies, they were not sufficiently compelling for us to do the same. The spectral information content in Fig. 1A clearly indicated the relevance of the investigated frequency range.

Although these frequency ranges isolate the hypothesized relevant spectral information of the BOLD signal and were shown to cohere significantly with infraslow LFPs under medetomidine anesthesia (Pan et al., 2013), inclusion of temporal content above 0.1 Hz risks contribution from slow frequency vascular phenomena such as vasomotion and Mayer waves (Baudrie et al., 2007; Bumstead et al., 2017; Drew et al., 2011; Julien, 2006; Tsai et al., 2015). Vasomotion is the intrinsic spontaneous oscillation of blood vessel tone leading to flow motion, while Mayer waves represent slow frequency changes in arterial blood pressure.

Given potential confounds from physiological noise and the fact that Mayer waves relate to hearth rate variability (HRV) (Elghozi and Julien, 2007), we used multiple linear regression analysis to investigate in LA subjects the relationship between two parameters of the observed QPPs, namely occurrence rate and power (i.e. the average correlation value for above-threshold peak detections), with four physiological parameters, namely cardiac rate, cardiac rate STD (i.e. HRV), respiration rate, respiration rate STD (Table S3). No significant interactions could be observed, only after GSR there was a trend towards correlation between breathing rate and QPP occurrence rate, and between cardiac rate STD and QPP power. GSR is generally considered to remove contributions from physiological noise (Chang and Glover, 2009; Murphy et al., 2013), making these results seem somewhat surprising. It would however be expected that with stronger CBF-weighing at shorter TRs, systemic parameters that affect CBF would correlate more to the BOLD signal and derived readouts. The latter might be accentuated by GSR.

As an additional control, we performed the QPP analysis at a lower frequency range (0.01–0.1 Hz) that should theoretically exclude contributions from vasomotion and Mayer waves. The same QPPs could be detected, with or without GSR, although be it with altered detection rates and slower temporal dynamics, which is to be expected due to temporal filtering (Fig. S13). The current experimental setup does not allow to fully exclude contributions from physiological signals, which should be investigated more in depth in future experiments together with the role of spectral range. Nonetheless, there seems to be substantial support for a neuronal component in the QPPs and their high similarity with known RSNs implicates their contribution to BOLD LF FC, regardless of their origin.

Global signal regression impact on spatiotemporal dynamics

GSR remains a controversial tool for rsfMRI processing, with the current consensus being that data should be compared with and without GSR (Murphy and Fox, 2016). In the investigation of the spatiotemporal dynamics in mouse BOLD, we observed that GSR removes PAT2-4 detection and decreases detection of subcortical patterns, leading to the sole detection of the lateral to medial cortical QPP (PAT1), which was also observed in rats (Majeed et al., 2011). The removal of PAT2-4 through GSR was further supported by their similar timing and spatiotemporal shape with the global signal CAP. In QPPs after GSR, subcortical dynamics are still present, indicating that their removal is targeted to the specific coincident timing with the global signal and potentially to periods between respective PAT1 occurrences. The removal of QPPs matches with a recently suggested mechanism for GSR, where it acts as a temporal down-weighting process, attenuating data from time points with a large global signal contribution and leaving data from low global signal time points largely unaffected (Nalci et al., 2017). With regard to the current study, PAT1 would represent the low global signal time points and PAT2-4 the high global signal time points, which appeared to fall between the first and second part of PAT1.

The ‘anti-correlated’ structure of PAT1 and the QPPs after GSR have also been shown for measures of RSN FC in several rodent studies and in humans, between analogues DMN (medial Cg, i.e. mouse DMN-like network) and TPN (lateral S2, i.e. mouse lateral cortical network) (Fox et al., 2005; Gozzi and Schwarz, 2015; Grandjean et al., 2014). It is very relevant to note here that the anti-correlated nature of these two networks has been debated to be a potential artifact of GSR (Fox et al., 2009; Murphy and Fox, 2016), but in the current study PAT1 was both detected before and after GSR. Similarly, Nalci et al. (2017) suggested that censoring of high global signal time points in the time series, rather than GSR, still allowed detection of anti-correlated interactions between DMN and TPN.

Although the suggested DMN-TPN interaction might thus be comparable with or without GSR (PAT1 is present in both cases), it does not address the question if GSR has a positive or negative role. We however show that without GSR, three separate QPPs could be observed, which resemble known RSNs and therefore suggest their neuronal relevance. A neural basis for QPPs was already directly indicated in rats, where a correlation is observed with infraslow LFPs (Thompson et al., 2014a,b; Thompson et al., 2015; Pan et al., 2013). All QPPs observed in the current study displayed a high coincidence with each other and the global signal. It was shown that the global signal itself, as measured with rsfMRI, might also be related to a global neural signal (Schölvinck et al., 2010). In the latter study, global BOLD signal coupling with direct neural recordings was increased during the eyes-closed condition, which has been correlated to changes in vigilance and attention (Wong et al., 2016). Similarly the presence and magnitude of the global signal has been related to the level of arousal (Liu et al., 2017; Wong et al., 2013, 2012) and global neuronal events were found to match with micro-arousal fluctuations (Liu et al., 2015). The relationship between arousal and the global signal provides a potential interpretation for the results of the current study, given that QPPs and spontaneous large-scale BOLD fluctuations have been linked with attention and behavior performance in humans (Abbas et al., 2016; Fox et al., 2007; Monto et al., 2008) & cfr. (Keilholz, 2014; Keilholz et al., 2016).

Based on our results, we suggested that GSR might be removing relevant information from neuronal origins related to arousal. Investigating and isolating QPPs that are related to the global signal thus provides a potentially more physiologically relevant alternative to standard GSR. For this interpretation, it should be stressed that global signal in this study is calculated from either one or three slices, and might thus not fully match the global signal as described in other studies. On the other hand, the observed impact of GSR on proposed DMN-like and TPN-like networks matches with preceding literature.

Study limitations

In section Earlier, we described the similarity of QPPs with RSNs in preceding literature. In the current study, QPPs also matched with RSNs determined in the presented data itself. However, while the overall configuration of RSNs appeared to match existing literature and mono-synaptic connectivity between different brain areas (Grandjean et al., 2017b), it is important to state that these RSNs also displayed some variability in their homotopic representation across the hemispheres. Furthermore, some RSNs displayed functional coupling that was not as strong and pronounced as in other studies. These observations were most noticeable for S1HL/FL/BF components. We also determined differences between short and long TR data, where in long TR data only a single Cpu component was observed when ICA was used to determine RSNs. These RSN topology differences and lower functional coupling, compared to preceding mouse rsfMRI literature, might be attributed to differences in sample size and pre-processing data cleanup strategies. When interpreting the presented results, these differences should be kept in mind.

Another potential limitation of the current study is the timing of HA followed by LA, which might bias LA results through habituation and interference with neural activity. A prior study however, which performed rsfMRI scans in young C57BL/6 J mice two weeks apart, showed no significant differences between both time points, addressing concerns about habituation. To address potential remaining concerns, we performed novel experiments in C57BL/6 J mice (n = 4) at the age of 3.5 months, which were prior not exposed to anesthesia. High temporal rsfMRI data was acquired under the same experimental conditions and same LA regime. Analysis of this data revealed reproducible QPPs, showing the same timing with respect to each other, similar clustering and interaction with the global signal (Fig. S14). This high reproducibility supports the validity of the presented findings.

A last limitation is reflected by this study’s restriction to single slice investigation, so that QPPs could only be investigated in a sub-sample of the brain. This was an active choice, to enable high spatial resolution EPI-acquisition with a short TR, so that earlier rat work could be reproduced. However, while normal low temporal rsfMRI could be used to relate QPPs to large-scale brain networks, QPP propagation across the rostro-caudal axis could not be investigated. In humans, QPPs propagate across the entire brain, involving mainly DMN and TPN areas (Majeed et al., 2011; Yousefi et al., 2017). Similarly, different whole-brain CAPs appeared to display some form of temporal sequence, suggestive of QPP-like behavior (Chen et al., 2015; Liu and Duyn, 2013). Finally, within the current study, it should be stated that the detection of multiple pattern types, which highly coincide with each other, might be a consequence of limited slice count and QPP variability across subjects. It is therefore not un-plausible that all observed patterns relate to a single QPP that shows a close interaction with the global signal. Future studies with larger brain coverage will be needed to investigate rostro-caudal and whole-brain properties of mouse QPPs, and to further elucidate their relationship with the global signal.

Conclusion & perspectives

Dynamic rsfMRI has been shown to reveal new insights into the macro-scale organization of functional networks, stepping closer to the underlying neural activity (Calhoun et al., 2014; Keilholz, 2014). In this study, we tease at the repertoire of dynamic processes, focusing in particular on the large-scale and repetitive background BOLD fluctuations that in recent years have become apparent as propagating spatiotemporal activity waves. We report the detection of a set of recurring QPPs in mice, which show similarity with known RSNs and represent promising contributors to BOLD FC. Their shape and properties confirm interspecies consistency and the importance of anesthesia in rodent rsfMRI research. High consistency of QPP detection, even at the single subject level, and a suggestive mechanistic role for GSR, marks advance towards more reliable and comprehensive rsfMRI research. These findings open up a new approach to study mouse LF BOLD spatiotemporal dynamics and mechanisms underlying FC, as was shown recently in humans (Wang et al., 2016).

It has been suggested that within the spectrum of neural activity, QPPs represent the infraslow LFP contribution, playing a role in attention and task performance, while SWA captures BOLD dynamics related with higher frequency LFPs, scoping state changes in cognitive processing (Abbas et al., 2016; Keilholz, 2014; Keilholz et al., 2016, 2013; Thompson et al., 2015). Together with the recent application of SWA in mice by Grandjean et al. (2017a), the findings in this study suggest that we can now tackle this dual dynamic repertoire in mice rsfMRI. This promises a considerable step forward in the field, encompassing a wide range of new research strategies and potential applications for pre-clinical disease models.

Abbreviations

CC

cross-correlation

GSR

global signal regression

HA

High anesthesia

LA

Low anesthesia

LF

Low frequency

PAT

Pattern

QPP

Quasi-Periodic Pattern

RSN

Resting State Network

STC

Sliding Template Correlation

CAP

Co-Activation Pattern

Appendix A. Supplementary data

Supplementary data related to this article can be found at https://doi. org/10.1016/j.neuroimage.2018.01.075.