Abstract
As a vital land surface parameter, soil moisture influences climate through its impact on water and energy cycles. However, the effect of soil moisture on precipitation has been strongly debated. In this study, a new causal detection method, convergent cross mapping (CCM), was applied to explore the causality between soil moisture and precipitation over low- and mid- latitude regions in the Northern Hemisphere. CCM method generally identified a strong effect of soil moisture on precipitation. Specifically, the optimal effect of soil moisture on precipitation occurred with a lag of one month and clearly decreased after four months, suggesting that soil moisture has potentials to improve the accuracy of precipitation forecast at a sub-seasonal scale. In addition, as climate (i.e., aridity index) changed from dry to wet, the effect of soil moisture on precipitation first increased and then decreased with peaks in semi-arid and semi-humid areas. These findings statistically support the hypothesis that soil moisture impacts precipitation and also provide a reference for the design of climate prediction systems.
Introduction
A growing body of evidence shows that variations in land surface conditions, particularly water storage1, vegetation2, and ice/snow cover3, can impact climate through the process of heat and water transfer between atmosphere and land surface. Soil moisture, a slowly varying surface parameter, can affect weather through its influence on energy and water fluxes4,5. Soil moisture-precipitation interaction is an important topic in the land-atmosphere coupling research, as it has the potential to improve the accuracy of precipitation prediction and the monitoring of extreme events such as floods and droughts6,7. Theoretically, the impact of soil moisture on precipitation can be dissected into two distinct parts: the impact of soil moisture on subsequent evapotranspiration, and the impact of evapotranspiration on subsequent precipitation8. The dependency of evapotranspiration on soil moisture is intuitive and easy to quantify9, while the effect of evapotranspiration on precipitation is uncertain due to complex atmospheric processes and has been strongly debated10.
Previous studies showed discrepancies on feedback signs and intensities of the impact of soil moisture on precipitation. The study in Illinois is an interesting example. Findell and Eltahir11 stated that soil moisture in early summer was positively correlated with subsequent precipitation based on direct observations. However, Salvucci et al.12 argued that antecedent soil moisture had no effect on precipitation in Illinois. Furthermore, D’Odorico and Porporato13 found that soil moisture can affect the frequency of subsequent precipitation rather than the precipitation amount. Given these conflicting findings, further research is necessary to explore the soil moisture-precipitation coupling mechanism.
Due to the paucity of continuous observation data on soil moisture, previous studies are mainly based on climate models, such as the Atmospheric General Circulation Models (AGCMs)14, the Consortium for Small-Scale Modeling Model in Climate Mode (CCLM)15, the Weather Research and Forecasting (WRF) Model16, and the regional climate model (CLM)17. Such analyses could be limited by parameter settings and assumed behavior in models, which influences the simulated responsiveness18,19. To avoid this dependency, it is essential to conduct researches based on the observed data. Nowadays, remote sensing technology provides global available data of soil moisture, which facilitates this study.
However, it is difficult to establish causality based on observation data. In the literature, correlation analysis is commonly used to study causality20,21, but it is neither necessary nor sufficient for a causal link22. Granger causality, which can detect causality between variables based on predictability instead of correlation, is widely applied in econometrics23. However, it is applicable only to separable and purely stochastic systems, rather than dynamic systems24. Recently, a new approach known as convergent cross mapping (CCM) has been proposed to detect causality in dynamical systems based on empirical dynamics and Takens’ theorem24. CCM can also identify time-delayed causality and distinguish real bidirectional causality from the phenomenon of synchrony caused by strong unidirectional causality25. This method has been successfully applied in climate system, such as the interaction between temperature and greenhouse gases26, the relationship between galactic cosmic rays and temperature variations27, and the sensitivity of the carbon cycle to tropical temperature variations28. However, CCM method has not yet been applied in researches on soil moisture-precipitation interaction.
Based on remote sensing and re-analysis data (i.e., ESA CCI soil moisture, MODIS evapotranspiration, and CRU precipitation), we detect the causal effect of soil moisture on precipitation over low- and mid- latitude regions in the Northern Hemisphere using CCM method, and try to address three questions: (1) whether soil moisture can affect precipitation, (2) if so, whether there is a time delay in the causality, and (3) how this causality varies spatially over different climate conditions.
Results
The spatial patterns of soil moisture, evapotranspiration, and precipitation
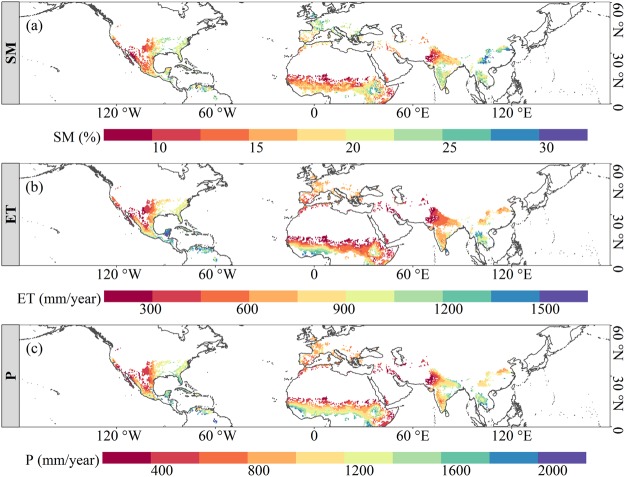
This study focuses on low- and mid- latitude regions in the Northern Hemisphere (latitude 0°N~60°N). However, due to gaps in the soil moisture data, we extract grids with valid soil moisture data from January 2010 to December 2014 for analysis. Additionally, the study area is limited to regions with aridity index (AI) between 0.03 and 1 by excluding hyper-arid regions (AI < 0.03) with negligible soil moisture and hyper-humid regions (AI > 1) with negligible soil moisture changes. The finally study area is demarcated in color in Fig. 1.
Figure 1.
Spatial patterns of mean annual soil moisture, evapotranspiration and precipitation for the period 2010–2014 (Generated by free software R, https://www.R-project.org/).
Over the study area, soil moisture (SM) ranged from 7% to 37%, and exhibited an obvious spatial heterogeneity (Fig. 1). High soil moisture appeared in the Southeastern United States, France, Italy, Southern China, and Thailand, which indicates a relatively wet climate in these areas. In contrast, low soil moisture, signifying a dry condition, mainly distributed in the south-central United States, north-central Mexico, Pakistan, parts of India, and some equatorial African nations. Evapotranspiration (ET) and precipitation (P) showed a similar spatial pattern as soil moisture. Over regions with high soil moisture, evapotranspiration and precipitation were relatively high, and vice versa. There are also strong correlations among these three variables, with R = 0.897 between SM and ET, R = 0.894 between ET and P, and R = 0.795 between SM and P.
Detecting causality in the soil moisture-precipitation process
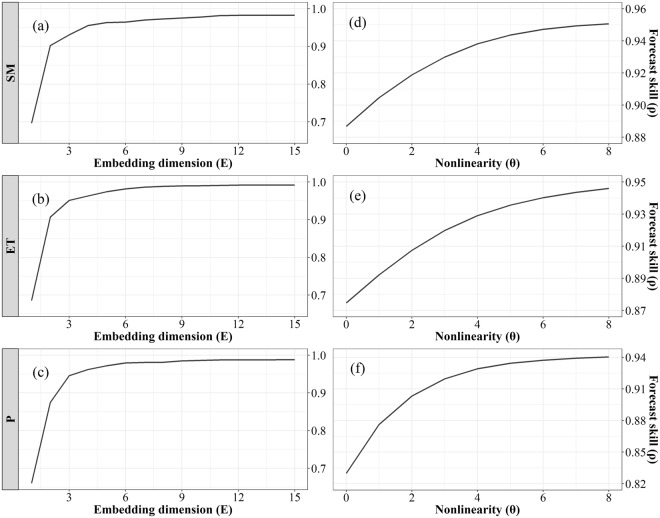
In CCM method, the first step is to determine the optimal embedding dimension (E) which describes the size of the time windows used for prediction. Here, the simplex projection was applied to determine the optimal E for soil moisture, evapotranspiration, and precipitation, by using the forecast skill (ρ) as an indicator. Figure 2(a–c) presents the variation in the forecast skill as a function of E, which shows that the forecast skill approached a saturating status with the increasing of E. E near the saturation point is usually chosen as the optimal E. From this figure, a relatively high forecast skill was achieved with E = 6 for these three variables.
Figure 2.
Forecast skill as a function of the embedding dimension (left column) and the nonlinearity index (right column) for soil moisture (a,d), evapotranspiration (b,e) and precipitation (c,f) (Generated by free software R, https://www.R-project.org/).
The second step of CCM is to use the S-map method to test the nonlinearity of the system. In this method, the nonlinear index (θ) is used to govern the weighting procedure, and the nonlinear dynamics system can be identified if the forecast skill improves as θ increases. In Fig. 2(d–f), the nonlinear models (θ > 0) gave better predictions than the linear model (θ = 0), which indicates statistical nonlinear behaviors in these three time series. Therefore, the CCM method can be applied to detect the causality between them.
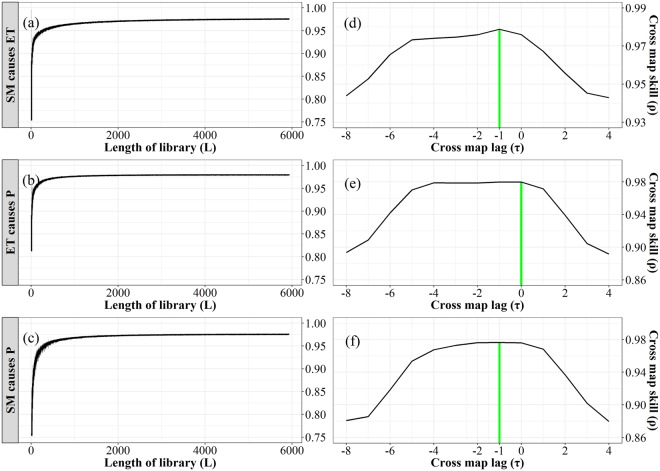
The effect of soil moisture on precipitation (SM-P) can be separated into two segments: the effect of soil moisture on evapotranspiration (SM-ET), and the effect of evapotranspiration on precipitation (ET-P). Here, CCM method was applied to analyze the causal relationships of SM-ET, ET-P, and SM-P, respectively. When applying CCM method, the cross map skill (ρ) is defined as the correlation coefficient between predictions and observations, and the length of library (L) refers to the number of historical observations. The causality is confirmed when ρ substantially increases with the increasing L. As presented in Fig. 3(a–c), for these three relationships, ρ increased with L and converged around L 1000, suggesting significant causal effects of SM on ET, ET on P, and SM on P, respectively. Additionally, CCM also showed a strong coupling within the system, as indicated by high cross map skills (ρ > 0.95).
Figure 3.
Cross map skill as a function of the length of library (left) and the cross map lag (right) for SM causing ET (a,d), ET causing P (b,e) and SM causing P (c,f) (Generated by free software R, https://www.R-project.org/).
In case of strong coupling, the phenomenon of synchrony must be addressed to infer the true causation. In this study, CCM method was repeated for different time lags (τ) to determine the optimal time lag which corresponds to the highest cross map skill. For real causality, the optimal cross map lag is non-positive. Conversely, the optimal cross map lag is positive. Figure 3(d–f) shows that the optimal effect of soil moisture on evapotranspiration occurred with a negative lag (τ = −1), meaning that an increase in soil moisture could not instantaneously translate into evapotranspiration increase. Evapotranspiration had a nearly instantaneous effect on precipitation, as the optimal cross map skill occurred with no time lag (τ = 0). CCM identified a true causal effect of soil moisture on precipitation with a negative optimal lag (τ = −1), suggesting that precipitation responded slowly to soil moisture change, due to a one month lag in converting soil moisture into evapotranspiration.
Figure 3(f) also shows that soil moisture had the strongest effect on precipitation with a one month lag, and the impact clearly decreased after four months, which reveals that soil moisture has the potential to predict precipitation at a sub-seasonal scale.
Identifying regions with strong effects of soil moisture on precipitation
Identifying regions with strong effects of soil moisture on precipitation is important for designing the precipitation prediction system. Here the range of AI (0.03–0.1) was divided into 65 sub-ranges at intervals of 0.015, and the corresponding sub-regions were extracted from the study area. Then CCM method was applied to the data from each sub-region at different time lags to calculate the optimal effect of soil moisture on precipitation.
Figure 4 displays the variation of cross map skill from dry to wet climate conditions. As AI increased, the cross map skill increased first and decreased afterward, with peaks in semi-arid and semi-humid area (0.3 < AI < 0.6), corresponding to the areas with soil volumetric moisture ranging between 15% and 20%.
Figure 4.
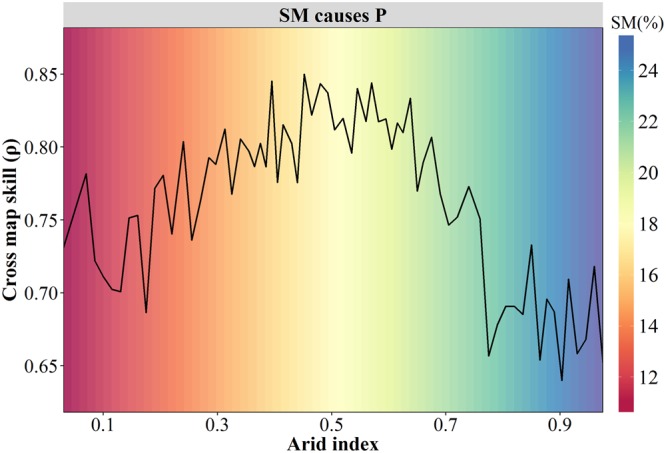
Variations of cross map skill across different climate regimes (Generated by free software R, https://www.R-project.org/).
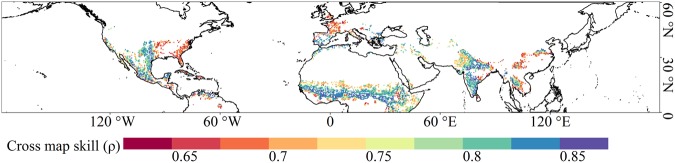
Figure 5 illustrates the spatial pattern of cross map skill over the study area. High cross map skills indicated strong effects of soil moisture on precipitation in the south-central United States, north-central Mexico, India, and some country of equatorial Africa.
Figure 5.
Spatial pattern of cross map skill (Generated by free software R, https://www.R-project.org/).
Discussions
Persistence is a distinctive attribute of soil moisture. A number of studies have investigated the soil moisture persistence, and indicated that the soil moisture persistence can span weeks to a couple of months29–31. Such persistence may turn out to be the main source of long-term weather prediction over mid-latitude continents32. However, the potential use of soil moisture persistence for precipitation forecasting has not been investigated as thoroughly. In this study, the persistence time in the effect of soil moisture on precipitation was quantified using CCM method, and the result shows that soil moisture has the potential to predict precipitation at a sub-seasonal scale. Furthermore, previous studies have demonstrated that surface soil moisture persistence was highly region and season dependent33. Hence, the persistence time in the effect of soil moisture on precipitation may vary with regions and seasons.
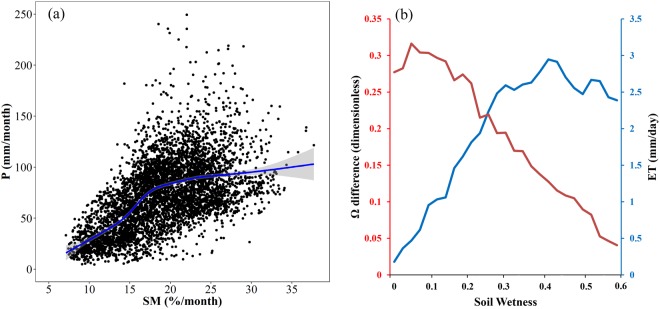
In addition, stronger effects of soil moisture on precipitation were detected in semi-arid and semi-humid areas compared to other regions (Fig. 4). To illustrate this phenomenon, Fig. 6(a) displays the variation of precipitation with soil moisture. The increasing rate of precipitation differed under different soil moisture conditions and exhibited an inverse tangent shape. The highest increasing rate was found in regions with soil moisture between 15% and 20%, which corresponds to regions with strong effects of soil moisture on precipitation (Fig. 4). Further, the relationship between soil moisture and evapotranspiration is depicted in Fig. 6(b). With soil moisture growth, the evapotranspiration (blue line) increased, while the dependency of evapotranspiration on soil moisture (Ω difference; red line) decreased. For hyper dry soil, both evaporation and its variation are too small to affect precipitation. As soil gets very wet and even approaches saturated, evapotranspiration is controlled by atmospheric condition rather than soil moisture, and thus soil moisture has little effect on precipitation34. Hence, the strong effect of soil moisture on precipitation mostly occurs in the transition between dry and wet soil, where a high sensitivity of evapotranspiration to soil moisture and a high variability of evapotranspiration are coexistent35. In addition, regions with stronger effects of soil moisture on precipitation identified by CCM method (Fig. 5) were in line with the results from Koster et al.36, that is, strong coupling regions were mainly distributed in the central Great Plains of North America, the Sahel, equatorial Africa, and India. This further increases the credibility of our results.
Figure 6.
Relationships of soil moisture with precipitation (a) and evapotranspiration (b). (a) presents scatterplots of mean monthly precipitation against soil moisture for all points over the study area, and the blue line is the fitted trend based on auto smoothing method, with shaded area denoting 95% confidence interval. (b) presents the variations of evapotranspiration and Ω difference (the fraction of variance in ET explained by soil moisture variations) with the increase of soil wetness (adjusted From Koster, R. D. et al. Regions of strong coupling between soil moisture and precipitation. Science 305, 1138–1140 (2004). Reprinted with permission from AAAS). (Generated by free software R, https://www.R-project.org/).
Finally, the soil moisture-precipitation relationship might be region dependent. In this study, a positive relationship between soil moisture and precipitation was discovered in the transitional regions with AI between 0.03 and 1, while Yang et al.37 observed a negative feedback over extreme dry and wet regions. This difference between the transitional regions and extremely dry/wet regions may arise from different relationships between soil moisture and evapotranspiration38. Vegetation can also affect precipitation through its influence on soil moisture and evapotranspiration39, thus there may be some discrepancies in soil moisture-precipitation relationship over different land types. Furthermore, the soil moisture-precipitation feedback at different spatiotemporal scales can also make a difference. For instance, Hohenegger et al.40 found a positive feedback at a 25-km spatial resolution and a negative feedback at a 2.2-km spatial resolution based on hourly data, and Guillod et al.41 suggested positive temporal effects and negative spatial effects of soil moisture on afternoon rainfall at a spatial resolution of 1.25 degree. Hence, it should be a future hotspot to explore the soil moisture-precipitation coupling mechanism in different regions and spatiotemporal resolutions.
Conclusions
In this study, CCM method was used to detect causality between soil moisture and precipitation over low- and mid- latitude regions in the Northern Hemisphere. A strong causality between SM-ET, ET-P, and SM-P was detected with cross map skill more than 0.95, which supports the assertion that soil moisture affects precipitation through evapotranspiration. The optimal cross map skill for soil moisture affecting precipitation occurred with a lag of one month, and then substantially decreased after four months, suggesting that soil moisture is potential to predict precipitation at a sub-seasonal scale. As the climate changed from dry to wet, the effect of soil moisture on precipitation increased first and then decreased, with the strongest effects appearing in semi-arid and semi-humid area, such as the south-central part of the United States, north-central of Mexico, India, and some country of equatorial Africa.
Although this study successfully detected the effect of soil moisture on precipitation at both temporal and spatial scales, there are still some spaces for improvement. For instance, we only detected the causal effect over regions with valid soil moisture data, while there are large areas without valid soil moisture data over low- and mid- latitude regions in the Northern Hemisphere. In addition, this study only considered the local effect rather than the remote effect, and the mechanisms for the remote effect need to be explored in the future.
Methods
Precipitation data (P)
Monthly precipitation data are collected from the Climate Research Unit time series data version 4.0 (CRU Ts4.0), for the period from January 2010 to December 2014. This dataset is gridded onto a 0.5° network, based on analysis of more than 4,000 weather station records42.
Soil moisture data (SM)
This study uses the soil moisture dataset released by the European Space Agency (ESA) Climate Change Initiative (CCI) program43. Version CCI v03.3 contains an active data set, a passive data set and a combined data set. The combined data set used in this study is derived from three active (AMI-WS, MetOp-A ASCAT, MetOp-B ASCAT) and seven passive (SMMR, SSM/I, TMI, WindSat, AMSR-E, AMSR2, SMOS) microwave sensors. The dataset has a temporal resolution of one day and a spatial resolution of 0.25°, and provides surface soil moisture information in volumetric units (m3·m−3). Monthly soil moisture data are calculated from ESA CCI daily data. To guarantee the accuracy of monthly average values, the averaging conversion is only applied to pixels where valid data have a length of more than 15 days a month44. The monthly soil moisture data are then averaged spatially to a resolution of 0.5°.
Evapotranspiration data (ET)
Evapotranspiration data downloaded from MODIS (MOD16) for the period January 2010 to December 2014 and at a spatial resolution of 0.5° are used in this study (http://files.ntsg.umt.edu/data/NTSG_Products/MOD16/MOD16A2_MONTHLY.MERRA_GMAO_1kmALB/GEOTIFF_0.5degree/). The MOD16 ET is calculated based on the Penman-Monteith theory, which performs well in generating global evapotranspiration data45.
Aridity index (AI)
To understand the dependency of precipitation on soil moisture across different climate regimes, the mean global aridity index (AI) from CGIAR-CSI (http://www.cgiar-csi.org) is used for climate classification. The AI is calculated as:
| 1 |
where MAP is the mean annual precipitation, and MAE is the mean annual potential evapotranspiration.
According to the United Nations Environment Programme (UNEP 1997), there are five climate classes: hyper-arid (AI < 0.03), arid (0.03 < AI < 0.2), semi-arid (0.2 < AI < 0.5), semi-humid (0.5 < AI < 0.65), and humid (AI > 0.65).
Convergent cross mapping (CCM)
It is a new approach for detecting the causal relationships in nonlinear dynamical systems. CCM is based on the Takens’ theorem, which states that in a multi-dimensional dynamical system, the essential information can be retained in the time series of any single variable of the system24,46. In CCM, causality is detected by measuring the extent to which the time series historical record of one variable can reliably estimate states of the other variable. That is, if variable X is influencing Y, then, based on the generalized Takens’ theorem, the causal variable X can be recovered from the historical record of the affected variable Y. The cross map skill is defined as the correlation coefficient ρ between predictions and observations of X. If the cross map skill increases with the length of the time series and convergence is present, then the causal effect of X on Y can be inferred. More details can be found in three one-minute animations from the supplementary material of Sugihara et al.24 (http://science.sciencemag.org/content/suppl/2012/09/19/science.1227079.DC1). CCM can also distinguish the true bidirectional causality from the phenomenon of synchrony resulting from extremely strong unidirectional forcing24. In case of synchrony, although variable X does influence Y, and Y has no effect on X, CCM can detect causal relationships in both directions. To resolve this problem, Hao et al.25 proposed an extension to CCM by considering time lags, i.e., a non-positive lag for optimal cross mapping for the true causal direction while a positive lag for the false causal direction.
In this study, the CCM analysis was implemented by using the free rEDM package47 and multispatialCCM package48 within the R language environment49, and the analysis was based on monthly data of grids in the study area for the period from January 2010 to December 2014. The implementation procedure includes following three steps:
Identify the optimal embedding dimension (E) using simplex projection. In this algorithm, the ability of one variable to predict its own dynamics is estimated using different embedding dimensions50. The correlation coefficient ρ between predictions and observations represents the forecast skill, and the optimal embedding dimension corresponds to the highest forecast skill.
Test the nonlinearity using the S-map test (sequential locally weighted global linear maps). The S-map method can describe the dynamics by fitting local linear maps51, and uses a nonlinearity index θ to govern the weight of points when fitting the local linear map. When θ = 0, all points are weighted equally, and the model corresponds to a simple linear model, and when θ > 0, the nearby points are weighted greater, and the forecast becomes more nonlinear. If the best forecast skill appears in a linear model (θ = 0), the system has only linear dynamics. In contrast, if forecast skill ρ improves with increasing θ, the system is nonlinear.
Calculate the cross map skill for different time lags. In the CCM method, the cross map skill (ρ) varies as a function of the length of the library (L), which represents the number of observations in the composite time series collapsing from multiple plots. The CCM method is executed at different time lags (τ) to distinguish the true bidirectional causality from the synchrony.
Acknowledgements
The research is supported by the Science and Technology Service Network Initiative Project of Chinese Academy of Sciences (KFJ-STS-ZDTP-036) and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA20100303).
Author Contributions
W.Y.Q. and Y.J. conceived the project and wrote the paper. C.Y.N., P.D.M. and L.Z. contributed to the discussion of the results and commented on the manuscript. D.W.L. contributed to the discussion and revised the manuscript.
Data Availability
No datasets were generated during the current study.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Schlosser CA, Milly PCD. A model-based investigation of soil moisture predictability and associated climate predictability. Journal of Hydrometeorology. 2002;3:483–501. doi: 10.1175/1525-7541(2002)003<0483:AMBIOS>2.0.CO;2. [DOI] [Google Scholar]
- 2.Yuan X, et al. Vegetation changes and land surface feedbacks drive shifts in local temperatures over Central Asia. Scientific Reports. 2017;7:3287. doi: 10.1038/s41598-017-03432-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gastineau G, García-Serrano J, Frankignoul C. The influence of autumnal Eurasian snow cover on climate and its link with Arctic sea ice cover. Journal of Climate. 2017;30:7599–7619. doi: 10.1175/JCLI-D-16-0623.1. [DOI] [Google Scholar]
- 4.Alexander L. Climate science: Extreme heat rooted in dry soils. Nature Geoscience. 2011;4:12. doi: 10.1038/ngeo1045. [DOI] [Google Scholar]
- 5.Dirmeyer, P. A. The terrestrial segment of soil moisture–climate coupling. Geophysical Research Letters38 (2011).
- 6.Tuttle S, Salvucci G. Empirical evidence of contrasting soil moisture–precipitation feedbacks across the United States. Science. 2016;352:825–828. doi: 10.1126/science.aaa7185. [DOI] [PubMed] [Google Scholar]
- 7.Dirmeyer PA, Halder S. Sensitivity of numerical weather forecasts to initial soil moisture variations in CFSv2. Weather and Forecasting. 2016;31:1973–1983. doi: 10.1175/WAF-D-16-0049.1. [DOI] [Google Scholar]
- 8.Wei J, Dirmeyer PA, Guo Z. How much do different land models matter for climate simulation? Part II: A decomposed view of the land–atmosphere coupling strength. Journal of Climate. 2010;23:3135–3145. doi: 10.1175/2010JCLI3178.1. [DOI] [Google Scholar]
- 9.Koster, R. D., Suarez, M. J., Higgins, R. W. & Van den Dool, H. M. Observational evidence that soil moisture variations affect precipitation. Geophysical Research Letters30 (2003).
- 10.Gentine P, Holtslag AA, D’Andrea F, Ek M. Surface and atmospheric controls on the onset of moist convection over land. Journal of Hydrometeorology. 2013;14:1443–1462. doi: 10.1175/JHM-D-12-0137.1. [DOI] [Google Scholar]
- 11.Findell KL, Eltahir EA. An analysis of the soil moisture‐rainfall feedback, based on direct observations from Illinois. Water Resources Research. 1997;33:725–735. doi: 10.1029/96WR03756. [DOI] [Google Scholar]
- 12.Salvucci GD, Saleem JA, Kaufmann R. Investigating soil moisture feedbacks on precipitation with tests of Granger causality. Advances in water Resources. 2002;25:1305–1312. doi: 10.1016/S0309-1708(02)00057-X. [DOI] [Google Scholar]
- 13.D’Odorico P, Porporato A. Preferential states in soil moisture and climate dynamics. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:8848–8851. doi: 10.1073/pnas.0401428101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Koster RD, Suarez MJ, Heiser M. Variance and predictability of precipitation at seasonal-to-interannual timescales. Journal of hydrometeorology. 2000;1:26–46. doi: 10.1175/1525-7541(2000)001<0026:VAPOPA>2.0.CO;2. [DOI] [Google Scholar]
- 15.Froidevaux P, Schlemmer L, Schmidli J, Langhans W, Schär C. Influence of the background wind on the local soil moisture–precipitation feedback. Journal of the atmospheric sciences. 2014;71:782–799. doi: 10.1175/JAS-D-13-0180.1. [DOI] [Google Scholar]
- 16.Su H, Dickinson RE. On the spatial gradient of soil moisture–precipitation feedback strength in the April 2011 drought in the Southern Great Plains. Journal of Climate. 2017;30:829–848. doi: 10.1175/JCLI-D-13-00185.1. [DOI] [Google Scholar]
- 17.Jaeger EB, Seneviratne SI. Impact of soil moisture–atmosphere coupling on European climate extremes and trends in a regional climate model. Climate Dynamics. 2011;36:1919–1939. doi: 10.1007/s00382-010-0780-8. [DOI] [Google Scholar]
- 18.Taylor CM, et al. Modeling soil moisture‐precipitation feedback in the Sahel: Importance of spatial scale versus convective parameterization. Geophysical Research Letters. 2013;40:6213–6218. doi: 10.1002/2013GL058511. [DOI] [Google Scholar]
- 19.Gallus WA, Jr., Segal M. Sensitivity of forecast rainfall in a Texas convective system to soil moisture and convective parameterization. Weather and forecasting. 2000;15:509–525. doi: 10.1175/1520-0434(2000)015<0509:SOFRIA>2.0.CO;2. [DOI] [Google Scholar]
- 20.Mei R, Wang G. Impact of sea surface temperature and soil moisture on summer precipitation in the United States based on observational data. Journal of Hydrometeorology. 2011;12:1086–1099. doi: 10.1175/2011JHM1312.1. [DOI] [Google Scholar]
- 21.Meng L, Long D, Quiring SM, Shen Y. Statistical analysis of the relationship between spring soil moisture and summer precipitation in East China. International Journal of Climatology. 2014;34:1511–1523. doi: 10.1002/joc.3780. [DOI] [Google Scholar]
- 22.Matin MA, Bourque CP. Relating seasonal dynamics of enhanced vegetation index to the recycling of water in two endorheic river basins in north-west China. Hydrology and Earth System Sciences. 2015;19:3387. doi: 10.5194/hess-19-3387-2015. [DOI] [Google Scholar]
- 23.Granger, C. W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society, 424–438 (1969).
- 24.Sugihara, G. et al. Detecting causality in complex ecosystems. Science, 1227079 (2012). [DOI] [PubMed]
- 25.Ye H, Deyle ER, Gilarranz LJ, Sugihara G. Distinguishing time-delayed causal interactions using convergent cross mapping. Scientific reports. 2015;5:14750. doi: 10.1038/srep14750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Van Nes EH, et al. Causal feedbacks in climate change. Nature Climate Change. 2015;5:445. doi: 10.1038/nclimate2568. [DOI] [Google Scholar]
- 27.Tsonis AA, et al. Dynamical evidence for causality between galactic cosmic rays and interannual variation in global temperature. Proceedings of the National Academy of Sciences. 2015;112:3253–3256. doi: 10.1073/pnas.1420291112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang X, et al. A two-fold increase of carbon cycle sensitivity to tropical temperature variations. Nature. 2014;506:212. doi: 10.1038/nature12915. [DOI] [PubMed] [Google Scholar]
- 29.Koster, R. D. et al. Contribution of land surface initialization to subseasonal forecast skill: First results from a multi‐model experiment. Geophysical Research Letters37 (2010).
- 30.Dirmeyer PA, Schlosser CA, Brubaker KL. Precipitation, recycling, and land memory: An integrated analysis. Journal of Hydrometeorology. 2009;10:278–288. doi: 10.1175/2008JHM1016.1. [DOI] [Google Scholar]
- 31.Seneviratne SI, et al. Soil moisture memory in AGCM simulations: analysis of global land–atmosphere coupling experiment (GLACE) data. Journal of Hydrometeorology. 2006;7:1090–1112. doi: 10.1175/JHM533.1. [DOI] [Google Scholar]
- 32.Koster RD, Suarez MJ. Soil moisture memory in climate models. Journal of hydrometeorology. 2001;2:558–570. doi: 10.1175/1525-7541(2001)002<0558:SMMICM>2.0.CO;2. [DOI] [Google Scholar]
- 33.Nicolai‐Shaw N, Gudmundsson L, Hirschi M, Seneviratne SI. Long‐term predictability of soil moisture dynamics at the global scale: Persistence versus large‐scale drivers. Geophysical Research Letters. 2016;43:8554–8562. doi: 10.1002/2016GL069847. [DOI] [Google Scholar]
- 34.Koster R, Schubert S, Suarez M. Analyzing the concurrence of meteorological droughts and warm periods, with implications for the determination of evaporative regime. Journal of Climate. 2009;22:3331–3341. doi: 10.1175/2008JCLI2718.1. [DOI] [Google Scholar]
- 35.Guo Z, et al. GLACE: the global land–atmosphere coupling experiment. Part II: analysis. Journal of Hydrometeorology. 2006;7:611–625. doi: 10.1175/JHM511.1. [DOI] [Google Scholar]
- 36.Koster RD, et al. Regions of strong coupling between soil moisture and precipitation. Science. 2004;305:1138–1140. doi: 10.1126/science.1100217. [DOI] [PubMed] [Google Scholar]
- 37.Yang L, Sun G, Zhi L, Zhao J. Negative soil moisture-precipitation feedback in dry and wet regions. Scientific reports. 2018;8:4026. doi: 10.1038/s41598-018-22394-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Seneviratne SI, et al. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Science Reviews. 2010;99:125–161. doi: 10.1016/j.earscirev.2010.02.004. [DOI] [Google Scholar]
- 39.Feng H, Zou B, Luo J. Coverage-dependent amplifiers of vegetation change on global water cycle dynamics. Journal of hydrology. 2017;550:220–229. doi: 10.1016/j.jhydrol.2017.04.056. [DOI] [Google Scholar]
- 40.Hohenegger C, Brockhaus P, Bretherton CS, Schär C. The soil moisture–precipitation feedback in simulations with explicit and parameterized convection. Journal of Climate. 2009;22:5003–5020. doi: 10.1175/2009JCLI2604.1. [DOI] [Google Scholar]
- 41.Guillod BP, Orlowsky B, Miralles DG, Teuling AJ, Seneviratne SI. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nature communications. 2015;6:6443. doi: 10.1038/ncomms7443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Harris I, Jones P, Osborn T, Lister D. Updated high‐resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. International Journal of Climatology. 2014;34:623–642. doi: 10.1002/joc.3711. [DOI] [Google Scholar]
- 43.Dorigo W, et al. ESA CCI Soil Moisture for improved Earth system understanding: state-of-the art and future directions. Remote Sensing of Environment. 2017;203:185–215. doi: 10.1016/j.rse.2017.07.001. [DOI] [Google Scholar]
- 44.Wang Y, Yang J, Chen Y, Wang A, De Maeyer P. The Spatiotemporal Response of Soil Moisture to Precipitation and Temperature Changes in an Arid Region, China. Remote Sensing. 2018;10:468. doi: 10.3390/rs10030468. [DOI] [Google Scholar]
- 45.Mu Q, Zhao M, Running SW. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sensing of Environment. 2011;115:1781–1800. doi: 10.1016/j.rse.2011.02.019. [DOI] [Google Scholar]
- 46.Takens, F. In Dynamical systems and turbulence, Warwick 1980 366–381 (Springer, 1981).
- 47.Ye, H. et al. and George Sugihara. rEDM: Applications of Empirical Dynamic Modeling from Time Series. R package version 0.6.9. https://CRAN.R-project.org/package=rEDM (2017).
- 48.Clark, A. multispatialCCM: Multispatial Convergent Cross Mapping. R package version 1.0. https://CRAN.R-project.org/package=multispatialCCM (2014).
- 49.Team, R. C. A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/ (2018).
- 50.Sugihara G, May RM. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature. 1990;344:734. doi: 10.1038/344734a0. [DOI] [PubMed] [Google Scholar]
- 51.Sugihara G. Nonlinear forecasting for the classification of natural time series. Phil. Trans. R. Soc. Lond. A. 1994;348:477–495. doi: 10.1098/rsta.1994.0106. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No datasets were generated during the current study.