Abstract
Neurons in primary visual cortex are selective to the orientation and spatial frequency of sinusoidal gratings. In the classic model of cortical organization, a population of neurons responding to the same region of the visual field but tuned to all possible feature combinations provides a detailed representation of the local image. Such a functional module is assumed to be replicated across primary visual cortex to provide a uniform representation of the image across the entire visual field. In contrast, it has been hypothesized that the tiling properties of ON- and OFF-center receptive fields in the retina, largely mirrored in the geniculate, may constrain cortical tuning at each location in the visual field. This model predicts the existence of local biases in tuning that vary across the visual field and would prevent the cortex from developing a uniform, modular representation as postulated by the classic model. Here, we confirm the existence of local tuning biases in the primary visual cortex of the mouse, lending support to the notion that cortical tuning may be constrained by signals from the periphery.
NEW & NOTEWORTHY Populations of cortical neurons responding to the same part of the visual field are shown to have similar tuning. Such local biases are consistent with the hypothesis that cortical tuning, in mouse primary visual cortex, is constrained by signals from the periphery.
Keywords: population coding, primary visual cortex, receptive fields
INTRODUCTION
Mice lack the precise spatial organization of neural preferences into radial columns and two-dimensional feature maps that are a hallmark of cat and monkey primary visual cortex (area V1; Grinvald et al. 1986; Hübener et al. 1997; Ts’o et al. 1990). Instead, neurons with diverse tuning preferences intermingle in the cortex to form “salt-and-pepper” maps (Bonin et al. 2011; Ohki et al. 2005; Van Hooser 2007). Despite this apparent disorder, the receptive field properties and tuning of individual neurons in mouse V1 are similar to those of their counterparts in higher mammals (Bonin et al. 2011; Lien and Scanziani 2013; Niell and Stryker 2008; Vaiceliunaite et al. 2013). In particular, they show similar tuning for the orientation and spatial frequency of sinusoidal gratings (Ringach et al. 2016). How populations of neurons in mouse V1 represent a local image and how such representation compares with that of higher mammals are central questions of visual neuroscience (Mazade and Alonso 2017; Van Hooser 2007).
The classic model of V1 in higher mammals posits that populations of neurons with overlapping receptive fields, comprising a hypercolumn, develop a full set of tuning preferences, such as all possible orientations and spatial frequencies (Hubel and Wiesel 1977). A cortical hypercolumn would then have all the machinery required to represent local image structure accurately (Daugman 1988). An alternative model of cortical organization postulates that the spatial tiling of ON/OFF receptive fields in the retina, and largely mirrored in the geniculate (Usrey et al. 1999), constrains cortical tuning at each location in the visual field (Ringach 2004, 2011, 2013; Soodak 1987). This model predicts the existence of local tuning biases that ought to be reflected in a tendency for the similarity of tuning between neurons to increase with a measure of their receptive field overlap. Here, we report evidence of a correlation between receptive field overlap and tuning similarity in primary visual cortex of the mouse, lending support to the notion that cortical tuning may be, in part, determined by biases originating in the periphery (Ringach 2013).
METHODS
Animals.
All procedures were approved by the University of California, Los Angeles, Office of Animal Research Oversight (the Institutional Animal Care and Use Committee) and were in accord with guidelines set by the US National Institutes of Health. A total of 6 C57BL/6J mice (The Jackson Laboratory), both male (3) and female (3), aged postnatal days 35–56, were used in this study. Mice were housed in groups of 2 or 3, in reversed light cycle. Animals were naïve subjects with no prior history of participation in research studies. We imaged 26 different fields to obtain the data discussed in this paper.
Surgery.
Carprofen and buprenorphine analgesia were administered preoperatively. Mice were then anesthetized with isoflurane (4–5% induction; 1.5–2% surgery). Core body temperature was maintained at 37.5°C using a feedback heating system. Eyes were coated with a thin layer of ophthalmic ointment to prevent desiccation. Anesthetized mice were mounted in a stereotaxic apparatus. Blunt ear bars were placed in the external auditory meatus to immobilize the head. A portion of the scalp overlying the two hemispheres of the cortex (~8 × 6 mm) was then removed to expose the underlying skull.
After the skull was exposed, it was dried and covered by a thin layer of Vetbond. After the Vetbond dried (~15 min), it provided a stable and solid surface to affix the aluminum bracket with dental acrylic. The bracket was then affixed to the skull, and the margins were sealed with Vetbond and dental acrylic to prevent infections.
Virus injection.
A 3-mm-diameter region of skull overlying the occipital cortex was removed. Care was taken to leave the dura intact. GCaMP6-fast (University of Pennsylvania Vector Core: AAV1.Syn.GCaMP6f.WPRE.SV40; #AV-1-PV2822) was expressed in cortical neurons using adeno-associated virus (AAV). AAV-GCaMP6-fast (titer: ~1013 genomes/ml) was loaded into a glass micropipette and slowly inserted into the primary visual cortex (V1) using a micromanipulator. Two injection sites were made centered around the center of V1 and separated ~200 μm apart. For each site, AAV-GCaMP6-fast was pressure-injected using a Picospritzer III (4 puffs at 15–20 psi with a duration of 10 ms, and each puff was separated by 4 s; Parker, Hollis, NH) starting at a depth of 350 μm below the pial surface and making injections every 10 μm moving up with the last injection made at 100 μm below the pial surface. The total volume injected across all depths was ~0.5 μl. The injections were made by a computer program in control of the micromanipulator and the Picospritzer.
A sterile 3-mm-diameter cover glass was then placed directly on the dura and sealed at its edges with Vetbond. When dry, the edges of the cover glass were further sealed with dental acrylic. At the end of the surgery, all exposed skull and wound margins were sealed with Vetbond and dental acrylic, and a small, sealed glass window was left in place over the occipital cortex. Mice were then removed from the stereotaxic apparatus, given a subcutaneous bolus of warm sterile saline, and allowed to recover on the heating pad. When fully alert, they were placed back in their home cage.
Imaging.
Once expression of GCaMP6f was observed in primary visual cortex, typically between 11 and 15 days after the injection, imaging sessions took place. Imaging was performed using a resonant, two-photon microscope (Neurolabware, Los Angeles, CA) controlled by Scanbox acquisition software (Los Angeles, CA). The light source was a Coherent Chameleon Ultra II laser (Santa Clara, CA) running at 920 nm. The objective was a ×16 water immersion lens (0.8 numerical aperture, 3-mm working distance; Nikon). The microscope frame rate was 15.6 Hz (512 lines with a resonant mirror at 8 kHz). Eye movements and pupil size were recorded via a Dalsa Genie M1280 camera (Teledyne Dalsa) fitted with a 740-nm long-pass filter that looked at the eye indirectly through the reflection of an infrared-reflecting glass. Images were captured at an average depth of 260 μm.
Visual stimulation.
Sequences of pseudorandom sinusoidal gratings (Malone and Ringach 2008; Ringach et al. 1997) and sparse noise stimuli were generated in real-time by a Processing sketch using OpenGL shaders (see https://processing.org). In generating pseudorandom gratings, the orientation domain was sampled in equal steps of 10° for a total of 18 possible orientations; the spatial frequency domain was sampled in equal steps on a logarithmic scale from 0.0079 to 0.1549 cycles/°, for a total of 12 possible spatial frequencies; and for each combination of orientation and spatial frequency, spatial phase was equally sampled in steps of 45°, leading to a total of 8 possible settings. The tuning curves were computed by averaging responses over spatial phase, as done in previous studies (Malone and Ringach 2008; Ringach et al. 2002). The duration of the sequences was either 20 or 30 min, and gratings were updated 4 times a second on a screen refreshed at 60 Hz. Thus each combination of orientation and spatial frequency appeared ≥22 times on average (for a 20-min sequence). Sparse noise consisted of flashed dark and bright disks with a diameter of 5°. Two disks of each contrast appeared at any one time. The lifetime of each disk was 250 ms, after which it was removed and repositioned randomly on the screen. Transistor-transistor logic signals generated by the stimulus computer were sampled by the microscope and time-stamped with the frame and line number being scanned at that time. The time stamps provided the synchronization between visual stimulation and imaging data.
In all experiments, we used a BenQ XL2720Z screen, which measured 60 × 34 cm and was viewed at 20-cm distance, subtending 112 × 80° of visual angle. The screen was calibrated using a Photo Research (Chatsworth, CA) PR-650 spectroradiometer, and the result was used to generate the appropriate γ-corrections for the red, green, and blue components via an NVIDIA Quadro K4000 graphics card. The contrast of the stimulus was 80%. The center of the monitor was positioned with the center of the receptive field population for the eye contralateral to the cortical hemisphere under consideration. The locations of the receptive fields were estimated by an automated process where localized, flickering checkerboard patches appeared at randomized locations within the screen. This experiment was run at the beginning of each imaging session to ensure the centering of receptive fields on the monitor.
We imaged the monocular region of V1 in the left hemisphere. The receptive fields of neurons were centered around 20–35° in azimuth and 0–20° in elevation on the right visual hemifield.
Image processing.
The image processing pipeline was the same as described in detail elsewhere (Ringach et al. 2016). Briefly, calcium images were aligned to correct for motion artifacts. Following motion stabilization, we used a MATLAB (MathWorks, Natick, MA) graphical user interface tool developed in our laboratory to define regions of interest corresponding to putative cell bodies manually. Following segmentation, we extracted signals by computing the mean of the calcium fluorescence within each region of interest and discounting the signals from the nearby neuropil. Spikes were then estimated via deconvolution (Berens et al. 2018).
Kernel estimation.
The estimation of the tuning kernel was performed as in earlier studies by fitting a linear model between the response and the stimulus (Ringach et al. 2016). Similarly, we computed the ON/OFF maps by fitting a linear model between the response and the location of bright and dark spots. The maps were smoothed with the Gaussian window of σ = 5°. For each cell, we used the map at the optimal time delay between stimulus and response. The optimal delay was defined as the time at which the variance of the kernel reached its maximum. A tuning kernel was defined as significant if the peak variance was at least two times that of the baseline measured at negative time lags. ON and OFF maps showed a distribution of values that was close to normal. We defined the optimal delay time as the one at which the map kurtosis reached its maximum. We considered a map significant if its peak kurtosis was >8. The results described below were robust to the selection of these thresholds.
Tuning similarity and overlap indices.
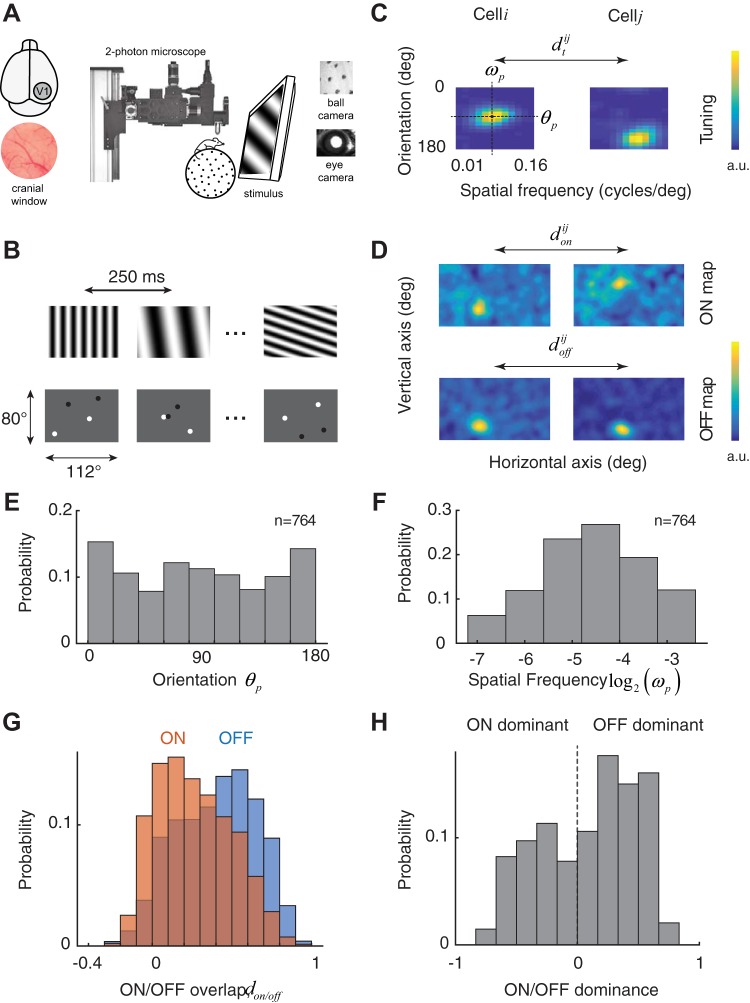
The similarity of tuning between two cells was defined as the cross-correlation coefficient between their tuning kernels. In some cases, we also investigated the similarity orientation preference, defined by the absolute difference between the preferred orientations, or the similarity of their peak spatial frequency, defined as the absolute difference of the logarithm (base 2) of the preferred frequency. The preferred parameters were computed as the center of mass of horizontal (for spatial frequency) and vertical (for orientation) slices of the tuning kernel passing through the peak response (Fig. 1C). As a measure of overlap between ON and OFF subregions, we computed the correlation coefficient between the maps. In some analyses, we also computed a normalized overlap measure between receptive field pairs, defined as the distance between the locations of their peaks normalized by the mean square root of their areas. The area of a receptive field was defined by the size of the region >90% of the maximum response. When assessing a statistical correlation between indices of overlap and tuning similarity, we used Spearman rank correlation, as these are bounded indices that are not normally distributed. The smoothed version of the scatterplot in Fig. 1E was generated by local regression using weighted least squares and a 1st degree polynomial model (as implemented by smooth function in MATLAB).
Fig. 1.
Experimental setup and basic measures of receptive fields and tuning selectivity. A: experimental setup: 2-photon imaging in awake behaving mouse. A cranial window is implanted over the primary visual cortex (area V1). Mice are head-restrained but otherwise free to walk, rest, or groom on a spherical treadmill. Eye movements and locomotion are monitored by cameras synchronized to the microscope. B: pseudorandom sequences of full-field, sinusoidal gratings were used to map the tuning for orientation and spatial frequency. Sparse noise stimuli consisting of randomly flashed dark and bright disks were used to map the ON and OFF subregions of each cell. C: 2 examples of tuning kernels in the orientation and spatial frequency domain. Kernels are normalized and presented in arbitrary units (a.u.). Spatial frequency was sampled in equal steps in a logarithmic scale. From the kernels, we estimate the preferred orientation of the cell, θp, as well as its preferred spatial frequency, ωp. Similarity between the tuning kernels of 2 cells, i and j, is denoted by . deg, Degrees. D: 2 examples of ON and OFF maps. Kernels are normalized and presented in arbitrary units. Dimensions of the image in visual space correspond to the ones displayed in B. Similarities between ON and OFF maps of 2 cells, i and j, are denoted by and , respectively. E: distribution of preferred orientation in the population. There is a slight overrepresentation of the cardinal orientations. F: distribution of preferred spatial frequency. G: distribution of ON and OFF subregion overlap in cells ≤100 μm apart from each other. There is a higher scatter for ON than OFF subregions. H: histogram of the relative amplitudes of ON and OFF kernels shows a slight dominance of OFF responses.
An ON/OFF dominance index was defined based on the peak amplitudes of the corresponding kernels, Aoff and Aon, by the equation (Aoff − Aon)/(Aoff + Aon). An index of +1 corresponds to a cell with a pure, dominant OFF subregion, an index of −1 corresponds to a cell with a pure, dominant ON subregion, and an index of 0 represents a cell with perfectly balanced ON and OFF responses. A Wilcoxon rank sign test was used to test the null hypothesis that the distribution is balanced.
Code and data availability.
All analyses were conducted in MATLAB. We are making the tuning and receptive field data available to the community so our analyses can be replicated and compared with data from other laboratories (see endnote).
RESULTS
We measured the visual properties of neurons in primary visual cortex using resonant, two-photon microscopy in the awake, behaving mouse (Fig. 1A). To measure the tuning of neurons to orientation and spatial frequency, we used a visual stimulus consisting of a sequence of flashed, high-contrast sinusoidal gratings having pseudorandom orientations and spatial frequencies (Fig. 1B, top). We estimated the tuning of each cell by linearly regressing the response on the stimulus (Fig. 1C; see methods). We denote the estimated tuning kernel of the i − th cell in the population by . As expected, cells were selective for orientation and band pass in spatial frequency (Niell and Stryker 2008). We define the tuning similarity between a pair of cells as the correlation coefficient between their tuning kernels, (Fig. 1C). The peak of the tuning curve also yielded a preferred orientation and spatial frequency (Fig. 1C).
We also measured the location of receptive fields in visual space using a sparse noise stimulus in which dark and bright disks were randomly flashed on the computer screen for a brief period before being relocated (Fig. 1B, bottom). We computed separate ON and OFF maps for each cell by correlating their responses with the location of the bright and dark disks, respectively (Jones and Palmer 1987; Fig. 1D). We denote the ON/OFF maps corresponding to the i − th cell in the population by and , respectively. We define the index of overlap between ON/OFF subregions, and , as the correlation coefficients of their respective maps (Fig. 1D). The distribution of preferred orientations shows a slight overrepresentation of the cardinal directions (Fig. 1E), and the distribution of the preferred spatial frequencies had a log-normal shape, with a geometric mean of 0.04 cycles/° (Fig. 1F). The results are consistent with previous reports (Kondo and Ohki 2016; Niell and Stryker 2008).
Interestingly, the average overlap of OFF subregions in a small cortical neighborhood (cells within 100 μm of each other) is significantly higher than ON subregions (Fig. 1G; non = 1,340, noff = 2,729, medians of 0.24 and 0.42 for ON and OFF, respectively, Wilcoxon rank sum test, P = 1.1 × 10−59). Moreover, there is a slight dominance of OFF over ON responses (Fig. 1H; Wilcoxon sign rank test, n = 679, P = 3.9 × 10−9; see methods). The relatively lower scatter of OFF compared with ON subregions and the slight dominance of OFF responses in the superficial layers of the cortex are two organizational features that resemble what is observed in higher mammals (Jin et al. 2008; Kremkow et al. 2016; Lee et al. 2016; Yeh et al. 2009).
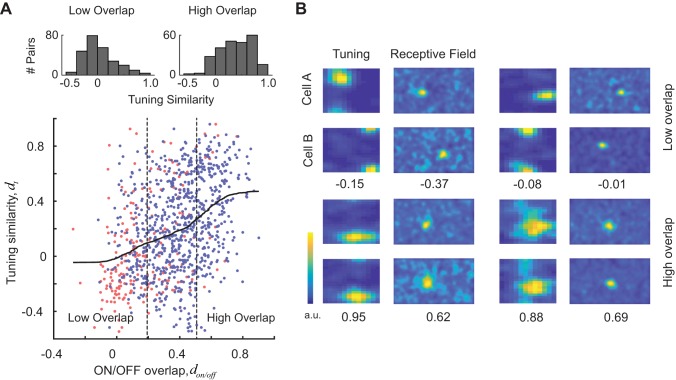
Our central finding is that there is a highly significant, positive correlation between tuning similarity and receptive field overlap (ON subregions, n = 209, r = 0.38, P = 2.4 × 10−8; OFF subregions, n = 790, r = 0.32, P = 2.9 × 10−21; ON/OFF subregions, n = 999, r = 0.38, P = 2.7 × 10−36; Fig. 2A). We defined groups of cell pairs with low and high overlap as those falling within the first and fourth quartiles of the overlap index distribution, respectively (Fig. 2A). Tuning similarity for cells with receptive fields with low overlap was significantly lower than that with receptive fields with high overlap (Fig. 2A, top histograms; median values of −0.03 and 0.39, Wilcoxon ranked-sum test, P = 6.2 × 10−30). The correlation between tuning similarity and receptive field overlap was significant in four out of the six mice when tested individually (P < 0.01). The two mice that failed to show an effect had the lowest number of cell pairs (n = 15 and 61). Four cell pairs showing different degrees of overlap and tuning similarity are shown in Fig. 2B.
Fig. 2.
Evidence of local tuning bias in mouse primary visual cortex. A, bottom: tuning similarity (dt) is positively correlated with receptive field overlap of both ON and OFF subregions (don and doff). Scatterplot shows tuning similarity against the overlap of ON or OFF subregions. Pairs of cells may be plotted twice, once showing the overlap of ON subregions (red points) and once showing the overlap with OFF subregions (blue points). Solid curve represents a smoothed version of the scatterplot obtained via local regression. Top: histograms of tuning similarity values for pairs with low and high overlap (defined by the vertical, dashed lines). Pairs with high degree of receptive field overlap have a significantly higher similarity of tuning than pairs with low degree of receptive field overlap. #, Number of. B: examples of 4 cell pairs with different degrees of receptive field overlap and tuning similarity. For each pair, the tuning similarity and receptive field overlap values are shown at the bottom. Top row shows examples of cell pairs with low degree of receptive field overlap and tuning similarity. Bottom row shows examples of cell pairs with high degree of receptive field overlap and tuning similarity. a.u., Arbitrary units.
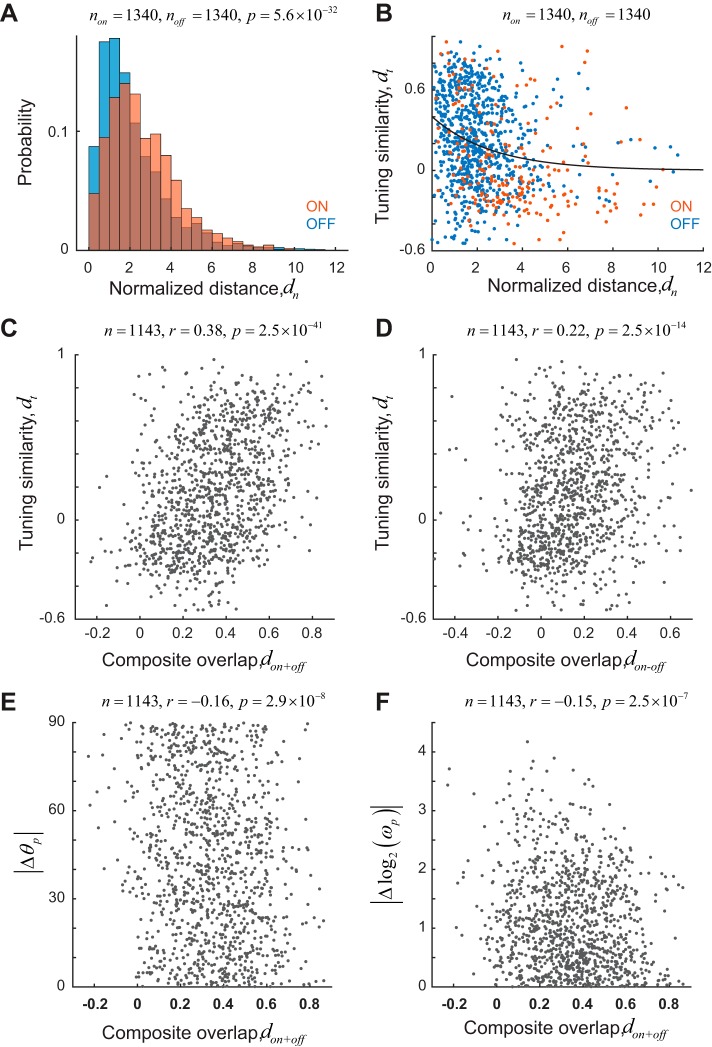
To probe the robustness of our finding, we also explored different measures of receptive field overlap and tuning similarity. A different measure of receptive field overlap is the normalized distance, defined as the distance between the peaks of receptive fields divided by the average, effective radius of their sizes. The size of a receptive field was defined as the area >90% of its maximum value. The normalized distance can be computed separately for both ON and OFF maps. We find that the median normalized distance of ON subregions is significantly greater than those of OFF subregions (Fig. 3A; non = 1,340, noff = 2,729, medians of 2.34 and 1.69 for ON and OFF subregions, respectively; rank sum test, P = 5.6 × 10−32), consistent with our earlier result (Fig. 1G). Finally, tuning similarity correlates with normalized distance [Fig. 3B; r = −0.24, P = 1.6 × 10−15, solid curve is an exponential fit y = Ae−bx, with A = 0.40 (0.33, 0.47) and b = 0.37 (0.26, 0.48), optimal fit values and 95% confidence intervals in parentheses]. Next, for each cell, we defined the composite sum map as hon+off = hon + hoff and a composite difference map as hon−off = hon − hoff. We defined the overlap measure don+off as the correlation coefficient between the composite sum maps of two cells and the measure don−off as the correlation coefficient between the composite difference maps. We find that tuning similarity is correlated with both don+off (Fig. 3C; r = 0.38, P = 2.5 × 10−41) and don−off (Fig. 3D; r = 0.22, P = 2.5 × 10−14). The weaker correlation with overlap based on difference maps arises from the fact that the composite difference maps tend to have increased amount of noise in background, which biases the values of correlation coefficients toward 0. We also find that the similarity of preferred orientation (Fig. 3E; r = −0.16, P = 2.9 × 10−8) and spatial frequencies (Fig. 3F; r = −0.15, P = 2.5 × 10−7) is significantly correlated with don+off. However, it is clear the strength of the correlation is not as high as seen when we measure tuning similarity based on the shapes of the full tuning kernels.
Fig. 3.
Robustness of correlation between tuning similarity and receptive field overlap. A: distribution of normalized distance (dn), a measure of receptive field overlap, for ON (red) and OFF (blue) subregions for pairs ≤100 μm apart on the cortex. ON subregions show larger positional scatter. B: tuning similarity is inversely correlated with normalized distance. Solid line represents an exponential fit to the data. Receptive fields with overlapping receptive fields tend to have higher tuning similarity than receptive fields that are far apart in the visual field. Blue dots represent OFF subregions. Red dots represent ON subregions. C and D: tuning similarity is correlated with receptive field overlap measures based on the sum (don+off) or difference (don−off) of ON and OFF maps. E and F: absolute differences of preferred orientation (|Δθp|) and spatial frequency [|Δlog2(ωp)|] are correlated with receptive field overlap based on the sum of ON and OFF maps.
Altogether, the data demonstrate the existence of local tuning biases, where cells with high degree of receptive field overlap tend to have higher tuning similarity than cells with low degrees of overlap.
DISCUSSION
Local tuning biases imply that populations of neurons responding to different parts of the visual field do not represent the local image in a uniform way, as assumed by modular cortical organization. The preferences of a population of neurons responding to one location of the visual field will be biased to one specific combination of orientation and spatial frequency, whereas populations responding to other locations will have a different bias. How can the cortex reconstruct the structure of the image given such incomplete information?
To draw an analogy, the situation is like the structure of the photoreceptor mosaic, where at any one retinal position we may find an L, M, or S cone. In other words, the retinal representation does not offer all three spectral measurements at each position. Nevertheless, a partial set of measurements along with the statistical regularities of natural scenes allow the brain to infer the image most likely to have produced a particular pattern of activation across the cone mosaic (Brainard 2015). A cortical representation where different parts of the visual field are represented by populations of cells with different tuning biases offers a similar challenge, and a similar solution based on the statistics of natural scenes can be offered.
In the mouse, at least three different factors may exert a tuning bias onto the cortex. First, there is a specialized circuit carrying direction-selective signals that arise in retinal ganglion cells. These cells target the lateral geniculate nucleus (LGN) “shell,” which, in turn, projects to the superficial layers of the cortex (Cruz-Martín et al. 2014). If some cells preferentially sample from one of these inputs, they are expected to inherit the same selectivity and location in the visual field. A different type of projection from the retina to cortex occurs via the core of the LGN and innervates layers 4 and 6. Recent studies reveal that geniculate afferents from the core are moderately tuned for the orientation and direction of a stimulus (Kondo and Ohki 2016; Piscopo et al. 2013; Sun et al. 2016). Thus it may be possible that some cortical cells reflect the biases of these individual thalamic inputs. At the same time, differences in the tuning of layer 4 neurons and their thalamic inputs indicate that not all cortical selectivity is inherited by sampling of individual LGN afferents. Cells in layer 4 have a band-pass spatial frequency tuning with peak spatial frequencies higher than those of thalamic afferents (Kondo and Ohki 2016). Layer 4 neurons also show higher selectivity than those of thalamic afferents and have a larger diversity of preferred orientations, whereas LGN inputs are biased heavily toward the cardinals (Kondo and Ohki 2016). Thus one can expect the structure of a population of simple cell receptive fields in layer 4 to arise from the combination of spatially displaced ON- and OFF-center thalamic afferents, as described in the classic Hubel and Wiesel (1977) model. When ON- and OFF-center receptive fields are combined in this way, tuning biases can still arise when their available number of inputs is limited or spatially unbalanced. Note that the relationship between tuning similarity and receptive field overlap holds separately for ON and OFF subregions (Fig. 2). In principle, a pair of simple cells could share just one subregion but still have very different orientation tuning. The fact that this is not observed is consistent with a scenario where a limited set of inputs constrains cortical tuning (Ringach 2011).
The next natural step would be to determine whether a comparable relationship exists in higher mammals. In cats, we know the sum of geniculate ON/OFF receptive fields converging onto a cortical column is biased, and the “population receptive field” profile resembles that of a simple cell with a preferred orientation that matches the preference of the target cortical column (Jin et al. 2011). Although this finding is partly consistent with local tuning biases, it leaves open the possibility that a nearby cortical column has a different tuning preference while responding to the same location in the visual field. A second study reported that cells with orientation preferences 90° apart could only be found if the centers of the corresponding receptive fields were at least one receptive field diameter apart in the visual field (Das and Gilbert 1997). Those findings have been controversial (Bosking et al. 2002) but are consistent with our results and deserve further consideration. If local tuning biases can be demonstrated in higher mammals, the data would favor a broader role of peripheral guidance in the development of cortical tuning and maps across species (Ringach 2004, 2011, 2013; Soodak 1987).
GRANTS
D. L. Ringach was supported by National Eye Institute Grant EY-018322 and National Institute of Biomedical Imaging and Bioengineering Grant EB-022915, and J. T. Trachtenberg was supported by National Eye Institute Grant EY-023871.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
D.L.R. conceived and designed research; L.O.J., E.T., and D.L.R. performed experiments; L.O.J. and D.L.R. analyzed data; L.O.J., J.T.T., and D.L.R. interpreted results of experiments; D.L.R. prepared figures; D.L.R. drafted manuscript; J.T.T. and D.L.R. edited and revised manuscript; L.O.J., E.T., J.T.T., and D.L.R. approved final version of manuscript.
ENDNOTE
At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at the Web site of the authors, which at the time of publication they indicate is: https://figshare.com/articles/database_tuning_on_off_mat/6553658. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the Web site address, or for any links to or from it.
REFERENCES
- Berens P, Freeman J, Deneux T, Chenkov N, McColgan T, Speiser A, Macke JH, Turaga SC, Mineault P, Rupprecht P, Gerhard S, Friedrich RW, Friedrich J, Paninski L, Pachitariu M, Harris KD, Bolte B, Machado TA, Ringach D, Stone J, Rogerson LE, Sofroniew NJ, Reimer J, Froudarakis E, Euler T, Román Rosón M, Theis L, Tolias AS, Bethge M. Community-based benchmarking improves spike rate inference from two-photon calcium imaging data. PLoS Comput Biol 14: e1006157, 2018. doi: 10.1371/journal.pcbi.1006157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonin V, Histed MH, Yurgenson S, Reid RC. Local diversity and fine-scale organization of receptive fields in mouse visual cortex. J Neurosci 31: 18506–18521, 2011. doi: 10.1523/JNEUROSCI.2974-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosking WH, Crowley JC, Fitzpatrick D. Spatial coding of position and orientation in primary visual cortex. Nat Neurosci 5: 874–882, 2002. doi: 10.1038/nn908. [DOI] [PubMed] [Google Scholar]
- Brainard DH. Color and the cone mosaic. Annu Rev Vis Sci 1: 519–546, 2015. doi: 10.1146/annurev-vision-082114-035341. [DOI] [PubMed] [Google Scholar]
- Cruz-Martín A, El-Danaf RN, Osakada F, Sriram B, Dhande OS, Nguyen PL, Callaway EM, Ghosh A, Huberman AD. A dedicated circuit links direction-selective retinal ganglion cells to the primary visual cortex. Nature 507: 358–361, 2014. doi: 10.1038/nature12989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A, Gilbert CD. Distortions of visuotopic map match orientation singularities in primary visual cortex. Nature 387: 594–598, 1997. doi: 10.1038/42461. [DOI] [PubMed] [Google Scholar]
- Daugman JG. Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression. IEEE Trans Acoust 36: 1169–1179, 1988. doi: 10.1109/29.1644. [DOI] [Google Scholar]
- Grinvald A, Lieke E, Frostig RD, Gilbert CD, Wiesel TN. Functional architecture of cortex revealed by optical imaging of intrinsic signals. Nature 324: 361–364, 1986. doi: 10.1038/324361a0. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Ferrier lecture. Functional architecture of macaque monkey visual cortex. Proc R Soc Lond B Biol Sci 198: 1–59, 1977. doi: 10.1098/rspb.1977.0085. [DOI] [PubMed] [Google Scholar]
- Hübener M, Shoham D, Grinvald A, Bonhoeffer T. Spatial relationships among three columnar systems in cat area 17. J Neurosci 17: 9270–9284, 1997. doi: 10.1523/JNEUROSCI.17-23-09270.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Wang Y, Swadlow HA, Alonso JM. Population receptive fields of ON and OFF thalamic inputs to an orientation column in visual cortex. Nat Neurosci 14: 232–238, 2011. doi: 10.1038/nn.2729. [DOI] [PubMed] [Google Scholar]
- Jin JZ, Weng C, Yeh CI, Gordon JA, Ruthazer ES, Stryker MP, Swadlow HA, Alonso JM. On and off domains of geniculate afferents in cat primary visual cortex. Nat Neurosci 11: 88–94, 2008. doi: 10.1038/nn2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones JP, Palmer LA. An evaluation of the two-dimensional Gabor filter model of simple receptive fields in cat striate cortex. J Neurophysiol 58: 1233–1258, 1987. doi: 10.1152/jn.1987.58.6.1233. [DOI] [PubMed] [Google Scholar]
- Kondo S, Ohki K. Laminar differences in the orientation selectivity of geniculate afferents in mouse primary visual cortex. Nat Neurosci 19: 316–319, 2016. doi: 10.1038/nn.4215. [DOI] [PubMed] [Google Scholar]
- Kremkow J, Jin J, Wang Y, Alonso JM. Principles underlying sensory map topography in primary visual cortex. Nature 533: 52–57, 2016. doi: 10.1038/nature17936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KS, Huang X, Fitzpatrick D. Topology of ON and OFF inputs in visual cortex enables an invariant columnar architecture. Nature 533: 90–94, 2016. doi: 10.1038/nature17941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien AD, Scanziani M. Tuned thalamic excitation is amplified by visual cortical circuits. Nat Neurosci 16: 1315–1323, 2013. doi: 10.1038/nn.3488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone BJ, Ringach DL. Dynamics of tuning in the Fourier domain. J Neurophysiol 100: 239–248, 2008. doi: 10.1152/jn.90273.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazade R, Alonso JM. Thalamocortical processing in vision. Vis Neurosci 34: E007, 2017. doi: 10.1017/S0952523817000049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niell CM, Stryker MP. Highly selective receptive fields in mouse visual cortex. J Neurosci 28: 7520–7536, 2008. doi: 10.1523/JNEUROSCI.0623-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohki K, Chung S, Ch’ng YH, Kara P, Reid RC. Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature 433: 597–603, 2005. doi: 10.1038/nature03274. [DOI] [PubMed] [Google Scholar]
- Piscopo DM, El-Danaf RN, Huberman AD, Niell CM. Diverse visual features encoded in mouse lateral geniculate nucleus. J Neurosci 33: 4642–4656, 2013. doi: 10.1523/JNEUROSCI.5187-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL. Haphazard wiring of simple receptive fields and orientation columns in visual cortex. J Neurophysiol 92: 468–476, 2004. doi: 10.1152/jn.01202.2003. [DOI] [PubMed] [Google Scholar]
- Ringach DL. Peripheral guidance of cortical organization. In: The New Visual Neurosciences, edited by Werner JS and Chalupa LM. Cambridge, MA: MIT Press, 2013. [Google Scholar]
- Ringach DL. You get what you get and you don’t get upset. Nat Neurosci 14: 123–124, 2011. doi: 10.1038/nn0211-123. [DOI] [PubMed] [Google Scholar]
- Ringach DL, Bredfeldt CE, Shapley RM, Hawken MJ. Suppression of neural responses to nonoptimal stimuli correlates with tuning selectivity in macaque V1. J Neurophysiol 87: 1018–1027, 2002. doi: 10.1152/jn.00614.2001. [DOI] [PubMed] [Google Scholar]
- Ringach DL, Mineault PJ, Tring E, Olivas ND, Garcia-Junco-Clemente P, Trachtenberg JT. Spatial clustering of tuning in mouse primary visual cortex. Nat Commun 7: 12270, 2016. doi: 10.1038/ncomms12270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL, Sapiro G, Shapley R. A subspace reverse-correlation technique for the study of visual neurons. Vision Res 37: 2455–2464, 1997. doi: 10.1016/S0042-6989(96)00247-7. [DOI] [PubMed] [Google Scholar]
- Soodak RE. The retinal ganglion cell mosaic defines orientation columns in striate cortex. Proc Natl Acad Sci USA 84: 3936–3940, 1987. doi: 10.1073/pnas.84.11.3936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun W, Tan Z, Mensh BD, Ji N. Thalamus provides layer 4 of primary visual cortex with orientation- and direction-tuned inputs. Nat Neurosci 19: 308–315, 2016. doi: 10.1038/nn.4196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ts’o DY, Frostig RD, Lieke EE, Grinvald A. Functional organization of primate visual cortex revealed by high resolution optical imaging. Science 249: 417–420, 1990. doi: 10.1126/science.2165630. [DOI] [PubMed] [Google Scholar]
- Usrey WM, Reppas JB, Reid RC. Specificity and strength of retinogeniculate connections. J Neurophysiol 82: 3527–3540, 1999. doi: 10.1152/jn.1999.82.6.3527. [DOI] [PubMed] [Google Scholar]
- Vaiceliunaite A, Erisken S, Franzen F, Katzner S, Busse L. Spatial integration in mouse primary visual cortex. J Neurophysiol 110: 964–972, 2013. doi: 10.1152/jn.00138.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hooser SD. Similarity and diversity in visual cortex: is there a unifying theory of cortical computation? Neuroscientist 13: 639–656, 2007. doi: 10.1177/1073858407306597. [DOI] [PubMed] [Google Scholar]
- Yeh CI, Xing D, Shapley RM. “Black” responses dominate macaque primary visual cortex V1. J Neurosci 29: 11753–11760, 2009. doi: 10.1523/JNEUROSCI.1991-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]