Significance
Almost 30 y ago, researchers discovered that a great variety of efficient swimmers cruise in a narrow range of Strouhal numbers, a dimensionless number describing the kinematics of swimming. Almost 15 y later, separate researchers discovered that fliers (bats, birds, and insects) also cruise in the same narrow range of Strouhal numbers. Attendant experiments on flapping airfoils have shown that this narrow range of Strouhal numbers gives rise to the most efficient kinematics. Here, we explain why this range of Strouhal numbers is the most efficient.
Keywords: swimming, flight, biolocomotion, drag
Abstract
Many swimming and flying animals are observed to cruise in a narrow range of Strouhal numbers, where the Strouhal number is a dimensionless parameter that relates stroke frequency , amplitude , and forward speed . Dolphins, sharks, bony fish, birds, bats, and insects typically cruise in the range , which coincides with the Strouhal number range for maximum efficiency as found by experiments on heaving and pitching airfoils. It has therefore been postulated that natural selection has tuned animals to use this range of Strouhal numbers because it confers high efficiency, but the reason why this is so is still unclear. Here, by using simple scaling arguments, we argue that the Strouhal number for peak efficiency is largely determined by fluid drag on the fins and wings.
Swimming and flying animals across many species and scales cruise in a relatively narrow range of Strouhal numbers (1, 2). The Strouhal number is a dimensionless parameter that relates stroke frequency , stroke amplitude , and forward speed . It has been hypothesized that for animals that range widely or migrate over long distances, natural selection should favor swimming and flying motions of high propulsive efficiency, and so the kinematics, described by the Strouhal number, should be tuned for high propulsive efficiency. Indeed, the cruising range of Strouhal numbers observed in nature overlaps the range of Strouhal numbers experimentally shown to result in high propulsive efficiency for simple propulsors (1, 3, 4).
A typical efficiency curve for a simple propulsor is shown in Fig. 1. We see that at low Strouhal numbers, the efficiency rapidly rises with increasing Strouhal number, reaches a maximum, and then falls off relatively slowly with further increases in Strouhal number. Here, the propulsive efficiency is defined as , where is the mean net thrust that propels the animal forward, is the mean forward cruising speed, and is the mean mechanical power required to create the thrust.
Fig. 1.
A typical efficiency curve showing efficiency as a function of . Data are for a heaving and pitching NACA0012 foil (5) (, and heaving leads pitching by ).
What dictates the Strouhal number that leads to maximum efficiency? Three prevailing theories have been proposed. The first (1, 6) argues that peak efficiency occurs when the kinematics result in the maximum amplification of the shed vortices in the wake, yielding maximum thrust per unit of input energy; this phenomenon has been termed “wake resonance” (7). The second theory (8) argues that the preferred Strouhal number is connected with maximizing the angle of attack allowed, while avoiding the shedding of leading edge vortices. The third (9) holds that, for aquatic animals, the ratio of the tail beat amplitude to the body length essentially dictates the Strouhal number for cruise, since it requires a balance between thrust and drag.
Here, we offer a simple alternative explanation for the observed peak in efficiency, and we also explain the rapid rise in efficiency at low and the more gradual decrease at high . Our explanation highlights the important role that fluid drag plays in determining the efficiency behavior.
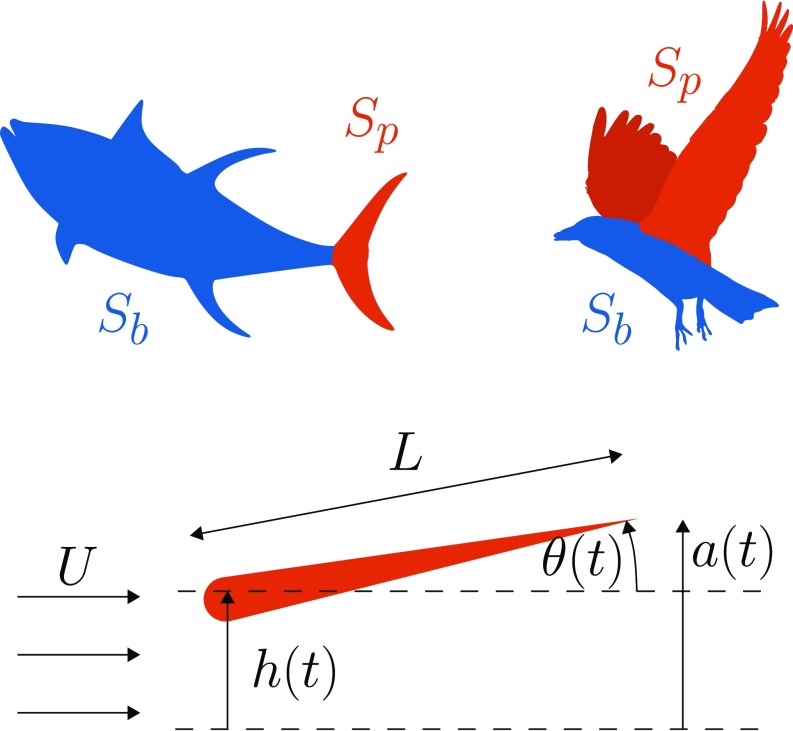
Consider a cruising animal, one that is moving at constant velocity. We make the assumption that the thrust is produced primarily by its propulsor (for example, caudal fin for a fish, fluke for a mammal, wing for a bird) and that the drag is composed of two parts: the drag due to its body (, proportional to the body surface area), and an “offset” drag due to its propulsor (, proportional to the propulsor frontal area projected over its range of motion). More details are given below.
This decomposition is illustrated in Fig. 2, where the thrust-producing propulsor is separated from the drag-producing body and represented by an oscillating airfoil (10). To be clear, fliers are distinct from swimmers in that fliers’ propulsors need to produce lift to combat gravity, in addition to thrust to propel themselves forward. As far as steady forward cruising is concerned, however, the physics of forward propulsion is not affected by the additional requirement of lift (10).
Fig. 2.
Swimmers and fliers can be decomposed into thrust-producing (orange) and drag-producing (blue) parts, with the propulsor aptly represented by an oscillating airfoil.
We also simplify the motion of the propulsor to model it as a combination of heaving (amplitude ) and pitching (amplitude ). Biologically relevant motions are ones where the heaving and pitching motions are in phase or where the heaving motion leads the pitching motion by (4). In cruise, our model requires that the thrust produced by the propulsor balances the total fluid drag experienced by the body and the propulsor.
We now consider the performance (thrust, power, and efficiency) of an isolated propulsor. For the net thrust , we use the scaling
| [1] |
where is the density of the fluid, is the area of the propulsor, and () is the characteristic speed of the transverse motion of the propulsor. The scaling is derived in SI Appendix, where it is also shown to be representative of biologically relevant flapping motions. In addition, the scaling is supported by theory (11, 12), empirical curve fits on fish performance (13, 14), and the performance of a large group of swimming animals (15). As indicated above, we will assume that for a cruising animal the net thrust of the propulsor balances the drag of the body , where , and is the surface area of the body. Hence, for a negligible offset drag,
| [2] |
Previous work has proposed that this thrust–drag balance alone yields a constant Strouhal number (15). However, Eq. 2 shows that this conclusion implicitly assumes that and that the area ratio remains constant, which will not hold across the many different species that cruise in the preferred range . To arrive at a more general result, we need to understand the energetics determining swimming and flying. The net thrust of the propulsor at peak efficiency then sets the cruising speed.
For the power expended, we adopt the scaling
| [3] |
where is a characteristic length scale of the propulsor, and and are the transverse velocity scales characteristic of the heaving and pitching motions, respectively. This scaling is derived in SI Appendix, where further details are given. It is based on established theory and analysis (11, 16, 17), and it is corroborated by a large set of experiments (4). It derives from the nonlinear interaction of the power produced by the propulsor velocity and its acceleration, an interaction that is critical to our understanding of the large-amplitude motions observed in nature.
We now consider the offset drag—that is, the drag of the propulsor in the limit of vanishing —which scales as
| [4] |
Here, is the amplitude of the pitching motion, and the function is positive when and increases with (3, 4). The offset drag can be viewed as scaling with the projected frontal area of the propulsor, as in bluff body flows (18).
Hence, we arrive at
| [5] |
where the constant sets the relative importance of the drag term compared with the thrust term (in general, we expect to be a function of Reynolds number , where is the fluid viscosity). The efficiency can be recast in terms of the Strouhal number and a dimensionless amplitude , so that
| [6] |
The other nondimensional terms, and , represent, respectively, the amplitudes of the heaving and pitching motions relative to the total amplitude of motion.
We see immediately that to achieve high efficiency, the dimensionless amplitude should be large. This observation is consistent with the argument put forth by R. M. Alexander, where he proposed that large-amplitude motions are more efficient than small-amplitude motions (19). However, there are two potential limiting factors. First, as becomes larger, the instantaneous angle of attack increases, dynamic stall effects may become important, and the drag model given here for will be invalidated. Second, animal morphology naturally sets a limit as to how large they can make . For efficient cruising, therefore, should be as large as an animal’s morphology allows, while avoiding dynamic stall at all times. Our argument is consistent with the experimental observations made by Saadat et al. (9) in what we called the third theory. The author of ref. 8 (the second theory) similarly argues for large-amplitude motions, although she argues that large-amplitude motions are connected to the optimal Strouhal number, whereas we argue that, all else fixed, the amplitude sets the total efficiency, but it does not dictate the optimal Strouhal number.
What about the optimal Strouhal number? When there is no offset drag (), the efficiency increases monotonically as decreases, and the optimal efficiency is achieved in the limit . However, in the presence of offset drag (), the efficiency will become negative as because the drag dominates the thrust produced by the propulsor. In general, Eq. 6 gives negative efficiencies at low , a rapid increase with to achieve a positive peak value at , and a subsequent slow decrease with further increase in as the influence of drag becomes weaker. The comparison between the form given by Eq. 6 and the data originally shown in Fig. 1 makes this clear, as displayed in Fig. 3. The offset drag is crucial in determining the low behavior and in setting the particular at which the peak efficiency occurs. Note that the maximum value of the efficiency is directly related to the value of the drag constant , which further emphasizes the critical role of the drag term in determining the efficiency behavior. The amplification of shed vortices described in the wake resonance theory (the first theory) may simply arise as a signature of the efficient production of net thrust, but this is purely speculative.
Fig. 3.
Efficiency as a function of . Data are as given in Fig. 1 for a heaving and pitching NACA0012 foil (5). Solid lines are given by Eq. 6 with a fixed proportionality constant of 0.155. The drag constant, , is set to 0.5, 0.35, 0.23, 0.15, 0.1, and 0.05 as the colors vary from dark to light, and we have set . The proportionality constant and the value of corresponding to the experimental data were calculated by a total least squares fit to the data.
Finally, we consider the composition of the motion—that is, the relative amounts of heaving and pitching. As shown in SI Appendix, for biologically relevant flapping motions, the denominator of Eq. 6 is minimized (and hence efficiency is maximized) when . In other words, optimally efficient propulsors should have heaving and pitching motions that contribute equally to the total motion. When we also take the numerator of Eq. 6 into account, we actually expect the heaving contribution to be a little larger because the offset drag is dominated by pitch. We are not aware of biological measurements that would allow us to test the optimal heaving and pitching balance, so at this point it remains a hypothesis.
We leave the reader with a final thought. We expect that the relative importance of the drag, captured by , will depend on the Reynolds number. Our drag model is similar to that for a bluff body, such as a sphere or cylinder, so we expect will be large at small Reynolds numbers and decrease as the Reynolds number increases until it reaches about 1,000, above which the drag will be almost constant (at least for , although biological measurements imply that the drag may remain constant up to ) (15, 20). Therefore, at low Reynolds numbers, the location of the peak efficiency will change with Reynolds number: As the Reynolds number increases, the optimal will decrease, until reaches its asymptotic value at a sufficiently high Reynolds number. Our conclusion is consistent with biological measurements (at least for swimmers), where the preferred Strouhal number appears to decrease as the Reynolds number increases, until it reaches an asymptotic value (15). This further substantiates our claim that the presence of fluid drag on the propulsor is the crucial factor in creating an efficiency peak, which dictates the cruising conditions of swimming and flying animals. In other words, energetic considerations set the kinematics of the propulsor to the most efficient one, and the net thrust of the propulsor at peak efficiency balances the drag of the body to set the cruising speed.
Materials and Methods
The experimental setup is the same as described by Van Buren et al. (4). Experiments on a heaving and pitching airfoil were conducted in a water tunnel with a m test section, with the tunnel velocity set to m/s. A teardrop airfoil of chord m, thickness 0.008 m, and span 0.279 m was used, yielding a chord-based Reynolds number of .
Heaving motions were generated by a linear actuator (Linmot PS01-23 80F-HP-R), pitching motions about the leading edge were generated by a servo motor (Hitec HS-8370TH), and both were measured by encoders. The heaving and pitching motions were sinusoidal, as described in SI Appendix, Eqs. S1 and S2, with frequencies to 0.8 Hz every 0.1 Hz, heaving amplitudes m, pitching amplitudes , and phase angles and , with experiments performed on all combinations of the kinematic parameters.
The forces and moments imparted by the water on the airfoil were measured by a six-component sensor (ATI Mini40) at a sampling rate of 100 Hz. The force and torque resolutions were N and Nm, respectively, in the streamwise and cross-stream directions, and N and Nm, respectively, in the spanwise direction. Each case was run for 30 cycles, with the first and last five cycles used for warmup and cooldown. All sensors were zeroed before every case.
Supplementary Material
Acknowledgments
This work was supported by Office of Naval Research Grant N00014-14-1-0533 (program manager, Robert Brizzolara).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 8063.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1805941115/-/DCSupplemental.
References
- 1.Triantafyllou MS, Triantafyllou GS, Gopalkrishnan R. Wake mechanics for thrust generation in oscillating foils. Phys Fluids A Fluid Dyn. 1991;3:2835–2837. [Google Scholar]
- 2.Taylor GK, Nudds RL, Thomas ALR. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature. 2003;425:707–711. doi: 10.1038/nature02000. [DOI] [PubMed] [Google Scholar]
- 3.Floryan D, Van Buren T, Rowley CW, Smits AJ. Scaling the propulsive performance of heaving and pitching foils. J Fluid Mech. 2017;822:386–397. [Google Scholar]
- 4.Van Buren T, Floryan D, Smits AJ. Scaling and performance of simultaneously heaving and pitching foils. AIAA J. March 8, 2018 doi: 10.2514/1.J056635. [DOI] [Google Scholar]
- 5.Quinn DB, Lauder GV, Smits AJ. Maximizing the efficiency of a flexible propulsor using experimental optimization. J Fluid Mech. 2015;767:430–448. [Google Scholar]
- 6.Triantafyllou GS, Triantafyllou MS, Grosenbaugh MA. Optimal thrust development in oscillating foils with application to fish propulsion. J Fluids Struct. 1993;7:205–224. [Google Scholar]
- 7.Moored KW, Dewey PA, Smits AJ, Haj-Hariri H. Hydrodynamic wake resonance as an underlying principle of efficient unsteady propulsion. J Fluid Mech. 2012;708:329–348. [Google Scholar]
- 8.Wang ZJ. Vortex shedding and frequency selection in flapping flight. J Fluid Mech. 2000;410:323–341. [Google Scholar]
- 9.Saadat M, Fish FE, Domel AG, Di Santo V, Lauder GV, Haj-Hariri H. On the rules for aquatic locomotion. Phys Rev Fluids. 2017;2:083102. [Google Scholar]
- 10.Wu TY. Fish swimming and bird/insect flight. Annu Rev Fluid Mech. 2011;43:25–58. [Google Scholar]
- 11.Garrick IE. 1936. Propulsion of a flapping and oscillating airfoil (National Advisory Committee for Aeronautics. Washington, DC), Technical Report 567.
- 12.Lighthill MJ. 1971. Large-amplitude elongated-body theory of fish locomotion. Proc R Soc B 179 125–138.
- 13.Bainbridge R. The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat. J Exp Biol. 1958;35:109–133. [Google Scholar]
- 14.Bainbridge R. Caudal fin and body movement in the propulsion of some fish. J Exp Biol. 1963;40:23–56. [Google Scholar]
- 15.Gazzola M, Argentina M, Mahadevan L. Scaling macroscopic aquatic locomotion. Nat Phys. 2014;10:758–761. [Google Scholar]
- 16.Theodorsen T. 1935. General theory of aerodynamic instability and the mechanism of flutter (National Advisory Committee for Aeronautics. Washington, DC), Technical Report 496; originally published as ARR-1935.
- 17.Sedov LI. Two-Dimensional Problems in Hydrodynamics and Aerodynamics. Interscience Publishers; New York: 1965. [Google Scholar]
- 18.White FM. Fluid Mechanics. McGraw Hill; New York: 2011. [Google Scholar]
- 19.Alexander RM. Principles of Animal Locomotion. Princeton Univ Press; Princeton: 2003. [Google Scholar]
- 20.Schlichting H. Boundary-Layer Theory. 7th Ed McGraw-Hill; New York: 1979. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.