Microrheology of DNA hydrogels

Significance

While widely known as the molecule of life, DNA is also an amazing building block at the nanoscale, since it allows us to design and program the structure and dynamics of functional nanomaterials. We exploit the programmability of DNA to achieve control over the rheology of self-assembled hydrogels, which have elastic or viscous behavior (similar to that of slime) that is finely regulated by temperature. Using microrheology to investigate the mechanical properties of DNA hydrogels at the microlength scale, we map the viscoelastic response over a broad range of frequencies and temperatures. The deep understanding in the fundamental physics provides a way to design DNA-based materials with precise control over the structure stability and rigidity at molecular level.

Abstract

A key objective in DNA-based material science is understanding and precisely controlling the mechanical properties of DNA hydrogels. We perform microrheology measurements using diffusing wave spectroscopy (DWS) to investigate the viscoelastic behavior of a hydrogel made of Y-shaped DNA (Y-DNA) nanostars over a wide range of frequencies and temperatures. We observe a clear liquid-to-gel transition across the melting temperature region for which the Y-DNA bind to each other. Our measurements reveal a cross-over between the elastic $G\prime \left(\omega \right)$ and loss modulus $G^{″}\left(\omega \right)$ around the melting temperature $T_m$ of the DNA building blocks, which coincides with the systems percolation transition. This transition can be easily shifted in temperature by changing the DNA bond length between the Y shapes. Using bulk rheology as well, we further show that, by reducing the flexibility between the Y-DNA bonds, we can go from a semiflexible transient network to a more energy-driven hydrogel with higher elasticity while keeping the microstructure the same. This level of control in mechanical properties will facilitate the design of more sensitive molecular sensing tools and controlled release systems.

DNA hydrogels made of well-defined small building blocks are a type of tenuous, semiflexible polymeric network that consists of precisely designed synthetic nucleotide strands as chemical or physical cross-linkers (1–5). These manmade bulk DNA hydrogels have been widely studied as functional materials that can be potentially used for controlled drug delivery, tissue engineering, biosensing, and other applications in the fields of nanotechnology and bioengineering mainly because of their biocompatibility and the ability to mix them with other (bio-)polymers (6–10). In particular, the vast combinations of the Watson–Crick pairing provide a unique way to achieve programmable self-assembly of thermally reversible gels with precise functionality (11, 12). While current studies mostly focus on the fabrication and utilization of DNA hydrogels, the fundamental physics relating the microstructure of these gels to their macroscopically observed viscoelastic properties still lacks good understanding (5, 8, 13). In recent years, a series of computational and experimental studies was carried out on the phase diagram of DNA hydrogels made of two-, three- and n-valent nanostars and their mixtures, providing a good reference for creating volume-spanning, percolating gels (11, 14–18).

The study of transient networks has been at the heart of many theoretical (19–21) and experimental studies (22, 23) for their display of complex phase diagrams and dynamics (24). The reversible cross-links in transient networks can be mediated by the short sticky ends of telechelic polymers (25), telechelic dendrimers (26), triblock copolymers (27), or charged end groups (28). These cross-links have a finite lifetime, and transient networks therefore behave like yield-stress fluids. In contrast, chemically cross-linked networks, such as rubbers, do not flow, but break like a solid when deformed extensively. Other transient but active networks are formed by semiflexible actin filaments cross-linked via proteins that give shape to cells and provide their locomotion (29). Vitrimers, in which the bonds or cross-links can be exchanged through a catalytic process, are another class of transient networks with self-healing properties relevant in biological tissue engineering (30–32). However, with the ability to program DNA with an almost unlimited amount of highly specific interactions, different DNA nanostars can be designed to form arbitrarily complex networks, which cannot be achieved with other natural thermally reversible hydrogels made, for instance, of agarose or gelatin (33) or for that matter, vitrimers. In particular, local inhomogeneities with well-defined nanopores and mechanical properties may be built into the network, as different DNA blocks can be made to hybridize at different temperatures (34). Indeed, recent shear rheological studies on macroscopic samples (3, 35, 36), here referred to as bulk rheological studies, showed that the specific structure and connectivity of DNA nanostars have a strong influence on their macroscopic mechanical response. However, these low-frequency measurements only describe the systems macroscopic, long-time viscoelastic response and cannot describe how more local relaxation times change as the system goes through the melting transition.

Here, we present microrheology studies using diffusing wave spectroscopy (DWS) (37, 38) to study the equilibrium elastic and viscous moduli of our DNA gels over a much larger frequency range than that available in bulk rheology (39–42). In particular, using sealed sample chambers allowed us to perform these measurements over a large temperature range without fear of changes in the samples due to evaporation, which is problematic in bulk rheology (35, 43). We show that DWS enables us to link the system’s characteristic binding–unbinding processes with the local and global viscoelastic properties of the gel over a temperature range that covers the full melting region between the DNA nanostars. The measured $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ curves reveal a clear, temperature-reversible percolation transition coinciding with the melting temperature of the systems sticky ends. Moreover, we exploit the fact that ssDNA is much more flexible than dsDNA to show that, by keeping the total number density of Y-shaped DNA (Y-DNA) the same, we can render the network more rigid when removing the flexible linkers between them.

Results

DNA Design.

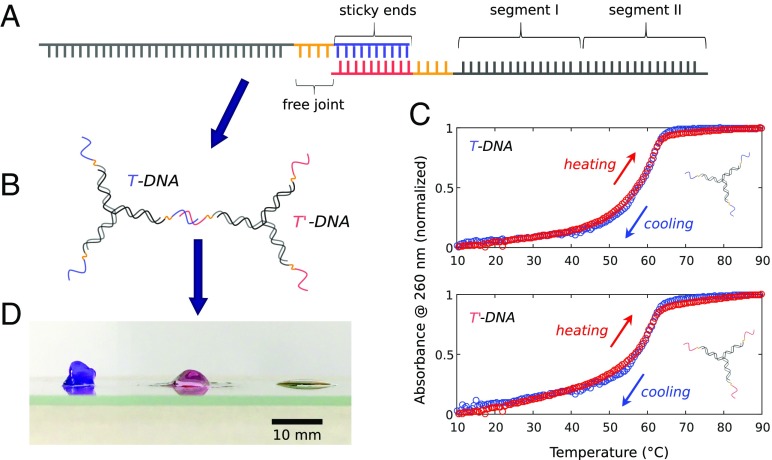
The DNA hydrogels used in this study are composed of Y-shaped DNA building blocks made of three partially complementary oligonucleotides, here denoted ${\mathrm{S}}_i$ (Fig. 1 and Table 1). These ss S-oligos are 43 bases long and consist of four functional parts: a sticky end (9 bases), a free joint of four Thymines providing flexibility, and two segments (I and II) that form the core of the Y shape. Segments I and II of, say, ssDNA S₁ are designed to be partially complementary to the respective segments of S₂ and S₃, thus making up the three dsDNA arms at the center of the Y shapes. Note that the center is created to be fully binding, leaving no nonbinding bases at the center and thus, reducing its flexibility. The respective binding sequences of the three dsDNA arms are given in Table 1, while the full sequences of the S-oligos are given in SI Appendix. The sticky ends can specifically bind to their complementary sequence due to Watson–Crick pairing. In all of the following gels, we use the same Y-shaped cores carrying either sticky ends named T or the complementary T′ DNA, such that Y shapes with T ends (T DNA) can only bind to those with T′ ends (T′ DNA). We keep the T to T′ DNA ratio 1:1, thus maximizing the system’s connectivity.

Fig. 1.

Design and characterization of the DNA hydrogel building blocks. (A) Schematic of the ssDNA S_i used. Each oligo strand consists of four functional parts: the sticky end, the free joint, segment I, and segment II. Segments I and II are part of the ds core DNA; sticky ends are for cross-linking the Y shapes to a network. (B) Cartoon of T and T′ DNA connected via hybridization of complementary sticky ends. (C) Melting (cooling) and heating (hybridization) curves of T and T′ DNA in Tris-EDTA buffer containing 150 mM NaCl measured using ultraviolet-visible (UV-vis) spectrometer. (D) From left to right are photographs of DNA hydrogels without free joint, with free joint, and with only one component. All three samples are made of [Y-shaped DNA] = 500 $\mathrm{\mu }$M. For clarity, the left and center gels were colored with the SYBR Safe DNA Gel Stain from Invitrogen. The sample maintains its original shape at a timescale of several minutes.

Table 1.

The sequences of dsDNA arms

Name	Segment I	Segment II
S1	5′-TGG ATC CGC ATG ATC	CAT TCG CCG TAA GTA-3′
S2	5′-TAC TTA CGG CGA ATG	ACA CCG AAT CAG CCT-3′
S3	5′-AGG CTG ATT CGG TGT	GAT CAT GCG GAT CCA-3′

The melting temperature profiles of the Y shapes carrying either T or T′ sticky ends (Fig. 1C) were determined by measuring the absorbance of 260 nm in 1 $\mathrm{\mu }$M DNA in Tris-EDTA buffer solution at pH 8.0 containing 150 mM NaCl, as ssDNA adsorbs 260 nm stronger than dsDNA. Starting at 90 ^○C, we observe a plateau in the absorbance until roughly 65 ^○C, marking the point at which hybridization (binding) sets in. Until this temperature, the individual ssDNAs are all in the unbound state. On further cooling, the absorption decreases continuously until the low-temperature plateau is reached, at which all single strands have hybridized into Y shapes. The melt temperature (denoted $T_{m1}$) is defined as the point at which one-half of all possible base pairs are dissociated. $T_{m1}$ was obtained from the median between the linear curves fitting the low- and high-temperature plateaus and found to be $T_m\approx$ 58 ^○C for both Y shapes with T or T′ overhangs for the concentrations used in the melt temperature measurements. As shown previously (44), nonbinding ssDNA tails slightly lowered the value of $T_m$ with respect to the value based on tabulated data by SantaLucia (45), which are, averaged over all three arms, $T_{m1}\ge$ 60 ^○C—details are given in SI Appendix.

DWS Microrhelogy.

DWS measurements rely on time correlations of diffusively scattered light caused by submicrometer-sized spherical tracer particles [here, 600-nm large, charge-stabilized polystyrene (PS) particles] embedded in the DNA hydrogel sample. The thermal motion of the particles is described by the mean-square displacement (MSD), denoted $⟨\mathrm{\Delta }r{\left(t\right)}^2⟩$. This is measured by the real-time fluctuations of the scattered light collected by a photodetector and presented as the intensity autocorrelation function (ICF), $g_2\left(\tau \right)={⟨I\left(\tau \right)I\left(0\right)⟩}_t/{⟨I\left(0\right)⟩}_t^2$, where $I\left(0\right)$ and $I\left(\tau \right)$ are the scattered intensities at time 0 and some delay time $\tau$ later. The decay of $g_2\left(\tau \right)$ is related to the time evolution of particle motion, allowing for the MSD of the particle to be measured (37). The complex viscoelastic modulus and MSD are related by the generalized Stokes–Einstein relation given in Eq. 1 (38, 39):

$$\tilde{G}\left(s\right)\approx \frac{k_{B}T}{\pi Rs⟨\mathrm{\Delta }{\tilde{r}}^2\left(s\right)⟩},$$ [1]

where G̃(s) and $⟨\mathrm{\Delta }\tilde{r}{\left(s\right)}^2⟩$ are the Laplace transforms of the complex shear modulus and the MSD, R is the radius of the tracer particles, and s is the Laplace frequency. Replacing $s$ with $i\omega$, we obtain the $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ from the complex shear modulus $G^{*}\left(\omega \right)=G\prime \left(\omega \right)+i{G}^{″}\left(\omega \right)$ (38, 39) (Materials and Methods).

Our DNA hydrogels were studied using a DWS RheoLab (LS Instrument AG) in echo mode, which allowed for long correlation times (Fig. 2A). The light source was a 685-nm-wavelength diode laser. The measured ICFs where fitted and then converted into MSDs using both the instrument software and for comparison, a home-written software. The procedures are detailed in SI Appendix.

Fig. 2.

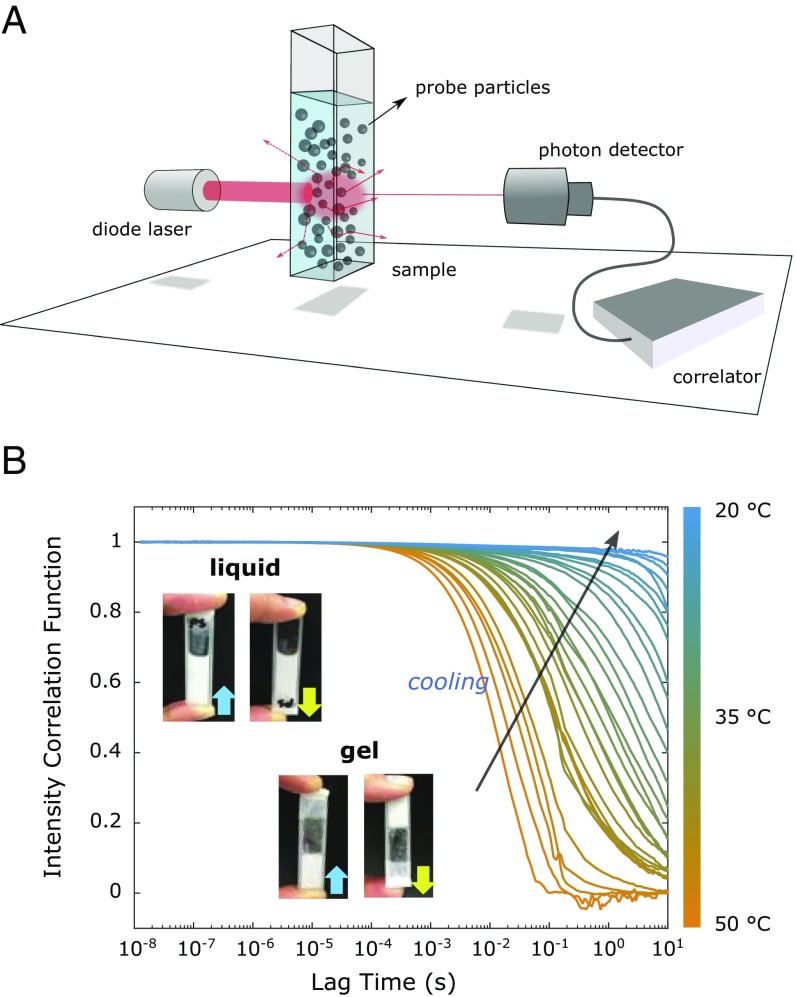
(A) Schematic illustration of the DWS setup. A 685-nm diode laser beam impinges on the sample, and the diffusely scattered light is collected by the photodiode on the other side of the sample. Tracer particles are uniformly embedded inside the sample. (B) Temperature-dependent ICF curves measured for the 500 $\mathrm{\mu }$M DNA hydrogel containing 1 (vol/vol %) 600-nm-large sterically stabilized PS tracer particles. The ICF curves were measured starting from 50 ^○C (orange lines) in 1 ^○C steps, cooling down to 20 ^○C (blue lines). The photographs show the sample cuvette showing the samples’ liquid state at 50 ^○C and the gel state at 20 ^○C.

DNA hydrogel samples were made by preparing T- and T′-DNA solutions separately at a DNA concentration of 500 $\mathrm{\mu }$M (Materials and Methods), already containing the tracer particles. The cuvettes (Fig. 2B) were filled with the respective T- and T′-DNA solutions, which are liquid at room temperature (RT), in a layer-by-layer fashion at RT for better mixing. The total filling volume was $\sim$500 $\mathrm{\mu }$L. Initially, the interfaces between the layers gelled due to the rapid hybridization at RT. To obtain well-mixed samples, we heated the cuvettes to 50 ^○C and incubated them for 20 min, which was sufficient to fully melt the sticky ends, rendering the sample a well-mixed fluid of Y shapes, but also cold enough to preserve the Y-shaped structure. Following this procedure, we ensured that the final DNA concentration in the fluid phase remained 500 $\mathrm{\mu }$M, corresponding to $\sim$20 mg/mL, containing 1% (wt/vol) PS particles.

DWS measurements were done starting at 50 ^○C and slowly cooled down to 20 ^○C. We measured the scattering intensity in 1 ^○C intervals and equilibrated the sample for 5 min before data acquisition, ensuring the full coverage of the melting transition of the sticky ends. The scattered intensities were then converted into ICFs and MSDs. We performed control experiments using 230-nm-large PS particles, testing both for a possible dependence of our results on particle size and for hysteresis in the gelation process by repeating the scattering measurements in a cooling and heating cycle following the same protocol as for the larger particles. The results, shown in SI Appendix, confirm that we only probe the viscoelastic properties of our DNA hydrogel and that it is a thermally reversible equilibrium gel. The ICF data for the cooling ramp are shown in Fig. 2B.

Bulk Rheology.

Bulk rheology measurements were performed to measure both the low-temperature behavior of $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ and their change when the flexible thymine linker was removed. Finally, differently long sticky overhangs were tested while keeping the centers of the Y shapes unchanged. These results are presented in SI Appendix.

Discussion

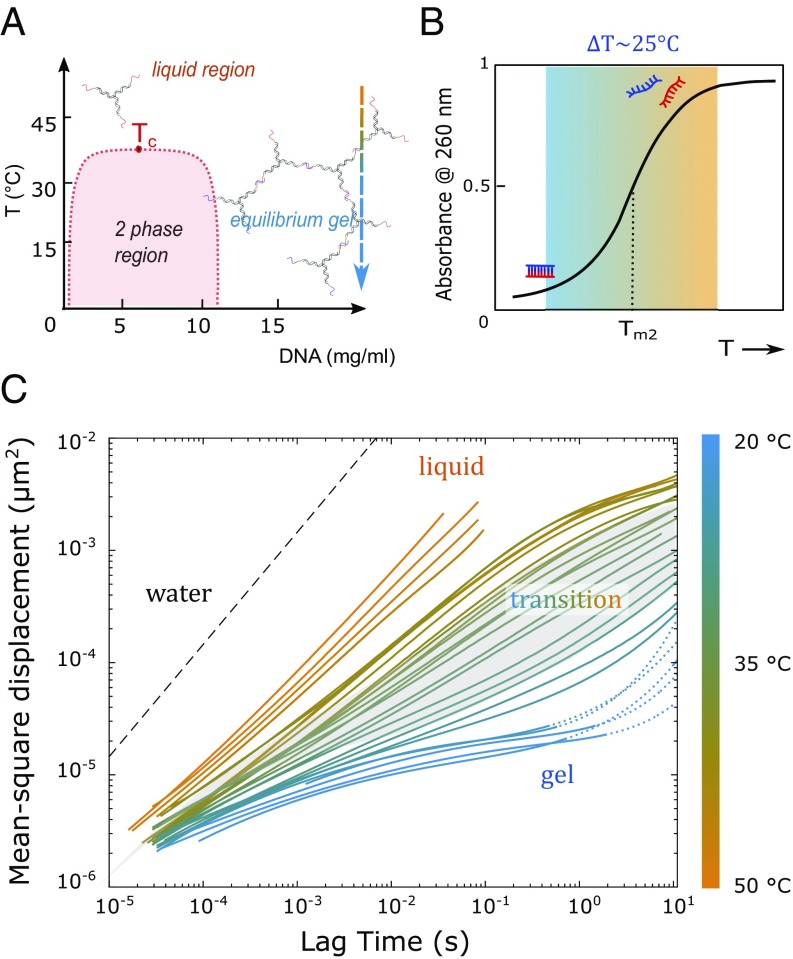
Several simulation and experimental studies explored the phase diagram of DNA hydrogels made of nanostars with two, three, and more bridging arms (14–16, 46). These studies showed that the range where the system phase separates into a nanostar-poor and a nanostar-rich region becomes increasingly more narrow, shifting to a lower DNA concentration for decreasing the number of bridging arms (14). Here, we used a total DNA concentration of 500 $\mathrm{\mu }$M, ensuring that we are firmly in the one-phase region (Fig. 3A) with the hydrogel spanning the entire sample. Hence, as we cool the sample from 50 ^○C to RT, the entire sample is brought continuously from a fluid phase containing free Y shapes to a percolating gel network. To obtain a clear signature of this network formation, its melt temperature $T_{m2}\approx$ 35 ^○C must be well below $T_{m1}$ of the individual Y shapes. This melt temperature separation was achieved by increasing the added salt concentration to 200 mM NaCl (44), shifting our systems’ $T_{m1}$ to $\sim$62 ^○C as shown in SI Appendix. More details on the $T_{m2}$ estimates are given in SI Appendix, where we also present data on the same Y shapes but with 12-base overhang.

Fig. 3.

(A) Schematic phase diagram of the Y-shaped DNA. The arrow indicates the concentration and temperature range of the ICF measurements shown in Fig. 2. The red area represents the two-phase region, and $T_c$ is the critical point. (B) Illustration of the hybridization range for the sticky ends of the two different Y shapes. The graded area signifies the range over which a fraction of base pairs is formed. (C) MSD extracted from the ICF curves in Fig. 2. The color of the lines gradually changes from orange to blue, standing for the transition region ranging from about 45 ^○C to 20 ^○C, which is centered around the melting temperature $T_{m2}$ = 35 ^○C of the sticky ends. The calculated MSD for the same 600-nm-large PS colloids in pure water at 50 ^○C is presented by the dashed line as guide to the eye.

The MSD results extracted from the ICF curves are shown in Fig. 3C. At temperatures well above $T_{m2}$ (Fig. 3C, orange lines), the MSD curves depend linearly on the lag time $\tau$ over the whole measured region, confirming the $⟨\mathrm{\Delta }r{\left(t\right)}^2⟩\propto \tau$ relation for Newtonian fluids and thus proving that, in the temperature window between about 55 ^○C and 45 ^○C, our system behaves like a fluid of disconnected Y shapes dispersed in a buffer colloid solution. Note that our sample displays a diffusivity that is two orders of magnitude lower than that extracted from MSDs for 600-nm PS particles dispersed in pure water having a diffusion constant $D=0.15$ ${\mathrm{\mu }}^2$ ms⁻¹ at 50 ^○C. A similar decrease is observed in control measurements using 230-nm-large PS particles and confirmed in bulk rheology measurements of a nongelling sample (SI Appendix). The related increased viscosity is purely due to the high DNA concentration. Indeed, assuming that the Y shapes take up an effective spherical volume due to rotational diffusion (assuming that each arm is $\sim$5 nm long), the approximate volume fraction occupied by the Y shapes is some 40%, although the actual DNA content is only 2 wt %.

At $T<$ 30 ^○C and short lag times, the MSD curves are similar to the high-$T$ measurements, increasing with increasing $\omega$; however, they have a slightly lower exponent, indicating subdiffusive motion of the local bridges between cross-links. At intermediate $\omega$ corresponding to longer relaxation times (for instance, of the “cages” formed by the cross-links), the MSD curves reach a plateau. Holding the sample at this lower temperature over 20 min and measuring the ICF in 5-min intervals show that there is no further increase in the plateau value (SI Appendix). This is also expressed in the flattening of the corresponding elastic moduli $G\prime$ presented in Fig. 4. This means that the tracer particles remain locally diffusive on short timescales (the diffusion coefficient of the particles in pure water is 1.65 ${\mathrm{\mu }}^2$ ms⁻¹ at 20 ^○C) but are confined by the percolating DNA network on long timescales. The transition region marked by the changing colors in Figs. 3 and 4 represents the melt temperature region over which the fraction of hydrogen bonds formed between two Y shapes with complementary sticky ends is gradually increasing as $T$ decreases. Using refined SantaLucia rules for hybridization (44), we estimate the width of this transition region to be $\mathrm{\Delta }T\sim$25 ^○C (Fig. 3B). With a $T_{m2}\hspace{0.17em}\sim \hspace{0.17em}$35 ^○C, this means that we should reach a fully bonded state and thus, a maximum network stiffness at around $T\hspace{0.17em}\sim \hspace{0.17em}$25 ^○C. A detailed discussion of the value of the stiffness is given in the following.

Fig. 4.

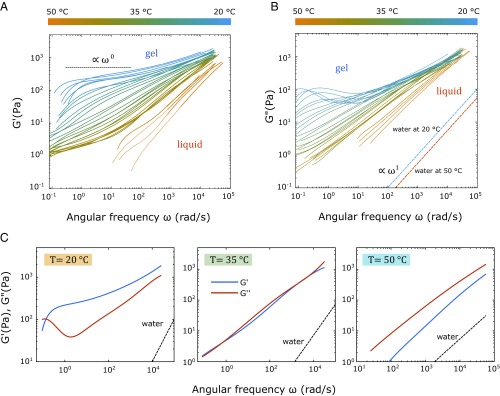
Temperature evolution of the complex moduli $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ as a function of frequency extracted from the MSDs in Fig. 3. (A) The elastic moduli $G\prime \left(\omega \right)$ measured in a cooling ramp. At temperatures above $T_{m2}$, $G\prime$ drops down at a frequency below $10^2\sim 10^4$rad/s, showing close to zero elasticity; below $T_{m2}$, only the onset of the decay in the ICF could be monitored. Hence, the low-frequency region is plotted as a dashed line using extrapolations. (B) The viscous modulus $G^{″}\left(\omega \right)$ in cooling (upper) ramp. (C) Comparison of $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ at temperatures of 20 ^○C, 35 ^○C, and 50 ^○C, representing typical behavior at temperatures below, around, and above $T_m$, respectively. At 20 ^○C, $G^{″}$ is higher than $G\prime$ at frequencies below the cross-over frequency $\sim 10^4$ rad/s; at 35 ^○C, $G\prime$ and $G^{″}$ are overlapping over almost the entire frequency range. At 50 ^○C, $G^{″}$ is higher than $G\prime$ over the whole measurable frequency range, showing no cross-over point at all.

The elastic, $G\prime \left(\omega \right)$, and viscous moduli, $G^{″}\left(\omega \right)$, measured in a cooling cycle are shown in Fig. 4. Again, similar results were obtained using the smaller tracer particles in a cooling and heating cycle (SI Appendix), suggesting that the equilibrium gels display only very small hysteresis effects. As expected, the elastic modulus, $G\prime \left(\omega \right)$, undergoes a significant change as the temperature changes over the melting temperature region, while $G^{″}\left(\omega \right)$ retains the same linear trend until about 30 ^○C. At high temperatures (orange lines in Fig. 4), $G\prime$ is nearly zero at long timescales, as the solution is in a fully fluid state of Y shapes; however, it is nonzero at high frequencies, reflecting the fact that the sample is a quasiconcentrated solution of elastic shapes behaving like soft colloids. Indeed, above $T_{m2}$, the loss modulus dominates (Fig. 4C). However, around the melting temperature (between 37 ^○C and 31 ^○C), $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ run parallel and on top of each other with a ${\omega }^{1/2}$ dependence, which we identify as the point of full percolation. Such a behavior is also associated with the gel point of cross-linked polymers (47). This percolation can be understood when looking at Fig. 3B: in the melt transition region, increasingly more Y shapes bind to each other, forming many clusters that grow in size as the temperature decreases. At $T_{m2}$, one-half of all possible hydrogen bonds or base pairs are bound, which does not mean that one-half of all Y-shaped arms are bound at all times but that they continuously form and break partially; thus, on average, they form a single cluster. Below $T_{m2}$, the fraction of hybridized base pairs continues to increase until about 25 ^○C, and also, their lifetime becomes longer. At even lower temperatures (blue lines in Fig. 4), the $G\prime$ reaches a plateau value of $\sim$ 200 Pa in the intermediate time range, which corresponds to a mesh size $\xi \sim$ 21.5 nm, assuming the scaling behavior of the bulk modulus $G_{bulk}\propto k_{B}T/{\xi }^3$. This is in good agreement with the calculated mesh size from the design that suggests an average distance between bonded Y-shaped centers of $\xi \sim$ 20 nm corresponding to a slightly higher elastic modulus.

Interestingly, below $T\sim$ 25 ^○C, our fully formed network is very similar to that of classical transient networks of flexible polymers held together by cross-links through physical interactions that constantly form and break (Fig. 4C) (20). The frequency behavior of such transient networks shows a typical Maxwellian $G^{″}\left(\omega \right)\propto \omega$ increase at long times, reflecting the fact that the TT′ bonds between the Y shapes are not irreversibly formed. In fact, we see a cross-over between the steeper increasing $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ at around 1 s⁻¹, which is known to correspond to the lifetime of the short ds bond between two Y shapes at RT and can be explained by the reptation model for associative polymers (19, 21). A similar observation was made in dynamic light scattering experiments on gels of four-armed nanostars (18). This cross-over is then followed by a plateau in $G\prime \left(\omega \right)$, while $G^{″}\left(\omega \right)$ decreases slightly for some intermediate frequency range before both moduli start increasing again at higher frequencies. In our case, this dip in $G^{″}\left(\omega \right)$ can be ascribed to the fact that the elastic network dominates in this time regime before a sufficient number of bonds break and the tracer colloids can move. Consequently, this dip in $G^{″}\left(\omega \right)$ disappears when the temperature reaches the melt transition region when the lifetime of the bonds decreases further and the viscous contributions increase. At even higher frequencies, $G^{″}\left(\omega \right)$ gradually reaches the linear behavior in $\omega$, as it reaches the fully liquid state by coming from a weakly subdiffusive behavior in the transition region, while $G\prime \left(\omega \right)$ reaches a power law behavior with a fractal power. In the gel phase, this upturn in $G\prime \left(\omega \right)$ at high frequencies is simply due to the fact that the bond lifetime is now longer than the typical motion due to thermal fluctuations; thus, the system shows the typical increase in elasticity, as the system cannot relax fast enough. This is associated with its second cross-over between the two moduli that appears to occur at ${\omega }_c\approx 4\times 10^4$ Hz at temperatures at $T\sim$ 35 ^○C to 50 ^○C (Fig. 3C). Estimating a second characteristic length scale $\xi \prime ={\left(2k_{B}T/\left(\eta {\omega }_c\right)\right)}^{-3}\hspace{0.17em}\approx \hspace{0.17em}$34 nm, assuming the viscosity of water. At this high frequency, the main elastic contribution must come from the cluster phase, with clusters forming cages of the Y shapes. These completely disappear at even higher temperatures.

We made an exciting observation when performing low-frequency bulk rheology measurements on the very same system in which we removed the flexible linkers. The measured $G\prime \left(\omega \right)$ and $G^{″}\left(\omega \right)$ curves showed an increase by a factor of up to 7, which was also observed when using samples with and without flexible linkers but 12 instead of 9 bases (data are shown in SI Appendix). This stiffening is particularly visible in the photograph in Fig. 1D. Moreover, further DWS data on the 12-bp sticky ends also confirm that the percolation transition coincides with the systems melting transition, only that now that transition occurs at $\sim$44 ^○C, the $T_{m2}$ for the 12 bases.

Finally, at $T\gtrsim$ 35 ^○C, we can plot the half time of the relaxation of the ICF as inverse function of temperature. The slope of the resulting Arrhenius plot (shown in SI Appendix) provides us with the strength of the bonds between two Y shapes, where the relaxation time $\tau =t_{1/2}={\tau }_0\exp \left(-\mathrm{\Delta }G/k_{B}T\right)$; here, $\mathrm{\Delta }G$ is the Gibbs free energy. Following the arguments by Nava et al. (18), this will happen when at least two bonds per Y shape are broken, which corresponds to about 60 kcal/mol in our case and is very close to the tabulated value.

To summarize, our microrheological measurements show how a transient cross-linked hydrogel is formed as it is brought from the high-temperature range, where the Y-shaped building blocks form a viscous fluid, into an equilibrium gel phase. Remarkably, after all possible bonds are formed below the melt transition region, the DNA hydrogel shows a frequency behavior very similar to that of transient networks of flexible polymers when the Y-shaped centers are connected via a stiff dsDNA bond and two short, flexible ssDNA linkers. Interestingly, when the flexible ssDNA linkers are removed while keeping the same Y-shaped density, the elasticity of such a network increases sevenfold, indicating that the network goes from flexible and entropy driven to a more elastic system that is dominated by the energy of the semistiff connectors between the Y-shaped centers. Testing two differently long sticky bonds, we also show that their melt temperatures $T_{m2}$ could be identified as the percolation transition. It should be noted that the results presented here cannot be easily obtained by regular bulk rheology unless evaporation is controlled carefully, and also, single-bead microrheology would lead to ambiguous results due to local heating around the laser-trapped probe particle.

Our findings show that we can develop a class of hydrogels with more ordered local structure or if “coding in” a cascade of hybridization temperature hierarchical structures. These could be achieved by introducing locally more rigid DNA building blocks. Such networks could be envisaged as builders of thermoresponsive materials that could provide controlled drug release or act as micrometer-sized actuators with well-defined elastic modulus.