Phantom Evaluations of Nonlinear Inversion MR Elastography

Abstract

This study evaluated non-linear inversion MRE (NLI-MRE) based on viscoelastic governing equations to determine its sensitivity to small, low contrast inclusions and interface changes in shear storage modulus and damping ratio. Reconstruction parameters identical to those used in recent in vivo MRE studies of mechanical property variations in small brain structures were applied. NLI-MRE was evaluated on four phantoms with contrast in stiffness and damping ratio. Image contrast to noise ratio was assessed as a function of inclusion diameter and property contrast, and edge and line spread functions were calculated as measures of imaging resolution. Phantoms were constructed from silicone, agar, and tofu materials. Reconstructed property estimates were compared with independent mechanical testing using dynamic mechanical analysis (DMA). The NLI-MRE technique detected inclusions as small as 8mm with a stiffness contrast as low as 14%. Storage modulus images also showed an interface edge response distance of 11mm. Damping ratio images distinguished inclusions with a diameter as small as 8mm, and yielded an interface edge response distance of 10mm. Property differences relative to DMA tests were in the 15%-20% range in most cases. In this study, NLI-MRE storage modulus estimates resolved the smallest inclusion with the lowest stiffness contrast, and spatial resolution of attenuation parameter images was quantified for the first time. These experiments and image quality metrics establish quantitative guidelines for the accuracy expected in vivo for MRE images of small brain structures, and provide a baseline for evaluating future improvements to the NLI-MRE pipeline.

Introduction

Magnetic resonance elastography (MRE) is an emerging imaging technique that quantifies mechanical properties of tissue, and has been applied to the breast [1, 2], liver [3, 4], heart [5, 6], and brain [7, 8]. For example, alterations in brain parenchyma caused by the demyelinating disease multiple sclerosis have been reported to decrease tissue stiffness. [9] Relationships between normal brain stiffness and pathology have also been found with MRE in Alzheimer’s Disease [10,11], malignant tumors [12], and normal pressure hydrocephalus [13].

MRE commonly recovers maps of the complex-valued viscoelastic shear modulus (μ = μ_S + iμ_L where μ_S is the storage modulus and μ_L is the loss modulus) which governs both elastic energy storage and viscous energy attenuation. A range of parameters derived from the complex shear modulus have been reported which can be classified broadly into stiffness and attenuation-based categories. Stiffness-based parameters include the storage modulus, μ_S, shear stiffness, ${\mu }_{\mathit{stiff}}=\rho {\nu }_s^2=\frac{2\left({\mu }_S^2+{\mu }_L^2\right)}{{\mu }_S+\sqrt{{\mu }_S^2+{\mu }_L^2}}$ (where ρ is the material density, and ν_s is the shear wavespeed) [14], and the magnitude of the complex modulus, $\left|\mu \right|=\sqrt{{\mu }_S^2+{\mu }_L^2}$ [15]; these quantities are related to how stiff a material would feel to the touch. Attenuation-based parameters include the damping ratio, $\xi =\frac{{\mu }_L}{2{\mu }_S}$, phase angle ϕ = atan(μ_L/μ_S), and dashpot powerlaw exponent, α where μ = κ(iω)^α [16–18]; these variables describe the relative level of attenuation of mechanical energy.

The relevance of stiffness parameters has been appreciated for some time; manual palpation is routinely used to distinguish variations in tissue elasticity. For instance, breast cancers are often found by palpation based on local increases in stiffness. [19] MRE has proven successful in discriminating between normal and fibrotic livers with ability to distinguish between stages of chronic liver disease. [3,4,20] Most groups have published simple phantom evaluations which confirm that techniques can recover known variations in stiffnesses simulating breast [21], muscle [22], heart [23], and soft tissue [24]. A more detailed contrast analysis was reported by Doyley et al.; however, most phantom studies to date have been limited to relatively large, high contrast stiffness inclusions. [25] Recent work in brain MRE has moved toward measuring small, low contrast structures to improve sensitivity to local changes in the mechanical microstucture as a vehicle to detect specific diseases. [26–28]

Attenuation related parameters have been reported to have clinical significance in many studies [1, 15, 29, 30]. Viscoelasticity in individuals with multiple sclerosis [16], Alzheimer’s Disease [31], and Parkinson’s Disease [32] exhibits an overall relative decrease with disease progression. Sack et al. provided evidence that attenuation related parameters also reveal information about brain tissue organization. [33]. Recently, Schwarb et al. reported a strong correlation between damping ratio of the hippocampus and memory task performance in a cohort of 20 volunteers which showed, for the first time, a relationship between viscoelastic properties and functional outcomes, as well as changes in hippocampal damping ratio after an exercise intervention in a group of multiple sclerosis patients. [34–36] Despite the potential clinical significance of attenuation in these studies, independent measurements are difficult to acquire in vivo. Phantom studies are a vital step in validation of a spatially resolved imaging modality; however, to the best of our knowledge, no images with known attenuation parameter contrasts have been published to date, which undermines confidence in the various MRE processing pipelines to accurately recover spatially distributed parameters. A detailed phantom study is required to determine limits of MRE inversions in detecting small, low contrast regions, at least under controlled conditions, and will lend confidence in MRE derived attenuation parameter estimates by characterizing imaging performance in a controlled system. In this study, we present four phantoms that were imaged using standardized nonlinear inversion (NLI) parameters applied in our brain MRE work to date. [34, 35] Recovered elasticity values are compared to independent mechanical testing. Image contrast to noise ratio was assessed as a function of inclusion diameter, and edge and line spread functions were calculated as measures of imaging performance for phantoms with stiffness and attenuation contrast. This collection of results provides the first phantom verification of attenuation imaging and confirms that the damping ratio of small structures can be accurately imaged under controlled conditions. The phantom system establishes a baseline of performance for assessing image quality produced by other inversions and improvements made to the NLI-MRE technique in the future.

Methods

Phantom Construction

Phantoms were fabricated from agar (Sigma-Aldrich), tofu (Mori-Nu), and A341 silicone soft gel (Factor II) with PMX-200 silicone fluid (Xiameter). Elastography phantoms have traditionally been constructed using gelatin [25] or agarose gels [37] because stiffness can be controlled through the gelatin or agar concentration. However, other factors, which are more difficult to control, can also have significant effects on resulting mechanical properties. The cooling rate is a good example; larger phantoms cool slower than smaller ones, which can lead to substantial variation in mechanical properties for a given gel concentration. [38] This difference can be influential when constructing inclusions of varying size, and significant changes in mechanical properties have been observed for both gelatin [38] and agarose [39]. Another alternative to gelatin phantoms is room temperature vulcanizing silicone which is formed by mixing a liquid with a catalyst. [21, 40, 41] A range of base materials are available with different mechanical properties, and dilution with silicone fluid provides control over mechanical stiffness. Silicone is safe, easy to handle, and simple to fabricate because the entire process is performed at room temperature. The lifespan of silicone phantoms are typically a few years. One disadvantage of silicone is potential variability of mechanical properties of the cured silicone between batches from the manufacturer. Mechanical testing samples need to be made from the same batch as the phantoms if mechanical property comparisons are of interest.

Four phantoms were fabricated for this study: (1) stiffness contrast-detail phantom, (2) stiffness interface phantom, (3) damping ratio inclusion phantom, and (4) damping ratio interface phantom. Rendered images of the phantoms and the external motion actuator used in this study can be seen in Figure 1.

Figure 1.

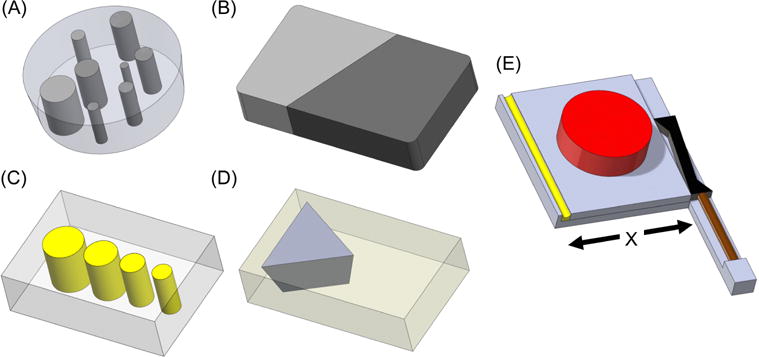
Rendered images of the four phantoms and motion actuator. (A) One layer (out of three) of the stiffness contrast-detail phantom with cylindrical inclusions of varying diameters and varying silicone composition (Table 1). (B) Stiffness interface phantom with 100% silicone A341 gel on left (light gray) and 70% silicone A341 gel on right (dark gray). (C) Damping ratio inclusion phantom with soft tofu background (gray) and 0.75% agar inclusions of varying diameters (yellow). (D) Damping ratio interface phantom with 0.65% agar background (yellow) and soft tofu (gray). (E) Motion actuator with a stack piezoelectric actuator (brown), lever (black), actuation plate (gray), phantom (red), and spring (yellow). The spring ensures constant contact of the actuation plate with the lever enabling shearing motion along the “X” direction.

Stiffness Contrast-Detail Phantom (see Fig. 1A)

The stiffness contrast-detail phantom was used to estimate the smallest inclusion that can be detected for a given stiffness contrast and was constructed using A341 silicone soft gel and silicone fluid. The recommended 10:1 ratio of A341 parts A and B were used. The components were mixed and placed into a vacuum chamber in order to remove air pockets. The silicone mixture was then carefully poured into molds which were coated with a thin layer of petroleum jelly to allow the cured phantoms to be easily extracted from their containers. A multi-inclusion cylindrical phantom (11 cm height and 10 cm diameter) was created using various concentrations of silicone soft gel A341 and silicone fluid to control stiffness. Higher percentage of silicone A341 produced a stiffer material. Twenty (20) cylindrical inclusions, 25mm in height, with varying diameters (8mm, 10mm, 15mm, 20mm, 29mm) and stiffness (55%, 60%, 65%, 70% A341) were embedded in a silicone background of 50% A341. Table 1 summarizes the composition, size, and stiffness of the inclusions along with their relative stiffness contrast which was determined by mechanical testing using DMA (dynamic mechanical analysis). Here, 4 different material stiffnesses were fabricated into 5 different diameters and all 20 inclusions were distributed among three layers.

Table 1.

Stiffness Contrast Detail Phantom Inclusion Composition and Storage Modulus (SM) Values

%Silicone A341 Gel	Inclusion Diameter(mm)	Orientation 1 SM		Orientation 2 SM		Orientation 3 SM		Combined		Stiffness Contrast vs Background
		Mean (Pa)	SD (Pa)	Mean (Pa)	SD (Pa)	Mean (Pa)	SD (Pa)	Mean (Pa)	Mean SD (Pa)
50%	Background	2488	305	2582	339	2453.2	387	2508	344	–
55%	8	2769	143	2264	164	3043	93	2692	133	14%
55%	10	2716	91	2482	129	2960	270	2720	163
55%	15	3213	208	3155	125	2857	241	3075	191
55%	20	3257	290	2944	348	2705	227	2969	288
55%	29	3174	223	3136	148	3219	323	3177	231
60%	8	3298	288	3606	186	2920	149	3275	208	33%
60%	10	3009	178	2947	223	2977	175	2978	192
60%	15	3398	232	2950	229	3194	194	3181	218
60%	20	3245	201	3621	313	3373	286	3413	267
60%	29	3376	299	3736	388	3012	254	3375	314
65%	8	3112	204	3631	171	2897	179	3214	184	40%
65%	10	3234	211	3421	279	3172	185	3275	225
65%	15	3616	516	3384	312	3575	461	3525	430
65%	20	3442	363	3613	306	3260	473	3438	381
65%	29	4148	379	3701	314	3747	417	3866	370
70%	8	3211	220	3264	366	3201	256	3225	281	50%
70%	10	3748	526	3914	349	3533	265	3732	380
70%	15	4104	496	3580	398	3559	307	3748	400
70%	20	3836	421	4464	464	3988	483	4096	456
70%	29	4580	666	4361	604	4180	519	4373	596

Stiffness Interface Phantom (see Fig. 1B)

The stiffness interface phantom was used to evaluate NLI-MRE image resolution of a step change in mechanical properties created by the interface. It was constructed from seventy percent (70%) and 100% silicone A341 following the same fabrication processes described for the stiffness contrast-detail phantom. The two materials formed an oblique interface relative to the scanning and actuation directions, as interfaces in tissue are unlikely to be aligned with coordinate directions. The dimensions of the phantom were 120mm × 60mm × 40mm with an interface length of 75mm.

Damping Ratio Inclusion Phantom (see Fig. 1C)

The damping ratio inclusion phantom was used to estimate the smallest diameter inclusion that could be resolved in damping ratio images with the NLI technique. It was comprised of a soft tofu background (which is known to have a higher damping ratio than gels due to the high proportion of mobile fluid [42]) with four inclusions of 0.75% agar, since silicone and tofu are incompatible as a mixed phantom. The dimensions of the phantom were approximately 100 mm × 50 mm × 38 mm. The inclusions were 38mm in height and varied in diameter (15 mm, 12 mm, 10 mm, and 8 mm). A 100ml volume of 0.75% agar solution consisting of 0.9% salt (sodium chloride) and 0.75% agar by weight was mixed at room temperature and heated to 85°C (the boiling point of agar) while being stirred frequently. The solution was then poured into 15 mm, 12 mm, 10 mm, and 8 mm diameter cylindrical holes cut into the soft tofu block. The phantom was cooled to room temperature and then refrigerated for at least two hours. Prior to MRE scanning, the phantom was returned to room temperature.

Damping Ratio Interface Phantom (see Fig. 1D)

The damping ratio interface phantom was used to evaluate NLI-MRE image resolution of a step change in damping ratio when the storage modulus was approximately equal across the interface. It was comprised of a soft tofu triangular prism, with one face cut at an angle, embedded in 0.65% agar solution; the phantom had a final cuboidal shape. The 0.65% agar material was prepared using the same procedures described for the damping ratio inclusion phantom except for the difference in agar weight percentage (0.65% instead of 0.75%). The two materials (soft tofu and 0.65% agar) were selected for their approximately equal storage modulus values. Two of the three faces of the tofu prism had interface angles that did not align with the scanning or actuation direction. The dimensions of the phantom were approximately 60 mm × 60 mm × 40 mm.

Motion Measurement

Each phantom was vibrated with a piezoelectric actuator (Fig. 1E) connected to a sinusoidal wave signal generator (Agilent Model HP33120A). Phantoms were placed on the actuation plate and then positioned in a Philips 8 channel RF head coil on a 3T Philips Achieva system with a motion encoding gradient amplitude of 31mT/m. The actuator produced a horizontal shearing motion along the × direction (see Fig. 1E). MRE motion data was collected over eight dynamic cycles using a spin-echo phase contrast pulse sequence with a motion gradient applied in three directions. Repetition and echo times were 900 ms and 40 ms, respectively. Coronal images were acquired using 2×2×2 mm³ voxels (2mm slices and no gap between slices). The field of view and number of slices for the stiffness contrast-detail phantom, stiffness interface phantom, damping ratio inclusion phantom and damping ratio interface phantom were 128×128×114mm with 52 slices, 130×130×40mm with 20 slices, 128×128×30mm with 15 slices, and 128×128×32mm with 16 slices respectively. The actuation frequency was 60Hz for the stiffness phantoms and 100Hz for the damping ratio phantoms to maintain a shear wavelength in the stiffer tofu similar to the softer silicone phantoms. The stiffness contrast-detail phantom and the damping ratio inclusion phantom were scanned in three different orientations to study the reproducibility of the reconstructed MRE images given different motion patterns. Octahedral shear strain signal to noise ratios (OSS-SNR) were calculated to measure the quality of motion acquired. [43]

Independent Mechanical Testing

Cylindrical samples of silicone, agar and tofu were formed for independent mechanical testing. The silicone samples were 10 mm thick and 35 mm in diameter, and contained the mixtures of silicone fluid and A341 soft gel listed in Table 1. They were constructed with the same process described for the stiffness contrast-detail phantom except that vacuum degassing was not required due to their small size. The four agar samples had the same dimensions as their silicone counterparts but varied in agar concentration: 0.65%, 0.75%, 0.85%, and 0.95%, and were formed using the steps described for the damping ratio inclusion phantom with a modified solution volume (10 ml instead of 100 ml). Tofu samples were cut from the three available tofu consistencies: soft, firm, and extra firm with dimensions of 10 mm in height and 28.5 mm in diameter. [44]

All samples were tested using a Q-800 DMA (TA Instruments, New Castle, DE) over a frequency range of 1-15 Hz at room temperature. Higher frequencies gave unstable results on the Q-800 system caused by machine resonance effects due to the very soft samples. Complex-valued shear modulus was calculated as a function of frequency using a dynamic viscoelastic model for comparison with the MRE estimations. A dynamic strain of 2% was applied with the force track set to 125% (approximately 3.5% pre-strain) for parallel plate compression. DMA measurements are sensitive to the level of pre-strain and dynamic strain due to material nonlinearities and geometric effects; these values were chosen to give reproducible results rather than attempt to match conditions in the phantom experiments. Damping ratio was calculated from the measured storage and loss modulus values using equation 2 (below).

To compare the values produced by the NLI-MRE and DMA methods, percent difference was calculated (NLI-DMA)/DMA where NLI and DMA are the values produced by NLI-MRE and Q-800 DMA, respectively. [45]. Intraclass correlation coefficient (ICC) was also computed to measure the consistency between the NLI estimates and DMA measurements with a one-way random effects model. [46,47]

Silicone NLI results were averaged over all inclusion diameters and over all three scanning orientations for each silicone composition. The 50% A341 silicone NLI storage modulus was an average of the background region also from the three orientations. Soft tofu and 0.65% agar results were averaged over their full volumes from the damping ratio interface phantom. NLI values for 0.75% agar were averaged over all inclusions within the damping ratio inclusion phantom.

Mechanical Property Estimation & Non-Linear Inversion

MRE image reconstruction was based on a heterogeneous nearly incompressible viscoelastic model in which the complex-valued shear modulus (storage and loss modulus) was estimated. The governing model is Navier’s time harmonic partial differential equation for viscoelastic materials described by

$$\nabla \cdot \left(\mu \left(\nabla \overrightarrow{u}+\nabla {\overrightarrow{u}}^T\right)\right)+\nabla \left(\lambda \nabla \cdot \overrightarrow{u}\right)=-\rho {\omega }^2\overrightarrow{u},$$ (1)

where $\overrightarrow{u}$ is the complex-valued 3D displacement amplitude vector, μ is the complex-valued shear modulus, λ is the first Lamé constant, ρ is the density, ω is the actuation frequency, and^T represents the transpose. Damping ratio, ξ, is a dimensionless quantity that indicates the level of attenuation in viscoelastic materials and can be quantified through

$$\xi =\frac{{\mu }_L}{2{\mu }_S}.$$ (2)

A value of ξ < 1 results in an oscillatory decay response to a step input, ξ =1 is critical damping and ξ > 1 is known as overdamping. [48]

NLI-MRE is an iterative technique that minimizes an objective function which compares the viscoelastic computational model in Eq. 1 with the measured displacement data of tissue under external harmonic excitation. [2,49–51] The objective function, Φ, is given by:

$$\Phi \left(\theta \right)={\displaystyle \sum _{i=1}^{N_m}\left\{\left(u_{c\left(i\right)}\left(\theta \right)-u_{m\left(i\right)}\right)\left(u_{c\left(i\right)}\left(\theta \right)-u_{m\left(i\right)}\right)\right\}},$$ (3)

where θ represents the material property estimates, u_c(i) is the computed displacements from the computational model for the i-th displacement measure, u_m(i) is the measured displacements, and N_m is the number of measurements. Calculating u_c(i) from Eq. 1 is known as the “forward problem”, and the “inverse problem” is the iterative estimation of the material properties on a set of overlapping subzones such that Φ(θ) is minimized. θ is initialized by an estimate of the 3D material property distribution and updated by the conjugate gradient method in this study. Type I boundary conditions on each subzone are used for the forward problem with u_m(i) for each node. Regularization is required to maintain stability during the inversion; Gaussian spatial filtering was employed using a filter kernel width of 1.5mm. Although NLI-MRE has the capability to employ other regularization techniques including soft prior regularization, total variation minimization and Tikhonov regularization, they were not used in this study in order to limit the influence of apriori knowledge on the results. NLI parameter updates involved 2 conjugate gradient and 2 line search iterations per subzone and the material property resolution was equal to the acquired data resolution. These parameters are the same as those applied to in vivo data acquired in recently published human studies and were chosen to ensure that the phantom analysis presented here is relevant to those clinical investigations. [26, 52–54] A 27-node hexahedral finite element mesh was generated from the acquired displacement data with nodal spacing equal to the measurement resolution. The unknown μ_S and μ_L values were supported on an 8-node hexahedral mesh at the same resolution. [53] A typical reconstruction of one phantom data set required 3-4 hours on 32 processors (2.6GHz core speed).

Image Evaluation Measures

Contrast-to-noise ratios were calculated using the following equation [25]:

$$\mathit{CNR}=\sqrt{\frac{2{\left({\mu }_I-{\mu }_B\right)}^2}{{\sigma }_I^2+{\sigma }_B^2}}$$ (4)

where μ_I and μ_B are the average property values for the inclusion and background, respectively, and σ_I and σ_B are their standard deviations. To quantify the interface resolution, the edge spread function (ESF) and line spread function (LSF) were calculated. The ESF captures the stiffness profile perpendicular to the interface, and the LSF is the first derivative of ESF, where the ideal LSF is a delta function. The profiles were calculated by manually selecting multiple points along the interface, creating an interface plane, and then plotting a profile of 25mm (spanning 12-13 pixels) normal to that plane.

Results

Stiffness Contrast-Detail Phantom

Figure 2A shows average storage modulus values (in kPa) for inclusions with respect to the 50% A341 background. The standard deviation was calculated by averaging property values for each inclusion across the three scanning orientations. Background (50% A341) stiffness value was an average of the three repeated scans from all three layers. Figure 2B shows the calculated CNR from Eq. 4 as a function of inclusion diameter. Based on a decision criterion of CNR>1, all inclusions were resolved from the background.

Figure 2.

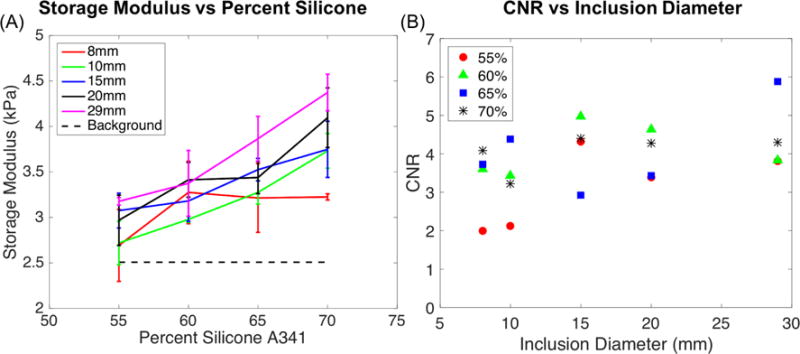
(A) Average values of storage modulus (kPa) of inclusions versus percent composition of silicone A341. (B) Calculated CNR (Contrast to Noise Ratio) values for inclusions compared to diameter size.

Figures 3 and 4 show storage modulus images reconstructed using the NLI technique. Representative cross-sections of the estimated stiffness property images from the three layers of the phantom are displayed in Figure 3. Figure 4 shows layer 1 stiffness images generated from data acquired in the three different scanning orientations. OSS-SNR for the three orientations were 17.2, 18.7, and 4.4. Table 1 presents the average storage modulus value for each inclusion with the standard deviation over the inclusion region for all three orientations. Inclusion ROIs were eroded one pixel layer (2mm) from the edges to avoid partial volume effects. Stiffness contrast with respect to the background was calculated using DMA results presented in Table 2.

Figure 3.

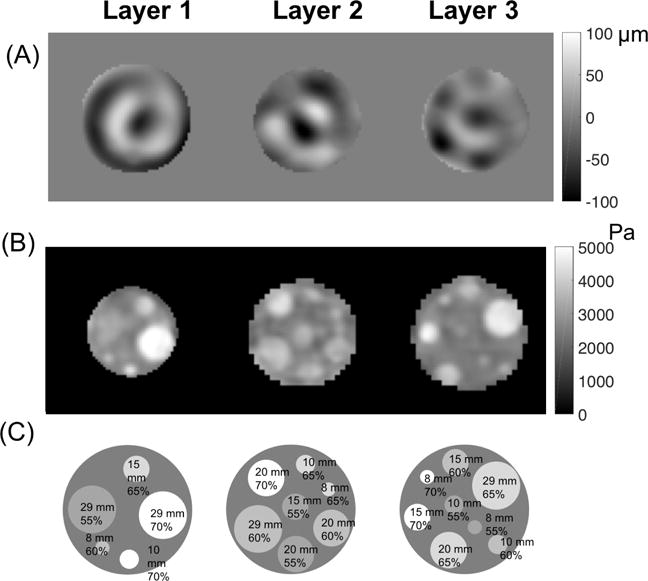
(A) Displacement images of motion in the Z direction, (B) storage modulus images and (C) corresponding locations of inclusions in each layer of the stiffness contrast-detail phantom indicating their size and A341 percentage for the first scanning orientation.

Figure 4.

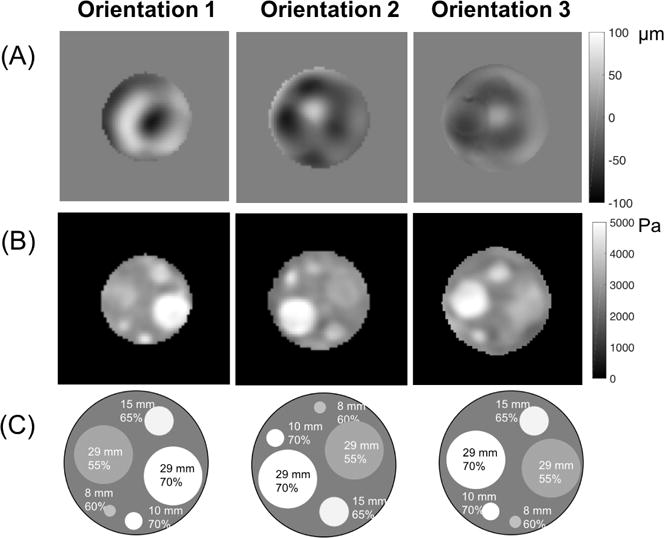
(A) Displacement images of motion in the Z direction, (B) storage modulus images and (C) corresponding locations, sizes and A341% of the inclusions for the three orientations of layer 1 in the stiffness contrast-detail phantom.

Table 2.

Percent Difference Storage Modulus (SM in PA) and Damping Ratio (DR) from NLI and DMA

	Silicone-SM					Agar-SM		Tofu-SM	Agar-DR		Tofu-DR
Composition	50%	55%	60%	65%	70%	0.65%	0.75%	Soft	0.65%	0.75%	Soft
NLI	2508	2926	3244	3464	3835	2909	3787	3312	0.033	0.081	0.083
DMA	2984	3424	3992	4237	4577	1800	2588	2667	0.057	0.07	0.097
% Difference	−16%	−15%	−19%	−18%	−16%	62%	46%	24%	−42%	16%	−14%

Results in Figure 2 and Figure 3 indicate the NLI technique was able to identify an 8mm inclusion with the lowest stiffness contrast (55% A341). As shown in Figure 4, the NLI technique produced similar storage modulus images in each of the three phantom orientations despite different motion fields for each case.

Stiffness Interface Phantom

Storage modulus inversion results from the stiffness interface phantom appear in Figure 5 where 5A and 5B are the magnitude and displacement images respectively. Figure 5D presents ESF and LSF profiles averaged over multiple slices. OSS-SNR was 14.3.

Figure 5.

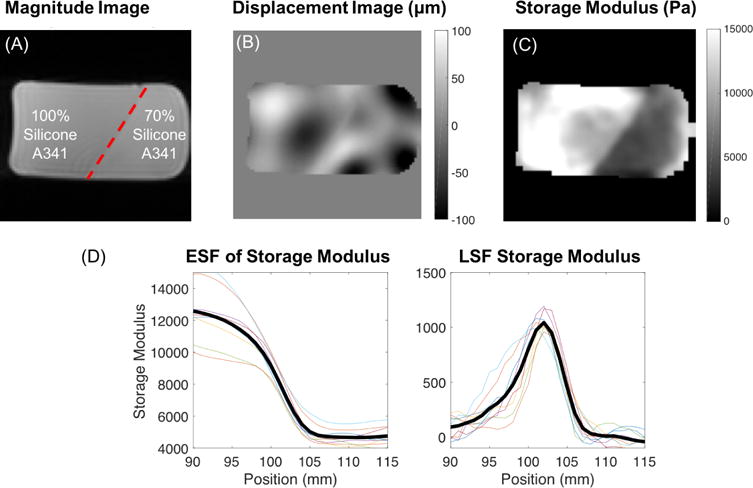
(A) Magnitude image, (B) displacement image of motion in the Z direction, and (C) storage modulus image of the stiffness interface phantom constructed from 100% A341 silicone soft gel (stiffer) and 70% A341 (softer). (D) ESF (left) and LSF (right) results from the storage modulus image of the stiffness interface phantom. Bolded line is an average across all sampled slices.

NLI storage modulus results yielded an edge response distance of 11mm at the interface of the 100% and 70% A341 silicone gel which was calculated as the distance for the ESF of storage modulus to decrease from 90% (~9200 Pa) to 10% (~5700Pa) of the step change across the interface. The full width half maximum (FWHM) value for the LSF of storage modulus was 5.0mm.

Damping Ratio Inclusion Phantom

Figure 6 presents the results of the damping ratio inclusion phantom where 6A and 6B are the magnitude and displacement images. Figures 6C and 6D show estimated storage modulus and damping ratio images for the damping ratio inclusion phantom in each scanned orientation. Red contours superimposed on the images indicate locations of the four 0.75% agar inclusions of diameters 8-15 mm. Average estimated properties from the reconstructed volume were calculated for the inclusions and compared to the soft tofu background in Figures 6E and 6F. Standard deviations plotted in Figure 6 were determined from the average values of the inclusion across the three scanning orientations. OSS-SNR was 26.7, 24.4, and 6.3 for the three orientations.

Figure 6.

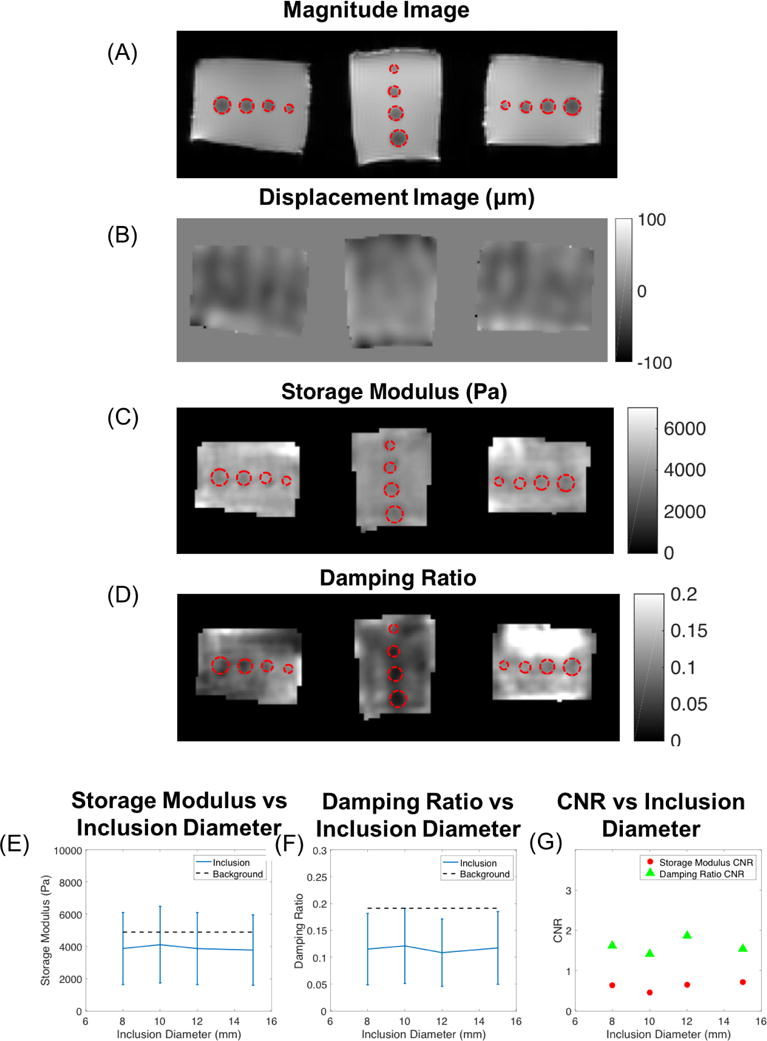
(A) Magnitude images, (B) displacement images of motion in the Z direction, (C) storage modulus, and (D) damping ratio images from the three scanning orientations of the damping ratio inclusion phantom. Red contours encircle regions of the 0.75% agar inclusions with diameters of 15mm, 12mm, 10mm, and 8mm. (E) Storage modulus (Pa) versus inclusion diameter (mm) is plotted with error bars indicating standard deviation across the three scanning orientations. (F) Damping ratio values versus inclusion diameter compared to average background value. (G) Storage modulus and damping ratio CNR for inclusions.

Figure 6 indicates that the spatial resolution of the damping ratio estimated from the NLI algorithm is at least 8mm. All inclusions (≥ 8mm in diameter) were resolved in the damping ratio images with CNR values greater than unity (Figure 6G). Inclusion regions were trimmed by one pixel layer from the outside to again reduce partial volume effects in the calculations.

Damping Ratio Interface Phantom

The reconstructed NLI results from the damping ratio interface phantom are presented in Figure 7 where 7A and 7B are the magnitude and displacement images. Previous experiments indicate tofu has high damping and agar has low damping [44]. Figures 7C and 7D show the NLI reconstructed storage modulus and damping ratio while Figures 7E and 7F present the corresponding ESF and LSF plots across the interface for damping ratio and storage modulus, respectively.

Figure 7.

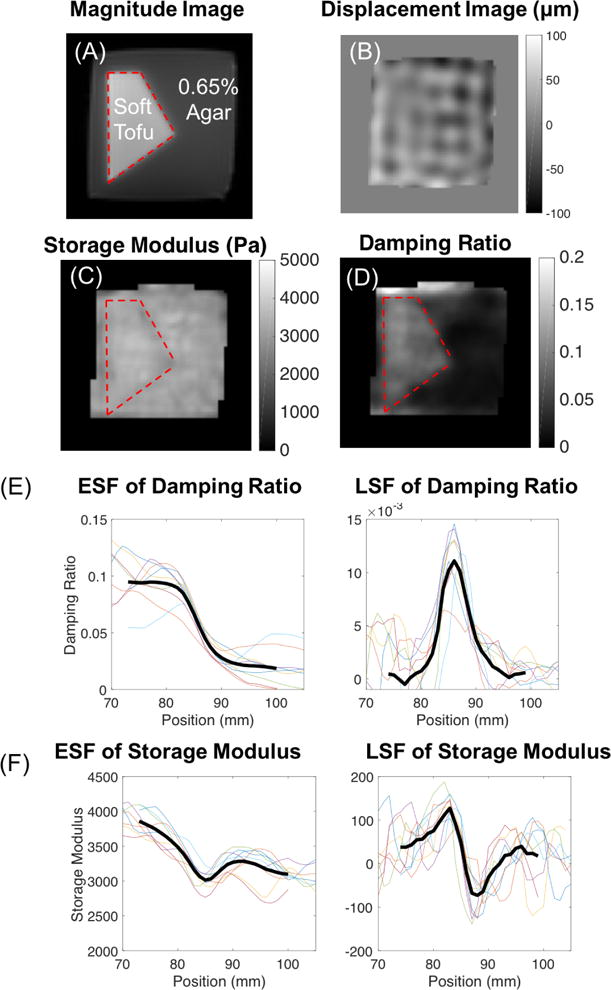
(A) Magnitude image, (B) displacement image of motion in the Z direction, (C) storage modulus, and (D) damping ratio images of the damping ratio interface phantom. Red contour encloses the soft tofu region. ESF and LSF plots from NLI reconstruction of the damping ratio interface phantom for (E) the damping ratio and (F) the storage modulus.

Figure 7 shows that the storage modulus image was relatively uniform (as expected since the tofu and agar were designed to have similar stiffness) whereas the damping ratio images distinguish the tofu-agar interface with an edge response (90%-10%) distance of 10mm in ESF of the damping ratio. The FWHM value for the LSF of the damping ratio was 7mm. OSS-SNR was 31.4.

Dynamic Mechanical Testing

Figure 8 shows measured shear storage and loss modulus values obtained from DMA experiments plotted versus frequency for the three materials used in the study. The reliable and reproducible frequency range for DMA of these materials is typically 1-10Hz. Table 2 summarizes averaged NLI-MRE property estimates and DMA (1-15Hz) results along with percent differences between the two techniques. Damping ratio values were calculated from the storage and loss modulus using Equation 2. NLI-MRE estimates fell within 20% of DMA measurements for silicone. ICC was 0.72 for storage modulus suggesting good agreement between the two measures. ICC was not calculated for the damping ratio values between the two techniques due to the lack of sufficient data. [55]

Figure 8.

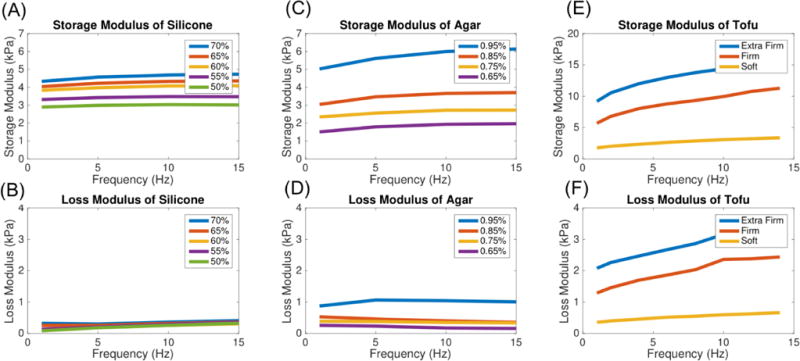
Dynamic mechanical analysis data (shear storage and loss moduli) for silicone soft gel A341 (A–B), agar (C–D), and tofu (E–F).

Discussion

This study was designed to investigate the performance limits of NLI-MRE by reconstructing mechanical property values, specifically the storage modulus and damping ratio, in four challenging phantoms with inversion parameters used to generate recently published in vivo results.

The stiffness contrast detail phantom provided a measure of the quantitative and spatial accuracy of the algorithm. A similar stiffness contrast detail analysis was performed by Doyley et al. [25] using an earlier version of the subzone based NLI technique. In that study the storage modulus contrast of spherical gelatin inclusions ranged from 1.1 to 8, whereas the results summarized in Figures 2 through 4 provided contrasts of approximately 1.3, 2.2, 2.8 and 3.7 corresponding to the 55%, 60%, 65% and 70% cylindrical A341 inclusions, respectively. In the Doyley paper, an inclusion with a contrast of 1.4dB (i.e. $20{\log }_{10}\frac{{\mu }_I}{{\mu }_B}$ where μ_I and μ_B are the inclusion and background storage moduli, respectively) was detected with a spherical diameter of 18mm, but not at a diameter of 10mm. Here, we showed that a lower contrast inclusion (1.3dB) with a smaller diameter (8mm) was detected. Although the results presented for the stiffness contrast-detail phantom appear to offer better resolution, comparisons between the two studies are indirect because of differences in the materials and inclusion shapes that were evaluated and advances in the NLI implementation. An increase in CNR as contrast increases would be expected under the assumption that noise is independent of stiffness contrast; however, Figure 2 does not suggest this trend. Noise may be correlated with stiffness contrast due to model-data mismatch at the interfaces of the inclusion and background matrix resulting from imperfect resolution of the interface caused by regularization and discretization. Other variations in the estimated property images could be attributed to fabrication errors such as imperfect mixing and/or differential cooling of the material components for large phantoms, which can affect the mechanical properties. Datasets with artifacts or imperfections in property images were not removed from this study or reimaged for better quality, since we aimed to evaluate NLI-MRE under day-to-day conditions that would be more indicative of clinical workflow.

Images or analyses of attenuation related parameters, such as the damping ratio, in a controlled phantom system have not been published despite a number of studies demonstrating clinical relevance of contrast in these parameters. [18, 28, 32, 56] In our study, the damping ratio inclusion phantom allowed us to evaluate spatial resolution in the estimated damping ratio images. This phantom indicated that the limit in damping ratio spatial resolution was 8mm using NLI. The inversion generated a contrast-to-noise value greater than unity for inclusions 8mm and larger in diameter. The NLI algorithm estimated the mechanical properties precisely when inclusion phantoms were scanned repeatedly and in different orientations. The damping ratio results presented here indicate that imaging the damping ratio of small regions with attenuation contrast accurately is possible. One example in the brain is the hippocampus, which has a volume of around 4 cm³ for each hemisphere, and plays a crucial role in memory function. Schwarb et al. used NLI-MRE to show that lower damping ratio in the hippocampus is strongly correlated with increased performance in memory-related tasks [34], and our study is the first phantom demonstration that damping ratio imaging at these scales is accurate.

The interface phantoms allowed us to evaluate spatial resolution at boundaries of step changes in material properties. The recovered storage modulus images from the stiffness interface phantom and the damping ratio images from the damping ratio interface phantom yielded high spatial resolution at the silicone-silicone interface (with an edge response distance of 11mm) and tofu-agar interface (with an edge response distance of 10mm), respectively.

Figures 2A, 6E and 6F show average inclusion values with standard deviations across the three scanning orientations. Moderate differences in recovered properties of the inclusion are evident (0.09-16% variance for inclusions from the stiffness contrast detail phantom) which could be due to noise and motion artifacts captured during motion acquisition. Placing phantoms in various orientations results in differences in pre-strain and strain amplitude; this fact is evident in the large spread in OSS-SNR in the stiffness contrast-detail phantom (highest OSS-SNR from the three orientations: 17.3, lowest: 4.4) and the damping ratio inclusion phantom (26.7 vs 6.3).

To test the accuracy of NLI, we compared the estimated property values to DMA measurements for materials used to construct the phantoms. DMA results and NLI storage modulus estimations have adequate agreement for the silicone materials used in this study, however, the two methods differed in the storage modulus and calculated damping ratio of agar and tofu. Differences between NLI-MRE property values and mechanical testing could be attributed to the low stiffness of the materials used here. DMA is sensitive to experimental conditions, for example, the amount of pre-strain and dynamic strain applied to the sample, and soft materials can be damaged with large compression and dynamic strain amplitude. [57] Pre-strain and dynamic strain vary across the phantom due to self-weight and positioning effects, and the phantom experiments were conducted at different frequencies so we do not expect an exact match between the two measurement modalities. However, DMA provides a good measure of the relative contrast that should be expected. Recently, Arunachalam et al. compared a Direct Inversion-MRE (DI-MRE) technique with DMA results for eight different polyvinyl chloride mixtures and reported a strong correlation between the two techniques across multiple frequencies (54Hz-134Hz). They reported an ICC of 0.99 for the magnitude of the complex shear modulus between DI-MRE of large homogeneous phantoms and DMA using 8 polyvinyl chloride samples. [45] In our study, the NLI-MRE and DMA techniques also revealed consistency with an ICC of 0.72 between the storage modulus of the silicone, agar, and tofu samples and the heterogeneous phantoms.

Recently Anderson et al. studied NLI subzone parameter variations and their influence on the reconstructed mechanical parameters and concluded that the stable subzone range was between 0.64L_s and 1.0L_s for phantoms. [58]. L_s is the shear wavelength of the material, and A341 silicone at 60Hz has an approximate L_s of 23.5 (0.64L_s ≈ 15mm). NLI reconstructions using 10, 15, 19.5, 25 and 30mm subzones sizes were performed on the phantoms in our study and we found less than ±2.5% difference between the estimated storage modulus images across all subzones. For human brain with an actuation frequency of 60Hz, L_s is approximately 30.5mm (0.64L_s ≈ 19.5mm). The stable subzone range for brain might be narrower (0.8L_s to 1.0L_s) and Anderson showed variable results in very thin stiff members like the falx when subzones were larger than 1.0L_s. Thin membranes are not adequately represented by the 2mm continuous mechanical property support of NLI, so they are significant sources of model data mismatch. Other regions of the brain further away from stiff membranes were only minimally affected by subzone size, as in this phantom study.

The achievable resolution of MRE is dependent on data quality and resolution. Higher resolution motion data and better SNR allows lower regularization levels to be applied to stabilize the inverse problem, which yields better resolution of recovered properties. This study used 2x2x2mm³ resolution for the motion acquisition and the same inversion parameters applied to brain studies in vivo. [52,59] Recent NLI-MRE studies in brain have used higher acquisition resolution (1.6×1.6×1.6mm³); hence, even smaller and lower contrast structures could be visible with high resolution MRI motion measurements and concomitant optimization of inversion parameters. [60] Higher actuation frequencies produce shorter shear wavelengths which could also improve resolution; however, the optimal frequency range for in vivo brain data is limited by attenuation to 50-60Hz. The actuation frequencies in this study were chosen to yield comparable shear wavelengths. Future work could investigate how data resolution and actuation frequency affect the achievable resolution, which is important for animal models where high frequency and resolution are often used due to smaller brain sizes.

Conclusion

The objective of this set of experiments was to evaluate the spatial resolution and accuracy of mechanical property distributions estimated by nonlinear inversion. Spatial resolution was assessed through contrast detail analysis and material interface studies. Edge spread and line spread functions were calculated. Results presented here also represent the first demonstration of accurate imaging of attenuation parameters in a controlled phantom system. To date, the spatial resolution of attenuation parameter images has not been evaluated to the extent considered in this paper, either in terms of detectable inclusion size or edge spread function despite conclusions made about attenuation based parameters in clinical studies. This set of experiments and image quality outcomes provide a baseline assessment for evaluating further improvements in the NLI and other MRE property mapping algorithms. Results also provide a size and contrast threshold for identifiable features for clinical and in vivo studies. Although the phantom dimensions and properties were designed to be representative of in vivo conditions, additional challenges for in vivo elastography such as physiological and patient motion, fluid spaces, anisotropy of white matter, and presence of thin membranes need to be considered when evaluating in vivo MRE data.