Use of random regression to estimate genetic parameters of temperament across an age continuum in a crossbred cattle population

Abstract

The objective was to estimate genetic parameters of temperament in beef cattle across an age continuum. The population consisted predominantly of Brahman-British crossbred cattle. Temperament was quantified by 1) pen score (PS), the reaction of a calf to a single experienced evaluator on a scale of 1 to 5 (1 = calm, 5 = excitable); 2) exit velocity (EV), the rate (m/s) at which a calf traveled 1.83 m upon exiting a squeeze chute; and 3) temperament score (TS), the numerical average of PS and EV. Covariates included days of age and proportion of Bos indicus in the calf and dam. Random regression models included the fixed effects determined from the repeated measures models, except for calf age. Likelihood ratio tests were used to determine the most appropriate random structures. In repeated measures models, the proportion of B. indicus in the calf was positively related with each calf temperament trait (0.41 ± 0.20, 0.85 ± 0.21, and 0.57 ± 0.18 for PS, EV, and TS, respectively; P < 0.01). There was an effect of contemporary group (combinations of season, year of birth, and management group) and dam age (P < 0.001) in all models. From repeated records analyses, estimates of heritability ($h^2$) were 0.34 ± 0.04, 0.31 ± 0.04, and 0.39 ± 0.04, while estimates of permanent environmental variance as a proportion of the phenotypic variance (c²) were 0.30 ± 0.04, 0.31 ± 0.03, and 0.34 ± 0.04 for PS, EV, and TS, respectively. Quadratic additive genetic random regressions on Legendre polynomials of age were significant for all traits. Quadratic permanent environmental random regressions were significant for PS and TS, but linear permanent environmental random regressions were significant for EV. Random regression results suggested that these components change across the age dimension of these data. There appeared to be an increasing influence of permanent environmental effects and decreasing influence of additive genetic effects corresponding to increasing calf age for EV, and to a lesser extent for TS. Inherited temperament may be overcome by accumulating environmental stimuli with increases in age, especially after weaning.

INTRODUCTION

Temperament is both an economically and logistically important trait during most phases of beef production. This may be because temperamental cattle have been reported to have reduced growth rates (Tulloh, 1961; Voisinet et al., 1997; Cafe et al., 2011), compromised immune function (Fell et al., 1999), increased difficulty to manage, and inferior carcass characteristics (King et al., 2006; Cafe et al., 2011). Temperament is highly heritable in beef cattle (Riley et al., 2014; Schmidt et al., 2014). It is of special interest in Bos indicus purebreds and crossbreds, because B. indicus-influenced cattle are considered to be more temperamental compared with British breeds. Limited efforts to characterize temperament in cattle across time have presented different results: either temperament was not different across some repeated measures of time (Riley et al., 2010) or temperament tended to improve across time (Cafe et al., 2011; Schmidt et al., 2014). Repeated record acquisition permits partitioning of phenotype in ways that may be beneficial for estimation and refinement of genetic merit. Random regression analyses facilitate assessment of traits along a continuous gradient such as time. In such analyses, additive genetic covariance values are modeled across a quantitative dimension (such as time) using a covariance function. Repeated temperament assessment in cattle is accomplished easily in conjunction with husbandry or data collection activities. The objective of this study was to assess genetic parameters of temperament across an age continuum in crossbred cattle with repeated records using random regression and compare with those from repeated records analyses.

MATERIALS AND METHODS

All animal procedures were in compliance with the Guide for the Care and Use of Agricultural Animals in Research and Teaching and were approved by the Mississippi State University Animal Care and Use Committee (IACUC #08-049 and #13-010).

Animals

Records were utilized from a population of mostly Brahman-British crossbred cattle with known breed composition. This herd is located at the Mississippi Agricultural and Forestry Experiment Station in Raymond, MS. Bos taurus breed types represented in this population included Angus, Hereford, Red Angus, Gelbvieh, Maine-Anjou, Charolais, and Limousin. Bos indicus breed types represented in this population included Brahman and Gyr. There were 4,891 animals in the five-generation pedigree including 118 sires and 1,292 dams with progeny that had records. Calves in the population with at least one record consisted of males (n = 2,063) and females (n = 1,958), born in the fall (n = 1,245) and spring (n = 2,776) between the years 2002 and 2015. Age at weaning was 217.38 ± 29.34 d of age on average.

Temperament Evaluation

Three measures of calf temperament, pen score (PS, a subjective measurement; Hammond et al., 1996), exit velocity (EV, an objective measurement; Burrow et al., 1988), and an overall temperament score (TS; King et al., 2006), were assessed at weaning. The PS was recorded prior to restraining animals for other measurements. To determine PS, an experienced observer visually evaluated (scored on a scale of 1 to 5; Table 1) individual calves in groups of three to five within a pen. The same experienced observer scored all calves. Subsequently, each group of calves was herded into a separate adjacent pen, where they remained until PS was recorded for all calves. After pen scoring, calves were walked into an enclosed handling facility and individually entered a squeeze chute for restraint. Exit velocity was defined as the rate, measured in m/s, at which an animal traversed 1.83 m upon exiting the squeeze chute using an infrared beam sensor system (FarmTek Inc., North Wylie, TX). Temperament score was defined as the numerical average of PS and EV, as previously reported (King et al., 2006).

Table 1.

Descriptions of subjective PS classifications (Hammond et al., 1996)¹

Score	Description
1	Calves walked slowly and were not excited by evaluator
2	Calves ran along fences and kept distance from evaluator
3	Calves heads were high, avoided the evaluator, and ran when approached by the evaluator but stopped before hitting fences
4	Calves stayed at the back of the group with their heads high, were very aware of humans, and often ran into fences
5	Calves were very excited or aggressive, ran into fences, and ran over anything in their path

¹PS is pen score, a subjective measure of temperament, in which reactions of an individual calf to a constant experienced evaluator within a pen of three to five calves are scored on a scale of 1 to 5 (1 = calm, 5 = excitable).

Statistical Analyses

All analyses were completed using ASReml (Gilmour et al., 2009).

Repeated Measures Analyses

Fixed effects were determined using repeated measures analyses, in which the random components modeled were additive genetic (obtained from an animal model) and permanent environmental effects. Fixed effects investigated included five dam age categories (2, 3, 4, 5 to 9, and older than 9 yr of age), which were slight modifications of those detailed in national genetic evaluation guidelines (Cundiff et al., 2016). Calf sex included three categories, and there were 650 bulls, 1,404 steers, and 1,950 heifers with EV records (all counts within groups that follow are of EV records; those for the other two traits are slightly different). Contemporary groups were constructed initially as combinations of year and season of birth. Heifers had identical breeding seasons as other cows, as well as similar nutrition and management conditions, but were pastured separately from the main herd, and therefore, separate contemporary groups were created for those within year-season combinations. These initial groupings were refined by limiting the age spread among calves in a contemporary group to a maximum of 90 d; most were 65 d or less. Those groups that initially exceeded 90 d of age spread were divided into groups of mostly equal numbers of animals, representing an older and younger group. Some of the original groups had large enough age spreads that required division into three groups based upon age. This procedure resulted in 77 contemporary groups ranging from 5 to 179 calves. Calves and dams in the research herd consisted primarily of two- or three-breed crosses of many breeds and purebreds of a few breeds (e.g., there were 3,860 crossbred and 144 purebred calves with at least one record; 3,545 calves had crossbred dams and 459 had purebred dams). All except 289 calves and 598 dams had some proportion B. indicus background. Many parameterizations of breed type of calves and their dams were investigated, but the large numbers of combinations of breed types (over 100), many with small numbers, made it impossible to appropriately estimate all combinations distinctly. Broad classifications of breed type such as British or Continental B. taurus were investigated, grouped proportions of each as classification variables (e.g., less than 0.25 British, 0.26 to 0.5 British, etc.), as well as fixed regressions on proportion of British breed or Continental breed. The final parameterization chosen was the most consistent with the magnitude and rank of least squares means of these and other modeled fixed effects in comparison to unadjusted means; no formal statistical test was employed. This included two fixed classification variables each with two levels consisting of purebred and crossbred calves, and purebred and crossbred dams. The proportions of B. indicus in calves and their dams were modeled as linear covariates (entire parameter space represented; averages for calves and dams were 0.179 and 0.195, respectively). Calf age in days at the time of record was included as a covariate.

The repeated measures models followed this form:

$$y=X\text{β}+Zu+Z\text{pe}+e,$$

in which y is a vector of response variables (temperament traits), β is a vector of estimated fixed effects as described above, u and $\text{pe}$ are vectors of random breeding values and permanent environmental effects, e is a vector of residuals, and X and Z are incidence matrices relating observations in y to values in $\text{β}, u,$ and $\text{pe}$ The random vectors have expectations equal to vectors of 0, with variances

$$\text{Var}\left[\begin{array}{c}u\\ \text{pe}\\ e\end{array}\right]=\left[\begin{array}{ccc}G& 0& 0\\ 0& C& 0\\ 0& 0& R\end{array}\right]$$

in which $G=A{\text{σ}}_a^2$ (A is the numerator relationship matrix constructed with pedigree information and ${\text{σ}}_a^2$ is the breeding value variance); $C=I{\text{σ}}_c^2$$\text{I}$ is an identity matrix and ${\text{σ}}_c^2$ represents the permanent environmental variance); R=$I{\text{σ}}_e^2$ (${\text{σ}}_e^2$ represents the residual variance). Likelihood ratio tests never supported inclusion of the maternal additive genetic component or the maternal permanent environmental component for any trait.

Estimates of additive genetic variance and permanent environmental variance, and as proportions of the phenotypic variance, were obtained from these repeated measures single-trait analyses.

Random Regression Analyses

These models were built for each trait separately with this general form:

$$y=X\text{β}+Qu+Zpe+e,$$

in which y is a vector of observed traits, β is a vector of estimated fixed effects as described above, u and $\text{pe}$ are vectors of random regression coefficients for additive genetic and permanent environmental effects, and e is a vector of residuals. The incidence matrix X relates observations in y to elements of β The incidence matrix Q contains the age covariate and relates observations in y to the additive genetic random regression coefficients in u; this matrix includes additional columns corresponding to increasingly higher order random regressions. Observations in y are related to the random regression coefficients for permanent environment in $\text{pe}$ by the incidence matrix Z, which contains age as a covariate. The vector e contains residuals. Expectations of the random vectors are all vectors of 0. The variance–covariance structure was

$$\text{Var}\left[\begin{array}{c}u\\ \text{pe}\\ e\end{array}\right]=\left[\begin{array}{ccc}A\otimes G& 0& 0\\ 0& \text{I}\otimes C& 0\\ 0& 0& R\end{array}\right],$$

in which A is the additive genetic numerator relationship matrix, G represents the covariance matrix of the additive genetic regression coefficients with order equal to the polynomial modeled, I is an identity matrix with order equal to number of animals with repeated records in the variance term for pe, and equal to the number of records in the variance term for e The matrix C is the covariance matrix of the permanent environmental regression coefficients. As before, $R=I{\text{σ}}_e^2$. There were 4,891 animals in the A matrix, including 118 sires and 1,292 dams.

The strategy for determining random regression models was similar to that described by Speidel et al. (2016). For each trait, random regression modeling used the fixed effects determined from the repeated measures models. The maximum number of records for individual animals in these data was 5. Those roughly corresponded to 1 mo before weaning, weaning (approximately 7 mo of age), 1 mo after weaning, 2 mo after weaning, and 1 yr of age. Therefore, the maximum possible polynomial regression supported by these data would be of order 4. Order is one less than the number of regression coefficients estimated and consists of the covariate raised to each power; for example, an order of 4 indicates age (in this case) raised to these powers: 0, 1, 2, 3, and 4.

Two random regressions of traits on age using orthogonal normalized Legendre polynomials (first suggested for this kind of use by Kirkpatrick et al., 1990) for age at the time of record were modeled for additive genetic and permanent environmental effects in models for each calf temperament trait. Model building was initiated with the order of the additive genetic random regression equal to 1 (i.e., an intercept and one linear covariate fitted). Speidel et al. (2016) reported that inclusion of the permanent environmental random regression component models the covariance of residuals and was preferred for random regression of days of age on weight rather than distinct residual error categories associated with measurement times. The random regression models of the present study included fixed regressions of trait on age using orthogonal Legendre polynomials, and these were equal to the order of the random additive genetic regression (Gilmour, 2009, as cited by Speidel et al., 2016). The order of this fixed regression was increased until the partial F-statistic (Gilmour, 2009, as cited by Speidel et al., 2016) of the highest coefficient was not significant.

After the fixed regression order was determined, while maintaining the order of the polynomial random regression for permanent environmental effects, the order of the polynomial random regression for additive genetic effects was increased by 1. Likelihood ratio tests of the higher order (2 times the absolute difference of log-likelihoods of nested models as a χ² with degrees of freedom equal to the difference in number of parameters estimated) were then conducted until the next higher order was not significant.

Subsequently, the order of the permanent environmental polynomial random regression was increased by 1. The order of the additive genetic polynomial random regression was reset to 1. All of the procedures for determination of the fixed and random regression orders described above were repeated for the higher order permanent environmental random regression. The addition of the higher order random regressions in each case was tested using likelihood ratio tests for random regression of either effect. Final models were concluded when the addition of terms was not significant. The maximum permissible order of any regression was 4.

The numbers of animals and records analyzed are reported in Table 2. Subsets of data were used for random regression analyses. That is, all records from animals that had fewer than the order of the polynomial modeled +1 were removed from analyses. For example, in a linear random regression analysis, all animals that had less than two records were removed from the data. The pedigree information included in the random regression analyses was limited to the subsets of the overall pedigree that corresponded to the animals with records in the random regressions.

Table 2.

Summary statistics from data used in random regression analyses for temperament traits

	Linear1			Quadratic2
	PS3	EV	TS	PS	EV	TS
Total records	9,831	10,099	9,798	9,831	10,099	9,798
Total animals	3,922	4,004	3,906	3,922	4,004	3,906
Records analyzed	8,070	8,373	8,048	6,758	6,988	6,740
Animals with records	2,165	2,282	2,160	1,508	1,588	1,505
Mean	2.83	2.61	2.709	2.84	2.59	2.71
SD	1.012	1.108	0.92	1.001	1.104	0.911
Minimum	1	0.22	0.61	1	0.22	0.61
Maximum	5	6.674	6.527	5	6.671	6.118
Age (d)
Mean	242.61	243.34	242.67	250.7	251.06	250.74
SD	67.198	68.611	67.216	69.099	70.535	69.095

¹All records of animals with less than two records were removed for linear random regression analyses.

²All records of animals with less than three records were removed for quadratic random regression analyses.

³PS = pen score, a subjective measure of temperament, in which reactions of an individual calf to a constant experienced evaluator within a pen of three to five calves are scored on a scale of 1 to 5 (1 = calm, 5 = excitable). EV = exit velocity, an objective measure of temperament, defined as the rate (m/s) in which a calf travels 1.83 m upon immediately exiting a squeeze chute. TS = temperament score, numerical average of pen score and exit velocity.

RESULTS AND DISCUSSION

Record summaries for the random regression analyses in Table 2 are limited to polynomials of orders 1 and 2, because increasing the random regression polynomials to order 3 was never appropriate, as log-likelihood values decreased.

Fixed Effects

Fixed effects were determined using the repeated records model. Although the primary intent of their inclusion was to adjust for those effects in these data, Table 3 summarizes that information as modeled. Probability values of the effects from repeated records analyses were not always identical when modeled in random regression analyses, but were similar. No fixed effect moved from inclusion to noninclusion model status (or vice versa) in repeated records and random regression analyses. Contemporary group was a highly significant component of all models (P < 0.001). Such differences are expected, due to known differences in calf temperament attributed to variability from year to year and season to season. The covariate for proportion of B. indicus in the calf indicated a strong positive relationship (regression coefficients were 0.41 ± 0.2, 0.85 ± 0.21, and 0.57 ± 0.18, for PS, EV, and TS, respectively; P < 0.01) with each calf temperament trait (greater proportions of B. indicus were associated with worse, larger, measures of temperament). This was consistent with all earlier comparisons of Brahman and Brahman-crossbreed types with British breeds (Fordyce et al., 1988; Riley et al., 2010; Chase et al., 2017). Alternatively, the covariate of proportion of B. indicus in dams was not influential for any calf temperament trait (P > 0.29) in this study. The Brahman maternal effect was influential on temperament of heifers produced in a diallel mating design (Riley et al., 2010). These results for modeling B. indicus may be due to the contribution of B. indicus influence by sire in calves in these data. Because of potential collinearity, these two covariates were confirmed independently, that is, without the presence of the other in the model, and similar significance levels were observed. Increasing calf age in days was associated with lower values (calmer temperaments) for all temperament traits (–0.001 ± 0.0002, –0.002 ± 0.0001, –0.002 ± 0.0001, for PS, EV, and TS, respectively; P < 0.001). Burdick et al. (2011) reported increased EV as suckling Brahman calves aged to weaning. Later, Schmidt et al. (2014) reported increased EV until weaning followed by a slight decrease with increasing ages. Such results may be due to an inverse relationship of PS, EV, or TS with BW in cattle; that is, the greater body mass in heavier cattle may cause them to exit the squeeze chute at a slower rate; this was first noted by Elzo et al. (2009). A similar inverse relationship of EV with BW was observed by Riley et al. (2010) in heifers between the ages of 7 and 19 mo, but the significance of that covariate may have been due to the pregnant status of most of the heifers in that study in latter months.

Table 3.

Least squares means for significant fixed effects (repeated measures analyses)

	Calf traits1
	PS	EV	TS
Dam age
2- and 3-yr olds	2.48 ± 0.07b	2.52 ± 0.06b	2.52 ± 0.05c
4-yr olds	2.64 ± 0.08a	2.75 ± 0.07ab	2.73 ± 0.06b
5-yr olds and older	2.72 ± 0.06a	2.85 ± 0.06a	2.81 ± 0.05a
Calf sex
Bulls	2.45 ± 0.06c	2.57 ± 0.06c	2.54 ± 0.06c
Steers	2.58 ± 0.07b	2.68 ± 0.06b	2.66 ± 0.05b
Heifers	2.79 ± 0.06a	2.87 ± 0.06a	2.85 ± 0.05a
Breed type2
Crossbred calves	2.70 ± 0.05a	2.67 ± 0.053	2.72 ± 0.053
Purebred calves	2.52 ± 0.09b	2.60 ± 0.09	2.59 ± 0.08

¹PS = pen score, a subjective measure of temperament, in which reactions of an individual calf to a constant experienced evaluator within a pen of three to five calves are scored on a scale of 1 to 5 (1 = calm, 5 = excitable). EV = exit velocity, an objective measure of temperament, defined as the rate (m/s) in which a calf travels 1.83 m upon immediately exiting a squeeze chute. TS = temperament score, numerical average of pen score and exit velocity.

²Because of the large numbers of breeds represented in the research population, breed type in calves was investigated as fixed effects with the levels listed in the table.

³The effect of breed type indicated no differences (P > 0.2) between purebred and crossbred calves for EV and TS.

^a,b,cWithin traits and effects (separated by empty lines in table), means that do not share a common superscript differ (P < 0.05).

Examination of unadjusted means and preliminary analyses showed minimal differences between 2- and 3-yr-old dams, and minimal differences between categories of dams 5 yr of age or older. Therefore, the effect of dam age was modeled as three levels (young cows 2 and 3 yr of age, 4-yr olds, and 5 yr or older). Dam age (P < 0.001 for all traits, Table 3) categories indicated that calves born to older cows often had greater, more excitable, temperaments relative to those born to younger dams. These results are in contrast to reports among purebred Brahman cattle that calves born to very young cows had greater PS (Schmidt et al., 2014). Riley et al. (2014) reported no effect of dam age on temperament measures approximately 1 mo after weaning in crossbred calves. No differences in calf PS were noted due to age of their dams, but those calves born to cows from 5 to 9 yr of age had slower exit velocities (Chase et al., 2017). All temperament variables in the present study were larger in females relative to males (Table 3), which is consistent with the vast majority of literature on temperament in cattle (Voisinet et al., 1997; Riley et al., 2014; Chase et al., 2017). An exception is that the effect of calf gender was not detected in temperament traits of Brahman calves (Schmidt et al., 2014). Crossbred calves in the present study had larger (P = 0.03) PS than purebreds (Table 3). This may be due to the majority of the purebreds in these data being British and the majority of crossbreds being B. indicus-influenced; however, no interactions of the terms representing breed type were detected (P > 0.3). Differences attributable to purebred vs. crossbred cows were not included in final models (P > 0.06) of any trait.

Estimates of Genetic Parameters—Repeated Measures

Estimates of genetic parameters for the three temperament traits from repeated measures analyses are shown in Table 4 from all data and from the subsets of data used in random regression analyses, that is, only from cattle that had three or more records. The estimates of heritability ($h^2$) were lower than those reported for Brahman (Schmidt et al., 2014) or Nellore-Angus crosses (Riley et al., 2014), but were similar to most included in the review by Adamczyk et al. (2013). The estimates of permanent environmental variance as a proportion of the phenotypic variance (c²) in Table 4 were of similar magnitude to narrow sense heritability estimates; all were less than 0.35 of phenotypic variance and differences ranged from 0.01 to 0.06. Permanent environmental variance as a proportion of the phenotypic variance ranged from 0.3 to 0.36 in the present study; Prayaga and Henshall (2005) estimated a similar value (0.25) for permanent environmental variance as a proportion of the phenotypic variance in evaluation of flight time (equivalent to the denominator of EV; i.e., elapsed time in seconds).

Table 4.

Genetic parameters of temperament estimates¹

Effect2	PS3		EV		TS
	All	Subset	All	Subset	All	Subset
${\text{σ}}_a^2$	0.240	0.313	0.305	0.266	0.238	0.263
${\text{σ}}_c^2$	0.321	0.288	0.301	0.352	0.260	0.272
${\text{σ}}_p^2$	0.945	0.958	1.01	1.017	0.710	0.748
$h^2$	0.26 ± 0.03	0.33 ± 0.05	0.30 ± 0.03	0.26 ± 0.04	0.34 ± 0.03	0.35 ± 0.05
$c^2$	0.35 ± 0.03	0.30 ± 0.04	0.30 ± 0.03	0.35 ± 0.03	0.37 ± 0.03	0.36 ± 0.05

¹All: parameters were estimated from repeated records analyses using all data. Subset: For comparison to random regression results, parameters were estimated from repeated record analyses that included only the data for each trait used in the quadratic random regression analyses (animals with less than three records were not included).

² ${\text{σ}}_a^2$, ${\text{σ}}_c^2$, ${\text{σ}}_p^2$, $h^2$ and $c^2$ represent estimates of additive genetic variance, permanent environmental variance, phenotypic variance, narrow sense heritability, and permanent environmental effects as a proportion of the phenotypic variance, respectively.

³PS = pen score, a subjective measure of temperament, in which reactions of an individual calf to a constant experienced evaluator within a pen of three to five calves are scored on a scale of 1 to 5 (1 = calm, 5 = excitable). EV = exit velocity, an objective measure of temperament, defined as the rate (m/s) in which a calf travels 1.83 m upon immediately exiting a squeeze chute. TS = temperament score, numerical average of pen score and exit velocity.

Random Regression

Pen score.

The sequence of modeling steps began with estimation of a fixed regression on Legendre polynomials of age, while the random regressions representing additive genetic and permanent environmental effects were set at an order of 1 (intercept and linear covariate). The order of the fixed regression on days of age was supported to an order of 2 (P < 0.001), that is, fitting an intercept, linear, and quadratic coefficients, but no higher (P = 0.99). Then, while holding the fixed regression at that order (2), increasing the orders of first the additive genetic random regression and then the permanent environmental random regression to 2 were highly significant, and within addition of each of those random regressions, attempts to increase the order of the fixed regression on days of age to 3 were not supported (P > 0.73). Increasing the random regressions to order 3 (intercept, linear, quadratic, and cubic covariates) was not merited, as the log-likelihood values decreased for each.

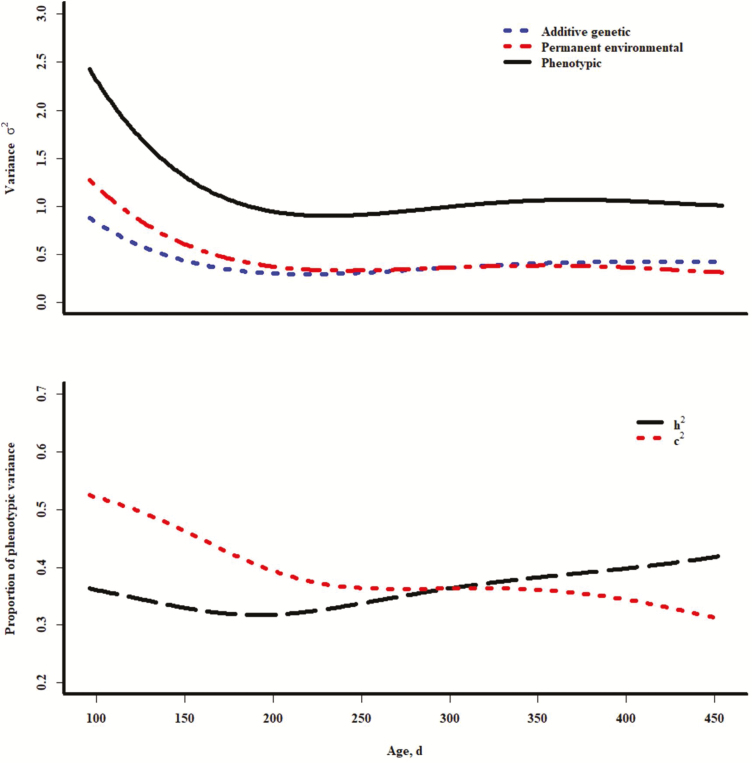
Estimates of variance from the best model (quadratic fixed and random regressions) are shown in Table 5. The SE for covariance terms of the intercept with either linear or quadratic estimates of both the additive genetic and permanent environmental random regressions was large. There were low correlations between coefficients of the intercept with either linear or quadratic terms of either permanent environmental or the additive genetic polynomials (ranged from –0.12 to 0.06). This differed from results of early implementations of this methodology in growth of cattle (Meyer, 2001b). However, the estimates of the correlation of the linear and quadratic coefficients in this study were strong and negative (–0.93 and –0.85 for additive genetic and permanent environmental regressions, respectively). The estimates of variance for the intercept were large, which was noted in other work (Meyer, 2001b). Plots of curves representing variances, narrow sense heritability (i.e., the ratio of the additive genetic and phenotypic variances that were estimated by evaluation of the random regression function at ages represented within the data), and permanent environmental variance as a proportion of the phenotypic variance across age in days within the limits of the project data (method previously demonstrated by Kirkpatrick et al., 1990) are shown in Figure 1. These plots suggest that variances and estimates of h² and c² at younger ages are initially larger than those estimates from repeated measures models (Table 4). Heritabilities decrease with age until approximately 200 d of age where the level is about the same as that from the repeated measures model. Estimates of heritability then increase and the permanent environmental effects as a proportion of the phenotypic variance decrease with age, and ultimately they are close to those estimated from the repeated measures analyses. Others have observed larger genetic variances on the extremes of the data ranges, which could be a consequence of using Legendre polynomials in the random regression (Schaeffer and Jamrozik, 2008; Schaeffer, 2016). However, multiple types of covariance functions will generate such fluctuations of parameters at those extremes (Mookprom et al., 2017). Erratic estimates at covariate boundaries may intensify with higher order polynomials (Meyer, 2001a). In the present study, the curve suggests that variances increase slightly after 300 d of age. Estimates of h² and c² suggest large repeatability of this trait, and therefore, additional records may have lower value for prediction purposes.

Table 5.

Estimates of residual variance and variances of coefficients of regression on Legendre polynomials of age for temperament traits¹

Component	PS2		EV		TS
	Estimate	SE	Estimate	SE	Estimate	SE
Residual	0.272	0.0068	0.322	0.0075	0.155	0.0039
Permanent environmental
Intercept	0.578	0.0850	0.768	0.0776	0.548	0.0700
Cov (intercept, linear)	–0.047	0.0418	0.043	0.0354	0.042	0.0258
Linear	0.269	0.0424	0.118	0.0302	0.135	0.0301
Cov (intercept, quadratic)	–0.018	0.0352			–0.042	0.0244
Cov (linear, quadratic)	–0.103	0.0266			–0.020	0.0156
Quadratic	0.056	0.0283			0.012	0.0168
Additive genetic
Intercept	0.620	0.1150	0.466	0.0970	0.522	0.0944
Cov (intercept, linear)	0.034	0.0514	–0.0004	0.0445	–0.005	0.0376
Linear	0.147	0.0437	0.205	0.0383	0.129	0.0296
Cov (intercept, quadratic)	0.004	0.0424	–0.023	0.0249	0.018	0.0283
Cov (linear, quadratic)	–0.074	0.0258	–0.106	0.0185	–0.073	0.0173
Quadratic	0.045	0.0231	0.066	0.0187	0.045	0.0152

¹Estimates for PS and TS are from a quadratic random regression model on Legendre polynomials for both permanent environmental and additive genetic effects. Estimates for EV were from a model that included a linear random regression of permanent environmental effects on Legendre polynomials of age and a quadratic random regression of additive genetic effects on Legendre polynomials of age.

²PS = pen score, a subjective measure of temperament, in which reactions of an individual calf to a constant experienced evaluator within a pen of three to five calves are scored on a scale of 1 to 5 (1 = calm, 5 = excitable). EV = exit velocity, an objective measure of temperament, defined as the rate (m/s) in which a calf travels 1.83 m upon immediately exiting a squeeze chute. TS = temperament score, numerical average of pen score and exit velocity.

Figure 1.

Plots of variance components for pen score across age (upper) and plots of heritability in the narrow sense and permanent environmental variance as a proportion of the phenotypic variance; all results from quadratic random regression models.

Exit velocity.

Beginning with linear random regressions (order 1) on days of age for permanent environmental effects and for additive genetic effects, the fixed linear regression on age was highly significant. However, increasing the order of this fixed regression to 2 was not supported (P = 0.89). Then a quadratic additive genetic random regression on age was fitted for the component, while maintaining a linear permanent environmental random regression. Comparison of log-likelihood values of the random regression models strongly favored quadratic additive genetic random regression (P < 0.001). Increasing the order of the permanent environmental random regression was not supported, because the log-likelihood of this model decreased relative to that of the linear permanent environmental/quadratic additive genetic model. Increasing the order of the fixed regression on days of age was not warranted (P = 0.9). Modeling of mature cow weight by Arango et al. (2004) required a larger order for the permanent environmental random covariate than for the additive genetic random covariate. Cubic random regressions for additive genetic effects resulted in decreases in log-likelihood values. Estimates of random regression coefficients are presented in Table 5.

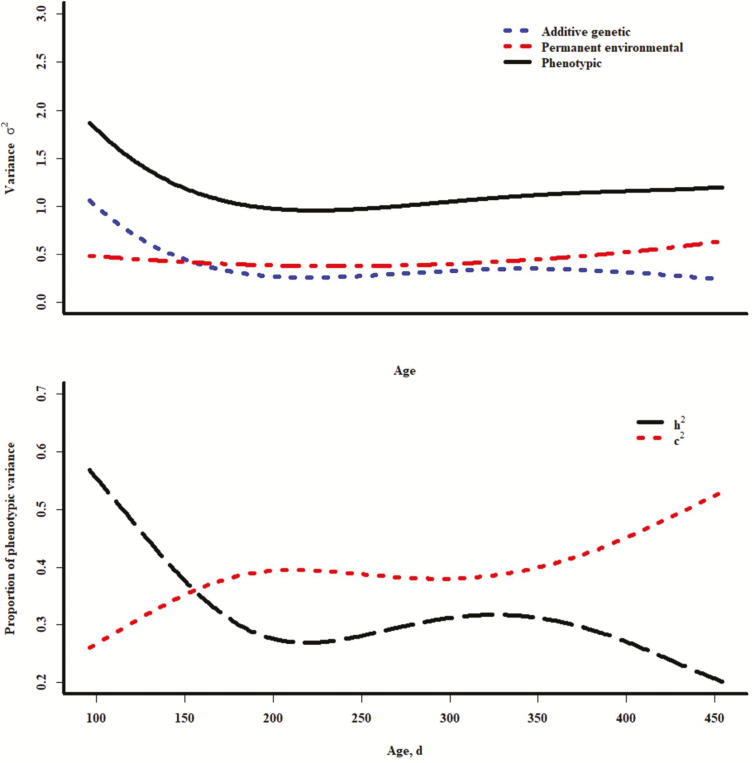
Curves representing variances and parameter estimates across age represented in these data are shown in Figure 2. The greatest values for the additive genetic and phenotypic variances for EV were at younger ages, and the permanent environmental component appeared to slightly increase at older ages. Although lower than the estimates from the repeated records models at young ages (Table 4), very notable in these curves was the increasing permanent environmental variance as a proportion of phenotypic variance, accompanied by an ultimate decrease in heritability with increasing age. From 200 to nearly 400 d of age, estimates of heritability appeared to be similar in magnitude to the estimates in Table 4 from repeated records models. Similar trends for additive genetic and permanent environmental variances as a proportion of phenotypic variance were reported for BW in pigs (Huisman et al., 2002). Arango et al. (2004) reported decreasing influence of permanent environmental effects and increasing additive genetic effects for mature cow body weights over time. Additive genetic and permanent environmental variances both increased in random regression analyses of observed days to weight in fed cattle (Speidel et al., 2016), and estimates of heritability for BW in quail increased with age (Karami et al., 2017). The present study indicated increasing c² and decreasing h² over time, suggesting an increasing influence of environmental and decreasing relative influence of additive genetic effects on EV with increasing age.

Figure 2.

Plots of variance components for exit velocity across age (upper) and plots of heritability in the narrow sense and permanent environmental variance as a proportion of the phenotypic variance; results from models with quadratic additive genetic random regression and linear permanent environmental random regression.

Temperament score.

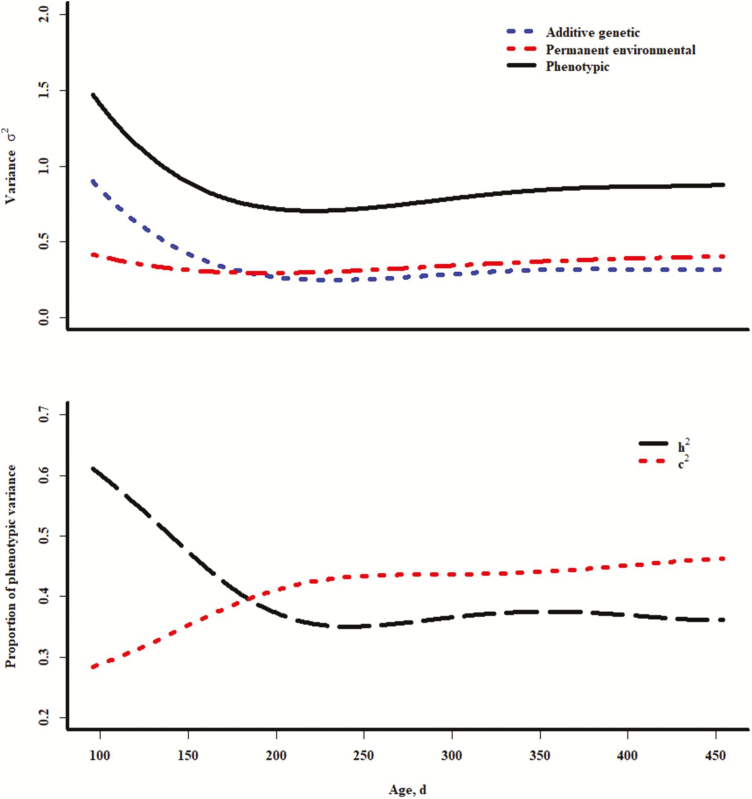
Within linear random regressions on Legendre polynomials of age for additive genetic and permanent environmental effects, the order of the fixed regression on days of age was best modeled as order 2 (P < 0.001). The cubic term was not appropriate (P = 0.99). Subsequently, quadratic random regressions on age were highly significant for additive genetic and permanent environmental effects. Within those regressions (order 2 for both additive genetic and permanent environmental random regressions), the quadratic fixed regression on age was preferred (P = 0.02), as a cubic fixed regression was not significant (P > 0.2). Log-likelihood values were not significantly improved (P > 0.31) by increasing the order of either random regression beyond 2. Estimates of variance of coefficients are shown in Table 5. Although a function of both PS and EV, results for TS may more closely resemble those of EV. Curves in Figure 3 show larger additive genetic, permanent environmental, and phenotypic variances at the younger compared with the older ages in these data. Similar to results for EV, the permanent environmental component as a proportion of phenotypic variance was initially lower than estimates from the repeated records models, but appears to show a relative increase with age. Estimates of heritability were high at younger ages and decreased to levels similar to those from the repeated records models by approximately 250 d of age. These results suggest that environmental influence at least partially overrides additive genetic influence over time, which may be as a consequence of exposure to accumulating environmental stimuli.

Figure 3.

Plots of variance components for temperament score across age (upper) and plots of heritability in the narrow sense and permanent environmental variance as a proportion of the phenotypic variance; all results from quadratic random regression models.

Dynamics of Components of Variance for Calf Temperament Accompanying Age

Changes in the variance components and associated parameters estimated by the random regression models for any of these temperament traits could occur as a result of increased sample variances at older ages. However, that does not seem likely, as variances (represented as a function of SD) of records that correspond roughly with records taken at 28 d before weaning, weaning, 28 and 56 d postweaning, and 1 yr of age increased substantially only for EV (Table 6). The permanent environmental effects from analyses of EV and TS appear to accumulate across time, particularly with repeated exposure to data collection. Additive genetic effects appear to be more influential early in life, becoming less over time as permanent environmental effects accumulate. The results from analyses of PS were opposite of this; that is, $h^2$ increased and $c^2$ decreased with increases in age. As a measure of temperament, PS appears to involve more direct human contact than EV. Pen score may more represent a very distinct component of temperament. It may be more reflective of fear, and acclimation to conditions of PS may be slower than for EV. Such acclimation to conditions seems natural from day-to-day observations of cattle exposed to repeated processing. Peixoto et al. (2016) reported a negative relationship for behavioral reactivity (mechanical measurement of movement while confined in a scale box) with age, that is, less movement was associated with older ages in B. indicus (Guzerat) dairy cows. Neither EV nor chute score (subjective score representing amount of movement when confined to a scale box) decreased with monthly measurements on heifers (Riley et al., 2010). Exit velocity increased in calves from weaning to 24 h postweaning and decreased at 72 h postweaning; PS from the same calves decreased (improved) at each of those measurement times (Chase et al., 2017). In that work, transported steers had lower EV at 4 wk after long -distance transportation than measurements at the time of shipment up to 2 wk after long-distance transportation. The content or characterization of the repeated exposure or handling might affect acclimation in different ways, for example, rough, traumatic handling could be detrimental (Petherick et al., 2009; Peixoto et al., 2016) and appear to have an effect opposite of acclimation. In such cases, the partitioning of variance might yield unexpected results.

Table 6.

Unadjusted means and SD for age and temperament traits by time of record¹

	Age (d)		PS		EV		TS
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Weaning − 28 d	183.32	25.26	2.98	1.06	2.74	1.09	2.86	0.94
Weaning	217.38	29.34	2.84	1.00	2.69	1.04	2.77	0.88
Weaning + 28 d	243.76	26.78	2.81	0.98	2.66	1.06	2.74	0.89
Weaning + 56 d	267.36	26.24	2.73	0.99	2.62	1.13	2.65	0.91
Yearling	387.52	31.13	2.80	1.01	2.32	1.17	2.51	0.95
Grand total	239.56	63.52	2.84	1.01	2.64	1.09	2.74	0.91

¹PS = pen score, a subjective measure of temperament, in which reactions of an individual calf to a constant experienced evaluator within a pen of three to five calves are scored on a scale of 1 to 5 (1 = calm, 5 = excitable). EV = exit velocity, an objective measure of temperament, defined as the rate (m/s) in which a calf travels 1.83 m upon immediately exiting a squeeze chute. TS = temperament score, numerical average of pen score and exit velocity.

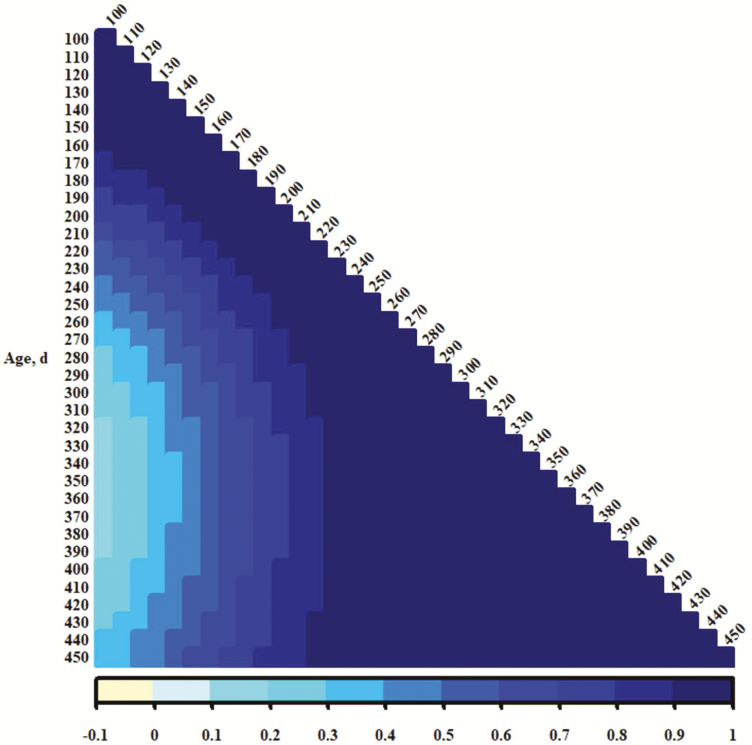
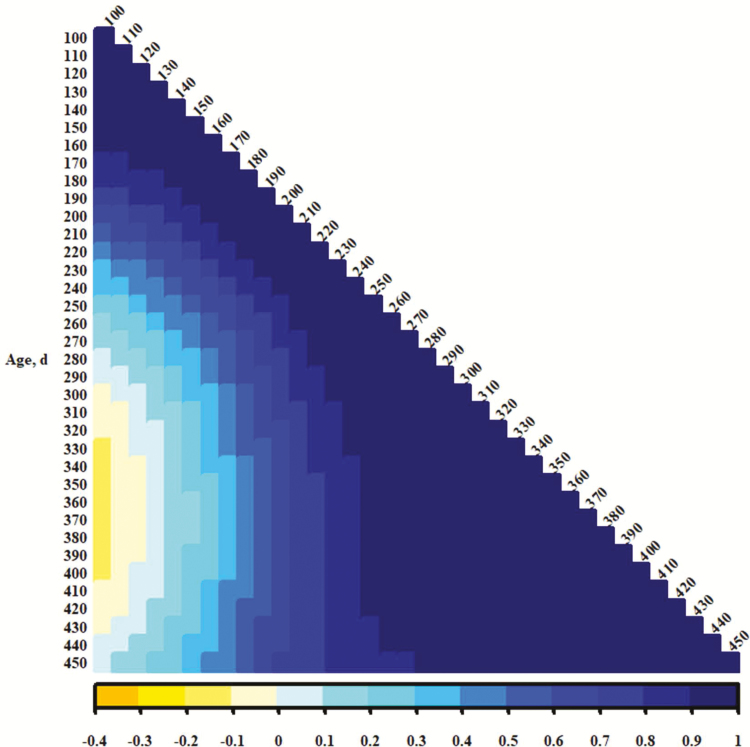
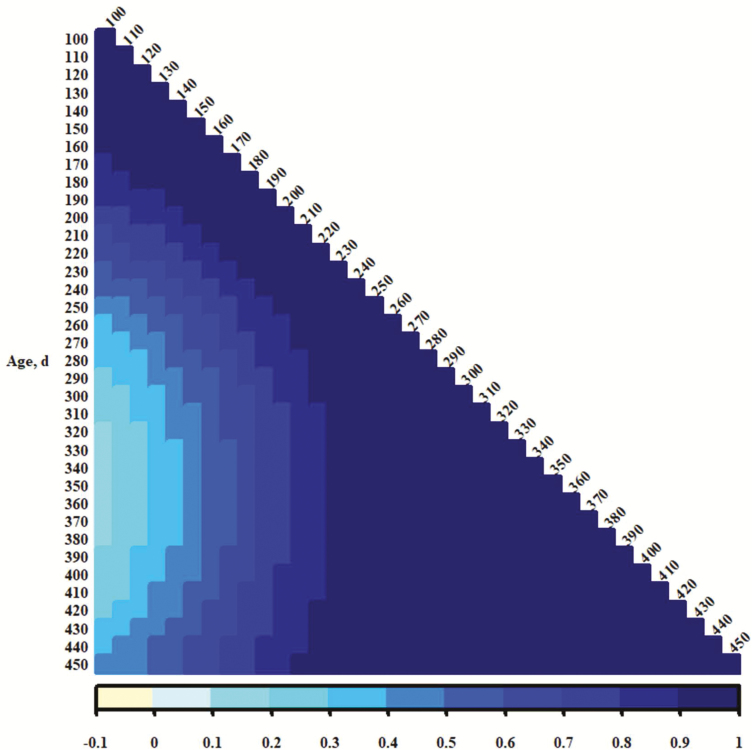
The genetic correlations between traits from different days of age (Figures 4, 5, and 6 show heat maps representing additive genetic correlation coefficients for PS, EV, and TS, respectively) suggest that temperament traits recorded at young ages were distinct from those recorded after weaning (250 d) to over 400 d. Correlation coefficients for PS or TS corresponding to those were near 0; some for EV (Figure 5) were negative. This could be indicative of a specific time period in which distinct genes or sets of genes are activated to influence temperament. It seems reasonable that maternal additive genetic or maternal permanent environmental influence is important in calf phenotypes recorded preweaning or in the proximity of weaning, although neither was detected in these analyses. An alternative is that maternal presence contributes to accumulation of permanent environmental effects, and those become substantial across time. Genes influencing temperament may act additively and constant across time (the heavy influence and heritability of the intercept terms in the present study may support this notion), but permanent environment accrues and becomes the more influential component of phenotypic variance. Since temperament records are easily accumulated, an estimate of producing ability (Lush, 1945; all genetic components and permanent environment, as described by Falconer and Mackay, 1996) might be an effective predictor of merit. However, a single evaluation at a young age may be appropriate for estimation of breeding value, although the higher additive genetic variances at younger ages may be a consequence of modeling. A final caveat for interpretation here is that if performance is worse for those cattle with poor (more excitable) temperaments, as is commonly assumed (e.g., Tulloh, 1961; Voisinet et al., 1997; King et al., 2006; Cafe et al., 2011), it could be expected that there would be negative selective pressure on their presence with increasing age. This might result in less phenotypic variance for temperament at older ages and be more of an issue for records in mature cows measured at times much later in life.

Figure 4.

Color representations (per scale at bottom of figure) of additive genetic correlation between pen scores from different days of age.

Figure 5.

Color representations (per scale at bottom of figure) of additive genetic correlation between exit velocities from different days of age.

Figure 6.

Color representations (per scale at bottom of figure) of additive genetic correlation between temperament scores (average of pen score and exit velocity) from different days of age.

The breed-type component of this population may influence these results in unknown ways. The majority of cattle with records were B. taurus–B. indicus crosses. Although heterosis may be important (yet unfavorable) for temperament traits (Chase et al., 2017), crossbred Brahman have also been reported to have similar temperament measurements as Brahman cattle (Riley et al., 2010; Schmidt et al., 2014; Chase et al., 2017). There was no convenient simple parameterization of breed type of calves and their dams in these data (and of course the two are functions of each other). When one of the breeds involved in temperament evaluation is Brahman, it becomes especially important. Most of the introduction of Brahman ancestry in animals in this project was more subtle, as through the use of Brangus bulls. These factors could have influenced breed-type effects on temperament in unrevealed manners.

CONCLUSIONS

Estimates of heritability were similar to those previously reported for temperament in beef cattle, which supports assertions that selection programs could be effectively implemented for these traits in beef cattle breeding programs. To our knowledge, this is the first report of genetic parameters of temperament in beef cattle estimated across time (as a calf ages) with random regression analyses. Random regression analyses of temperament in cattle seemed to emphasize the increasing influence of permanent environmental effects and the decreasing influence of additive genetic effects across time as the bovine matures. This suggests inherited temperament traits are predictable and observable in early life, but may become gradually overridden as calves age, maybe due to accumulating exposure to environmental stimuli.