Estimation of direct and maternal genetic parameters for individual birth weight, weaning weight, and probe weight in Yorkshire and Landrace pigs

Abstract

As a result of selecting for increased litter size, newborn piglets are being born lighter and have a lower chance of survival. Raising fewer pigs to market weight would have a negative impact on the industry and farmer profitability; thus, understanding the genetics of individual growth performance traits will determine whether these traits will play an important role in pig breeding schemes. This study aimed to estimate genetic parameters for individual birth weight (BW), weaning weight (WW), and probe weight (PW) in Canadian-purebred Yorkshire and Landrace pigs. PW is a live weight taken at the time of the ultrasound measurements, when pigs weigh about 100 kg. Data were collected from 2 large and related breeding herds from 2003 to 2015. Four linear animal models were used, which included the following: Model 1—direct additive genetic effect; Model 2—direct additive genetic and maternal genetic effect; Model 3—direct additive genetic and common litter effect; and Model 4—direct additive genetic, maternal genetic, and common litter effect. The model which included all 3 random effects (Model 4) was determined to be the best fit to the data. Low to moderate direct heritability estimates were observed as follows: 0.15 ± 0.03 for BW, 0.04 ± 0.01 for WW, and 0.33 ± 0.03 for PW for the Yorkshire breed; and 0.05 ± 0.01 for BW, 0.01 ± 0.01 for WW, and 0.27 ± 0.03 for PW in the Landrace breed. As expected, the direct heritability estimates increased with age as a result of decreased maternal influence on the trait. Bivariate animal models were also used to estimate genetic and environmental correlations between traits. Strong direct genetic correlations were observed between BW and WW in both breeds. Based on the estimates of genetic parameters, individual BW could be evaluated and considered in breeding programs aiming to increase BW and improve subsequent performance. Different selection emphasis could also be applied on direct and maternal additive genetic effects on BW to optimize the breeding programs and improve selection efficiency.

INTRODUCTION

The profitability of the pig industry is largely associated with efficient growth performance. Early growth performance is largely dependent on the individual piglet’s birth weight (BW), as BW is directly correlated with piglet survival, behavior, and weight gain (Caceres et al., 2001; Fix et al., 2010; Muns et al., 2013). Improving the early growth performance of a piglet could increase profit for producers for several reasons, including reducing the need for management interventions and decreasing days to market (Beaulieu et al., 2010; Baxter et al., 2013). To make genetic progress for growth performance, it is crucial to understand the genetic control of indicator traits such as BW and weaning weight (WW). However, WW is typically overlooked by breeders and piglets are usually not individually weighed at weaning. Yet, breeding programs in other livestock species such as sheep and cattle are recording and selecting for individual BW and WW aiming to make genetic improvements in growth performance (Koots et al., 1994; Assan et al., 2002). Genetic parameters for individual BW and WW in pigs have been reported in countries such as Switzerland, Ghana, Japan, Belgium, and United States (Kaufmann, 2000; Darfour-Oduro et al., 2009; Tomiyama et al., 2010; Dufrasne et al., 2014; Jiao et al., 2014). However, to the best of our knowledge, no estimates of variance components for direct and maternal effects on individual BW and WW have been reported for purebred Canadian pigs. Miar et al. (2014), however, evaluated BW, WW, nursery weight (~38 kg), and end weight (~110 kg) in 6,408 Canadian commercial crossbred pigs (Duroc × F1 Landrace × Yorkshire). Information on individual BW and WW might be valuable to breeders and commercial production systems for predicting the early growth performance of piglets and their probe weight (PW), which is a live weight, taken at the time of the ultrasound measurements, when pigs weigh about 100 kg, following national standards. Therefore, the objectives of this study were as follows: 1) to evaluate the importance of direct additive genetic effects, maternal additive genetic and permanent environmental effects, and common litter effects in the estimation of variance components for individual BW, WW, and PW; and 2) to estimate genetic correlations between these traits.

MATERIALS AND METHODS

Ethics Statement

No Animal Care Committee approval was necessary for the purposes of this study, as all information required was obtained from existing databases.

Phenotypes and Datasets

Phenotypes.

Piglet information from 2 large breeding herds in Quebec and Manitoba was provided by the Canadian Centre for Swine Improvement (CCSI, www.ccsi.ca; accessed May 12, 2018). Individual weights recorded from 2003 to 2015 were available for this study.

Datasets.

As the focus of this study was on maternal traits, the maternal breeds Yorkshire and Landrace were of primary interest. Due to the reduced number of individual WW available, 2 datasets were created for both the Yorkshire and Landrace breeds: 1) the CORE dataset and 2) the MERGED dataset.

• 1) CORE dataset: All animals in the CORE dataset had BW, WW, and PW records and consisted of 24,460 and 24,884 records for Yorkshire and Landrace breeds, respectively. Cross-fostering information was not available for these animals.

• 2) MERGED dataset: The MERGED dataset combines the core dataset with the animals with BW and PW records, but not individually weighed at weaning and those were not cross fostered. There were 151,101 BW and PW records and 24,460 WW records for the Yorkshire breed, whereas there were 122,133 records for BW and PW and 24,884 WW records for Landrace.

Both datasets (CORE and MERGED) were used for the following analyses. It was known that farms that record individual WWs record all pigs from a litter. Therefore, no selective recording was done and it was expected that the CORE dataset would provide unbiased estimates of genetic parameters for BW, WW, and PW. For assessing possible unknown selective recording, the MERGED dataset was also analyzed, which also included BW and PW records of animals not individually weighed at weaning and that were not cross fostered. As mentioned before, unfortunately cross-fostering information was not available for the farms that recorded individual WWs, so the effect of cross-fostering could not be modeled.

Descriptive statistics.

Data were edited using the PROC UNIVARIATE procedure of SAS 9.2 (SAS Institute, 2011). This procedure identified the inter-quartile range (IQR), the first quartile (Q1), and the third quartile (Q3) (Supplementary Table S1). Outliers were removed from the data using the IQR test as described by Lin and Sherman (2007). Outlier limits were set 50% further away than the IQR. Outliers were removed for 1) BW, WW, and PW; and 2) age of recording of BW, WW, and PW.

All of the statistical analyses performed were generated using SAS software Version 9.2 of the SAS System for Unix (SAS Institute, 2011). The PROC MEANS procedure was performed to determine the descriptive statistics of the variables in the datasets. The PROC UNIVARIATE procedure was then used to test BW, WW, and PW for the Yorkshire and Landrace breeds for a Gaussian distribution by calculating skewness and kurtosis.

Pedigree.

The pedigree consisted of 23 generations of ancestors, with a total of 1,140,696 animals and 54,291 parents. Of those parents, 8,003 were sires and 44,312 were dams. For all animals in the pedigree, 99.8% have both parents known, whereas 95% of the animals had no progeny. In the pedigree, 96% of the animals were inbred with an average inbreeding coefficient of 0.05. The pedigree was analyzed using the software package CFC (Sargolzaei et al., 2006).

Model Definitions

Models.

Four linear animal models excluding or including maternal additive genetic effect, common litter effect, or a combination thereof were used in the univariate analyses for BW, WW, and PW. The random terms in the models, besides the direct additive genetic effect (i.e. maternal additive genetic effect and common litter effect), were evaluated one by one to determine their effects on the estimation of variance components. The fixed effects in each of the models included sex (female or male for BW; female, male, or castrated male for WW and PW), age at recording (defined as a linear covariate for each trait), and contemporary group (herd, year, and season). Variance components and genetic parameters were estimated by fitting all models using the Restricted Maximum Likelihood (REML) procedure implemented in the software ASReml 4.0 (Gilmour et al., 2009). The models were described as follows:

Model 1: Animal model with a direct additive genetic effect:

$$\mathit{y}=\mathit{Xb}+{\mathit{Z}}_{\mathit{d}}{\mathit{a}}_{\mathit{d }}+\mathit{e},$$

Model 2: Animal model with a direct additive genetic effect and maternal genetic effect:

$$\mathit{y}=\mathit{Xb}+{\mathit{Z}}_{\mathit{d}}{\mathit{a}}_{\mathit{d }}+{\mathit{Z}}_{\mathit{m}}{\mathit{a}}_{\mathit{m }}+\mathit{e},$$

Model 3: Animal model with a direct additive genetic effect and common litter effect:

$$\mathit{y}=\mathit{Xb}+{\mathit{Z}}_{\mathit{d}}{\mathit{a}}_{\mathit{d }}+\mathit{Wc}+\mathit{e},\text{ and}$$

Model 4: Animal model with a direct additive genetic effect, maternal genetic effect and common-litter effect:

$$\mathit{y}=\mathit{Xb}+{\mathit{Z}}_{\mathit{d}}{\mathit{a}}_{\mathit{d }}+{\mathit{Z}}_{\mathit{m}}{\mathit{a}}_{\mathit{m }}+\mathit{Wc}+\mathit{e,}$$

where y is the vector of observations; $\mathit{X},{\mathit{Z}}_{\mathit{d}}, {\mathit{Z}}_{\mathit{m}}, \mathit{W}$ are known incidence matrices relating observations to fixed and random effects; $\mathit{b}$ is the vector of unknown fixed effects; ${\mathit{a}}_{\mathit{d }}$ is the vector of unknown random direct additive genetic effects; ${\mathit{a}}_{\mathit{m }}$ is the vector of unknown random maternal genetic effects; $\mathit{c}$ is the vector of unknown random nongenetic effects common to individuals born in the same litter (common litter effect); and $\mathit{e}$ is a vector of residuals. The models assumptions are as follows: $a_d|A,{\text{σ}}_d^2~\text{ N}(0,A{\text{σ}}_d^2)$ where A is the additive relationship matrix, ${\text{σ}}_d^2$ is the direct additive genetic variance; $a_m|A, {\text{σ}}_m^2~\text{ N}(0,A{\text{σ}}_m^2),$ where ${\text{σ}}_{m }^2$is the maternal genetic variance; $c|I, {\text{σ}}_c^2~\text{N}(0,I{\sigma }_c^2),$ where $I$ is an identity matrix, ${\text{σ}}_c^2$ is the common litter variance; and $\mathit{e}~\text{ N}(0,I{\text{σ}}_e^2),$ where ${\text{σ}}_e^2$is the residual variance. Distributions of the random effects in the univariate models were assumed as follows:

$$\text{Var}\left[\begin{array}{c}{a}_d\\ a_m\\ c\\ e\end{array}\right]=\left[\begin{array}{c}A{\sigma }_d^2 \mathit{A}{\sigma }_{dm} 0 0\\ \mathit{A}{\mathit{\sigma }}_{\mathit{dm}} A{\sigma }_m^2 0 0 \\ 0 0 I{\sigma }_c^2 0\\ 0 0 0I{\sigma }_e^2\end{array}\right],$$

where ${\text{σ}}_{dm}$ is the covariance between the direct and maternal genetic effects. The model shows that the direct and maternal genetic effects have a covariance structure depending on the genetic relationships, and there is a correlation between the direct additive genetic effect and maternal genetic effect. The common litter effect is independent of the other random effects and uncorrelated for different animals. Preliminary analyses also included the maternal permanent environmental effect in the models 2 and 4; however, this effect explained only a negligible proportion of the phenotypic variance, being removed from further analyses for sake of computation time.

Likelihood ratio test.

To determine the most suitable model for estimating the genetic parameters, the Log-likelihood values (LogL) for the 4 different models were compared. The chi-square test statistic ($X^2$) was used according to Bouwman et al. (2014) and was calculated as follows:

$$X^2 =–\text{2}\left({\text{LogL}}_{\text{reduced model}}–{\text{LogL}}_{\text{full model}}\right),$$

where LogL_{reduced model} is the log likelihood for a simpler model, LogL_{full model} is the log likelihood for a more complete model, and $X^2$ is distributed as a mixture of 2 chi-square distributions: $0.5x_{df,\text{α }}^2+ 0.5x_{0,\text{α}}^2$, where df is the degrees of freedom equal to the difference in number of parameters (random effects) fitted for the 2 models, and α is the level of significance set at 0.05. The chi-square distribution follows this distribution because likelihood ratio test (LRT) is testing the variance of the models with differing numbers of random effects, and the variance is bounded at zero (Self and Liang, 1987).

Estimating Variance Components

Variance components.

After estimating the variance components and genetic parameters for the 4 models, the most suitable one was chosen using the X² test statistic. After significance testing, Model 4 was determined to be the most suitable and was then used to estimate total heritability and genetic correlations within breed between each pair of growth traits using bivariate models. The fixed effects included sex, age in days at which the trait was recorded, and contemporary group; the random effects included direct additive genetic, maternal genetic, and common litter effects. Assumptions and estimates of the proportion of variance due to the random effects were calculated as shown above. The covariance structures of the random effects in the bivariate models were assumed as follows:

$$\text{Var}\left[\begin{array}{c}{a}_{d_1}\\ a_{d_2}\\ a_{m_1}\\ a_{m_2}\end{array}\right]=\left[\begin{array}{c} {\sigma }_{d_1}^2 {\sigma }_{d_{21}} {\sigma }_{d_1{m}_1} {\sigma }_{d_1{m}_2}\\ {\sigma }_{d_{12}} {\sigma }_{d_2}^2 {\sigma }_{d_2{m}_1} {\sigma }_{d_2{m}_2}\\ {\sigma }_{d_1{m}_1} {\sigma }_{d_2{m}_1} {\sigma }_{m_1}^2 {\sigma }_{m_{21}} \\ {\sigma }_{d_1{m}_2} {\sigma }_{d_2{m}_2} {\sigma }_{m_{12}} {\sigma }_{m_2}^2 \end{array}\right] \otimes A=G_0\otimes A.$$

$$\text{Var}\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]=\left[\begin{array}{cc} {\sigma }_{c_1}^2& {\sigma }_{c_{12}}\\ {\sigma }_{c_{12}}& {\sigma }_{c_2}^2\end{array}\right]\otimes I =C_0\otimes I.$$

$$\text{Var}\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]=\left[\begin{array}{cc} {\sigma }_{e_1}^2& {\sigma }_{e_{12}}\\ {\sigma }_{e_{12}}& {\sigma }_{e_2}^2\end{array}\right]\otimes I =E_0\otimes I.$$

where A is the additive genetic relationship matrix based on available pedigree information containing 1,140,696 animals; G₀ is a 4 × 4 direct additive genetic and maternal genetic variance-covariance matrix between traits; I is an identity matrix; and C₀ is a 2 × 2 common litter effect variance-covariance matrix between traits. Furthermore, ${\text{σ}}_{d_i}^2$ is a direct additive genetic variance for trait i, ${\text{σ}}_{m_i}^2$ is the maternal additive genetic variance for trait i, ${\text{€ σ}}_{d_i{m}_j}$is the additive genetic covariance between the direct additive genetic effect for trait i and maternal additive genetic effect for trait j, ${\text{ σ}}_{d_{ij }}$ is the additive genetic covariance between the direct additive genetic effects for trait i and trait j, ${\text{ σ}}_{m_{ij}}$ is the additive genetic covariance between the maternal additive genetic effects for trait i and trait j, ${\sigma }_{c_i}^2$ is the common litter variance for trait i, ${\text{ σ}}_{c_{ij }}$is the covariance between the common litter effect for trait i and trait j, ${\sigma }_{e_i}^2$ is the error variance for trait i, and ${\text{ σ}}_{e_{ij}}$ is the covariance between the errors for trait i and trait j. The common litter effect and residual effects were assumed independent of the other random effects within and across the traits.

Heritability.

Estimates of direct heritability $\left(h_{\mathit{d}}^2\right)$ maternal heritability $\left(h_{\mathit{m}}^2\right)$ and common litter effects $\left({\mathit{C}}^2\right)$ were calculated as ratios of estimates of direct additive genetic variance $({\text{σ}}_d^2)$ maternal additive genetic variance $\left({\text{σ}}_m^2\right)$ and common litter variance $\left({\text{σ}}_c^2\right)$ to the total phenotypic variance $\left({\text{σ}}_p^2\right)$ respectively. The significance of these estimates was tested using a Z-test with the null hypothesis that the estimates are equal to zero (α = 0.05).

The total phenotypic variance was calculated as follows:

$${\sigma }_p^2 ={\sigma }_d^2+{\sigma }_m^2+{\sigma }_{dm}+{\sigma }_c^2+{\sigma }_e^2,$$

Total heritability $(h_{\mathit{t}}^2)$ is a measure of the fraction of the selection differential that would be realized if selection was based on the phenotypic value of the offspring and were calculated as defined by Willham (1972):

$$h_t^2=\frac{{\sigma }_d^2+ 0.5{\sigma }_m^2+ 1.5{\sigma }_{dm}}{{\sigma }_p^2}.$$

RESULTS

For both Yorkshire and Landrace breeds, BW, WW, and PW did not substantially deviate from an expected normal distribution, having skewness and kurtosis within acceptable ranges, varying from −0.01 to 0.18, and −0.58 to 0.25, respectively, as illustrated in Figure 1 for Yorkshire breed.

Figure 1.

Histograms of the distribution of birth weight, weaning weight, and probe weight in the Yorkshire breed.

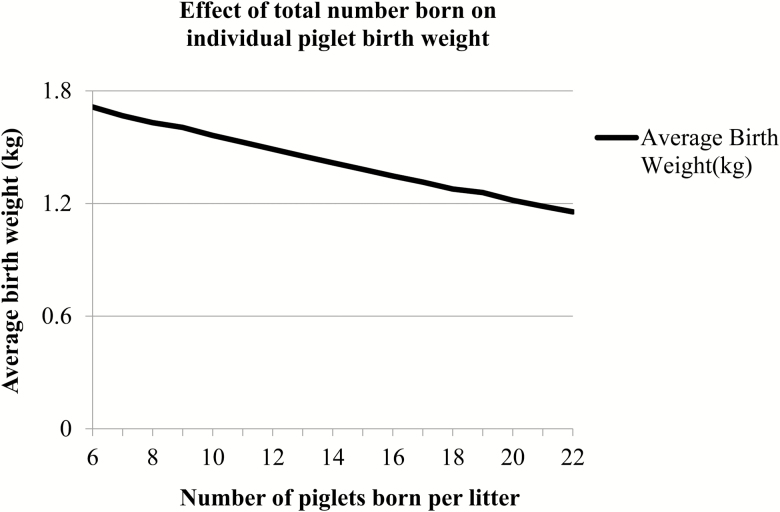
Figure 2 shows the relationship between the total number of piglets born per litter and the average piglet BW per litter. As the total number born increased from 6 piglets per litter to 22 piglets per litter, the average BW decreased 0.55 kg. Descriptive statistics for both breeds including mean, standard deviation (SD), and minimum and maximum for the weights and age traits from both datasets are presented in Table 1.

Figure 2.

Relationship between total number of piglets born per litter and the average individual birth weight within each litter size.

Table 1.

Descriptive statistics of the datasets used in this study

Trait1	N2	Mean3	SD4	Minimum	Maximum
CORE5 dataset—Yorkshire
BW (kg)	24,460	1.48	0.32	0.56	2.40
WW (kg)	24,460	5.06	1.15	1.70	8.26
PW (kg)	24,460	103.45	12.24	75.00	139.00
ageBW (d)	24,460	1	1	0	2
ageWW(d)	24,460	16	3	10	21
agePW (d)	24,460	151	13	124	183
MERGED6 dataset—Yorkshire
BW (kg)	151,010	1.45	0.31	0.48	2.40
WW (kg)	24,460	5.06	1.15	1.70	8.26
PW (kg)	151,010	102.18	13.55	75.00	150.00
ageBW (d)	151,010	1	1	0	2
ageWW(d)	24,460	16	3	10	21
agePW (d)	151,010	155	11	124	183
CORE dataset—Landrace
BW (kg)	24,884	1.52	0.32	0.48	2.40
WW (kg)	24,884	5.14	1.15	1.70	8.26
PW (kg)	24,884	102.49	13.00	75.00	139.00
ageBW (d)	24,884	1	1	0	2
ageWW(d)	24,884	15	3	10	21
agePW (d)	24,884	150	13	124	183
MERGED dataset—Landrace
BW (kg)	122,133	1.58	0.32	0.48	2.40
WW (kg)	24,884	5.14	1.15	1.70	8.26
PW (kg)	122,133	104.00	12.88	75.00	150.00
ageBW (d)	122,133	1	1	0	2
ageWW(d)	24,884	15	3	10	21
agePW (d)	122,133	153	11	124	183

¹BW = birth weight; WW = weaning weight; PW = probe weight; ageBW = age BW was recorded; ageWW = age WW was recorded.

²N = number of records.

³Mean = mean of the trait.

⁴SD = standard deviation of the trait.

⁵CORE = all animals have BW, WW, and PW records.

⁶MERGED = combines the CORE dataset with animals that have BW and PW recorded, but not individual WW.

When using either dataset and for both breeds, Model 4, which contained all 3 random effects (direct additive genetic, maternal genetic, and common litter effects), outperformed the other models based on the LRT statistic (data shown for CORE dataset in Table 2). According to LRT, the difference between each of the reduced models and full models tested was significant (α = 0.05, P < 0.0001). Therefore, the full model (Model 4) was determined to have the best fit to the data and was used in further analyses.

Table 2.

Log likelihood (LogL) values and likelihood ratio test (LRT) of comparable models in the Yorkshire and Landrace CORE datasets

Trait1	Model2	LogL3	Compared4	LRT5	df6	P-value
Yorkshire
BW	Model 1	7,223.8	1 vs. 4	1,985.8	2	<0.0001
	Model 2	7,674.8	2 vs. 4	1,083.8	1	<0.0001
	Model 3	8,130.2	3 vs. 4	173.0	1	<0.0001
	Model 4	8,216.7
WW	Model 1	−10,911.0	1 vs. 4	1,632.0	2	<0.0001
	Model 2	−10,571.2	2 vs. 4	952.4	1	<0.0001
	Model 3	−10,155.9	3 vs. 4	121.8	1	<0.0001
	Model 4	−10,095.0
PW	Model 1	−5,239.3	1 vs. 4	446.2	2	<0.0001
	Model 2	−5,172.2	2 vs. 4	312.0	1	<0.0001
	Model 3	−5,032.4	3 vs. 4	32.4	1	<0.0001
	Model 4	−5,016.2
Landrace
BW	Model 1	8,343.2	1 vs. 4	2,379.0	2	<0.0001
	Model 2	9,028.7	2 vs. 4	1,008.0	1	<0.0001
	Model 3	9,331.4	3 vs. 4	402.6	1	<0.0001
	Model 4	9,532.7
WW	Model 1	−10,300.2	1 vs. 4	1,691.2	2	<0.0001
	Model 2	−9,997.3	2 vs. 4	1,085.4	1	<0.0001
	Model 3	−9,531.2	3 vs. 4	153.2	1	<0.0001
	Model 4	−9,454.6
PW	Model 1	−5,823.0	1 vs. 4	607.6	2	<0.0001
	Model 2	−5,709.3	2 vs. 4	380.2	1	<0.0001
	Model 3	−5,552.7	3 vs. 4	67.0	1	<0.0001
	Model 4	−5,519.2

¹BW = birth weight; WW = weaning weight; PW = probe weight.

²1. Direct additive genetic effect; 2. Direct additive genetic effect and maternal genetic effect; 3. Direct additive genetic effect and common litter effect; 4. Direct additive genetic, maternal genetic and common litter effect.

³LogL= Log likelihood.

⁴Compared reduced model (Models 1, 2, and 3) vs. full model (Model 4).

⁵LRT: $X^2$ test statistic for the likelihood ratio test = −2 (LogL_{reduced model} – LogL_{full model}).

⁶Degrees of freedom for the $X^2$ test statistic.

Variance components and genetic parameters for BW, WW, and PW estimated using bivariate models from both datasets and breeds are reported in Table 3. The direct heritability for BW, WW, and PW ranged from 0.05 to 0.15, 0.01 to 0.05, and 0.27 to 0.34, respectively. The maternal heritability decreased as the animals got older and the common litter effect decreased as a proportion of total variance after weaning age. The heritability estimates, except for the direct heritability for WW, were all significantly different from zero (P < 0.05).

Table 3.

Estimates of variance components, direct $\left(h_d^2\pm SE\right)$, maternal $\left(h_m^2\pm SE\right)$, and total heritability $\left(h_t^2\right)$, and common litter effect $\left(C^2\pm SE\right)$ for individual weights of Yorkshire pigs (York) and Landrace pigs (Land) using bivariate analysis and model 4

Dataset1	Breed	Trait2	Variance component3				$h_d^2\pm SE$	$h_m^2\pm SE$	$h_t^2{}^{\text{4}}$	$C^2\pm SE$
			${\sigma }_d^2$	${\sigma }_m^2$	${\sigma }_c^2$	${\sigma }_e^2$
CORE	York	BW	0.017	0.022	0.019	0.059	0.15 $\pm$ 0.03	0.18 $\pm$ 0.02	0.17	0.17 $\pm$ 0.01
		WW	0.046	0.13	0.18	0.69	0.04 $\pm$ 0.01	0.13 $\pm$ 0.02	0.06	0.17 $\pm$ 0.01
		PW	30.76	4.90	7.23	51.73	0.33 $\pm$ 0.03	0.05 $\pm$ 0.01	0.25	0.08 $\pm$ 0.01
MERGED	York	BW	0.0094	0.033	0.019	0.047	0.10 $\pm$ 0.01	0.22 $\pm$ 0.01	0.15	0.20 $\pm$ 0.004
		WW	0.033	0.12	0.18	0.63	0.03 $\pm$ 0.01	0.13 $\pm$ 0.02	0.06	0.18 $\pm$ 0.01
		PW	36.58	5.70	12.98	56.84	0.34 $\pm$ 0.01	0.05 $\pm$ 0.004	0.31	0.12 $\pm$ 0.003
CORE	Land	BW	0.0044	0.024	0.015	0.046	0.05 $\pm$ 0.01	0.27 $\pm$ 0.02	0.13	0.17 $\pm$ 0.01
		WW	0.0046	0.098	0.15	0.54	0.01 $\pm$ 0.01	0.12 $\pm$ 0.01	0.02	0.19 $\pm$ 0.01
		PW	23.37	5.91	7.38	51.48	0.27 $\pm$ 0.03	0.07 $\pm$ 0.01	0.27	0.08 $\pm$ 0.01
MERGED	Land	BW	0.0064	0.027	0.020	0.043	0.07 $\pm$ 0.01	0.28 $\pm$ 0.01	0.11	0.21 $\pm$ 0.004
		WW	0.0071	0.099	0.16	0.53	0.01 $\pm$ 0.01	0.12 $\pm$ 0.01	0.02	0.20 $\pm$ 0.01
		PW	30.65	6.70	11.39	52.33	0.30 $\pm$ 0.01	0.07 $\pm$ 0.01	0.27	0.11 $\pm$ 0.003

¹CORE = all animals have BW, WW, and PW records; MERGED = combines the CORE dataset with animals that have BW and PW recorded, but not individual WW.

²BW= birth weight; WW= weaning weight; PW= probe weight.

^{3 ${\text{σ}}_d^2$}= direct additive genetic variance; ${\text{σ}}_m^2$= maternal genetic variance; ${\sigma }_c^2$= common litter variance; ${\text{σ}}_e^2$= residual variance.

⁴SE were not available.

In the Yorkshire breed, the direct additive genetic correlation using the CORE dataset (MERGED dataset) were 0.78 ± 0.09 (0.68 ± 0.11) for BW and WW; 0.23 ± 0.10 (0.19 ± 0.04) for BW and PW; and 0.33 ± 0.15 (0.33 ± 0.15) for WW and PW. The maternal additive genetic correlations were 0.71 ± 0.06 (0.71 ± 0.05) for BW and WW, 0.77 ± 0.08 (0.72 ± 0.03) for BW and PW, and 0.78 ± 0.09 (0.77 ± 0.09) for WW and PW. The correlation between the direct and maternal additive genetic effects for each of the traits was moderate and negative at −0.27 (−0.28) for BW, −0.39 (−0.37) for WW, and −0.43 (−0.24) for PW. All these correlations were statistically significant (P < 0.05).

In the Landrace breed, the direct additive genetic correlation using the CORE dataset (MERGED dataset) between BW and WW was 0.71^NS ± 0.44 (0.75 ± 0.34); between BW and PW was −0.10^NS ± 0.15 (0.12 ± 0.05); and between WW and PW was −0.41^NS ± 0.36 (−0.31^NS ± 0.35), where NS indicates nonsignificant (P > 0.05) or the correlation was significant (P < 0.05) otherwise. The maternal additive genetic correlations were 0.74 ± 0.05 (0.75 ± 0.05) for BW and WW, 0.77 ± 0.06 (0.82 ± 0.02) for BW and PW, and 0.73 ± 0.08 (0.70 ± 0.09) for WW and PW were all significant (P < 0.05). The significant (P < 0.05) correlations between the direct and maternal additive genetic effects for each of the traits were low to moderate and negative at −0.25 (−0.41) for BW, −0.07 (−0.21) WW, and −0.13 (−0.30) for PW.

Genetic parameters estimated using CORE and MERGED datasets did not substantially differ, indicating no evidence for selective recording, as it would be expected, because it was known that farms that recorded individual WWs also recorded all pigs from a litter.

DISCUSSION

The main goal of this study was to determine whether BW would be useful for selection on early growth performance in purebred Yorkshire and Landrace pigs from Canadian breeding herds. Early growth performance of a piglet is dependent on a combination of management decisions including diet complexity and space allocation, as well as the individual performance of the sow and piglets (Hafez, 1963; Wolter et al., 2003). Early growth performance is largely dependent on the individual piglet’s BW, as this trait is directly correlated with piglet survival, behavior, and weight gain (Muns et al., 2013). Therefore, BW is a trait of potential economic importance, but it is typically overlooked. The lack of means to select pigs based on early growth performance information, such as individual BW or WW, has been identified by CCSI (www.ccsi.ca) as a Canadian issue that should be addressed. BW was found to be directly correlated with the preweaning mortality of pigs (Caceres et al., 2001; Fix et al., 2010); smaller pigs are at an increased risk of suffering from hypothermia, crushing, litter competition, and starvation (English and Morrison, 1984; Oksbjerg et al., 2013) and dead piglets are an obvious loss to swine producers. BW is also important when defining hierarchal capabilities common in production when piglets are grouped. A heavier litter mate was found to be dominant when establishing its place in the group for a functional teat (Milligan et al., 2001; Andersen et al., 2011) and also had a physical advantage during the weaning process when having to cope with sudden changes in the piglet’s environment, nutrition, and social group (Cox and Cooper, 2001; Muns et al., 2013). BW is also important for weight gain; Smith et al. (2007) found that piglets heavier at birth were found to still be heavier 42-d postweaning. Since heavy piglets are better able to stimulate the sows teat to produce milk (King et al., 1997), differences in body weight between light and heavy piglets are often maintained or increased throughout lactation (Milligan et al., 2002). Piglets with lower growth rates are costly to produce because they require extra facility costs, eat more per gram of pork produced, and complicate management through supplemental diets, space allocation, and cross-fostering (Deen et al., 1998; Wolter et al., 2003; Baxter et al., 2013). Thus, information on individual BW would be valuable to breeders and commercial production systems for predicting the early growth performance of piglets.

Since individual BW and WW genetic parameters have yet to be estimated in Canada, there is no agreement in the literature as to which random effects should be included in the model. It was determined in the present study that the model that included all 3 random effects (Model 4) was the best fit to the data. Knol et al. (2002) also looked at the effect of adding random terms to the models and observed that the direct heritability estimates were larger when the maternal genetic effect was ignored. This is expected, as exclusion of the maternal genetic effect could inflate the direct additive genetic effect as some of the maternal genetic variation would appear to be contributed by the direct additive genetic effect. When Knol et al. (2002) included both direct and maternal genetic effects, the estimates of heritability were in agreement with those estimates from this study. Therefore, differences in the random terms included in the model seem to play a significant role in the value and quality of the genetic parameter estimates.

As a result of differences in age at measurement, breed, and method of estimation of the genetic parameters for growth, there is considerable variation in estimates of heritabilities reported in the literature. For instance, Dufrasne et al. (2014) estimated a greater heritability for BW compared with literature reports, which could have been due to the fact they recorded BW up until 4 d of age; as the animal gets older, the direct genetic effect is expected to increase. However, it is concluded that the parameter estimates for individual BW, WW, and PW fall within the range of the estimates reported in the literature (Kaufmann, 2000; Arango et al., 2006; Tomiyama et al., 2010; Akanno et al., 2013; Dufrasne et al., 2014). Generally, direct heritability estimates for BW from the literature were low. This is as expected because most of the influence on weight at this point is contributed by the maternal genetic component and the uterine environment by the sow.

It is difficult to make comparisons between the genetic parameter estimates for individual weight traits as those reported in the literature are from different countries and breeds, or from crossbred animals. Yet, the heritability estimates for WW were lower than expected, even though they were in agreement with some reported in the literature (Kaufmann, 2000; Zhang et al., 2000; Akanno et al., 2013; Jiao et al., 2014). This might be due to the different weaning ages when compared with studies with high heritability estimates. For instance, the average pig was weaned at 15 d in this study, 21 d by Akanno et al. (2013), and 28 d by Zhang et al. (2000), whereas studies with high heritability estimates weaned at 42 d Darfour-Oduro et al. (2009). There is a lack of scientific reports on estimates of variance components for individual BW and WW in purebred Canadian pigs. Miar et al. (2014) evaluated BW, WW, nursery weight, and end weight in 6,408 Canadian commercial crossbred pigs (Duroc × F1 Landrace × Yorkshire). Hsu and Johnson (2014), investigating long-term selection in U.S. pigs, reported genetic parameters for various reproduction, growth (including BW), and carcass traits in a Yorkshire–Landrace composite population. Putz et al. (2015) estimated genetic parameters for litter size traits in U.S. Landrace and Yorkshire pigs. However, differently from the current study, Putz and colleagues reported average litter BWs, which represent the average weight of the alive piglet at weighing. For Duroc pigs in United States, Jiao et al. (2014) reported genetic parameters for both BW and WW. However, the estimates had very large standard errors, for BW the h² estimate was = 0.34 (±0.28) and, for WW, h² estimate was 0.05 (± 0.09).

Maternal genetic effects are presumably due to genetically controlled components of uterine nutrient supply, uterine capacity, and milk production (Kaufmann, 2000). Maternal heritability estimates in this study were in agreement with those reported in the literature. For BW, it ranged from 0.15 to 0.24 (Kaufmann, 2000; Knol et al., 2002; Arango et al., 2006; Tomiyama et al., 2010; Dufrasne et al., 2014), from 0.06 to 0.24 for WW (Kaufmann, 2000; Tomiyama et al., 2010; Dufrasne et al., 2014), and from 0.01 to 0.05 for PW (Tomiyama et al., 2010; Dufrasne et al., 2014). As the animal gets older, especially postweaning, the maternal influence on that animal decreases. Therefore, a decrease in the maternal genetic effect as the animal ages as found in this study is to be expected.

Common litter effects are also important to litter bearing species as they share a common environment which contributes to their resemblance (Neto et al., 2009). The origin of common environmental variances among families could be due to similar diet and/or climatic conditions (Kaufmann, 2000; Zhang et al., 2000; Akanno et al., 2013; Dufrasne et al., 2014). Several studies outside of Canada have incorporated the common litter effect to estimate genetic parameters for individual piglet BW and WW (Kaufmann, 2000; Zhang et al., 2000; Akanno et al., 2013; Dufrasne et al., 2014). The common litter effect estimates from this study were moderate and favorable in both breeds, and dissipated with age. Dufrasne et al. (2014) estimated that the common litter effect would decrease at each age demarcation, ranging from 0.19 at BW to 0.09 at weaning and 0.03 at PW, whereas Kaufmann (2000) found that the common litter effect increased from 0.11 at birth to 0.23 at weaning. The finding by Kaufmann (2000) is logical as the common litter effect will play an important role in growth until the piglets are weaned and new groupings are established. The trend in the common litter effect in the present study is in agreement with Kaufmann (2000) as the common litter effect for the Yorkshire and Landrace breeds ranged from 0.17 to 0.21, 0.17 to 0.20, and 0.08 to 0.12 for BW, WW, and PW, respectively.

The correlation between the direct and maternal genetic effects for BW, BW, and PW in the Yorkshire and Landrace breeds was moderate and negative. These moderate and negative correlations were in agreement with the literature (Arango et al., 2006; Roehe et al., 2010; Dube et al., 2014; Dufrasne et al., 2014). The negative correlation between the direct and maternal genetic effects suggest antagonism between these effects. Therefore, it is important to consider both effects in genetic evaluation and breeding programs. However, this negative correlation might be an artifact of the data structure that does not allow disentangling direct and maternal effects when there is not enough number of dams that have daughters with their own offspring with records in the data file (Heydarpour et al., 2008). This might be the case here, since only 417 Landrace sows and 376 Yorkshire sows have daughters with offspring with WW records in the date sets.

The greatest direct genetic correlation in both the Yorkshire and Landrace breeds was found between BW and WW, as also reported in the literature (Darfour-Oduro et al., 2009; Dufrasne et al., 2014). The moderate direct genetic correlations found in the Yorkshire breed suggest that BW is a good predictor of later performance (Darfour-Oduro et al., 2009; Dufrasne et al., 2014). Yet on the other hand, the moderate and unfavorable direct genetic correlations between BW and PW, and WW and PW in the Landrace breed suggest otherwise. However, the standard errors reported for the direct genetic correlations in the Landrace breed are high, suggesting that these results should be interpreted with caution. A negative genetic correlation between BW or WW and PW might also reflect compensatory gain, which is likely not the case here, since estimates of direct genetic correlations between BW and PW, and WW and PW in the Landrace from the literature are generally moderate and favorable (e.g. Darfour-Oduro et al., 2009; Dufrasne et al., 2014). Therefore, using individual BW should improve performance in WW and PW if it is included in a selection program. This finding also strengthens the importance of accounting for BW when selecting for greater prolificacy, as current selection programs will increase total born and therefore influence BW negatively as shown in Figure 2 of this study, and also demonstrated by Dufrasne et al. (2013).

Maternal genetic correlations between traits were high and favorable in both breeds. Therefore, the dam providing favorable genes for high BW also seemed to provide favorable genes for growth, i.e. sows that give birth to heavier piglets also wean heavier piglets. Other studies also estimated high maternal genetic correlations (Kaufmann, 2000; Darfour-Oduro et al., 2009). However, relatively few estimates of maternal genetic correlations were available in the literature for individual weight traits in swine, and those that were reported had large standard errors (e.g. Dufrasne et al., 2014). Therefore, it is likely that the high and favorable maternal genetic correlations estimated in this study are closer to the true values.

The correlations due to common litter effects were moderate and favorable in both breeds. Therefore, the environment common to littermates affected BW, WW, and PW in the same way. Dufrasne et al. (2014) had similar results between BW and WW, but estimated negative correlations between the other 2 weights; again, there was a large standard error for the negative estimates. Therefore, it is likely that the common litter effect correlations among BW, WW, and PW are closer to moderate and favorable as found in this study.

An additional difficulty with modeling direct and maternal effects in pigs comes from the use of cross-fostering as a management technique. As a litter bearing species, there is variation between sows in the total number of piglets born and the weight of the piglets within the litter (Milligan et al., 2002; Wolf et al., 2008; Zindove, 2013). Therefore, piglets are fostered in from or out to other sows to balance numbers across litters. If cross-fostering is performed properly, it should be beneficial for the piglet in regard to growth or survival. However, it creates problems when modeling maternal effects as the birth sow provides the direct maternal genetics and prepartum maternal environment, and the foster sow provides the postpartum maternal environment. Cross-fostering was not addressed in this study, because the animals with individual WW did not have available information on cross-fostering. However, cross-fostering is a practical issue that should be modeled in the future using cross-fostering data. Based on herds with recorded cross-fostering, only a relatively small fraction of piglets were cross-fostered (<11% of pigs), so cross-fostering likely did not greatly affect results. However, reliability of WW results should decrease as amount of fostering increases.

CONCLUSIONS

This study set out to explore the importance of direct additive genetic effects, maternal additive genetic effects, and common litter effects in the estimation of variance components for individual weight traits. It was determined that all 3 random terms should be included in the models as they each explain a portion of the variation in individual pig weight. This study also aimed to estimate genetic parameters including heritability and genetic correlations for individual BW, WW, and PW. The heritabilities estimated for BW, WW, and PW, and the positive correlations between traits suggest that selection decisions made early in a piglet’s life are possible. Making selection decisions earlier in the pig’s life is beneficial to breeders as it could reduce costs due to feeding and management. Future genetic evaluations should aim to model cross-fostering effect, since it was not addressed in this study.

SUPPLEMENTARY DATA

Supplementary data are available at Journal of Animal Science online.