Abstract
Benefits of hormonal growth promotants (HGPs) include production efficiency, profit, and reduced environmental effects for beef cattle. Questions remain about effects of HGP on beef quality, particularly on measures of toughness such as Warner-Bratzler shear force (WBSF), tenderness, and other taste-panel attributes of beef. The objective of this meta-analysis was to assess the effects of HGP on beef quality using the results of randomized controlled trials identified from 3 searched databases. Thirty-one experiments with 181 treatment comparisons were used to evaluate the effects of HGP on WBSF and sensory measures of beef quality. Experiments varied in design, used many different hormonal treatments and combinations, which were single or repeated, in different breeds and sex groups of cattle, with or without electrical stimulation, and with different lengths of time on feed and beef aging. The effects of multiple treatment comparisons in experiments were evaluated using robust regression models and compared to Knapp–Hartung and permutation meta-analytical methods. Increased WBSF was associated with HGP treatment. Use of multiple HGP implants was associated with an increase in WBSF of 0.248 kg (95% CI = 0.203 to 0.292). Effects of a single implant only increased WBSF by 0.176 kg (95% CI = 0.109 to 0.242). Aging of beef did not alter the association of HGP with increased WBSF (P = 0.105); however, the point direction was toward a reduced effect with aging (standardized mean difference [SMD] = −0.005 per day aged). While aging lowered WBSF, it did not reduce the SMD between HGP treatment and reference groups. Comparisons using trenbolone acetate did not differ in WBSF from those using other implants (P > 0.15). The findings on sensory panel tenderness differ from those using WBSF as HGP treatment was not associated with reduced tenderness (P > 0.3) and multiple HGP treatments improved tenderness (SMD = 0.468) compared to a single implant. Further, juiciness, flavor, and connective tissue were not associated with HGP use, whereas there was a marked 5.5-point decrease in the Meat Standards Australia meat quality 4 score, albeit with limited experiments. In general, the true variance of experiments, tau2 (τ2) was low (<0.1), but heterogeneity, I2 was high (>50%) indicating that much of the variance was due to factors other than measurement error. More targeted studies on the role of HGP in influencing beef quality are needed.
Keywords: beef aging, beef quality, hormonal growth promotant, meta-analysis, tenderness, trembolone acetate
INTRODUCTION
Hormonal growth promotant (HGP) implants are widely used in the beef industries of United States, Australia, Argentina, and South Africa. The impacts of these HGP on the efficiency of beef production are substantial with many individual reports and reviews highlighting responses including increased weight gain and feed efficiency from the HGP. There are also substantial environmental benefits (Capper and Hayes, 2012) from the use of these interventions and the production responses are profitable for beef producers (Hunter, 2010). However, questions remain about the effect of HGP on beef quality, particularly on measures of toughness such as Warner-Bratzler shear force (WBSF), and other attributes of beef palatability, for instance, tenderness, juiciness, flavor, and connective tissue that have been consumer and trained panel tested (Watson, 2008).
There have been a number of quantitative and semiquantitative reviews of the effects of HGP on the quality of beef as assessed by WBSF. In a traditional review of the literature, there was evidence of increased toughness of the beef with HGP use that the authors chose to consider to be negligible (Nichols et al., 2002). In a semiquantitative review, Duckett and Pratt (2014) considered that the impacts of the increase in WBSF may be more associated with repeated treatments with HGP and with androgenic rather than estrogenic steroids. Hunter (2010) noted the quantitative review by Watson (2008) on the effects of HGP in increasing WBSF and toughness but considered that there may be mitigating factors such as repeated number of implants and potential for postmortem aging to influence the responses. The aim of this meta-analysis was to evaluate the effects of HGP, primarily on WBSF, but also to consider effects on other beef palatability outcomes. We hypothesized that responses to HGP may be mediated by factors such as aging of beef, type of implant, number of implants used, and freezing of beef prior to quality evaluations.
MATERIALS AND METHODS
Literature Search
A comprehensive search of English language literature published from 1975 to 2017 was conducted to identify research experiments involving treatment comparisons designed to evaluate the effects of HGP on beef quality, primarily on the change in WBSF and taste-panel data for the tenderness, juiciness, flavor, connective tissue content, and Meat Standards Australia meat quality 4 score of beef (MQ4). Three search engines, ISI Web of Science (http://wokinfo.com/), Google Scholar (http://scholar.google.com/), and PubMed (http://www.ncbi.nlm.nih.gov/pubmed), were utilized between May 1 and 14, 2017 with a defined and repeatable search strategy using the terms “(HGP OR hormonal OR implants) AND (palatability OR shear-force OR tenderness) AND (beef or steer)” to identify relevant experiments. The searches were conducted independently by 2 workers. For Google Scholar many thousands of hits were identified and a systematic approach of ceasing investigation of papers identified was made when a sequence of 30 papers did not yield experiments that were relevant. Experiments were initially included for further investigation based on title, citation, and abstract. Experiments were then assessed as being suitable for inclusion or exclusion based on detailed review by 2 reviewers who checked the extraction and validation of the data. Additional experiments were examined from the references of experiments identified from the primary databases searches.
Inclusion and Exclusion Criteria
All published experiments were screened using standardized criteria according to the following criteria established a priori, but following a search to establish that sufficient new studies were published subsequent to Watson (2008) to merit a new meta-analysis. For inclusion into the meta-analysis, experiments needed to have the following: be English language, use HGP, be randomized, have replicated experimental units (pen or cattle) in which a reference group was present, beef quality outcomes were measured, there were sufficient data to determine the standardized mean difference (SMD) for continuous data, and they included a measure of variance (SE or SD) for each effect estimate or treatment and reference/control comparisons. In order to reduce variability in the evaluation and ensure that multiple comparisons on the 1 carcass were not included, Musculus longissimus thoracis et lumborum or longissimus muscle (LM; which was variously described by terms including strip loin) was assessed and data from other muscle groups were excluded with a single exception of treatments by Hunter et al. (2000) that were only conducted on the M. semitendinosus and no other muscle group. Two studies (Foutz et al., 1997; Cheatham et al., 2008) used rib cross sections that would have contained LM. Other treatments such as the use of beta-agonists were balanced within treatment comparison, such that both groups were either treated or not treated.
Data Extraction
Response means and measures of variance (SD or SE) were organized into an Excel spreadsheet with the following experimental details: authors, year, source of information, details of the HGP used, days the HGP were implanted, aging details on the beef, country in which experiments were conducted, breed, sex, feeding system (pens or pasture), number of days that cattle were fed, whether carcasses were electrically stimulated or not, days that carcasses were chilled before processing, the cut or muscle group tested, whether beef was frozen or not, whether beef was vacuum packed or not, number of cattle (or pens) per treatment, and details of the outcomes and their measures of dispersion. Outcomes for this experiment included WBSF and taste-panel data for the tenderness, juiciness, flavor, connective tissue content, and Meat Standards Australia MQ4 score. Some experiments reported different units of shear strength and Newtons were corrected to kilograms by dividing by 9.807. The MQ4 score is reported on a 100-point scale and is based on consumer panel testing with higher scores representing beef of higher quality. The Meat Standards Australia MQ4 score pre-2009 was calculated by the following equation using consumer assessed sensory variables (Watson et al., 2008):
Post-2009 the MQ4 was calculated by the following equation using consumer assessed sensory variables (unpublished data):
The sensory measures were inconsistently reported and the most frequently reported term relating to those measures was the one selected for inclusion. However, where this term was not reported, alternate, but similar, measures were used. Specifically, the term juiciness included “juiciness,” “initial juiciness,” and “sustained juiciness.” If more than 1 of these 3 measures were used in a treatment comparison, “juiciness” was used by preference. “Tenderness” terms included “myofibrillar tenderness,” “overall tenderness,” “initial tenderness,” and “sustained tenderness.” By preference, when more than 1 measure was present, “overall tenderness” was used. “Flavor” terms included “flavor intensity,” “flavor desirability,” and “beef flavor.” The terms “off flavor” or “flavor of lean” were not used. Some experiments reported different scales on which sensory outcomes were evaluated and these, with their respective measures of dispersion, were retained on the basis that these were amenable to SMD analysis, but would not allow a weighted mean difference (WMD) to be calculated.
Statistical Analysis
Data were structured to allow a classical meta-analytical evaluation of differences in responses of the experimental groups to be assessed. The SE and n (pens or animals) of a comparison were used to calculate SD, if SD was not provided. There is a hierarchical structure in these data as many experiments used multiple treatment comparisons. Consequently, there is dependence within experiment and the effects of experiment and treatment need to be evaluated by meta-regression using multi-level models (St-Pierre, 2001; Hedges et al., 2010; Van den Noortgate et al., 2013). The comparison between a reference/control and a HGP treatment group is defined as a “treatment comparison.” Within an experiment, there could be 1 comparison or several (i.e., a multi-arm experiment). The reference/control group was that not treated with HGP and was used for each comparison.
While HGP use was the treatment category, many different HGP treatments were applied and these were used in a large variety of different combinations. In order to evaluate some aspects of the treatment regimens, the use of trenbolone acetate (TBA) in a treatment comparison was examined as was the use of multiple or single implants. Variables that were examined by meta-regression included the length of time that beef was aged (“aging”), use of multiple implants or not (yes or no), use of TBA (yes or no), breed (British, European, Holstein and crosses; Brahman and Brahman crosses; crossbred undescribed; not stated), sex (steer, bull, heifer, mixed [steers and heifers]), days on feed, and electrical stimulation of the carcass (yes, no, not stated). Freezing of the beef before evaluation was almost universal and length of time that beef was frozen before evaluation was not often reported. Consequently, this was not evaluated, nor was days chilled or vacuum packing of the beef as these were not consistently reported.
Model development.
Initial data exploration included production of basic statistics using Stata (Version 15.1, StataCorp LP, College Station, TX) to examine the data for errors and to estimate the means and measures of dispersion. Normality of the data was examined for continuous variables, by visual and statistical appraisal.
Univariable analyses were performed for each dependent variable analyzed and predictors with P < 0.20 were considered for multivariable models. This method was used to reduce the potential for overfitting models to the data (Dohoo et al., 2009). The effect of treatment comparison within experiment was examined as a random effect using GLAMM (Stata Version 15.1) to partition the variance components of the nested model (Rabe-Hesketh and Skrondal, 2005), and this effect explained a substantial amount (43.6%) of variation in responses above that explained by experiment alone.
Stata Version 15.1 was also used to analyze differences in beef quality responses by SMD analysis which is also called effect size (ES) analysis. These methods have been published in detail in Lean et al. (2009) and Golder and Lean (2016). The difference between treatment and reference groups means, which is termed “treatment comparison” in the following description, was standardized using the SD of reference and treatment groups. The SMD estimates were pooled using the DerSimonian and Laird (1986) random effects models. Only random effects models were used, as previous work concluded that when there was uncertainty in the evaluative units caused by clustering of observations, the random effects model was appropriate (White and Thomas, 2005).
If an experiment or comparison reported separate estimates of measures of variance (SE or SD) for each group, these were recorded as such. Many comparisons reported a common SE or SD and these estimates were applied to both reference and treatment groups. Efforts were made to clearly identify the units of interest used in the studies and to clarify the measures of dispersion reported in papers. If there was a lack of clarity in regards to the unit of measure, a more conservative measure was used. Specifically, if muscle characteristics were measured and evaluated as the unit of analysis, but the muscles were obtained from pen-fed studies, pen was used in our analyses. A random effects WMD between treatment comparisons and reference is provided for WBSF and MQ4, with the weighting reflecting the inverse of the variance of the treatments included according to the nostandard method in the “metan” program of Stata to allow an interpretation of treatment effects in familiar units (kg of force), rather than ES. The other variables studied used scales that differed within the variable and were not amenable to WMD analysis.
Assessment of heterogeneity.
Variations among the treatment comparison SMD were assessed using a chi-squared (Q) test of heterogeneity. Heterogeneity in treatment responses reflects underlying differences in clinical diversity of the experimental populations and interventions, differences in experimental design and analytical methods, and statistical variation around responses. The clinical diversity of the experimental population includes all the nonstudy design aspects of variation, such as facility design, environment, animal management that may be measured and controlled for in meta-analysis, but are often not reported or measured. Identifying the presence and sources of the heterogeneity improves understanding of the responses to the interventions used. An α level of 0.10 was used because of the relatively poor power of the chi-square test to detect heterogeneity among small numbers of treatment comparisons (Clarke and Stewart, 2001). Heterogeneity of results among the treatment comparisons was quantified using the I2 statistic (Higgins and Thompson, 2002), which was developed to measure the impact of heterogeneity on a meta-analysis from mathematical criteria that are independent of the number of treatment comparisons and the treatment effect measure. The measure, I2 is a transformation of the square root of the χ2 heterogeneity statistic divided by its degrees of freedom and describes the proportion of total variation in treatment estimates that is due to heterogeneity. Further, I2 provides an estimate of the proportion of the true variance of effects of the treatment, that is, the true variance, tau2 (τ2) divided by the total variance observed in the treatment (Borenstein et al., 2017) that reflect measurement error. Negative values of I2 are assigned a value of 0, consequently the value I2 lies between 0% and 100%. An I2 value between 0% and 40% might not be important, 30% to 60% may represent moderate heterogeneity, 50% to 90% might represent substantial heterogeneity, and 75% to 100% might represent considerable heterogeneity (Higgins and Green, 2011). A 95% CI for I2 was calculated using the heterogi command in Stata according to methods recommended by Ioannidis et al. (2007). Both I2 and τ2 are provided to allow readers the opportunity to evaluate both metrics.
Meta-regression.
A key focus of meta-analysis is to identify and understand the sources of heterogeneity or variation of response, using the individual SMD for each treatment as the outcome and the associated SE as the measure of variance. Meta-regression is also a technique that can formally test whether there is evidence of different effects in different subgroups of treatments (Knapp and Hartung, 2003). The equations used in meta-regression have previously been published (Rabiee et al., 2012) and we refer readers to these for a description of meta-regression using the methods of Thompson and Sharp (1999) and Knapp and Hartung (2003).
Backward stepping models were used for meta-regression that included variables with a univariable value of P-value < 0.2 obtained using the Knapp–Hartung method (Knapp and Hartung, 2003). Models were derived using the Knapp–Hartung method until the variables retained had a P-value < 0.1 when a permutation model was used to develop final models. The permutation test approach for assessing the statistical significance of meta-regression methods suggested by Higgins and Thompson (2004), and programmed by Harbord and Higgins (2008) and Harbord and Steichen (2004), was used to reduce the risk of type I error as described by Rabiee et al. (2012). The data are simulated under the null hypothesis of no association between effect estimates and any covariate, yet with an unexplained component of heterogeneity according to the standard random effects meta-analysis model (Higgins and Thompson, 2004). Without loss of generality the average effect was assigned to zero (Higgins and Thompson, 2004):
where an ES θi is estimated by yi in treatment comparison i for experiment 1,…,k with a mean of zero and variance τ2 and vi represents the within experiment variances.
Covariates are simulated from a multivariable (standard) normal distribution so that correlation is imposed between pairs of covariates. This process provides an assessment less likely to produce type I statistical error (Higgins and Thompson, 2004).
The results of the permutation test, which do not account for the hierarchical structure of the effects of treatment comparison within experiment, are provided for comparison to robust regression models. The robust regression models are derived using the same starting variables that account for the nested effect of treatment comparisons within experiment (Hedges et al., 2010) and were programmed as robumeta in Stata (Tanner‐Smith and Tipton, 2014). Hedges et al. (2010) developed the robust regression models to account for the 2-stage cluster sampling inherent when the ES estimates are derived from a total of n = k1 + k2 + ··· + km estimates from treatment comparisons that were collected by sampling m clusters of experiments, that is, several treatment comparison estimates are derived from the same experiment. Hence, sampling kj ≥ 1 estimates within the jth cluster for j = 1,…,m. Briefly, in this test the mean ES from a series of experiments is described as follows: in this case, the regression model has only an intercept b1 and the weighted mean has the form:
where m is the total number of studies, k the total number of treatment comparisons and wij is the weighting for treatment comparisons within experiments and Tij is the vector of the ES estimates of treatment comparisons within experiments. If all the treatment comparison estimates in the same experiment are given identical weights, the robust variance estimate (vR) reduces to:
where Ťj is the unweighted mean of the treatment comparison estimates in the jth cluster, b1 is the estimate of the weighted mean, and wj is the total weight given to estimates in the jth cluster. This is a kind of weighted variance which reduces to (m − 1)/m2 times the variance, when the weights within experiment are identical, and (since the correlation coefficient = 1 in this case) the robust regression SE equals 1/m times the variance of Ťj estimated when the weights are equal. Hedges et al. (2010) highlight several important aspects of the robust model and the underlying assumptions that: the correlation structure of the Tj does not need be known to compute the pooled ES or vR, only that the vectors of estimates from different experiments are independent and that regularity conditions are satisfied; the experiment or treatment comparison level regressors do not need to be fixed; the theorem is asymptotic based on the number of experiments, rather than the number of treatment comparisons; and the theorem is relatively robust to regularity assumptions. The centered mean effects of covariates within experiment and treatment comparison were evaluated according to the methods outlined by Tanner-Smith and Tipton (2014).
Publication bias.
Presence of publication bias was investigated using funnel plots, which are a simple scatter plot of the intervention effect estimates from individual treatment comparisons plotted against precision. The name “funnel plot” arises because precision of the intervention effect increases as the size and precision of a treatment comparison increases. Effect estimates from treatments with a small number of animal units will scatter more widely at the bottom of the graph and the spread narrows for those with higher numbers of units. In the absence of bias, the plot should approximately resemble a symmetrical (inverted) funnel. If there is bias, for example, because smaller treatment comparisons without statistically significant effects remain unpublished, this will lead to an asymmetrical appearance of the funnel plot and a gap will be evident in a bottom corner of the graph. In this situation, the effect calculated in a meta-analysis will tend to overestimate the intervention effect. The more pronounced the asymmetry, the more likely it is that the bias will be substantial. Data were screened for plausible quadratic relationships for these variables by visual appraisal of univariable scatter plots between the covariate and SMD of each treatment comparison.
RESULTS
Over 3,000 experiments resulted from the literature searches with 182 experiments identified for review based on the pertinence of the title to this experiment and only 129 were pertinent and not repeated. Of these, 59 were excluded that did not meet the topic of interest or were rejected as review papers. Of the 70 remaining experiments, 38 were rejected for reasons that are outlined in Supplementary Table 1. This left 32 experiments, one of which was rejected on the basis that the units of variation (rsd) produced an improbable SD, leaving 31 experiments containing 181 treatment comparisons accepted for analysis. A PRISMA flow chart of the exclusions is provided as Supplementary Fig. 1. The tabulation of information on treatment comparisons is provided in Table 1 that lists the variables analyzed. Countries where treatment comparisons were conducted are United States (157), Australia (25), United Kingdom (1), and France (1). Information on descriptive statistics for the treatment comparisons is provided in Tables 2 and 3. There were relatively few observations in some categories for breed, for example, undescribed crossbreds, and sex, for example, bulls, or mixed heifers and steers. The lack of observations for breeds, other than the British category, Brahman and Brahman crosses and sex groups other than steers, limited the opportunities to evaluate these effects in detail.
Table 1.
Summary of descriptors for each treatment comparison used in the meta-analysis including a list of authors, year of publication, number of animals in the reference and treatment comparisons, sex of cattle, name of first hormonal implant used, use of multiple implants (yes or no), the number of days beef was aged, the number of days cattle were fed, and the mean WBSF for the reference and treatment groups
| Author | Year | Number of animals | Sexa | Hormonal implant 1 | Multiple implants | TBAb use | Days aged | Days fed | Mean WBSFc, kg | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference | Treatment | Reference | Treatment | ||||||||
| Apple et al. | 1991 | 3 | 3 | S | Ralgro | No | No | 6 | 249 | 4.01 | 4.01 |
| Apple et al. | 1991 | 3 | 3 | S | Synovex-S | No | No | 6 | 249 | 4.01 | 3.93 |
| Apple et al. | 1991 | 3 | 3 | S | Finaplix-S | No | Yes | 6 | 249 | 4.01 | 4.06 |
| Apple et al. | 1991 | 3 | 3 | S | Finaplix-S | Yes | Yes | 6 | 249 | 4.01 | 4.35 |
| Apple et al. | 1991 | 3 | 3 | S | Finaplix-S | Yes | Yes | 6 | 249 | 4.01 | 4.30 |
| Barham et al. | 2003 | 1368 | 660 | S | Synovex-S | Yes | No | 3 | 210 | 3.44 | 3.57 |
| Barham et al. | 2003 | 1368 | 720 | S | Synovex-S | Yes | Yes | 3 | 210 | 3.44 | 3.51 |
| Boles et al. | 2009 | 32 | 32 | S/H | Ralgro | Yes | Yes | 120 | 5.90 | 6.50 | |
| Boles et al. | 2009 | 37 | 37 | S/H | Vet Life | No | Yes | 120 | 6.80 | 7.90 | |
| Cafe et al. | 2010 | 83 | 81 | S/H | Revalor-H | No | Yes | 1 | 117 | 7.59 | 8.42 |
| Cafe et al. | 2010 | 83 | 81 | S/H | Revalor-H | No | Yes | 7 | 117 | 7.29 | 7.66 |
| Cafe et al. | 2010 | 83 | 81 | S/H | Revalor-H | No | Yes | 1 | 117 | 4.55 | 4.90 |
| Cafe et al. | 2010 | 83 | 81 | S/H | Revalor-H | No | Yes | 7 | 117 | 4.50 | 4.84 |
| Cafe et al. | 2010 | 71 | 72 | S | Revalor-H | No | Yes | 1 | 80 | 4.98 | 5.59 |
| Cafe et al. | 2010 | 71 | 72 | S | Revalor-H | No | Yes | 7 | 80 | 4.77 | 5.41 |
| Cafe et al. | 2010 | 71 | 72 | S | Revalor-H | No | Yes | 1 | 80 | 5.19 | 5.65 |
| Cafe et al. | 2010 | 71 | 72 | S | Revalor-H | No | Yes | 7 | 80 | 4.54 | 4.87 |
| Calkins et al. | 1986 | 4 | 4 | B | Ralgro | Yes | No | 10 | 232 | 2.31 | 2.32 |
| Calkins et al. | 1986 | 4 | 4 | S | Ralgro | Yes | No | 10 | 232 | 2.16 | 2.31 |
| Calkins et al. | 1986 | 4 | 4 | B | Compudose 200 | Yes | No | 10 | 232 | 2.31 | 2.20 |
| Calkins et al. | 1986 | 4 | 4 | S | Compudose 200 | Yes | No | 10 | 232 | 2.16 | 2.33 |
| Cheatham et al. | 2008 | 5 | 5 | S | Ralgro | Yes | No | 2 | 259 | 1.98 | 2.14 |
| Cheatham et al. | 2008 | 5 | 5 | S | Ralgro | Yes | Yes | 2 | 259 | 1.98 | 2.25 |
| Cheatham et al. | 2008 | 5 | 4 | S | Ralgro | Yes | Yes | 2 | 259 | 1.98 | 2.52 |
| Ebarb et al. | 2016 | 11 | 11 | H | Component TE-200 | No | No | 35 | 75 | 4.37 | 4.52 |
| Ebarb et al. | 2017 | 11 | 11 | H | Component TE-200 | No | No | 2 | 90 | 5.09 | 5.54 |
| Ebarb et al. | 2017 | 11 | 11 | H | Component TE-200 | No | No | 7 | 90 | 4.27 | 4.78 |
| Foutz et al. | 1997 | 4 | 4 | S | Synovex-S | No | Yes | 7 | 119–126 | 4.00 | 4.43 |
| Foutz et al. | 1997 | 4 | 4 | S | Revalor | No | Yes | 7 | 119–127 | 4.00 | 4.32 |
| Foutz et al. | 1997 | 4 | 4 | S | Finaplix-S | No | Yes | 7 | 119–128 | 4.00 | 4.12 |
| Foutz et al. | 1997 | 4 | 4 | S | Finaplix-S | Yes | Yes | 7 | 119–129 | 4.00 | 4.41 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 7 | 152–174 | 2.43 | 2.79 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 14 | 152–174 | 2.55 | 2.78 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 21 | 152–174 | 2.50 | 2.63 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 28 | 152–174 | 1.87 | 2.12 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 35 | 152–174 | 2.60 | 2.87 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 7 | 152–174 | 2.43 | 2.74 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 14 | 152–174 | 2.55 | 2.95 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 21 | 152–174 | 2.50 | 2.90 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 28 | 152–174 | 1.87 | 2.30 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 35 | 152–174 | 2.60 | 2.62 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 7 | 152–174 | 3.58 | 4.19 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 14 | 152–174 | 3.59 | 4.14 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 21 | 152–174 | 3.29 | 3.86 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 28 | 152–174 | 2.58 | 3.42 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor-S | No | Yes | 35 | 152–174 | 2.89 | 3.21 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 7 | 152–174 | 3.58 | 3.80 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 14 | 152–174 | 3.59 | 4.06 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 21 | 152–174 | 3.29 | 3.68 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 28 | 152–174 | 2.58 | 2.85 |
| Garmyn et al. | 2011 | 16 | 16 | S | Revalor XS | No | Yes | 35 | 152–174 | 2.89 | 2.88 |
| Gerken et al. | 1995 | 6 | 6 | S | Synovex-S | No | No | 14 | 112 | 3.98 | 4.56 |
| Gerken et al. | 1995 | 6 | 6 | S | Finaplix-S | No | Yes | 14 | 112 | 3.98 | 3.93 |
| Gerken et al. | 1995 | 6 | 6 | S | Revalor-S | No | Yes | 14 | 112 | 3.98 | 4.65 |
| Hopkins and Dikeman | 1987 | 3 | 3 | B | Compudose | Yes | No | 10 | 205 | 5.20 | 4.40 |
| Hunt et al. | 1991 | 5 | 5 | S | Finnaplix-120 | Yes | Yes | 7 | 160 | 3.40 | 3.30 |
| Hunt et al. | 1991 | 5 | 5 | B | Finnaplix-120 | Yes | Yes | 7 | 160 | 4.40 | 3.50 |
| Hunt et al. | 1991 | 5 | 5 | S | Finnaplix-120 | Yes | Yes | 7 | 160 | 3.40 | 3.20 |
| Hunt et al. | 1991 | 5 | 5 | B | Finnaplix-120 | Yes | Yes | 7 | 160 | 4.40 | 3.60 |
| Hunter et al. | 2000 | 17 | 16 | S | Compudose 400 | No | No | Unknown | 420 | 5.10 | 5.50 |
| Hunter et al. | 2000 | 17 | 16 | S | Compudose 100 | Yes | No | Unknown | 420 | 5.10 | 5.60 |
| Hunter et al. | 2001 | 20 | 17 | S | Compudose 100 | No | No | 1 | 100 | 4.30 | 4.80 |
| Hunter et al. | 2001 | 16 | 16 | S | Compudose 100 | No | No | 1 | 150 | 4.70 | 5.40 |
| Hunter et al. | 2001 | 18 | 17 | S | Compudose 100 | No | No | 1 | 70 | 4.40 | 4.50 |
| Hunter et al. | 2001 | 17 | 12 | S | Compudose 100 | No | No | 1 | Unknown | 6.00 | 6.30 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor XS | No | Yes | 14 | 145–174 | 3.20 | 3.00 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor IS | Yes | Yes | 14 | 145–174 | 3.20 | 3.20 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor XS | No | Yes | 21 | 145–174 | 2.90 | 2.90 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor IS | Yes | Yes | 21 | 145–174 | 2.90 | 2.90 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor XS | No | Yes | 14 | 145–174 | 3.00 | 2.90 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor IS | Yes | Yes | 14 | 145–174 | 3.00 | 3.30 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor XS | No | Yes | 21 | 145–174 | 2.70 | 2.60 |
| Igo et al. | 2011 | 4 | 7 | S | Revalor IS | Yes | Yes | 21 | 145–174 | 2.70 | 2.80 |
| Kerth et al. | 2003 | 8 | 8 | H | Revalor-H | No | Yes | 16 | Unknown | 3.49 | 3.54 |
| Kerth et al. | 2003 | 8 | 8 | H | Revalor-H | No | Yes | 16 | Unknown | 3.49 | 2.93 |
| Kerth et al. | 2003 | 8 | 8 | H | Revalor-H | Yes | Yes | 16 | Unknown | 3.49 | 3.18 |
| Kerth et al. | 2003 | 8 | 8 | H | Revalor-IH | Yes | Yes | 16 | Unknown | 3.49 | 3.34 |
| Kerth et al. | 2003 | 8 | 8 | H | Synovex-H | Yes | Yes | 16 | Unknown | 3.49 | 3.39 |
| Nute and Dransfield | 1984 | 12 | 12 | S | Ralgro | No | No | 6 | Unknown | ||
| Ouali et al. | 1988 | 10 | 10 | S | Revalor-S | No | Yes | 7 | 130 | ||
| Packer et al. | In press | 100 | 100 | S | Compudose 100 | No | No | 7 | 73 | 4.40 | 4.60 |
| Packer et al. | In press | 100 | 100 | S | Compudose 100 | No | No | 35 | 73 | 3.40 | 3.50 |
| Packer et al. | In press | 100 | 100 | S | Component TE-200 | No | Yes | 7 | 73 | 4.40 | 4.70 |
| Packer et al. | In press | 100 | 100 | S | Component TE-200 | No | Yes | 35 | 73 | 3.40 | 3.50 |
| Phelps et al. | 2014 | 16 | 16 | S | Component E-S | Yes | No | 21 | 175 | 3.20 | 3.42 |
| Phelps et al. | 2014 | 16 | 16 | S | Component E-S | Yes | No | 21 | 175 | 3.00 | 3.55 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-S | Yes | Yes | 17.5 | Various | 3.54 | 3.95 |
| Platter et al. | 2003 | 50 | 50 | S | Ralgro | Yes | Yes | 17.5 | Various | 3.54 | 4.46 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-S | Yes | Yes | 17.5 | Various | 3.54 | 4.19 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-C | Yes | Yes | 17.5 | Various | 3.54 | 4.19 |
| Platter et al. | 2003 | 50 | 50 | S | Ralgro | Yes | Yes | 17.5 | Various | 3.54 | 4.15 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-C | Yes | Yes | 17.5 | Various | 3.54 | 4.12 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-C | Yes | Yes | 17.5 | Various | 3.54 | 4.05 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-C | Yes | Yes | 17.5 | Various | 3.54 | 4.05 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-C | Yes | Yes | 17.5 | Various | 3.54 | 4.14 |
| Platter et al. | 2003 | 50 | 50 | S | Synovex-C | Yes | Yes | 17.5 | Various | 3.54 | 4.38 |
| Reiling and Johnson | 2003 | 40 | 41 | S | Ralgro | Yes | Yes | 14 | 105 | 3.06 | 3.28 |
| Reiling and Johnson | 2003 | 40 | 42 | S | Revalor-S | Yes | Yes | 14 | 105 | 3.06 | 3.58 |
| Reiling and Johnson | 2003 | 41 | 41 | S | Component TE-S | Yes | No | 5 | 105 | 3.76 | 4.09 |
| Reiling and Johnson | 2003 | 41 | 41 | S | Component TE-S | Yes | No | 14 | 105 | 3.54 | 3.72 |
| Robinson et al. | 2012 | 187 | 176 | S/H | Revalor-H | No | Yes | 7 | 390–660 | ||
| Robinson et al. | 2012 | 187 | 176 | S/H | Revalor-H | No | Yes | 7 | 390–661 | ||
| Roeber et al. | 2000 | 36 | 39 | S | Encore | Yes | Yes | 14 | 140 or 141 | 2.97 | 3.18 |
| Roeber et al. | 2000 | 36 | 38 | S | Ralgro | Yes | Yes | 14 | 140 or 141 | 2.97 | 3.41 |
| Roeber et al. | 2000 | 36 | 38 | S | Ralgro | Yes | Yes | 14 | 140 or 141 | 2.97 | 3.31 |
| Roeber et al. | 2000 | 36 | 36 | S | Revalor-S | Yes | Yes | 14 | 140 or 141 | 2.97 | 3.28 |
| Roeber et al. | 2000 | 36 | 36 | S | Revalor-S | No | Yes | 14 | 140 or 141 | 2.97 | 3.51 |
| Roeber et al. | 2000 | 36 | 37 | S | No | Yes | 14 | 140 or 141 | 2.97 | 3.42 | |
| Roeber et al. | 2000 | 36 | 37 | S | Synovex Plus | No | Yes | 14 | 140 or 141 | 2.97 | 3.29 |
| Rumsey et al. | 1990 | 10 | 10 | S | Synovex-S | Yes | No | 2 | 160 | 3.69 | 3.87 |
| Rumsey et al. | 1990 | 19 | 19 | S/H | Synovex-S | Yes | No | 2 | 160 | 4.70 | 6.05 |
| Samber et al. | 1996 | 8 | 8 | S | Ralgro | Yes | Yes | 14 | 212 | 2.58 | 2.74 |
| Samber et al. | 1996 | 8 | 8 | S | Ralgro | Yes | Yes | 14 | 212 | 2.58 | 2.75 |
| Samber et al. | 1996 | 8 | 8 | S | Synovex-S | Yes | Yes | 14 | 212 | 2.58 | 2.64 |
| Samber et al. | 1996 | 8 | 8 | S | Revalor-S | Yes | Yes | 14 | 212 | 2.58 | 3.01 |
| Samber et al. | 1996 | 8 | 8 | S | Revalor-S | Yes | Yes | 14 | 212 | 2.58 | 2.92 |
| Scheffler et al. | 2003 | 4 | 4 | S | Component TE-S | Yes | Yes | 14 | 269 | 2.50 | 2.60 |
| Scheffler et al. | 2003 | 4 | 4 | S | Component TE-S | Yes | Yes | 14 | 269 | 2.50 | 2.80 |
| Scheffler et al. | 2003 | 4 | 4 | S | Component TE-S | Yes | Yes | 14 | 269 | 2.50 | 3.00 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | No | Yes | 3 | 140 | 4.67 | 4.51 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | No | Yes | 7 | 140 | 4.22 | 4.22 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | No | Yes | 14 | 140 | 3.80 | 3.59 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | No | Yes | 21 | 140 | 3.33 | 3.36 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | No | Yes | 28 | 140 | 3.27 | 3.24 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | No | Yes | 3 | 140 | 4.67 | 4.57 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | No | Yes | 7 | 140 | 4.22 | 4.06 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | No | Yes | 14 | 140 | 3.80 | 3.56 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | No | Yes | 21 | 140 | 3.33 | 3.26 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | No | Yes | 28 | 140 | 3.27 | 3.13 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 3 | 140 | 4.67 | 4.67 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 7 | 140 | 4.22 | 4.33 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 14 | 140 | 3.80 | 3.84 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 21 | 140 | 3.33 | 3.45 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 28 | 140 | 3.27 | 3.23 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 3 | 140 | 4.67 | 4.74 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 7 | 140 | 4.22 | 4.37 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 14 | 140 | 3.80 | 3.71 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 21 | 140 | 3.33 | 3.44 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | No | Yes | 28 | 140 | 3.27 | 3.19 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | Yes | Yes | 3 | 140 | 4.67 | 4.65 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | Yes | Yes | 7 | 140 | 4.22 | 4.30 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | Yes | Yes | 14 | 140 | 3.80 | 3.73 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | Yes | Yes | 21 | 140 | 3.33 | 3.43 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA | Yes | Yes | 28 | 140 | 3.27 | 3.39 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 3 | 140 | 4.67 | 5.03 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 7 | 140 | 4.22 | 4.47 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 14 | 140 | 3.80 | 3.87 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 21 | 140 | 3.33 | 3.51 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 28 | 140 | 3.27 | 3.26 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | Yes | Yes | 3 | 140 | 4.67 | 5.06 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | Yes | Yes | 7 | 140 | 4.22 | 4.66 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | Yes | Yes | 14 | 140 | 3.80 | 4.05 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | Yes | Yes | 21 | 140 | 3.33 | 3.67 |
| Schneider et al. | 2007 | 42 | 41 | H | TBA + E2 | Yes | Yes | 28 | 140 | 3.27 | 3.39 |
| Schneider et al. | 2007 | 42 | 40 | H | TBA + E2 | Yes | Yes | 3 | 140 | 4.67 | 5.41 |
| Schneider et al. | 2007 | 42 | 40 | H | TBA + E2 | Yes | Yes | 7 | 140 | 4.22 | 4.87 |
| Schneider et al. | 2007 | 42 | 40 | H | TBA + E2 | Yes | Yes | 14 | 140 | 3.80 | 4.20 |
| Schneider et al. | 2007 | 42 | 40 | H | TBA + E2 | Yes | Yes | 21 | 140 | 3.33 | 3.74 |
| Schneider et al. | 2007 | 42 | 40 | H | TBA + E2 | Yes | Yes | 28 | 140 | 3.27 | 3.50 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 3 | 140 | 4.67 | 5.31 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 7 | 140 | 4.22 | 4.73 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 14 | 140 | 3.80 | 4.11 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 21 | 140 | 3.33 | 3.62 |
| Schneider et al. | 2007 | 42 | 42 | H | TBA + E2 | Yes | Yes | 28 | 140 | 3.27 | 3.42 |
| Schneider et al. | 2007 | 42 | 44 | H | TBA + E2 | Yes | Yes | 3 | 140 | 4.67 | 5.46 |
| Schneider et al. | 2007 | 42 | 44 | H | TBA + E2 | Yes | Yes | 7 | 140 | 4.22 | 5.00 |
| Schneider et al. | 2007 | 42 | 44 | H | TBA + E2 | Yes | Yes | 14 | 140 | 3.80 | 4.21 |
| Schneider et al. | 2007 | 42 | 44 | H | TBA + E2 | Yes | Yes | 21 | 140 | 3.33 | 3.77 |
| Schneider et al. | 2007 | 42 | 44 | H | TBA + E2 | Yes | Yes | 28 | 140 | 3.27 | 3.36 |
| Schneider et al. | 2007 | 42 | 43 | H | TBA + E2 | Yes | Yes | 3 | 140 | 4.67 | 5.56 |
| Schneider et al. | 2007 | 42 | 43 | H | TBA + E2 | Yes | Yes | 7 | 140 | 4.22 | 5.09 |
| Schneider et al. | 2007 | 42 | 43 | H | TBA + E2 | Yes | Yes | 14 | 140 | 3.80 | 4.36 |
| Schneider et al. | 2007 | 42 | 43 | H | TBA + E2 | Yes | Yes | 21 | 140 | 3.33 | 3.76 |
| Schneider et al. | 2007 | 42 | 43 | H | TBA + E2 | Yes | Yes | 28 | 140 | 3.27 | 3.66 |
| Shackelford et al. | 1992 | 48 | 48 | B | Ralgro | No | No | 10 | 190, 246, 315 | 4.30 | 5.10 |
| Shackelford et al. | 1992 | 48 | 48 | B | Synovex-S | No | No | 10 | 190, 246, 315 | 4.30 | 5.10 |
| Thompson et al. | 2008 | 20 | 20 | S | Revalor-S | No | Yes | 5 | 55 or 65 | 3.60 | 4.00 |
| Thompson et al. | 2008 | 20 | 20 | H | Revalor-H | No | Yes | 5 | 55 or 65 | 4.30 | 5.20 |
| Thompson et al. | 2008 | 20 | 20 | S | Revalor-S | No | Yes | 21 | 55 or 65 | 3.00 | 3.30 |
| Thompson et al. | 2008 | 20 | 20 | H | Revalor-H | No | Yes | 21 | 55 or 65 | 3.20 | 3.60 |
| Thompson et al. | 2008 | 240 | 235 | S | Compudose 100 | No | No | 1 | 55 or 65 | 5.80 | 5.80 |
aSex categories; S, steers; H, heifers; B, bulls.
bTBA, trenbolone acetate implants.
cWBSF, Warner-Bratzler shear force.
Table 2.
Descriptive statistics for number of experiments, treatment comparisons used for multiple HGP implants, treatments using TBA, length of time that beef was aged before evaluation, length of time that cattle were fed, and number of animals or pens per treatment
| Variable | Number of treatment comparisons | Percentage or mean | SD | Minimum | Maximum |
|---|---|---|---|---|---|
| Multiple implants, % of treatments | 181 | 50 | 0.5 | NA | NA |
| TBA, % of treatments | 181 | 83 | 0.4 | NA | NA |
| Aging of beef, d | 177 | 13 | 8.8 | 1 | 35 |
| Length of feeding, d | 160 | 151 | 54.1 | 60 | 420 |
| Number of animals or pens per treatment | 181 | 39.9 | 75.5 | 3 | 720 |
Table 3.
Frequency distribution of breed, sex, and electrical stimulation at slaughter categories for 181 treatments comparisons
| Variable | Frequency | Percentage, % |
|---|---|---|
| Breed | ||
| British and European breeds, British and European cross, and Holstein | 129 | 71.3 |
| Brahman and Brahman crosses | 32 | 17.7 |
| Crossbred (undescribed) | 16 | 8.8 |
| Not stated | 4 | 2.2 |
| Sex | ||
| Steers | 100 | 55.3 |
| Bull | 7 | 3.9 |
| Heifers | 65 | 35.9 |
| Mixed (steers and heifers) | 9 | 5.0 |
| Electrical stimulation at slaughter | ||
| Not stimulated | 23 | 12.7 |
| Stimulated | 77 | 42.5 |
| Not stated | 81 | 44.8 |
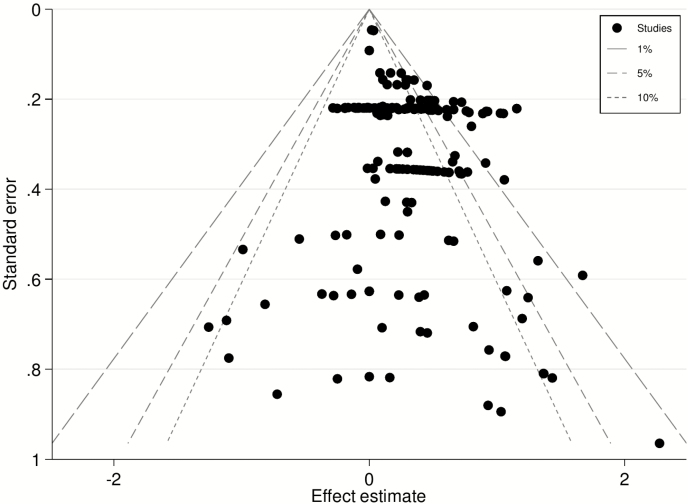
There was no evidence of publication bias in the funnel plots. The funnel plot for WBSF is shown in Fig. 1 and those for sensory panel tenderness, juiciness, and flavor are provided in Supplementary Figs. 2 to 4. It should be noted that the results for beef quality measures other than WBSF are less reliable than for WBSF because these were only extracted from papers identified in the search for effects of HGP on WBSF. Consequently, papers evaluating these other beef quality measures are likely missing from the evaluations conducted in this study and could alter findings.
Figure 1.
Contour-enhanced funnel plot showing the effect estimate for HGPs on the difference in WBSF (kg) of primarily the Longissimus dorsi muscle in beef cattle against the SE of that estimate (y-axis). The gray broken lines represent the 90%, 95%, and 99% CI for treatment comparisons. Effect estimates from small studies will scatter more widely at the bottom of the graph and the spread narrows for larger treatments (Sterne and Harbord, 2004). In the absence of heterogeneity or bias the plot should approximately resemble a symmetrical (inverted) funnel with studies lying within these lines. If there is bias, for example, because smaller treatments without statistically significant effects remain unpublished, this will lead to an asymmetrical appearance of the funnel plot and a gap will be evident in a bottom corner of the graph.
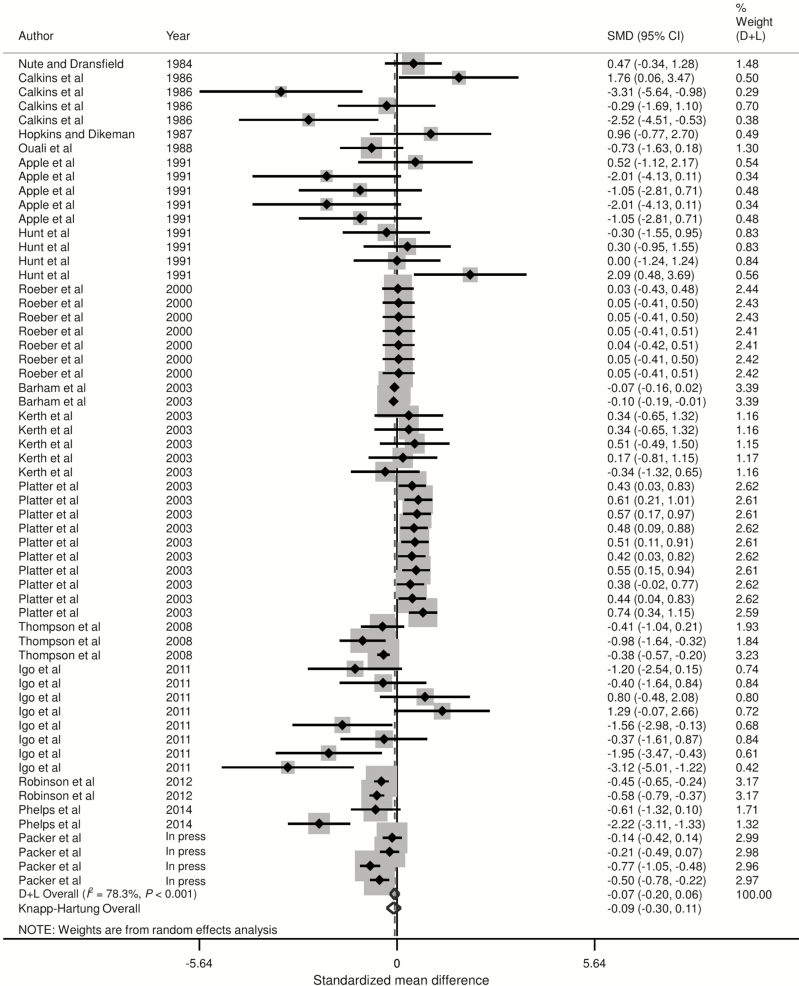
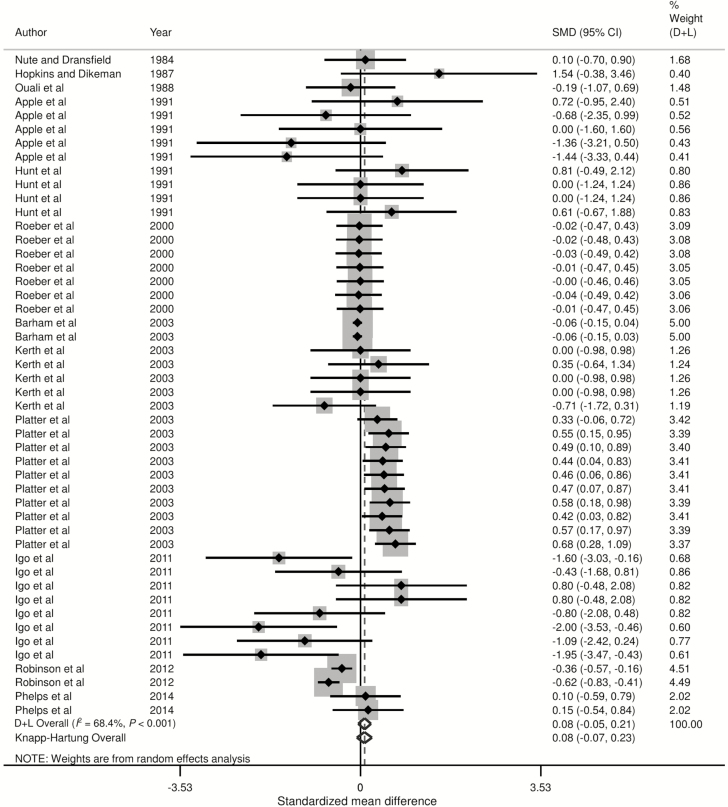
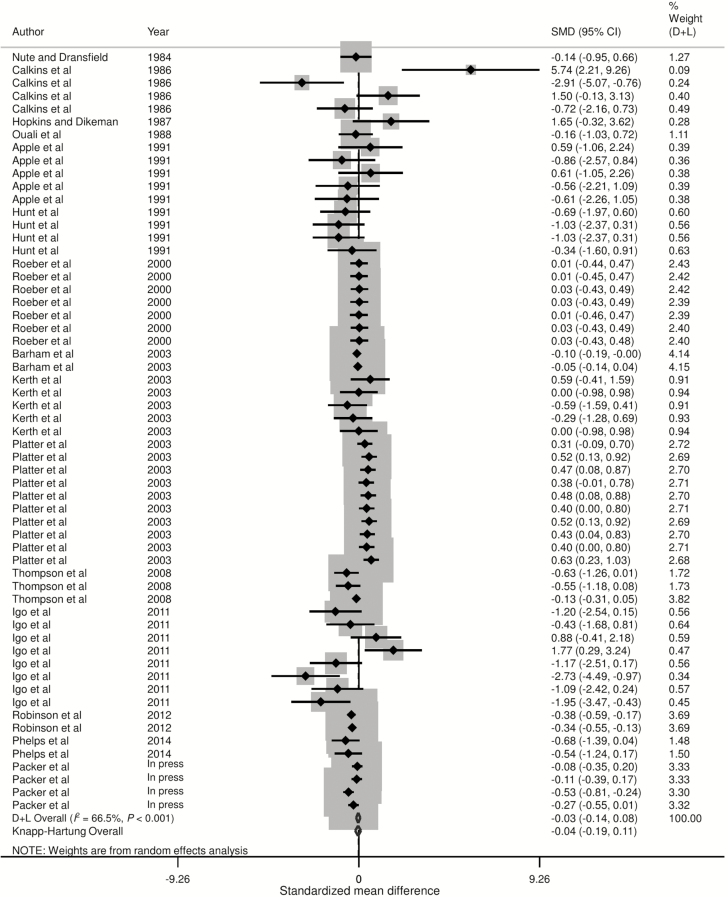
Forest plots of the responses were created and associations between HGP treatments and sensory panel tenderness, juiciness, and flavor are displayed in Figs. 2 to 4, using the estimated SMD of the outcomes with both the DerSimonian and Laird (1986) and the Knapp–Hartung summary estimates. Due to the large number of treatment comparisons for WBSF, the forest plot for this outcome is provided as Supplementary Fig. 5.
Figure 2.
Forest plot of the ES or SMD (standardized using the z-statistic) and 95% CI of the effect of hormonal growth promotants on sensory panel tenderness of primarily the Longissimus dorsi muscle in beef cattle. The solid vertical line represents a mean difference of zero or no effect. Points to the left of the line represent a decrease in sensory panel tenderness, while points to the right of the line indicate an increase. Each square around the point effect represents the mean ES for that treatment comparison and reflects the relative weighting of the treatment comparison to the overall ES estimate. The larger the box, the greater the treatment comparison contribution to the overall estimate. The weight that each treatment comparison contributed is in the right-hand column. The upper and lower limit of the line connected to the square represents the upper and lower 95% CI for the ES. The overall pooled effects size or SMD and 95% CI pooled using the DerSimonian and Laird (D + L; DerSimonian and Laird, 1986) and Knapp–Sidak–Jonkman (Knapp–Hartung; IntHout et al., 2014) methods for random effects models are indicated by the respective diamonds at the bottom. The heterogeneity measure, I2 is a measure of variation beyond chance among treatments included in the meta-analysis. The effect of HGP treatment on sensory panel tenderness was substantially heterogeneous as indicated by the I2 of 78.3%.
Figure 4.
Forest plot of the ES or SMD (standardized using the z-statistic) and 95% CI of the effect of hormonal growth promotants on flavor of primarily the Longissimus dorsi muscle in beef cattle. The solid vertical line represents a mean difference of zero or no effect. Points to the left of the line represent a decrease in flavor, while points to the right of the line indicate an increase. Each square around the point effect represents the mean ES for that treatment comparison and reflects the relative weighting of the treatment comparison to the overall ES estimate. The larger the box, the greater the treatment comparison contribution to the overall estimate. The weight that each treatment comparison contributed is in the right-hand column. The upper and lower limit of the line connected to the square represents the upper and lower 95% CI for the ES. The overall pooled effects size or SMD and 95% CI pooled using the DerSimonian and Laird (D + L; DerSimonian and Laird, 1986) and Knapp–Sidak–Jonkman (Knapp–Hartung; IntHout et al., 2014) methods for random effects models are indicated by the respective diamonds at the bottom. The heterogeneity measure, I2 is a measure of variation beyond chance among treatments included in the meta-analysis. The effect of HGP treatment on flavor was moderately heterogeneous as indicated by the I2 of 68.4%.
Figure 3.
Forest plot of the ES or SMD (standardized using the z-statistic) and 95% CI of the effect of hormonal growth promotants on juiciness of primarily the Longissimus dorsi muscle in beef cattle. The solid vertical line represents a mean difference of zero or no effect. Points to the left of the line represent a decrease in juiciness, while points to the right of the line indicate an increase. Each square around the point effect represents the mean ES for that treatment comparison and reflects the relative weighting of the treatment comparison to the overall ES estimate. The larger the box, the greater the treatment comparison contribution to the overall estimate. The weight that each treatment comparison contributed is in the right-hand column. The upper and lower limit of the line connected to the square represents the upper and lower 95% CI for the ES. The overall pooled effects size or SMD and 95% CI pooled using the DerSimonian and Laird (D + L; DerSimonian and Laird, 1986) and Knapp–Sidak–Jonkman (Knapp–Hartung; IntHout et al., 2014) methods for random effects models are indicated by the respective diamonds at the bottom. The heterogeneity measure, I2 is a measure of variation beyond chance among treatments included in the meta-analysis. The effect of HGP treatment on juiciness was moderately heterogeneous as indicated by the I2 of 66.5%.
Table 4 provides detail on the SMD estimates of the effect of HGP on beef quality outcomes. The estimates are based on Knapp–Hartung methods and provide the SMD, SE, and 95% CI of the SMD, P-value, I2 and 95% CI of I2, and τ2. The estimates of effect based on robust regression methods provide the SMD, SE, and 95% CI of the SMD, P-value, and I2; however, the low number of treatment comparisons and experiments available precluded evaluation based on robust regression of the effects on connective tissue and MQ4. Of the outcomes investigated, only WBSF and MQ4 were significantly affected by HGP treatment. The WMD of WBSF was 0.248 kg with a 95% CI of 0.203 to 0.292. The estimates of effect were similar for the Knapp–Hartung and robust models for WBSF (Table 4). The estimates of I2 for all beef quality outcomes were all moderate to substantial and the 95% CI indicated that all estimates had significant heterogeneity associated with treatment, but estimates of τ2 were low, almost all being close to or below 0.1, indicating that there was considerable variance in response that is not explained by the true effects.
Table 4.
Standardized mean difference estimates of the effect of HGPs on beef quality outcomes
| Variable | SMD | SE | 95% CI | P-value | I 2, % (95% CI) | τ2 |
|---|---|---|---|---|---|---|
| WBSFa, kg (KH) | 0.299 | 0.027 | 0.246 to 0.352 | 0.001 | 47.3 (37–56) | 0.046 |
| WBSFa, kg (robust) | 0.306 | 0.053 | 0.181 to 0.431 | 0.001 | 0.001 | |
| Juiciness (KH) | −0.038 | 0.075 | −0.189 to 0.112 | 0.610 | 66.5 (56–75) | 0.102 |
| Juiciness (robust) | −0.115 | 0.137 | −0.424 to 0.193 | 0.421 | 0.001 | |
| Tenderness (KH) | −0.094 | 0.101 | −0.296 to 0.109 | 0.360 | 78.3 (72–83) | 0.129 |
| Tenderness (robust) | −0.223 | 0.219 | −0.717 to 0.270 | 0.333 | 0.001 | |
| Flavor (KH) | 0.077 | 0.074 | −0.071 to 0.226 | 0.301 | 68.4 (57–77) | 0.101 |
| Flavor (robust) | −0.003 | 0.177 | −0.426 to 0.418 | 0.983 | 0.001 | |
| Connective tissue (KH) | −0.060 | 0.207 | −0.502 to 0.382 | 0.776 | 34.1 (0–64) | 0.215 |
| Meat quality 4 score (KH) | −0.490 | 0.107 | −0.737 to −0.243 | 0.002 | 81.5 (66–90) | 0.075 |
The estimates based on Knapp–Hartung methods (KH) provide a SMD, SE, and 95% CI of the SMD, significance (P-value), and measures of heterogeneity I2 (with 95% CI) and tau2 (τ2). Estimates based on robust regression methods (robust) provide a SMD, SE, and 95% CI of the SMD, P-value, and τ2. Treatment and experiment numbers were too small to evaluate robust regression results for the amount of connective tissue or Meat Standards Australia meat quality 4 score.
aWarner-Bratzler shear force.
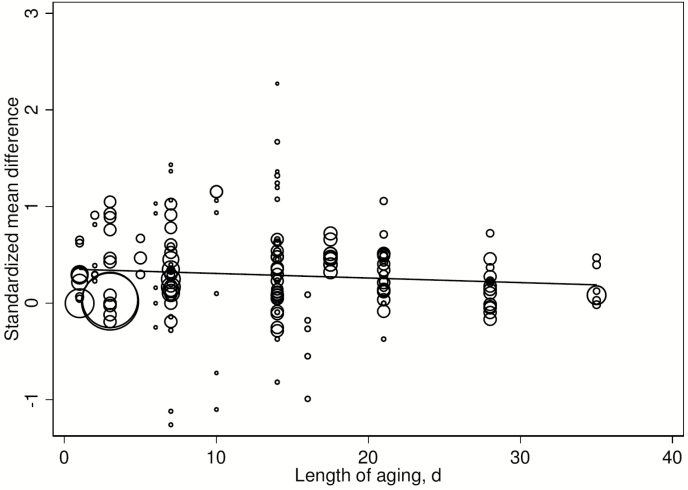
Univariable meta-regression analyses were conducted using Knapp–Hartung methods to evaluate the association of potential effect modifiers with beef quality outcomes (Tables 5 to 9). Multiple implants increased the SMD for WBSF by 0.196 and explained 18.1% of the variance in treatment (Table 5). The heterogeneity for this remained high, as was the case for the other variables examined in meta-regression. The robust regression had a larger ES (0.487, P = 0.026). Further investigation of the effects of implants on WBSF indicated that the Knapp–Hartung SMD for a single implant only on WBSF was 0.195 (95% CI = 0.126 to 0.264; P < 0.001) and had a lower heterogeneity (I2 = 28.9) and very low τ2 (0.03). Evaluation of the effect of a single HGP implant only on the SMD for WBSF using the robust regression model provided an estimate of 0.219 (95% CI = −0.010 to 0.447; P = 0.06). The aging of beef (Knapp–Hartung P = 0.105; Fig. 5) and robust regression (P = 0.315), with single implants, was not associated with altering the ES for WBSF. It is a limitation of the study that the evaluations of the effect of single or multiple HGP implants could not be derived from direct comparisons and reflect a mixture of differing HGP implant approaches.
Table 5.
Meta-regression estimates (univariable analyses) for the effects of length of time that beef was aged before evaluation, length of time that cattle were fed, use of multiple HGP implants (yes or no), treatment comparisons using TBA (yes or no), breed of cattle, sex of cattle, and electrical stimulation of the carcass on WBSF responses
| Variable | SMD | SE | 95% CI | P-value | R 2 | I 2, % | τ2 |
|---|---|---|---|---|---|---|---|
| Aging of the beef, d (KH) | −0.005 | 0.003 | −0.010 to 0.001 | 0.105 | −0.55 | 46.7 | 0.043 |
| Aging of the beef, d (robust) | −0.009 | 0.008 | −0.029 to 0.011 | 0.315 | 0.001 | ||
| Length of feeding, d (KH) | 0.001 | 0.0006 | −0.0002 to 0.002 | 0.125 | −5.06 | 39.9 | 0.035 |
| Length of feeding, d (robust) | 0.001 | 0.0026 | −0.010 to 0.013 | 0.705 | 0.001 | ||
| Multiple implants, % of studies (KH) | 0.196 | 0.051 | 0.095 to 0.296 | 0.001 | 18.1 | 46.9 | 0.036 |
| Multiple implants, % of studies (robust) | 0.487 | 0.164 | 0.083 to 0.892 | 0.026 | 0.001 | ||
| TBA, % of studies (KH) | −0.100 | 0.077 | −0.252 to 0.052 | 0.196 | −3.17 | 47.1 | 0.045 |
| TBA, % of studies (robust) | 0.241 | 0.232 | −0.290 to 0.772 | 0.327 | 0.001 | ||
| Breeda (reference British, British cross, European, and Holstein) | |||||||
| Brahman and Brahman crosses (KH) | −0.017 | 0.064 | −0.144 to 0.110 | 0.789 | 4.39 | 42.7 | 0.042 |
| Crossbred (undescribed; KH) | 0.189 | 0.087 | 0.018 to 0.360 | 0.031 | |||
| Not stated (KH) | 0.423 | 0.217 | −0.006 to 0.853 | 0.053 | |||
| Sexa (reference steers) | |||||||
| Bull (KH) | 0.289 | 0.186 | −0.077 to 0.656 | 0.121 | 9.21 | 44.3 | 0.040 |
| Heifer (KH) | −0.084 | 0.055 | −0.193 to 0.024 | 0.127 | |||
| Mixed (KH) | 0.082 | 0.115 | −0.145 to 0.308 | 0.477 | |||
| Stimulation (reference not stimulated) | |||||||
| Stimulated (KH) | 0.059 | 0.090 | −0.119 to 0.238 | 0.512 | 4.08 | 47.9 | 0.042 |
| Not stated (KH) | 0.197 | 0.094 | 0.012 to 0.383 | 0.037 | |||
The estimates based on Knapp–Hartung methods (KH) provide a SMD, SE, and 95% CI of the SMD, significance (P-value), model fit (R2), and measures of heterogeneity I2 and τ2. Estimates based on robust regression methods (robust) at the treatment level provide a SMD, SE, and 95% CI of the SMD, P-value, and τ2. There were 177 treatment comparisons and 28 experiments.
aThe distribution of data leads to small degrees of freedom for sex and breed, resulting in unreliable P-values for the robust regression.
Table 9.
Meta-regression estimates for the association of length of time that beef was aged before evaluation, length of time that cattle were fed, use of multiple HGP implants (yes or no), and treatment comparisons using TBA (yes or no) on connective tissue responses
| Variable | SMD | SE | 95% CI | P-value | R 2 | I 2, % | τ2 |
|---|---|---|---|---|---|---|---|
| Aging of beef, d | 0.005 | 0.377 | −0.076 to 0.086 | 0.900 | −28.80 | 38.53 | 0.277 |
| Length of feeding, d | −0.009 | 0.006 | −0.021 to 0.003 | 0.115 | 6.8 | 28.3 | 0.200 |
| Multiple implants, % of studies | 0.729 | 0.611 | −0.582 to 2.040 | 0.253 | 1.89 | 33.43 | 0.211 |
| TBA, % of studies | 0.063 | 0.436 | −0.872 to 0.998 | 0.887 | −16.77 | 38.31 | 0.251 |
The estimates are based on Knapp–Hartung methods and provide a SMD, SE, and 95% CI of the ES, significance (P-value), model fit (R2), and measures of heterogeneity I2 and τ2. There were 16 treatment comparisons and 4 experiments.
Figure 5.
Standardized mean difference between reference and HGP treatment for WBSF of primarily the Longissimus dorsi muscle in beef cattle with increasing length of aging of beef in beef cattle.
The tenderness of the beef (Table 6), as assessed by taste panels, was evaluated using different scoring systems. The only variable that was significantly associated with tenderness was the use of multiple implants that increased tenderness compared to a single implant (SMD = 0.468). Treatments using crossbreds of undescribed breed and unstated breed treatments had more tender outcomes than those using British, British breed cross, European, and Holstein, cattle. The limited number of bull treatments tended to produce beef assessed as more tender. All the results had substantial heterogeneity with estimates of I2 being all >60%. The τ2 were moderately low (<0.3), indicating that the remaining heterogeneity was substantial and influenced by factors other than the true effects.
Table 6.
Meta-regression estimates for the effects of length of time that beef was aged before evaluation, length of time that cattle were fed, use of multiple HGP implants (yes or no), treatment comparisons using TBA (yes or no), breed of cattle, sex of cattle, and electrical stimulation of the carcass on tenderness responses
| Variable | SMD | SE | 95% CI | P-value | R 2 | I 2, % | τ2 |
|---|---|---|---|---|---|---|---|
| Aging of the beef, d | 0.011 | 0.014 | −0.167 to 0.038 | 0.435 | 0.10 | 78.11 | 0.273 |
| Length of feeding, d | −0.001 | 0.002 | −0.005 to 0.005 | 0.872 | −18.6 | 65.3 | 0.277 |
| Multiple implants, % of studies | 0.468 | 0.182 | 0.104 to 0.832 | 0.013 | 41.46 | 71.34 | 0.16 |
| TBA, % of studies | 0.364 | 0.246 | −0.129 to 0.858 | 0.145 | 7.06 | 78.43 | 0.254 |
| Breed (reference British, British cross, European, and Holstein) | |||||||
| Brahman and Brahman crosses | −0.211 | 0.182 | −0.576 to 0.154 | 0.252 | 68.21 | 73.03 | 0.087 |
| Crossbred (undescribed) | 0.537 | 0.177 | 0.181 to 0.892 | 0.004 | |||
| Not stated | −1.167 | 0.547 | −2.083 to −0.251 | 0.014 | |||
| Sex (reference steers) | |||||||
| Bull | 0.974 | 0.493 | −0.013 to 1.962 | 0.053 | 0.55 | 76.0 | 0.272 |
| Heifer | 0.068 | 0.349 | −0.630 to 0.767 | 0.845 | |||
| Mixed | −0.390 | 0.447 | −1.29 to 0.505 | 0.386 | |||
| Stimulation (reference not stimulated) | |||||||
| Stimulated | −0.341 | 0.235 | −0.812 to 0.129 | 0.151 | 55.02 | 72.25 | 0.123 |
| Not stated | 0.371 | 0.192 | −0.141 to 0.756 | 0.059 | |||
The estimates are based on Knapp–Hartung methods and provide a SMD, SE, and 95% CI of the SMD, significance (P-value), model fit (R2), and measures of heterogeneity I2 and τ2. There were 59 treatment comparisons and 15 experiments.
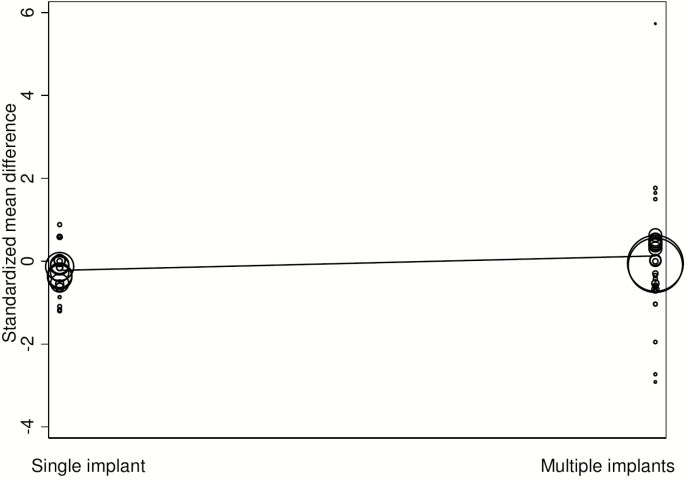
Use of multiple HGP implants was associated (P = 0.008; R2 = 56%) with increased juiciness of the meat compared with a single HGP implant (Table 7); however, the overall effect of implant use was to restore juiciness toward the level of no HGP implant (Fig. 6). Treatment comparisons using crossbred cattle with no description of the breeds used resulted in juicier meat than the British breed category. There was marked heterogeneity in all the meta-regression estimates for juiciness with estimates of I2 being moderate to substantial; all were >50% (Table 7). Again, the τ2 were low (<0.05), indicating that the remaining heterogeneity was substantial and influenced by factors other than the true effects.
Table 7.
Meta-regression estimates for the association of length of time that beef was aged before evaluation, length of time that cattle were fed, use of multiple HGP implants (yes or no), treatment comparisons using TBA (yes or no), breed of cattle, sex of cattle, and electrical stimulation of the carcass on juiciness responses
| Variable | SMD | SE | 95% CI | P-value | R 2 | I 2, % | τ2 |
|---|---|---|---|---|---|---|---|
| Aging of the beef, d | 0.013 | 0.009 | −0.006 to 0.031 | 0.179 | 6.2 | 65.7 | 0.096 |
| Length of feeding, d | 0.001 | 0.0006 | −0.0003 to 0.002 | 0.135 | 100.0 | 50.7 | 0.001 |
| Multiple implants, % of studies | 0.348 | 0.126 | 0.096 to 0.600 | 0.008 | 54.5 | 61.2 | 0.044 |
| TBA, % of studies | 0.134 | 0.185 | −0.237 to 0.504 | 0.473 | 2.58 | 66.7 | 0.099 |
| Breed (reference British, British cross, European, and Holstein) | |||||||
| Brahman and Brahman crosses | −0.065 | 0.127 | −0.321 to 0.190 | 0.611 | 73.5 | 54.8 | 0.027 |
| Crossbred (undescribed) | 0.513 | 0.132 | 0.248 to 0.778 | 0.001 | |||
| Not stated | −0.455 | 0.355 | −1.167 to 0.257 | 0.206 | |||
| Sex (reference steers) | |||||||
| Bull | 0.425 | 0.502 | −0.580 to 1.430 | 0.400 | 8.89 | 64.3 | 0.093 |
| Heifer | −0.178 | 0.293 | −0.765 to 0.409 | 0.546 | |||
| Mixed | −0.351 | 0.294 | −0.941 to 0.308 | 0.239 | |||
| Stimulation (reference not stimulated) | |||||||
| Stimulated | −0.117 | 0.168 | −0.454 to 0.238 | 0.487 | 58.6 | 62.3 | 0.042 |
| Not stated | 0.325 | 0.143 | 0.012 to 0.039 | 0.027 | |||
The estimates are based on Knapp–Hartung methods and provide a SMD, SE, and 95% CI of the ES, significance (P-value), model fit (R2), and measures of heterogeneity I2 and τ2. There were 55 treatment comparisons and 12 experiments.
Figure 6.
Standardized mean difference between reference and HGP treatment for juiciness of primarily the Longissimus dorsi muscle in beef cattle implanted with single or multiple HGPs.
Although there was no significant association between treatment with HGP and measures of flavor, there were many significant meta-regression effects (Table 8). Aging of the beef was associated with higher flavor (P = 0.003; R2 = 51%) as was use of multiple implants (P = 0.004; R2 = 46%); however, the I2 for these interventions were high (>50%). The mixed sex groups were associated with less flavor than the steers. Differences in beef flavor were present between breeds with crossbred cattle being associated with beef with more flavor than the British breed category. There was increased beef flavor in cattle that were administered with HGPs with unknown presence or absence of stimulation of the meat (not stated stimulation) compared with those whose meat was not stimulated. Again, estimates of I2 were moderate to substantial, with the exception of breed that was moderate. Estimates of τ2 were small.
Table 8.
Meta-regression estimates for the association of length of time that meat was aged before evaluation, length of time that cattle were fed, use of multiple HGP implants (yes or no), treatment comparisons using TBA (yes or no), breed of cattle, sex of cattle, and electrical stimulation of the carcass on flavor responses
| Variable | ES | SE | 95% CI | P-value | R 2 | I 2, % | τ2 |
|---|---|---|---|---|---|---|---|
| Aging of the beef, d | 0.036 | 0.011 | 0.013 to 0.059 | 0.003 | 51.08 | 59.11 | 0.049 |
| Length of feeding, d | −0.0004 | 0.002 | −0.005 to 0.005 | 0.872 | −18.60 | 55.3 | 0.277 |
| Multiple implants, % of studies | 0.436 | 0.141 | 0.151 to 0.722 | 0.004 | 45.89 | 59.79 | 0.055 |
| TBA, % of studies | −0.023 | 0.229 | −0.485 to 0.439 | 0.920 | −5.28 | 68.98 | 0.107 |
| Breed (reference British, British cross, European, and Holstein) | |||||||
| Brahman and Brahman crosses | −0.158 | 0.114 | −0.388 to 0.073 | 0.175 | 81.65 | 37.24 | 0.019 |
| Crossbred (undescribed) | 0.577 | 0.114 | 0.348 to 0.807 | 0.001 | |||
| Not stated | 0.203 | 0.286 | −0.373 to 0.780 | 0.481 | |||
| Sex (reference steers) | |||||||
| Bull | 0.369 | 0.495 | −0.629 to 1.36 | 0.460 | 52.28 | 57.26 | 0.048 |
| Heifer | −0.223 | 0.287 | −0.802 to 0.357 | 0.443 | |||
| Mixed | −0.651 | 0.208 | −1.070 to −2.233 | 0.003 | |||
| Stimulation (reference not stimulated) | |||||||
| Stimulated | −0.344 | 0.462 | −1.274 to 0.585 | 0.460 | 45.20 | 63.09 | 0.055 |
| Not stated | 0.385 | 0.131 | 0.121 to 0.649 | 0.005 | |||
The estimates are based on Knapp–Hartung methods and provide a SMD, SE, and 95% CI of the ES, significance (P-value), model fit (R2), and measures of heterogeneity I2 and τ2. There were 48 treatment comparisons and 11 experiments.
There were limited number of observations (n = 16 treatment comparisons) on the effects of HGP on connective tissue content of beef and none of the meta-regression effects studied were significant (Table 9). Also, there were limited observations (n = 9 treatment comparisons) for MQ4 and meta-regressions were not explored. The WMD for MQ4 was −5.52 (95% CI = −7.94 to −3.10).
Effects of HGPs on WBSF and sensory panel tenderness, juiciness, flavor, connective tissue, and MQ4 were further investigated in multivariable models using Knapp–Hartung, permutation, and robust analysis methods. In Table 10, the results of these analyses are provided for WBSF. The P-values for the Knapp–Hartung meta-regressions are provided as results of the permutation analyses (Harbord and Higgins, 2008). These models show that the use of multiple implants was associated with an increased WBSF and that the treatment comparisons that did not include a description of electrical stimulation were associated with a greater WBSF than those that reported no stimulation. The relatively small number of experiments reporting other beef quality metrics precluded multivariable analysis.
Table 10.
Multivariable meta-regression estimates for the association of use of multiple HGP implants (yes or no) and electrical stimulation of the carcass on WBSF responses
| Variable | SMD | SE | 95% CI | P-value | R 2 | I 2, % | τ2 |
|---|---|---|---|---|---|---|---|
| Multiple implants, % of studies (KH) | 0.215 | 0.051 | 0.114 to 0.315 | 0.001 | 20.4 | 47.4 | 0.035 |
| Stimulation (reference not stimulated) | |||||||
| Stimulated (KH) | 0.084 | 0.088 | −0.089 to 0.257 | 0.654 | |||
| Not stated (KH) | 0.237 | 0.092 | 0.057 to 0.419 | 0.035 | |||
| Multiple implants, % of studies (robust experiment level) | −0.030 | 0.069 | −0.380 to 0.320 | 0.852 | 0.001 | ||
| Multiple implants, % of studies (robust treatment level) | 0.461 | 0.175 | 0.312 to 0.890 | 0.039 | |||
| Stimulation (reference not stimulated) | |||||||
| Stimulated (robust experiment level) | 0.128 | 0.162 | −0.288 to 0.544 | 0.465 | |||
| Not stated (robust experiment level) | 0.241 | 0.196 | −0.244 to 0.725 | 0.267 | |||
The estimates based on Knapp–Hartung (KH) methods provide a SMD, SE, and 95% CI of the SMD, significance (P-value), model fit (R2), and measures of heterogeneity I2 and τ2. The estimates based on robust regression methods (robust) at the experiment and treatment level provide a SMD, SE, and 95% CI of the SMD, P-value, and τ2.
DISCUSSION
There were sufficient experiments and treatment comparisons to provide a rigorous evaluation of the effects of HGP treatment on WBSF. Almost all experiments evaluated in the current meta-analysis refer exclusively to the effects of HGP on LM, with only 2 treatments from 1 experiment using M. semitendinosus. The evidence base for muscles other than LM would have been considerably less. However, LM differs from other muscles in terms of aging. Gruber et al. (2006) found a large aging response for LM tenderness with a decrease of 2.5 kg in muscles obtained for USDA Select grade carcasses aged for 26 d and 2.0 kg lower shear force for muscles from USDA Choice carcasses from aging for 15 d. These were the greatest improvements in tenderness of any of the 17 muscles tested for change in tenderness with aging for the respective carcass quality categories across all publications assessed.
There were essentially 2 approaches taken to the analysis of these data. The results of classical meta-analysis, with a random effect of experiment, are provided and meta-regression methods are used to explore the heterogeneity in the SMD using Knapp–Hartung and permutation methods. The second robust method contains the random effect of experiment and treatment, and while it is possible to explore other variables using meta-regression, there were no factors that were significant in this model used to examine variability in WBSF. The 2 methods are included to provide a less conservative, but more informative evaluation of effects that may modify the response in WBSF with HGP treatments using the Knapp–Hartung and permutation model.
The SMD for the effect of HGP on WBSF obtained from the Knapp–Hartung and robust regression are very similar and both significant, showing an increase of approximately 0.30 SMD (Table 4) with a WMD of 0.25 kg of force between HGP treated and reference cattle. This increase is consistent with the estimates of effect for HGP treatment on WBSF (WMD = 0.27 kg) derived by Watson (2008) with fewer experiments and treatments.
It has been proposed that aging can reduce the effects of HGP on WBSF (Thompson et al., 2008). Some experiments support this finding (Schneider et al., 2007; Thompson et al., 2008; Igo et al., 2011; Packer et al., 2018), while others did not (Platter et al., 2003), and many experiments did not explicitly examine the effect of aging on the WBSF response to HGP. There was limited evidence to support a diminished effect of the HGP on WBSF from this experiment (Table 5; Fig. 4). However, the nonsignificant point effect of aging on SMD was −0.005 SMD per day or −0.15 SMD over 30 d; representing half the overall effect of HGP on WBSF, but aging explained little of the overall variance in SMD. The largest experiments had relatively short aging periods. The nonsignificant difference in WBSF of −0.15 SMD from 30 d of aging between treatments and references estimated in this experiment is much smaller than the effect on WBSF of aging alone over 15 and 26 d of 2.0 to 2.5 kg less force, respectively, in LM as reported by Gruber et al. (2006).
The effect of multiple implants in increasing WBSF has been consistently reported (Dikeman, 2007) and strongly supported in this experiment. The low heterogeneity for the effects of multiple implants suggests that these responses were relatively consistent across treatments. The use of a single implant, whether this be a single agent or combination had a more limited effect on WBSF than multiple treatments.
It has been suggested that TBA may have a greater effect on increasing WBSF than other HGP treatments (Gerken et al., 1995; Packer et al., 2018). There are few experiments that test this hypothesis with single treatments, as many TBA treatments are conducted with combined TBA and estrogen treatments. Gerken et al. (1995) using 6 cloned steers per group found no significant difference in WBSF between treatment with a single estrogenic implant, containing 20 mg of estradiol benzoate and 200 mg of progesterone (Synovex-S) to a single androgenic implant, containing 140 mg of TBA (Finaplex). However, in our experiment, the point effect was toward TBA, associated with a reduced WBSF and the effect was not significant. The TBA implants were used in 81% of treatments either as a single, or more typically, as a combined HGP. Descriptions of the large number of different HGP products used in experiments were not always definitively provided and it was not assumed that product equivalency existed for different formulations with similar active agents. Consequently, a specific analysis for the different TBA products used was not indicated.
The evidence base for this experiment is a little unusual, because there was considerable variation in the experimental designs used. Most experiments had multiple treatment comparisons, with Schneider et al. (2007) containing 55 treatment comparisons. Fifty percent of treatments used more than 1 implant; some treatments used up to 5 implants. Experiments represented a wide range in productivity and diet composition, some reflecting feedlot practice, and some extensive pasture-based production. Further, the treatments were conducted, primarily using British and European breeds (71%) and 18% were on Brahman and Brahman cross cattle and mostly on steers (55%) or heifers (36%). Some experiments were conducted at the pen level (Foutz et al., 1997; Kerth et al., 2003; Igo et al., 2011), whereas others were conducted with individual cattle as the unit of interest (Barham et al., 2003; Cafe et al., 2010; Packer et al., 2018). This variation in experimental design was reflected in the variance attributable to treatment within experiment being 44% of the total variance. Other meta-analytical experiments found the variance attributable to treatment level was much lower, in the order of 3% to 6% (Lean et al., 2018). The τ2 representing the variance in the SMD were low, rarely exceeding 0.2 and often <0.1, but the heterogeneity attributable to random sampling errors are high, almost all with I2 > 50 (Tables 4 to 10). The considerable variation in experimental design suggested a need for caution in interpretation of meta-regression results, such as those for TBA, because confounding of HGP treatment effects with breed, sex, or stimulation of carcass was present for single implant TBA data. However, evaluation of these TBA results controlling for the effect of breed, provided no evidence that the estimates were affected by breed “British” or “Brahman” and that TBA use was not associated with a higher WBSF than other HGP interventions (data not shown). There was little evidence to support breed or sex differences in modifying the effect of HGP on WBSF, with the possible exception of treatments using undescribed crossbred cattle (Table 5). However, this effect was not present in the robust regression (results not shown). Similarly, the treatments that did not report whether electrical stimulation of the carcass was used differed for WBSF to the unstimulated studies (SMD = 0.2), but only for the Knapp–Hartung and permutation model. There were few experiments represented by the undescribed crossbreds (n = 3) and while 19 experiments with unstated stimulation categories were present, the more conservative results of the robust regression models indicating no effect of crossbreds or electrical stimulation are appropriate.
The overall nonsignificant effect of HGP on tenderness based on the sensory evaluation was consistent with that presented in Table 2 of Nichols et al. (2002), but not with Watson (2008) who found that HGP reduced the tenderness of LM by approximately 5 units on a 100-point scale. None of these 3 quantitative evaluations use identical evidence bases, but many of the experiments used are the same. Watson (2008) converted the scales of assessment used in the original papers to provide a WMD, whereas Nichols et al. (2002) provided the data, but no pooled estimates of effect and this experiment evaluated ES, thus using the original data from experiments to provide the pooled estimate, albeit in z-score units.
The sensory panel tenderness responses did not support the WBSF findings in that use of multiple implants was associated with increased tenderness by 0.47 SMD. It should be noted that there are 13 less experiments in the sensory panel tenderness and juiciness evaluations than for the WBSF database. Further, use of both a single, or multiple HGP implants were associated with improved tenderness. It is also possible that time on feed, which differed between use of single (mean days on feed were 132 ± 15 d) compared to multiple implants (mean days on feed were 183 ± 8 d), may have influenced this result. While there are strong correlations between WBSF and sensory panel tenderness scores for LM, Shackelford et al. (1995) discussed the variability and inconsistency in relationships between WBSF and sensory panel tenderness scores. Duckett and Pratt (2014) also comment on the variability in responses between WBSF and sensory measures. Despite the strong correlations between WBSF and sensory panel tenderness scores for LM, it appears that sensory panel tenderness assessment of LM treated with HGP or not differed from the WBSF assessed response.
Aging did not influence the difference in sensory panel tenderness; however, the point direction was to increased tenderness. Undescribed breed crosses were associated with more sensory panel tenderness than “British” cattle and “not stated breed” were associated with being less tender than British cattle. Bulls were present in a very low number of experiments (n = 4), but tended (P = 0.055) to be associated with more tenderness than steers, possibly reflecting an earlier time to slaughter or other confounding factors.
There were limited observations for juiciness which was not significantly reduced with HGP use, nor associated with increased aging or length of feeding. The juiciness was associated with multiple implant use, and undescribed crossbred cattle compared to “British” cattle, a result consistent with the findings for tenderness, but not WBSF. Similarly, the use of multiple implants, undescribed crossbred cattle compared to “British” cattle, and treatments that did not state whether carcass stimulation occurred, were associated with increased flavor of the beef. There is a pattern of improved sensory panel performance for the treatments that had these characteristics, that is, multiple implant use, undescribed crossbred cattle compared to “British” cattle, and treatments that did not state whether carcass stimulation occurred for sensory panel tenderness, juiciness, and flavor. It is unclear if these effects have a biological basis, or whether these findings reflect confounding for these relatively sparse observations. Both sensory panel tenderness and juiciness were conducted using the same evidence base of 15 experiments and 59 treatment comparisons, but flavor had less observations. It is notable; however, that aging was associated with increased flavor, an observation with a biological basis.
There were very limited observations on connective tissue (n = 16 treatments) and MQ4 (n = 9 treatments) responses to HGP treatment, highlighting the need for further studies. While connective tissue content was not altered by HGP treatment, MQ4 was reduced by HGP treatment by 5.54 units on the 100-point scale. This effect is large, but the number of studies from which it is derived is very low. Given the limited number of MQ4 comparisons and studies further evaluation of responses was not undertaken.
CONCLUSIONS
The responses in this meta-analysis showed treatment with HGP increased WBSF in meat. While use of multiple HGP implants was associated with a large increase in WBSF, a single implant had limited effects. Aging of HGP-treated beef did not significantly reduce the increased SMD for WBSF compared to the reference group; however, the point direction was toward a reduced difference in effect on WBSF as the number of days of aging increased. Tenderness, juiciness, flavor, and connective tissue content in beef, as assessed by sensory methods were not associated with HGP use, whereas there was a marked 5.5-point decrease in MQ4 in cattle treated with HGPs, albeit in limited studies. There is a need for more targeted studies on the role of HGP in influencing beef quality. These studies need to address limitations in the data including further exploration of the effects of single or multiple implants with matched treatments, comparative studies of the effects of implants and effects of genetic differences on implant responses. These studies would help address limitations of the current study.
SUPPLEMENTARY DATA
Supplementary data are available at Journal of Animal Science online.
ACKNOWLEDGMENTS
We acknowledge J. Perovic (Meat and Livestock Australia Ltd, Armidale, NSW, Australia) for her contribution to paper review. Funding support for this research was provided by Meat and Livestock Australia Ltd.
LITERATURE CITED
- Apple J. K., Dikeman M. E., Simms D. D., and Kuhl G.. 1991. Effects of synthetic hormone implants, singularly or in combinations, on performance, carcass traits, and longissimus muscle palatability of Holstein steers. J. Anim. Sci. 69:4437–4448. doi:10.2527/1991.69114437x [DOI] [PubMed] [Google Scholar]
- Barham B. L., Brooks J. C., Blanton J. R. Jr, Herring A. D., Carr M. A., Kerth C. R., and Miller M. F.. 2003. Effects of growth implants on consumer perceptions of meat tenderness in beef steers. J. Anim. Sci. 81:3052–3056. doi:10.2527/2003.81123052x [DOI] [PubMed] [Google Scholar]
- Boles J. A., Boss D. L., Neary K. I., Davis K. C., and Tess M. W.. 2009. Growth implants reduced tenderness of steaks from steers and heifers with different genetic potentials for growth and marbling. J. Anim. Sci. 87:269–274. doi:10.2527/jas.2008-1256 [DOI] [PubMed] [Google Scholar]
- Borenstein M., Higgins J. P. T., Hedges L. V., and Rothstein H. R.. 2017. Basics of meta-analysis: I2 is not an absolute measure of heterogeneity. Res. Synth. Methods 8:5–18. doi:10.1002/jrsm.1230 [DOI] [PubMed] [Google Scholar]
- Cafe L. M., McIntyre B. L., Robinson D. L., Geesink G. H., Barendse W., Pethick D. W., Thompson J. M., and Greenwood P. L.. 2010. Production and processing studies on calpain-system gene markers for tenderness in Brahman cattle: 2. Objective meat quality. J. Anim. Sci. 88:3059–3069. doi:10.2527/jas.2009–2679 [DOI] [PubMed] [Google Scholar]
- Calkins C. R., Clanton D. C., Berg T. J., and Kinder J. E.. 1986. Growth, carcass and palatability traits of intact males and steers implanted with zeranol or estradiol early and throughout life. J. Anim. Sci. 62:625–631. doi:10.2527/jas1986.623625x [DOI] [PubMed] [Google Scholar]
- Capper J. L. and Hayes D. J.. 2012. The environmental and economic impact of removing growth-enhancing technologies from U.S. beef production. J. Anim. Sci. 90:3527–3537. doi:10.2527/jas.2011-4870 [DOI] [PubMed] [Google Scholar]
- Cheatham R., Duff G., Bailey C., Sanders S., Collier R., Marchello J., and Baumgard L.. 2008. Effects of implant programs on performance, carcass characteristics, and lipogenic gene expression in Holstein steers. S. Afr. J. Anim. Sci. 38:238–246. http://www.scielo.org.za/scielo.php?script=sci_arttext&pid=S0375-15892008000300011&lng=en&nrm=iso>. ISSN: 2221-4062. [Google Scholar]
- Clarke M. J., and Stewart L. A.. 2001. Principles of and procedures for systematic reviews. In: M. Egger, G. D. Smith, and D. G. Altman, editors, Systematic reviews in health care meta-analysis in context no. 23-41. British Medical Journal Books, London. [Google Scholar]
- DerSimonian R. and Laird N.. 1986. Meta-analysis in clinical trials. Control. Clin. Trials. 7:177–188. doi:10.1016/0197-2456(86)90046-2 [DOI] [PubMed] [Google Scholar]
- Dikeman M. E. 2007. Effects of metabolic modifiers on carcass traits and meat quality. Meat Sci. 77:121–135. doi:10.1016/j.meatsci.2007.04.011 [DOI] [PubMed] [Google Scholar]
- Dohoo I. R., Martin S. W., and Stryhn H.. 2009. Veterinary epidemiologic research. VER, Incorporated, Charlottetown, Prince Edward Island, Canada. [Google Scholar]
- Duckett S., and Pratt S.. 2014. Meat science and muscle biology symposium—anabolic implants and meat quality. J. Anim. Sci. 92:3–9. doi:10.2527/jas.2013-7088 [DOI] [PubMed] [Google Scholar]
- Ebarb S. M., Drouillard J. S., Maddock-Carlin K. R., Phelps K. J., Vaughn M. A., Burnett D. D., Van Bibber-Krueger C. L., Paulk C. B., Grieger D. M., and Gonzalez J. M.. 2016. Effect of growth-promoting technologies on Longissimus lumborum muscle fiber morphometrics, collagen solubility, and cooked meat tenderness. J. Anim. Sci. 94:869–881. doi:10.2527/jas.2015-9888 [DOI] [PubMed] [Google Scholar]
- Ebarb S. M., Phelps K. J., Drouillard J. S., Maddock-Carlin K. R., Vaughn M. A., Burnett D. D., Noel J. A., Van Bibber-Krueger C. L., Paulk C. B., Grieger D. M., et al. 2017. Effects of anabolic implants and ractopamine-HCl on muscle fiber morphometrics, collagen solubility, and tenderness of beef Longissimus lumborum steaks. J. Anim. Sci. 95:1219–1231. doi:10.2527/jas.2016.1263 [DOI] [PubMed] [Google Scholar]
- Foutz C. P., Dolezal H. G., Gardner T. L., Gill D. R., Hensley J. L., and Morgan J. B.. 1997. Anabolic implant effects on steer performance, carcass traits, subprimal yields, and longissimus muscle properties. J. Anim. Sci. 75:1256–1265. doi:10.2527/1997.7551256x [DOI] [PubMed] [Google Scholar]
- Gerken C. L., Tatum J. D., Morgan J. B., and Smith G. C.. 1995. Use of genetically identical (clone) steers to determine the effects of estrogenic and androgenic implants on beef quality and palatability characteristics. J. Anim. Sci. 73:3317–3324.doi:10.2527/1995.73113317x [DOI] [PubMed] [Google Scholar]
- Golder H. M. and Lean I. J.. 2016. A meta-analysis of lasalocid effects on rumen measures, beef and dairy performance, and carcass traits in cattle. J. Anim. Sci. 94:306–326. doi:10.2527/jas.2015-9694 [DOI] [PubMed] [Google Scholar]
- Gruber S. L., Tatum J. D., Scanga J. A., Chapman P. L., Smith G. C., and Belk K. E.. 2006. Effects of postmortem aging and USDA quality grade on Warner-Bratzler shear force values of seventeen individual beef muscles. J. Anim. Sci. 84:3387–3396. doi:10.2527/jas.2006-194 [DOI] [PubMed] [Google Scholar]
- Harbord R. M., and Higgins J.. 2008. Meta-regression in Stata. Meta. 8:493–519. https://www.stata.com/meeting/uk10/UKSUG10.Harbord.pdf. [Google Scholar]
- Harbord R. M., and Steichen T. J.. 2004. “Metareg: stata module to perform meta-analysis regression,” statistical software components S4446201. Boston College, Department of Economics, Revised 5 January 2009. [Google Scholar]
- Hedges L. V., Tipton E., and Johnson M. C.. 2010. Robust variance estimation in meta-regression with dependent effect size estimates. Res. Synth. Methods 1:39–65. doi:10.1002/jrsm.5 [DOI] [PubMed] [Google Scholar]
- Higgins J. P. T., and Green S.. 2011. Cochrane handbook for systematic reviews of interventions version 5.1.0 [updated March 2011]. The Cochrane Collaboration. [Google Scholar]
- Higgins J. P. T., and Thompson S. G.. 2002. Quantifying heterogeneity in a meta-analysis. Stat. Med. 21:1539–1558. doi:10.1002/sim.1186 [DOI] [PubMed] [Google Scholar]
- Higgins J. P. T., and Thompson S. G.. 2004. Controlling the risk of spurious findings from meta-regression. Stat. Med. 23:1663–1682. doi:10.1002/sim.1752 [DOI] [PubMed] [Google Scholar]
- Hopkins T. D. and Dikeman M. E.. 1987. Effects of oestradiol-17β implantation on performance, carcass traits, meat sensory traits and endocrine aspects of bulls and steers. Meat Sci. 21:51–65. doi:10.1016/0309-1740(87)90041-6 [DOI] [PubMed] [Google Scholar]
- Hunt D. W., Henricks D. M., Skelley G. C., and Grimes L. W.. 1991. Use of trenbolone acetate and estradiol in intact and castrate male cattle: effects on growth, serum hormones, and carcass characteristics. J. Anim. Sci. 69:2452–2462. doi:10.2527/1991.6962452x [DOI] [PubMed] [Google Scholar]
- Hunter R. 2010. Hormonal growth promotant use in the Australian beef industry. Anim. Prod. Sci. 50:637–659. doi:10.1071/AN09120 [Google Scholar]
- Hunter R. A., Burrow H. M., and McCrabb G. J.. 2001. Sustained growth promotion, carcass and meat quality of steers slaughtered at three liveweights. Aust. J. Exp. Agr. 41:1033–1040. doi:10.1071/EA00016 [Google Scholar]
- Hunter R. A., Magner T., and Allingham P. G.. 2000. Sustained growth promotion, carcass characteristics, and meat quality of steers treated with oestradiol-17β. Aust. J. Agric. Res. 51:133–138. doi:10.1071/AR99048 [Google Scholar]
- Igo J. L., Brooks J. C., Johnson B. J., Starkey J., Rathmann R. J., Garmyn A. J., Nichols W. T., Hutcheson J. P., and Miller M. F.. 2011. Characterization of estrogen-trenbolone acetate implants on tenderness and consumer acceptability of beef under the effect of 2 aging times. J. Anim. Sci. 89:792–797. doi:10.2527/jas.2010-3115 [DOI] [PubMed] [Google Scholar]
- IntHout J., Ioannidis J. P., and Borm G. F.. 2014. The Hartung-Knapp-Sidik-Jonkman method for random effects meta-analysis is straightforward and considerably outperforms the standard Dersimonian-Laird method. BMC Med. Res. Methodol. 14:25. doi:10.1186/1471-2288-14-25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis J. P., Patsopoulos N. A., and Evangelou E.. 2007. Uncertainty in heterogeneity estimates in meta-analyses. BMJ 335:914–916. doi:10.1136/bmj.39343.408449.80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerth C. R., Montgomery J. L., Morrow K. J., Galyean M. L., and Miller M. F.. 2003. Protein turnover and sensory traits of longissimus muscle from implanted and nonimplanted heifers. J. Anim. Sci. 81:1728–1735. doi:10.2527/2003.8171728x [DOI] [PubMed] [Google Scholar]
- Knapp G. and Hartung J.. 2003. Improved tests for a random effects meta-regression with a single covariate. Stat. Med. 22:2693–2710. doi:10.1002/sim.1482 [DOI] [PubMed] [Google Scholar]
- Lean I. J., de Ondarza M. B., Sniffen C. J., Santos J. E. P., and Griswold K. E.. 2018. Meta-analysis to predict the effects of metabolizable amino acids on dairy cattle performance. J. Dairy Sci. 101:340–364. doi:10.3168/jds.2016-12493 [DOI] [PubMed] [Google Scholar]
- Lean I. J., Rabiee A. R., Duffield T. F., and Dohoo I. R.. 2009. Invited review: use of meta-analysis in animal health and reproduction: methods and applications. J. Dairy Sci. 92:3545–3565. doi:10.3168/jds.2009-2140 [DOI] [PubMed] [Google Scholar]
- Nichols W. T., Galyean M. L., Thomson D. U., and Hutcheson J. P.. 2002. Effects of steroid implants on the tenderness of beef. Prof. Ani. Sci. 18:202–210. doi:10.15232/S1080-7446(15)31523-0 [Google Scholar]
- Nute G., and Dransfield E.. 1984. The quality of sirloin from zeranol implanted steers. Int. J. Food Sci. Tech. 19:21–28. doi:10.1111/j.1365–2621.1984.tb00324.x [Google Scholar]
- Ouali A., Zabari M., Renou J. P., Touraille C., Kopp J., Bonnet M., and Valin C.. 1988. Anabolic agents in beef production: effects on muscle traits and meat quality. Meat Sci. 24:151–161. doi:10.1016/0309- 1740(88)90074-5 [DOI] [PubMed] [Google Scholar]
- Packer D., Geesink G., Polkinghorne R., Thompson J., and Ball A.. 2018. The impact of two different hormonal growth promotants (HGPs) on the eating quality of feedlot finished steer carcasses. Anim. Prod. Sci. (in press). [DOI] [PubMed] [Google Scholar]
- Phelps K. J., Drouillard J. S., Jennings J. S., Depenbusch B. E., Van Bibber-Krueger C. L., Miller K. A., Vaughn M. A., Burnett D. D., Ebarb S. M., Houser T. A., et al. 2014. Effects of the programmed nutrition beef program on meat quality characteristics. J. Anim. Sci. 92:1780–1791. doi:10.2527/jas.2013-7231 [DOI] [PubMed] [Google Scholar]
- Platter W. J., Tatum J. D., Belk K. E., Scanga J. A., and Smith G. C.. 2003. Effects of repetitive use of hormonal implants on beef carcass quality, tenderness, and consumer ratings of beef palatability. J. Anim. Sci. 81:984–996. doi:10.2527/2003.814984x [DOI] [PubMed] [Google Scholar]
- Rabe-Hesketh S., and Skrondal A.. 2005. Multilevel and longitudinal modeling using Stata. STATA Press, College Station, TX. [Google Scholar]
- Rabiee A. R., Breinhild K., Scott W., Golder H. M., Block E., and Lean I. J.. 2012. Effect of fat additions to diets of dairy cattle on milk production and components: a meta-analysis and meta-regression. J. Dairy Sci. 95:3225–3247. doi:10.3168/jds.2011-4895 [DOI] [PubMed] [Google Scholar]
- Reiling B. A. and Johnson D. D.. 2003. Effects of implant regimens (trenbolone acetate-estradiol administered alone or in combination with zeranol) and vitamin D3 on fresh beef color and quality. J. Anim. Sci. 81:135–142. doi:10.2527/2003.811135x [DOI] [PubMed] [Google Scholar]
- Robinson D. L., Cafe L. M., McIntyre B. L., Geesink G. H., Barendse W., Pethick D. W., Thompson J. M., Polkinghorne R., and Greenwood P. L.. 2012. Production and processing studies on calpain-system gene markers for beef tenderness: consumer assessments of eating quality. J. Anim. Sci. 90:2850–2860. doi:10.2527/jas.2011-4928 [DOI] [PubMed] [Google Scholar]
- Roeber D. L., Cannell R. C., Belk K. E., Miller R. K., Tatum J. D., and Smith G. C.. 2000. Implant strategies during feeding: impact on carcass grades and consumer acceptability. J. Anim. Sci. 78:1867–1874.doi:10.2527/2000.7871867x [DOI] [PubMed] [Google Scholar]
- Rumsey T. S., Elsasser T. H., Kahl S., and Solomon M. B.. 1999. The effect of roasted soybeans in the diet of feedlot steers and Synovex-S ear implants on carcass characteristics and estimated composition. J. Anim. Sci. 77:1726–1734. doi:10.2527/1999.7771726x [DOI] [PubMed] [Google Scholar]
- Samber J. A., Tatum J. D., Wray M. I., Nichols W. T., Morgan J. B., and Smith G. C.. 1996. Implant program effects on performance and carcass quality of steer calves finished for 212 days. J. Anim. Sci. 74:1470–1476.doi:10.2527/1996.7471470x [DOI] [PubMed] [Google Scholar]
- Scheffler J. M., Buskirk D. D., Rust S. R., Cowley J. D., and Doumit M. E.. 2003. Effect of repeated administration of combination trenbolone acetate and estradiol implants on growth, carcass traits, and beef quality of long-fed Holstein steers. J. Anim. Sci. 81:2395–2400. doi:10.2527/2003.81102395x [DOI] [PubMed] [Google Scholar]
- Schneider B. A., Tatum J. D., Engle T. E., and Bryant T. C.. 2007. Effects of heifer finishing implants on beef carcass traits and longissimus tenderness. J. Anim. Sci. 85:2019–2030. doi:10.2527/jas.2007-0004 [DOI] [PubMed] [Google Scholar]
- Shackelford S. D., Savell J. W., Crouse J. D., Cross H. R., Schanbacher B. D., Johnson D. D., and Anderson M. L.. 1992. Palatability of beef from bulls administered exogenous hormones. Meat Sci. 32:397–405. doi:10.1016/0309-1740(92)90081-E [DOI] [PubMed] [Google Scholar]
- Shackelford S. D., Wheeler T. L., and Koohmaraie M.. 1995. Relationship between shear force and trained sensory panel tenderness ratings of 10 major muscles from Bos indicus and Bos taurus cattle. J. Anim. Sci. 73:3333–3340. doi:10.2527/1995.73113333x [DOI] [PubMed] [Google Scholar]
- Sterne J. A., and Harbord R. M.. 2004. Funnel plots in meta-analysis. Stata J. 4:127–141. [Google Scholar]
- St-Pierre N. 2001. Invited review: integrating quantitative findings from multiple studies using mixed model methodology. J. Dairy Sci. 84:741–755. doi:10.3168/jds.S0022-0302(01)74530–4 [DOI] [PubMed] [Google Scholar]
- Tanner‐Smith E. E., and Tipton E.. 2014. Robust variance estimation with dependent effect sizes: practical considerations including a software tutorial in Stata and SPSS. Res. Synth. Methods 5:13–30. doi:10.1002/jrsm.1091 [DOI] [PubMed] [Google Scholar]
- Thompson J., McIntyre B., Tudor G., Pethick D., Polkinghorne R., and Watson R.. 2008. Effects of hormonal growth promotants (HGP) on growth, carcass characteristics, the palatability of different muscles in the beef carcass and their interaction with aging. Aust. J. Exp. Agr. 48:1405–1414. doi:10.1071/EA07131 [Google Scholar]
- Thompson S. G. and Sharp S. J.. 1999. Explaining heterogeneity in meta-analysis: a comparison of methods. Stat. Med. 18:2693–2708. doi:10.1002/(SICI)1097-0258(1999 1030)18:20<2693::AID-SIM235>3.0.CO;2-V [DOI] [PubMed] [Google Scholar]
- Van den Noortgate W., López-López J. A., Marín-Martínez F., and Sánchez-Meca J.. 2013. Three-level meta-analysis of dependent effect sizes. Behav. Res. Methods 45:576–594. doi:10.3758/s13428-012-0261-6 [DOI] [PubMed] [Google Scholar]
- Watson R. 2008. Meta-analysis of the published effects of hgp use on beef palatability in steers as measured by objective and sensory testing. Aust. J. Exp. Agr. 48:1425–1433. doi:10.1071/EA07174 [Google Scholar]
- Watson R., Gee A., Polkinghorne R., and Porter M.. 2008. Consumer assessment of eating quality–development of protocols for Meat Standards Australia (MSA) testing. Anim. Prod. Sci. 48:1360–1367. doi:10.1071/EA07176 [Google Scholar]
- White I. R. and Thomas J.. 2005. Standardized mean differences in individually-randomized and cluster-randomized trials, with applications to meta-analysis. Clin. Trials 2:141–151. doi:10.1191/1740774505cn081oa [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.