Coupled Yu–Shiba–Rusinov States in Molecular Dimers on NbSe₂

Abstract

Magnetic impurities have a dramatic effect on superconductivity by breaking the time-reversal symmetry and inducing so-called Yu–Shiba–Rusinov (YSR) low energy bound states within the superconducting gap. The spatial extent of YSR states is greatly enhanced in two-dimensional (2D) systems, which should facilitate the formation of coupled states. Here, we observe YSR states on single cobalt phthalocyanine (CoPC) molecules on a 2D superconductor NbSe₂ using low-temperature scanning tunneling microscopy (STM) and spectroscopy. We use STM lateral manipulation to create controlled CoPc dimers and demonstrate the formation of coupled YSR states. The experimental results are corroborated by theoretical analysis of the coupled states in lattice and continuum models.

Magnetic impurities have a dramatic effect on superconductivity by breaking the time-reversal symmetry and inducing so-called Yu–Shiba–Rusinov (YSR) low energy bound states within the superconducting gap.¹⁻⁵ These states can be detected in real space by scanning tunneling microscopy (STM) and their energy spectrum has been studied in great detail by scanning tunneling spectroscopy (STS) on a variety of traditional s-wave superconductors.⁵⁻¹¹ In addition to individual impurities, self-assembled dimers at atomic separations⁶ and atomic wires of magnetic atoms have been investigated.¹²⁻¹⁴

Coupling between two impurities that have parallel spins results in YSR states that hybridize and split into bonding and antibonding states.^6,15−17 Atomic chains with a suitable spin-texture have been suggested to support one-dimensional (1D) topological superconductivity¹⁸ and Majorana modes at each end,¹⁹ which have been recently realized in iron chains on Pb(110).^12,13 In general, controlled coupling of YSR states should enable realizing designer quantum materials with novel topological phases.²⁰ However, the experimentally observed YSR states on s-wave superconductors (Pb and Nb) are localized within a few atomic distances from the impurity center and their energies vary strongly depending on the adsorption site of the impurity. This greatly hampers forming assemblies of controllably coupled YSR states.

Recently, Ménard et al. demonstrated that the spatial extent of the YSR states depends on the dimensionality of the superconductor and is greatly enhanced in 2D systems, where the impurity bound state can extend over several nanometers away from the impurity.²¹ Although long-range bound states have also been observed on Pb (e.g., the Majorana modes at the ends of atomic iron chains),^10,12,13,22 the functional form of the YSR wave function decay is expected to depend on the dimensionality of the superconductor. This was experimentally tested recently by Ménard et al., and they showed that impurity bound state can extend over several nanometers away from the impurity on 2D superconductors.²¹ This was demonstrated on iron impurities embedded into a niobium diselenide (NbSe₂) substrate, which is layered material with a superconducting transition at 7.2 K. Because of the weak van der Waals interaction between adjacent layers, it behaves essentially as a 2D system. However, coupling between YSR states on 2D superconductors has not yet been demonstrated. Here, we observe YSR states on single cobalt phthalocyanine (CoPC) molecules on NbSe₂ using low-temperature scanning tunneling microscopy (STM) and spectroscopy (STS). In contrast to the embedded or adsorbed atomic impurities on NbSe₂,^21,23 we can use STM lateral manipulation to controllably move the CoPc molecules. We use this technique to form CoPc dimers and demonstrate the formation of coupled YSR states. The experimental results are corroborated by theoretical analysis of the coupled states in lattice and continuum models.

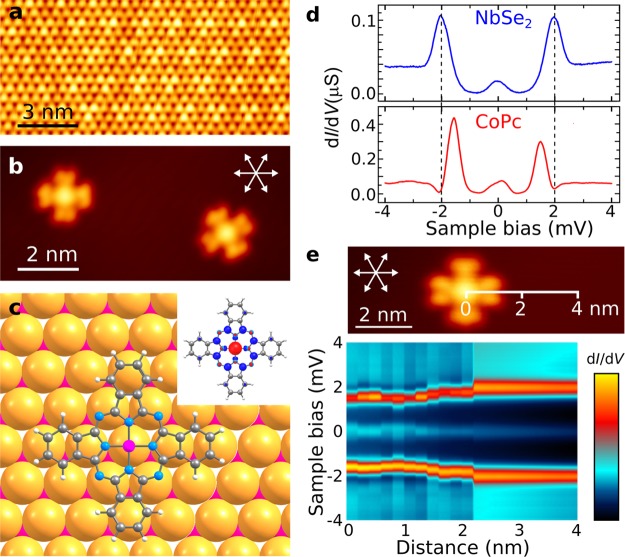
Figure 1a shows an atomic resolution STM image of a NbSe₂ surface at 4.2 K (see Supporting Information for details on the experiments). It reveals the hexagonal arrangement of the outermost Se atoms, and the well-known 3 × 3 charge-density wave (CDW) superstructure.^21,24Figure 1b displays a topographic STM image of two isolated cobalt phthalocyanine (CoPc) molecules on NbSe₂, where the principal directions of the substrate have been marked with arrows. We have determined the adsorption site of CoPc from atomically resolved images (Supporting Information), which is relevant as the molecular properties (e.g., spin state and more importantly, the magnetic coupling to the superconductor) might depend on this. Our STM measurements indicate that independent of the molecular orientation, the central Co atom always sits on top of an underlying Se atom. This experimentally observed adsorption configuration is confirmed by density functional theory (DFT) calculations, with Figure 1c showing the most stable adsorption structure.

Figure 1.

CoPc molecules deposited on NbSe₂ surface. (a) Atomically resolved STM image of the NbSe₂ surface (V = 20 mV, I = 1 nA). (b) STM image of two CoPc molecules (V = 0.6 V, I = 5 pA). The arrows indicate the principal directions of the underlying NbSe₂ substrate. (c) DFT results on the CoPc adsorption on NbSe₂. Inset shows the calculated spin density on the CoPc molecule. (d) Measured dI/dV spectra on the bare NbSe₂ substrate (top panel, feedback set point: V = 100 mV, I = 50 pA, z_offset = 100 pm) and on an isolated CoPc molecule (bottom panel, feedback set point: V = 100 mV, I = 50 pA, z_offset = 50 pm) with a superconducting STM tip. (e) dI/dV spectra acquired at different distances from the center of a CoPc molecule showing the evolution of the YSR resonances (feedback set point: V = 100 mV, I = 50 pA, z_offset = 50 pm). Color scale between 0–1 μS. In the upper panel, the arrows indicate the principal directions of the underlying NbSe₂ substrate.

dI/dV spectroscopy was performed with NbSe₂-coated SC tip to increase the energy resolution beyond the thermal limit.^6,7,24Figure 1d (upper panel) shows a typical dI/dV spectrum acquired on bare NbSe₂ substrate. It exhibits a gap that is twice the size of the SC gap of NbSe₂ with sharp coherence peaks at ±2Δ ∼ ±2 meV.^25,26 The small peak close to V = 0 is due to the tunneling of thermally excited quasiparticles. dI/dV curve taken on a CoPC molecule (Figure 1d, lower panel) shows that the coherence peaks at ±2Δ are replaced by pronounced peaks of asymmetric heights within the SC gap and two replicas of those peaks close to V = 0, similarly to an earlier report on MnPC on Pb surface.⁷ These asymmetric peaks in the SC gap arise from the interaction between an isolated spin on CoPC and Cooper pairs in NbSe₂, that is, the formation of YSR states. Despite CoPc adsorption being driven by the weak van der Waals forces, the magnetic coupling is still sufficiently strong to result in the formation of YSR states. DFT calculations predict that CoPC on NbSe₂ has the same spin as in the gas phase, S = 1/2. The inset of Figure 1c shows the spin density of CoPC on NbSe₂ surface, which is derived from the cobalt d_z² orbital, as expected.

Because of the anisotropy of NbSe₂, the YSR states have been shown to have a large spatial extent and to decay differently than on a 3D superconducting substrate.²¹ We have probed the spatial extent of the YSR states in our system by recording spectra along a line over a single CoPc as shown in Figure 1e (zero corresponds to the center of the molecule). It is seen from the figure that the YSR states persist >2 nm from the center of the molecule. In addition to the very slight energy variations of the YSR resonance over the molecule (distances <1 nm), the smooth energy variation of the resonances at larger distances is likely to result from tip–molecule interactions (see Supporting Information for more details). The sudden change in the spectra (at the distance of 2.1 nm, when the tip is no longer on the molecule) may also be related to tip–molecule interactions. The YSR wave functions on NbSe₂ are expected to have 6-fold symmetry with larger spatial extent along the principal crystal directions of the surface.²¹ We have tested this effect by recording another set of line spectra at a 45° angle with respect to the data shown in Figure 1e and carried out grid spectroscopy experiments (Supporting Information). These experiments suggest that YSR wave functions are anisotropic also in our system.

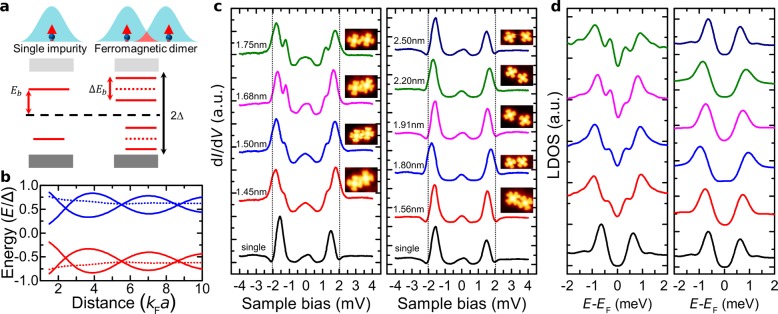
The coupling of subgap states is illustrated in Figure 2a, which shows schematically how two nearby YSR states hybridize and form bonding and antibonding combinations. In this case, phenomenological theory predicts a splitting that depends on the dimensionless coupling strength α (i.e., the energy of an individual YSR state), the relative orientations of the two (classical) spins and the separation between the spins^4,15,20,27 (Supporting Information). α can be determined from experiments on a single impurity and we estimate a value of α ≈ 0.5. The splitting oscillates with a period determined by k_F (See Figure 2b) and obtains its maximum value for a ferromagnetic alignment of the spins. Coupling of antiparallel spins (dotted line in Figure 2b) does not result in energy splitting but the degenerate energy level is slightly shifted from the individual YSR energy.

Figure 2.

Formation of coupled YSR states on CoPc dimers. (a) Schematic of the formation of coupled YSR states. (b) Calculated evolution of the YSR state energies as a function of the impurity dimer separation for a ferromagnetic (solid lines) and antiferromagnetic (dotted lines) dimer. (c) Set of dI/dV spectra showing split (left panel) and nonsplit YSR states (right panel). A spectrum measured on an isolated CoPc (black line) is shown in both panels for comparison (feedback set point: V = 100 mV, I = 50 pA, z_offset = 100 pm). The dotted line shows the position of the SC gap edge at ±2Δ/e. (d) The LDOS extracted by numerical convolution from the experimental dI/dV curves.

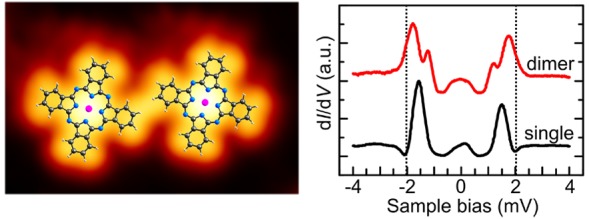
Using STM lateral manipulation,²⁸ we successfully constructed molecular dimers with different separations (see Supporting Information for details). In all cases, we have manipulated one molecule of the dimer and have recorded the spectrum on the one which has not been moved. In this way, we have made sure that the target molecule is always at the same adsorption side. Figure 2c shows point spectra on the molecular dimers with different separations (STM images of the dimers are shown in the insets). Unlike in the case of a single CoPc molecule where we observed only one pair of YSR resonances in the SC gap, now the main YSR peaks are split to two peaks (left panel). In order to remove the influence of the superconducting density of states of the tip, numerical deconvolution was performed to directly extract the local density of states (LDOS) of the YSR states due to the CoPc molecules. Figure 2d shows the measured LDOS, where the split YRS states (left panel) can be compared to the single YSR peaks at ±0.63 meV. It is evident that the energy positions of split peaks change depending on distance between the dimers.

We observe a maximum splitting of ∼0.5 meV, which is very similar to the predictions from a simple continuum model for experimentally relevant distances (Figure 2b). Magnetic coupling between the spins (through, for example, RKKY interaction or superexchange) is expected to be weak compared to kT at T = 4.2 K. While the observed YSR coupling and possible RKKY-induced magnetic coupling between the two spins vanish if the s–d coupling J = 0, these two effects are governed by different dependence on system parameters and are not expected to have similar magnitude. The YSR splitting scale varies as 1/(k_FR) for two spins separated by R (when k_FR ≫ 1) and the RKKY coupling J_eff would decay much more rapidly as 1/(k_FR)² in 2D. Therefore, it is possible to observe significant YSR splitting, while the direct magnetic interactions between the spins are weak. Moreover, CoPc is not expected to have significant magnetic anisotropy,²⁹⁻³² and the spins in a dimer are expected to be randomly oriented (thermal average). The majority of random orientations give rise to energy splittings comparable to the maximum splitting, and we would observe experimentally essentially the same splitting as the maximum value (see Supporting Information for details).

Other possible reasons for splitting of the YSR states include different angular momentum scattering contributions, individual d orbitals acting as separate scattering potentials, or low-energy excitations due to magnetic anisotropy or vibrations.^{8−10,33−36} All of the above scenarios are predicted on a single magnetic impurity, where we always observe only a single pair of YSR states. This leaves the magnetic coupling between the impurities through the SC medium and the formation of coupled YSR states as the natural explanation of the observed spectra.

The right panel of Figure 2c shows a different set of dI/dV spectra on the molecular dimers. While not identical, the intradimer distances are over a similar range as in left panel of Figure 2c. Surprisingly, small changes in the distance result in drastic changes in the spectra and we observe alternating single and split YSR state behavior. Once the impurity separations exceed ∼2.5 nm, we only observe response consistent with single impurity YSR states. As indicated above, we do not expect the spins to be strictly antiparallel, and the expected distance dependence (period of k_F) is not consistent with these rapid changes between split and nonsplit dimer states.

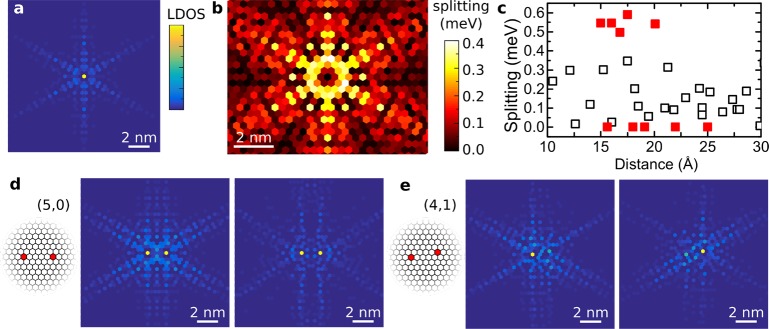
In order to understand this behavior, we have to go beyond the continuum description of the SC substrate. The Fermi surface of the NbSe₂ is anisotropic,³⁷ which gives rise to star-shaped structures in the LDOS around a magnetic impurities and vortices.²¹ In addition, the YSR wave functions have atomic scale oscillations arising from the Bloch part of the wave function. As the coupling of the YSR states is determined by the wave function overlap, these oscillations are a potential source for the atomic scale variations in the observed YSR splitting (see below). We model these effects using a next-nearest neighbor tight-binding model¹⁵ (see Supporting Information for details). Calculated LDOS of a single impurity is shown in Figure 3a. The wave function strongly reflects the crystal symmetry and it is easy to see that the coupling might strongly depend on the relative orientation of the dimer. We have calculated coupled dimers for different positions of the magnetic impurities and the splitting of the YSR states is shown in Figure 3b. In addition to a very clear 6-fold symmetry stemming from the crystal lattice, there are strong atomic scale variations. These variations result from strong changes in the wave function overlap (due to the Bloch part of the wave function), when one of the impurities is moved by a single lattice site. This is highlighted in Figure 3c, which shows the YSR splitting as a function of the dimer separation over the experimentally relevant range. The experimental data oscillate with distance but seem to be clustered around two values. While the theoretical values are also seen to vary strongly with distance, the experimental data (shown with solid red squares) show discrete alteration between split and nonsplit states. YSR splitting as a function of the dimer angle is shown in the Supporting Information.

Figure 3.

Atomic scale details of the coupling between two magnetic impurities. (a) Calculated LDOS of single impurity in the next-nearest neighbor tight-binding model. (b) Calculated splitting as a function of the impurity position (the other impurity is at (0,0)). (c) Calculated (open symbols) and measured (closed symbols) splitting of the YSR states as a function of the distance between the impurities. (d,e) Calculated bonding (left panels) and antibonding (right panels) state LDOS for a strongly coupled (5,0) (panel d) and weakly coupled (4,1) (panel e) dimer.

In Figure 3d,e, we have illustrated the bonding and antibonding wave functions of two dimers where one of the impurities has been moved by a single lattice site from (5,0) to (4,1) (the other impurity is at (0,0)). The calculated YSR splitting in these two dimers is 0.35 meV (5,0) and 0.02 meV (4,1). The latter is far below our experimental energy resolution and would not result in an observable splitting of the YSR resonances. The calculated wave functions reflect this; whereas they are delocalized on both impurities in the strongly coupled dimer (Figure 3d, analogous to H₂ molecule), they are mostly localized on a single impurity in the weakly coupled dimer (Figure 3e). This highlights that the atomic scale details are important for a detailed understanding of the coupled YSR states.

In conclusion, we have demonstrated the formation and coupling of YSR states on CoPc molecules on NbSe₂. Using STM lateral manipulation, we have constructed well-defined CoPc dimers and observed coupled YSR states. Experimentally, we find strong variations of the coupling strength depending on the detailed geometry of the CoPc dimer, which can be understood based on the details of the wave function overlap of the two impurity states. The demonstration of coupled YSR states is promising for the realization of novel topological phases in designer magnetic lattices on superconductors.^20,38

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b05050.

• Experimental and theoretical methods, adsorption geometry determination of the CoPc molecules, additional grid and line dI/dV spectroscopy over a single CoPc molecule, dI/dV spectroscopy as a function of the tip–sample distance, and YSR splitting analyzed as a function of the dimer angle (PDF)

The authors declare no competing financial interest.