Uncertainty Quantification in Alchemical Free Energy Methods

Abstract

Alchemical free energy methods have gained much importance recently from several reports of improved ligand–protein binding affinity predictions based on their implementation using molecular dynamics simulations. A large number of variants of such methods implementing different accelerated sampling techniques and free energy estimators are available, each claimed to be better than the others in its own way. However, the key features of reproducibility and quantification of associated uncertainties in such methods have barely been discussed. Here, we apply a systematic protocol for uncertainty quantification to a number of popular alchemical free energy methods, covering both absolute and relative free energy predictions. We show that a reliable measure of error estimation is provided by ensemble simulation—an ensemble of independent MD simulations—which applies irrespective of the free energy method. The need to use ensemble methods is fundamental and holds regardless of the duration of time of the molecular dynamics simulations performed.

1. Introduction

A major concern in the scientific community is the lack of reproducible results in the published literature.¹ This holds irrespective of the field of research and applies to both experimental and computational methods. A recent survey by Nature revealed that more than 70% of researchers failed to reproduce another scientist’s results, and more than half were unable to reproduce their own.² In the case of experiments, a variety of reasons ranging from mixed up chemicals, through fluctuations in the environment, variations in the experimental setup, to confirmation bias^3,4 can be found responsible for nonreproducible results.^5,6 In the case of molecular simulations, the reasons reside in a combination of theory and the model used, including the accuracy of force fields, convergence of the calculations, reliability of the software, and so on.⁷ However, for all classical molecular dynamics (MD)-based methods, the underlying lack of reproducibility is intrinsic and is independent of these other issues. This is because the prediction of macroscopic properties, such as the Gibbs free energy, requires ensemble averaging over microscopic states. Given the sensitivity of Newtonian dynamics to initial conditions, a manifestation of the mixing ergodic properties of any system that will reach an equilibrium state, two different MD simulations exhibit trajectories that diverge rapidly over time no matter how close their initial conditions.⁸ This is true for essentially all MD simulations of complex systems; however, in this article we shall focus only on MD-based free energy calculation methods for determining ligand–protein binding affinities.

In silico free energy prediction is increasingly gaining importance given its application in drug design and personalized medicine. However, it is necessary to perform accurate, precise, and reliable free energy predictions rapidly to make actionable decisions in clinical or industrial settings.^4,8 A large number of reviews are available in the literature describing various classical molecular dynamics-based methods to calculate free energies for macromolecules.⁹⁻²⁰ There has been considerable effort put into developing new sampling protocols to accelerate phase space sampling: umbrella sampling,²¹ metadynamics,²² tempering approaches,^23,24 steered molecular dynamics,^25,26 blue moon sampling,²⁷ adaptive biasing force algorithm,²⁸ slow growth,²⁹ fast growth,³⁰ and Gaussian accelerated MD³¹ to name a few. Numerous reviews are available in the literature on various approaches.^{23,24,32−35} Among these, replica exchange molecular dynamics (REMD) (also known as parallel tempering)³⁶ has proved to be fruitful in the case of biomolecular simulations. In its original form, it was only applicable to small molecules due to the large number of replicas required, but this problem was addressed by Hamiltonian-replica exchange (H-REMD),³⁷ which extended its applicability to large solvated biomolecules. Thereafter, several variants of H-REMD have been reported. Wang et al. proposed an improved version of the original replica exchange with solute tempering (REST),³⁸ called REST2,³⁹ as well as FEP/REST⁴⁰ (which we will refer to as λ-REST2 in this paper) for alchemical free energy calculations. In this study, we shall use the latter two as a representative set for all the other variants of H-REMD. We shall also consider the multistate Bennett acceptance ratio (MBAR)⁴¹ free energy estimator in this study, which has been claimed to be the best free energy estimator by some authors.⁴¹⁻⁴³

There is a wealth of evidence in the literature and in unpublished work on in silico free energy methods that one-off MD simulation-based methods are not reproducible for the reasons mentioned above.⁴⁴⁻⁶² To our knowledge, the idea that multiple short MD simulations sample better than a single long MD simulation was first mentioned a couple of decades ago.⁴⁴⁻⁴⁶ There are several reports in the literature where this idea has been applied to MD simulation-based free energy calculations to obtain a meaningful uncertainty of the results.⁵⁶⁻⁵⁸ However, the systematic application of this idea waited until Genhenden et al.⁵⁵ and Sadiq et al.⁴⁷ independently published their studies using MMGBSA and MMPBSA methods, respectively, thoroughly investigating the effect of performing multiple (up to 50) short MD simulations on the reported free energies and comparing their results with those from a single long simulation. Thereafter, several studies employing their ideas have been published leading to the approaches named “enhanced sampling of molecular dynamics with approximation of continuum solvent (ESMACS)”,^{48−51,53,54} “velocity-induced independent trajectories (VIIT)”, and “solvation-induced independent trajectories (SIIT)”.⁵⁹⁻⁶¹ Similarly, in the case of alchemical methods, Lawrenz et al.⁶² reported their method called “independent trajectory thermodynamic integration (IT-TI)” showing that the averaged free energy from multiple independent TI calculations yields more accurate results. Bhati et al.⁵² recently published their method called “thermodynamic integration with enhanced sampling (TIES)” using up to 105 independent short MD simulations in combination with the concept of stochastic integration to yield accurate and precise free energy predictions for a variety of biomolecular systems. The underlying reason for such variations between independent MD simulations is their sensitivity to the initial conditions, as explained by Coveney and Wan.⁸

The ESMACS and TIES approaches (mentioned above) involve performing an ensemble simulation unlike the traditional one-off simulation approach and have been shown to consistently improve the accuracy and precision of predicted free energies over a range of protein systems. Ensemble simulation in the context of ESMACS and TIES means an ensemble of independent MD simulations (termed as “replicas”), where independent MD simulations vary only in their initial conditions which are randomly chosen from the phase space. Several different approaches to vary the initial conditions of replicas have been reported including varying only the initial velocities^{44,45,47,48,52,55,57−59,62} or the initial velocities in combination with other properties like the initial structures, protonation states, solvation boxes, initial conformations, ligand charges, and so on.^59,63−67 In this work, all the replicas have identical initial configurations, and their initial velocities were randomly drawn from a Maxwell–Boltzmann distribution.

Statistical mechanics uses ensemble averaging over microstates to determine the macroscopic properties of a system. For systems at equilibrium, if we could run a single simulation for “long enough”, then their time-averaged properties would be equivalent to the ensemble average via the ergodic theorem. In such a case, the duration of the simulation would need to be of the order of a Poincaré recurrence time, which is inordinately long and completely out of reach of simulation on any computer now and in the foreseeable future.⁸ Moreover, time averaging is generally meaningless for systems out of equilibrium as their properties are time-dependent. In the case of ensemble simulations, the microstates are generated by the replicas. Therefore, ensemble averages can be computed by running a sufficiently large number of replicas as defined in the following paragraph, an approach applicable for systems in as well as out of equilibrium.

The number of replicas needed in an ensemble to obtain a converged result is such that the result should not differ on adding another replica to the ensemble. There is no general theory to determine this number, which needs to be assessed for each case under investigation.⁸ The size of the ensemble one uses in practice is a trade-off between the size of the uncertainty of the predictions and the associated computational cost. Extensive investigations show that the properties computed from classical molecular dynamics trajectories are essentially those generated by a Gaussian random process. Ensemble simulations provide a direct route to uncertainty quantification.⁸ A single simulation, or a small number of repeats, provides no control over the errors in these calculations.^48,50,52 Our previous studies have established that, to achieve a precision of ≤1 kcal/mol in the case of ESMACS and ≤0.5 kcal/mol in the case of TIES, no less than 25 and 5 replicas should be run for ESMACS and TIES, respectively, where the length of each replica is 4 ns.⁴⁷⁻⁵⁴ It is worth mentioning here that the error bars on the results can be further reduced by increasing the number of replicas. These numbers depend on a number of factors including the nature of the system studied, level of precision desired, type of free energy method employed, and so forth, and may need to be increased. For instance, in the current study, the absolute binding affinity method comprises a series of stages, a few of which require 10 replicas whereas others require only 5 for the same level of precision.

It is sometimes claimed that, by using enhanced sampling methods, for instance REST2³⁹ and λ-REST2,⁴⁰ and improved free energy estimators such as MBAR,⁴¹ the problem of nonreproducibility can be overcome. Yet in virtually all reported cases only one replica, that is a single MD trajectory, is performed from which the results are calculated. In this study, we apply the concept of ensemble simulation from TIES⁵² to a few popular alchemical free energy techniques, thereby providing a systematic route to uncertainty quantification in such methods. We show that the stochastic variation in predicted free energies is intrinsic to all MD-based methods when using one-off MD trajectories and that the correct approach to quantify the concomitant errors is to perform ensemble-based calculations. We also demonstrate that running single simulations for long times does not lead to controlled errors and is not an alternative to ensemble simulation. We provide a comparison of TIES results for a biomolecular system from two different sources that vary in the software and hardware employed as well as the implementation of the protocols used for free energy calculation. Excellent agreement betweeen the two results proves that the reproducibility of TIES holds irrespective of such variations in software and hardware. Indeed, although the current study is confined to a selected set of free energy methods, the conceptual basis laid out here is general and is directly applicable to other methods of calculation based on classical molecular dynamics.⁶⁸

2. Methods

In this section, we describe the protein targets and associated ligands chosen for the purpose of this study and the different protocols used to calculate their free energies. We chose to study three different classes of protein targets here to exhibit the wide applicability of our methods. We employ the AMBER ff99SBildn force field⁶⁹ for all protein targets and GAFF⁷⁰ for all ligands in this study, which are consistent with the previous TIES studies for comparison purpose (details in section 2.1). These force fields are known to be reliable for the present systems, and hence, our protein–ligand systems are well validated.⁴⁷⁻⁵⁴

2.1. Protein Targets and Ligands

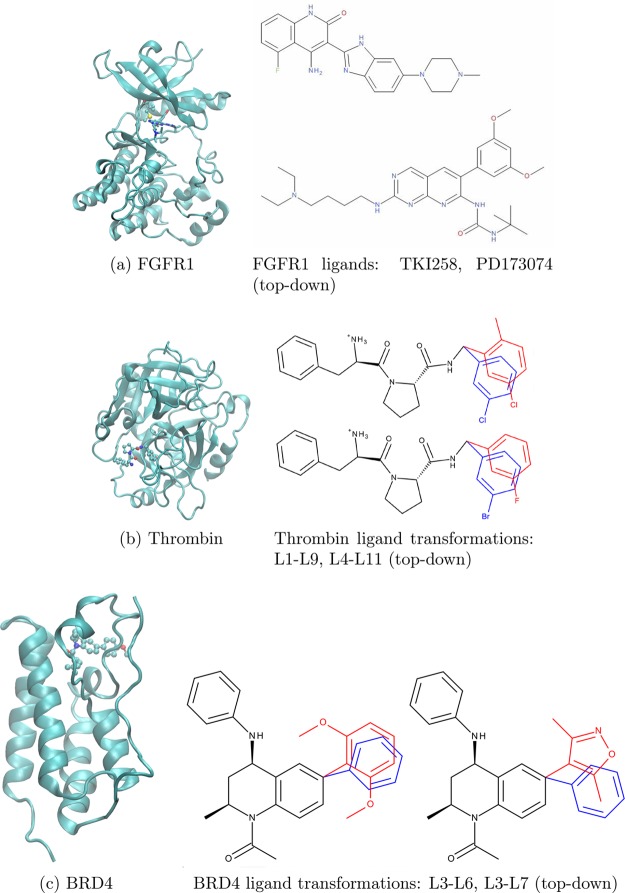
In this paper, we consider three different protein systems (see Figure 1) that have already been studied using the TIES method, namely, fibroblast growth factor receptor 1 (FGFR1),⁵¹ thrombin,⁵² and bromodomain-containing protein 4 (BRD4).⁵³ FGFR1 is a well-known therapeutic target given its involvement in the pathology of many cancer types with most inhibitors binding to its kinase domain (KD).

Figure 1.

Structures of all the target proteins (ribbon representation) studied, in each case shown bound to a ligand: (a) Fibroblast growth factor receptor 1 (FGFR1), (b) Serine protease thrombin, and (c) Bromodomain-containing protein 4 (BRD4). The ligand is shown in stick representation; the hybrid side chain is shown in ball-line representation for FGFR1, and the ligand is shown in ball–stick representation for the others. The alchemically mutating atoms in the case of Thrombin and BRD4 ligand transformations are marked in red and blue. In the case of V561M mutation, the side chains comprise the alchemical region.

The inhibitor binding is known to be altered by mutations in the FGFR1 KD, rendering some drugs ineffective.⁵¹ Here, we study the transformation of FGFR1 wild-type to V561M mutant (where, V and M denote valine and methionine, respectively), both bound to two inhibitors, namely PD173074 and TKI258 (Dovitinib). V561M is the gatekeeper mutation. It occurs very frequently and is responsible for resistance against several drugs. The serine protease thrombin is involved in the regulation of hemostasis and thrombosis, and its increased activation may result in several disorders.⁷¹ In this paper, we have chosen four thrombin inhibitors (two pairs corresponding to two alchemical transformations) to study with our methods.

The development of drugs to inhibit bromodomain-containing proteins is an area of active research due to their application in pathologies ranging from cancer to inflammation.⁵³ Here, we have chosen to study bromodomain-containing protein 4 (BRD4) and three associated inhibitors (two pairs corresponding to two alchemical transformations). In addition, BRD4 and 15 associated inhibitors have been chosen to perform repeat TIES calculations with GPUs using the pmemdGTI⁷² software patch for the AMBER 16 package.⁷³ The structures for all of these BRD4 inhibitors can be found in Wan et al.⁵³ All the parameters and pre-equilibrated structures for the simulations as well as the alchemically modified regions of all complexes were taken from the previous TIES studies.⁵¹⁻⁵³

2.2. Free Energy Schemes

In this paper, we use the thermodynamic integration with enhanced sampling (TIES) method⁵² to calculate the absolute or relative free energy corresponding to an alchemical transformation (ΔG_alch). We denote the alchemical coupling parameter as λ. ΔG_alch is given by the equation

1

where ⟨···⟩_λ denotes an ensemble average in state λ and ∂V(λ,x)/∂λ is the derivative of the hybrid potential function. For ⟨∂V/∂λ⟩ to be calculated, an ensemble of MD simulations is run at each window corresponding to an intermediate value of λ. We evaluate eq 1 using a stochastic integration method because the integrand comprises points that are Gaussian random processes.⁵² In TIES analysis, the integral in eq 1 is treated as a stochastic integral, and the associated uncertainty is calculated accordingly, as described by Bhati et al.⁵² It should be noted that this procedure is not the same as computing the integral multiple times and assessing its error. The relative free energy change (ΔΔG) is given by the difference in the free energy changes associated with the alchemical transformation in the complex (ΔG_alch^complex) and apo (ΔG_alch) states.

We now describe the different schemes used in this study to calculate absolute as well as relative binding free energies for the systems described in section 2.1. Note that the original TIES method (as employed in our previous studies) does a very good job of computing rapid, accurate, precise, and reproducible binding free energies.⁵¹⁻⁵³ However, employing further enhanced sampling methods, such as REST2 and λ-REST2, may be useful in cases where there are multiple energy minima separated by energy barriers that are inaccessible at room temperature. Therefore, in this study, we employ the enhanced sampling versions of TIES wherein REST2 and λ-REST2 simulations are performed, unlike in the case of original TIES where standard MD simulations are used.

It should be noted that the term “replica” in the context of ensemble simulation means an independent calculation initiated from a randomly selected initial condition. It is different from the use of the term “replica” within the context of replica-exchange simulation. In this paper, the term replica will always be used to refer to the former, whereas the latter will be denoted as a “REST2 replica”.

2.2.1. Relative Binding Affinity Calculation

The calculation of relative binding affinities is based on two popular versions of the Hamiltonian replica-exchange method, namely, replica exchange with solute tempering (REST2)³⁹ and λ-REST2.⁴⁰ We categorize these free energy calculation methods into four schemes as described below:

I. TIES-REST2

This performs an ensemble of REST2 simulations at each window with a fixed value of the alchemical parameter λ. Each REST2 simulation involves running a predefined number of parallel REST2 replicas varying only in their solute potential scaling factors (i.e., effective temperatures, T_eff) with regular exchange of configurations attempted between neighboring replicas. Only samples from the REST2 replica at T_eff = 300 K are used to obtain ∂V/∂λ at each window for each REST2 simulation followed by standard TIES analysis⁵² to yield ΔG_alch and associated uncertainty.

II. TIES-REST2-M

In this scheme, MBAR⁴¹ is employed as a reweighting technique to calculate ∂V/∂λ using samples from REST2 replicas at all T_eff values from scheme I at each λ window for each REST2 simulation. Standard TIES analysis then follows. It should be noted that scheme II amounts to reanalyzing the simulation output from scheme I and does not require any additional molecular dynamics simulation. It is designed to provide more precise results by utilizing all the REST2 replicas generated from these replica exchange simulations unlike scheme I, where all but the ones from T_eff = 300 K are discarded.

III. TIES-λ-REST2

An ensemble of λ-REST2 simulations is performed. Each λ-REST2 simulation involves running a predefined number of parallel REST2 replicas varying in both their T_eff as well as λ with regular exchange of configurations attempted between neighboring λ replicas. The λ value varies linearly from 0 to 1 with replicas, whereas T_eff varies such that it attains its maximum for the middle λ value and has minima at the end-points. Samples from a specific REST2 replica are used to calculate ∂V/∂λ at that state (the state here being defined by the pair (λ,T_eff)) for each λ-REST2 simulation followed by standard TIES analysis to yield ΔG_alch and associated uncertainty.

IV. TIES-λ-REST2-M

Here, the simulation output from scheme III is analyzed such that for each λ-REST2 simulation MBAR is employed so as to include samples from multiple REST2 replicas to calculate ∂V/∂λ at a given state (the state here again being defined by the pair (λ,T_eff)). Standard TIES analysis then follows. Note that no further simulations in addition to scheme III are needed for scheme IV. The latter maximizes utilization of the available REST2 replicas from scheme III to obtain more precise results.

For schemes I and II, we use a total of 13 λ-windows: 0.00, 0.05, 0.10, 0.20,···, 0.80, 0.90, 0.95, and 1.00. At each window, 10 REST2 replicas are taken with T_eff varying from 300 to 600 K. This amounts to a total of 130 MD simulations per REST2 simulation. Therefore, a single TIES-REST2 run (taking ensemble size as 5) requires performing 650 MD simulations.

For schemes III and IV, we use a total of 13 REST2 replicas with λ varying linearly between 0 and 1 for them. T_eff corresponding to λ = 0.5 is 600 K, and it symmetrically goes to 300 K at both end-points, that is, for λ = 0 and 1. This amounts to 13 MD simulations per λ-REST2 simulation and 65 MD simulations for a single TIES-λ-REST2 run (taking the ensemble size to be 5).

2.2.2. Absolute Binding Affinity Calculation

As for the relative free energy calculations, the absolute binding affinity calculation method is based on a double annihilation technique that was first proposed nearly three decades ago.⁷⁴ It had until recently not been applied to druglike ligands and pharmacologically relevant proteins. In this study, the thermodynamic cycle approach shown in Figure 2 is used, as described by Aldeghi et al.⁷⁵ Five nonphysical processes are involved, linking the unbound state to the bound state through a series of intermediate alchemical states. Insertion or annihilation of the ligand from both its bound and unbound states is performed in several steps as described below. Corrections for electrostatic finite-size effects^76,77 were made for charged ligands as they involve perturbing the net charge of the system along the alchemical path. The five processes are

Figure 2.

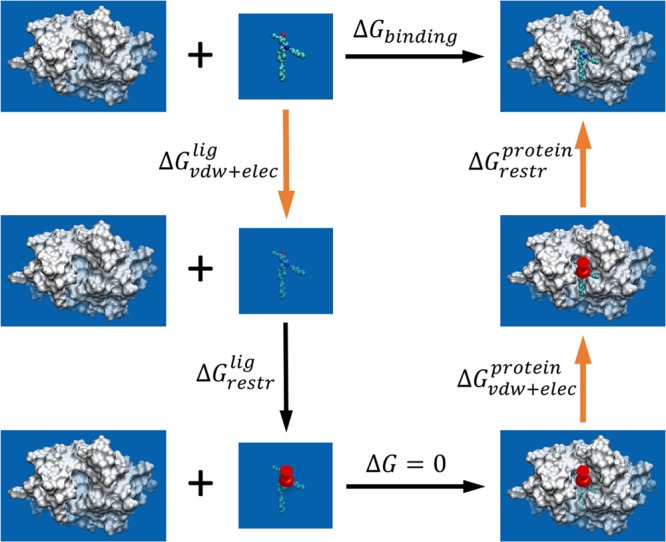
Thermodynamic cycle employed for the absolute binding free energy calculations. The process of binding is divided into a series of nonphysical transformations each with an associated ΔG. The binding free energy, ΔG_binding, is the sum of all these ΔG values. Three of them (corresponding to the transformations denoted by bold orange arrows) are computed using ensemble simulations. The noninteracting ligand is represented with faded colors. A set of restraints (denoted by a push pin) is used to restrict the position and the orientation of the noninteracting ligand.

1. Decoupling the ligand from solution (i.e., from physically solvated ligand to one with no interaction with its environment), for which a free energy difference ΔG_vdw+elec^lig is calculated by an alchemical approach.

2. Introducing a set of restraints to keep the position and orientation of the noninteracting ligand at a conformation close to that of the bound state, associated with a free energy difference (ΔG_restr^lig) that can be calculated analytically, as described by Boresch et al.⁷⁸

3. Transferring the noninteracting ligand from an aqueous environment to the protein in which no free energy changes are introduced as the two states are effectively equivalent (the ligand has no interaction with its environment in both states).

4. Turning on the ligand’s interactions with the environment in which a free energy difference ΔG_vdw+elec^protein is calculated by an alchemical approach.

5. Removing the set of restraints through a series of simulations that progressively reduce restraint strengths with a free energy difference ΔG_restr^protein being calculated.

Five replicas were used for the calculations of ΔG_vdw+elec^lig and ten replicas for ΔG_vdw+elec as well as ΔG_restr^protein to attain the desired precision (<1 kcal/mol). The latter quantity exhibits larger fluctuations and hence needs more replicas compared to the former terms to attain a similar level of precision. Thirteen λ windows were used for the processes of turning on/off the van der Waals and electrostatic interactions with λ = 0.0, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 (the electrostatic and van der Waals components are scaled differently with λ; see section 2.3 for details) and 12 λ windows for the removal of restraints in the ligand–protein complexes with λ = 1.0, 0.75, 0.5, 0.3, 0.2, 0.15, 0.1, 0.075, 0.05, 0.025, 0.01, 0.0. Both of these series of λ windows are more closely spaced near the λ = 0 end-point due to the steeper energy gradient in that region of the phase space.

Once all of the free energy differences for the nonphysical processes have been calculated, the physical binding free energy (ΔG_calc) of the ligand can be determined and compared with the experimental data (ΔG_exp).⁵¹ All ΔG values and associated uncertainties are computed using the standard TIES analysis method.⁵²

2.3. Simulation Setup

All the pre-equilibrated solvated structures and corresponding parameters for FGFR1, thrombin, and BRD4 were taken from the previous TIES studies.⁵¹⁻⁵³ The systems were maintained at a temperature of 300 K and a pressure of 1 bar in an NPT ensemble using the standard NAMD protocol of Langevin dynamics (with a damping coefficient of 5 ps^–1) and a Berendsen barostat (compressibility of 4.57 × 10^–5 bar^–1 and relaxation time of 100 fs). A time step of 2 fs was used. The simulation length of 4 ns and ensemble size of 5 were taken as per the standard TIES protocol.⁵² Van der Waals contributions were perturbed using linearly varying λ across the full range (0 to 1). A soft core potential was used for the van der Waals interactions of all atoms in the alchemical space to avoid divergent potential energy due to the sudden appearance of atoms close to the end points of the alchemical transformation, often called “end point catastrophes”.^79,80 Moreover, the electrostatic interactions of the disappearing atoms were linearly decoupled from the simulations between λ values of 0 and 0.55 and completely turned off beyond that, whereas those of the appearing atoms were linearly coupled to the simulations from λ values of 0.45 to 1 and completely extinguished otherwise.

2.3.1. Relative Binding Affinity Calculation

The customized version of the NAMD 2.11 package,⁸¹ based on the patch developed by Jo and Jiang⁸² to implement the REST2 algorithm in NAMD, was used for all the REST2 and λ-REST2 simulations using three-dimensional periodic boundary conditions. An exchange was attempted after every 1 ps, and conformations were saved after every 10 ps. The dual topology scheme as described by Bhati et al.⁵² was employed for alchemical hybrid parameters and structures. In the case of the ligand alchemical transformations, the REST2 region for unbound ligand calculations is defined as being all the alchemically mutating atoms. For bound ligand calculations, the REST2 region comprises all alchemically mutating atoms and all protein residues within 3 Å distance of the former. In the case of protein mutations, the REST2 region for unbound protein calculations is defined as the mutant residue and all protein residues within 3 Å distance of the former. For bound protein calculations, it is defined as the mutant residue, all protein residues within 3 Å of the mutant residue and 4 Å of the ligand, and all ligand atoms within 4 Å of the mutant residue.

2.3.2. Absolute Binding Affinity Calculation

All simulations were performed using NAMD 2.12⁸¹ with three-dimensional periodic boundary conditions imposed. The set of restraints used here consists of six harmonic potentials for one distance, two angles, and three dihedrals (refer to Boresch et al.⁷⁸ for details) with force constants of 10 kcal mol^–1 Å^–2 for the distance and 500 kcal mol^–1 rad^–2 for the angles and dihedrals.

2.4. Simulation Setup for Binding Affinity Calculations Using pmemdGTI

The pmemdGTI software package is an implementation of the thermodynamic integration (TI) free energy method within the pmemd module of the AMBER 16 package, which runs on GPUs.⁷² It is available as a patch to the AMBER 16 software package (http://lbsr.rutgers.edu/software-downloads). In this study, we performed relative binding affinity calculations employing the original TIES protocol for a set of BRD4 inhibitor transformations using pmemdGTI and compared the results with those obtained using the NAMD 2.9 software package taken from a previous TIES study by Wan et al.⁵³ The initial structures and parameters for the protein and inhibitors were taken from the previous TIES study⁵³ and so were the definitions of alchemical regions for all inhibitor transformations studied. The single topology method was employed for all TI calculations. The ligands and complexes were neutralized with Na⁺ and Cl^– ions and then solvated in a TIP3P water box extending at least 11 Å in each direction from the solute. A time step of 1 fs was used for the integration of the equations of motion, and a cutoff of 9 Å was used for long-range electrostatic interactions with the particle-mesh Ewald method (PME). Softcore potentials were applied to all atoms in the alchemical domain for both electrostatic as well as van der Waals interactions. Eleven λ-windows were used, where the λ value varied from 0.0 to 1.0 with Δλ = 0.1, and the electrostatic and van der Waals forces were coupled/decoupled simultaneously. All the starting structures were first minimized and relaxed at 300 K with the NVT ensemble. The initial conformations for each λ window were sequentially generated with 1.4 ns equilibration for each λ-window such that the equilibrated conformation of the current λ-window was used as the starting conformation for the next λ-window. Ten replicas were run at each λ-window to calculate the ensemble averages using the TIES analysis. Each replica was run for 5 ns, and the last 4 ns data were collected at a sampling frequency of 1 ps to calculate free energies.

2.5. Computational Resources

Note that each of the above calculations requires a large number of MD simulations to be performed. However, given the architecture of modern large-scale high-performance computers, all simulations can be run in parallel and completed in the same wall clock time as needed to complete a single MD simulation. Thus, the time to solution remains short (∼6–8 h; using GPUs, one can reduce this to as little as 1–2 h (see below)), which is a further major advantage of the above-mentioned schemes. It should also be noted that, in the case of the relative free energy calculations, schemes I/II are an order of magnitude more expensive computationally compared to schemes III/IV. The latter are slightly more expensive than standard TIES calculations. Table 1 provides a comparison of computational costs for the different types of calculations. All simulations for the relative free energy calculations were run on SuperMUC at the Leibniz Supercomputing Center (LRZ; https://www.lrz.de/english/) in Germany and on the UK supercomputer ARCHER (http://www.archer.ac.uk/).

Table 1. A Comparison of Computational Costs for Different Free Energy Calculations Using L1-L9 Ligand Alchemical Transformation Bound to Thrombin (∼60k Atoms)^a.

calculation type	number of cores	wall clock time (hrs)	core hours
TIES	8320	5.75	47840
schemes I/II	83200	6.82	567424
schemes III/IV	8320	6.82	56742

^aAll the data are taken from 4 ns duration production MD simulations performed on SuperMUC, a machine at the Leibniz Supercomputing Center (LRZ).

For the absolute free energy calculations, all three simulation steps (steps 1, 4, and 5) were performed on the BlueWaters machine at the National Center for Supercomputing Applications, University of Illinois at Urbana–Champaign (https://bluewaters.ncsa.illinois.edu). Note that step 2 was done analytically and did not require any HPC resources. Five replicas of step 1 required negligible resources as compared to the ten replicas of steps 4 and 5 (ΔG_vdw+elec^protein and ΔG_restr; 10 ns each), which collectively required 661,419 core hours (32000 cores for 20.67 h; these numbers correspond to thrombin–ligand complex, ∼60k atoms). It is important to note that these numbers correspond to 10 ns simulation duration using 10 replicas as compared with 4 ns and 5 replicas in the case of relative free energy calculations. All replicas can be run in parallel, and the results can be obtained within 1 day. Given the estimate of computational cost involved, it is evident that the absolute free energy calculations performed using ensemble simulation are very expensive calculations (they are ∼3-times more expensive than standard TIES calculations with the same number of replicas and simulation length and ∼1 order of magnitude more expensive than ESMACS calculations).

All the simulations for the pmemdGTI calculations were performed using Merck’s GPU resources comprising NVIDIA Tesla K80 and P100 nodes. A single GPU chip was used for each replica. For the L3-L4 ligand alchemical transformation bound to BRD4 (∼33k atoms), a single P100 chip needed 2 h to complete a 5 ns long simulation.

2.6. Uncertainty Quantification

The error bars reported on all of the results in this paper are derived from the bootstrapped standard error from the ensemble of potential derivatives produced by the ensemble simulation (see section 3.3 of Bhati et al.⁵²). Recall that the TIES analysis does not amount to merely running five (or ten) versions of the conventional TI calculation, computing the integral five (or ten) times and assessing its error. As explained earlier, it involves evaluating that integral as a stochastic one, so we compute it by numerical quadrature such that the error in the integral is given by the convolution of the errors in the integrand at the various points within the quadrature. Such error bars furnish a statistical estimate of the reproducibility of our results. This approach provides a reliable quantification of uncertainty, which is missing in most of the existing publications on free energy calculations.

3. Results

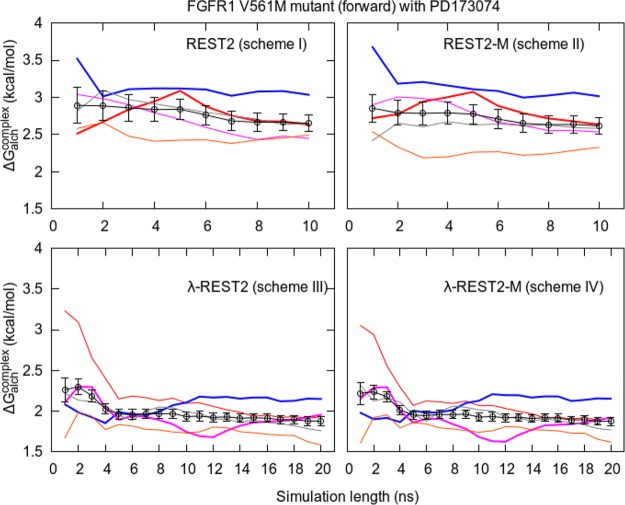
Table 2 contains the ΔΔG values for all of the protein–ligand systems studied using all four schemes. We borrow the notation of “forward” and “reverse” transformations from our earlier FGFR1 TIES study,⁵¹ where “forward” denotes the V → M mutation and “reverse” denotes the M → V mutation, and their initial structures are taken from different PDB files. Calculating ΔΔG in both directions eliminates the “hysteresis effect”, where hysteresis is the difference between the ΔΔG values in forward and reverse directions, which should theoretically be zero.^51,83 The variation in ΔΔG for 5 replicas is also shown. Note that each replica here is an independent calculation and should not be confused with the notion of a REST2 replica, as per terminology discussed above. Unsurprisingly, on the basis of our earlier work, the results vary by 0.8–1.3 kcal/mol for all schemes in the case of FGFR1 complexes, whereas in the case of thrombin and BRD4, the variation goes up to as high as 1.6 and 1.2 kcal/mol, respectively. The limits of this range are the differences between the largest value of ΔG_alch^complex and the smallest value of ΔG_alch, and vice versa. These values are provided in Table S1. It is important to note that such variation is system-dependent and could be larger for more flexible protein–ligand systems and larger alchemical transformations. This is due to the fact that MD simulations are sensitive to the initial configuration of the system.⁸ As is evident from Figure 6, in the case of the FGFR1 V561M mutant, one of the replicas may get trapped within a region of conformational space.

Table 2. Relative Binding Affinity Predictions for All Complexes Using the Four Schemes (I–IV^a)^b.

system	scheme	range using 5 replicas	ΔΔGTIES	ΔΔGexpc
V561M mutant (forward) with PD173074	I	2.86 to 3.95 (1.09)	3.56(0.18)	2.73(0.13)
	II	2.80 to 4.08 (1.28)	3.54(0.17)
	III	2.84 to 3.70 (0.86)	3.23(0.08)
	IV	2.82 to 3.61 (0.79)	3.19(0.06)
V561M mutant (reverse) with PD173074	I	2.20 to 2.97 (0.70)	2.65(0.13)
	II	2.14 to 3.17 (1.03)	2.65(0.12)
	III	2.91 to 3.87 (0.96)	3.42(0.10)
	IV	3.00 to 3.82 (0.82)	3.42(0.09)
V561M mutant (forward) with TKI258	III	–0.67 to 0.25 (0.92)	–0.15(0.09)	–0.60(0.82)
	IV	–0.73 to 0.31 (1.04)	–0.19(0.08)
L1-L9 with thrombin	III	0.29 to 1.14 (0.85)	0.67(0.10)	0.43
	IV	0.38 to 1.14 (0.76)	0.67(0.08)
L4-L11 with thrombin	III	0.29 to 1.82 (1.53)	1.06(0.14)	1.08
	IV	0.24 to 1.82 (1.58)	1.05(0.12)
L3-L6 with BRD4	III	–1.60 to –0.45 (1.15)	–1.14(0.10)	–1.65(0.05)
	IV	–1.61 to –0.38 (1.23)	–1.14(0.08)
L3-L7 with BRD4	III	–0.07 to 0.61 (0.68)	0.27(0.10)	–1.37(0.10)
	IV	–0.18 to 0.67 (0.85)	0.27(0.09)

^aIn scheme IV, the samples from states which are electrostatically fully decoupled from the state of interest are excluded from MBAR analysis. This is because the energies of such samples at the state of interest may approach infinitely high values due to overlapping atoms by virtue of the nonsoftcore electrostatic potential used in these simulations.

^bThe range of ΔΔG values is derived from the differences between the largest ΔG_alch^protein/lig and smallest ΔG_alch and vice versa, whose values are provided in Table S1. ΔG_alch^complex and ΔG_alch are the free energy changes associated with the alchemical transformation in the complex and apo states, respectively. All values are in kcal/mol.

^cThe experimental error bar is the standard error of repeated measurements. It is unavailable for thrombin complexes.

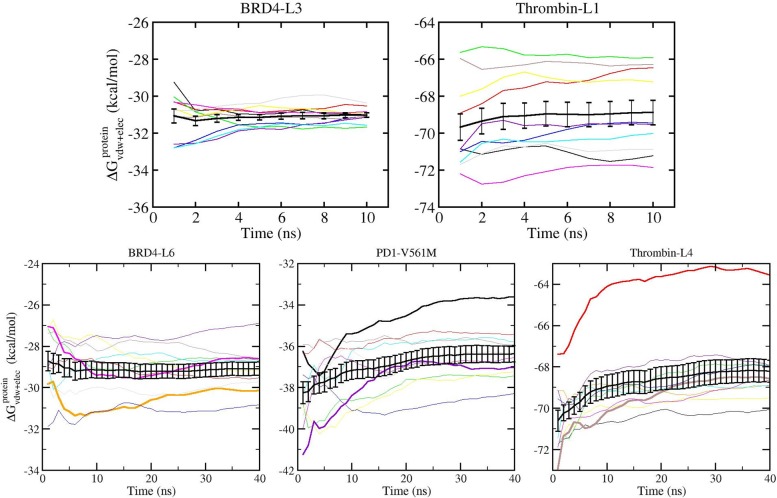
Figure 6.

Variation of cumulative ΔG_alch^complex with simulation length for five replicas of relative free energy calculations (shown in different colors) and their combined TIES analysis result (shown in black with error bars) for all four schemes. The simulations were extended up to 10 ns for schemes I and II and up to 20 ns for schemes III and IV. Some of the replicas are highlighted (thick lines) to show how a single replica may fluctuate substantially or become trapped in a local potential minimum, whereas the ensemble average overcomes such problems.

Figure 3 shows a comparison of the absolute binding affinity predictions (ΔG) with the corresponding experimental values. The predictions are of modest accuracy with mean unsigned errors (MUEs) of 1.3, 1.9, and 2.7 kcal/mol for BRD4, FGFR1, and thrombin, respectively. Although a smaller MUE was reported in the literature for broad-spectrum inhibitors to bromodomain families,⁸⁴ similar or larger MUEs were obtained for other molecular systems, including fragmentlike ligands binding to a T4 lysozyme,^85,86 druglike ligands to FK506-binding protein,⁸⁷ and ATP-competitive inhibitors to CDK2 and ERK2 kinases.⁸⁸ Our calculations correctly predict the resistance of PD173074 for the gatekeeper mutation V561M. The calculations cannot distinguish the binding affinities for dovitinib for which experiments report the same binding affinity within errors for both variants. The calculations also correctly predict the free energy differences for selected pairs of ligands and for the FGFR1 variants (see Figure 5). The largest uncertainties in these calculations arise from the step where the interactions of the ligands are turned on/off in the ligand–protein complexes (see Table S2). This is not surprising as, in this alchemical step, there are large conformational changes occurring in the protein and relatively large-scale water molecular redistribution. The ΔG_vdw+elec^protein and ΔG_restr terms are correlated, which account for the annihilation of the ligand from the complex. The sum of these two terms (ΔG_vdw+elec^protein + ΔG_restr) differs by up to 2.5, 6.2, and 7.1 kcal/mol for ligand binding to BRD4, FGFR1, and thrombin systems, respectively, from the 10 replica simulations. The finite size electrostatic corrections are important and significantly improve the predicted binding free energies (Table S2).⁷⁷

Figure 3.

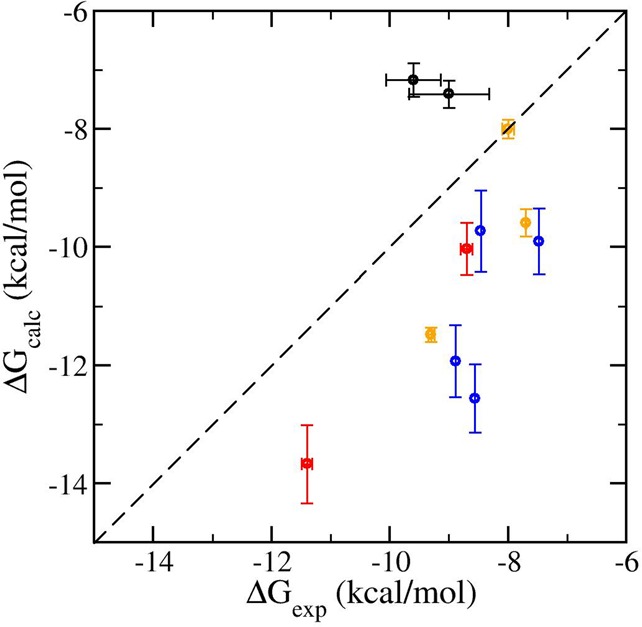
Comparison of calculated and experimental absolute binding free energies of dovitinib (black) and PD173074 (red) with wild-type and V561M mutant FGFR1, three ligands with BRD4 (orange), and four ligands with thrombin (blue).

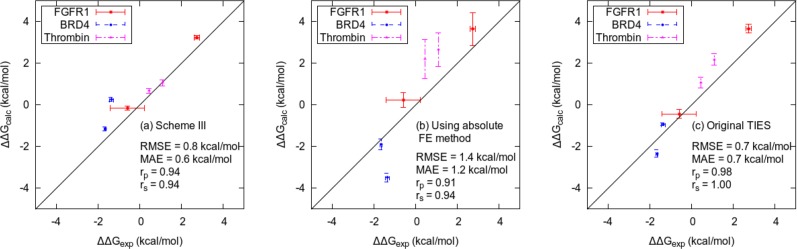
Figure 5.

Comparison of the relative binding affinities for all complexes using (a) scheme III, (b) the absolute free energy calculation method, and (c) the original TIES scheme with normal MD simulations without REST2. The correlation coefficients (Pearson (r_p) and Spearman (r_S)) for all the three schemes are good (>0.9). The root mean squared error (RMSE) and mean unsigned error (MUE) for scheme (b) are almost double those of schemes (a) and (c).

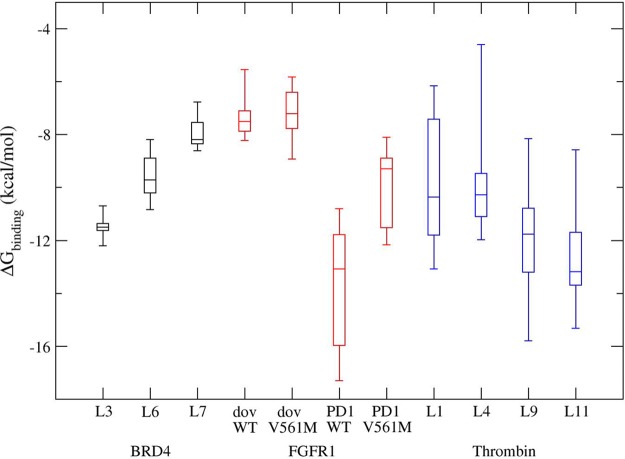
The binding free energies, calculated from a random combination of 10 replicas of complex simulations and 5 replicas of ligand-only simulations, can vary by as much as 2.6, 6.5, and 7.6 kcal/mol for BRD4, FGFR1, and thrombin, respectively (Figure 4). The accuracies and the precisions of these calculations appear to depend on the flexibility of the proteins and the ligands, the conformational changes upon binding, the accessibility of water molecules to the binding sites, and so on. The BRD4 systems exhibit the most consistent results from different replicas along with FGFR1 complexed with dovitinib; thrombin has the largest variations for all four ligands studied here. All of these findings are based on the 10 ns production runs. There is no doubt that further studies on a broad data set, consisting of both diverse ligands and various proteins, are necessary to determine the most optimal simulation protocol, the length of the various simulations, and the number of replicas to achieve desired statistical significance.

Figure 4.

Box plots of calculated absolute binding free energies for ligand binding to BRD4 (black), FGFR1 (red), and thrombin (blue). The binding free energies are generated by combining results from all steps in the thermodynamic cycle (Figure 2); there are 500 possible combinations from the replicas used in the three simulation steps. The graph displays the distribution of data based on the five number summary: minimum, first quartile, median, third quartile, and maximum. The central rectangles span the first quartile to the third quartile: the interquartile range.

Our results show, yet again, the variation that can occur between replicas using the same structure and parameters but with different initial velocities. This phenomenon is intrinsic to classical molecular dynamics and is independent of the force field used for the calculations.⁸

It is interesting to note from Table 2 that the predicted ΔΔG values obtained using schemes II and IV are very close, if not identical, to those using schemes I and III, respectively. However, the former always have marginally lower uncertainties than the latter. This implies that MBAR has no effect on the accuracy of results but improves their precision, although only very slightly in our case. It is important to highlight here that the precision of our results is an indicator of the distribution of free energies across replicas. It should be noted that all proteins we study are small and compact. Larger proteins might benefit from MBAR in a way these do not. In addition, a comparison of results from scheme I with III tells us that the differences between ΔΔG values for V561M mutant bound with PD173074 are 0.33(0.20), 0.77(0.16), and 0.22(0.26) kcal/mol for the forward direction, reverse direction, and their average, respectively. The results from schemes II and IV are also almost identical. This suggests that REST2 and λ-REST2 give the same results within the error bars in the forward direction as well as on averaging results in both directions. However, the results in the reverse direction are statistically different. The data set presented here is too small to make any general conclusion on the relative accuracies of the different schemes. Nevertheless, it is clear that λ-REST2 provides similar results to REST2 for an order of magnitude less computational cost and is, hence, preferable. Thus, on the basis of the data in Table 2, we can conclude that scheme IV provides the most cost-effective way of obtaining reliable predictions. Because in this study the results from schemes III and IV are almost identical, we have used the results from the former in further discussions hereafter. The results from scheme III have a high degree of accuracy with the differences from the experimental values of all but one transformation lying in the range of 0.0–0.7 kcal/mol. Figure 5(a) shows the excellent agreement of ΔΔG values predicted from scheme III with those reported experimentally.

It is worth noting that the hysteresis in ΔΔG for FGFR1 V561M mutant bound to PD173074 (that is the difference between the forward and reverse transformations) has vanished (0.2 kcal/mol, in the case of scheme III, which is essentially the same within error bars) from 0.8 kcal/mol in the case of the previous TIES study (ref (51); based on 5 replicas; note, however, that a larger number of replicas reduces it further). For ligand alchemical transformation L4-L11 bound to thrombin, the difference between predicted and experimental ΔΔG values has been brought down from 1.1 kcal/mol in the case of the previous TIES study (ref (52)) to 0.0 kcal/mol (in the case of scheme III). This shows that replica exchange, in combination with the TIES methodology, can accelerate convergence of results from different initial structures and improve the accuracy of results.

Figure 5 shows a comparison of the relative binding affinities for all protein–ligand complexes using scheme III, the absolute free energy calculation method, and the original TIES (without REST2). All of them are reasonably accurate (correlation coefficients >0.9) with scheme III having the smallest error bars as expected for any REST2 simulation. However, RMSE and MUE for the absolute free energy calculation method are almost double those for scheme III and for the TIES (∼0.7 and 0.6 kcal/mol, respectively). In the case of thrombin, REST2 improves the accuracy of predictions over the straightforward TIES scheme. For other proteins, there is no substantial change except the L3-L7 transformation bound with BRD4, where the results from scheme III are less accurate. This suggests that, unlike thrombin, the other complexes do not have multiple local minima separated by an energy barrier. The absolute free energy calculation method has the largest error bars as it involves disappearance of the entire ligand, unlike the other two methods.

Another important remark is that, although the methods discussed in this study are all based on thermodynamic integration, our conclusions are general and apply equally to other alchemical methods such as FEP because FEP is merely a simple variant on this. For instance, the recently published methods by Wang et al.⁸⁹ and Aldeghi et al.⁷⁵ are both very similar to the methods used in this study and are expected to exhibit similar variation in results from different replicas, which, however, have not been reported.

In the case of relative free energy calculations, it is not uncommon for practitioners to perform calculations over a closed thermodynamic cycle and to use the magnitude of the hysteresis, which in this case is the sum of all ΔΔG values in the closed cycle, to adjust the individual ΔΔG values.⁸⁹ However, there is no sense in using such closed cycles to attempt to control errors. This procedure is itself unreliable because it may distribute a large error arising in one prediction over the entire thermodynamic cycle, thereby distorting other correct predictions.⁵² The hysteresis value of 0 is a necessary but not sufficient condition for convergence of predictions. In addition, when only a single replica is computed, the magnitude of the hysteresis itself may fluctuate considerably, just like the ΔΔG values themselves. Performing only a single replica calculation gives no control over errors in the predictions.

3.1. Dependence of Free Energies on Duration of Simulation

Figure 6 shows the variation of predicted relative free energies with simulation time for simulations extended up to 10 ns for schemes I and II (top panel) and up to 20 ns for schemes III and IV (bottom panel). The cumulative ΔG_alch^complex for individual replicas as well as their ensemble average calculated using TIES analysis is shown. A similar representation corresponding to the predicted absolute free energies is exhibited in Figure 7 for simulation time extended up to 40 ns. In Figure 7, the top panel shows the variation of cumulative free energies with simulation time for the two complexes with maximum and minimum spread in results from individual replicas for simulation length up to 10 ns (similar plots up to 10 ns for all complexes are shown in Figure S1), and the bottom panel shows the results of extending simulations to 40 ns for three complexes, one from each biomolecular system. For both relative and absolute binding affinity calculations, the results do not vary significantly for simulations extended beyond 4 ns except for two complexes that require longer simulation lengths for their absolute binding affinities to converge (see bottom panel of Figure 7). As can be seen in the top panel of Figure 7, the calculated ΔG values at 4 ns are –31.1 ± 0.2 and –69.0 ± 0.7 kcal/mol, which become –31.0 ± 0.1 and –68.9 ± 0.7 kcal/mol at 10 ns for BRD4-L3 and thrombin-L1, respectively. Not surprisingly, longer simulations do not change the predictions, which are already stable within 4 ns simulation length, as shown for BRD4-L6 in Figure 7. However, extension of simulations led to converged predictions for the two complexes (PD1-V561M and thrombin-L4), which did not converge within 4 ns duration. It should be noted that, for some complexes, although the ΔG value has converged using the TIES analysis, some of the individual replicas have not reached convergence in the whole 40 ns duration (see the bottom panel of Figure 7). Figure 6 exhibits similar behavior (see black line) for all schemes with the difference between ΔG_alch values at 4 and 10 ns being less than 0.2 kcal/mol for schemes I/II and less than 0.1 kcal/mol for schemes III/IV. The error bars are also reduced marginally with simulation time for all cases. It is worth mentioning here that this behavior is system-dependent. For more flexible protein targets/ligands or for larger alchemical transformations, the number of replicas and/or simulation length may need to be increased to achieve a similar level of precision.

Figure 7.

Convergence of the absolute binding free energy calculations. ΔG_vdw+elec^protein has the largest variance and requires the longest time to converge among all of the steps for the absolute binding free energy calculation and hence is used to display the convergence in the calculation. An ensemble of 4 ns production trajectories is capable of producing well-converged free energy estimates for most of the molecular systems studied here. The top panel displays the representative convergence behavior for systems with the smallest (BRD4-L3) and the largest (thrombin-L1) differences between replicas, and the complete figure is provided in Figure S1. The bottom panel shows that longer simulations do not change the estimates for those complexes that are already stable within 4 ns, as shown for BRD4-L6, whereas extension of simulations can lead to improved convergence behavior for the ones (PD1-V561M and thrombin-L4) that are not converged within 4 ns. Some of the replicas are highlighted (thick lines) to show how a single replica may fluctuate substantially or become trapped in a local potential minimum, whereas the ensemble average overcomes such problems.

The most important thing to note in both Figures 6 and 7 is the variation of individual replica behavior with simulation length. The colored lines (corresponding to results from individual replicas) fluctuate much more than the black lines (the results from TIES analysis of all 5 or 10 replicas). This means that a single replica consistently generates a larger variation in results. The highlighted lines in both of these figures show that a single replica may fluctuate considerably or get trapped in a local potential minimum; the ensemble average, however, can overcome such behavior. Although single replica variation is small for the FGFR1-PD173074 complex (on the order of 0.5 kcal/mol; Figure 6) and ∼6 kcal/mol for the thrombin-L1 complex (Figure 7), it might be larger for other biomolecular systems and hence is unreliable. Thus, it is clear that ensemble simulations are needed irrespective of the length of the simulation. As noted earlier, such a variation in results from one-off MD simulations has been reported in the literature for other in silico free energy methods.^{44−55,58,59,62} Moreover, running a single replica does not allow any meaningful assessment of statistical uncertainty associated with results. In addition, a single replica may become trapped within a region of conformation space. For instance, REST2 simulations (schemes I and II) could not bring the blue line in Figure 6 closer to the black one. A similar observation can be made from Figure 7. However, when TIES analysis is performed by applying the ensemble simulation approach to combine the output from all 5 or 10 replicas (denoted by the black line in Figures 6 and 7), the results are very precise.

3.2. Reproducibility of the TIES Protocol Under Variation of Topology, Code, Software, and Hardware

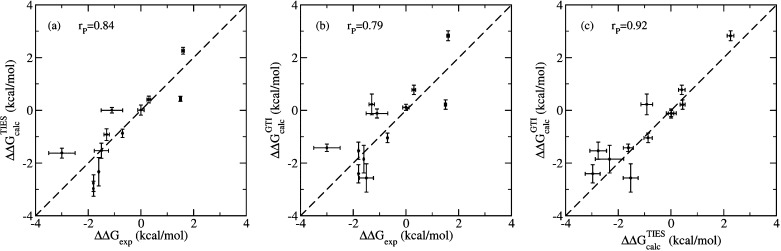
To exhibit the reproducibility of the TIES protocol, we performed TIES calculations for a set of BRD4 inhibitor transformations in this study using the method described in section 2.4 and compared the results with those from our previous TIES study⁵³ (referred to as the original TIES study here). The two differ in the software and hardware employed for the calculations as well as the simulation setup. Table 3 provides the details of the differences in the two methods. The key differences to be noted are those in the MD engines employed (NAMD vs AMBER), the hardware used (CPU vs GPU), and the topology schemes employed (dual vs single). Figure 8 shows a comparison of the predicted relative binding affinities from both methods with the corresponding experimental data as well as with each other. Both methods display good accuracy with Pearson correlation coefficients of 0.84 and 0.79 for the original TIES method and the pmemdGTI method, respectively, when compared with the experimental data. Moreover, a correlation coefficient of 0.92 is obtained when comparing the results from both methods with each other, confirming that the TIES protocol has excellent reproducibility irrespective of the variations in the software, hardware, and implementation of the free energy method employed.

Table 3. Comparison of Different Parameters Used by Wan et al.⁵³ for the Original TIES Calculations of the BRD4 Inhibitor Transformations with Those Used in This Study for the TIES Calculations Using the pmemdGTI Software Package.

parameter	original TIES	pmemdGTI
MD engine	NAMD	AMBER
processor	CPU	GPU
method	dual topology	single topology
ensemble	NPT (300 K, 1 bar)	NVT (300 K)
timestep	2 fs	1 fs
electrostatic cutoff	12 Å	9 Å
electrostatic decoupling/coupling	0–0.55/0.45–1 (see ref (53))	0–1
softcore potential	vdW	vdW + elec
buffer size	14 Å	11 Å
number of λ-windows	13 (0, 0.05, 0.1, ···, 0.9, 0.95, 1)	11 (0,0.1, ···, 0.9,1)
initial structures for each λ	minimization	minimization, sequential equl. (1.4 ns/λ)
simulation run	2 ns equl., 4 ns prod.	1 ns equl., 4 ns prod.
number of replicas	5	10

Figure 8.

Correlation plots for the TIES results from two different sources when compared with the experimental data as well as with each other. Relative binding affinities: (a) from the original TIES study by Wan et al.⁵³ compared with the experimental data, (b) using pmemdGTI software employing GPUs compared with the experimental data, and (c) from the two calculations compared with each other. Pearson’s correlation coefficients are shown for each plot to quantify the degree of agreement in each case.

4. Conclusions

In this article, four approaches to predict relative binding free energies, namely TIES-REST2, TIES-REST2-M, TIES-λ-REST2, and TIES-λ-REST2-M, and one approach to predict absolute binding free energies, all based on thermodynamic integration, are described. All these approaches rely upon ensemble simulations and are conceptually identical to the TIES method recently proposed by Bhati et al.⁵² They are shown to be accurate and precise with in-built control of errors for a range of target proteins and ligands. The importance of ensemble simulations for proper assessment of statistical uncertainty has been emphasized here yet again by providing an account of the variation in results between different replicas of the ensemble. In the case of relative free energy calculations, TIES-λ-REST2 is shown to yield similar results for an order of magnitude less computational cost compared to TIES-REST2, indicating that the former scheme is clearly preferable. The free energy estimator, MBAR,⁴¹ does not affect the accuracy of the predictions but offers a marginal improvement in their precisions. Replica exchange simulations are found to improve the accuracy of results over normal MD simulations for some cases. Results from an ensemble of longer simulations are presented and enable us to conclude that ensemble simulation is a requirement irrespective of the simulation length. The TIES protocol is shown to reproduce the relative binding affinity predictions for a set of BRD4 inhibitor transformations when the calculations are repeated using a different MD code, different hardware, and a different topology scheme.

The absolute free energy calculation method is found to have larger error bars compared to the relative free energy calculation methods. This is not surprising given that the former involves the complete disappearance of the ligand. The former is computationally a very expensive calculation, which is ∼1 order of magnitude more costly than other ensemble simulation-based approaches for calculating absolute free energies, namely ESMACS,^48,53,54 VIIT, and SIIT.⁵⁹⁻⁶¹ However, the absolute free energy method described here is an alchemical one and in principle is able to predict accurate free energies unlike the others, which involve several approximations and are primarily of value for ranking purposes as their results are often highly precise albeit inaccurate.

This study provides a systematic approach to uncertainty quantification based on ensemble simulations, which is generally applicable to all free energy calculation methods that draw on classical molecular dynamics. Owing to the intrinsic instability of molecular dynamics trajectories, there is no escape from it even when using other forms of enhanced sampling method; rather, they need to be combined with ensemble averaging. Indeed, ensemble averaging should become an integral aspect of scientific results reported from the use of molecular dynamics as it is the one reliable way in which errors may be estimated from these kinds of calculations.⁶⁸

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b01143.

• Tables containing individual ΔG_alch values for all the relative free energy calculations and its decomposition into different energy components for all absolute free energy calculations; figure exhibiting the convergence of accumulated absolute ΔG values using ensembles of simulations up to 10 ns for all complexes studied; and table showing a comparison of results for absolute free energies with and without MBAR analysis (PDF)

Author Present Address

^¶ Y.H.: Modeling & Informatics, Discovery, Alkermes Inc., 852 Winter Street, Waltham, MA, 02451, USA

Author Contributions

^§ A.P.B. and S.W. contributed equally to this work.

The authors declare no competing financial interest.