The Mechanics of Omitted Variable Bias: Bias Amplification and Cancellation of Offsetting Biases

Abstract

Causal inference with observational data frequently requires researchers to estimate treatment effects conditional on a set of observed covariates, hoping that they remove or at least reduce the confounding bias. Using a simple linear (regression) setting with two confounders – one observed (X), the other unobserved (U) – we demonstrate that conditioning on the observed confounder X does not necessarily imply that the confounding bias decreases, even if X is highly correlated with U. That is, adjusting for X may increase instead of reduce the omitted variable bias (OVB). Two phenomena can cause an increasing OVB: (i) bias amplification and (ii) cancellation of offsetting biases. Bias amplification occurs because conditioning on X amplifies any remaining bias due to the omitted confounder U. Cancellation of offsetting biases is an issue whenever X and U induce biases in opposite directions such that they perfectly or partially offset each other, in which case adjusting for X inadvertently cancels the bias-offsetting effect. In this article we discuss the conditions under which adjusting for X increases OVB, and demonstrate that conditioning on X increases the imbalance in U, which turns U into an even stronger confounder. We also show that conditioning on an unreliably measured confounder can remove more bias than the corresponding reliable measure. Practical implications for causal inference will be discussed.

Introduction

Causal inference with observational studies frequently requires researchers to estimate treatment effects conditional on a set of observed baseline covariates in order to remove confounding bias. Covariate-adjusted effect estimates can be obtained by controlling for the observed covariates in a regression analysis, or by matching cases on the observed covariates or the corresponding propensity score. It is well known that the confounding bias can be removed if all the confounding covariates that simultaneously determine treatment selection and the outcome are observed. This condition is frequently referred to as the conditional independence assumption, selection on observables, strong ignorability assumption, unconfoundedness, or the backdoor or adjustment criterion [1–4]. If one fails to reliably measure all the confounding covariates, the causal effect is not identified and the covariate-adjusted treatment effect will usually remain biased. In the linear regression context, the bias due an omitted variable is formalized in the omitted variable bias (OVB) formula [2, 5–7].¹

Though OVB is well known and has been discussed for decades, the mechanics of OVB are not yet fully understood which regularly leads to misguided advice regarding the reduction of confounding bias in practice. Applied and methodological articles and textbooks regularly suggest that including more variables in a regression model will more likely establish the conditional independence assumption and thus reduce or at least not increase confounding bias (e. g., [8–10], see [7], for a brief discussion of this ill-advised rationale for including more rather than less covariates). Similarly, there is a strong belief that adjusting for an observed variable that is correlated with unobserved confounders necessarily removes a part of the bias induced by the unobserved confounders and, thus, further reduces bias. Particularly the matching literature suggests that matching on variables that are correlated with unobserved confounders reduces the imbalance in and the bias due to unobserved confounders (e. g., [11–13]). We will show that even a high correlation neither guarantees a decrease in imbalance in the unobserved confounders nor a decreasing bias. We will also show that measurement error in covariates (unreliability) does not imply that less bias is removed.

Recently, researchers started looking at the mechanics of OVB in more detail. In particular, they have been investigating what happens if one conditions on covariates that have the potential to induce or amplify bias. Such covariates are collider variables that induce their own bias in addition to any OVB [14–16], or instrumental variables (IVs) that amplify any bias left after conditioning on a set of observed covariates [17, 18]. Another class of bias-amplifying covariates are near-IVs that strongly determine treatment selection but affect the outcome only weakly (the weak instead of absent association with the outcome turns them into a near-IV). Pearl [17, 19], see also [20, 21], formally showed that adjusting for a near-IV removes the near-IV’s own confounding bias but also amplifies any bias left due to omitted confounders. Also simulation studies have been used to demonstrate that the inclusion of additional variables can actually increase OVB [7, 21, 22].

In this article we give a thorough formal characterization of the mechanics that lead to OVB. In particular, we discuss conditions under which adjusting for a confounder actually increases instead of reduces OVB. We use a linear setting with only two continuous confounders, X and U, that confound the relationship between a continuous treatment Z and a continuous outcome variable Y. This allows us to keep the complexity of the OVB formulas low, and thus to better understand the OVB mechanics.

In the following we first review and explain the phenomenon of bias amplification when one conditions on an IV in the presence of an omitted variable. Then we focus on the case of two uncorrelated confounders (one observed, the other unobserved), followed by the more general case with two correlated confounders. Slowly increasing the complexity of the confounding structure – from the IV case to two correlated confounders – allows us to clearly disentangle the effects of bias amplification, cancellation of offsetting biases, correlated confounders, and unreliable covariate measurement. We conclude with a discussion of practical implications. The appendices contain (a) an explanation of bias amplification in the context of matching or stratifying on an IV (Appendix A), (b) OVB formulas for a dichotomous treatment variable (Appendix B), and (c) proofs of results discussed in this article (Appendix C).

Amplification of bias and imbalance: the instrumental variable case

Several publications [17–20] demonstrated that conditioning on an instrumental variable (IV) amplifies any remaining bias due to an omitted variable.² The causal graph in Figure 1 represents a simple data generating model (DGM) for the outcome Y and treatment Z with one confounder U and an instrumental variable IV (which is a variable that has no effect on the outcome Y except for the indirect effect via treatment Z). The corresponding linear structural causal model (SCM) is given by

Figure 1.

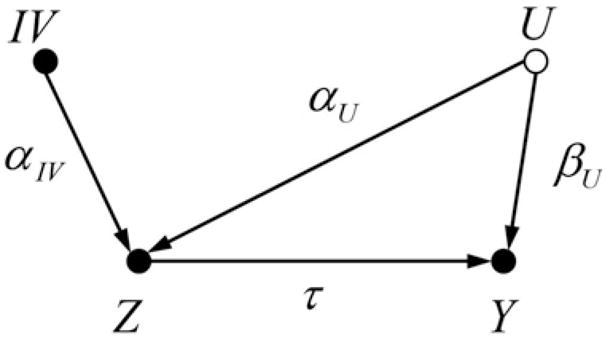
Causal graph with an instrumental variable (IV). Z is the treatment, Y the outcome, and U an unobserved confounder (represented by the vacant node).

$$\begin{gathered} IV={\epsilon }_{IV}, \\ U={\epsilon }_U, \\ Z={\alpha }_{IV}IV+{\alpha }_{U}U+{\epsilon }_Z, \\ Y=\tau Z+{\beta }_{U}U+{\epsilon }_Y, \end{gathered}$$

where α_U, β_U, and τ are standardized parameters and ε_IV, ε_U, ε_Z, and ε_Y are mutually independent error terms (representing unknown factors or measurement error) with variances that ensure that

$$\mathit{Var}(IV)=\mathit{Var}(U)=\mathit{Var}(Z)=\mathit{Var}(Y)=1.$$

Conducting a linear regression analysis that neither conditions on U nor on IV, Ŷ = γ̂ + τ̂Z, results in a biased regression estimator τ̂ for the treatment effect with E(τ̂) = τ + α_Uβ_U. Thus, the initial OVB, that is, the bias before conditioning on IV, is given by OVB(τ̂ | {}) = E(τ̂) − τ = α_Uβ_U. The empty set in OVB(τ̂ | {}) indicates that we did not adjust for any covariates. Note that the initial OVB, α_Uβ_U, represents the confounding bias due to the unblocked (open) backdoor path Z ← U → Y.³

Bias amplification

Omitting U but including IV in the regression model, Ŷ = γ̂ + τ̂Z + α̂_IVIV, also results in bias [17]:

$$\mathit{OVB}(\widehat{\tau }\mid IV)=\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_{IV}^2}.$$ (1)

However, conditioning on IV amplifies any bias left due to an unblocked backdoor path because $0<1-{\alpha }_{IV}^2<1$. Thus, the absolute OVB after adjusting for IV is always greater than the absolute initial $\text{OVB}:\left|\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_{IV}^2}\right|>\mid {\alpha }_U{\beta }_U\mid$. If we were to condition on U in addition to IV (in case U would be observed), no OVB would be left because U blocks the backdoor path Z ← U → Y. Thus, if all confounders (or at least a set of variables that blocks all backdoor paths) are reliably measured, conditioning on an IV does not result in any OVB because there is no bias left to be amplified (provided the functional form of the regression is correctly specified). However, adjusting for the IV still reduces the efficiency of the treatment effect estimate [21, 23].

Imbalance in the unobserved confounder U

Bias amplification occurs because conditioning on the IV increases the imbalance in the unobserved confounder U. For our linear framework, we define imbalance as the difference in the expected value of U for subpopulations with Z = z and Z = z + 1 (if Z would be dichotomous the imbalance would measure the mean difference between the two groups). That is, without conditioning on the IV or any other covariate the imbalance in U is obtained by regressing U on Z: Imbalance(U |{}) = E(U | Z = z + 1) − E(U | Z = z) = α_U. After conditioning on IV, we get $\mathit{Imbalance}(U\mid IV)=E(U\mid Z=z+1,IV)-E(U\mid Z=z,IV)=\frac{{\alpha }_U}{1-{\alpha }_{IV}^2}$ (Proof 1 in Appendix C). The comparison of the two imbalance formulas reveals that conditioning on the IV amplifies U’s imbalance by the factor $1/(1-{\alpha }_{IV}^2)$. Thus, we can write the OVB as the product of the amplified imbalance in U and U’s direct effect on the outcome: $\mathit{OVB}(\widehat{\tau }\mid IV)=\frac{{\alpha }_U}{1-{\alpha }_{IV}^2}\times {\beta }_U$. This formula highlights that conditioning on IV turns U into a relatively stronger confounder.

The increased imbalance in U can be explained as follows (similar explanations can be found in [21], and [24]): Since Z = α_IVIV + α_UU + ε_Z is a function of IV, U, and the error term ε_Z, conditioning on the IV removes IV’s effect on Z such that the remaining variation in Z is determined by U and the error term alone. With only two sources of variation left (U and ε_Z), U now explains a larger portion of variance in Z. Hence, the association between U and Z for a given IV = v is necessarily greater than before conditioning on IV. The increased association between U and Z implies an increase in U’s absolute imbalance: $\mid \mathit{Imbalance}(U\mid IV)\mid =\left|\frac{{\alpha }_U}{1-{\alpha }_{IV}^2}\right|>\mid \mathit{Imbalance}(U\mid \{\})\mid =\mid {\alpha }_U\mid$. Appendix A contains a more intuitive explanation within the context of matching or stratifying treatment and control cases on an IV.

OVB and imbalance due to conditioning on an uncorrelated confounder

Bias-amplification occurs not only when one conditions on an IV but also when one conditions on a confounder. For an unobserved confounder U and an uncorrelated confounder X that both induce bias in the same direction (i. e., either positive or negative selection bias), prior studies have shown that conditioning on a confounder, where X is a near-IV that is highly predictive of treatment Z but only weakly predictive of the outcome, has two effects: it removes X’s own confounding bias and amplifies any remaining bias due the omitted confounder [17, 19, 21]. The bias-amplifying effect may actually dominate the bias-reducing effect such that conditioning on a confounder X may increase instead of reduce OVB in the treatment effect. In order to fully characterize the mechanics of OVB, we discuss the more general case where X and U (a) are (un)correlated, (b) induce biases in different directions, and (c) where X is unreliably measured. We first discuss the case of uncorrelated confounders and then the case where X and U are correlated.

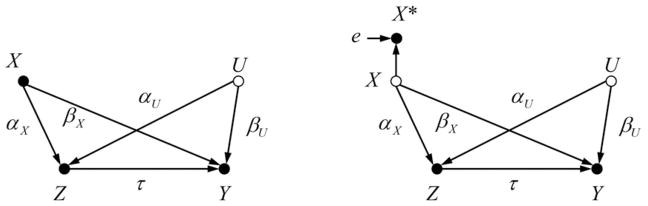
The left graph in Figure 2 shows the DGM with two uncorrelated confounders, an observed confounder X and an unobserved confounder U. The corresponding linear SCM is given by

Figure 2.

Causal graphs with two uncorrelated confounders X and U, with X reliably measured in the left graph, and X measured with error in the right graph.

$$\begin{gathered} X={\epsilon }_X, \\ U={\epsilon }_U, \\ Z={\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z, \\ Y=\tau Z+{\beta }_{X}X+{\beta }_{U}U+{\epsilon }_Y, \end{gathered}$$ (2)

with the same constraints as before such that the parameters represent standardized coefficients. For this linear SCM, the initial OVB due to omitted confounders X and U is OVB(τ̂ | {}) = α_Xβ_X + α_Uβ_U, which represents the biases induced by the two open backdoor paths Z ← X → Y and Z ← U → Y. It is important to note that the two bias terms add up if both terms are either positive or negative, but partially or fully offset each other if one term is positive and the other negative.

Reliably measured confounder X

Adjusting for a reliably measured confounder X results in a biased regression estimator with

$$\mathit{OVB}(\widehat{\tau }\mid X)={\alpha }_U{\beta }_U\times \frac{1}{1-{\alpha }_X^2}.$$ (3)

A comparison of this bias formula (Proof 3 in Appendix C) with the initial OVB indicates that conditioning on X has two effects: First, a bias-reducing effect because X blocks the backdoor path Z ← X → Y and thus eliminates its own confounding bias (α_Xβ_X). Second, a bias-increasing effect because the bias due to the unblocked backdoor path Z ← U → Y (α_Uβ_U) is amplified by the factor $1/(1-{\alpha }_X^2)$.

If the bias-increasing effect dominates the bias-reducing effect then conditioning on X leads to an increase in the absolute OVB, that is, the OVB after conditioning on the confounder X is greater than without conditioning on $X:\left|\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_X^2}\right|>\mid {\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U\mid$. The discussion of the conditions under which the absolute OVB actually increases requires a distinction between the case where X and U induce bias in the same direction (no offsetting biases) and where they induce bias in different directions such that their respective confounding biases partially or fully offset each other.

Biases in the Same Direction

If both confounders induce bias in the same direction, sgn(α_Xβ_X) = sgn(α_Uβ_U), then conditioning on X results in an increasing OVB only if the bias-amplifying effect dominates the bias-reducing effect, which is the case if

$$\left|\frac{{\alpha }_U{\beta }_U}{{\alpha }_X{\beta }_X}\right|>\frac{1-{\alpha }_X^2}{{\alpha }_X^2}.$$ (4)

⁴

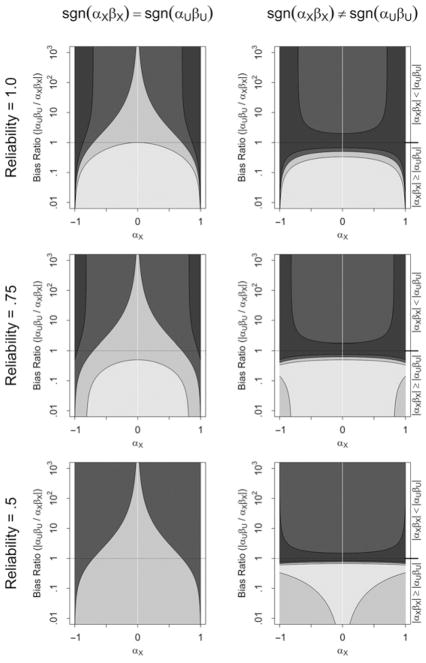
Conditioning on X very likely increases the absolute OVB in two situations. First, if the bias induced by U (α_Uβ_U) is much larger than the bias induced by X (α_Xβ_X), implying that the bias ratio on the left-hand side in (4) is large. And second, if X strongly determines Z (|α_X| close to 1) such that the right-hand side in (4) is close to zero. Thus, adjusting for a confounder with |α_X| close to 1 and β_X close to zero (i. e., a near-IV) very likely increases the absolute bias.

In the upper left plot of Figure 3 the two dark grey areas show combinations of α_X values and bias ratios $\left|\frac{{\alpha }_U{\beta }_U}{{\alpha }_X{\beta }_X}\right|$ for which the absolute OVB increases. The two light grey areas indicate areas of decreasing OVB. The line separating the dark and light grey areas represents the 100%bias contour line where conditioning on X neither reduces nor increases OVB (i. e., 100% of the initial OVB is left). The darker shade of the two dark grey areas indicates the region where conditioning on X leads to a bias that is at least twice as large as the initial bias. Thus, the contour line that separates the two dark grey areas represents the 200%bias contour line. Similarly, the very light grey area indicates that less than 50% of the initial bias is remaining. The contour line separating the two light grey areas represents the 50% bias contour line. For example, conditioning on a confounder with α_X = .1 results in an increasing OVB only if the bias ratio $\left|\frac{{\alpha }_U{\beta }_U}{{\alpha }_X{\beta }_X}\right|$ is greater than $\frac{1-{.1}^2}{{.1}^2}=101$, that is, if the bias induced by the unobserved confounder U is at least 101 times greater than the bias induced by X. However, if X is strongly related to treatment, α_X = .9, conditioning on X results in an increasing OVB if the bias induced by U is at least one fourth ( $\frac{1-{.9}^2}{{.9}^2}=.23$) of X’s bias. In this case, bias amplification dominates bias reduction: though conditioning on X removes its own bias α_Xβ_X which amounts to 81% (= 1/(1 + .23)) of the total confounding bias,⁵ the amplification of the remaining 19% (= .23/(1 + .23)) due to omitting U (α_Uβ_U) is strong enough to offset the bias-reducing effect because the bias amplification factor is 1/(1 − .9²) = 5.26.

Figure 3.

Increasing and decreasing OVB due to conditioning on an uncorrelated confounder X. The two dark grey areas indicate an increasing OVB, with 100%–200% (lighter shade) and 200% or more (darker shade) remaining bias. The two light grey areas indicate a decreasing OVB, with 50%–100% (darker shade) and 50% or less (lighter shade) remaining bias.

Offsetting Biases

For sgn(α_Xβ_X) ≠ sgn(α_Uβ_U), the confounding biases induced by X and U partially or even completely offset each other such that |α_Xβ_X + α_Uβ_U| < max(|α_Xβ_X| |, α_Uβ_U|). If U induces less bias than X, |α_Uβ_U| ≤|α_Xβ_X|, adjusting for the observed confounder X increases rather than reduces OVB only if

$$\left|\frac{{\alpha }_U{\beta }_U}{{\alpha }_X{\beta }_X}\right|\ge \frac{1-{\alpha }_X^2}{2-{\alpha }_X^2}(\text{Proof}4\text{in}\text{Appendix}\mathrm{C}).$$ (5)

But if U induces more bias than X, |α_Uβ_U| >|α_Xβ_X|, then conditioning on X always increases OVB because the remaining bias due to the unblocked backdoor path Z ← U → Y is necessarily greater than the initial bias: |α_Uβ_U| > |α_Xβ_X + α_Uβ_U|.

The upper right plot in Figure 3 shows areas of increasing and decreasing absolute OVB when biases (partially) offset each other. For |α_X| → 0, OVB increases as long as the bias induced by U is at least half of X’s bias: $\underset{{\alpha }_X\to 0}{lim}\frac{1-{\alpha }_X^2}{2-{\alpha }_X^2}=\frac{1}{2}$. For α_X = .5, OVB increases if the bias ratio exceeds $\frac{1-{.5}^2}{2-{.5}^2}=.43$. If α_X is close to 1, say .95, then OVB increases as long as the bias induced by U is at least about one tenth of X’s bias ( $\frac{1-{.95}^2}{2-{.95}^2}=.09$).

To summarize, for offsetting biases, the absolute OVB increases in two situations: First, if the confounding biases induced by X and U nearly offset each other (α_Xβ_X ≈ − α_Uβ_U). In fact, independent of the value of α_X, OVB always increases if the bias induced by the unobserved confounder U is at least half of X’s bias (|α_Uβ_U| > |α_Xβ_X|/2). And second, if X strongly determines Z such that |α_X| is close to 1, then the absolute OVB increases even when |α_Xβ_X | > > |α_Uβ_U|. The increase in the absolute OVB is mostly a result of the cancellation of the bias-offsetting effect, but the amplification of the remaining bias adds to the increase. Also note that the sign of the initial and adjusted OVB may differ. For instance, the initial OVB might be positive, but adjusting for X might turn the positive OVB into a negative OVB.

Unreliably measured confounder X

The OVB formula in (3) only holds for a reliably measured uncorrelated confounder X. The right graph in Figure 2 shows the case with a fallibly measured X. The node of X now turns into a vacant node (open circle) indicating that X is not directly observed. Instead, we only have an unreliable measure X* which is given by X*= X + e, where e is an independent error with mean zero and variance ${\sigma }_e^2$.⁶ Since Var(X) = 1, the reliability of X* is given by $\gamma =1/(1+{\sigma }_e^2)$. Measurement error in X* has no influence on the initial OVB, OVB(τ̂ | {}) = α_Xβ_X + α_Uβ_U, but affects OVB after adjusting for the fallible X* (Proof 3 in Appendix C):

$$\mathit{OVB}(\widehat{\tau }\mid X^{\ast })=\{{\alpha }_U{\beta }_U+{\alpha }_X{\beta }_X(1-\gamma )\}\times \frac{1}{1-{\alpha }_X^2\gamma }.$$ (6)

In comparison to the OVB for a reliably measured confounder X in (3), measurement error has two effects: First, the bias left due to (partially) unblocked backdoor paths now consists of two components, α_Uβ_U and α_Xβ_X(1 − γ). Besides the open backdoor path Z ← U → Y (due to omitting U), adjusting for X* no longer fully blocks the backdoor path Z ← X → Y such that(1 − γ)% of X’s bias is left. That is, X* removes the bias induced by X only to the degree of its reliability (γ). The less reliable the measurement, the more of X’s bias will remain. Second, measurement error attenuates the bias amplification factor since $1/(1-{\alpha }_X^2\gamma )$ is always less than $1/(1-{\alpha }_X^2)$ because 0 ≤ γ ≤ 1. A completely unreliable measure X* with γ → 0 neither removes nor amplifies any bias such that the initial OVB remains: $\underset{\gamma \to 0}{lim}\mathit{OVB}(\widehat{\tau }\mid X^{\ast })={\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U$ (also see [25]). On the other extreme, with a perfectly reliable measure X (γ = 1), the OVB formula in (6) reduces to the OVB formula in (3).

Biases in the Same Direction

The second and third row of plots in Figure 3 show the areas of increasing OVB (the two dark grey areas) and decreasing OVB (the two light grey areas) for an unreliably measured confounder X (γ = .75 in the second row and γ = .5 in the third row). In the left columns of plots for sgn(α_Xβ_X) = sgn(α_Uβ_U), the 100% bias contour lines are the same as for the reliably measured confounder (upper left plot), but the 200% and 50% bias contour lines change. Unreliability in X does not change the 100% contour line because measurement error always results in an attenuation of OVB toward the initial OVB [26] (see Proof 5 in Appendix C which also contains a more detailed discussion). Since the 100% contour line represents situations where conditioning on X does not alter the initial OVB (i. e., bias reduction is exactly offset by bias amplification), measurement error has no effect. But if adjusting for the reliable X increases OVB then measurement error attenuates the increase as shown by the retreating 200% contour line (as one moves from the plot in the first row to the plots in the second and third row). If conditioning on the reliable X reduces OVB then measurement error attenuates bias reduction as indicated by the retreating 50% contour line.

Offsetting Biases

For offsetting biases (sgn(α_Xβ_X) ≠ sgn(α_Uβ_U), shown in the right column of Figure 3), all bias contour lines depend on the extent of measurement error. In comparison to the reliably measured confounder (upper right plot), more measurement error in X* results in an expansion of the light grey areas of diminishing OVB, that is, measurement error makes an increasing OVB less likely because the cancellation of the offsetting biases is attenuated. Though unreliability decreases the chances of an increasing OVB, it does not imply that the fallible X* necessarily removes more bias than the corresponding reliable measure. A comparison of the 50% bias contour lines (or the very light grey area) across the three plots reveals that the fallibly X* can remove less OVB than the reliably X.

Imbalance in confounders U and X

For both reliably and unreliably measured confounders X, bias amplification operates via increasing the imbalance in U and X. For an unreliably measured confounder X*, the initial imbalance in U (α_U) and remaining imbalance in X (α_X(1 − γ)) are inflated by the factor $1/(1-{\alpha }_X^2\gamma ):\mathit{Imbalance}(U\mid X^{\ast })=\frac{{\alpha }_U}{1-{\alpha }_X^2\gamma }$ and $\mathit{Imbalance}(X\mid X^{\ast })=\frac{{\alpha }_X(1-\gamma )}{1-{\alpha }_X^2\gamma }$ (Proof 1 in Appendix C). The imbalance formula for U indicates that adjusting for X* always increases the absolute imbalance in U because the amplification factor $1/(1-{\alpha }_X^2\gamma )$ is less than one (but note that measurement error attenuates bias amplification and thus the decrease in U’s absolute imbalance). Regarding the imbalance in X, conditioning on X* cannot fully balance X because the unreliable X* fails to completely remove the association between Z and X. However, the unreliable measure X* will be balanced, Imbalance(X*|X*) = 0. Thus, balance in a fallible covariate X* does not imply that the underlying data-generating confounder X will be balanced. Particularly if |α_X| ≫ 0 or γ < .75, then the absolute imbalance in X after adjusting for X* may still be large but it will never exceed the absolute initial imbalance, |Imbalance(X|{})| = |α_X| (Proof 2 in Appendix C). This result does not generalize to the more general case with multiple observed confounders. If one conditions not only on a single unreliable confounder but on multiple, possibly uncorrelated confounders simultaneously, the resulting imbalance in the latent X might exceed the initial imbalance. This is so because the remaining imbalance in X after conditioning on X*, Imbalance(X|X*), is further amplified by any other confounder we condition on (just like the imbalance in U).

OVB and imbalance due to conditioning on a correlated confounder

The mechanics of OVB become slightly more complex when confounders are correlated. Intuitively, one might think that the correlation between an observed (X) and unobserved confounder (U) always helps in reducing OVB when conditioning on X. But this is not necessarily true because the correlation also triggers the bias-amplifying potential of the hidden confounder or might result in a cancellation of offsetting biases (e. g., if both X and U induce positive bias on their own, a negative correlation would partially offset their biases). These bias-increasing effects can actually dominate the bias-reducing effects. Since bias amplification, cancellation of offsetting biases, and measurement error operate as before, we only highlight the changes due to the correlation of confounders.

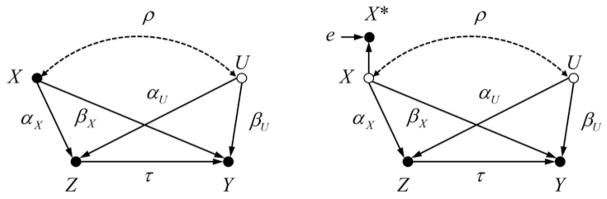
The left graph in Figure 4 shows the DGM with correlated confounders X and U. The linear SCM is the same as for the uncorrelated case in Eq. (1), except that X and U are correlated with Cor(X, U) = ρ. The correlation between X and U might be due to a common cause C (X ← C → U), a causal effect of X on U (X → U), or a causal effect of U on X (U → X). The initial OVB is then given by OVB(τ̂ | {}) = α_Xβ_X + α_Uβ_U + α_Xρβ_U + α_Uρβ_X, which reflects the biases due to all four backdoor paths between Z and Y in Figure 4: Z ← X → Y, Z ← U → Y, Z ← X U → Y, and Z ← U X → Y.

Figure 4.

Causal graphs with two correlated confounders X and U, with X reliably measured in the left graph and X measured with error in the right graph.

Reliably measured confounder X

Adjusting for the reliably measured confounder X but omitting U results in

$$\mathit{OVB}(\widehat{\tau }\mid X)={\alpha }_U{\beta }_U(1-{\rho }^2)\times \frac{1}{1-{({\alpha }_X+{\alpha }_U\rho )}^2}.$$ (7)

The OVB formula indicates that conditioning on a correlated confounder X has three effects. First, it eliminates its own confounding bias (α_Xβ_X) but also the entire confounding bias induced by X’s correlation with U (α_Xρβ_U + α_Uρβ_X). That is, conditioning on X blocks all backdoor paths going through X (i. e., Z ← X → Y, Z ← X U → Y, and Z ← U X → Y). Second, because of X and U’s correlation, X partially blocks the backdoor path Z ← U → Y to the extent of the squared correlation ρ², thus the bias due to the unobserved U reduces to α_Uβ_U(1 − ρ²). And third, the correlation also affects the bias amplification factor 1/(1 − (α_X + α_Uρ)²) because conditioning on X triggers U’s bias-amplifying potential to the extent of their correlation as reflected by the additional term α_Uρ in the denominator.

Depending on the sign of α_Uρ, the correlation can strengthen, weaken, or even neutralize the bias amplification factor. If sgn(α_Uρ) = sgn(α_X) then the correlation boosts bias amplification in comparison to the uncorrelated case because |α_X + α_Uρ| > |α_X|. The stronger the correlation and the larger α_U, the stronger the bias-amplifying effect. If sgn(α_Uρ) ≠ sgn(α_X), the correlation can strengthen (if |α_X + α_Uρ| > |α_X|), weaken (if |α_X + α_Uρ| < |α_X|) or completely cancel bias amplification (if α_X = − α_Uρ). Thus, even with highly correlated confounders X and U, there is no guarantee that conditioning on a correlated X reduces OVB (examples are briefly discussed at the end of the following subsection).

Unreliably measured confounder X

The right graph in Figure 4 shows the same causal diagram as before but with the fallible covariate X*. In this case, one can show (Proof 3 in Appendix C) that conditioning on X* results in an OVB of

$$\mathit{OVB}(\widehat{\tau }\mid X^{\ast })=\{{\alpha }_U{\beta }_U(1-{\stackrel{\sim }{\rho }}^2)+({\alpha }_X{\beta }_X+{\alpha }_X\rho {\beta }_U+{\alpha }_U\rho {\beta }_X)(1-\gamma )\}\times \frac{1}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }.$$ (8)

All four terms of the initial bias appear in the OVB formula, but the biases induced by the four backdoor paths are not fully effective. First, the correlation of the unreliable X* with the unobserved confounder U, $\mathit{Cor}(X^{\ast },U)=\stackrel{\sim }{\rho }=\rho \sqrt{\gamma }$, reduces the bias induced by U to the extent of the squared correlation ρ̃², leaving a bias of α_Uβ_U(1 − ρ̃²). Second, the unreliable X* blocks the three backdoor paths via X only to the extent of its reliability (γ) and thus leaves a bias of (α_Xβ_X + α_Xρβ_U + α_Uρβ_X)(1 − γ). Finally, the remaining bias due to the four partially unblocked backdoor paths is amplified but the bias amplification factor is attenuated by the reliability γ.

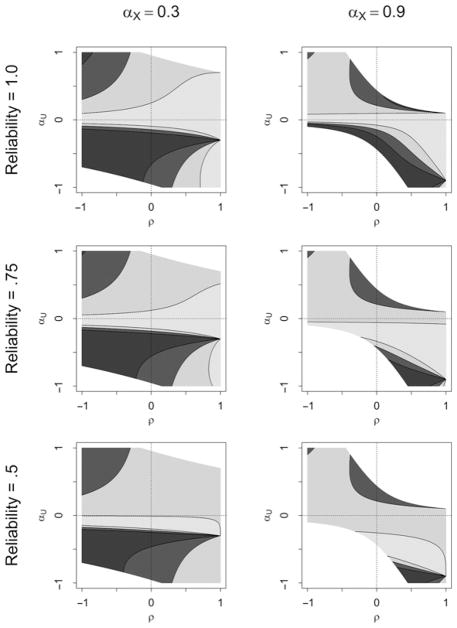
Due to the increased complexity of the OVB formulas, an easily interpretable inequality as for the uncorrelated confounder case is not derivable. Thus, we illustrate the effect of correlated confounders with two examples. The first row of plots in Figure 5 shows for two different parameter settings the areas of increasing (dark grey) and decreasing OVB (light grey) as a function of the correlation ρ (abscissa) and the unobserved confounder’s coefficient α_U (ordinate). For both plots we set β_X = β_U = .1, but α_X = .3 in the left plot and α_X = .9 in the right plot (making X a near-IV in the latter case). In each plot, quadrant I (with ρ ≥ 0 and α_U ≥ 0) represents the situation where all biases induced by X and U go into the same direction because all five data-generating parameters are positive. Quadrants II, III, and IV show the results for partial or completely offsetting biases (because the signs of the parameters differ).

Figure 5.

Increasing and decreasing OVB due to conditioning on a correlated confounder X. The two dark grey areas indicate an increasing OVB, with 100%–200% (lighter shade) and 200% or more (darker shade) remaining bias. The two light grey areas indicate a decreasing OVB, whith 50%–100% (darker shade) and 50% or less (lighter shade) remaining bias. The white areas indicate parameter combinations that are impossible for standardized path coefficients.

Consider quadrant I of the top right plot in Figure 3, where the confounder X strongly affects Z (α_X = .9): OVB can exceed the initial bias even if one conditions on a confounder X that is almost perfectly correlated with U. In general, it is hard to derive a generalizable pattern from the two example plots. Without knowing the sign and magnitude of the five parameters it is impossible to predict whether conditioning on a correlated X or X* reduces or increases OVB even if X is highly correlated with U. The second and third row in Figure 3 shows the effect of measurement error, which is the same as for the uncorrelated case (i. e., attenuation to the initial bias; Proof 5 in Appendix C).

Imbalance in confounders U and X

As for the case of uncorrelated confounders, the bias-amplifying effect of conditioning on a reliably or unreliably measured confounder X can be explained by the amplified imbalance in U and X. The absolute initial imbalance in U, |Imbalance(U | {})| = |α_U + α_Xρ|, might increase or decrease once one conditions on X*, even when U is correlated with X*. Adjusting for the correlated X* changes the initial imbalance in U to α_U(1 − ρ̃²) + α_Xρ(1 − γ), which then is amplified by the factor 1/(1 − (α_X + α_Uρ)²γ) such that we obtain $\mid \mathit{Imbalance}(U\mid X^{\ast })\mid =\left|\frac{{\alpha }_U(1-{\stackrel{\sim }{\rho }}^2)+{\alpha }_X\rho (1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }\right|$. Compared to the absolute value of the initial imbalance (before adjusting for X*), the absolute imbalance in U after adjusting for X* might be smaller or larger (Proof 2 in Appendix C). Despite the correlation, conditioning on X* can increase the imbalance in U because the term α_Uρ may strengthen the bias amplification factor.

Correspondingly, conditioning on X* first reduces the absolute initial imbalance in X from |Imbalance(X|{})| = |α_X + α_Uρ| to |(α_X + α_Uρ)(1 − γ)|, which again is amplified such that $\mid \mathit{Imbalance}(X\mid X^{\ast })\mid =\left|\frac{({\alpha }_X+{\alpha }_U\rho )(1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }\right|$. Multiplying U’s imbalance by β_U and X’s imbalance by β_X, and then adding the two terms results in the OVB formula (8). As for the uncorrelated confounder case, the absolute imbalance in X after adjusting for X* will always be smaller than before the adjustment, |Imbalance(X|X*)|≤|Imbalance(X|{})|(Proof 2 in Appendix C). Again, this only holds for the case with a single observed confounder X. Conditioning on multiple confounders, including X*, can actually increase the imbalance in X (but as for the imbalance in U, whether the imbalance in X decreases or increases depends on the correlation among the observed confounders).

With a perfectly reliably measured X (γ = 1), X will be fully balanced but U remains imbalanced with $\mid \mathit{Imbalance}(U\mid X^{\ast })\mid =\left|\frac{{\alpha }_U(1-{\rho }^2)}{1-{({\alpha }_X+{\alpha }_U\rho )}^2}\right|$. Note that neither the imbalance in U nor in X (given it is unreliably measured) can be tested empirically since both are unobserved.

Discussion

The investigation of the OVB mechanics revealed that conditioning on a confounder provokes two opposing effects, a bias-removing effect and a bias-increasing effect. If the bias-increasing effect dominates the bias-removing effect, then OVB increases. The increase in OVB can be caused by the amplification of any bias left due to unblocked backdoor paths, the cancellation of offsetting biases, or by both together. The overall extent of bias amplification is driven by two factors: (i) the bias left due to unblocked backdoor paths and (ii) the size of the multiplicative bias amplification factor. Both factors depend on the strength of the correlation between the observed and unobserved confounder and the degree of measurement error in the observed confounder. Though the correlation helps in partially removing the bias induced by the unobserved confounder, it also picks up the bias-amplifying potential of the unobserved confounder, and thus can further boost bias amplification. Therefore, even a high correlation between the observed and unobserved confounder does not guarantee that OVB will decrease. Though measurement error attenuates the bias amplification factor it also attenuates the confounder’s potential to remove bias such that measurement error may have a positive or negative effect on OVB. Bias amplification is not an issue if conditioning on a set of confounders removes all the bias (i. e., no bias is left to be amplified) or if the amplification factor is one (i. e., α_X = − α_Uρ). Table 1 and Table 2 summarize the formulas and results for uncorrelated and correlated confounders, respectively. Appendix B shows that the very same OVB mechanics operate with dichotomous instead of continous treatment variables (though the formulas a slightly different).

Table 1.

Uncorrelated confounders X and U: Omitted variable bias (OVB) and imbalance before and after adjusting for X*.

	Initial OVB and Imbalance	OVB and Imbalance after adjusting for X*
Omitted variable bias	OVB(τ̂ | {}) = αXβX + αUβU	$\mathit{OVB}(\widehat{\tau }\mid X^{\ast })=\frac{{\alpha }_U{\beta }_U+{\alpha }_X{\beta }_X(1-\gamma )}{1-{\alpha }_X^2\gamma }$
Imbalance in U	Imbalance(U | {}) = αU	$\mathit{Imbalance}(U\mid X^{\ast })=\frac{{\alpha }_U}{1-{\alpha }_X^2\gamma }$
Imbalance in X	Imbalance(X|{}) = αX	$\mathit{Imbalance}(X\mid X^{\ast })=\frac{{\alpha }_X(1-\gamma )}{1-{\alpha }_X^2\gamma }$
	Effect of conditioning on X* when …
	biases are in the same direction	biases offset each other
Absolute omitted variable bias	Increase in OVB is most likely if the bias induced by the unobserved confounder U is much larger than the bias induced by confounder X or confounder X strongly affects Z.	If the bias induced by the unobserved confounder U exceeds half of the bias induced by X, OVB always increases (this case also includes almost perfectly offsetting biases). If the bias induced by the unobserved confounder U is less than half of the bias induced by X, OVB most likely increases if X strongly affects Z (provided X is reliably measured).
Absolute imbalance	Imbalance in U always increases. Imbalance in X always decreases.	Imbalance in U always increases. Imbalance in X always decreases.
Effect of measurement error	Attenuates any increase in OVB and attenuates any decrease in OVB.	If the bias induced by the unobserved confounder U exceeds half of the bias induced by X, measurement error attenuates any increase in OVB. If the bias induced by the unobserved confounder U is less than half of the bias induced by X, measurement error attenuates any increase in OVB (and might even turn an increase into a decrease) but may attenuate or strengthen any decrease in OVB.

Table 2.

Correlated confounders X and U: Omitted variable bias (OVB) and imbalance before and after adjusting for X*.

	Initial OVB and Imbalance	OVB and Imbalance after adjusting for X*
Omitted variable bias	OVB(τ̂ | {}) = αXβX + αUβU + αXρβU + αUρβX	$\mathit{OVB}(\widehat{\tau }\mid X^{\ast })=\frac{{\alpha }_U{\beta }_U(1-{\stackrel{\sim }{\rho }}^2)+({\alpha }_X{\beta }_X+{\alpha }_X\rho {\beta }_U+{\alpha }_U\rho {\beta }_X)(1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }$
Imbalance in U	Imbalance(U | {}) = αU + αXρ	$\mathit{Imbalance}(U\mid X^{\ast })=\frac{{\alpha }_U(1-{\stackrel{\sim }{\rho }}^2)+{\alpha }_X\rho (1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }$
Imbalance in X	Imbalance(X|{}) = αX + αUρ	$\mathit{Imbalance}(X\mid X^{\ast })=\frac{({\alpha }_X+{\alpha }_U\rho )(1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }$
	Effect of conditioning on X* when …
	biases are in same the direction	biases offset each other
Absolute omitted variable bias	Increase in OVB is most likely if the bias induced by the unobserved confounder U is much larger than the bias induced by confounder X and the correlation between X and U is low, or confounder X strongly affects Z –a high correlation between X and U strongly boosts bias amplification.	Whether OVB increases strongly depends. on the signs and magnitudes of all five parameters. If the biases induced by X and U strongly offset each other, an increase in OVB almost surely results – unless the correlation between X and U is close to 1.
Absolute imbalance	Imbalance in U may increase or decrease. Imbalance in X always decreases.	Imbalance in U may increase or decrease. Imbalance in X always decreases.
Effect of measurement error	Attenuates any increase in OVB and attenuates any decrease in OVB.	Attenuates any increase in OVB (and might even turn an increase into a decrease) but may attenuate or strengthen any decrease in OVB.

Though we restricted our discussion of OVB to the case with a single observed and unobserved confounder, the principles of the OVB mechanics also apply to the multiple confounder case where X and U represent sets of observed and unobserved confounders. However, the OVB formulas would be by far more complex because the correlation structure within and between the two sets of confounders also needs to be considered (for an OVB formula in matrix notation, see [27]). Moreover, cancellation of offsetting biases and bias amplification are not restricted to the linear case, they also occur in nonlinear settings [17]; but it is much harder to derive closed OVB formulas that are informative about the OVB mechanics.

We also showed that bias amplification operates via increasing the imbalance in unobserved confounders. That is, conditioning on an observed confounder can significantly increase the unobserved confounders’ imbalance and, thus, turn them into even stronger confounders. If the observed and unobserved confounders are uncorrelated, the imbalance in the unobserved confounders always increases. Thus, balancing a large set of observed covariates via matching or regression adjustment does not imply that the imbalance in unobserved confounders decreases.

In the presence of omitted or unobserved variables, is it possible to select a subset of observed covariates that minimizes OVB? Or, is it at least possible to make sure that the selected covariates do not increase OVB? With almost perfect knowledge about the data-generating selection and outcome models one could actually select the set of covariates that minimizes OVB. But such knowledge is rarely available. Without reliable knowledge about the true DGM it seems impossible to know whether conditioning on a set of covariates minimizes or even reduces the confounding bias. While empirical covariate selection strategies, that rely on observed relations between the covariates and the treatment or outcome, can be very successful when all confounding covariates are reliably measured, it is not clear how good or bad these strategies perform in the presence of unobserved or unreliably measured confounders. However, partial knowledge might occasionally allow an informed assessment of whether adjusting for a set of covariates brings us at least closer to a causal effect estimate (for instance, we might know that only positive selection took place and that the observed covariates cover the most important confounders but no near-IVs).

The OVB mechanics discussed in this article have far-reaching implications for practice. Given unobserved confounders, neither conditioning on all or a large set of observed pre-treatment covariates (as publicized in [28], or [9]), nor conditioning on a small set of covariates that has been selected on subject-matter or empirical grounds [21] can guarantee that OVB will decrease. For matching designs like propensity score matching this means that achieving balance on all observed pre-treatment covariates neither implies that the confounding bias has been minimized or even reduced nor that the imbalance in unobserved covariates, including the latent constructs of fallible measures, diminished. The same holds for all methods dealing with bias due to nonresponse or attrition – conditioning on a large set of covariates does not imply that nonresponse or attrition bias in the statistic of interest is successfully addressed [22]; Or for two-stage least-squares analyses (2SLS) of conditional IV designs, conditioning on a set of observed covariates does not guarantee that the bias due to a potential violation of the exclusion restriction is minimized. Whenever covariate adjustments are made in the hope to reduce different types of confounding bias, a thoughtless or automated selection of covariates may increase instead of reduce the bias.

Since we used a very simple data-generating model to explain the mechanics of OVB, one needs to be careful in deriving practical guidelines about when to condition on an observed covariate and when not. The decision about adjusting for a given covariate strongly depends on the presumed real-world data-generating model. For instance, if there would be only a single confounder X but which has been unreliably measured, then conditioning on X* would always reduce selection bias. But when there is one or multiple unobserved confounders, then it is already less clear whether conditioning on X* actually reduces OVB. In practice, the situation is usually even more complex because a confounding path might be blocked in more than one way. For instance, if we observed an intermediate covariate W on U’s confounding path, Z ← W ← U → Y, then conditioning on W would not result in any OVB despite the omission of confounder U (provided there are no other unobserved confounders). But if one conditions neither on U nor on W the OVB mechanics are in place again.

Sometimes it is also possible to circumvent unobserved confounding by using designs that exploit other observed covariates. For instance, if the observed set of covariates contains an instrumental variable then we could use an instrumental variable design to identify the complier average treatment effect. Or, if data contain a pretest measure of the outcome then a gain score or difference-in-differences design can deal with unobserved time-invariant confounding [29]. However, the assumptions underlying these designs might be less credible than the conditional independence assumption such that covariate adjustments via regression or matching methods might be preferable. But given the uncertainty about the magnitude of OVB left after adjusting for a set of covariates, it is important to conduct sensitivity analyses that assess the estimated treatment effect’s sensitivity to unobserved confounders [30–32]. Or, with partial knowledge about the data-generating process, one can pursue a partial identification strategy and compute bounds on the treatment effect [33]. In any case, lacking strong subject-matter theory, researchers should abstain from making strong causal claims from a single observational study. Causal claims are much more credible when built on multiple independent replications with different study designs.

Appendix A: Bias amplification when matching or stratifying on an IV

Bias amplification can also be intuitively explained within the context of matching or stratifying treatment and control cases on the IV (i. e., with a dichotomous treatment Z). Consider the case of exact full matching on IV, that is, all treatment and control cases with IV = v are matched together (this is equivalent to exact stratification because the set of matched cases forms a unique stratum with IV = v). For simplicity, we first assume that the dichotomous treatment Z is a deterministic function of IV and U: Z = f (IV, U) = 1_{[IV + U> c]}, where Z = 1 if the sum IV + U exceeds a threshold c, otherwise Z = 0 (indicating the control condition). Now assume that we match on the observed IV in the hope to remove potential confounding bias. Then, for a given stratum with IV = v, the treatment status Z = f (U | IV = v) = 1_{[U>c− v]} is now exclusively determined by U: Cases with U > c − v received the treatment and cases with U ≤ c − v received the control condition. Thus, all treatment cases with IV = v must have strictly larger values in U than the control cases, that is, the treatment and control cases distribution of U no longer overlap. But without matching on IV, the distributions of U would have overlapped, enabling exact matches on U. Thus, matching on the IV increases the treatment and control group’s heterogeneity in U which is reflected by the increased imbalance.

The same argument holds for a treatment function with an independent error term (i. e., unobserved factors determining Z): Z = f (IV,U, ε) = 1_{[IV + U+ ε > c]}. Matching on IV then restricts the pool of potential matches with regard to U – if one were to match on the unobserved U. Due to the error term, we still could find exact matches on U but, nonetheless, the difference in the treatment and control cases distribution of U is larger than before matching on IV. Note that the imbalance in U does not necessarily have to increase within each stratum, but it will necessarily increase on average across strata.

Appendix B: Bias amplification and cancellation of offsetting biases for a dichotomous treatment

All the bias formulas we discussed so far referred to regression estimators for a continuous treatment variable. Since treatment variables are frequently dichotomous, we briefly characterize the bias for a dichotomous treatment indicator Z* (this section follows the formalization used by [14]). Figure 6 shows the DGM with two correlated confounders, one measured with error and the other one unobserved. The corresponding SCM we used for the following derivations is given by

Figure 6.

Causal graph for two correlated confounders X and U. The vacant nodes for X, Z and U indicate that they are unobserved. Z* is dichotomous.

$$\begin{gathered} X={\epsilon }_X \\ {X}^{\ast }=X+e \\ U={\epsilon }_U \\ Z={\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z \\ {Z}^{\ast }=1\text{if}Z\ge c\text{and}{Z}^{\ast }=0\text{if}Z<c \\ Y=\tau Z^{\ast }+{\beta }_{X}X+{\beta }_{U}U+{\epsilon }_Y \end{gathered}$$

In order to derive corresponding OVB formulas, we assume that X and U are distributed according to a bivariate normal distribution with zero expectation, unit variances, and a correlation ρ. Consequently, also Z is normally distributed with zero expectation. We further assume that the treatment effect is zero which considerably simplifies the derivation of the OVB formulas. As before, coefficients of α_X, α_U, β_X, and β_U represent standardized coefficients, and the normally distributed error terms ε_Z and ε_U were chosen such that Var(Z) = 1 and Var(Y) = 1. The dichotomous treatment Z* is obtained from the continuous Z and the cutoff c. The cutoff value c refers to the quantiles of a standard normal distribution ϕ(c) because Z ~N(0, 1). The unreliable measure X* is given by X* = X + e with $e~N(0,{\sigma }_{\mathrm{e}}^2)$.

Under these assumptions the standardized effect of X on Z* is given by ${\alpha }_X^{\ast }={\alpha }_X\frac{\varphi (c)}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}$ and the standardized effect of U on Z* is given by ${\alpha }_U^{\ast }={\alpha }_U\frac{\varphi (c)}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}$ where ϕ(c) and Φ(c) denote the standard normal probability density and cumulative distribution function, respectively (the Proof is given at the end of the section). Then, the regression estimator’s initial bias before any conditioning (i. e., Ŷ = γ̂ + τ̂_Z*Z*) is

$$\mathit{OVB}({\widehat{\tau }}_{Z^{\ast }}\mid \{\})=({\alpha }_X^{\ast }{\beta }_X+{\alpha }_U^{\ast }{\beta }_U+{\alpha }_X^{\ast }\rho {\beta }_U+{\alpha }_U^{\ast }\rho {\beta }_X)\times \frac{1}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}.$$ (9)

After conditioning on X*, we obtain

$$\mathit{OVB}({\widehat{\tau }}_{Z^{\ast }}\mid X^{\ast })=\{{\alpha }_U^{\ast }{\beta }_U(1-{\stackrel{\sim }{\rho }}^2)+({\alpha }_X^{\ast }{\beta }_X+{\alpha }_X^{\ast }\rho {\beta }_U+{\alpha }_U^{\ast }\rho {\beta }_X)(1-\gamma )\}\times \frac{1}{1-{({\alpha }_X^{\ast }+\rho {\alpha }_U^{\ast })}^2\gamma }+\frac{1}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}.$$ (10)

Both OVB formulas are identical to the OVB formulas for a continuous treatment variable, except for the constant $1/\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}=1/\sqrt{\mathit{Var}(Z^{\ast })}$ which ensures that OVB refers to the change in Z* from 0 to 1 (without the constant the OVB formula would refer to a change in Z* by one standard deviation, just as in the continuous case). Thus, we have the same OVB mechanics and conditions under which conditioning on X* increases OVB as for the continuous treatment case. However, since ${\alpha }_X^{\ast }<{\alpha }_X$ and ${\alpha }_U^{\ast }<{\alpha }_U$ the bias-amplifying effects will always be weaker for a dichotomous treatment than for a corresponding continuous treatment (because the dichotomized version of the continuous treatment will always be less strongly correlated with the continuous confounders). But this does not imply that bias amplification and an increasing OVB is less of an issue with a dichotomous treatment. Just assume that the dichotomous Z* is directly affected by dichotomous confounders X and U (i. e., with respect to Figure 6, X and U are dichotomous and there is no continuous Z on the causal pathway from the dichotomous confounders to Z*; instead X and U directly affect Z*: X → Z* and U → Z*). In this case, the dichotomous confounders can affect Z* at least as strongly as continuous confounders can affect a continuous Z ( ${\alpha }_X^{\ast }$ and ${\alpha }_U^{\ast }$ are no longer attenuated and the correlation between the confounder and the treatment can theoretically be one as in the continuous treatment and confounder case).

Proof

OVB with a Dichotomous Treatment

Using the data generating model in Figure 6 with a treatment effect of zero (τ = 0), we derive the OVB formula for the treatment effect from the regression of Y on Z* and X*. We assume that X and U are bivariate normally distributed with zero means, unit variances, and a correlation ρ. This implies that also Z is normally distributed. The unstandardized OLS estimator for the treatment effect can be written in terms of observed correlations as $b_{Z^{\ast }}=\frac{r_{Y{Z}^{\ast }}-r_{Y{X}^{\ast }}{r}_{Z^{\ast }{X}^{\ast }}}{1-r_{Z^{\ast }{X}^{\ast }}^2}\times \frac{1}{SD(Z)}$. To obtain the three correlation coefficients, we use the corresponding covariances:

$$\begin{gathered} \mathit{Cov}(Y,Z^{\ast })=\varphi (c)({\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U+\rho {\alpha }_X{\beta }_U+\rho {\alpha }_U{\beta }_X) \\ \mathit{Cov}(Y,X^{\ast })=\mathit{Cov}(X+e,Y)=\mathit{Cov}(X,Y)=\mathit{Cov}(X,{\beta }_{X}X+{\beta }_{U}U+eY)={\beta }_X+\rho {\beta }_U, \\ \mathit{Cov}(Z^{\ast },X^{\ast })=\mathit{Cov}(Z^{\ast },X+e)=\mathit{Cov}(Z^{\ast },X)=\varphi (c)({\alpha }_X+\rho {\alpha }_U), \end{gathered}$$

where ϕ(x) denotes the standard normal density function. While Cov(Y, X*) directly follows from the structural equations, Cov(Y, Z*) and Cov(Z*, X*) need some further explanations which we exemplify for Cov(Y, Z*).

Assuming a constant treatment effect of zero, the treatment effect’s regression estimator from the regression of Y on Z* can be written as the expected difference in the outcome Y for Z*=1 and Z* = 0, that is, E(Y|Z*= 1) − E(Y|Z*=0). Since the OLS estimator is given by Cov(Y, Z*)/Var(Z*), we obtain Cov(Y, Z*) = Var(Z*){E(Y|Z*= 1) − E(Y|Z*=0)}. Then, using Var(Z*) =Φ(c)Φ( − c) and $E(Y\mid Z^{\ast }=1)-E(Y\mid Z^{\ast }=0)=E(Y\mid Z\ge c)-E(Y\mid Z<c)=\frac{r_{ZY}\varphi (c)}{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}$ from Lemma 1 and Lemma 2 (see below), and r_ZY = Cov(α_XX + α_UU + eZ, β_XX + β_UU + eY) = α_Xβ_X + α_Uβ_U + ρα_Xβ_U + ρα_Uβ_X, we get Cov(Y, Z*) = ϕ(c)(α_Xβ_X + α_Uβ_U + ρα_Xβ_U + ρα_Uβ_X).

The covariances and Lemma 1 are then used to obtain expressions for the correlations:

$$\begin{gathered} r_{Y{Z}^{\ast }}=\mathit{Cov}(Y,Z^{\ast })/SD(Z^{\ast })=\varphi (c)({\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U+\rho {\alpha }_X{\beta }_U+\rho {\alpha }_U{\beta }_X)/\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)} \\ {r}_{Y{X}^{\ast }}=\mathit{Cov}(Y,X^{\ast })/SD(X^{\ast })=({\beta }_X+\rho {\beta }_U)\sqrt{\gamma }, \\ {r}_{Z^{\ast }{X}^{\ast }}=\mathit{Cov}(Z^{\ast },X^{\ast })/\{SD(Z^{\ast })SD(X^{\ast })\}=\varphi (c)({\alpha }_X+\rho {\alpha }_U)\sqrt{\gamma }\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)} \end{gathered}$$

Plugging the correlations into the formula for the treatment effect’s regression estimator results in $b_{Z^{\ast }}=\mathit{OVB}({\widehat{\tau }}_{Z^{\ast }}\mid X^{\ast })=\frac{\varphi (c)\{{\alpha }_U{\beta }_U(1-{\stackrel{\sim }{\rho }}^2)+({\alpha }_X{\beta }_X+\rho {\alpha }_X{\beta }_U+\rho {\alpha }_U{\beta }_X)(1-\gamma )\}}{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)-\varphi {(c)}^2{({\alpha }_X+\rho {\alpha }_U)}^2\gamma }$ which is equivalent to the OVB since the derivations are based on a treatment effect of zero. The initial bias in the treatment effect of Z* on Y can be obtained by regressing Y onto Z*, that is,

$$\begin{gathered} \mathit{OVB}({\widehat{\tau }}_{Z^{\ast }}\mid \{\})=\mathit{Cov}(Z^{\ast },Y)/\mathit{Var}(Z^{\ast }) \\ =\varphi (c)({\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U+\rho {\alpha }_X{\beta }_U+\rho {\alpha }_U{\beta }_X)/\mathrm{\Phi }(c)\mathrm{\Phi }(-c). \end{gathered}$$

The two OVBs can be rewritten as

$$\begin{gathered} \mathit{OVB}({\widehat{\tau }}_{Z^{\ast }}\mid \{\})=({\alpha }_X^{\ast }{\beta }_X+{\alpha }_U^{\ast }{\beta }_U+{\alpha }_X^{\ast }\rho {\beta }_U+{\alpha }_U^{\ast }\rho {\beta }_X)\times \frac{1}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}\text{and} \\ \mathit{OVB}({\widehat{\tau }}_{Z^{\ast }}\mid X^{\ast })=\{{\alpha }_U^{\ast }{\beta }_U(1-{\stackrel{\sim }{\rho }}^2)+({\alpha }_X^{\ast }{\beta }_X+{\alpha }_X^{\ast }\rho {\beta }_U+{\alpha }_U^{\ast }\rho {\beta }_X)(1-\gamma )\}\times \frac{1}{1-{({\alpha }_X^{\ast }+\rho {\alpha }_U^{\ast })}^2\gamma }\times \frac{1}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}, \end{gathered}$$

where ${\alpha }_X^{\ast }={\alpha }_X\frac{\varphi (c)}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}$ is the standardized effect of X on Z* and ${\alpha }_U^{\ast }={\alpha }_U\frac{\varphi (c)}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}$ is the standardized effect of U on Z*. ${\alpha }_X^{\ast }$ is the product of the effect of X on Z (α_X) and the standardized effect of Z on Z* ( $\frac{\varphi (c)}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}$). The latter is obtained from the regression of Z* on Z together with Lemmas 1 and 2, that is,

$$\begin{gathered} \frac{\mathit{Cov}(Z,Z^{\ast })}{\mathit{Var}(Z)}\times \frac{SD(Z)}{SD(Z^{\ast })}=\frac{\mathit{Cov}(Z,Z^{\ast })}{\mathit{Var}(Z^{\ast })}\times \frac{SD(Z^{\ast })}{SD(Z)} \\ =\{E(Z\mid Z^{\ast }=1)-E(Z\mid Z^{\ast }=0)\}\times SD(Z^{\ast }) \\ =\left\{\frac{\varphi (c)}{\mathrm{\Phi }(-c)}-\frac{-\varphi (c)}{\mathrm{\Phi }(c)}\right\}\times \sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)} \\ =\frac{\varphi (c)}{\sqrt{\mathrm{\Phi }(c)\mathrm{\Phi }(-c)}}. \end{gathered}$$

The first equality follows from inverting the regression, that is, regressing Z on Z* (using the fact the standardized coefficients of the original and inverted regression are equivalent), the second equality rewrites the effect of Z* on Z in terms of conditional expectations and uses SD(Z) = 1, and the third equality directly follows from Lemma 1 and 2.

Lemma 1

Assume Z is distributed according to a standard normal distribution and a binary variable Z* is determined from Z using a cutoff c such that Z = 1 if Z ≥ c and Z = 0 otherwise. Then the new random variable Z* follows a Bernoulli distribution with Pr(Z*= 1) = p. Since p= Pr(Z*= 1)= Pr(Z ≥ c) = 1 −Φ(c) =Φ(− c), we get Var(Z*) = p(1 − p) =Φ(c)Φ(− c).

Lemma 2. [14]

Assume X and Y follow a bivariate normal distribution with zero means, unit variances, and correlation coefficient ρ. Under these assumptions we have E(Y|X < c) = ρE(X|X < c). Since $E(X\mid X<c)=\frac{1}{\mathrm{\Phi }(c)}{\int }_{-\infty }^{c}x\varphi (x)dx=\frac{1}{\mathrm{\Phi }(c)}{\int }_{-\infty }^{c}d\varphi (x)=\frac{-\varphi (c)}{\mathrm{\Phi }(c)}$, we obtain $E(Y\mid X<c)=\rho \frac{-\varphi (c)}{\mathrm{\Phi }(c)}$. Similarly, we obtain $E(Y\mid X\ge c)=\rho \frac{-\varphi (-c)}{\mathrm{\Phi }(-c)}=\rho \frac{\varphi (c)}{\mathrm{\Phi }(-c)}$ since E(Y|X ≥ c) = E(Y|X < − c).

Appendix C: Proofs

Proof 1 Imbalance in confounders U and X

For the linear structural model formulated in Eq. (2) and represented by the right causal diagram in Figure 4, we prove for the general case with a correlated and unreliably measured confounder X* the imbalance formula

$$\mathit{Imbalance}(U\mid X^{\ast })=E_{X^{\ast }}\{E(U\mid Z=z+1,X^{\ast })-E(U\mid Z=z,X^{\ast })\}=\frac{{\alpha }_U(1-{\stackrel{\sim }{\rho }}^2)+{\alpha }_X\rho (1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma },$$

where X, U, Z, and Y are unit-variance variables and X* is a fallible measure of X with reliability $\gamma =1/(1+{\sigma }_e^2)$ (i. e., X*=X + e with $e~N(0,{\sigma }_{\mathrm{e}}^2)$). The correlation between X and U is given by cor(X,U) = ρ < 1, and the corresponding correlation with X* is $\mathit{cor}(X^{\ast },U)=\rho \sqrt{\gamma }=\stackrel{\sim }{\rho }$. Due to the linearity of the structural model, the difference in expectations of the above imbalance formula is given by the partial regression coefficient for Z of the regression of U on Z and $X^{\ast }:b_Z=\frac{r_{UZ}-r_{U{X}^{\ast }}{r}_{Z{X}^{\ast }}}{1-r_{Z{X}^{\ast }}^2}$, where r_AB is the correlation coefficient between A and B (note that the difference in expectations represents the change due to a one-unit increase in Z). Then, using correlations

$$\begin{gathered} r_{UZ}=\mathit{Cov}(U,Z)=\mathit{Cov}(U,{\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z)={\alpha }_X\rho +{\alpha }_U \\ {r}_{U{X}^{\ast }}=\mathit{Cov}(U,X^{\ast })/SD(X^{\ast })=\mathit{Cov}(U,X+e)\sqrt{\gamma }=\rho \sqrt{\gamma },\text{and} \\ {r}_{Z{X}^{\ast }}=\mathit{Cov}(Z,X^{\ast })/SD(X^{\ast })=\mathit{Cov}({\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z,X+e)\sqrt{\gamma }=({\alpha }_X+{\alpha }_U\rho )\sqrt{\gamma } \end{gathered}$$

we obtain

$$\mathit{Imbalance}(U\mid X^{\ast })=\frac{r_{UZ}-r_{U{X}^{\ast }}{r}_{Z{X}^{\ast }}}{1-r_{Z{X}^{\ast }}^2}=\{{\alpha }_U(1-{\stackrel{\sim }{\rho }}^2)+{\alpha }_X\rho (1-\gamma )\}\frac{1}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }.$$

In setting ρ=0 or γ = 1 all other imbalance formulas presented in this article can be directly derived.

Analogously, the imbalance formula for X is given by the partial regression coefficient for Z from the regression of X on Z and X*. Using

$$\begin{gathered} r_{XZ}=\mathit{Cov}(X,Z)=\mathit{Cov}(X,{\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z)={\alpha }_X+{\alpha }_U\rho \text{and} \\ {r}_{X{X}^{\ast }}=\mathit{Cov}(X,X^{\ast })/SD(X^{\ast })=\mathit{Cov}(X,X+e)\sqrt{\gamma }=\sqrt{\gamma } \end{gathered}$$

we get

$$\mathit{Imbalance}(X\mid X^{\ast })=\frac{r_{XZ}-r_{X{X}^{\ast }}{r}_{Z{X}^{\ast }}}{1-r_{Z{X}^{\ast }}^2}=\frac{({\alpha }_X+{\alpha }_U\rho )(1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }.$$

Proof 2 Imbalance inequalities

We prove the following three results: (i) Conditioning on a fallible X* does not fully balance the latent X, and the imbalance can never exceed the initial imbalance (i. e., without conditioning on X or X*): |Imbalance(X|X*)|≤|Imbalance(X|{})|. (ii) If X and U are uncorrelated, conditioning on a fallible X* increases the imbalance in U:|Imbalance(U | X*)|>|Imbalance(U | {})|. (iii) For correlated X and U, conditioning on a fallible X* may increase or decrease the imbalance in U.

1. We show that |Imbalance(X|X*)|≤|Imbalance(X|{})|, that is, $\left|\frac{({\alpha }_X+{\alpha }_U\rho )(1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }\right|\le \mid {\alpha }_X+{\alpha }_U\rho \mid$. For ease of notation, we use a = α_X + ρα_U such that the inequality simplifies to $\left|\frac{a(1-\gamma )}{1-a^2\gamma }\right|\le \mid a\mid$ which is identical to writing $\frac{(1-\gamma )}{1-a^2\gamma }\mid a\mid \le \mid a\mid$ since 0 < γ ≤ 1 and a² ≤ 1 (because the path coefficients refer to variables with unit variances). Because of the constraints on γ and a we know that $\frac{(1-\gamma )}{1-a^2\gamma }\le 1$, proving our result. Note that conditioning on X* does not reduce the imbalance in X if a = α_X + ρα_U = 0 (another setting would be a = α_X + ρα_U = 1 but this is not possible due to the parameter constraints).

2. For uncorrelated X and U we show that |Imbalance(U | X*)|>|Imbalance(U | {})|, that is, $\left|\frac{{\alpha }_U}{1-{\alpha }_X^2\gamma }\right|>\mid {\alpha }_U\mid$. Using 0 < γ ≤ 1 and α_X² < 1, we get $\frac{\mid {\alpha }_U\mid }{1-{\alpha }_X^2\gamma }>\mid {\alpha }_U\mid$. And knowing that $1-{\alpha }_X^2\gamma <1$ verifies the inequality.

3. For correlated X and U conditioning on X* can increase or decrease the imbalance in U, that is, |Imbalance(U | X*)|>|Imbalance(U | {})| or |Imbalance(U | X*)|≤|Imbalance(U | {})|. Using two different restrictions on α_U, we show that the difference in absolute imbalances, $\mid \mathit{Imbalance}(U\mid \{\})\mid -\mid \mathit{Imbalance}(U\mid X^{\ast })\mid =\mid {\alpha }_U+{\alpha }_X\rho \mid -\left|\frac{{\alpha }_U(1-{\stackrel{\sim }{\rho }}^2)+{\alpha }_X\rho (1-\gamma )}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }\right|$, can be negative or positive. Using α_U = − α_Xρ with |α_Xρ|> 0 as first restriction results in a negative difference. Since |Imbalance(U | {})|= 0 and $\mid \mathit{Imbalance}(U\mid X^{\ast })\mid =\frac{\gamma (1-{\rho }^2)}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }\mid {\alpha }_X\rho \mid >0$ we obtain |Imbalance(U | {})|−|Imbalance(U | X*)|<0. Using ${\alpha }_U=\frac{-{\alpha }_X\rho (1-\gamma )}{1-{\stackrel{\sim }{\rho }}^2}$ with |α_Xρ|> 0 as second restriction results in a positive difference. Since $\mid \mathit{Imbalance}(U\mid \{\})\mid =\frac{\gamma (1-{\rho }^2)}{1-{\rho }^2\gamma }\mid {\alpha }_X\rho \mid >0$ and |Imbalance(U | X*)|= 0 we get |Imbalance(U | {})|− |Imbalance(U | X*)|>0.

Proof 3 Bias in the linear regression estimator τ̂

Using the same linear setting as in Proof 1, we show that, after conditioning on X*, the bias in the linear regression estimator τ̂ is given by

$$\mathit{OVB}(\widehat{\tau }\mid X^{\ast })=\{{\alpha }_U{\beta }_U(1-{\stackrel{\sim }{\rho }}^2)+({\alpha }_X{\beta }_X+{\alpha }_X\rho {\beta }_U+{\alpha }_U\rho {\beta }_X)(1-\gamma )\}\times \frac{1}{1-{({\alpha }_X+{\alpha }_U\rho )}^2\gamma }.$$

The estimator τ̂ for the effect of treatment Z is obtained from regressing Y onto Z and $X^{\ast }:\widehat{\tau }=\frac{r_{YZ}-r_{Y{X}^{\ast }}{r}_{Z{X}^{\ast }}}{1-r_{Z{X}^{\ast }}^2}$. Plugging the population correlations

$$\begin{gathered} r_{YZ}=\mathit{Cov}(Y,Z)=\mathit{Cov}({\beta }_{X}X+{\beta }_{U}U+\tau Z+{\epsilon }_Y+{\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z) \\ =\tau +{\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U+{\alpha }_X{\beta }_U\rho +{\alpha }_U{\beta }_X\rho , \\ {r}_{Y{X}^{\ast }}=\mathit{Cov}(Y,X^{\ast })/SD(X^{\ast })=\mathit{Cov}({\beta }_{X}X+{\beta }_{U}U+\tau Z+{\epsilon }_Y,X+e)\sqrt{\gamma } \\ =({\beta }_X+\tau {\alpha }_X+{\beta }_U\rho +\tau {\alpha }_U\rho )\sqrt{\gamma }, \\ {r}_{Z{X}^{\ast }}=\mathit{Cov}(Z,X^{\ast })/SD(X^{\ast })=\mathit{Cov}({\alpha }_{X}X+{\alpha }_{U}U+{\epsilon }_Z,X+e)\sqrt{\gamma }=({\alpha }_X+{\alpha }_U\rho )\sqrt{\gamma } \end{gathered}$$

into the above OVB formula we get $\widehat{\tau }-\tau =\frac{r_{YZ}-r_{Y{X}^{\ast }}{r}_{Z{X}^{\ast }}}{1-r_{Z{X}^{\ast }}^2}-\tau$. In setting ρ=0 or γ = 1 all other bias formulas contained in this article directly follow from this general formula.

Proof 4 Inequalities for increasing bias when conditioning on an uncorrelated and reliably measured confounder X

For uncorrelated confounders X and U (with standardized coefficients), we prove the inequalities (i) $\frac{\mid {\alpha }_U{\beta }_U\mid }{\mid {\alpha }_X{\beta }_X\mid }>\frac{1-{\alpha }_X^2}{{\alpha }_X^2}$ if sgn(α_Xβ_X) = sgn(α_Uβ_U), (ii) $\frac{\mid {\alpha }_U{\beta }_U\mid }{\mid {\alpha }_X{\beta }_X\mid }>\frac{1-{\alpha }_X^2}{2-{\alpha }_X^2}$ if sgn(α_Xβ_X) ≠ sgn(α_Uβ_U) and |α_Xβ_X | > |α_Uβ_U|, and (iii) $\frac{\mid {\alpha }_U{\beta }_U\mid }{\mid {\alpha }_X{\beta }_X\mid }>1-\frac{1}{{\alpha }_X^2}$ if sgn(α_Xβ_X) ≠ sgn(α_Uβ_U) and |α_Xβ_X | < |α_Uβ_U|. Given the biases before and after conditioning on X, OVB(τ̂ | {}) = α_Xβ_X + α_Uβ_U and $\mathit{OVB}(\widehat{\tau }\mid X)=\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_X^2}$, adjusting for X increases the absolute bias if

$$\left|\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_X^2}\right|>\mid {\alpha }_X{\beta }_X+{\alpha }_U{\beta }_U\mid$$ (C1)

First, if sgn(α_Xβ_X) = sgn(α_Uβ_U), (C1) is equivalent to $\mid \frac{{\alpha }_U{\beta }_U}{1-{\alpha }_X^2}\mid >\mid {\alpha }_X{\beta }_X\mid +\mid {\alpha }_U{\beta }_U\mid$. In dividing both sides by |α_Uβ_U| we obtain $\frac{1}{1-{\alpha }_X^2}>\frac{\mid {\alpha }_X{\beta }_X\mid }{\mid {\alpha }_U{\beta }_U\mid }+1$ and, finally, $\frac{\mid {\alpha }_U{\beta }_U\mid }{\mid {\alpha }_X{\beta }_X\mid }>\frac{1-{\alpha }_X^2}{{\alpha }_X^2}$.

Second, if sgn(α_Xβ_X) ≠ sgn(α_Uβ_U) and |α_Xβ_X | > |α_Uβ_U|, then (C1) can be written as $\left|\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_X^2}\right|>\mid {\alpha }_X{\beta }_X\mid -\mid {\alpha }_U{\beta }_U\mid$. Dividing both sides by |α_Uβ_U| we obtain $\frac{1}{1-{\alpha }_X^2}>\frac{\mid {\alpha }_X{\beta }_X\mid }{\mid {\alpha }_U{\beta }_U\mid }-1$, and thus $\frac{\mid {\alpha }_U{\beta }_U\mid }{\mid {\alpha }_X{\beta }_X\mid }>\frac{1-{\alpha }_X^2}{2-{\alpha }_X^2}$.

Third, if sgn(α_Xβ_X) ≠ sgn(α_Uβ_U) and |α_Xβ_X | < |α_Uβ_U|, then (C1) is equivalent to $\left|\frac{{\alpha }_U{\beta }_U}{1-{\alpha }_X^2}\right|>\mid {\alpha }_U{\beta }_U\mid -\mid {\alpha }_X{\beta }_X\mid$. Then, dividing both sides by |α_Uβ_U| we obtain $\frac{1}{1-{\alpha }_X^2}>1-\frac{\mid {\alpha }_X{\beta }_X\mid }{\mid {\alpha }_U{\beta }_U\mid }$ and finally $\frac{\mid {\alpha }_U{\beta }_U\mid }{\mid {\alpha }_X{\beta }_X\mid }>1-\frac{1}{{\alpha }_X^2}$. For |α_Xβ_X | < |α_Uβ_U| this inequality is always true because the left-hand side is always greater than one while the right-hand side is always less than one. That is, for sgn(α_Xβ_X) ≠ sgn(α_Uβ_U) and |α_Xβ_X | < |α_Uβ_U|, conditioning on X always increases rather than reduces the bias.

Proof 5 Inequalities among absolute biases

It is important to note that measurement error in X* always attenuates OVB towards the initial bias [26], that is,

$$\begin{gathered} \mathit{OVB}(\widehat{\tau }\mid X)<\mathit{OVB}(\widehat{\tau }\mid X^{\ast })<\mathit{OVB}(\widehat{\tau }\mid \{\})\text{if}\mathit{OVB}(\widehat{\tau }\mid X)<\mathit{OVB}(\widehat{\tau }\mid \{\})\text{and} \\ \mathit{OVB}(\widehat{\tau }\mid X)>\mathit{OVB}(\widehat{\tau }\mid X^{\ast })>\mathit{OVB}(\widehat{\tau }\mid \{\})\text{if}\mathit{OVB}(\widehat{\tau }\mid X)>\mathit{OVB}(\widehat{\tau }\mid \{\}). \end{gathered}$$

Since the initial OVB and the OVB after adjusting for X can be of opposite signs, the two inequalities do not imply that measurement error necessarily increases the absolute OVB. Thus, the corresponding inequalities with absolute OVBs,

$$\begin{gathered} \mid \mathit{OVB}(\widehat{\tau }\mid X)\mid <\mid \mathit{OVB}(\widehat{\tau }\mid X^{\ast })\mid <\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid \text{if}\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid <\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid \text{and} \\ \mid \mathit{OVB}(\widehat{\tau }\mid X)\mid >\mid \mathit{OVB}(\widehat{\tau }\mid X^{\ast })\mid >\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid \text{if}\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid >\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid \end{gathered}$$

do not hold in general. They only hold if X and U induce bias in the same direction, that is, all four terms in the initial bias formula have the same sign. To show the impact of measurement error on the bias, we prove the following four inequalities:

1. |OVB(τ̂ | X)|≤|OVB(τ̂ | X*)|≤|OVB(τ̂ | {})| holds

   if $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }\le 1$ and sgn(OVB(τ̂ | {})) = sgn(OVB(τ̂ | X)),

2. |OVB(τ̂ | {})|<|OVB(τ̂ | X*)|<|OVB(τ̂ | X)| holds

   if $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }>1$ and sgn(OVB(τ̂ | {})) = sgn(OVB(τ̂ | X)),

3. |OVB(τ̂ | X*)|≤|OVB(τ̂ | X)|≤|OVB(τ̂ | {})| holds

   if $k<\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }\le 1$ and sgn(OVB(τ̂ | {})) ≠ sgn(OVB(τ̂ | X)),

4. |OVB(τ̂ | X*)|≤|OVB(τ̂ | {})|<|OVB(τ̂ | X)| holds

   if $1<\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }\le k$ and sgn(OVB(τ̂ | {}))≠ sgn(OVB(τ̂ | X)),

where $k=\frac{1-\gamma }{\gamma \{1-{({\alpha }_X+\rho {\alpha }_U)}^2\}}$ and γ is the reliability of X*.

For ease of notation we use a = α_X + ρα_U, u= (1− ρ²)α_Uβ_U and ini = OVB(τ̂ | {}) = α_Xβ_X + α_Uβ_U + ρα_Xβ_U + ρα_Uβ_X. Then, we can write the absolute OVB differences as

$$\begin{gathered} B_0=\mid \mathit{OVB}(\widehat{\tau }\mid X^{\ast })\mid -\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid =\left|\frac{u}{1-a^2+{\sigma }^2}+\frac{\mathit{ini}}{1-a^2+{\sigma }^2}{\sigma }^2\right|-\mid \mathit{ini}\mid , \\ {B}_X=\mid \mathit{OVB}(\widehat{\tau }\mid X^{\ast })\mid -\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid =\left|\frac{u}{1-a^2+{\sigma }^2}+\frac{\mathit{ini}}{1-a^2+{\sigma }^2}{\sigma }^2\right|-\left|\frac{u}{1-a^2}\right|. \end{gathered}$$

We first prove that a² < 1. Due to the constraints of our parameters (unit variance of variables) we have ${\alpha }_X^2+{\alpha }_U^2+2\rho {\alpha }_X{\alpha }_U<1$. Adding $(1-{\rho }^2){\alpha }_U^2$ to both sides we get $1-{({\alpha }_X+\rho {\alpha }_X)}^2>(1-{\rho }^2){\alpha }_U^2$. Since −1 < ρ < 1 we obtain the true inequality (α_X + ρα_U)² < 1. Consequently, 1 − a² + σ² > 0 in both B₀ and B_X.

Now consider the situation where sgn(OVB(τ̂ | {}))= sgn(OVB(τ̂ | X))holds (inequalities (i) and (ii)). The equality of signs directly implies sgn(u) = sgn(ini) such that

$$B_0=\frac{1}{1-a^2+{\sigma }^2}(\mid u\mid -(1-a^2)\mid \mathit{ini}\mid )\text{and}{B}_X=\frac{-{\sigma }^2}{1-a^2+{\sigma }^2}\left(\frac{\mid u\mid }{1-a^2}-\mid \mathit{ini}\mid \right).$$

Then, inequality (i) holds if $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }\le 1$ because B₀ ≤ 0 and B_X ≥ 0. Inequality (ii) holds if $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }>1$ because B₀ > 0 and B_X <0.

Now consider the situation where sgn(OVB(τ̂ | {})) ≠ sgn(OVB(τ̂ | X))and |u|>|ini|σ² (inequality (iii)). The two absolute OVB differences are given by

$$B_0=\frac{1}{1-a^2+{\sigma }^2}(\mid u\mid -(1-a^2+2{\sigma }^2)\mid \mathit{ini}\mid )\text{and}{B}_X=\frac{-{\sigma }^2}{1-a^2+{\sigma }^2}\left(\frac{\mid u\mid }{1-a^2}+\mid \mathit{ini}\mid \right).$$

Then, inequality (iii) holds if $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }\le 1$ and $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }>\frac{1-\gamma }{\gamma \{1-{({\alpha }_X+\rho {\alpha }_U)}^2\}}$ because B₀ ≤ 0 and B_X ≤ 0. Note that B₀ ≤ 0 holds because |u| − (1 − a² + 2σ²) |ini| ≤ |u| − (1 − a²)|ini| ≤ 0.

Finally consider the situation where sgn(OVB(τ̂ |{})) ≠ sgn(OVB(τ̂ |X)) and |u| ≤ |ini|σ² (inequality (iv)). The two absolute OVB differences are given by

$$B_0=\frac{-1}{1-a^2+{\sigma }^2}(\mid u\mid +(1-a^2)\mid \mathit{ini}\mid )\text{and}{B}_X=\frac{{\sigma }^2}{1-a^2+{\sigma }^2}\left(\mid \mathit{ini}\mid -\frac{\mid u\mid }{1-a^2}-\frac{2\mid u\mid }{{\sigma }^2}\right).$$

Inequality (iv) holds if $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }>1$ and $\frac{\mid \mathit{OVB}(\widehat{\tau }\mid X)\mid }{\mid \mathit{OVB}(\widehat{\tau }\mid \{\})\mid }\le \frac{1-\gamma }{\gamma \{1-{({\alpha }_X+\rho {\alpha }_U)}^2\}}$ because B₀ ≤ 0 and B_X ≤ 0. Note that B_X ≤ 0 hold because $\mid \mathit{ini}\mid -\frac{\mid u\mid }{1-a^2}-\frac{2\mid u\mid }{{\sigma }^2}\le \mid \mathit{ini}\mid -\frac{\mid u\mid }{1-a^2}<0$.