Abstract
The governing international standard for the development of prosthetic heart valves is International Organization for Standardization (ISO) 5840. This standard requires the assessment of the thrombus potential of transcatheter heart valve substitutes using an integrated thrombus evaluation. Besides experimental flow field assessment and ex vivo flow testing, computational fluid dynamics is a critical component of this integrated approach. This position paper is intended to provide and discuss best practices for the setup of a computational model, numerical solving, post-processing, data evaluation and reporting, as it relates to transcatheter heart valve substitutes. This paper is not intended to be a review of current computational technology; instead, it represents the position of the ISO working group consisting of experts from academia and industry with regards to considerations for computational fluid dynamic assessment of transcatheter heart valve substitutes.
Introduction
Surgical aortic valve replacement (SAVR) is the standard of care for patients with aortic stenosis (AS) [1, 2]. Patients who are deemed intermediate or greater surgical risk are eligible for transcatheter aortic valve replacement (TAVR) [3–6]. Currently, there is substantial effort to expand TAVR to lower surgical risk patients [7, 8], after positive clinical results in intermediate risk patients [7, 9–11]. However, recent evidence of leaflet thrombosis and reduced leaflet mobility in TAVR devices [11] has led to concerns of stroke and long-term valve durability. Risk factors for thrombosis in TAVR patients remain poorly defined. It is unclear whether this is a device-specific effect or class finding [12].
Thrombosis in the cardiovascular system is described in terms of Virchow’s triad: hemodynamics (fluid stasis and/or elevated fluid shear stresses), endothelial injury (surface phenomena related to foreign materials), and hypercoagulability (altered blood biochemistry). In a recent study by Makkar et al., 21% of valve replacement patients (including surgical and transcatheter devices) had reduced leaflet motion. However, not all patients with the same prosthetic valve (foreign materials) experienced leaflet thrombosis, nor was there a substantial trend in these patients towards abnormal blood chemistry [11]. While materials and blood chemistry are likely to be compounding factors [11–18], data suggest that the hemodynamic environment in the vicinity of the valve prosthesis is a critical factor in the development of leaflet thrombosis. The US Food and Drug Administration (FDA) perspective also alludes to the fact that hemodynamics play a significant role in the development of leaflet thrombosis [19].
Computational fluid dynamic (CFD) analyses can greatly augment the knowledge gained from experiments for thrombus assessment related to artificial heart valves. It is a cost-effective tool which can be used for high-resolution evaluation of flow parameters which are otherwise difficult to measure in vivo or/and in vitro (e.g. wall shear stress, or WSS, and blood damage). These parameters can be used to optimize the design of artificial heart valves. Additionally, computational simulation allows for patient-specific evaluation of artificial heart valve performance [20–22]. While promising early results exist, fully patient-specific computational simulation is relatively new and not yet thoroughly validated for a wide range of applications.
Due to the complexity of thrombus formation and limitations in the flow field investigation using either computational simulation, in vitro (e.g. by digital particle image velocimetry, DPIV), or ex vivo methods, the International Organization for Standardization (ISO) working group recommends an integrated approach combining complementary methods for establishing a potential thrombus assessment (Fig. 1).
Figure 1.
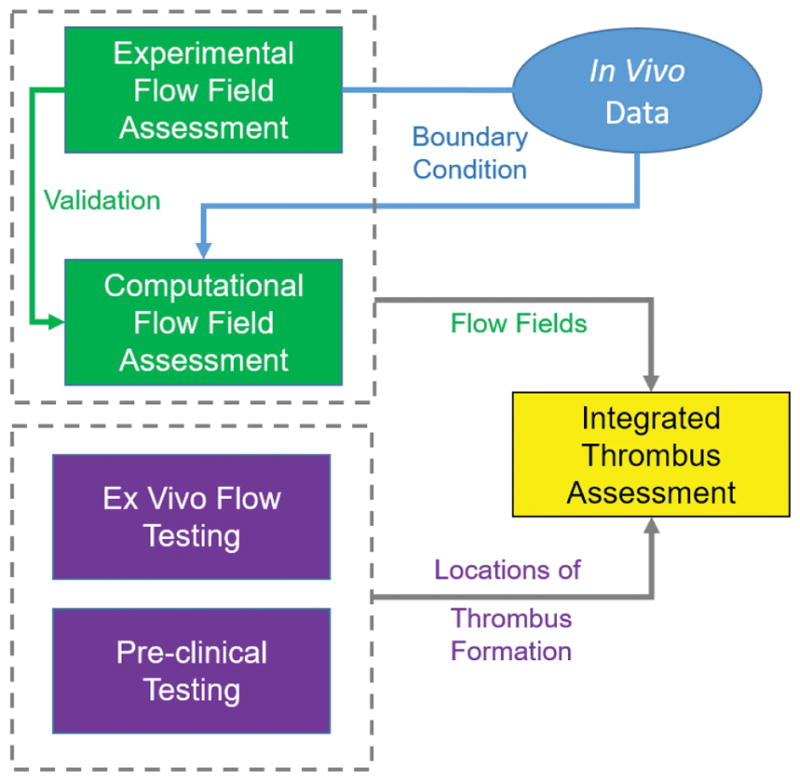
Example of integrated thrombus assessment approach
The first step of this integrated approach is to validate the CFD or fluid-structure interaction (FSI) methods against in vitro experiments (e.g. by DPIV). Appropriate boundary and hemodynamic conditions shall be defined using in vivo data or published data in the literature. It is important noting that, because of its high cost, the experiment setup and targeted quantities for validation should be planned ahead of the development and simulation of the computational model. The experiment is usually more expensive to adjust than the computational model; therefore, the latter model has to be adjusted to the limitations of the former one. Once the computational methods are validated, the computational results should be compared with ex vivo flow testing, e.g. blood loops, and pre-clinical testing. Here the task is to correlate hemodynamic parameters from the computational results (e.g. presence of high shear stresses and recirculation/flow stagnation regions) with locations of thrombus formation in the experiment. Once a correlation is achieved, the thrombus assessment can be performed based on the results of these complementary approaches.
Currently, there is no standard approach for the CFD assessment of transcatheter heart valve prostheses. For this reason, the ISO working group has drafted this position paper to provide guidance for performing computational investigations. In the first section, different strategies and numerical methods are described and discussed. This is followed by a best practice workflow.
Simulation Techniques
In CFD, the governing equations for the flow field are the Navier-Stokes equations. Any numerical solver that has proven to provide an accurate numerical solution of the Navier-Stokes equations can be used. The following are examples of the commercially available CFD solvers:
Fluent and CFX from ANSYS (Canonsburg, PA)
Star-CCM from CD-Adapco - Siemens (Plano, Texas)
Comsol Multiphysics from COMSOL (Stockholm, Sweden)
Adina from Adina R&D (Watertown, MA)
AcuSolve from ACUSIM Software (Mountain View, CA)
LS-DYNA from Livermore Software Technology Corp (Livermore, CA)
Many open-source CFD packages are also available, such as:
OpenFoam (openfoam.org)
FEniCS (fenicsproject.org)
LifeV (cmcsforge.epfl.ch/projects/lifev/)
SimVascular (simvascular.github.io)
These CFD solvers have been extensively verified, validated and adopted for industrial engineering applications [23, 24]. However, their application to the study of the cardiovascular system is limited. Simulations involving the cardiovascular system are challenging due to the complex geometries and materials properties, transitional turbulent effects, and boundaries with large deformation and moving interfaces. Therefore, before using the simulation results for thrombus assessment, the setup of the numerical framework has to be thoroughly considered and justified. A proper validation against controlled experiments of these systems is necessary.
Geometry
A transcatheter bioprosthesis typically consists of three biological leaflets mounted inside a self-expanding or mechanically-expandable stent frame which may be covered with an internal and/or external skirt to facilitate the leaflet attachment to the stent and reduce paravalvular leakage, as shown Fig. 2. Manufacturing a TAVR device is a complex process that involves a series of manual steps to suture the leaflets and skirt to the stent. A complete model including all manufacturing components of a TAVR may not be necessary. Additionally, deployment of a TAVR into a patient-specific calcified aortic root often results in a non-circular, asymmetric stent configuration, thus, the in vivo valve geometry can be substantially different from the nominal, circular geometry defined by the valve CAD drawings. Hence, simplifications of the TAVR geometry should be made with caution and with understanding of their potential impacts. Simplifications usually reduce model complexity and computation time, but may compromise accuracy.
Figure 2.
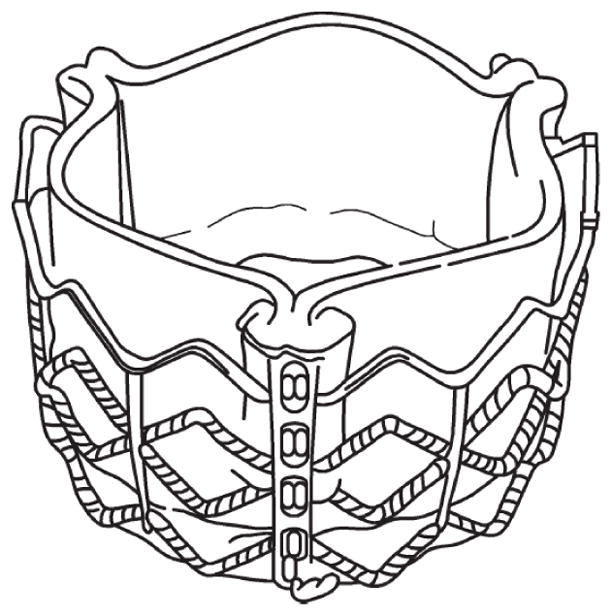
An example of transcatheter heart valve substitutes adapted from ISO 5840-3:2013, Annex B [26]. More representative examples of transcatheter heart valve substitutes, components and delivery systems can be found in this Annex;
Possible simplifying assumptions and modifications for modeling the valve prosthesis and the fluid domain are listed below.
Assumptions of valve prosthesis model:
Sewing suture between stent frame and leaflets/skirt can be neglected [25].
Homogeneous thickness of the leaflets for pericardial valves.
Flow channel for validation against ex vivo hydrodynamic experiments:
A straight tube with symmetric sinuses can be used. An asymmetric domain may affect shear stress estimations.
Coronary arteries and native leaflets can be neglected.
General assumptions:
Geometric symmetries can be used to reduce computation time. However, such symmetries may be limited in capturing the non-symmetric opening and closing of the leaflets.
It is important to have developed flow entering and leaving the flow domain and to minimize the influence of the boundary conditions (BCs) in the flow region of interest. For this purpose, an appropriate length of flow extension can be added to the inlet and outlet boundaries.
For patient-specific models, the anatomical geometies are segmented and reconstructed to three-dimensional (3D) surface models from multi-slice medical images like computed tomography (CT) or magnetic resonance imaging (MRI). Hounsfield unit thresholding is usually applied to segment the structure followed by image processing tools (e.g. region growing), morphologic operations, manual editing of the slices and a subsequent smoothing and wrapping to fix inconsistencies in the model due to image noise. This reconstruction process has potential limitations, such as limited reproducibility due to manual steps, possible deviations from the original anatomy and high dependency of the outcome on the image quality [27–29]. Deviations may have a strong impact on the results, e.g. WSS ~ 1/D3 where D is the diameter.
The following are some of the commercially available solutions for 3D reconstruction of medical images:
Mimics from Materialise (Leuven, Belgium)
Simpleware from Synopsys (Mountain View, CA)
Amira-Avizo from FEI (Hillsboro, OR)
Open-source packages are also available, such as:
VMTK (http://www.vmtk.org)
3D slicer (https://www.slicer.org)
ITK-SNAP (www.itksnap.org)
InVesalius (https://www.cti.gov.br/invesalius)
Material Modeling
An important aspect of the analysis of the dynamics of native tissue and bioprosthetic heart valves is the choice of material and fluid properties.
The complex nature of native tissues (e.g. aortic leaflets, sinus, ascending aorta, adjacent myocardium and calcification) and bioprosthetic leaflets (e.g., bovine or porcine pericardial tissues) involves non-linear, anisotropic material responses which should be considered to obtain realistic simulation results [30]. Hyperelastic material models such as Fung-elastic model [31, 32] and Holzapfel-Gasser-Ogden material model [33], may be used. Material properties should represent the mechanical behavior of the native tissues as closely as possible. Justifications of adopting a simplified material model should be provided. The use of linear elastic material models (e.g., Hooke’s law) for native tissues is not recommended. However, depending on the case, sometimes simplifying assumptions are necessary.
The stent is modeled using shape memory alloy models representing Nitinol material or an isotropic, linear elastic material model for stainless steel or cobalt-chromium. Shape memory alloy models that consider the superelastic and shape memory effect can be applied. Plastic deformation of the stent should be considered and modeled if the valve crimping and un-crimping process, and/or the deployment process are simulated.
Although blood is a non-Newtonian fluid, it can be assumed to be Newtonian in regions of high shear rates where the diameter of the vessel is quite large. The fluid is, therefore, often approximated as homogeneous, isothermal, incompressible, and Newtonian with blood-like properties of the density and viscosity. Non-Newtonian blood models (e.g. based on Ballyik et al. [34] or the Carreau model) can be applied. In this case, the dynamic viscosity is a function of the computed shear-strain rate. A comparison between various non-Newtonian blood models can be found in Ref. [35]. More sophisticated approaches include the modeling of the red blood cells and platelets. [36, 37]. However, such a micro-scale computational analysis is only possible today for performing research in a small computational domain and not practical yet for industrial application related to transcatheter heart valves. For validation purposes, the same fluid properties as in the in vitro setup (e.g. water-glycerin mixture) should be used.
Turbulence Modeling
While blood flow in a healthy heart can be modeled as laminar, in the presence of diseased heart valves (obstructive and regurgitant valvular lesions) or prosthetic heart valves, the transition to turbulence cannot be neglected. It is important to capture turbulence effects since they affect the flow field, and consequently the estimation of parameters such as shear stress. Several methods exist for modeling turbulence, including direct numerical simulation (DNS), large eddy simulation (LES) and Reynold-averaged Navier-Stokes (RANS). DNS is considered the “gold standard” as it provides the numerical solution of the Navier-Stokes equations by resolving all spatial and temporal scales. However, due to large computational costs associated with DNS, LES and RANS alternatives are more feasible. Most commercial or open-source CFD solvers incorporate a variety of these turbulence models including
-
Reynolds Averaged Navier-Stokes (RANS) Models
k-ε model
k-ω model
shear stress transport (SST) model
Large Eddy Simulations (LES)
-
Hybrid RANS-LES Simulations
Detached eddy simulation
Traditional RANS models, i.e. k-ε model and k-ω model, are very popular in industrial applications. While the k-ω model allows for a more accurate near wall treatment, the k-ε model is advantageous in the bulk flow. They are robust and computationally efficient in the assistance of special wall treatment. However, their accuracy to resolve turbulent fluctuations and transition from laminar to turbulent flow is not optimal. These RANS models were originally derived assuming fully developed turbulent flow, while heart valves function in the transitional flow regime, from laminar to turbulent. Hence, the SST model, which combines the advantages of the k-ε model and k-ω model using a blending function, is a better option, but it still creates artificial turbulent effects for non-turbulent regions. The appropriate mesh resolution for RANS models depends on the choice of the turbulence modeling approach and the wall treatment.
LES can be used to achieve improved accuracy for modeling transitional turbulence. However, the excessive requirement for mesh resolution delays the wider use of the LES in the industrial field. Hybrid RANS-LES simulations resolve the near-wall-resolution issue by employing the RANS model for the near wall region while using the LES for the rest of the computational domain. Though the Hybrid RANS-LES models are ideal for capturing the fluid dynamics through a heart valve, these models contain much more equations compared to the traditional RANS model, and consequently, its implementation is time-consuming and computationally expensive. After all, it is always challenging to simulate transitional turbulence with existing turbulence models. Recent publications demonstrated the feasibility of using DNS to resolve the transitional turbulence in the flow through a heart valve [36, 37]. However, it is generally not practical to apply such simulations to industrial problems without a substantial increase of computational power.
Fluid-Structure Interaction (FSI)
The principle of FSI is to resolve the coupling between the fluid and structural components. Heart valves involve complex dynamics during opening and closing in which solid structures interact with the fluid. For physiologically accurate simulations, the fluid dynamics associated with the valves and the structural mechanics of the valves and tissue should be modeled together. However, an FSI analysis presents several challenges and significant additional computation time.
FSI simulations can be divided into three major categories:
Pseudo-State simulations [38]: This is commonly used to study the downstream flow fields of heart valves under the assumption that the valve is stationary, usually at peak systole, and can be modeled using aforementioned CFD techniques for flow fields.
One-way FSI: One-way FSI allows heart valves to move under a prescribed geometric deformation. The prescribed structure dynamic motion affects the fluid flow but not vice versa.
Two-way FSI: This is the most challenging type of FSI simulations. In a two-way FSI, the structural and fluid fields affect each other. The structural model of a two-way FSI solver needs to adequately represent material properties and the interaction between the leaflets and the surrounding fluid. Most two-way FSI solvers can solve one-way FSI problems.
For the coupling between the fluid and structure, mainly two approaches are used:
Partitioned approach: The fluid and solid domains are separately treated with two distinct solvers. Information between the two solvers is communicated across a domain interface. An “explicit/weakly” coupling allows information communication at the end of a time step. Alternatively, for an “implicit/strong” coupling, several coupling iterations are performed for each domain per time step until the data converges to the solution of the monolithic system. Since each domain uses its own solver, independent numerical methods as well as more efficient and developed algorithms can be applied to solve the flow and structural equations. Furthermore, less memory storage is required compared to the monolithic approach (as described in the following section). However, FSI simulations involving strong couplings, such as in the case of the flexible membrane, do generally not converge due to stability problems. [38]
Monolithic approach: The fluid and structural domains are solved simultaneously by discretizing the problem into one system of equations using a single numerical method (e.g. FEM). This leads to a stable solution process for most of the cases since the mutual influence of the two fields are incorporated directly. However, for a large three dimensional engineering problem, a prohibitively amount of memory storage is needed. Moreover, since only one numerical method is applied for both physical domains, the applicability of the monolithic approach using commercial packages is limited. This is because structural problems are generally solved using the FEM while most commercial packages use the Finite Volume Method (FVM) to numerically describe CFD problems.
An alternative way to categorize FSI techniques to (1) body-fitted and (2) non body-fitted methods [39, 40]. This categorization depends on the whether computational mesh for fluid domain conforms the boundaries of the structures. The Arbitrary Lagrangian-Eulerian (ALE) Method [41] is an example of a body-fitted method, and the Immersed-boundary (IB) method is one of non body-fitted methods.
To date, the ALE Method is the most common method adopted in industrial applications. This conforming mesh method separates the computational domains related to the structure and fluid. Due to the large movements of the leaflet structures and contact between the solid elements, it requires mesh adaptation for the fluid domain, which greatly reduces computational efficiency and results in poor mesh quality. Remeshing is necessary which may result in artificial diffusivity and instabilities. The IB method embeds the structure to the static fluid mesh implicitly, which provides a great advantage for simulating largely moving/morphing structures [42]. However, the near wall flow resolution of the leaflets of the IB method may be inferior to the ALE method [43]. Many commercial softwares also offer the sliding mesh technique, however, it is only possible to model axially rotating blood pumps and mechanical valves.
Examples of commercial structural mechanic solvers include:
ANSYS Mechanical from ANSYS (Canonsburg, PA)
Abaqus from Dassault Systèmes Simulia Corp (Providence, Rhode Island)
IMPETUS from IMPETUS Afea (Flekkefjord, Norway)
LS-DYNA from Livermore Software Technology Corp (Livermore, CA)
Adina from ADINA Research & Development, Inc. (Watertown, MA)
COMSOL Multiphysics® Modeling Software from Comsol Multiphysics GmbH (Göttingen, Germany)
Boundary Condition
Numerical results are sensitive to the choice of BCs [44] and therefore, these should be based on physiologically accurate flows and pressures. When validating the numerical results using benchtop experiments, flows and pressures used in the corresponding experiments should be applied as inflow and outflow BCs in the computational simulations.
For patient-specific modeling, physiological or pathological boundary conditions such as cardiac output, flowrates, flow profiles, pressure measurements and displacements (e.g. leaflet motion and wall deformation) should be used. Flowrates, pressures and displacements can obtained from clinical modalities including, but not limited to, Echocardiography, phase-contrast MRI, and cardiac catheterization. Inlet BCs usually make use of the flowrate, while pressure is used for outlet BCs. Commonly, however, in the absence of clinical pressure measurements, alternative methods must be used to simulate the effect of peripheral vasculature on pressure and flows in the region of interest. These methods can include resistance BCs, Windkessel models, and cardiovascular lumped parameter network (cLPN) [45, 46]. They belong to the family of zero-dimensional lumped parameter models (0D-LPMs), but the former two methods focus on modeling terminal vessels, while the cLPN models the cardiovascular system as a closed loop that has feedback mechanisms.
Coupling a 0D-LPM with a 3D solver is not trivial, and one major challenge is stability. The coupling scheme can be categorized into monolithic and partitioned approaches. The former approach solves the 0D and 3D together, therefore, results in a more stable system than the latter one; however, this approach also requires an analytic relationship between pressure and flow and demands modifications to the 3D solver, hence, its range of applicability is limited. Conversely, the partitioned approach solves the 0D and 3D solutions separately and exchange data via well-defined interfaces. This approach is a more generalized method and very attractive to users of commercial software. Hence, careful numerical algorithms should be implemented to handle this data exchange to avoid instability [47, 48, 45].
Contact Modeling
Appropriate contact modeling is necessary to handle the complicated, highly dynamic contact behavior between the leaflets, between the leaflets and the stent as well as between the stent and the surroundings. A self-contact among the leaflets is typically applied, although it is a common challenging to model the self-contact in body-fitted methods, e.g. ALE. It is usually necessary to enforce a small gap between the leaflets to allow for the expansion of the moving mesh. This gap may result in unrealistic fluid dynamics during valve closure [40]. On the contrary, non-body fitted methods, e.g. IB methods, can readily handle the contact between leaflets without further treatment of mesh [40, 49].
Furthermore, the leaflets are usually connected with the stent frame using a tied-type/bonded contact method to mimic the attachment between the stent and the leaflets. A tied-type contact is usually used between the stent frame and the compartment model of the experimental flow channel, which means the sliding between the model interfaces is prohibited. When the deployment procedure of the valve prosthesis into the anatomic structure is incorporated, a frictional contact may be applied between the stent frame and the tissue [22], which allows for the evaluation of the contact forces between the native annulus and the stent.
Thrombus Assessment
In the past decades, many numerical approaches have been developed to investigate the blood damage through artificial heart valves and the risk of thrombus formation. They can primarily be categorized into two types:
These two methods depend on the flow field results simulated by aforementioned numerical methods. The Eulerian methods provide information about hemolysis and platelet activation, based on the shear stress of the flow field. The Lagrangian methods can model the behavior of the blood cell, estimate the washout time of blood cells, and record the shear stress history and exposure time for blood cells. Therefore, the Lagrangian methods offer much better accuracy for blood damage estimation, but with a much higher computational expense. Additionally, the results depend on the number of particles and it is possible that certain areas are not covered by particles. Examples of the Lagrangian methods are:
To evaluate the thromboresistance of cardiovascular devices, the device thrombogenicity emulation (DTE) methodology by Bluestein et al. [55] and Piatti et al. [56] combines in silico and in vitro measurements by correlating device hemodynamics with platelet activity coagulation markers. Several approaches that combine the mechanical aspects of the simulation with biochemical interactions of platelet activation and aggregation have been presented in the past [57, 58]. Some of the multi-scale models attempt to include part or even the complete coagulation cascade [59], e.g. by using a set of convection–reaction–diffusion equations [60], the Dissipative Particle Dynamics-Partial Differential Equation (DPD-PDE) method [61] or a discrete stochastic Cellular Potts Method (CPM) [62] to track the movement of platelets and red blood cells. These models are intended to take into account irregular thrombus shapes, alteration of flow field due to growth of the thrombus, and thrombus embolization due to shear Due to the large computational cost, these models are, however, only applicable for two-dimensional cases or a very small domain. Beyond that, many unknowns and assumptions in the model development limit the validity of this complex approach.
As there is currently no validated numerical model that can reliably predict the formation and growth of thrombosis related to heart valves, the recommended strategy of the ISO working group is an integrated thrombus assessment approach combining in vitro (e.g. using PIV) and CFD assessment with ex vivo flow testing (e.g. blood loops) and pre-clinical testing (Fig. 1). Individual or combined hemodynamic parameters that may lead to an adverse effect are identified in the validated computational results and correlated with locations of thrombus formation in the in vitro, ex vivo, or pre-clinical testing. These hemodynamic parameters may include information such as shear rate, wall shear stress, estimation of the washout time, flow recirculation or separation, and any adverse effects of device flow on tissues or organs.
Best Practice Workflow
Though many numerical techniques are available, it is important to select an appropriate numerical solver with correct governing equations, adequate physical representation, and sufficient accuracy to perform flow field characterization and thrombus assessment. The definition of rigid rules for setup and validation of a computational simulation for flow field assessment associated with heart valve prostheses is difficult and impractical. Therefore, in this section, a best practice recommendation is given.
Code Verification
The software code used for the intended study must have been verified against accepted solutions of benchmark analytical cases or another already verified code. A description of the software quality assurance (SQA) and numerical code verification (NCV) should exist. Commonly, code verification is constantly performed by the software developers themselves. Therefore, it may be referred to available documentation and verification results from the software developer.
Numerical Stability [63, 64]
All numerical models must prove their robustness and applicability for the intended study. Adequate convergence criteria for momentum, continuity, fluid-structure coupling, and turbulent quantities, if applicable, should be selected to assure minimal numerical errors. All convergence criteria values should be explicitly stated and proved to yield converged solutions. Sufficient temporal and spatial resolutions should be applied. The mesh should be constructed with appropriate structure and resolution. Mesh- and time-independence studies should be performed, and flow quantities used to verify independent results should be explicitly stated and consistent with the purpose of the study. The total simulation time should be sufficiently long to ensure periodically stable results.
Validation [65–68]
Modeling approximations (e.g. geometry, material and fluid properties, boundary conditions, turbulence) may be used in the study which can affect the accuracy of the solution. To validate that the physical model is accurately represented, the computational model should be validated against in vitro experimental data of high measurement resolution and accuracy, e.g. DPIV measurements. DPIV is a non-invasive, optical flow visualization technique and based on the motion-detection of illuminated particles to calculate the velocity field. The hemodynamic waveforms produced by the in vitro system should reasonably simulate physiological conditions as shown in ISO 5840-1:2015. While this is still a simplification compared to clinical data, it allows an estimation of the predictability of numerical studies.
The dimensions of the numerical domain should correspond to the respective dimensions of the experimental apparatus as closely as possible. The same fluid properties as in the in vitro setup (e.g. water-glycerin mixture) should be used. For validation, quantitative comparisons of the following metrics against experimental data should be considered:
Leaflet kinematics: leaflet open area (temporal profile, maximum, and mean), rapid valve opening/closing times, etc.;
Fluid dynamics: pressure, flow rates, cardiac output, velocity (maximum and spatial profiles), total ejection time, etc.;
Flow Dynamics [69–71]
Once the computational model is successfully validated, the numerical framework can be utilized in a subsequent step to investigate the flow field for deployment and anatomical variations that the device may encounter. As it is impractical to validate all the simulated cases, the variations are extrapolated out of the validation frame.
Dimensions of the intended implant site (e.g. based on CT scans) and all aspects of the implantation scenario should be considered. Consideration should be given to deployment variations as anticipated during implantation. The fluid properties should mimic the properties of blood. Appropriate operating condition should be employed that represent the intended condition as closely as possible.
In unsteady numerical simulation, intermediate solutions should be saved for visualizing intermediate vortical structures and local blood damage index contours, as well as constructing particle paths. The displacement of the two-way FSI components should be recorded over the simulation.
The evaluation of the results may include, but is not limited to, information about blood damage estimation, shear rates, platelet activation, wall shear stress, behavior of the blood cells, estimation of the washout time/recirculation/separation and any adverse effects of device flow on tissues or organs. Any averaged quantities should be obtained based on data after the simulation passes the transition period bridging from the initial condition to a periodically stable solution.
Final Report
The FDA guidance document on reporting of computational studies [72] should be considered for the final report. Information should be given regarding, but is not limited to, the software tools employed (e.g. commercial solvers or open-source CFD packages, software used to generate the geometry (CAD) and anatomical models); the numerical implementation used to solve the governing equations; system configuration (e.g. the geometry of the device, the computational domain, dimensions); the governing equations and/or constitutive laws used to perform the computational analysis; the biological, chemical, and physical properties of the system (e.g. fluid properties, material properties) including the testing conditions to get the data; and the conditions that were imposed on the system, such as the boundary and loading conditions, initial conditions, and other constraints that control the system.
Additionally, the final report should demonstrate the applicability of the used software and numerical setup to the flow field assessment. The code verification and validation activities should be extensively described. If applicable, rationale for differences between the numerical setup used for validation and for the computational application should be explicitly elucidated. Experimental uncertainty estimates should be described. Information and results of the grid- and time-independence studies should be given.
The results of the computational fluid dynamics assessment should be presented and discussed. Quantitative results should be provided with sufficient details, including labels and legends. For evaluation and interpretation of the hemodynamic data and the following assessment of thrombus formation, the results of the computation should be correlated/validated with results from ex vivo flow testing, e.g. blood loops, and pre-clinical testing. Here the task is to correlate the hemodynamic parameters from the computational results (e.g. presence of high shear stresses and recirculation/flow stagnation regions) with locations of thrombus formation in the experiment. These correlations should be rigorously justified by knowledge and phenomenon demonstrated by previously published literature. Once a correlation is determined, the computational model can be used for the assessment of thrombogenic potential.
Limitations of the study (e.g. assumptions/simplifications) should be stated and justified. Finally, a conclusion should be made.
Acknowledgments
The authors would like to thank Dr. Ajit Yoganathan and other ISO TC 150 committee members for their suggestions and comments on the paper. Dr. Wei Sun and Dr. Simon Johannes Sonntag in the author list are ISO members, and Dr. Zhenglun Alan Wei, Dr. Milan Toma, and Dr. Shelly Singh-Gryzbon are not ISO members but they are experts in relevant fields who work with the ISO group to develop this document.
Footnotes
COMPLIANCE WITH ETHICAL STANDARDS
Funding: No funding was received for this work.
Conflict of Interest
Zhenglun Wei, Milan Toma, Shelly Singh, and Wei Sun report no conflict of interest; Simon J. Sonntag is an employee of enmodes GmbH.
Ethical Approval
NA
Informed Consent
NA
References
- 1.Leon MB. Transcatheter Aortic-Valve Implantation for Aortic Stenosis in Patients Who Cannot Undergo Surgery. The New England journal of medicine. 2010;363(17):1597–607. doi: 10.1056/NEJMoa1008232. [DOI] [PubMed] [Google Scholar]
- 2.Nishimura RA, Otto CM, Bonow RO, Ruiz CE, Skubas NJ, Sorajja P. 2014 AHA/ACC Guideline for the Management of Patients With Valvular Heart Disease A Report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. 2014 doi: 10.1016/j.jacc.2014.02.536. [DOI] [PubMed] [Google Scholar]
- 3.Smith C. Transcatheter versus Surgical Aortic-Valve Replacement in High-Risk Patients. N Engl J Med. 2011;364(23):2187–98. doi: 10.1056/NEJMoa1103510. [DOI] [PubMed] [Google Scholar]
- 4.Adams DH, Popma JJ, Reardon MJ, Yakubov SJ, Coselli JS, Deeb GM, et al. Transcatheter Aortic-Valve Replacement with a Self-Expanding Prosthesis. New England Journal of Medicine. 2014;370(19):1790–8. doi: 10.1056/NEJMoa1400590. [DOI] [PubMed] [Google Scholar]
- 5.Popma JJ, Adams DH, Reardon MJ, Yakubov SJ, Kleiman NS, Heimansohn D, et al. Transcatheter Aortic Valve Replacement Using a Self-Expanding Bioprosthesis in Patients With Severe Aortic Stenosis at Extreme Risk for Surgery. J Am Coll Cardiol. 2014;63(19):1972–81. doi: 10.1016/j.jacc.2014.02.556. [DOI] [PubMed] [Google Scholar]
- 6.Thyregod HGH, Daniel Andreas S, Nikolaj I, Nissen H. Transcatheter Versus Surgical Aortic Valve Replacement in Patients With Severe Aortic Valve Stenosis. J Am Coll Cardiol. 2015;65(20):2184–94. doi: 10.1016/j.jacc.2015.03.014. [DOI] [PubMed] [Google Scholar]
- 7.Gravel GM, Généreux P. Exploring the Role of Transcatheter Aortic Valve Replacement as the Preferred Treatment for Lower-Risk Patients. Journal of the American College of Cardiology. 2015;66(14):1638. doi: 10.1016/j.jacc.2015.06.1346. [DOI] [PubMed] [Google Scholar]
- 8.Piazza N, Kalesan B, van Mieghem N, Head S, Wenaweser P, Carrel TP, et al. A 3-Center Comparison of 1-Year Mortality Outcomes Between Transcatheter Aortic Valve Implantation and Surgical Aortic Valve Replacement on the Basis of Propensity Score Matching Among Intermediate-Risk Surgical Patients. JCIN. 2013;6(5):443–51. doi: 10.1016/j.jcin.2013.01.136. [DOI] [PubMed] [Google Scholar]
- 9.Tamburino C, Barbanti M, Rs PDE, Ranucci M, Onorati F, Covello RD, et al. 1-Year Outcomes After Transfemoral Transcatheter or Surgical Aortic Valve Replacement. Journal of the American College of Cardiology. 2015;66(7):804–12. doi: 10.1016/j.jacc.2015.06.013. [DOI] [PubMed] [Google Scholar]
- 10.Leon MB, Smith CR, Mack MJ, Makkar RR, Svensson LG, Kodali SK, et al. Transcatheter or Surgical Aortic-Valve Replacement in Intermediate-Risk Patients. New England Journal of Medicine. 2016;374(17):1609–20. doi: 10.1056/NEJMoa1514616. [DOI] [PubMed] [Google Scholar]
- 11.Makkar RR, Fontana G, Jilaihawi H, Chakravarty T, Kofoed KF, de Backer O, et al. Possible Subclinical Leaflet Thrombosis in Bioprosthetic Aortic Valves. New England Journal of Medicine. 2015;373(21):2015–24. doi: 10.1056/NEJMoa1509233. [DOI] [PubMed] [Google Scholar]
- 12.Hansson NC, Grove EL, Andersen HR, Leipsic J, Mathiassen ON, Jensen JM, et al. Transcatheter Aortic Valve Thrombosis: Incidence, Predisposing Factors, and Clinical Implications. Journal of the American College of Cardiology. 2016;68(19):2059–69. doi: 10.1016/j.jacc.2016.08.010. [DOI] [PubMed] [Google Scholar]
- 13.De Marchena E, Mesa J, Pomenti S, Marin y Kall C, Marincic X, Yahagi K, et al. Thrombus Formation Following Transcatheter Aortic Valve Replacement. 2015;8(5):728–39. doi: 10.1016/j.jcin.2015.03.005. [DOI] [PubMed] [Google Scholar]
- 14.Egbe AC, Pislaru SV, Pellikka PA, Poterucha JT, Schaff HV, Maleszewski JJ, et al. Bioprosthetic Valve Thrombosis Versus Structural Failure: Clinical and Echocardiographic Predictors. Journal of the American College of Cardiology. 2015;66(21):2285–94. doi: 10.1016/j.jacc.2015.09.022. [DOI] [PubMed] [Google Scholar]
- 15.Chakravarty T, Søndergaard L, Friedman J, De Backer O, Berman D, Kofoed KF, et al. Subclinical leaflet thrombosis in surgical and transcatheter bioprosthetic aortic valves: an observational study. The Lancet. 2017;6736(17):1–10. doi: 10.1016/S0140-6736(17)30757-2. [DOI] [PubMed] [Google Scholar]
- 16.Holmes DR, Mack MJ. Aortic Valve Bioprostheses: Leaflet Immobility and Valve Thrombosis. Circulation. 2017;135(18):1749–56. doi: 10.1161/CIRCULATIONAHA.116.025429. [DOI] [PubMed] [Google Scholar]
- 17.Midha PA, Raghav V, Sharma R, Condado JF, Okafor IU, Rami T, et al. The Fluid Mechanics of Transcatheter Heart Valve Leaflet Thrombosis in the Neo-Sinus. Circulation. 2017 doi: 10.1161/CIRCULATIONAHA.117.029479. CIRCULATIONAHA.117.029479. [DOI] [PubMed] [Google Scholar]
- 18.Leetmaa T, Hansson NC, Leipsic J, Jensen K, Poulsen SH, Andersen HR, et al. Early aortic transcatheter heart valve thrombosis: diagnostic value of contrast-enhanced multidetector computed tomography. Circ Cardiovasc Interv. 2015;8(4) doi: 10.1161/CIRCINTERVENTIONS.114.001596. [DOI] [PubMed] [Google Scholar]
- 19.Laschinger JC, Wu C, Ibrahim NG, Shuren JE. Reduced Leaflet Motion in Bioprosthetic Aortic Valves--The FDA Perspective. The New England journal of medicine. 2015;373(21):1996–8. doi: 10.1056/NEJMp1512264. [DOI] [PubMed] [Google Scholar]
- 20.Dasi LP, Hatoum H, Kheradvar A, Zareian R, Alavi SH, Sun W, et al. On the Mechanics of Transcatheter Aortic Valve Replacement. Annals of Biomedical Engineering. 2017;45(2):310–31. doi: 10.1007/s10439-016-1759-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang Q, Kodali S, Primiano C, Sun W. Simulations of transcatheter aortic valve implantation: implications for aortic root rupture. Biomech Model Mechanobiol. 2015;14(1):29–38. doi: 10.1007/s10237-014-0583-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang Q, Primiano C, McKay R, Kodali S, Sun W. CT image-based engineering analysis of transcatheter aortic valve replacement. JACC: Cardiovascular Imaging. 2014;7(5):526–8. doi: 10.1016/j.jcmg.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Oberkampf WL, Trucano TG. Verification and validation benchmarks. Nucl Eng Des. 2008;238(3):716–43. doi: 10.1016/j.nucengdes.2007.02.032. [DOI] [Google Scholar]
- 24.Hariharan P, D’Souza GA, Horner M, Morrison TM, Malinauskas RA, Myers MR. Use of the FDA nozzle model to illustrate validation techniques in computational fluid dynamics (CFD) simulations. Plos One. 2017;12(6) doi: 10.1371/journal.pone.0178749. ARTN e0178749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mao W, Li K, Sun W. Fluid-Structure Interaction Study of Transcatheter Aortic Valve Dynamics Using Smoothed Particle Hydrodynamics. Cardiovascular Engineering and Technology. 2016;7(4):374–88. doi: 10.1007/s13239-016-0285-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.International Standards O. ISO 5840-3:2013 Cardiovascular implants - cardiac valve prostheses. Part 3: Heart valve substitutes implanted by transcatheter techniques. 2013:104p. [Google Scholar]
- 27.Sonntag SJ, Kutting M, Ghalati PF, Kaufmann T, Vazquez-Jimenez J, Steinseifer U, et al. Effect of pulmonary conduit oversizing on hemodynamics in children. Int J Artif Organs. 2015;38(10):548–56. doi: 10.5301/ijao.5000443. [DOI] [PubMed] [Google Scholar]
- 28.Berg P, Saalfeld S, Voß S, Redel T, Preim B, Janiga G, et al. Does the DSA reconstruction kernel affect hemodynamic predictions in intracranial aneurysms? An analysis of geometry and blood flow variations. Journal of NeuroInterventional Surgery. 2017 doi: 10.1136/neurintsurg-2017-012996. [DOI] [PubMed] [Google Scholar]
- 29.Bianchi M, Marom G, Ghosh RP, Fernandez HA, Taylor JR, Jr, Slepian MJ, et al. Effect of Balloon-Expandable Transcatheter Aortic Valve Replacement Positioning: A Patient-Specific Numerical Model. Artif Organs. 2016;40(12):E292–E304. doi: 10.1111/aor.12806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sun W, Martin C, Pham T. Computational Modeling of Cardiac Valve Function and Intervention. Annual Review of Biomedical Engineering. 2014;16(1):53–76. doi: 10.1146/annurev-bioeng-071813-104517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fung Y-C. Biomechanics: Mechanical Properties of Living Tissues. Springer; New York: 1993. [Google Scholar]
- 32.Sun W, Sacks MS. Finite element implementation of a generalized Fung-elastic constitutive model for planar soft tissues. Biomechanics and Modeling in Mechanobiology. 2005;4(2–3):190–9. doi: 10.1007/s10237-005-0075-x. [DOI] [PubMed] [Google Scholar]
- 33.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61(1–3):1–48. doi: 10.1023/A:1010835316564. [DOI] [Google Scholar]
- 34.Ballyk PD, Steinman DA, Ethier CR. Simulation of non-Newtonian blood flow in an end-to-side anastomosis. Biorheology. 1994;31(5):565–86. doi: 10.3233/bir-1994-31505. [DOI] [PubMed] [Google Scholar]
- 35.Karimi S, Dabagh M, Vasava P, Dadvar M, Dabir B, Jalali P. Effect of rheological models on the hemodynamics within human aorta: CFD study on CT image-based geometry. Journal of Non-Newtonian Fluid Mechanics. 2014;207:42–52. doi: 10.1016/j.jnnfm.2014.03.007. [DOI] [Google Scholar]
- 36.Yun BM, Dasi LP, Aidun CK, Yoganathan AP. Computational modelling of flow through prosthetic heart valves using the entropic lattice-Boltzmann method. Journal of Fluid Mechanics. 2014;743:170–201. doi: 10.1017/jfm.2014.54. [DOI] [Google Scholar]
- 37.Yun BM, Dasi LP, Aidun CK, Yoganathan AP. Highly resolved pulsatile flows through prosthetic heart valves using the entropic lattice-Boltzmann method. Journal of Fluid Mechanics. 2014;754:122–60. doi: 10.1017/jfm.2014.393. [DOI] [Google Scholar]
- 38.Ge L, Jones SC, Sotiropoulos F, Healy TM, Yoganathan AP. Numerical simulation of flow in mechanical heart valves: grid resolution and the assumption of flow symmetry. Journal of biomechanical engineering. 2003;125(5):709–18. doi: 10.1115/1.1614817. [DOI] [PubMed] [Google Scholar]
- 39.Marom G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Archives of Computational Methods in Engineering. 2014;22(4):595–620. doi: 10.1007/s11831-014-9133-9. [DOI] [Google Scholar]
- 40.Zakaria MS, Ismail F, Tamagawa M, Aziz AFA, Wiriadidjaja S, Basri AA, et al. Review of numerical methods for simulation of mechanical heart valves and the potential for blood clotting. Medical & Biological Engineering & Computing. 2017;55(9):1519–48. doi: 10.1007/s11517-017-1688-9. [DOI] [PubMed] [Google Scholar]
- 41.Toma M, Krdey A, Oshima M. STRONGLY COUPLED FLUID-STRUCTURE INTERACTION CARDIOVASCULAR ANALYSIS WITH THE EFFECT OF PERIPHERAL NETWORK. Institute of Industrial Science, The University of Tokyo Department of Mechanical Engineering, School of Engineering, The University of Tokyo; [Google Scholar]
- 42.Wei Z, Zheng ZC. Mechanisms of wake deflection angle change behind a heaving airfoil. J Fluid Struct. 2014;48:1–13. doi: 10.1016/j.jfluidstructs.2014.02.010. [DOI] [Google Scholar]
- 43.Wei ZA, Zheng ZC. Fluid-structure-interaction simulation on energy harvesting from vortical flows by a passive heaving foil. Journal of Fluids Engineering. 2017 [Google Scholar]
- 44.Bruening J, Hellmeier F, Yevtushenko P, Kelm M, Nordmeyer S, Sündermann SH, et al. Impact of patient-specific LVOT inflow profiles on aortic valve prosthesis and ascending aorta hemodynamics. Journal of Computational Science. 2017 doi: 10.1016/j.jocs.2017.11.005. [DOI] [Google Scholar]
- 45.Quarteroni A, Veneziani A, Vergara C. Geometric multiscale modeling of the cardiovascular system, between theory and practice. Computer Methods in Applied Mechanics and Engineering. 2016;302:193–252. doi: 10.1016/j.cma.2016.01.007. [DOI] [Google Scholar]
- 46.Marsden AL. Multi-scale Modeling of Cardiovascular Flows. 2015. [Google Scholar]
- 47.Quarteroni A, Ragni S, Veneziani A. Coupling between lumped and distributed models for blood flow problems. Computing and Visualization in Science. 2001;4(2):111–24. doi: 10.1007/s007910100063. [DOI] [Google Scholar]
- 48.Moghadam ME, Migliavacca F, Vignon-Clementel IE, Hsia T-Y, Marsden AL. Optimization of shunt placement for the Norwood surgery using multi-domain modeling. Journal of biomechanical engineering. 2012;134(5):051002. doi: 10.1115/1.4006814. [DOI] [PubMed] [Google Scholar]
- 49.Kheradvar A, Groves EM, Falahatpisheh A, Mofrad MK, Hamed Alavi S, Tranquillo R, et al. Emerging Trends in Heart Valve Engineering: Part IV. Computational Modeling and Experimental Studies. Ann Biomed Eng. 2015;43(10):2314–33. doi: 10.1007/s10439-015-1394-4. [DOI] [PubMed] [Google Scholar]
- 50.Fraser KH, Taskin ME, Griffith BP, Wu ZJ. The use of computational fluid dynamics in the development of ventricular assist devices. Medical Engineering and Physics. 2011;33(3):263–80. doi: 10.1016/j.medengphy.2010.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Min Yun B, Aidun CK, Yoganathan AP. Blood damage through a bileaflet mechanical heart valve: a quantitative computational study using a multiscale suspension flow solver. Journal of biomechanical engineering. 2014;136(10):101009. doi: 10.1115/1.4028105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Yun BM, McElhinney DB, Arjunon S, Mirabella L, Aidun CK, Yoganathan AP. Computational simulations of flow dynamics and blood damage through a bileaflet mechanical heart valve scaled to pediatric size and flow. Journal of Biomechanics. 2014;47(12):3169–77. doi: 10.1016/j.jbiomech.2014.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fogelson AL, Neeves KB. Fluid Mechanics of Blood Clot Formation. Annu Rev Fluid Mech. 2015;47(1):377–403. doi: 10.1146/annurev-fluid-010814-014513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Filipovic N, Ravnic D, Kojic M, Mentzer SJ, Haber S, Tsuda A. Interactions of blood cell constituents: experimental investigation and computational modeling by discrete particle dynamics algorithm. Microvasc Res. 2008;75(2):279–84. doi: 10.1016/j.mvr.2007.09.007. [DOI] [PubMed] [Google Scholar]
- 55.Bluestein D, Einav S, Slepian MJ. Device thrombogenicity emulation: A novel methodology for optimizing the thromboresistance of cardiovascular devices. Journal of Biomechanics. 2013;46(2):338–44. doi: 10.1016/j.jbiomech.2012.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Piatti F, Sturla F, Marom G, Sheriff J, Claiborne TE, Slepian MJ, et al. Hemodynamic and thrombogenic analysis of a trileaflet polymeric valve using a fluid-structure interaction approach. Journal of Biomechanics. 2015;48(13):3650–8. doi: 10.1016/j.jbiomech.2015.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Sagar A, Varner J. Dynamic Modeling of the Human Coagulation Cascade Using Reduced Order Effective Kinetic Models. Processes. 2015;3(4):178–203. doi: 10.3390/pr3010178. [DOI] [Google Scholar]
- 58.Anand M, Rajagopal K. A Short Review of Advances in the Modelling of Blood Rheology and Clot Formation. Fluids. 2017;2(4) doi: 10.3390/fluids2030035. [DOI] [Google Scholar]
- 59.Xu Z, Lioi J, Mu J, Kamocka MM, Liu X, Chen DZ, et al. A multiscale model of venous thrombus formation with surface-mediated control of blood coagulation cascade. Biophys J. 2010;98(9):1723–32. doi: 10.1016/j.bpj.2009.12.4331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wu WT, Jamiolkowski MA, Wagner WR, Aubry N, Massoudi M, Antaki JF. Multi-Constituent Simulation of Thrombus Deposition. Sci Rep. 2017;7:42720. doi: 10.1038/srep42720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tosenberger A, Ataullakhanov F, Bessonov N, Panteleev M, Tokarev A, Volpert V. Modelling of platelet-fibrin clot formation in flow with a DPD-PDE method. J Math Biol. 2016;72(3):649–81. doi: 10.1007/s00285-015-0891-2. [DOI] [PubMed] [Google Scholar]
- 62.Xu Z, Chen N, Kamocka MM, Rosen ED, Alber M. A multiscale model of thrombus development. J R Soc Interface. 2008;5(24):705–22. doi: 10.1098/rsif.2007.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ferziger JH, Peric M. Computational methods for fluid dynamics. Springer Science & Business Media; 2012. [Google Scholar]
- 64.Wei ZA, Tree M, Trusty PM, Wu W, Singh-Gryzbon S, Yoganathan A. The Advantages of Viscous Dissipation Rate over Simplified Power Loss as a Fontan Hemodynamic Metric. Ann Biomed Eng. 2017 doi: 10.1007/s10439-017-1950-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Committee V. Standard for verification and validation in computational fluid dynamics and heat transfer. American Society of Mechanical Engineers; New York: 2009. [Google Scholar]
- 66.Schwer LE. An overview of the PTC 60/V&V 10: guide for verification and validation in computational solid mechanics. Eng Comput-Germany. 2007;23(4):245–52. doi: 10.1007/s00366-007-0072-z. [DOI] [Google Scholar]
- 67.Malinauskas RA, Hariharan P, Day SW, Herbertson LH, Buesen M, Steinseifer U, et al. FDA benchmark medical device flow models for CFD validation. ASAIO Journal. 2017;63(2):150–60. doi: 10.1097/MAT.0000000000000499. [DOI] [PubMed] [Google Scholar]
- 68.Taylor JO, Good BC, Paterno AV, Hariharan P, Deutsch S, Malinauskas RA, et al. Analysis of Transitional and Turbulent Flow Through the FDA Benchmark Nozzle Model Using Laser Doppler Velocimetry. Cardiovasc Eng Technol. 2016;7(3):191–209. doi: 10.1007/s13239-016-0270-1. [DOI] [PubMed] [Google Scholar]
- 69.Vy P, Auffret V, Badel P, Rochette M, Le Breton H, Haigron P, et al. Review of patient-specific simulations of transcatheter aortic valve implantation. International Journal of Advances in Engineering Sciences and Applied Mathematics. 2015;8(1):2–24. doi: 10.1007/s12572-015-0139-9. [DOI] [Google Scholar]
- 70.Siguenza J, Pott D, Mendez S, Sonntag SJ, Kaufmann TAS, Steinseifer U, et al. Fluid-structure interaction of a pulsatile flow with an aortic valve model: A combined experimental and numerical study. Int J Numer Method Biomed Eng. 2017 doi: 10.1002/cnm.2945. [DOI] [PubMed] [Google Scholar]
- 71.Wu W, Pott D, Mazza B, Sironi T, Dordoni E, Chiastra C, et al. Fluid–Structure Interaction Model of a Percutaneous Aortic Valve: Comparison with an In Vitro Test and Feasibility Study in a Patient-Specific Case. Annals of Biomedical Engineering. 2016;44(2):590–603. doi: 10.1007/s10439-015-1429-x. [DOI] [PubMed] [Google Scholar]
- 72.Reporting of Computational Modeling Studies in Medical Device Submissions. https://www.fda.gov/downloads/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/UCM381813.pdf.


