Computational Fluid Dynamics Modeling of the Human Pulmonary Arteries with Experimental Validation

2. ABSTRACT AND KEY TERMS

Pulmonary hypertension (PH) is a chronic progressive disease characterized by elevated pulmonary arterial pressure, caused by an increase in pulmonary arterial impedance. Computational fluid dynamics (CFD) can be used to identify metrics representative of the stage of PH disease. However, experimental validation of CFD models is often not pursued due to the geometric complexity of the model or uncertainties in the reproduction of the required flow conditions. The goal of this work is to validate experimentally a CFD model of a pulmonary artery phantom using a particle image velocimetry (PIV) technique. Rapid prototyping was used for the construction of the patient-specific pulmonary geometry, derived from chest computed tomography angiography images. CFD simulations were performed with the pulmonary model with a Reynolds number matching those of the experiments. Flow rates, the velocity field, and shear stress distributions obtained with the CFD simulations were compared to their counterparts from the PIV flow visualization experiments. Computationally predicted flow rates were within 1% of the experimental measurements for three of the four branches of the CFD model. The mean velocities in four transversal planes of study were within 5.9% to 13.1% of the experimental mean velocities. Shear stresses were qualitatively similar between the two methods with some discrepancies in the regions of high velocity gradients. The fluid flow differences between the CFD model and the PIV phantom are attributed to experimental inaccuracies and the relative compliance of the phantom. This comparative analysis yielded valuable information on the accuracy of CFD predicted hemodynamics in pulmonary circulation models.

3. INTRODUCTION

Pulmonary hypertension (PH) is a chronic, progressive disease that causes remodeling of the pulmonary vasculature leading to failure of the right ventricle (RV) and ultimately death.⁸ The progression of PH is caused by the response of the vascular tissue to the increase in pulmonary arterial pressure above normal physiological values. A prolonged exposure to this high blood pressure causes an increase in arterial wall thickness, decrease of arterial compliance and remodeling of the vasculature.^11,40 PH is diagnosed when the mean pressure in the main pulmonary artery, measured by right heart catheterization (RHC), is equal or higher than 25 mmHg at resting conditions.⁷

The current approach to diagnose and evaluate the mortality risk in patients with PH is based on monitoring cardiac output (CO), mean pulmonary artery pressure (mPAP), pulmonary vascular resistance, and other metrics to assess RV response to the increase in pressure characteristic of the disease.³⁵ A definitive diagnosis of PH relies on invasive methods such as RHC. Non-invasive techniques to measure PH severity include echocardiographic imaging and magnetic resonance imaging (MRI). However, these methods can only provide screening level diagnostics (e.g., echocardiographic imaging) and are generally expensive (e.g., MRI). Non-invasive methods based on computational models of the pulmonary circulation as a diagnostic tool could prove to be invaluable for clinical scientists.²³ Currently, for computational fluid dynamics (CFD) simulations of the pulmonary vasculature, pressure and flow data are collected from RHC procedures to derive patient-specific boundary conditions. Recent studies describe non-invasive techniques to obtain such data.^24,27,31 Using CFD as an investigative tool to provide insight into cardiovascular disease progression has great potential within the field of medicine. With this traditional computational method, blood flow in arteries and the ensuing flow-induced wall stress distribution can be computed. Such computations can be used to understand and guide the course of treatment of cardiopulmonary diseases,^{5,13,17,37,38} including PH where studies show that WSS –a mechanism of endothelial dysfunction– exhibits a relationship with the progression of the disease.^17,38 Recent efforts have been made to pursue a thorough understanding of the roles of elastin and collagen,^20,26,44 arterial mechanical properties^12,45 and relative area change of the pulmonary arteries,³⁹ as well as their remodeling¹⁸ using animal models of PH. New experimental approaches involve the use of imaging tools to study arterial stiffness by analyzing smooth muscle cells and their interaction in the extracellular matrix of the pulmonary vasculature.³⁴

An experimental method for computational data validation is important to verify the accuracy and reliability of the predictions made using CFD models. One such method is particle image velocimetry (PIV), which consists of a non-invasive optical technique for studying bench-top flow phantoms and providing quantitative fluid velocity measurements. PIV can provide accurate quantitative measurements of instantaneous fluid velocity across a planar area of the flow field within an optically transparent phantom. Validation of CFD simulations have been performed using PIV with phantoms of abdominal aortic and cerebral aneurysms,^5,6,32 pulmonary airways,^22,43 and for the fluid dynamics quantification in stents and ventricular assist devices.^3,48

The primary goal of the present work is to validate experimentally the CFD model of a pulmonary arterial phantom using a PIV technique. Such validation is based on the quantification of flow rates, fluid velocities and shear stress at specific locations of interest within the phantom while circulating a blood-mimicking fluid (BMF). To the authors’ knowledge, this is the first known bench-top experimental validation of a CFD model of the pulmonary arterial circulation. The outcome is expected to yield confidence in the computational predictions of hemodynamics in a pulmonary arterial geometry so that future CFD studies can be carried out with a focus on pulmonary hypertensive arterial models.

4. MATERIALS AND METHODS

4.1 Patient-specific pulmonary artery flow model fabrication

The patient-specific pulmonary arterial phantom was built from chest computed tomography (CT) images of a human subject acquired retrospectively after Institutional Review Board approval at Allegheny General Hospital (Pittsburgh, PA). The contrast-enhanced images were segmented using a thresholding based algorithm in the application Mimics (Materialise, Belgium). Due to the complexity of the human pulmonary vasculature, as illustrated in Fig. 1, the images were segmented up to the first bifurcation of the right pulmonary artery. Upon completion of the image segmentation protocol, a stereolithography file was created using the solid model editing application 3-Matic (Materialise, Belgium).

Figure 1.

Anatomy of the human pulmonary vascular system. The main pulmonary artery (MPA) carries blood from the heart to the lungs and bifurcates into the right and left pulmonary arteries (RPA and LPA, respectively). The RPA subdivides into two branches, the superior trunk (or truncus anterior, TA) and inferior trunk (or interlobar, IA). The TA supplies blood to the right upper lobe and the IA supplies the middle and lower lobes. The LPA also subdivides into two branches. Unlike the RPA, there is no TA in the left side of the vasculature and the segmental branches originate directly from the LPA. In the basal trunk (BT) of both lungs, lower lobe segmental branches arise.^9,15 Reproduced from https://www.med-ed.virginia.edu/courses/rad/cxr/anatomy6chest.html.

The phantom was constructed using the silicone elastomer polydimethylsiloxane or PDMS (Dow Corning, Midland, MI), using a lost-core technique as illustrated in Fig. 2. This process involved the creation of a negative mold from a positive core and subsequently removing the core so that the mold is left intact. The positive core was 3D printed using a MakerBot Replicator2 printer (MakerBot, Brooklyn, NY) with a polylactide acid (PLA) resin filament. Due to the intrinsic uneven topology of objects printed using fused deposition manufacturing, a material removal technique was applied before the surface of the negative mold was suitable for coating. A reduced surface roughness is essential for the coating solution (i.e., the silicone elastomer) to flow easily around the core allowing the endoluminal surface to be smooth and have optical clarity for the PIV experiments.⁴⁷ The surface roughness was reduced by incremental sanding techniques and chemical treatment. Large surface imperfections were removed manually by locally sanding the area with different sand paper grits starting from the larger abrasive particles (100) to a superfine grain (600). After this mechanical treatment, the core was chemically finished with dichloromethane (Dow Corning, Midland, MI) to produce a nearly glass-smooth surface. Dichloromethane (DCM) is a solvent that readily dissolves PLA. Therefore, the sanded mold was submerged into the solvent for approximately 2 seconds, allowing the removal of small imperfections and greatly reducing the surface roughness.

Figure 2.

Pulmonary phantom development protocol. First, a positive mold of the patient-specific pulmonary artery geometry was printed using polylactic acid on a 3D printer (a). The model was then chemically treated and placed in an acrylic housing (b). Polydimethylsiloxane was poured into the mold housing and left to cure for at least 24 hours (c). Dichloromethane was used to dissolve the mold so that its negative remains intact. The negative mold of the pulmonary phantom is ready to be connected to the flow loop (d). Phantom attached to PIV flow loop with a refractive index matching the blood mimicking fluid flowing through it. Note that the lumen of the phantom is nearly undetectable (e).

The PDMS solution was prepared as a two-part solution where the parts were mixed according to the manufacturer’s specifications at a 1:10 ratio of activator to base. Since this mixing process can draw ambient air into the solution, the solution was placed in a vacuum to remove any existing air pockets. This step is necessary to make the phantom optically clear after curing. An acrylic box was constructed to hold the core in place while the silicone was poured over it. The core and mold were placed in an oven to cure the silicone at approximately 45°C for 48 hours. The core was subsequently removed by injection of DCM and the resulting negative mold was representative of the endoluminal surface of the patient-specific pulmonary vasculature.

4.2 Flow-loop setup

The phantom was placed in a flow circuit driven by a constant flow rate submersible utility pump (Little Giant, Oklahoma City, OK) that delivered a continuous, non-pulsatile flow rate. The flow-loop was assembled on a large optical table with vinyl tubing (Thermo Fisher Scientific, Waltham, MA), tube fittings (Qosina, Edgewood, NY), electromagnetic flow meters (Kobold Instruments Inc., Pittsburgh, PA), pressure transducers (Honeywell, Morristown, NJ), and custom made dampers and resistors. Signals from the flow meters and pressure transducers were recorded using a data acquisition card and in-house LabVIEW program (National Instruments, Austin, TX).

To ensure fully developed flow conditions entering the phantom, an inlet rigid tube at least ten hydraulic diameters long was 3D printed with a matching inlet cross-section and connected to the phantom. Similar connectors were 3D printed for each of the outlet cross-sections of the phantom. The working fluid for the PIV system is a BMF made to match the refractive index (RI) of PDMS (RI = 1.41) to reduce the optical distortion of light passing through the interface between the phantom and the fluid circulating within. An Abbe refractometer (Atago USA, Inc., Bellevue, WA) was used to measure the RI of both the PDMS and the BMF. The composition of the BMF was determined based on the recommendations by Yousif et al.^49,50 as follows: 47.38% deionized water, 36.94% glycerol, and 15.68% sodium iodide to ensure a match in RI while maintaining a dynamic viscosity similar to that of whole human blood. This BMF exhibits a natural discoloration (yellowing) over time due to the ionization of sodium iodide (releasing $I_3^{-}$ ions) after exposure to air or light.²⁵ Adding 0.1% aluminum thiosulphate to the BMF solution before use counteracts the discoloration without altering the dynamic viscosity or RI appreciably. The BMF is a Newtonian fluid with a measured dynamic viscosity of 4.17 cP (Brookfield Engineering, Middleboro, MA) while the density was measured to be 1.245 g/cm³ (at 22.4°C). In large vessels, such as the human main pulmonary artery (MPA), it is acceptable to consider blood as a Newtonian fluid. The temperature of the BMF was maintained at 37°C by an immersion circulator (VWR International, Radnor, PA) to match a typical body temperature.

4.3 PIV configuration

A LaVision PIV system (LaVision, Goettingen, Germany) was used for the flow visualization experiments with the flow-loop setup. The system consists of a dual-cavity pulsed neodymium-doped yttrium aluminum garnet (Nd:YAG) laser, cylindrical optics to provide a laser sheet for visualization of the working fluid, two CCD cameras for stereoscopic (i.e., three-dimensional) imaging, and a proprietary desktop computer with the necessary software for data analysis and post-processing. The laser operates at a wavelength of 1064 nm; however, once the laser light passes through a frequency doubling crystal, the output has a wavelength of 532 nm with energy of ~65 mJ per pulse and a repetition rate of 15 Hz. Images were captured using two 14-bit high-speed digital cameras with 1600 × 1200 pixel CCD sensors, 30 Hz frame rate, and a minimum time interval of 110 nanoseconds. The cameras and laser were controlled by a LaVision hardware processing unit designed specifically for PIV. To minimize the RMS error in velocity vector measurements, the angle of separation between the two cameras was fixed at approximately 35 degrees.

The velocity vector fields were calculated from double-frame acquired images of the seeding particle displacement while image analysis was performed using the LaVision DaVis 8.2 software. A built-in stereoscopic calibration process was performed with the software prior to experimentation.⁵ To improve the signal to noise ratio in the raw PIV images, fluorescent Rhodamine-B particles (Thermo Scientific, Waltham, MA) of approximately 10 microns in transverse dimension were used instead of silica microspheres, which are typically implemented for PIV systems. Silica microspheres scatter incident light, which can cause higher noise at the fluid-solid interface in flow phantoms; fluorescent particles are preferred to reduce light scattering.

4.4 PIV image post-processing and data analysis

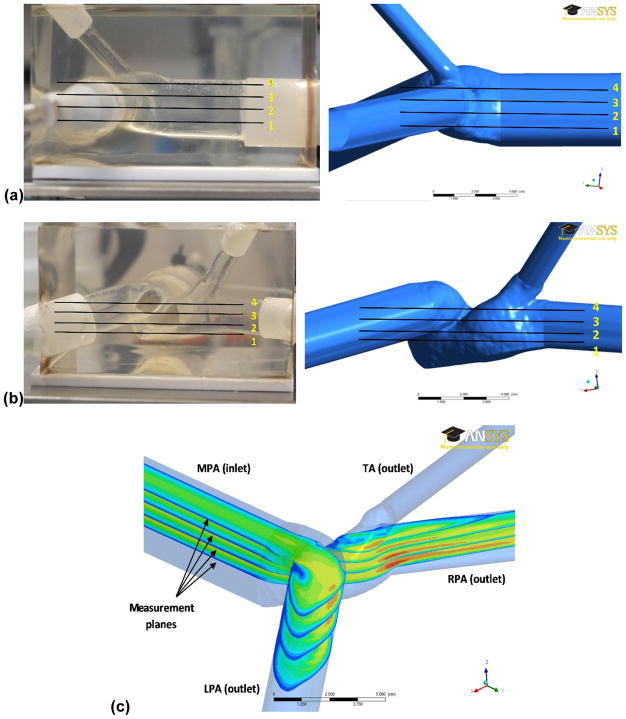
From the acquired PIV time lapse images, the shear stress distributions in four selected planes, as shown in Figs. 3(a) and 3(b), were calculated using in-house Matlab scripts (The MathWorks Inc., Natick, MA). The shear stress (τ) for each plane was calculated using Eq. (1),

Figure 3.

Location of the four planes of study chosen for the evaluation of velocity fields and shear stress distributions; (a) side view of the pulmonary phantom (left) and computational geometry (right) with measurement planes overlaid; (b) front view of the pulmonary phantom (left) and computational geometry (right) with measurement planes overlaid; (c) isometric view of the four planes with exemplary velocity fields and labeling of the major pulmonary branches in the model.

$$\tau =\mu \left[\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right]$$ (1)

where μ is the dynamic viscosity of the BMF (4.17 cP), and ∂u/∂y and ∂v/∂x represent the x and y components of the fluid velocity gradient along the x and y directions, respectively. The wall shear stress (τ_w) in the aforementioned four planes was calculated using Eq. (2),

$${\tau }_w=\mu \frac{\partial u}{\partial n}$$ (2)

where ∂u/∂n represents fluid velocity gradient along the wall-normal unit vector n. Considering the difficulty associated with the transformation of the local vessel coordinate system to the experimental measurement coordinate system to calculate∂u/∂n, Poelma et al.²⁸ assumed two conditions so that ∂u/∂n can be reduced to a simpler form. First, the flow close to the vessel wall is assumed parallel to the wall, i.e. $u\approx V_{\mathit{abs}}=\sqrt{u^2+v^2}$. Second, the flow is assumed to be fully developed. With these two aforementioned conditions, ∂u/∂n can be reduced to the form of Eq. (3),

$$\frac{\partial u}{\partial n}\approx \sqrt{{\left[\frac{\partial \left(\sqrt{u^2+v^2}\right)}{\partial x}\right]}^2+{\left[\frac{\partial \left(\sqrt{u^2+v^2}\right)}{\partial y}\right]}^2}$$ (3)

where u and v represent the x and y components of the velocity vector. Moreover, the flow is considered 2D Newtonian and incompressible, so the wall shear stress (WSS) can be calculated using Eq. (2).

4.5 CFD simulations

The phantom geometry used for the computational simulations was modified using solid model editing software by adding an inlet extension to ensure fully developed flow conditions entering the main pulmonary artery. Likewise, outlet extensions were added to apply outflow boundary conditions far from the fluid domain of interest and to minimize discrepancies between the experimental and computational flows.^4,30,42 To ensure the results were independent of the mesh size, a WSS-based grid convergence analysis was performed.²⁸ The error of the L2-norm of the WSS is considered to be a quantitative representation of grid independence.¹⁶ The mesh was considered size independent when the error of the L2-norm of the WSS was less than 10%, which corresponded to approximately 5.9 million cells with a maximum edge length of 0.84 mm. The CFD simulations were carried out with the solver Ansys Fluent (Ansys Inc., Canonsburg, PA), which is based on the finite volume method where the Navier-Stokes equations are solved in discrete form. The boundary conditions applied to the mesh were a constant inlet flow rate, a no-slip condition at the endoluminal surface and a pure resistance structured-tree outflow boundary condition at each of the three outlet cross-sections.

The CFD simulations were performed by matching the Reynolds number used in the PIV experiments. The fluid was considered incompressible and Newtonian, with an inlet velocity of 9.16 cm/s and a flow rate of 95 mL/s. The latter was obtained following a similarity analysis performed on the basis of matching the Reynolds number corresponding to the time-averaged flow rate obtained from a patient-specific MPA flow waveform. This waveform was measured with a catheter introduced in the MPA of a PH human subject (following a protocol approved for an alternate human subjects research study), such that the inlet velocity corresponds to the time-averaged flow rate calculated from the in vivo flow rate. The vascular resistance was calculated using Eq. (4) for each outlet considering the length of the outflow arterial segment (L), the hydraulic radius (α), and the dynamic viscosity of the fluid (μ).

$$R=\frac{8\mu L}{\pi a^4}$$ (4)

Each outflow resistance was adjusted following an iterative process until the flows calculated in the right pulmonary artery (RPA), left pulmonary artery (LPA), and truncus anterior (TA) matched those measured in the PIV experiment. The labeling of each branch (MPA, RPA, LPA, and TA) in the computational geometry is illustrated in Fig. 3(c).

5. RESULTS

A comparison was made with PIV measurements on the flow phantom to validate the results of the CFD simulation. The comparison of volume flow rates is presented in Table 1, where it can be seen that the relative difference in the flow rates obtained at the inlet and the primary outlets (MPA, RPA and LPA) between the PIV experiment and CFD simulations are less than 1%. Conversely, the relative different in flow rate at the TA outlet was 12.1%. The flow characteristics were computed and measured at the four planes of interest for both the CFD model and the PIV experiments, as seen in Fig. 3. In Fig. 4 the velocity vectors were computed in the CFD model at planes 1–4 and compared to the corresponding PIV velocity vectors. From the PIV experiments it was observed that once the flow is distal to the main pulmonary trunk bifurcation, the fluid impinges on the anterior side of the LPA endoluminal surface, creating a large recirculation region seen in all the planes of study. Additionally, a smaller recirculation zone in the RPA is observed consistently in both the CFD model and the PIV phantom for all four planes.

Table 1.

Comparison of the flow rates calculated by CFD simulation and those measured during the PIV experiments.

Pulmonary model branch	QCFD (cm3/s)	QPIV (cm3/s)	Relative difference with respect to QPIV (%)
MPA (inlet)	95.00	94.97	+0.03
RPA	36.08	36.28	−0.55
LPA	39.32	39.22	+0.25
TA	19.59	22.28	−12.1

Figure 4.

Velocity vectors in planes 1–4 (rows a–d, respectively) for the CFD model (left) and PIV phantom (right). The velocity scale is identical for both columns, as shown in the first frame, and the orientation of the MPA, LPA and RPA is the same for all planes of study.

The mean velocities at the planes of interest for the CFD model and PIV phantom were calculated from discrete velocity measurements and are presented in Table 2. The non-dimensional velocity profiles at three specific cross-sections in the MPA, RPA and LPA were obtained as a function of the non-dimensional transverse dimension, as shown in Fig. 5. The profiles were non-dimensionalized relative to the mean velocity at the inlet cross-section of the models. Relative root mean square errors for each velocity profile were calculated to assess the difference between the computationally predicted profiles and the experimentally measured ones, yielding values of 0.21, 0.34 and 0.20 (non-dimensional) for the MPA, RPA and LPA, respectively.

Table 2.

Comparison of the mean velocities at the planes of study calculated by the CFD simulation and measured during the PIV experiments.

Plane of study	Mean VCFD (cm/s)	Mean VPIV (cm/s)	Relative difference with respect to VPIV (%)
1	10.1	11.3	−10.4
2	9.47	10.9	−13.1
3	9.13	9.70	−5.87
4	7.95	8.81	−9.76

Figure 5.

Comparison of the velocity profiles obtained with the CFD model and the PIV phantom along a cross-section at each major branch (MPA, RPA and LPA). The velocity and the location of each point of interest in the cross-sections were non-dimensionalized by the average velocity at the inlet (V_inlet) and the minimum (y_a) and maximum (y_b) coordinates of the points in each cross-section.

Flow velocity vectors and shear stress distributions on the four planes of interest were quantified and are illustrated in Fig. 6 for the PIV phantom. To avoid terminological confusion and to elucidate the results properly, the proximal arterial region (MPA) is coined the primary branch, while the two daughter arteries (RPA and LPA) are coined the upper and lower branches, respectively, in Fig. 6. Regardless of plane location, positive and negative shear stresses were found to be distributed continuously throughout the aforementioned branches. This shear stress distribution can be described by shedding light on the equations used for the calculation of shear stress, where its magnitude is directly proportional to the velocity gradients. A mostly uniform shear stress is evident in the primary branch corresponding to the steady and uniform laminar flow observed in the MPA. However, at the entrance and proximal end of the upper and lower branches, higher shear stresses were observed due to the increase in velocity gradients, in turn due to the narrowing of the lumen in the RPA and LPA. In addition, a high shear stress was observed at the bifurcation of the MPA into the RPA and LPA due to the impinging flow jet. This localized increase in shear stress translates into an elevated WSS, which can be seen in Fig. 7.

Figure 6.

PIV phantom velocity vectors (left column) and its corresponding shear stress distributions (right column) at planes of study 1–4 (rows a–d, respectively). The velocity and shear stress scales are identical for all frames in the left and right columns, respectively.

Figure 7.

Wall shear stress distribution calculated for the CFD model shown herein after removal of inlet and outlet extensions. The spatially-averaged wall shear stress (SAWSS) is approximately 8.5 dyne/cm².

WSS is the mechanical drag force per unit area acting on the vessel wall due to circulating blood flow and it is known to be responsible for endothelial cell geometric arrangement and mechanotransduction. It has been considered a non-clinical measure of vascular health and its relationship with the etiology of many diseases is well established in the literature.^5,19,46 Figure 6 illustrates that irrespective of the location of the planes of interest, the average and maximum shear stresses in the phantom were 1.5 dyne/cm² and 3.5 dyne/cm², respectively. A spatially-averaged wall shear stress (SAWSS) was also calculated for the CFD model, resulting in 8.5 dyne/cm². In general, higher WSS were evident at (i) the distal end of the upper branch, corresponding to the narrowing of the RPA, and (ii) the upper and lower branches near the bifurcation, likely due to a flow stagnation point at that location. Shear stress was also calculated for each plane of study for the CFD simulations and compared with the PIV results, as shown in Fig. 8. There is generally good agreement in the location of the maximum and minimum shear stresses in both models, indicating that the velocity gradients obtained computationally and measured experimentally are of similar magnitude.

Figure 8.

Shear stress distributions at planes 1–4 (rows a–d, respectively) for the CFD model (left) and PIV phantom (right). The computational and experimental shear stress scales are identical for all frames in the left and right columns, respectively.

6. DISCUSSION

Experimental validation is of vital importance for any computational modeling study. For the present work, an in vitro bench-top flow loop coupled with a PIV system was utilized to test the predictions made by CFD simulations of a patient-specific truncated model of the human pulmonary arteries. The experimental setup was used with a flow phantom fabricated with identical dimensions as the CFD model geometry. Four measurement planes were used to provide detailed information of the flow, velocity and shear stress distribution within the phantom.

In the last two decades, CFD has become a valuable tool used to reproduce, evaluate and analyze complex living systems. CFD simulations can be conducted to analyze blood flow in the pulmonary arterial system where hemodynamics plays an important role in subjects suffering from pulmonary hypertension. By matching closely computational predictions with experimental results, we can develop more complex models of the pulmonary arterial network with the objective of addressing, on a patient-specific basis, the potential role of computational hemodynamics as an aid to right heart catheterization in the diagnosis or follow-up of PH patients. A recent study by Zhang et al.⁵¹ reports on the three-dimensional reconstruction of the MPA from patient-specific images and the use of CFD for such reconstructed models. They analyzed the effect of different LPA angulations on the MPA hemodynamics and found that acute angulation of the LPA is associated with adverse hemodynamic performance. In PH, the impact of blood shear stress on progressive vascular dysfunction has been extensively documented. In the study of pediatric PH, computational simulations have shown to be an invaluable tool to understand the disease mechanism and progression. Hunter et al.¹³ presented an analysis of different applications of computational methods. These studies, while promising, lack proper experimental validation that is essential to assess the accuracy of the computational results. To this end, the present work presents quantitative evidence on the accuracy and precision of a pulmonary computational model relative to a physical model that is nearly identical.

A fundamental understanding of the mechanical behavior of the vascular wall in pulmonary arteries of patients with PAH and the significance of WSS in this disease was recently reported in the literature.^33,38 Our average and maximum shear stresses in the phantom were in agreement with the findings of Sotelo et al.³⁶ and Truong et al.⁴¹ using phase-contrast MRI. Our results show agreement with the work of Tang et al.³⁸ in that the SAWSS of the CFD model is within the range of WSS of the proximal pulmonary arteries in patients with PH. The general location of the high WSS regions in the proximal vasculature also shows similarities with the results reported in ³⁸. The importance of hemodynamic predictions in patient-specific models of the pulmonary circulation is underscored by WSS being a known mechanism of endothelial dysfunction and studies that show its relationship with the progression of PAH.^14,38

The flow rates calculated in the CFD simulations demonstrated an excellent agreement with the PIV phantom with no percentage differences larger than 1% in the MPA as well as in the two major branches, LPA and RPA. The larger percentage difference in the TA flow rate is attributed to an experimental error of unknown source with the flow meter connected to the TA outlet. The quantitative analysis of the velocity profiles along three specific cross-sections in the major branches of the pulmonary bifurcation revealed relative non-dimensional RMS errors of 0.21, 0.34, and 0.20. We infer that good agreement was obtained for these fluid velocity profiles, both qualitatively and quantitatively.

Qualitatively, it was shown that the four planes of study yielded similar results for both methods with regards to the regions of fluid acceleration, recirculation and stagnation. Maximum and minimum wall shear stresses within planes 1–4 had good agreement considering the sensitivity of shear stress to velocity gradients. Further analysis indicates that small differences in the hydraulic diameter of the phantom and the CFD model may be the source of these discrepancies. To this end, the compliance of the silicone elastomer used to fabricate the phantom may have led to changes in the hydraulic diameter during data acquisition. Deformation of the phantom wall (enlargement of the lumen due to internal pressures) would yield the discrepancies in the average velocities compared to the rigid-wall CFD model.¹

An accurate discretization of the geometry is essential when conducting CFD simulations. Therefore, agreement between CFD and experimental results depends heavily on the reproduction of the actual geometry.¹⁰ A slight dissimilarity between the physical model and the computational geometry can result in non-negligible changes to the flow field and yield far greater discrepancies in the derivatives of the velocity field and hemodynamic metrics. Near-wall hemodynamic metrics, such as wall shear stress (WSS), are particularly sensitive to discrepancies in geometry as changes in surface curvature, bifurcations or branching influence the flow patterns greatly.^2,14 In addition, CFD simulations possess the inherent limitation of a finite discretization of the computational geometry, which may be unable to resolve the gradients of shear stress near solid boundaries with the same accuracy as the flow field. This is compounded by inaccuracies in the estimation of patient-specific outflow boundary conditions and a rigid wall assumption.

Obtaining perfect agreement between CFD models and PIV experiments can be a challenging task. Due to experimental uncertainties inherent to the PIV equipment and human error involved in the fabrication of the phantoms, it may not be possible to mitigate all sources of discrepancies in the results. There was experimental error introduced due to small misalignments in the positions of the measurement planes relative to the planes where the CFD results were computed. In addition, the PIV phantom was not entirely rigid. While a quantitative assessment of the elastic properties of the PDMS block was not performed, a small expansion of the phantom wall was visible when the laser sheet illuminated the phantom while taking velocity measurements. Moreover, PIV spatial velocity resolution may have contributed to the discrepancies observed in the shear stresses. As spatial resolution is limited by seeding density, if there are insufficient particles within an interrogation spot to make a reliable measurement, this will require a larger interrogation spot and in turn reduce the spatial resolution of the velocity field. If the seeding number density is sufficiently high to give a valid measurement for a majority of interrogations then the spot size will still tend to smooth the velocity field due to spatial averaging. Therefore, for the estimation of spatial velocity gradients required to calculate shear stress there will be a reduction in the shear stresses due to spatial averaging. We speculate that the seeding density of the 10-micron fluorescent Rhodamine-B particles affected the spatial resolution of the PIV measurements, specifically close to the flow boundaries. This is evident in Fig. 8, where the large shear stresses seen close to the walls of the MPA, RPA, and LPA (due to high velocity gradients near the wall) are underestimated for the PIV-predicted shear stresses.

Overall, qualitatively and quantitatively, the PIV measurements and CFD results showed relatively good agreement, indicating that CFD simulations could be used in a clinical setting to assess the hemodynamics in the pulmonary circulation. However, more research is warranted to assess the pulmonary vasculature constitutive mechanical properties and compare fluid-structure interaction (FSI) simulation results with in-vivo flow in patients with pulmonary hypertension.