Machine Learning Adaptive Basis Sets for Efficient Large Scale Density Functional Theory Simulation

Abstract

It is chemically intuitive that an optimal atom centered basis set must adapt to its atomic environment, for example by polarizing toward nearby atoms. Adaptive basis sets of small size can be significantly more accurate than traditional atom centered basis sets of the same size. The small size and well conditioned nature of these basis sets leads to large saving in computational cost, in particular in a linear scaling framework. Here, it is shown that machine learning can be used to predict such adaptive basis sets using local geometrical information only. As a result, various properties of standard DFT calculations can be easily obtained at much lower costs, including nuclear gradients. In our approach, a rotationally invariant parametrization of the basis is obtained by employing a potential anchored on neighboring atoms to ultimately construct a rotation matrix that turns a traditional atom centered basis set into a suitable adaptive basis set. The method is demonstrated using MD simulations of liquid water, where it is shown that minimal basis sets yield structural properties in fair agreement with basis set converged results, while reducing the computational cost in the best case by a factor of 200 and the required flops by 4 orders of magnitude. Already a very small training set yields satisfactory results as the variational nature of the method provides robustness.

1. Introduction

The rapid increase in computational power and the development of linear scaling methods^1,2 now allow for easy single-point density functional theory (DFT) energy calculations of systems with 10,000–1,000,000 atoms.^3,4 However, the approach is computationally demanding for routine application, especially if first-principles molecular dynamics or relaxation is required. The computational cost of a DFT calculation depends critically on the size and condition number of the employed basis set. Traditional linear scaling DFT implementations employ basis sets which are atom centered, static, and isotropic. Since molecular systems are never isotropic, it is apparent that isotropic basis sets are suboptimal. Therefore, in this work a scheme is presented to define small adaptive basis sets as a function of the local chemical environment. These chemical environments are subject to change, e.g., during the aforementioned relaxations or sampling. In order to map chemical environments to basis functions in a predictable fashion, a machine learning (ML) approach is used. The analytic nature of a ML framework allows for the calculation of exact analytic forces, as required for dynamic simulations.

The idea of representing the electronic structure with adapted atomic or quasi-atomic basis functions dates back several decades. It underlays, e.g., many early tools used for the investigation of bonding order.⁵⁻¹⁰ Also more recent methods for extracting atomic orbitals from molecular orbitals build on this idea.¹¹⁻¹⁶ Besides using adaptive basis sets for analytic tasks, they can also be used to speed up SCF algorithms, which was pioneered by Adams.¹⁷⁻¹⁹ The approach was later refined by Lee and Head-Gordon^20,21 and subsequently applied to linear scaling DFT by Berghold et al.²² Many linear scaling DFT packages have also developed their own adaptive basis set scheme: The CONQUEST program⁴ uses local support functions, derived either from plane waves²³ or pseudoatomic orbitals.²⁴ The ONETEP program²⁵ uses nonorthogonal generalized Wannier functions (NGWFs).²⁶ The BigDFT program²⁷ uses a minimal set of on-the-fly optimized contracted basis functions.²⁸ Other related methods include numeric atomic orbital²⁹⁻³² and localized filter diagonalization.³³⁻³⁷ Recently Mao et al. used perturbation theory to correct for the error introduced into a DFT calculation by a minimal adaptive basis.³⁸

Here, we focus on polarized atomic orbitals (PAOs) and build on the work of Berghold et al.²² PAOs are linear combinations of atomic orbitals (AOs) on a single atomic center, called primary basis in the following, that minimize the total energy when used as a basis. As a result, small PAO basis sets are usually of good quality and their variational aspect is advantageous when computing properties, such as, e.g., nuclear gradients. While there is no fundamental restriction on the PAO basis size, minimal PAO basis sets have been studied in the most detail and are also the focus of this work. Despite their qualities, the use of PAOs in simulation has been very limited, which we attribute to the difficulty of optimizing these PAOs for each molecular geometry in addition to the implied approximation. Our aim is to exploit the adaptivity of the PAO basis but to avoid this tedious optimization step by a machine learning approach.

The application of machine learning techniques to quantum chemistry is a rather young and very active field. For a recent review see Ramakrishnan and von Lilienfeld.³⁹ Its aim is to mitigate the high computational cost associated with quantum calculations. Initially, the research focused mostly on predicting observable properties directly from atomic positions.⁴⁰ For example, very successful recent applications include the derivation of force fields using neural network descriptions.⁴¹⁻⁴³ However, such end-to-end predictions pose a very challenging learning problem. As a consequence they require large amounts of training data with increasing system size, and the learning must be repeated for each property. Fortunately, the past decades of research have provided a wealth of quantum chemical insights. One can therefore build onto established approximations, such as DFT, and apply machine learning only to small, but expensive, subparts of the algorithms. Examples are schemes for learning the kinetic energy functional to perform orbital free DFT⁴⁴ or learning the electronic density of states at the Fermi energy.⁴⁵ Alternatively, machine learning can be used to improve the accuracy of semiempirical methods by making their parameters configuration-dependent.^46,47 In this work, machine learning is used to predict suitable PAO basis sets for a given chemical environment. The present method is thus essentially a standard DFT calculation in a geometry-dependent, optimized basis. Contrary to methods learning specific properties, including the total energy, the present method thus provides access to all properties in DFT calculations.

2. Methods

2.1. Polarized Atomic Orbitals

The polarized atomic orbital basis is derived from a larger primary basis through linear combinations among functions centered on the same atom. In the following, the notation from Berghold et al.²² has been adopted. Variables with a tilde denote objects in the smaller PAO basis, while undecorated variables refer to objects in the primary basis. Formally, a PAO basis function φ̃_μ can be written as a weighted sum of primary basis functions φ_ν, where μ and ν belong to the same atom:

1

As a consequence of the atom-wise contractions, the transformation matrix B assumes a rectangular block-diagonal structure. Since the primary basis is nonorthogonal, the tensor property of the involved matrices has to be taken into account.⁴⁸ Covariant matrices such as the Kohn–Sham matrix H and the overlap matrix S transform differently than the contravariant density matrix P. Hence, two transformation matrices A and B are introduced.

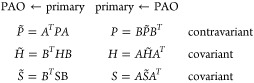2

Notice that A^TB = B^TA = 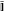gives the identity matrix in the PAO basis, while AB^T = BA^T is the projector onto the subspace spanned by the PAO basis within the primary basis. In order to treat the matrices A and B in a simple and unified fashion, they are rewritten as a product of three matrices:

3

Due to the atom-wise contractions, the matrices N, U, and Y are block-diagonal as well. The matrices N^±1 transform into the orthonormal basis, in which co- and contravariance coincide and the distinction can be dropped. The unitary matrix U rotates the orthonormalized primary basis functions of each atom such that the desired PAO basis functions become the first m_I components. The selector matrix Y is a rectangular matrix, which selects for each atom the first m_I components. Each atomic block Y_I of the selector matrix is a rectangular identity matrix of dimension n_I·m_I, where n_I denotes the size of the primary basis and m_I the PAO basis size for the given atom I:

4

In the formulation from eq 3 the PAO basis is now solely determined by the unitary diagonal blocks of matrix U, without any loss of generality. None of the matrix multiplications required in the transformation is expensive to compute, because the matrices either are block-diagonal or expressed in the small PAO basis.

2.2. Potential Parametrization

The PAO basis is determined by the unitary matrix U. In order to ensure the unitariness of U, it is constructed from the eigenvectors of an auxiliary atomic Hamiltonian H_aux:

5

6

Effectivly, the lowest m states of the auxiliary Hamiltonian are taken as PAO basis functions. Here, the atomic Hamiltonian H₀ describes the isolated spherical atom, and V is the polarization potential that models the influence of neighboring atoms. In the absence of V the PAO basis will reproduce the isolated atom exactly.

In the context of machine learning a parametrization should also be rotationally invariant. A parametrization without rotational invariance, on the contrary, would require training data for all possible orientations and still bear the risk of introducing artificial torque forces. In this work rotational invariant parameters X are obtained by expanding the potential V into terms V_i that are anchored on the neighboring atoms:

7

When the system is rotated, the potential terms V_i change accordingly, while the X_i remain invariant. As a consquence, the optimal X⃗ is independent of the system’s orientation.

Explicit Form of the Potential Terms

The explicit form of the potential terms V_i must be sufficiently flexible to span the relevant subspace. Yet, they must also depend smoothly on atomic positions, be independent of the atom ordering, and be sufficiently local in nature. While we expect that more advanced forms can be found, the following scheme has been employed:

8

where

9

is a potential that results from spherical Gaussian potentials centered on all neighboring atoms.

10

is a projector on shells of basis functions that share a common radial part, and the same angular momentum number l, but have different m quantum numbers. Specializing the terms by different l quantum number and radial part introduces the needed flexibility, while retaining the rotational invariance. Nonlocal pseudopotentials have some resemblance to this scheme. Finally, additional terms are added that just result from the central atom, these are give by

11

Trivially degenerated terms with l_u = l_v = 0 are included only once. The weights w_J and exponents β_J could be used for fine-tunning the potential terms. However, througout this work simply w_J = 1, β_J = 2, and k ≤ 2 are used.

2.3. Machine Learning

Machine learning essentially means to approximate a complex, usually unknown, function from a given set of training points. The amount of required training data grows with the difficulty of the learning problem. Therefore, the learning problem should be kept as small as possible by exploiting a priori knowledge about the function’s domain and codomain.

For the co-domain side this simplification is achieved through the previously described potential parametrization. It takes as input a PAO parameter vector and returns the unitary matrix that eventually determines the PAO basis: X⃗ → U.

For the domain side a so-called descriptor is used. It takes as input all atom positions and returns a low-dimensional feature vector that characterizes the chemical environment: {R⃗_I} → q⃗. The search for a good general-purpose descriptor is an ongoing research effort.⁴⁹⁻⁵¹ For this work a variant of the descriptor proposed by Sadeghi et al.⁵² and inspired by Rupp et al.⁵³ was chosen. For each atom I an overlap matrix of its surrouding atoms is constructed:

12

The eigenvalues of this overlap matrix are then used as descriptor. They are invariant under rotation of the system and permutation of equivalent atoms. The exponent σ_I acts as a screening parameter, while β_J allows the descriptor to distinguish between different atomic species. With these two simplifications in place, the learning machinery only has to perform the remaining mapping of feature vectors onto PAO parameter vectors: q⃗ → X⃗. A number of different learning methods have been proposed, including neural networks⁵⁴ and regression.⁴⁰ For this work a Gaussian process (GP)⁵⁵ was chosen as a relatively simple, but well characterized, ML procedure. As kernel served the popular squared exponential covariance function:

13

However, the PAO-ML scheme makes no assumptions about the employed ML algorithm and can be used in combination with any other machine learning method. Finally, a small number of hyper-parameters had to be optimized to achieve good results. While fixing the descriptor screening to σ_I = 1 and the GP noise level to ϵ = 10^–4, the descriptor’s β_J and the GP length scale σ were determined with a derivative-free optimizer as β_O = 0.09, β_H = 0.23, and σ = 0.46 au. For an overview of the entire PAO-ML scheme see Figure 1.

Figure 1.

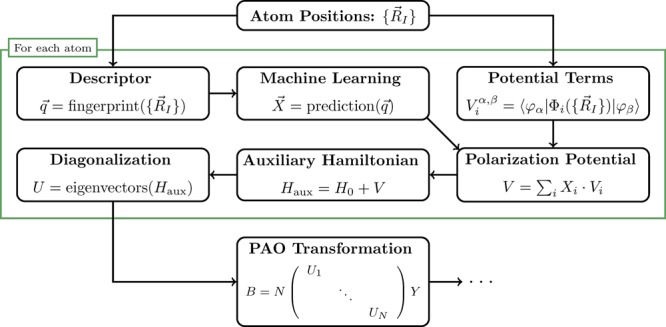
Overview of the PAO-ML scheme for using the potential parametrization and machine learning to calculate the PAO basis from given atomic positions.

2.4. Analytic Forces

In order to run molecular dynamics simulations, accurate forces are essential. Forces are the derivative of the total energy with respect to atom positions. While a variationally optimized PAO basis does not contribute any additional force terms, the same does not hold for approximately optimized PAO basis sets. The advantage of using a pretrained machine learning scheme is the possibility to calculate accurate forces nevertheless.

The PAO-ML scheme contributes two force terms that have to be added to the common DFT forces F⃗_DFT. One term originates from the potential terms V_i from eq 8, which are anchored on neighboring atoms. The other force term arises from the descriptor, which takes atom positions as input. Both additional terms can be calculated analytically:

14

2.5. Training Data Acquisition

Training data are obtained by explicitly optimizing the PAO basis for a set of training structures. This poses an intricate minimization problem because the total energy must be minimal with respect to the rotation matrix U and the density matrix P̃. Additionally, the solution has to be self-consistent because the Kohn–Sham matrix H depends on the density matrix. Significant speedups can be obtained from temporarily relaxing the self-consistency by fixing the Kohn–Sham matrix H during an optimization cycle of P̃ and U.

Regularization

For high-quality training data the optimal parameters X⃗ should be unique and vary smoothly with atomic positions. To this end, two carefully designed regularization terms were introduced. The first term is inspired by Tikhonov regularization⁵⁶ and penalizes expansion on linearly dependent potential terms in eq 7. The second term is a L₂ regularization for the excess degrees of freedom in the potential V. Together both regularizations can be expressed via the overlap matrix of the potential terms:

15

as

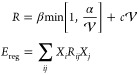16

Througout this work the values α = 10^–6 and β = c = 1 mHa are used.

3. Results

In this section, the performance of the method for bulk liquid water is explored. This system has a long tradition within the first-principles MD community, as it is both important and difficult to describe.⁵⁷ From an energetic point of view, the challenge arises from the delicate balance between directional hydrogen bonding and nondirectional interactions such as van der Waals interactions.⁵⁸ The relatively weak interaction can furthermore be influenced by technical aspects, such as basis set quality. Additionally, the liquid is a disordered state, which requires sampling of configurations for a proper description. The disorder makes it also an interesting test case for the ML approach, as the variability of the environment of each molecule can be large.

3.1. Learning Curve

In order to validate the PAO-ML method a learning curve is recorded. To do this, 71 frames containing 64 water molecules, spaced 100 fs apart, are taken from an earlier MP2 MD simulation at ambient temperature and pressure.⁵⁹ The first 30 frames are used as training data while the last 30 frames serve as a test set. For each training frame the optimal PAO basis is determined via explicit optimization using DZVP-MOLOPT-GTH as the primary basis. The PAO-ML method is then used to predict basis sets for all test frames based on an increasing number of training frames. The learning curve in Figure 2 shows the standard deviation of the energy difference with respect to the primary basis taken across all 64 water molecules in all 30 test frames. It shows that already a single frame, i.e., 64 molecular geometries, is sufficient training data to yield an error below 0.1 mHa per water molecule. The curve furthermore shows good resilience against overfitting as the error continues to decrease even for large training sets, eventually reaching 0.083 mHa per molecule. In comparison, a traditional minimal (SZV-MOLOPT-GTH) basis set exhibits an error of 0.360 mHa. The learning can at best reach the accuracy of the underlying PAO approximation (0.074 mHa). It is unlikely that the current descriptor would be sufficient to attain that bound.

Figure 2.

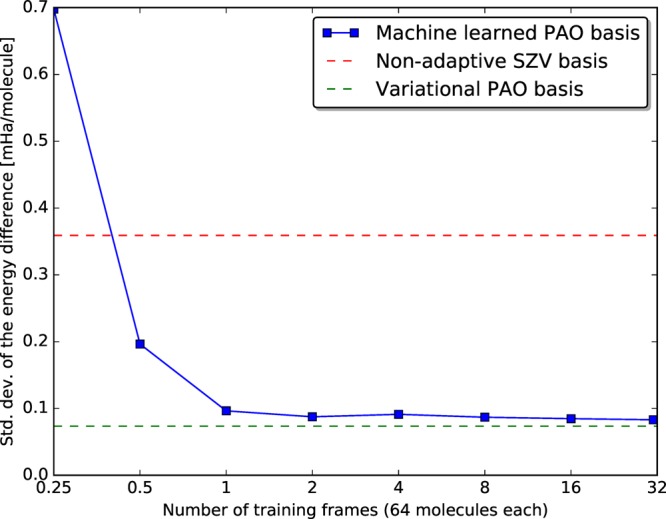
Learning curve showing the decreasing error of PAO-ML (blue) with increased training set size. For comparison the error of a variationally optimized PAO basis (green) and a traditional minimal SZV-MOLOPT-GTH (red) basis set are shown. With very little training data, the variational limit is approached by the ML method.

3.2. Consistency of Energy and Forces

In order to validate that the forces provided by the PAO-ML implementation are consistent with its energies, a series of short molecular dynamics simulations with different time steps was performed on a water dimer. For the integration of Newton’s law of motion the velocity–Verlet algorithm⁶⁰ has been employed, which has an integration error that is of second order in the time step. Figure 3 shows the fluctuations obtained with time steps of 0.4, 0.2, and 0.1 fs. The standard variations extracted from these fluctuation curves are 5.00, 1.23, and 0.31 μHa. This matches nicely the 4-fold decrease expected for a time step halving and confirms the consistency of the PAO-ML implementation.

Figure 3.

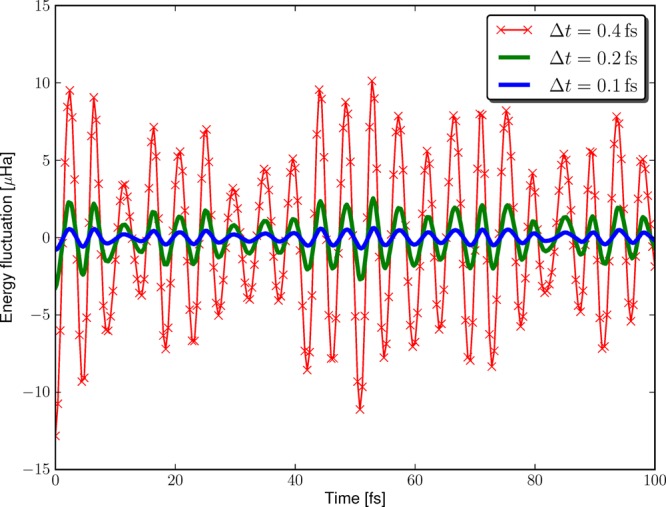
Energy fluctuation during a series of MD simulation of a water dimer using the PAO-ML scheme. The simulations were conducted in the NVE ensemble using different time steps Δt to demonstrate the consistency of the forces and thus the controllability of the integration error.

3.3. PAO-ML Molecular Dynamics of Liquid Water

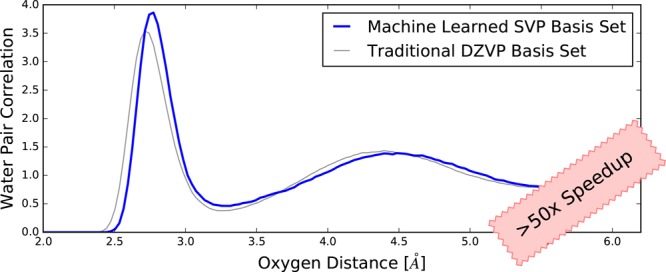
So far, we have tested the performance of the method based on frames sampled with a traditional approach. More challenging for a ML method is sampling configurations based on predicted energies, in particular, to verify that instabilities and unphysical behavior are absent when the method is given the freedom to explore phase space. To test and verify the performance, molecular dynamics simulations have been performed for 64 molecules of water at experimental density and 300 K, producing trajectories between 20 and 40 ps depending on the method. Besides PAO-ML, a traditional minimal (SZV-MOLOPT-GTH) basis set, a standard basis sets of triple-ζ quality (TZV2P-MOLOPT-GTH), and density functional tight binding (DFTB)^61,62 were used. TZV2P serves as a reference converged result, while SZV and DFTB provide insight in the performance of methods with a basis set size identical to PAO-ML. The oxygen–oxygen pair correlation functions of liquid water are shown in Figure 4. First, these results show that the PAO-ML simulation is similar to the reference TZV2P-MOLOPT-GTH. The position of the first peak in the O–O pair correlation function matches well the one of the experimental reference, which is a significant improvement over the result obtained with a SZV-MOLOPT-GTH basis. Compared to the experiment, overstructuring of the first peak can be mostly attributed to the employed PBE exchange and correlation functional, as it also shows up with the triple-ζ basis set. Comparing to the DFTB results, the difference is most significant near the second solvation shell, which is mostly absent or strongly shifted to larger distances with DFTB, whereas the PAO-ML reproduces the reference results rather accurately.

Figure 4.

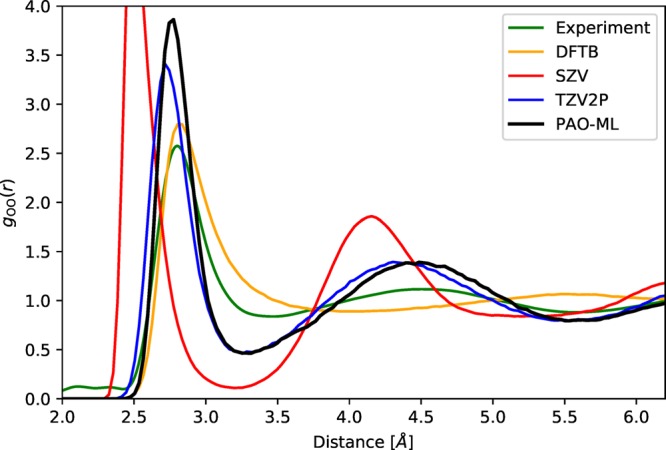
Shown are oxygen–oxygen pair correlation functions for liquid water at 300 K. As reference the experimental (green, ref (63)) and TZV2P-MOLOPT-GTH basis sets (blue) results are shown. The SZV-MOLOPT-GTH curve (red) and DFTB (orange) are examples of results typically obtained from a minimal basis sets. The adaptive basis set PAO-ML (black) reproduces the reference (TZV2P) better than any of the alternative minimal basis set methods.

3.4. Check for Unphysical Minima

We checked that the PAO-ML potential energy surface is free from unphysical minima. To this end, the 30 test frames of bulk liquid water employed in section 3.1 were geometry optimized using PAO-ML. During this optimization the energy dropped on average by 3.14 mHa per water molecule and each atom moved on average 0.212 Å. Afterward, starting from the PAO-ML minima configuration, a second geometry optimization was performed using the DZVP-MOLOPT-GTH basis. Confirming the physical nature of the PAO-ML minima, the average energy difference between the configurations optimized with PAO-ML and DZVP is a neglibile 0.028 mHa per molecule and the positions changed on average by only 0.014 Å per atom. This confirms the quality of the PAO-ML basis.

3.5. PAO-ML Speedup

The speedup obtained with PAO-ML in the context of linear scaling calculations will be quantified. As a test system, a cubic unit cell containing 6912 water molecules (∼20000 atoms) is employed. The simulations were run on a Cray XC40 using between 64 and 400 nodes each with two CPUs. Table 1 shows the timings for both the full energy calculation and the sparse matrix multiplication part alone. Linear scaling calculations are typically dominated by matrix multiplication, which made it the target of the PAO-ML method. The largest speedup for this part is observable on a few nodes, in which case the PAO-ML scheme yields a 200× wall time reduction. The number of flops actually executed decreases by 4 orders of magnitude from 61.63 × 10¹⁵ flops for DZVP-MOLOPT-GTH to only 4.07 × 10¹² flops for PAO-ML. This speedup can only be partially attributed to the smaller basis set, as the reduction in flops in the dense case would be only 56× (6 vs 23 basis functions per water molecule). This demonstrates the importance of the condition number of the overlap matrix in sparse linear algebra, because the PAO basis exhibits a condition number around 6, which is more than 2 orders of magnitude lower than for the primary DZVP basis set. Due to the large speedup of the matrix multiplication, the Kohn–Sham matrix construction becomes a major contribution to the timings. Nevertheless, on 64 nodes the PAO-ML method speedup the full calculation by 60×. Running on 400 nodes allows one to perform an SCF step in just 3.3 s.

Table 1. Timings (seconds) for the Complete CP2K Energy Calculation (Full) and the Matrix Multiplication Part (mult) on a System Consisting of ∼20000 Atoms, As Described in the Text^a.

nodes	64	100	169	256	400
PAO-ML
full	87	58	41	33	24
mult	23	17	13	11	8
DZVP-MOLOPT-GTH
full	5215	2765	1996	1840	1201
mult	5036	2655	1922	1779	1165

^aThe PAO-ML method outperforms a standard DFT run with a DZVP-MOLOPT-GTH basis by a factor of at least 50×.

3.6. Computational Setup

All the calculations were performed using the CP2K software.⁶⁴⁻⁶⁶ CP2K combines a primary contracted Gaussian basis with an auxiliary plane-wave (PW) basis. This Gaussian and plane-wave (GPW)⁶⁷ scheme allows for an efficient linear-scaling calculation of the Kohn–Sham matrix. The auxiliary PW basis is used to calculate the Hartree (Coulomb) energy in linear-scaling time using fast Fourier transforms. The transformation between the Gaussian and PW basis can be computed rapidly. The cutoff for the PW basis set was chosen to be at least 400 Ry in all simulations. While the PW basis is efficient for the Hartree energy, the primary Gaussian basis set is local in nature and allows for a sparse representation of the Kohn–Sham matrix. For the simulations, the Perdew–Burke–Ernzerhof⁶⁸ (PBE) exchange and correlation (XC) functional and Goedecker–Teter–Hutter (GTH) pseudopotentials⁶⁹ were used. The linear-scaling calculations were performed with the implementation as described in ref (3), which in particular allows for variable sparsity patterns of the matrices. All SCF optimization used the TRS4⁷⁰ algorithm. The SCF optimization was converged to a threshold (EPS_SCF) of 10^–8 or tighter; the filtering threshold EPS_FILTER was to 10^–7 or tighter. The default accuracy (EPS_DEFAULT) was set to 10^–10 or tighter. All simulations were run in double precision. CP2K input files are available in the Supporting Information.

4. Discussion and Conclusions

In this work, the PAO-ML scheme has been presented and tested. PAO-ML employs machine learning techniques to infer geometry adapted atom centered basis sets from training data in a general way. The scheme can serve as an almost drop-in replacement for conventional basis sets to speedup otherwise standard DFT calculations. The method is similar to semiempirical models based on minimal basis sets but offers improved accuracy and quasi-automatic parametrization.

The PAO-ML approach has the interesting property that the optimal prediction of the parameters makes the energy minimal with respect to these parameters. During the actual simulation, this implies a certain stability of the simulation, as regions with poorly predicted parameters will be avoided due to their higher energy. Ultimately, the whole PAO-ML method provides basis sets that depend in an analytical way on the atomic coordinates. As such, analytic nuclear forces are available, making the method suitable for geometry optimization and energy conserving molecular dynamics simulations.

The performance of the method was demonstrated using MD simulations of liquid water, where it was shown that small basis sets yield structural properties that outperform those of other minimal basis set approaches. Interestingly, very small samples of training data yielded satisfactory results. Compared to the standard approach, the number of flops needed in matrix–matrix multiplications decreased by over 4 orders of magnitude, leading to an effective 60-fold run-time speedup.

Finally, it is clear that the approach presented in this work can be further refined and extended. Some early results have been published in a Ph.D. thesis.⁷¹ Possible directions for improvements include the following: (a) systematic storage and extension of reference data to yield a general purpose machine learned framework for large scale simulation, including a more rigorous quantification of the expected error, which will improve usability; (b) refined parametrization of the PAO basis sets, reducing the number of parameters needed and the enhancing the robustness of the method; (c) nonminimal PAO basis sets; (d) extensions of the method to yield basis sets for fragments or molecules rather than atoms, which will increase accuracy and efficiency; (e) more advanced machine learning techniques and alternative descriptors, which will allow for larger training sets and improved transferability of reference results. These directions should be explored in future work.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00378.

• Representative input files for most simulations (ZIP)

This work was supported by the European Union FP7 with an ERC Starting Grant under Contract No. 277910 and by a grant from the Swiss National Supercomputing Centre (CSCS) under Project ID ch5.

The authors declare no competing financial interest.