Kinetic-Energy Density-Functional Theory on a Lattice

Abstract

We present a kinetic-energy density-functional theory and the corresponding kinetic-energy Kohn–Sham (keKS) scheme on a lattice and show that, by including more observables explicitly in a density-functional approach, already simple approximation strategies lead to very accurate results. Here, we promote the kinetic-energy density to a fundamental variable alongside the density and show for specific cases (analytically and numerically) that there is a one-to-one correspondence between the external pair of on-site potential and site-dependent hopping and the internal pair of density and kinetic-energy density. On the basis of this mapping, we establish two unknown effective fields, the mean-field exchange-correlation potential and the mean-field exchange-correlation hopping, which force the keKS system to generate the same kinetic-energy density and density as the fully interacting one. We show, by a decomposition based on the equations of motions for the density and the kinetic-energy density, that we can construct simple orbital-dependent functionals that outperform the corresponding exact-exchange Kohn–Sham (KS) approximation of standard density-functional theory. We do so by considering the exact KS and keKS systems and comparing the unknown correlation contributions as well as by comparing self-consistent calculations based on the mean-field exchange (for the effective potential) and a uniform (for the effective hopping) approximation for the keKS and the exact-exchange approximation for the KS system, respectively.

1. Introduction

Density-functional theory (DFT) has become over the past decades a standard approach to the quantum many-body problem. Its success comes from the fact that it combines low computational cost with a reasonable accuracy, which helps to understand and predict experimental results for systems not accessible with wave function-based methods. DFT avoids the exponential numerical costs of wave function-based methods by reformulating quantum mechanics in terms of the density. The major drawback of DFT is that the exact energy expression of the quantum system in terms of the density is not available, and in practice approximations need to be employed. Already before the rigorous formulation of DFT,¹ a heuristic method based on the density instead of the wave function existed, which was called the Thomas–Fermi theory.^2,3 While this theory proved to be very important for the derivation of fundamental results, for example, the stability of quantum matter,⁴ in practice it is not very accurate (only in the limit of atoms with arbitrarily high atomic number or for homogeneous systems) and does not provide basic properties such as the shell structure of atoms or the binding of molecules. As it was quickly realized, it is the approximation to the kinetic-energy expression that prevents Thomas–Fermi density-functional approximations from leading to accurate results. What has made DFT popular for determining properties of complex many-body systems is the Kohn–Sham (KS) construction,⁵ where instead of modeling the kinetic energy directly in terms of the density an auxiliary noninteracting quantum system is used that has the same density. The kinetic energy of this computationally cheap auxiliary system is then corrected by so-called Hartree-exchange-correlation (Hxc) contributions that incorporate the missing interaction and kinetic-energy contributions. Already simple approximations to this unknown expression give reasonably accurate answers. However, it is hard to systematically increase the accuracy of approximations while still keeping the favorable numerical costs.⁶ Moreover, it has been shown recently that numerous functionals, although accurate when it comes to total energies, fail to reproduce the true density.⁷ The difficulty in functional construction can be attributed to the fact that it is not easy to find the appropriate expression of Hxc contributions in terms of the auxiliary KS wave function or the density.

There are several other approaches for dealing with the quantum many-body problem that also avoid the many-body wave function, while the basic variable used makes it easier to model the desired physical quantities. Green’s function techniques can be systematically improved in accuracy by including higher-order Feynmann diagrams, but are computationally much more expensive.^8,9 Reduced density-matrix (RDM) functional theories^10,11 provide a compromise between accuracy and computational cost. In one-body RDM (1RDM) functional theory,¹¹ the kinetic energy is an explicit functional of the 1RDM, thus only part of the interaction energy needs to be approximated, while in the two-body case¹⁰ even the interaction is given by an explicit functional. Although the explicit use of wave functions can be avoided in these cases, it is still necessary for the RDM to be representable by a wave function. However, the so-called N-representability conditions that guarantee an underlying wave function associated with an RDM are anything but trivial.¹²⁻¹⁵ Moreover, it is not possible to associate to every RDM an auxiliary system of noninteracting particles that would allow one to replace the N-representability conditions by a numerically simpler auxiliary wave function, like in the DFT case. The Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy, where the time propagation of an RDM of certain order is related to the RDM of the next order, suffers from similar N-representability issues.¹⁶

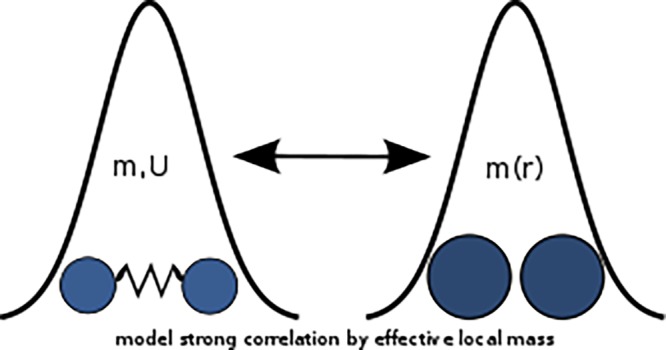
There are now several possible ways to remedy the above-mentioned deficiencies. For 1RDM theory, it is helpful to consider the many-body problem at finite temperature and indefinite numbers of particles.¹⁷⁻¹⁹ In this case, the representability conditions in terms of an ensemble of wave functions are known and easy to implement, and one can even find a noninteracting auxiliary system that generates the same 1RDM. Another possibility is to construct approximate natural orbitals, which are eigenfunctions of single-particle Hamiltonians with a local effective-potential.^20,21 On the DFT side, besides changing the auxiliary system for the KS construction,²²⁻²⁴ a possible way out is to include the kinetic-energy density as a basic functional variable along with the density, simplifying the modeling of the exchange-correlation potentials because they will not include any more kinetic-energy contributions. This however implies that an additional auxiliary potential, which couples to the kinetic-energy density, has to be introduced. A similar approach has recently appeared in a different context, that is, in thermal DFT,^25,26 where the additional auxiliary potential corresponds to a proxy for local temperature variations and couples to the entire energy density, including kinetic and interaction contributions. The concept of local temperature was also introduced in the local thermodynamic ansatz of DFT.²⁷⁻²⁹ Furthermore, it is important to note that the kinetic-energy density is already used extensively in DFT, for instance, as an integral part of the so-called meta-GGAs. When treated within the generalized KS framework,³⁰ meta-GGAs lead to a local potential coupling to the kinetic-energy density, which can be interpreted as a position-dependent mass.³¹

In this Article, we investigate the possibility to include the kinetic-energy density as a basic functional variable in DFT alongside the density. The idea is that by doing so one can increase the accuracy of density-functional approximations. We investigate this by constructing the exact density functionals of standard DFT and comparing them to the combined kinetic-energy density and density functionals of this extended approach we call kinetic-energy density-functional theory (keDFT). In this way, we want to assess possible advantages of such an approach when considering strongly correlated systems. The so-called kinetic contribution³² to the exchange correlation potential is important for the description of such systems. It has been shown that standard DFT functionals fail to describe the effects of this kinetic contribution such as the band narrowing due to interactions.³³ By including the kinetic-energy density as a fundamental variable, this contribution is taken into account explicitly.

Further, we want to consider the quality of possible approximation schemes to keDFT based on a kinetic-energy KS (keKS) construction and test them in practice. As is clear from the extent of the proposed program, this is not possible for real systems. Similar to investigations of the exact functionals in DFT³⁴⁻³⁶ and other extensions of DFT,³⁷ we restrict our study to a finite lattice approximation for the Hamiltonian, where the particles are only in specific states/positions. We therefore consider lattice keDFT. In this way, we not only avoid the prohibitively expensive calculation of reference data for realistic interacting many-body systems but also avoid mathematical issues connected to the continuum case, like the nonexistence of ground states and nondifferentiability of the involved functionals^38,39 or having to deal with the kinetic-energy operator, which is unbounded.⁴⁰ All of the operators that appear on the lattice are Hermitian matrices, which yield lowest energy eigenstates, and exact solutions can be easily calculated contrary to the continuum where one always has to resort to basis set approximations. We also highlight how simple approximations carry over from our model systems to more complex lattice systems and even to the full continuum limit. The results hint at the possibility to treat weakly and strongly correlated systems with the same simple approximation to keDFT.

This Article is structured as follows: In section 2 we introduce our lattice model, define the density and kinetic-energy density on the lattice, and highlight for a simple two-site case that the kinetic-energy density is a natural quantity to be reproduced by an extended KS construction. We then introduce the resulting keKS construction assuming the existence of the underlying maps between densities and fields. In section 3 we discuss these mappings and show how by allowing a spatially dependent mass/hopping a large gauge freedom is introduced. Still we can provide a bijective mapping between densities and fields for specific cases. In section 4 we then show how we numerically construct the mappings beyond these specific cases and hence find that keDFT on a lattice can be defined also for more general situations. In section 5 we then use the constructed mappings to determine the exact correlation expressions for the KS and the keKS construction, respectively. In section 6 we then compare the results of self-consistent calculations for similar approximations for the KS and the keKS systems, respectively. Finally, we conclude in section 7.

2. Formulation of the Lattice Problem

In the following, we consider quantum systems consisting of N Fermions (electrons) on a one-dimensional lattice of M discrete sites. We assume that these particles can move from site to site only via nearest-neighbor hopping (corresponding to a second-order finite-differencing approximation to the Laplacian) and employ zero boundary conditions for definiteness (the extension to periodic boundary conditions is straightforward). This leads to a Hamiltonian of the following type:

1

The nonlocal first term corresponds to the kinetic energy. Without loss of generality, we can assume that the hopping amplitude obeys t_i > 0. Let us point out that usually the hopping amplitude is site-independent. We employ this more general form (corresponding to a site-dependent mass) to establish the necessary mappings (see eq 10). However, when we numerically consider interacting systems, we always employ a site-independent hopping, which corresponds to the standard Hubbard Hamiltonian. The second term corresponds to a local scalar electrostatic potential v_i acting on the charged particles at site i. U ≥ 0 is the on-site Hubbard interaction between the Fermions, which is reminiscent of the Coulomb interaction. Further, the Fermionic creation and annihilation operators obey the anticommutation relations {ĉ_i^σ†,ĉ_j} = δ_ijδ_σσ′, where σ corresponds to the spin degrees of freedom of the particles, n̂_i^σ = ĉ_iĉ_i^σ is the spin-density operator, and n̂_i = n̂_i + n̂_i^↓ is the density operator that couples to the electrostatic potential. Because we fix the number of particles, the potential v_i is physically equivalent to a potential that differs by only a global constant. In the following, this arbitrary constant is fixed by requiring

2

Now, if Ψ is the ground-state wave function of Hamiltonian 1, we can associate to every point in space a ground-state density n_i = ⟨Ψ|n̂_i|Ψ⟩. From the lattice-version of DFT,⁴¹ we know that for every fixed set of parameters (t,U), there is a bijective mapping between the set of all possible potentials (in the above gauge) to all possible densities for a fixed number of particles. To ease notation, we introduce a vector for the density n ≡ (n₁,...,n_M) and accordingly for the potential v ≡ (v₁,...,v_M), which allows us to write the underlying mapping as 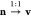. Accordingly, for the potential of an interacting system (U > 0) as a functional of the density, we write v_i[n]. We further note that because the total number of particles is fixed to N, the density is constrained by ∑_i = 1^Mn_i = N. This means that instead of the density at every point one can equivalently use the density differences between sites Δn_i = ⟨Ψ|n̂_i – n̂_i+1|Ψ⟩ to establish the above mapping at a fixed number of particles. Similarly, knowing the local potential v_i at every site together with the gauge condition 2 is equivalent to knowing Δv_i = v_i – v_i+1. In certain situations, for example, for figures, it is more convenient to use the density and potential differences instead of the density and potential.

Clearly a similar mapping between density and potential also holds for a noninteracting Hamiltonian, that is, U = 0. Because it is bijective, we can invert the mapping and find a potential v^s (where we follow the usual convention and denote the potential of a noninteracting system with an s) for a given density n. The noninteracting mapping allows one to define v_i^s[n], which in turn leads to

3

The noninteracting Hamiltonian reproduces the prescribed density n as its ground state by construction. This is not yet the KS construction, because we need to know the target density in advance. Only upon connecting the interacting with the noninteracting system by introducing the Hxc potential:

4

which can also be defined as a derivative of the corresponding Hxc energy functional with respect to n, we find the nonlinear KS equation for a given and fixed external potential v of the interacting system:

5

This problem has as the unique solution the noninteracting wave function that generates the density of the interacting problem without knowing it in advance.⁴² It is imperative at this point to understand the (often overlooked) difference between Ĥ^s[n] together with the density functional v_i^s[n] and H^KS together with the KS-potential functional v_i[v;n] = v_i + v_i^Hxc[n]. Only the latter provides an iterative scheme to predict the density of an interacting references system. Also, only at the unique fixed point of the KS iteration procedure, where v_i = v_i[n], do both Hamiltonians give rise to the same noninteracting wave function. When we later present results for the exact KS construction in section 5, we refer always to the results at the unique fixed point of the KS construction. In practice, however, we do not have the exact v_i[v;n] available, and hence we need to devise approximations to the unknown Hxc functional. The simplest such approximation would be a mean-field ansatz of the form v_i^Hxc[n] ≈ Un_i. To comply with the chosen gauge of eq 2, we could use v_i[n] ≈ U(n_i – N/M).

As we will see in section 5, the major problem in these approximations is that the kinetic-energy density of the KS and the interacting system become dramatically different with an increasing U. Here, the kinetic-energy density T_i at site i is defined nonlocally (because it involves the hopping) with the help of the first off-diagonal of the (spin-summed) 1RDM in site basis representation:

6

where γ_i,i+1 is given by

7

By analogy to the continuum case, one can also define the charge current J_i as

8

With no external magnetic field present, that is, no complex phase of the hopping amplitude, the ground-state wave functions are real valued, which implies γ_i,i+1 = γ_i+1,i, leading to zero current. We note that the current obeys the lattice version of the continuity equation:

9

in a time-dependent situation, where 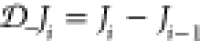is the backward derivative of J_i. Equation 9 is an equation of motion (EOM) (see also Appendix B for further EOMs) that physical wave functions need to adhere to. It is important to note that it is not only the variational (minimum-energy) principle that ground states have to fulfill, but there are many more exact relations. While for the case of the ground state the EOM of eq 9 is trivial because both sides are individually zero, there are many other nontrivial exact relations that can be based on EOMs and that provide us with exact relations between the densities, the fields, and other physical quantities. For instance, the second-time derivative of the density provides us with the local force balance of the equilibrium quantum system,⁴³ which we will use in section 4. Also, while the most common way to find approximations for the Hxc potentials is by obtaining approximate Hxc energy expressions and then taking a functional derivative, the EOMs provide an alternative way to construct approximate Hxc potentials without the need to perform functional variations.^44,45 In section 5 we will show how one can obtain such approximations, for instance, the exact-exchange approximation of standard DFT.

Clearly, if we could enforce that an auxiliary noninteracting system has the same 1RDM as the interacting one, then also the kinetic-energy densities T of the two systems would coincide. This suggests that one can establish a mapping between the interacting 1RDM and a nonlocal potential, that is, a v_i,j that connects any two sites of the lattice and thus couples directly to the full 1RDM. However, in general this is not possible as has been realized early on in 1RDM functional theory.⁴⁶ A concrete example is the two-site homogeneous Hubbard problem at half filling forming a singlet. In this case, we have i = 1,2 and v_i = 0. So we have a homogeneous density n_i = 1, and we can analytically determine all eigenfunctions of the interacting and noninteracting system. Further, in the case of only two sites, the full spin-summed 1RDM is a 2 × 2 matrix, where the diagonals are merely γ_i,i = n_i = 1 and the off-diagonals are given explicitly by 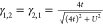. Because the density fixes the potential of the interacting and KS system to be exactly zero, our only freedom is to adopt the nonlocal potential, which is equivalent to just adopting the hopping of the KS system (in this case, the nonlocal potential v_1,2 ≡ t). Yet because the off-diagonals for the KS system are γ_1,2^s = γ_2,1 ≡ 1 irrespective of the hopping amplitude, no nonlocal KS potential exists that reproduces the interacting 1RDM. This is also true in more general lattice situations as has been shown in, for example, ref (47). For the 1RDM, two solutions to this problem are known. One is to include temperature and possibly an indefinite number of particles, which introduces off-diagonals that depend on the temperature and the hopping, that is, the nonlocal potential.¹⁹ We note that for the homogeneous two-site case, this can still be solved analytically and verified explicitly. The other possibility is to make the system degenerate such that we can reproduce any density matrix.¹⁹

Here, we apply a different strategy. While we cannot force the density matrices to coincide, it is possible to require the kinetic-energy densities to be the same. The crucial difference is that we include the coupling in the Hamiltonian in the definition of the quantity to be reproduced by the KS system. For example, in the two-site case, we merely need to use an interaction-dependent hopping 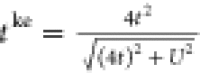. Thus, the auxiliary noninteracting system reproduces now the pair (n,T) of the interacting system. Before we move on, let us note that similarly to the continuum case, one could use 1RDM functional theory at zero temperature also on the lattice if one avoids the use of a noninteracting auxiliary system and merely uses functionals based directly on the interacting 1RDM.^48,49 Note that N-representability conditions would still need to be enforced in such a scheme.

Let us now assume that similar to DFT we can establish a bijective mapping:

10

which would allow us to define hopping parameters and potentials that generate a given kinetic-energy density and density, that is, (t_i[n,T], v_i[n,T]). Specifically we can then consider a noninteracting auxiliary problem that generates a prescribed pair (n,T):

11

by its ground state. Whether we can construct such an auxiliary system that reproduces the density and kinetic-energy density of an interacting system is something we do not know a priori. In this Article, we provide numerical evidence as well as proofs for specific situations that suggest that such a construction is possible (see section 3). If we introduce then the corresponding mapping differences similar to eq 4 and denote them by mean-field exchange-correlation (Mxc):

12

13

we find the corresponding keKS system:

14

such that

15

and

16

where Φ^ke is the corresponding ground state. This construction gives rise to the keKS hopping t_i^ke[t;n,T] and the keKS potential v_i[v;n,T]. Similarly to standard DFT, it is important to realize the difference between Ĥ^s[n,T] together with (t_i^s[n,T],v_i[n,T]) and the keKS Hamiltonian Ĥ^ke together with the keKS functionals (t_i^ke[t;n,T],v_i[v;n,T]). Only the latter provides an iterative scheme to predict the physical pair (n,T) of the interacting reference system. At the unique fixed point of the keKS iteration procedure, where v_i = v_i[n,T] and t_i = t_i[n,T], both Hamiltonians coincide and give rise to the same noninteracting wave function. When we in the following present results for the exact keKS construction, we refer always to the results at the unique fixed point of the keKS construction. This also allows us in the following to only use t_i^ke and v_i to highlight the difference between the usual KS and the keKS construction. To make the scheme practical, we now need two approximations: one for the Mxc potential and one for the Mxc hopping. Possible routes on how to construct approximations and how this could help to more accurately capture strongly correlated systems we consider in section 5.

At this point, we want to make a first connection to the continuum by considering the appropriate choice of the kinetic-energy density for that case. There are different possible definitions for a local kinetic-energy density, which will give rise to the same total kinetic energy.⁵⁰ For instance, we can choose the gauge-independent definition¹⁰⁰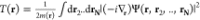, where Ψ corresponds to the interacting wave function, such that the kinetic-energy density is positive at every point in space. Here, we have defined a spatially dependent mass m(r) > 0 that takes the role of the site-dependent hopping in the lattice case. For the noninteracting system, the corresponding kinetic-energy density (provided we assume a Slater determinant) reads 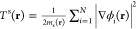, where m_s(r) > 0 is the spatially dependent noninteracting mass and ϕ_i the single particle orbitals. The single-particle kinetic-energy operator then becomes accordingly , where m(r) should be substituted with m_s(r) in the noninteracting case.

3. Generalized Mappings from Densities to Potentials

Similarly to fixing the constant of the local potential, one needs to fix the gauge of the hopping parameter t_i^(ke) (where the superscript ke in parentheses is used to denote that we refer both to interacting and to noninteracting keKS systems). One of the first things to note is that by letting t_i change from site to site, we encounter a large equivalence class for the site-dependent hopping parameters. Indeed, we can arbitrarily change the signs of the hopping from t_i^(ke) → −t_i without changing the density and the kinetic-energy density. However, the wave function and also, for example, the 1RDM change. For instance, for the noninteracting single particle Hamiltonian, we see that changing the sign locally, say at site i, will transform the single-particle wave function at this site ϕ_i to −ϕ_i (see Figure 1 for an example and Appendix D for further details). This leaves the density unchanged, as it is just a sum of the squared absolute values of the single-particle wave functions. Also, the kinetic-energy densities stay the same, because the 1RDM switches signs at the same place as the hopping amplitude. As it follows from the discussion above, the sign of t_i^(ke) is just a gauge choice, and we need to fix the gauge to establish the sought-after mapping. In the following, we choose t_i > 0.

Figure 1.

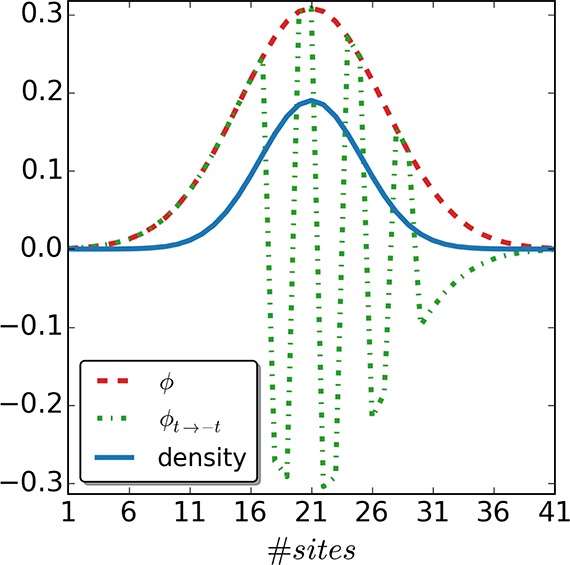
Doubly occupied orbital ϕ that corresponds to a two-electron singlet-state of a single particle Hamiltonian with all hopping parameters t_i^ke = t positive and the corresponding one ϕ_t→–t with alternating hopping parameters ±t from site 17 to 29. Every time we alternate t to – t at site i, the orbital ϕ changes sign from that site on. Because we replace t to −t from site to site, the orbital will recover its original sign after two sites. As one can readily see, the density stays the same in both cases, as a consequence of the sign of t being only a gauge choice.

A further complication that one encounters in establishing the necessary mappings is that the usual Hohenberg–Kohn approach does not work in our case. The reason is that the control fields t now become explicitly part of the control object T. A similar problem is encountered in current-density-functional theory, when trying to establish a mapping in terms of the gauge-independent physical charge current.⁵¹⁻⁵⁵ While in the time-dependent case having the field as part of the control objective is actually an advantage and a general proof has been established,⁵⁴ these complications unfortunately prohibit a simple general proof of the existence of the mapping (n,T) → (v,t) for the time-independent case. However, for specific situations, we are able to show that the discussed mapping is possible. The most important one in our context is the case of the two-site Hubbard model (see Appendix A for details). In this case, we only have a single potential difference Δv and density difference Δn. So we can simply rescale the auxiliary Hamiltonian and thus prove the existence of the mapping in the noninteracting case by employing the Hohenberg–Kohn results. A further simple case is two noninteracting particles, forming a singlet, in a general M-site lattice. Here, the density fixes the single-particle orbital (doubly occupied) up to a sign, and thus for a given T_i only a unique site-dependent hopping t_i is possible. Finally, in the homogeneous case, where the local potential v_i = 0 and periodic boundary conditions are employed, the density 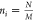and the kinetic-energy density of the interacting system will be constant at every site i, T_i = T. The matrix elements γ_i,i+1 will also be constant from site to site, γ_i,i+1 = γ. In this case, the mapping is invertible and a unique (up to a sign choice) 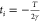is associated from site to site. Note that in this case the KS system and the keKS system yield the same wave function and 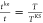. This last example, although it only shows the invertibility of the mapping (v,t) → (n,T) at the specific points t_i = t > 0 and v_i = 0, has very important consequences. It allows us in a simple yet exact way to connect the auxiliary keKS system to the interacting system. We will use this later to construct a first approximation to t_i^Mxc.

To show that the keDFT mapping can also be defined for other, more general cases, we construct in the following the mappings numerically. Afterward, we make use of the constructed mappings to investigate the properties of the Mxc potentials and the basic functionals, which for the continuum case would be numerically prohibitively expensive.

4. Inversion of (n,T)

Because, as discussed above, it is not straightforward to show that the mapping 10 is 1:1 in general, we investigate this question numerically. Therefore, we construct sets of densities and kinetic-energy densities (n,T) by solving the interacting problem specified by the Hamiltonian given in eq 2 (with a site-independent hopping, which corresponds to the usual Hubbard Hamiltonian), and for every set we determine the potentials (v,t) of the noninteracting Hamiltonian specified in eq 14, which yields the target densities (n,T). To determine these potentials, we set up an inversion scheme by using the EOM for the density and the kinetic-energy density, respectively. These provide not only physical relations that connect the quantities (v,t) with (n,T), but they are also suitable to define correlation potentials, as we will explain in the following.

Note that in principle the inversion can be done with other techniques, which are used to find the exact local KS potential for a given interacting target density.⁵⁶⁻⁵⁹ However, it is not straightforward how to transfer these techniques to the current situation. For instance, in ref (56), an iteration scheme is introduced that adopts the potential based on the intuition that where the density is too low the potential is made more attractive and where the density is too high it is made less attractive. It is not so clear how to transfer this intuitive procedure to the kinetic-energy density T_i, which is nonlocal, and the control field is part of the observable itself. In the continuum, one could perform an inversion and define the corresponding auxiliary potentials again by EOMs.^42,60 Another possibility would be to exploit techniques where the kinetic-energy density of the KS and the interacting system are used to model the exchange-correlation potential.⁵⁹

Because the first-order EOM for the density, that is, the continuity eq 9, is trivially satisfied as the current is just zero in the ground state, we consider the second time derivative of the density n̈_i. Because the first time derivative of the kinetic-energy density vanishes for ground-state wave functions, we use again the second-order EOM T̈_i.

As examples, we give here the EOMs for n̈₁ and T̈₁ for two sites in the noninteracting case that we use in our numerical inversion scheme:

17

18

In Appendix B, the general expressions for any number of sites can be found. Here, we have dropped the site index because everything corresponds to site 1, Δn = (n₁ – n₂) is the density difference between the two sites, Δv^ke = (v₁^ke – v₂) is the local potential difference, and T = −2t^keγ_1,2^ke. As one can readily see for the two-site case, there is no additional information in the equation for T̈, as once n̈ is 0 T̈ is also 0. Nevertheless, once we go to more sites, T̈_i will also give us new equations. For a detailed discussion of this issue, see Appendix B.

The inversion scheme we employ is an iterative procedure based on the above introduced EOMs (see eqs 44 and 48 in Appendix B for the general expressions), which provide us with relations between (Δv^ke,t^ke) and the target quantities (n,T). We obtain the target quantities (n,T) by finding the ground state of the corresponding interacting Hamiltonian of eq 1, with a position-indepent hopping t_i = t. We then choose as an initial guess for the auxiliary keKS system the values of the interacting system v_i^ke,0 = v_i and t_i = t.

(a) We solve the auxiliary noninteracting Schrödinger eq 11 with the values v_i^ke,0 and t_i:

19

(b) We next calculate the density and kinetic-energy density that correspond to the state |Φ^ke,0⟩, that is, n_i⁰ = ⟨Φ^ke,0|n̂_i|Φ^ke,0⟩ and T_i = −2t_i^ke,0⟨Φ^ke,0|γ̂_i,i+1|Φ^ke,0⟩ as well as the matrix elements γ_i,j that enter the EOMs 44 and 48.

(c) In a last step, we then calculate the variables of the next iteration v_i^ke,1 and t_i. The EOM for n̈_i = 0 of eq 44 provides us with analytic expressions of v_i^ke,1 in terms of the target densities, the hopping amplitudes t_i, and the reduced density matrix elements γ_i,j⁰ of the previous iteration. For calculating the t_i, we use a numerical solver on all of the available EOMs for n̈_i = 0 (eq 44) and T̈_i = 0 (eq 48), with the target kinetic-energy densities, but updated densities n_i⁰ and γ_i,j from the last iteration and the renewed local potentials v^ke,1. We repeat steps (a)–(c) until convergence of the calculated fields.

As an example in the two-site case, one can update in every iteration the local potential:

20

and the hopping parameter:

21

where Δn is the target density difference between the two sites and T is the target kinetic-energy density.

We want to point out that the procedure to update v^ke,i and t^ke,i is not the only one possible. For example, one could have used instead of the EOMs that we get for n̈_i = 0 the ones for J̈_i = 0. Further note that there are always M – 1 independent equations from n̈_i = 0 because of particle number conservation, thus as many as the independent v_i^ke that we have (although it is not clear that we need all of them as we do not have a linear system of equations). The number of EOMs that we get for the kinetic-energy density T̈_i is M – 2, as we explain in Appendix B. The interacting ground state was obtained using the single-site DMRG⁶¹ routine, implemented in the SyTen toolkit.⁶²

We successfully performed inversions for systems of up to four sites with different total number of electrons for different on-site interaction strengths U and local potentials v. Some representative results for half-filling are shown in the next section, where we use the constructed mappings to consider the exact keKS system. Note that we also successfully performed inversions beyond half-filling. We also performed successful inversions for the same systems for the interacting problem; that is, we chose random values (n,T) and reproduced them with a nonzero Hubbard interaction. This makes the equations involved slightly more complex (and we refrained from showing them here explicitly), but the inversion procedure stays the same. The fact that we could indeed construct a keKS auxiliary system for these cases as well as perform inversions for the interacting problems provides us with indications for the existence of a keKS system for an arbitrary number of electrons/sites.

5. Comparing the Exact KS and keKS Construction

Next, we assess the practical implications of using the kinetic-energy density as basic functional variable along with the density. First, we use the construction of the exact keKS system and the corresponding KS system to compare the Hxc energy E_Hxc^KS of the KS system with the corresponding quantity E_Mxc of the keKS system. This gives us a first indication of whether a keKS approach might help to capture also strong correlation effects more easily. For the KS system, the Hxc energy is

22

where T_i^KS = −2t⟨Φ^KS|γ̂_i,i+1|Φ^KS⟩ is the kinetic-energy density of the KS system and |Φ^KS⟩ its ground-state wave function. By E_gs, we denote the total ground-state energy of the interacting system and v_i is its external potential. The corresponding energy contribution of the keKS system reads

23

where T_i^ke = −2t_i⟨Φ^ke|γ̂_i,i+1|Φ^ke⟩. Because the kinetic energy of the keKS system is identical to the interacting one by construction, the E_Mxc^ke ≡ E_int = U∑_i = 1⟨Ψ|n̂_i^↑n̂_i|Ψ⟩ is equal only to the interaction energy in this case. The corresponding term of the KS system includes kinetic-energy contributions as well. In Figure 2, we plot E_Mxc^ke and E_Hxc for a Hubbard dimer at half-filling with local potential Δv/t = 1 as a function of the interaction strength U/t. Note that the data from the numerical inversion are used. Thus, both energy quantities are exact, and there is no approximation involved.

Figure 2.

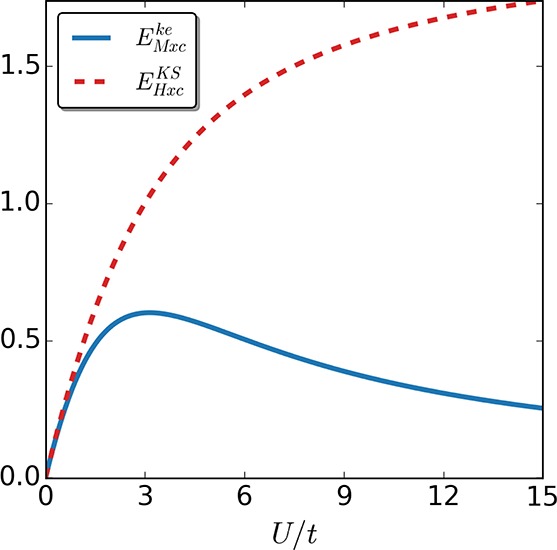
Hxc energy E_Hxc^KS (dashed line) and the corresponding energy term of the keKS system E_Mxc (continuous line) for a Hubbard dimer at half-filling with local potential Δv/t = 1 as a function of U/t. We see that for U > 0 it holds that E_Mxc^ke < E_Hxc.

In Figure 3, we show the corresponding plot for a four-site Hubbard system at half-filling with Δv₁/t = −Δv₃/t = 0.625 and Δv₂/t = 0.375. These two systems for two-site and four-site will serve as our test systems, and in the following we will refer to them as the two-site case and four-site case, respectively.

Figure 3.

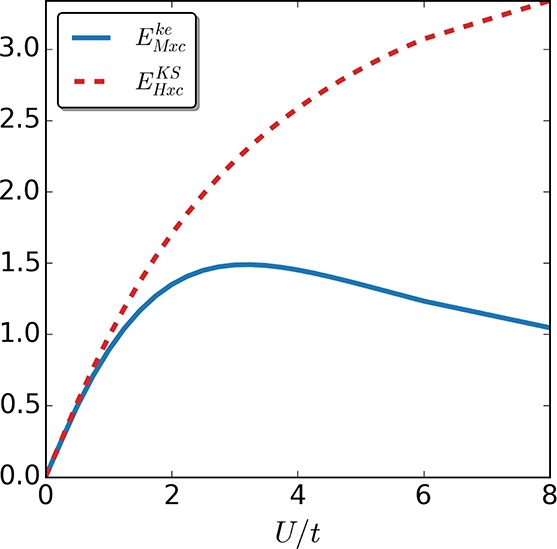
Hxc energy E_Hxc^KS (dashed line) and E_Mxc (continuous line) for a four-site Hubbard model at half-filling with local potential Δv₁/t = −Δv₃/t = 0.625 and Δv₂/t = 0.375 as a function of U/t. We again find that for U > 0 it holds that E_Mxc^ke < E_Hxc.

As one can readily see in Figures 2 and 3, for every interaction strength U > 0 it holds that E_Mxc^ke < E_Hxc. In the strong correlation limit, the kinetic-energy of the KS system is far from the interacting one. Having in mind the following relation:

24

it becomes apparent why E_Mxc^ke and E_Hxc are so different for strong interactions. As a consequence, the exchange-correlation potential derived from E_Hxc^KS will need to take into account this difference in the strong interaction regime. In the keKS system, on the other hand, one needs to introduce a second field t^Mxc, which is responsible for reproducing the kinetic-energy density along with the potential v^Mxc that ensures the density is reproduced. Furthermore, due to the fact that E_Mxc does not contain kinetic contributions, it offers a simple scaling relation in contrast to E_Hxc^KS.⁶³

While the energy functionals are an interesting first indication that the keKS approach can be useful to treat also strongly correlated systems, the real quantities of interest are the effective fields that the KS and keKS constructions employ, especially those parts of the Hxc potential and of the Mxc hopping and potential that are not accessible by simple approximation strategies. Those parts, which one usually assumes to be small in practice, we will denote as correlation terms. Let us in the following, based on the EOMs we used to derive the iteration scheme, define parts of the effective fields that we can express explicitly in terms of the KS and keKS wave functions. Similar constructions based on the EOM of the density have been employed in DFT and TDDFT.^44,45 For simplicity, we present the expressions only for the two-site case. The expressions for four-sites are given in Appendix C. The Hxc potential is defined as Δv^Hxc[n] = Δv^s[n] – Δv[n] (eq 4), where n is the target density of the interacting system, Δv^s[n] is the local potential difference of the KS system, and Δv[n] is just the external potential of the interacting system. The EOMs for the noninteracting/interacting density, eq 17/53, provide expressions for the local potential Δv^s[n] and Δv[n] of the noninteracting/interacting system. Thus, the Hxc potential in the two-site case reads

25

We can decompose Δv^Hxc in a Hartree-exchange part Δv^Hx[n,Φ^KS]:

26

which corresponds to the usual Hartree plus exchange approximation in standard DFT, and a remaining correlation part:

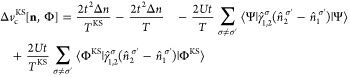27

Here, we include the KS wave function in the functional dependencies to highlight that it is an orbital functional; that is, it depends on the KS wave function. We note, however, that in the exact case the KS wave function is uniquely determined by the density. The above decomposition is similar to that of the continuum case introduced in ref (44) and later used in, for example, refs (45) and (64). In eq 12, we have defined the Mxc potential v^Mxc for the keKS system, which in the two-site case (by using the same EOMs as before) reads

28

We see that the first two terms are completely determined by the keKS system, contrary to Δv^Hxc of the KS system, where the second term cannot be given in terms of Δn or Φ explicitly. The first term, however, depends explicitly on the hopping in the keKS system, which has to be approximated in practice. Keeping this in mind, one can identify a mean-field exchange potential, similarly to the Hartree-exchange potential of the KS system:

29

which depends explicitly on the density, the kinetic-energy density, and the ground state of the keKS system. Let us at this point remark that if there is no approximation for the hopping parameter involved, that is, when t^ke = t, the expression of v^Mx in eq 29 is identical to the expression for v^Hx in eq 26. In the mean-field approximation, γ_i,i+1 ≈ γ_i,i+1^ke, it follows immediately that t_i = t, because we require the kinetic-energy densities to be the same, that is, t_i^keγ_i,i+1 = tγ_i,i+1. We note that for the exact case we consider here, that is, at the solution point of the exact keKS nonlinear equation (see also discussion about the keKS construction below eq 16), t^ke can be explicitly given in terms of t and the exact Φ^ke. In practice, however, we do not know t^ke[t,n,T] = t + t^Mxc[n,T] a priori, and we need to include further an extra approximation for t^Mxc[n,T]. Which approximations are possible (and how accurate they are) will be discussed next, and in the following section we will see how the practical form of v^Mx[n,T,Φ^ke], that is, including an approximate t^Mxc[n,T], performs. The remaining local potential correlation term contains now only contributions from the difference in interaction:

30

We stress that the definition of the correlation contribution to the local potential 30 only contains part of what is usually referred to as correlations in the context of KS DFT. The so-called kinetic correlation is taken care of in the hopping amplitudes t^ke and via definition 29 in v^Mx. In Figure 4 we plot for the two-site case the correlation KS and keKS potentials, which are given by eqs 27 and 30, respectively. In Figure 5 we plot the correlation potentials for the four-site case, which are given for the KS system by eqs 63–65 and for the keKS by eqs 72–74. As one can readily see for the two sites, the correlation potential is smaller in absolute value for the keKS system than in the KS one for all interaction strengths tested, apart from a small region at vanishing interaction. This follows from the fact that the kinetic contributions are included in the mean-field exchange potential Δv_i^Mx in the keKS case. For the four sites we see the same trend. However, in the keKS construction, we have a second effective field, which we so far did not take into account in our comparison. One needs to find an analogous decomposition into a term that corresponds to the v_i in the KS case, which can be approximated with a relatively simple functional, and a term that requires more advanced approximations, in correspondence to v_i^c. Of course, if the latter part is large as compared to the former, we did not gain anything by introducing the additional field t_i.

Figure 4.

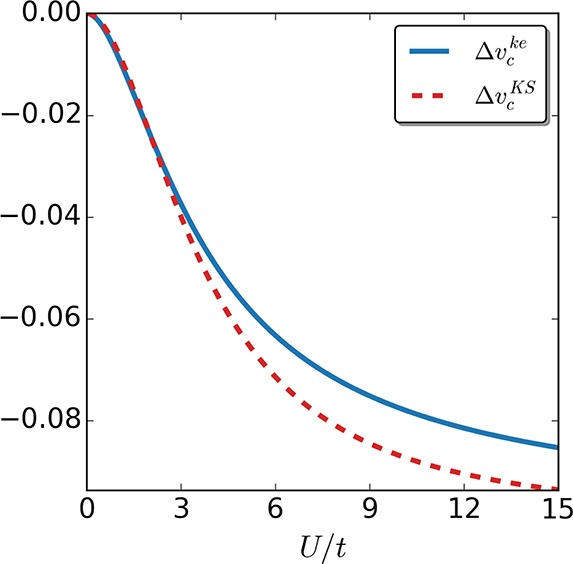
Correlation potential of the keKS Δv_c^ke (continuous curve) and KS system Δv_c (dashed curve) for the two-site case as a function of the interaction strength U/t. Apart from a small region at vanishing interaction strength U, |Δv_c^ke| < |Δv_c|.

Figure 5.

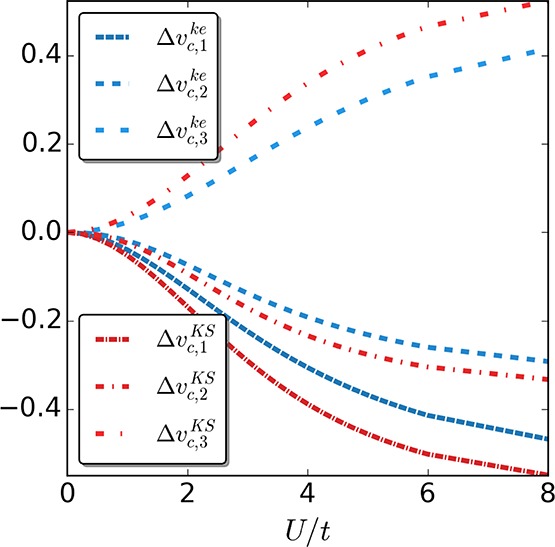
Correlation potentials of the keKS Δv_c,i^ke (dashed) and KS system Δv_c,i (dotted-dashed) for the four-site case as a function of the interaction strength U/t. Again, we find that, apart from a small region at vanishing interaction strength U, |Δv_c,i^ke| < |Δv_c,i|.

Starting from the definition of t_i^Mxc[n,T] = t_i[n,T] – t_i[n,T], and using the fact that the kinetic-energy density T_i has to be the same in the interacting and keKS system, we get that

31

which by substituting T_i = t_i[n,T]γ_i,i+1[n,T] and reordering the various terms yields the form:

32

where we have defined δγ_i,i+1 ≡ γ_i,i+1 – γ_i,i+1^ke. Up to here, there is no approximation involved. As the term δγ_i,i+1 involves the solution of an interacting and noninteracting problem, an approximation based on a reference solution suggests itself. The simplest such reference solution would be to use the homogeneous case of the interacting and the keKS system, respectively, similar to the local-density approximation in standard DFT. Because in the homogeneous case with periodic boundary conditions, as discussed in section 3, the keKS and the KS density matrices are the same, we can directly use well-known results such as the Bethe-ansatz solution at half filling. In this way, it becomes also straightforward to extend the introduced approximation to the continuum case, where we can use reference calculations for interacting homogeneous continuum systems. Let us also do the same uniform approximation for the zero boundary condition case that we discuss here, although the uniform KS and keKS density matrices will not be the same apart from the two-site case. Here, we assume that we have reference data for the homogeneous problems for different local hopping parameters t_i > 0, local fillings 0 < n_i < 2, and for the local interactions U > 0. Further we ignore the dependence of the t_i in the numerator on the internal pair (n,T) and use an explicit dependence on Φ^ke in the denominator. In the following, we will simplify the explicit parts even further and will just take the homogeneous solution at half filling, that is, calculate δγ_i,i+1 for two-site and four-site cases with different U. The update formula for t_i, which we will denote as t_i^unif to stress that the approximation comes from using uniform reference data for the 1RDM, reads:

33

Let us point out here that when 33 is used in a self-consistent loop, the t_i^unif is updated using the γ_i,i+1 of the previous iteration as the enumerator is fixed and taken from the reference calculation. In the two-site case such an ansatz seems appropriate, because despite the zero-boundary conditions the keKS and the KS systems are the same by construction. For the four-site case, however, the zero-boundary conditions make the keKS and KS density matrices different. Hence, the four-site case is a very challenging test for the accuracy of such a simple approximation. In accordance to the above introduced approximation, we will then define the remainder of the hopping field as t_c,i[n,T,Φ^ke] = t_i^Mxc[n,T] – t_i[Φ^ke], where we emphasize that strictly speaking t_c,i includes correlations beyond the correlations present in a uniform system. In Figure 6 we plot the (beyond uniform) correlation hopping field t_c/t as a function of the interaction strength U/t for the two-site case. We see that the value of t_c is small as compared to the chosen t for all interaction strengths and especially for weak and strong interactions. For strong interactions, the system resembles a homogeneous one as the interaction strength becomes more prominent in comparison to the local potential difference, and thus t_c becomes smaller in this regime. From this we can infer that for the case of a general system with periodic boundary conditions, the homogeneous ansatz will capture not only the weak but also the strong-interaction limit accurately.

Figure 6.

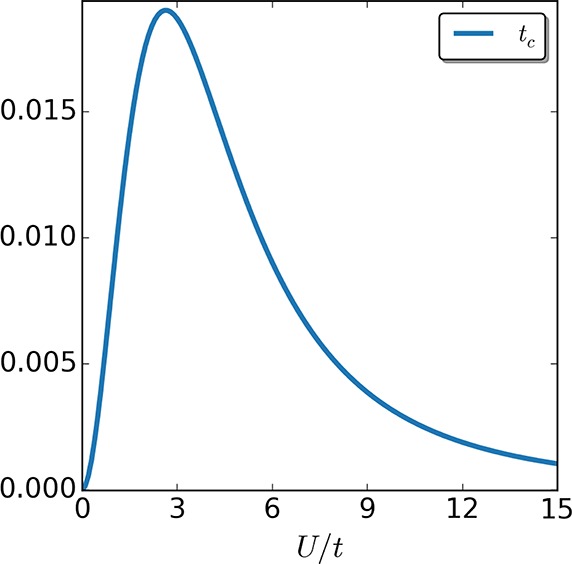
Correlation part of the hopping t_c,i in units of t, for the two-site case as a function of interaction strength U/t. For strong interaction strength, the system resembles a homogeneous one so that the uniform type of approximation we employed becomes very good.

In Figure 7 we turn to the more challenging case of four sites with zero boundary conditions and plot the three different t_c,i/t components as a function of the interaction strength. As one can readily see, all three t_c,i are small for every interaction strength U. However, only two of them seem to converge to a value that is close to zero for strong interactions, at least for the parameter range we investigated. (We want to point out that for larger values of U we encountered some convergence issues in the four-site case. The reason is that while the density matrices are not homogeneous, the density is, which causes some problems in the iteration scheme, where we divide by the density difference between two neighboring sites in each iteration. This problem, however, can be potentially overcome by using different update equations.) We remind the reader that this difference in accuracy between the two-site and the four-site cases is not surprising. In the two-site case, the uniform KS γ_i,i+1^KS, which is used to construct the approximation for t^unif, coincides with the corresponding uniform γ_i,i+1 of the keKS system. For four sites this is no longer the case. Still, comparing the numerical values of the correlation hopping t_c,i to those of the correlation potential v_c,i^ke, there is an order of magnitude difference. This gives some hope that crude approximations like the t_i can still lead to accurate predictions. Let us test this in the following section.

Figure 7.

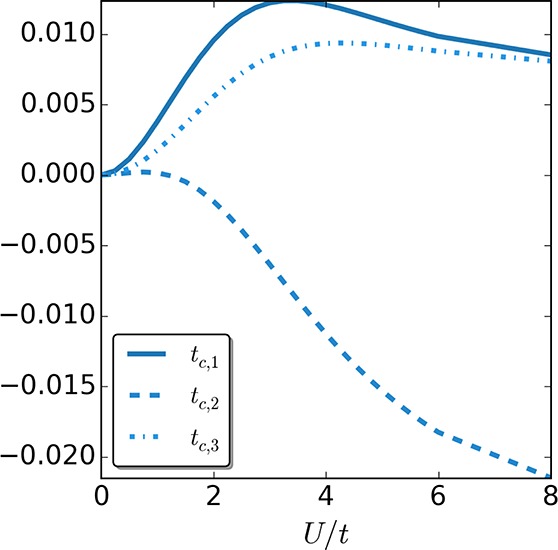
Correlation part of the hopping t_c,i in units of t, for the four-site case as a function of interaction strength U/t.

6. Comparing a Self-Consistent KS and keKS Calculation

While the above considerations about the exact correlation energies, potentials, and hopping parameters are crucial to understand what the different approximations to the unknown exchange-correlation terms are able to capture, it is not their performance at the exact solutions that matters in practice. A self-consistent calculation with the approximate functionals is not at all clear that will converge to a sensible solution or even converge at all. For instance, even for the prime example of a nonlinear problem in quantum chemistry, that is, the ground-state Hartree–Fock equation, the convergence to a unique solution has not been shown except for highly unusual cases.⁶⁵ To finally test whether the proposed keDFT and its keKS construction can be used in practice to predict the properties of correlated many-electron systems, we perform self-consistent calculations for our two-site and four-site Hubbard models. We use the mean-field exchange approximation of eq 29 for two sites and of eqs 69–71 for four sites together with the uniform approximation for the hopping term of eq 33. This leads to

34

where we update the involved effective fields in every iteration until convergence is achieved. We then compare the densities and kinetic-energy densities that we get with the KS ones within the exact-exchange approximation (thus t_i = t and v^Hx given by eq 26 for two sites and eqs 60–62 for four sites). We do so as in this way we have for both the KS and the keKS construction the same level of approximation as v^Mx will reduce to v^Hx for t_i^ke = t. This allows us to judge whether including the kinetic-energy density in the modeling of many-particle systems has any advantages over the usual density-only approach.

We first quantify the density difference between the calculated quantities and the exact ones using the following measure: δn^ke/KS = ∑_i=1^M|n_i – n_i|, where n_i is the interacting density at site i while n_i^ke/KS is the corresponding density of the keKS/KS system.

Indeed, for both the two-site case (see Figure 8) as well as the more challenging four-site case (see Figure 9), the self-consistent keKS approximation performs better than the corresponding self-consistent KS exact-exchange approximation. Because the main difference lies in the error correction to the local kinetic-energy density, we next also compare a measure for the difference in local kinetic-energy density: δT^ke/KS = ∑_i=1^M–1|T_i – T_i|, where T_i^ke/KS is the kinetic-energy density between site i and i+1, while T_i is the corresponding interacting one. Not surprisingly, in both cases (see Figures 10 and 11), the approximate kinetic-energy density of the keKS system is much closer to the actual one than the bare KS energy density. We see that for large interaction strengths the error is basically zero for the two-site case because in this limit the interaction is much larger than the asymmetry induced by the local potential. In the four-site case, our approximation for the kinetic-energy density is not as accurate, although it is still better than the corresponding KS one. The reason for this drop in accuracy is, as discussed around eq 33, the assumption that γ_i,i+1 = γ_i,i+1^unif,ke, which is violated for the four-site case. Nevertheless, for large systems (where the boundaries will not be significant) or for systems with periodic boundary conditions, this issue will essentially vanish because then the uniform reference system obeys γ_i,i+1 = γ_i,i+1^unif,ke and the strong-interaction limit is captured highly accurately. Consequently, it can be expected that including the kinetic-energy density can help to treat multiparticle systems accurately from the weak to strong interaction regime.

Figure 8.

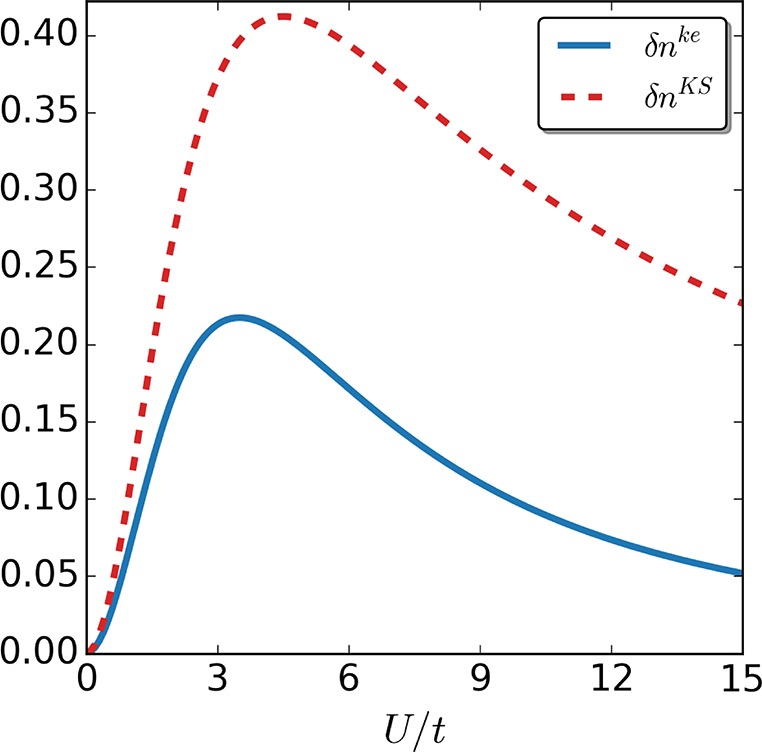
Density difference δn^ke/KS between the self-consistent calculations in the keKS system and the exact one (continuous, blue line), as well as for the self-consistent solution in the KS system and the exact one (dotted, red line), for the two-site case as a function of interaction strength U/t.

Figure 9.

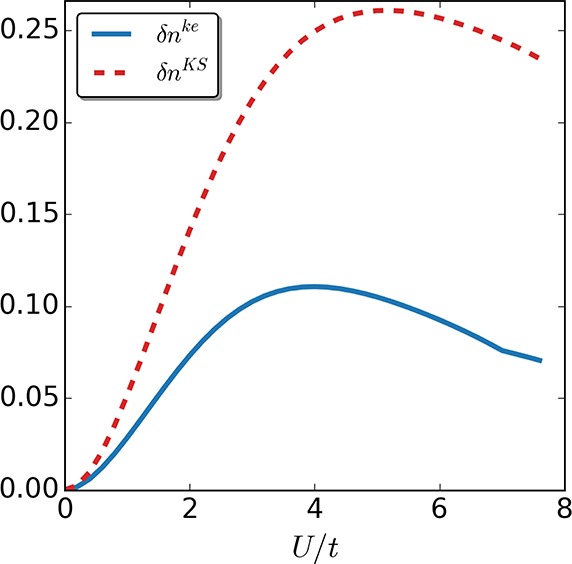
Density difference δn^ke/KS between the self-consistent calculations in the keKS system and the exact one (continuous, blue line), as well as for the self-consistent solution in the KS system and the exact one (dotted, red line), for the four-site case as a function of interaction strength U/t.

Figure 10.

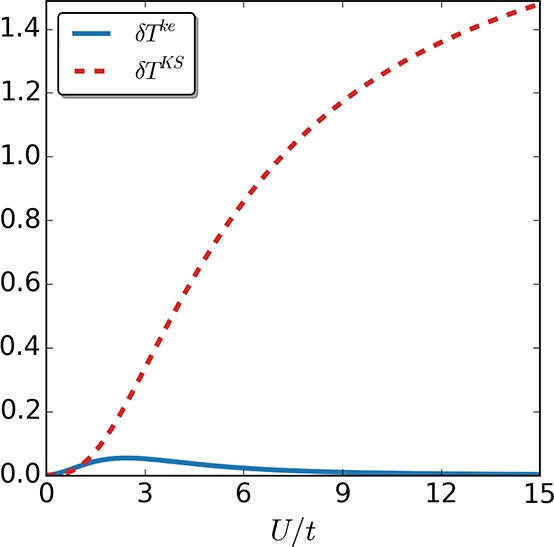
Kinetic-energy density difference δT^ke/KS between the self-consistent calculations in the keKS system and the exact one (continuous line), as well as for the self-consistent solution in the KS system and the exact one (dotted line), for the two-site case as a function of interaction strength U/t.

Figure 11.

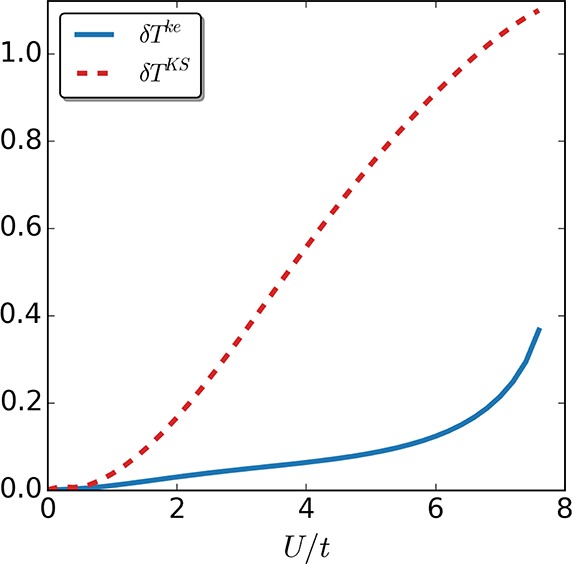
Kinetic-energy density difference δT^ke/KS between the self-consistent calculations in the keKS system and the exact one (continuous line), as well as for the self-consistent solution in the KS system and the exact one (dotted line), for the four-site case as a function of interaction strength U/t.

7. Conclusion and Outlook

In this work, we have introduced a kinetic-energy density-functional theory (keDFT) and the resulting kinetic-energy Kohn–Sham (keKS) scheme on a lattice. The idea was that by lifting the kinetic-energy density T to a fundamental variable along with the density n, the resulting effective theory becomes easier to approximate because more parts are known explicitly. Because the new external field, a site-dependent hopping t, is part of the kinetic-energy density, the usual Hohenberg–Kohn-type proof strategy to establish the necessary one-to-one correspondence between (v,t) and (n,T), where v is the usual on-site potential, does not work. However, besides giving proofs for specific cases and discussing the gauge freedom of the approach, we provided an indication that the necessary bijectivity holds by numerically constructing the inverse maps from a given pair (n,T) to (v,t) for two- to four-site Hubbard models. We did so by introducing an iterative scheme based on the equations of motion (EOMs) of the density and the kinetic-energy density. We then introduced a decomposition of the two unknown effective fields of the keKS scheme, the mean-field-exchange-correlation potential v_i^Mxc[n,T] and the mean-field exchange-correlation hopping t^Mxc[n,T], into explicitly known mean-field exchange (for the effective potential) and uniform (for the effective hopping) as well as unknown correlation parts. By comparing the unknown parts of the standard Kohn–Sham (KS) approach to the keKS approach, we saw that including the kinetic-energy density in the fundamental variables reduced the unknown parts considerably. Finally, we tested the keKS approach in practice by solving the resulting nonlinear equations with the introduced approximations. We found that the mean-field exchange and uniform keKS outperform the corresponding exact-exchange KS from weak to strong interactions and hence hold promise to become an alternative approach to treat many-particle systems efficiently and accurately.

While the presented approach was thoroughly investigated only for simple few-sites problems, its extension to many sides, arbitrary dimensions, and even the continuum is straightforward. Following ref (50) in the continuum, we can choose a gauge-independent and strictly positive definition of the kinetic-energy density with a spatially dependent mass term. The main reason why the keKS scheme can be more accurate than the usual KS scheme also in the continuum is that we can model explicitly the kinetic-energy density in this case. Because the simple kinetic-energy density approximations we introduced proved to be already quite reasonable, the extension to the continuum seems especially promising. For homogeneous systems, many reference calculations exist that can be used to derive a universal local kinetic-energy density approximation that resembles the uniform approximation introduced in this work.

Appendix A: Two-Sites Proof of (Δv^ke,t^ke) ↔ (Δn,T)

In this Appendix, we provide a proof of the bijectiveness of the mapping between density and kinetic-energy density and the corresponding fields in the case of a noninteracting system of up to N ≤ 3 electrons on a two-site lattice. For this case, the noninteracting Hamiltonian reads:

35

where 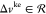and t^ke > 0. The mapping that we wish to show that is bijective is the following:

36

with T > 0 and Δn∈[–N,N]. Here, Δv^ke ≡ v₁^ke – v₂ and Δn ≡ n₁ – n₂, where the lower indexes refer to different site points. Note that t^ke ≥ 0 is a certain gauge choice as {(t^ke,Δv^ke),(−t^ke,Δv^ke)} → (T,Δn). Moreover, due to particle hole symmetry, it holds also that {(−t^ke,−Δv^ke),(t^ke,−Δv^ke)} → (T,Δn). Thus, from now on, when we refer to different potentials and hopping parameters, we will mean that they differ by more than a sign change. For the local potential, the gauge choice is v₁^ke + v₂ = 0 as throughout the document.

Proof: We are going to prove eq 36 through different cases.

Case 1: Two Hamiltonians Ĥ, Ĥ′ have the same hopping parameters t^ke = t^ke′ but different local potentials Δv^ke ≠ Δv^ke′.

From the Hohenberg–Kohn theorem, we then have that the corresponding wave functions are different, that is, Φ ≠ Φ′, and the same holds also for the densities Δn ≠ Δn′ and consequently (T,Δn) ≠ (T′,Δn′).

Case 2: Two Hamiltonians Ĥ, Ĥ′ have different hopping parameters t^ke ≠ t^ke′ but the same local potentials Δv^ke ≠ Δv^ke′.

Assume that (T,Δn) = (T,Δn′). We then have two wave functions Φ and Φ′ that are ground states of the corresponding Hamiltonians:

37

We can multiply Ĥ′ with a scaling factor 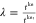so that we get a Hamiltonian Ĥ″, which has the same hopping as the Ĥ.

38

We assume that Δn = Δn′, which means that we have two different ground-state wave functions with different local potentials 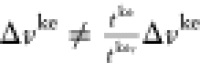that still give the same densities. This is clearly in contradiction with Case 1.

Case 3: Two Hamiltonians Ĥ, Ĥ′ have different hopping parameters t^ke ≠ t^ke′ and different local potentials Δv^ke ≠ Δv^ke′.

Again, we assume that (T,Δn) = (T′,Δn′), and we scale such that we find:

39

This requires that Δn = Δn′ can only hold if also the local potentials are the same as we showed in Case 1. Thus, it has to hold that

40

which means that the two Hamiltonians Ĥ and Ĥ′ are connected through the scaling relation Ĥ = λĤ′. Thus, we have

41

which contradicts our initial assumption.

Appendix B: Equations of Motion

In this Appendix, we derive the EOMs that we use in our numerical inversion scheme and to define the v^Hxc and v^Mxc potentials. Furthermore, we provide the explicit expressions of v^Hxc and v^Mxc for four sites. Finally, we discuss how the number of useful EOMs for our numerical inversion scheme depends on the number of sites.

The EOM for a generic operator A, which has no explicit time dependence, is given by

42

We are interested in obtaining EOM for a non interacting Hamiltonian of type 11. For a state Φ it follows that

43

which is an EOM for the observable associated with the operator Â. When Ψ is the ground state, eq 43 equals zero. Let us take now this operator to be the density. Because the first-order EOM for the density, that is, the continuity eq 9, is trivially satisfied as the current is just zero in the ground state, we consider the second time derivative of the density:

44

where we have introduced the forward (backward) difference operators (), which act on one-index objects: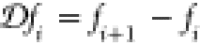, 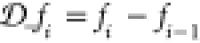. Here we note that in this Appendix we stray from the convention that we only use t_i^ke and v_i because we use the same EOMs for the KS and the keKS scheme as well. In eq 44, we furthermore introduced

45

which, by analogy to the continuum case, can be identified as the kinetic contribution to the momentum-stress tensor. The time derivative of the kinetic energy density also leads to

46

where we introduced the kinetic-energy current

47

Both Ξ_i and J_i vanish trivially for real-valued wave functions such as the ground state, so eq 46 is fulfilled trivially. Taking yet another time derivative leads to

48

In eq 48, there are two more EOMs involved. The one for Ξ_i is

49

with

50

The EOM for the current is

51

Moreover, we use the second-order EOM for the interacting density, obtained from a Hamiltonian of Case 2, to define the v^Hxc and v^Mxc potentials:

52

As an example, let us show here the EOM for n̈₁ for the two-site interacting Hamiltonian:

53

Formally, eq 44 defines M equations, that is, one for every site. However, because the sum of densities at every site has to give the total number of electrons, it holds that

54

We get M – 1 nontrivial equations. Now for M sites we do have M – 1 different T_i of the form eq 48. Yet as the total energy of the keKS system is fixed to some value E, that is:

55

taking the second time derivative of the above equation shows us that we have M – 2 nontrivial equations for T_i. Taking into account the gauge choice of v_i^s (eq 2) and the particle number conservation eq 54, we see that the equations for n̈_i and T̈_i connect through the following relation:

56

At this point, we have to mention that eq 54 still holds for the interacting system; however, eqs 55 and 56 will not hold anymore because the on-site repulsion term enters the energy expression in this case.

Appendix C: Exchange-Correlation Potentials for Four Sites

From the EOMs 44 and 52, one can derive the v^Hxc and v^Mxc for any number of sites. We give here their expressions for four sites because it is one of our test cases in this Article.

57

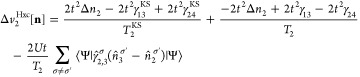58

59

Similarly to the two-site case, we can decompose v^Hxc to a v^Hx and a v^c contribution:

60

61

62

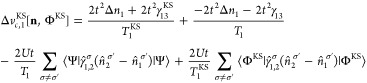63

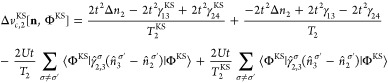64

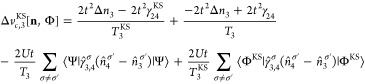65

Next, we give the corresponding expressions for the keKS system:

66

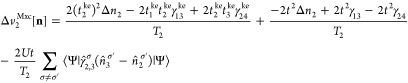67

68

Similarly to v^Hxc, we decompose v^Mxc in a v^Mx and a correlation part v^c. This is analogous to the decomposition for the two-site case presented in section 5:

69

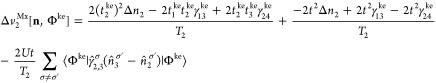70

71

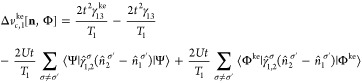72

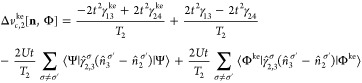73

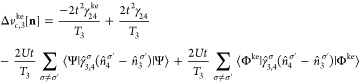74

Appendix D: Gauge Choice for Hopping

In this Appendix, we demonstrate that the sign of the hopping is just a gauge choice. Let us consider a single-particle Hamiltonian H. In the site basis, it corresponds to the matrix:

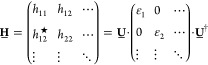75

where we also introduced its spectral decomposition with the unitary matrix U̲ having its eigenvectors as columns. Suppose we transform the Hamiltonian by

76

where 1̲_n is the n × n unit matrix and N is the total number of sites. Note that G̲^† = G̲^–1; that is, G̲ is unitary. It is straightforward to verify that the transformed Hamiltonian is given by

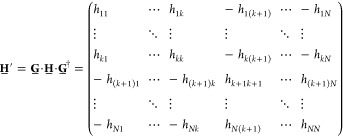77

We can see that the effect of the transformation is to change the sign of all matrix elements in the “off-diagonal” parts determined by the site k after which the sign in G̲ changes. For a one-dimensional nearest-neighbor tight-binding Hamiltonian with “zero boundary conditions”, like the one we consider in this Article, this corresponds to flipping the sign of the hopping amplitude between site k and k + 1. Obviously the eigenvalues of H̲′ are the same as the eigenvalues of H̲, and the eigenstates are simply given by U̲′ = G̲U̲, which means that the signs of the wave function in position representation are flipped from site k + 1 on. All Hamiltonians, which can be connected by such a transformation, are to be considered equivalent.

Financial support from the European Research Council (ERC-2015-AdG-694097), by the European Unions H2020 program under GA no. 676580 (NOMAD), is acknowledged. F.G.E. has received funding from the European Unions Framework Programme for Research and Innovation Horizon 2020 (2014–2020) under the Marie Skłodowska-Curie Grant agreement no. 701796.

The authors declare no competing financial interest.