Abstract
We investigate the performance of a class of compact and systematically improvable Jastrow–Slater wave functions for the efficient and accurate computation of structural properties, where the determinantal component is expanded with a perturbatively selected configuration interaction scheme (CIPSI). We concurrently optimize the molecular ground-state geometry and full wave function—Jastrow factor, orbitals, and configuration interaction coefficients—in variational Monte Carlo (VMC) for the prototypical case of 1,3-trans-butadiene, a small yet theoretically challenging π-conjugated system. We find that the CIPSI selection outperforms the conventional scheme of correlating orbitals within active spaces chosen by chemical intuition: it gives significantly better variational and diffusion Monte Carlo energies for all but the smallest expansions, and much smoother convergence of the geometry with the number of determinants. In particular, the optimal bond lengths and bond-length alternation of butadiene are converged to better than 1 mÅ with just a few thousand determinants, to values very close to the corresponding CCSD(T) results. The combination of CIPSI expansion and VMC optimization represents an affordable tool for the determination of accurate ground-state geometries in quantum Monte Carlo.
1. Introduction
Quantum Monte Carlo methods are a class of ab initio approaches which solve the interacting Schrödinger equation stochastically. The most widely used variants of QMC are the variational (VMC) and diffusion Monte Carlo (DMC). Thanks to their favorable scaling with the number of particles and the ease of parallelization, they have often been employed to benchmark electronic properties, in particular, total energies of relatively large molecules as well as solids. Recently, it has been shown1,2 that it is possible to compute derivatives of the energy at the same computational cost per Monte Carlo step as evaluating the energy itself, also when employing large determinantal expansions in the commonly used Jastrow–Slater QMC wave functions. Consequently, one can compute all derivatives necessary for the optimization of the structure of a system very efficiently and, simultaneously, of the variational parameters in the wave function, as was demonstrated on the structural optimization of short polyenes with expansions comprising over 200 000 determinants.2 These developments also allow us to thoroughly explore the sensitivity of QMC calculations to the choice of the Slater expansion, namely, the set of orbitals which one must correlate and the truncation of the active space. It was shown that an instructed guess of the orbitals based on chemical intuition can lead to significant variations in VMC energies and structures of a molecule as small as butadiene even when employing large expansions in the presence of a Jastrow correlation factor.2
To overcome the limitations of an a priori approach in the choice of the orbital set and achieve a compact description of the determinantal component in QMC, a promising alternative is to employ a selected CI algorithm such as the CIPSI (configuration interaction using a perturbative selection done iteratively) method. CIPSI was originally introduced by Huron et al. in 19733 and continually tested,4−10 improved,10−13 and assessed in comparison to full-CI (FCI) expansions10,14,15 in combination with a variety of orbital descriptions.16 In the past few years, there has been renewed interest in the development of selected CI approaches17−22 to accurately calculate the ground- and excited-state energies of small molecules, establishing the competence of these approaches for benchmarking applications. The use of these expansions has however only been marginally explored within the QMC framework,23−28 where it was shown to yield very good DMC energies at the price of employing large CIPSI wave functions. Good selection in multideterminantal expansions is also likely to improve the accuracy and efficiency in the phaseless auxiliary-field Monte Carlo method.29
Here, we complement the perturbatively selected CIPSI determinants with a Jastrow factor and VMC optimization of the full wave function (Jastrow parameters, orbitals and CI coefficients), and investigate the ability of the resultant Jastrow–CIPSI wave functions to obtain accurate molecular geometries in VMC, as well as corresponding VMC and DMC energies, with relatively compact expansions. We focus on the butadiene molecule, where an accurate estimation of the bond length alternation (BLA) is theoretically quite challenging, demanding a proper description of correlation effects, both static and dynamic. As mentioned above, significant variations in energies and structural parameters were observed in VMC when correlating different sets of σ and π orbitals in a fully optimized Jastrow-Slater wave function:2 with a large expansion comprising over 45 000 determinants in a restricted active space, good agreement with coupled cluster with singles, doubles, and perturbative triples in the complete basis set limit (CCSD(T)/CBS) was obtained in the bond lengths. This number of determinants is however surprisingly large for the description of the ground state of such a small system. Indeed, we find here that a determinantal description with CIPSI yields a much smoother convergence in the structural parameters and QMC energies when the size of the expansion is systematically incremented. Correspondingly, very accurate values for these physical properties are already obtained with only a few thousand determinants.
To construct the CIPSI component of the QMC trial wave functions, we follow two different schemes: one where we systematically “expand” the wave function by adding important determinants at every step, and the other where we first generate an extremely large wave function and subsequently “truncate” it to obtain requisite sizes. For a fixed size of the CI expansion, the “truncation” scheme is expected to be more accurate than the “expansion” one since the overlap of the wave function with the FCI wave function is larger. The difference can be important in systems where the CI coefficients change dramatically with the number of determinants in the wave function,30 but generation of the large wave function to initiate “truncation” might not be entirely feasible for larger systems where the “expansion” scheme would therefore represent a computationally less expensive route. For small systems such as butadiene, however, we can employ both strategies and, consequently, draw an assessment of their relative performance. Here, we find that the truncation scheme provides a faster and smoother convergence of the bond lengths of butadiene, while the convergence of the VMC energies is comparable for both schemes. We note that we are looking at extremely small variations in the structural parameters (well below mÅ) when comparing and establishing the convergence. Finally, while we primarily employ multiconfigurational self-consistent field (MCSCF) canonical orbitals in the CIPSI algorithm and as starting orbitals in QMC, we additionally test the use of natural orbitals. Rather peculiarly, expansions with natural orbitals commensurate in size with those with canonical orbitals consistently converge to slightly higher VMC energies.
The paper is organized as follows. In section 2, we describe the CIPSI algorithm and the functional form of the Jastrow-Slater wave functions and, in section 3, we report the computational details. The numerical results obtained for the structural optimization of butadiene and a comparison with our previous Jastrow–CAS results2 are given in section 4.
2. Methods
CIPSI is an iterative CI selection algorithm that allows us to perturbatively select determinants from the FCI space. Starting with an initial reference wave function, additional determinants are added to the expansion based on their effective second-order energy contribution which is required to be greater than a fixed or an iteratively modifiable threshold. Selection iterations can be performed until a target number of determinants is reached or until some other selection criterion is met.31 In the process, the quality of the wave function is systematically improved and converges toward the FCI solution.
A step-by-step description of the CIPSI algorithm is provided in refs (23, 25, 26, and 32) The scheme is briefly reiterated here. The reference wave function is composed of a linear combination of Slater determinants, Di , spanning a space, S:
| 1 |
Typically, this reference wave function
is
initially the single determinant with the lowest energy, which is
also the case here. At every iteration, the many-body Hamiltonian,  , is diagonalized in the reference space S to obtain
the variationally minimized energy Eref and the corresponding ci coefficients. Then, all the determinants Dj outside of this reference
space that are connected to S by
, is diagonalized in the reference space S to obtain
the variationally minimized energy Eref and the corresponding ci coefficients. Then, all the determinants Dj outside of this reference
space that are connected to S by  are generated, and their individual contributions
to the energy are estimated with the Epstein–Nesbet33,34 perturbation theory,
are generated, and their individual contributions
to the energy are estimated with the Epstein–Nesbet33,34 perturbation theory,
| 2 |
If |δEj(2)| is greater than a given threshold, determinant Dj is selected for the next iteration. Summing all these contributions gives EPT2, namely, the second-order perturbative energy correction to Eref, and the CIPSI energy of the current iteration is given by
| 3 |
Finally, all the selected determinants are added to the reference space S for the next iteration.
For the generation of different lengths of the CIPSI component of the QMC wave function, one could either follow (a) an “expansion” scheme where we repeat the above process as many times as necessary, thereby systematically increasing the size of the wave function, or (b) a “truncation” scheme after generating a very large CIPSI wave function, typically to a point where the CIPSI energy (eq 3) is reasonably converged. The large wave function created for the second scheme can contain millions of determinants and one needs to reorder them in decreasing order of the absolute value of their CI coefficients and then truncate the expansion, keeping their coefficients the same as in the large CIPSI wave function. This strategy is said to be a better starting point for VMC optimization as the determinant coefficients are from a near FCI calculation.26 We use complete active space SCF (CASSCF) orbitals for the majority of these calculations; however, (c) the use of natural orbitals obtained from a large CIPSI calculation is another aspect of our investigation.
In the expansion scheme, we choose to impose that the wave function is an eigenstate of the S2 operator. Therefore, after each selection, we apply all possible spin flips on the selected determinants keeping the number of α and β electrons unchanged. All spin-flipped determinants which are not already present in the set of selected determinants are added. This larger set of determinants spans the same space as all the configuration state functions to which the selected determinants belong. Consequently, when the Hamiltonian is diagonalized in this larger basis of determinants, the eigenfunctions are also eigenfunctions of S2. Note that, in the truncation scheme, the truncation is made in the determinant space, so the truncated wave functions are not eigenfunctions of S2. Hence, the comparison of the two schemes is not exactly one to one.
After generating the CIPSI expansion,
we introduce a positive Jastrow
correlation factor  and
construct the Jastrow–CIPSI
wave function as
and
construct the Jastrow–CIPSI
wave function as
| 4 |
where 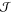 explicitly
describes electron–electron
and electron–nucleus (two-body,
explicitly
describes electron–electron
and electron–nucleus (two-body, 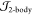 ) and electron–electron–nucleus
(three-body,
) and electron–electron–nucleus
(three-body, 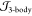 ) correlations35 while imposing the electron–electron
cusp conditions. Ndet represents the number
of determinants in
the CIPSI wave function spanning the space S.
) correlations35 while imposing the electron–electron
cusp conditions. Ndet represents the number
of determinants in
the CIPSI wave function spanning the space S.
3. Computational Details
The QMC calculations are carried out with the program package CHAMP.36 We employ scalar-relativistic energy-consistent Hartree–Fock pseudopotentials and the cc-pVTZ Gaussian basis set specifically constructed for our pseudopotentials.37,38 In particular, we perform all calculations with the cc-pVTZ basis set and test the convergence of the results with the cc-pVQZ basis set. To generate the Slater component of the QMC wave functions, CIPSI calculations are performed in Quantum Package39 using canonical orbitals obtained from a CAS(10,10) MCSCF calculation for the ground state of butadiene carried out with the program GAMESS(US).40,41
All parameters (Jastrow, orbital, and CI coefficients) are variationally optimized in VMC using the stochastic reconfiguration method42 in a conjugate gradient implementation.43 Most calculations are performed with a two-body Jastrow factor and the impact of the electron–electron–nucleus terms on the energy is tested for a few cases. Exploiting the low-numerical-scaling computation of energy and wave function derivatives,2 the ground-state geometry of butadiene is simultaneously optimized with the wave function following the path of steepest descent and an appropriate rescaling of the interatomic forces. To avoid spikes in forces, an improved estimator of the interatomic forces is used in all calculations, which is obtained by sampling the square of a modified wave function close to nodes.44 In the DMC calculations, we treat the pseudopotentials using the so-called T-move scheme45 and employ an imaginary time step of 0.015 au. As shown in the Supporting Information (SI), this time step yields DMC energies converged to better than 0.1 mHartree for a simple Jastrow–CIPSI wave function with only two determinants and is therefore appropriate for all wave functions of higher quality considered in this work.
We employ Gaussian0946 to perform CCSD(T) geometry optimization in combination with our pseudopotentials and in all-electron calculations in the frozen core (FC) approximation with the cc-pVXZ (X = D, T, Q, and 5) and aug-cc-pVXZ (X = D, T, and Q) basis sets. For CCSD(T) geometry optimization without the FC approximation, we use the PSI4 code47 with the cc-pCVXZ, cc-pwCVXZ, and corresponding augmented (X = D, T, and Q) basis sets. The results of these optimizations and their extrapolations to the CBS limit are detailed in the SI.
4. Results and Discussion
We investigate the merits of the choice of a CIPSI expansion to describe the Slater component of a QMC wave function when optimizing the ground-state geometry of butadiene over the conventional CAS description. We start all structural optimizations with the Jastrow–CIPSI wave functions from the same initial MP2/cc-pVQZ optimized geometry and, as described above, variationally optimize the Jastrow parameters, CI coefficients, and orbitals simultaneously with the geometry in VMC. Post convergence of the VMC energy and stabilization of the bond lengths, we perform 40 additional iterations and average these geometries. A final VMC and DMC energy calculation is done on this average geometry with the wave function obtained in the last iteration. As detailed in the SI, reoptimizing the wave function on the average geometry leads to equivalent energies within the statistical error.
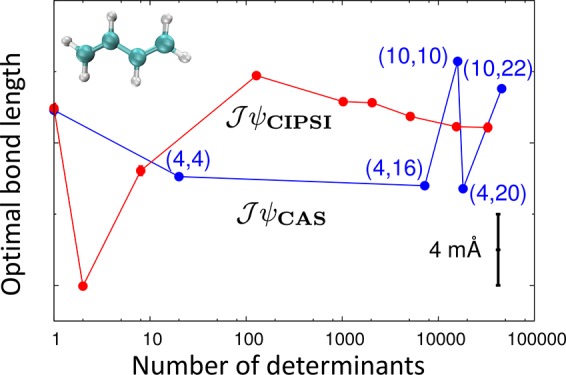
We primarily focus our discussion on the use of the “truncation” scheme for the CIPSI-determinant selection since, unlike the expansion scheme, no added selection criterion has been used. An initial CIPSI wave function is constructed including as many as 1.17 million determinants and then truncated to generate a set of determinantal expansions of increasing size. The results are summarized in Table 1 and illustrated in Figures 1 and 2, where the final VMC and DMC energies, and corresponding structural parameters are plotted against the size of the CIPSI expansions. We also compare our results with previous QMC calculations2 of the structural optimization of butadiene, which employed various CAS expansions: a CAS(4,4), CAS(4,16), and CAS(4,20) correlating four π electrons in the orbitals constructed from the 2pz, 3pz, 3dxz, 3dyz, and 4pz atomic orbitals; a CAS(10,10) consisting of 6 σ and 4 π electrons in 10 bonding and antibonding orbitals; a truncated RAS(10,22) that includes single and double excitations in additional 12 π and δ orbitals over the CAS(10,10) space. Since the cc-pVTZ and cc-pVQZ basis sets yield VMC and DMC energies compatible to better than 2 and 0.2 mHartee, respectively, and structural parameters differing by less than 0.4 mÅ (see SI), we can directly compare our cc-pVTZ calculations with the results obtained with the optimization of Jastrow–CAS wave functions in the cc-pVQZ basis.
Table 1. Optimal Ground-State Structural Parameters of Butadiene and Corresponding VMC and DMC Energies (au) with Increasing Number of CIPSI Determinants Obtained in the Truncation Schemea.
| bonds
(Å) |
energies
(au) |
|||||
|---|---|---|---|---|---|---|
| no. det | no. param | C—C | C=C | BLA | VMC | DMC |
| 1 | 749 | 1.45595(28) | 1.32415(11) | 0.13180(30) | –26.24310(32) | –26.30426(28) |
| 2 | 782 | 1.44596(20) | 1.33025(14) | 0.11571(29) | –26.24912(32) | –26.30681(14) |
| 8 | 822 | 1.45244(28) | 1.33245(15) | 0.11999(50) | –26.25644(31) | –26.31044(26) |
| 128 | 1594 | 1.45778(12) | 1.33564(20) | 0.12214(20) | –26.26562(30) | –26.31223(24) |
| 1024 | 5514 | 1.45632(22) | 1.33493(08) | 0.12139(25) | –26.28829(26) | –26.31908(20) |
| 2048 | 7726 | 1.45626(15) | 1.33456(09) | 0.12170(17) | –26.29386(25) | –26.32147(16) |
| 5114 | 12147 | 1.45549(08) | 1.33434(11) | 0.12115(07) | –26.29980(24) | –26.32424(09) |
| 15469 | 24818 | 1.45491(06) | 1.33406(08) | 0.12085(10) | –26.30880(22) | –26.32873(22) |
| 32768 | 44265 | 1.45487(25) | 1.33414(21) | 0.12072(37) | –26.31194(12) | –26.32928(20) |
The total number of optimized parameters in the wave function is listed. The statistical error is given in parentheses.
Figure 1.
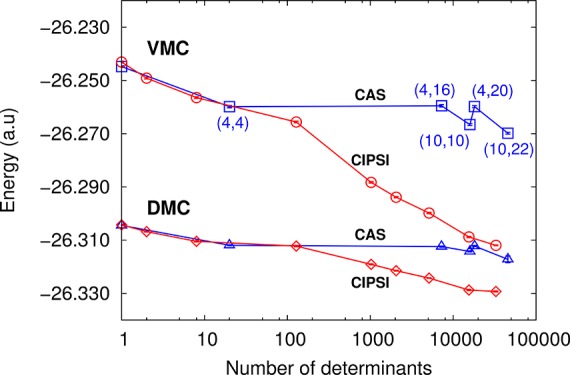
Convergence of the VMC and DMC energies on the optimal geometry with the number of determinants in the CIPSI expansion (red). Previous results2 obtained with Jastrow–CAS wave functions are also presented (blue).
Figure 2.
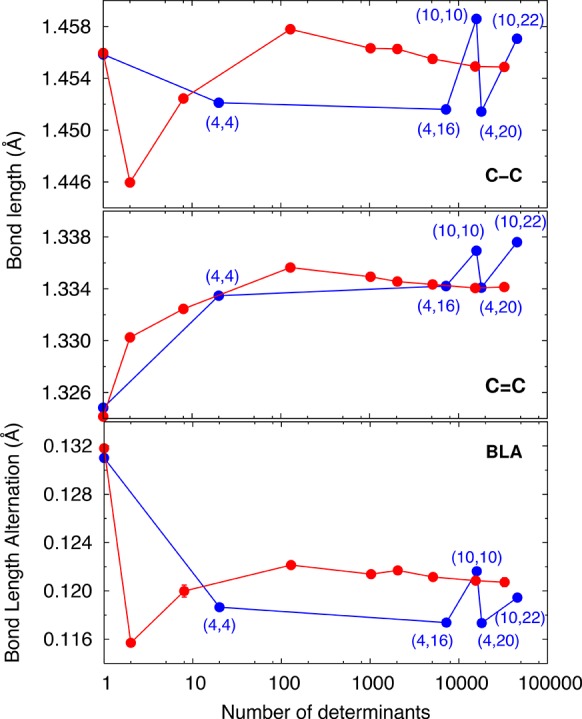
Convergence of the single bond (C–C), double bond (C=C), and bond length alternation (BLA) (Å) with the number of determinants in the CIPSI wave function (red). Previous results2 obtained with a Jastrow–CAS wave function are presented in blue.
As shown in Figure 1, a CIPSI wave function with roughly 100 determinants yields a VMC energy which is only about 1 and 4 mHartree higher than the energies of the CAS(10,10) and RAS(10,22) expansions consisting of 15 912 and 45 644 Slater determinants, respectively. Unlike the Jastrow–CAS case, where the energies are scattered around a relatively flat value, CIPSI expansions of increasing size yield a monotonic decrease in the VMC energy, with our largest considered expansion of 32 768 determinants amounting to an energy which is about 40 mHartree lower than the best RAS(10,22) value. In fact, the VMC energy obtained with our largest CIPSI expansion is within 5 mHartree of the seemingly converged DMC energy obtained with the Jastrow–CAS wave functions. Therefore, a smart selection of determinants from the approximate FCI space helps us attain much lower VMC energies in comparison to CAS expansions over conventionally used active-space definitions, which instead lead to the inclusion of many determinants with little contribution to the energy.
The behavior of DMC parallels the VMC results with the energy of the Jastrow–CAS wave functions being lowered by about 8 mHartree when the size of the wave function is increased from 1 to 20 determinants, and stagnating afterward as shown in Figure 1. The Jastrow–CIPSI wave function yields a DMC energy which is comparable with the Jastrow–CAS case when the CIPSI expansion has only about 100 determinants, while the largest CIPSI expansion gives a DMC energy 12 mHartree lower than the truncated RAS(10,22) case. We also note that the estimate of the FCI limit in the current basis set on the initial geometry is about −26.275 hartree (see SI) and, therefore, as much as 37 and 54 mHartree higher than our best VMC and DMC energies. Our best DMC energies are also superior to the CCSD(T) optimized values obtained with a quintuple-ζ basis set (see SI).
Importantly, the use of CIPSI expansions (in combination with a Jastrow factor and the optimization of all wave function parameters) is not only beneficial in terms of the quality of the final total energies: the smooth and monotonic convergence of the VMC and DMC energies with the number of determinants demonstrates the effectiveness of such an approach in identifying energetically relevant determinants in a systematic manner. These important excitations are not easily accessible through manual selection as demonstrated by the energy plateau one reaches in constructing very large expansions based on an a priori choice of an apparently reasonable set of active orbitals. Besides being completely automated, this feature of the CIPSI scheme is also crucial for obtaining a smooth convergence of the structural properties (to better than 1 mÅ) with the number of determinants as discussed next.
In Figure 2, we illustrate the variation of the carbon–carbon single and double bonds and of the bond length alternation (BLA) obtained with the Jastrow–CIPSI expansions. The convergence of the bond lengths and BLA is smooth with the increase in the size of the wave function. While the double bond is already converged to better than 0.5 mÅ with little over 2000 determinants, the single bond and, consequently, the BLA show a somewhat slower convergence and reach the same level of accuracy with about 5114 determinants. We stress however that we are here looking at extremely small differences while establishing the degree of convergence. For all practical purposes, the BLA is already converged to better than 1 mÅ within the limits of statistical error with just over 1000 determinants, again proving the ability of CIPSI expansions to obtain optimal geometry descriptions with a very small set of determinants. Besides overcoming the non-uniform convergence of the structural parameters when expanding the wave function on different active spaces, these calculations also confirm the need for a rather subtle multireference description for such conjugated systems.48,49 The converged single bond length is in excellent agreement with the CCSD(T)/CBS value of 1.455 Å obtained with the same pseudopotentials used in the QMC calculations (see SI). Our double bond is instead less than 0.003 Å smaller than the corresponding CCSD(T)/CBS value, consequently resulting in a difference of about 0.002 Å on the BLA.
To investigate the impact of the inclusion of three-body terms in the Jastrow factor, we add them to the CIPSI wave functions with 2048 and 5114 determinants and reoptimize all wave function parameters on the fixed average geometries we have determined with the two-body Jastrow factor. These optimizations result in the VMC and DMC energies presented in Table 2. While there is an expected gain in the VMC energies, the DMC energies are equivalent within the statistical error of 0.2 mHartree to the energies obtained with a two-body Jastrow factor. Consequently, given the quality of our determinantal component, a two-body Jastrow recovers most of the missing dynamical correlation contribution and is sufficient for our purposes.
Table 2. Effect of the Inclusion of Three-Body
Jastrow Terms ( ) on the Total VMC and DMC Energies (au)a.
) on the Total VMC and DMC Energies (au)a.
| no. det | EVMC | EDMC | ΔEVMC | ΔEDMC |
|---|---|---|---|---|
| 2048 | –26.29908(15) | –26.32162(20) | –0.00522(29) | –0.00015(26) |
| 5114 | –26.30333(23) | –26.32412(16) | –0.00353(33) | 0.00012(18) |
ΔE denotes
the gain in energy with respect to the values obtained with a two-body
Jastrow factor ( ). The structures optimized with the two-body
Jastrow factor are used.
). The structures optimized with the two-body
Jastrow factor are used.
All results presented so far have been obtained by selecting the CIPSI determinants out of a much larger CIPSI wave function according to the “truncation” scheme. The VMC energies obtained with the “expansion” scheme where one constructs CIPSI expansions of increasing size are compared with the “truncation” scheme in Figure 3. Both schemes lead to very comparable convergence in the energy as a function of the number of determinants in the Jastrow–CIPSI wave function and to compatible converged structural parameters. However, as shown in the SI, the variation of the bond lengths and BLA is not as smooth as in the truncation case. This difference probably arises from the added requirement of having an eigenstate of S2 in the expansion scheme. In fact, if we follow the expansion scheme without this requirement and construct a wave function of 5114 determinants, we obtain an optimal VMC single and double bonds of 1.45564(26) and 1.33496(11) Å, respectively, and a BLA of 0.12068(26) Å. The VMC energy converges to −26.29960(24) au. These results are in good agreement with the corresponding values obtained with the truncation scheme.
Figure 3.
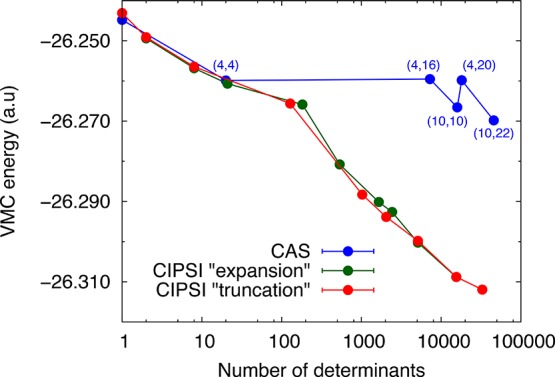
Optimal ground-state VMC energies obtained with Jastrow–CAS and Jastrow–CIPSI wave functions constructed with the “expansion” and “truncation” schemes.
Finally, we explore a potentially better orbital description in terms of natural orbitals obtained from a CIPSI calculation instead of the canonical orbitals resulting from a CAS(10,10) self-consistent calculation as done above. To this aim, we determine the natural orbitals for a very large CIPSI wave function of 2 million determinants and construct three expansions of roughly 2000, 5000, and 15 000 determinants with the truncation scheme. Surprisingly, we consistently obtain higher VMC energies compared to the expansions generated with canonical orbitals. The reason behind this observation is unclear. The bond lengths and BLA obtained with 5000 determinants are in excellent agreement with the corresponding values for the truncated canonical set of comparable size but the other test cases do not provide as compatible values. The results of these calculations are given in the SI.
5. Conclusion
We demonstrated the excellent performance of compact perturbatively selected CIPSI determinantal expansions in obtaining significantly lower VMC and DMC energies as compared to conventional active space definitions for the challenging case of butadiene. With the use of these wave functions, we were able to obtain converged ground-state structural parameters with the use of only a few thousand determinants. We tested two different schemes for the selection of the CIPSI expansions either by constructing a large CIPSI wave function and then truncating it (“truncation” scheme), or by considering successive sets of determinants in the CIPSI construction (“expansion” scheme). We found that the two representations are rather equivalent in terms of energy but that the truncation scheme possibly leads to a somewhat smoother convergence of the structural parameters with the size of the CIPSI expansion. CCSD(T) calculations with the same pseudopotentials yield a CBS estimate of the carbon–carbon single bond in very good agreement with our converged value but a double bond and corresponding BLA smaller by about 0.002 Å. We do not expect any significant change in the bond lengths upon inclusion of additional determinants, in view of their weak variations observed over a wide range of the number of determinants already considered.
Our study therefore shows that the automated selection of determinants from a CIPSI wave function is an extremely suitable and less cumbersome alternative for the fast optimization of ground-state geometries in QMC than a choice based on correlating electrons in active spaces constructed from energetically low-lying orbitals. The latter results in large expansions with many determinants which contribute little to the energy and to the convergence of the structural parameters. The use of CIPSI-based wave functions in combination with the low-scaling algorithms for simultaneous wave function and geometry optimization opens the way to the accurate and efficient QMC optimization of large molecular systems.
Acknowledgments
This work is part of the Industrial Partnership Programme (IPP) “Computational sciences for energy research” of The Netherlands Organisation for Scientific Research (NWO-I, formerly FOM). This research program is co-financed by Shell Global Solutions International B.V. This work was carried out on the Dutch national supercomputer Cartesius with the support of SURF Cooperative, and using HPC resources from CALMIP (Toulouse) under allocation 2017-0510.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00393.
CIPSI energies and FCI extrapolation; impact of reoptimizing the wave function on the average geometry; basis-set convergence of geometry and corresponding VMC and DMC energies; bond-length and BLA convergence obtained with the “expansion” scheme; energy and geometry convergence with the use of natural orbitals; DMC time-step extrapolation and CCSD(T) geometry optimizations with pseudopotential and all-electron basis sets (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Filippi C.; Assaraf R.; Moroni S. Simple formalism for efficient derivatives and multi-determinant expansions in quantum Monte Carlo. J. Chem. Phys. 2016, 144, 194105. 10.1063/1.4948778. [DOI] [PubMed] [Google Scholar]
- Assaraf R.; Moroni S.; Filippi C. Optimizing the Energy with Quantum Monte Carlo: A Lower Numerical Scaling for Jastrow–Slater Expansions. J. Chem. Theory Comput. 2017, 13, 5273–5281. 10.1021/acs.jctc.7b00648. [DOI] [PubMed] [Google Scholar]
- Huron B.; Malrieu J.; Rancurel P. Iterative perturbation calculations of ground and excited state energies from multiconfigurational zeroth-order wavefunctions. J. Chem. Phys. 1973, 58, 5745–5759. 10.1063/1.1679199. [DOI] [Google Scholar]
- Gouyet J.; Prat M. SPIN–CIPSI calculations on H2CO. J. Chem. Phys. 1976, 64, 946–955. 10.1063/1.432288. [DOI] [Google Scholar]
- Povill A.; Rubio J.; Illas F. Treating large intermediate spaces in the CIPSI method through a direct selected CI algorithm. Theor. Chim. Acta 1992, 82, 229–238. 10.1007/BF01113255. [DOI] [Google Scholar]
- Trinquier G.; Malrieu J. P. Silabutadienes and their silylene isomers. An ab initio study. J. Am. Chem. Soc. 1981, 103, 6313–6319. 10.1021/ja00411a008. [DOI] [Google Scholar]
- Castex M.; Morlais M.; Spiegelmann F.; Malrieu J. Comparison between experimentally and theoretically determined potential curves of the Ar2* lowest states. J. Chem. Phys. 1981, 75, 5006–5018. 10.1063/1.441890. [DOI] [Google Scholar]
- Pelissier M. Bonding between transition metal atoms. Ab initio effective potential calculations of Cu2. J. Chem. Phys. 1981, 75, 775–780. 10.1063/1.442119. [DOI] [Google Scholar]
- Nebot-Gil I.; Malrieu J.-P. CI calculations concerning the styrene cis-trans photoisomerization. Chem. Phys. Lett. 1981, 84, 571–574. 10.1016/0009-2614(81)80410-1. [DOI] [Google Scholar]
- Cimiraglia R.; Persico M. Recent advances in multireference second order perturbation CI: The CIPSI method revisited. J. Comput. Chem. 1987, 8, 39–47. 10.1002/jcc.540080105. [DOI] [Google Scholar]
- Evangelisti S.; Daudey J.-P.; Malrieu J.-P. Convergence of an improved CIPSI algorithm. Chem. Phys. 1983, 75, 91–102. 10.1016/0301-0104(83)85011-3. [DOI] [Google Scholar]
- Cimiraglia R. Second order perturbation correction to CI energies by use of diagrammatic techniques: An improvement to the CIPSI algorithm. J. Chem. Phys. 1985, 83, 1746–1749. 10.1063/1.449362. [DOI] [Google Scholar]
- Cimiraglia R.; Persico M.; Tomasi J. Ab initio study of the photodissociation of nitrosoalkanes and nitrosamines. J. Am. Chem. Soc. 1985, 107, 1617–1622. 10.1021/ja00292a026. [DOI] [Google Scholar]
- Illas F.; Rubio J.; Ricart J.; Bagus P. Selected versus complete configuration interaction expansions. J. Chem. Phys. 1991, 95, 1877–1883. 10.1063/1.461037. [DOI] [Google Scholar]
- Harrison R. J. Approximating full configuration interaction with selected configuration interaction and perturbation theory. J. Chem. Phys. 1991, 94, 5021–5031. 10.1063/1.460537. [DOI] [Google Scholar]
- Illas F.; Rubio J.; Ricart J. Approximate natural orbitals and the convergence of a second order multireference many-body perturbation theory (CIPSI) algorithm. J. Chem. Phys. 1988, 89, 6376–6384. 10.1063/1.455405. [DOI] [Google Scholar]
- Ohtsuka Y.; Hasegawa J. Selected configuration interaction method using sampled first-order corrections to wave functions. J. Chem. Phys. 2017, 147, 034102. 10.1063/1.4993214. [DOI] [PubMed] [Google Scholar]
- Schriber J. B.; Evangelista F. A. Adaptive configuration interaction for computing challenging electronic excited states with tunable accuracy. J. Chem. Theory Comput. 2017, 13, 5354–5366. 10.1021/acs.jctc.7b00725. [DOI] [PubMed] [Google Scholar]
- Schriber J. B.; Evangelista F. A. Communication: An adaptive configuration interaction approach for strongly correlated electrons with tunable accuracy. J. Chem. Phys. 2016, 144, 161106. 10.1063/1.4948308. [DOI] [PubMed] [Google Scholar]
- Holmes A. A.; Tubman N. M.; Umrigar C. J. Heat-bath configuration interaction: An efficient selected configuration interaction algorithm inspired by heat-bath sampling. J. Chem. Theory Comput. 2016, 12, 3674–3680. 10.1021/acs.jctc.6b00407. [DOI] [PubMed] [Google Scholar]
- Sharma S.; Holmes A. A.; Jeanmairet G.; Alavi A.; Umrigar C. J. Semistochastic Heat-bath Configuration Interaction method: selected configuration interaction with semistochastic perturbation theory. J. Chem. Theory Comput. 2017, 13, 1595–1604. 10.1021/acs.jctc.6b01028. [DOI] [PubMed] [Google Scholar]
- Chien A. D.; Holmes A. A.; Otten M.; Umrigar C. J.; Sharma S.; Zimmerman P. M. Excited States of Methylene, Polyenes, and Ozone from Heat-Bath Configuration Interaction. J. Phys. Chem. A 2018, 122, 2714–2722. 10.1021/acs.jpca.8b01554. [DOI] [PubMed] [Google Scholar]
- Giner E.; Scemama A.; Caffarel M. Using perturbatively selected configuration interaction in quantum Monte Carlo calculations. Can. J. Chem. 2013, 91, 879–885. 10.1139/cjc-2013-0017. [DOI] [Google Scholar]
- Scemama A.; Applencourt T.; Giner E.; Caffarel M. Accurate nonrelativistic ground-state energies of 3 d transition metal atoms. J. Chem. Phys. 2014, 141, 244110. 10.1063/1.4903985. [DOI] [PubMed] [Google Scholar]
- Giner E.; Scemama A.; Caffarel M. Fixed-node diffusion Monte Carlo potential energy curve of the fluorine molecule F2 using selected configuration interaction trial wavefunctions. J. Chem. Phys. 2015, 142, 044115. 10.1063/1.4905528. [DOI] [PubMed] [Google Scholar]
- Giner E.; Assaraf R.; Toulouse J. Quantum Monte Carlo with reoptimised perturbatively selected configuration-interaction wave functions. Mol. Phys. 2016, 114, 910–920. 10.1080/00268976.2016.1149630. [DOI] [Google Scholar]
- Caffarel M.; Applencourt T.; Giner E.; Scemama A. Communication: Toward an improved control of the fixed-node error in quantum Monte Carlo: The case of the water molecule. J. Chem. Phys. 2016, 144, 151103. 10.1063/1.4947093. [DOI] [PubMed] [Google Scholar]
- Scemama A.; Garniron Y.; Caffarel M.; Loos P.-F. Deterministic construction of nodal surfaces within quantum Monte Carlo: the case of FeS. J. Chem. Theory Comput. 2018, 14, 1395–1402. 10.1021/acs.jctc.7b01250. [DOI] [PubMed] [Google Scholar]
- Motta M.; Zhang S. Computation of ground-state properties in molecular systems: back-propagation with auxiliary-field quantum Monte Carlo. J. Chem. Theory Comput. 2017, 13, 5367–5378. 10.1021/acs.jctc.7b00730. [DOI] [PubMed] [Google Scholar]
- Caffarel M.; Giner E.; Scemama A.; Ramírez-Solís A. Spin Density Distribution in Open-Shell Transition Metal Systems: A Comparative Post-Hartree–Fock, Density Functional Theory, and Quantum Monte Carlo Study of the CuCl2 Molecule. J. Chem. Theory Comput. 2014, 10, 5286–5296. 10.1021/ct5004252. [DOI] [PubMed] [Google Scholar]
- Angeli C.; Persico M. Multireference perturbation CI II. Selection of the zero-order space. Theor. Chem. Acc. 1997, 98, 117–128. 10.1007/s002140050285. [DOI] [Google Scholar]
- Caffarel M.; Applencourt T.; Giner E.; Scemama A. Recent Progress in Quantum Monte Carlo. ACS Symp. Ser. 2016, 1234, 15–46. 10.1021/bk-2016-1234.ch002. [DOI] [Google Scholar]
- Epstein P. S. The stark effect from the point of view of Schroedinger’s quantum theory. Phys. Rev. 1926, 28, 695. 10.1103/PhysRev.28.695. [DOI] [Google Scholar]
- Nesbet R. K. Configuration interaction in orbital theories. Proc. R. Soc. London, Ser. A 1955, 230, 312–321. 10.1098/rspa.1955.0134. [DOI] [Google Scholar]
- Filippi C.; Umrigar C. J. Multiconfiguration wave functions for quantum Monte Carlo calculations of first-row diatomic molecules. J. Chem. Phys. 1996, 105, 213–226. 10.1063/1.471865. [DOI] [Google Scholar]; As Jastrow correlation factor, we use the exponential of the sum of three-fifths-order polynomials of the electron–nuclear (e-n), the electron–electron (e-e), and of pure three-body mixed e-e and e-n distances, respectively. The e-n and e-e-n terms have different coefficients for different atom types. The Jastrow factor is further adapted to deal with pseudoatoms, and the scaling factor κ is set to 0.60 au. The three-body e-e-n terms are not included in the two-body Jastrow factor.
- Umrigar C. J.; Filippi C.; Moroni S.. CHAMP: Cornell-Holland Ab-initio Materials Package, 2018.
- Burkatzki M.; Filippi C.; Dolg M. Energy-consistent pseudopotentials for quantum Monte Carlo calculations. J. Chem. Phys. 2007, 126, 234105. 10.1063/1.2741534. [DOI] [PubMed] [Google Scholar]
- For the hydrogen atom, we use a more accurate BFD pseudopotential and basis set.; Dolg M., Filippi C., private communication. [Google Scholar]
- Scemama A.; Applencourt T.; Garniron Y.; Giner E.; David G.; Caffarel M.. Quantum Package v1.0, 2016; https://github.com/LCPQ/quantum_package.
- Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Nguyen K. A.; Su S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
- Gordon M. S.; Schmidt M. W.. Theory and applications of computational chemistry; Elsevier, 2005; pp 1167–1189. [Google Scholar]
- Sorella S.; Casula M.; Rocca D. Weak binding between two aromatic rings: Feeling the van der Waals attraction by quantum Monte Carlo methods. J. Chem. Phys. 2007, 127, 014105. 10.1063/1.2746035. [DOI] [PubMed] [Google Scholar]
- Neuscamman E.; Umrigar C. J.; Chan G. K.-L. Optimizing large parameter sets in variational quantum Monte Carlo. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 045103. 10.1103/PhysRevB.85.045103. [DOI] [Google Scholar]
- Attaccalite C.; Sorella S. Stable liquid hydrogen at high pressure by a novel ab initio molecular-dynamics calculation. Phys. Rev. Lett. 2008, 100, 114501. 10.1103/PhysRevLett.100.114501. [DOI] [PubMed] [Google Scholar]
- Casula M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 161102. 10.1103/PhysRevB.74.161102. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian09, Revision A.02; Gaussian, Inc., Wallingford, CT. 2016. [Google Scholar]
- Parrish R. M.; Burns L. A.; Smith D. G.; Simmonett A. C.; DePrince A. E. III; Hohenstein E. G.; Bozkaya U.; Sokolov A. Y.; Di Remigio R.; Richard R. M.; et al. Psi4 1.1: An open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. 10.1021/acs.jctc.7b00174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenti L.; Giner E.; Malrieu J.-P.; Angeli C. Strongly localized approaches for delocalized systems. I. Ground state of linear polyenes. Comput. Theor. Chem. 2017, 1116, 102–111. 10.1016/j.comptc.2017.01.021. [DOI] [Google Scholar]
- Smith J. E. T.; Mussard B.; Holmes A. A.; Sharma S. Cheap and Near Exact CASSCF with Large Active Spaces. J. Chem. Theory Comput. 2017, 13, 5468–5478. 10.1021/acs.jctc.7b00900. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


