Estimation of an IRT Model by Mplus for Dichotomously Scored Responses Under Different Estimation Methods

Abstract

The purpose of this article is twofold. The first is to provide evaluative information on the recovery of model parameters and their standard errors for the two-parameter item response theory (IRT) model using different estimation methods by Mplus. The second is to provide easily accessible information for practitioners, instructors, and students about the relationships between IRT and item factor analysis (FA) parameterizations. Specifically, this is done using the “Theta” and “Delta” parameterizations in Mplus for unidimensional and multidimensional modeling with dichotomous and polytomous responses with and without the scaling constant D. The first objective aims at investigating differences that may occur when using different estimation methods in Mplus for binary response modeling. The second objective was motivated by practical interest observed among graduate students and applied researchers. The relations between IRT and Mplus FA “Theta” and “Delta” parameterizations are described using expressions without the use of matrices, which can be understood efficiently by applied researchers and students.

Mplus (L. K. Muthén & Muthén, 1998-2012) is a widely used program in structural equation modeling (SEM) research. Mplus software has flexible modeling capacity and can implement factor analysis, mixture modeling, and complex SEM for categorical and continuous variable data that have multilevel structure, to name a few (e.g., B. Muthén & Asparouhov, 2006; Nylund, Asparouhov, & Muthén, 2007). Mplus is also equipped with a variety of model estimation methods, such as maximum likelihood–based estimation, least square–based estimation, and Bayesian Markov chain Monte Carlo (MCMC).

From the factor analysis and Mplus users’ point of view, popular item response theory (IRT) models, such as one-parameter and two-parameter IRT models, are the measurement modeling part of SEM and are special cases of factor analysis with categorical ordinal data; thus, those who are mainly the users of Mplus for factor analysis with categorical ordinal data might wonder the degree of performance of those IRT model estimation by Mplus. In addition, because Mplus provides several different estimation options, users may be curious about the comparative performance of different estimation options embedded in Mplus for the estimation of IRT models. The same curiosity regarding the performance of SEM software for IRT model estimation may also exist among the IRT software users and researchers. Thus, this study aims at generating practical information regarding the unidimensional IRT model implementation by the Mplus IRT model estimation for dichotomously scored data. The IRT model under investigation in this study is the unidimensional two-parameter logistic model. To characterize psychometric behaviors of item responses, the two-parameter model has slope (discrimination) and location (difficulty) parameters in the item response function (IRF), which relates the latent trait (measured construct) to the probability of a correct (or yes) response (see also Lord & Novick, 1968, for the detailed development of the two-parameter model). When a cognitive test consists of short answer items or when a psychological test has items with two options (e.g., agree or disagree; yes or no), the two-parameter model can be a useful tool for test construction, scaling, and scoring (e.g., Yen & Fitzpatrick, 2006 for applications of the two-parameter and other IRT models).

There have been many studies on factor analysis model estimation for categorical data. Such studies typically focused on the investigation of different estimation methods. Previous studies that used both limited and full information estimation approaches with relatively rigorous simulations (i.e., 100 or more replications for simulations) include Boulet (1996), Gosz and Walker (2002), Reiser and VanderBerg (1994), and Forero and Maydeu-Olivares (2009). The work by Forero and Maydeu-Olivares was more systematic and comprehensive than the other works in their simulation. Forero and Maydeu-Olivares conducted simulations with over 324 conditions (1,000 replications per condition) where unidimensional and multidimensional models were simulated with dichotomous and polytomous item response data, in addition to accommodating other variations such as sample sizes and test lengths. However, previous studies have not investigated all available estimation methods in Mplus for the estimation of IRT models. For instance, Forero and Maydeu-Olivares (2009) restricted their choices to two estimation methods: marginal maximum likelihood (MML) estimation (full information approach) and unweighted least squares (limited information approach). Asparouhov and Muthén (2016) and L. K. Muthén and Muthén (2013) listed variations of weighted least squares (including the unweighted least squares) as legitimate choices in the Mplus IRT model estimation. In this study, we considered all estimation methods currently available in Mplus. Specifically, this study included three types of least square estimations (two weighted least squares and one unweighted least squares methods) in the limited information estimation approach and the full information maximum likelihood estimations with different standard error estimation methods for the two-parameter IRT model estimation. Providing more detailed results about the Mplus undimensioanl IRT estimation using different estimation approaches can help practitioners with their applications of an IRT model in Mplus, specifically regarding the choice of an estimation method. The current study investigated two aspects of the two-parameter model calibration with different estimation methods in Mplus: (1) recovery of the structural parameters (item slope or discrimination and difficulty parameters) and (2) the standard errors of the structural parameters. The next section describes details of the estimation methods used in the study.

Another objective is to provide a clear and easily accessible summary of the closed form relations between the IRT and the item factor analysis (FA) parameterizations under the “Theta” and the “Delta” parameterization used in Mplus for the normal ogive and logistic IRT IRFs, with and without the scaling constant of $D$ = 1.7 in unidimensional and multidimensional modeling for dichotomous and polytomous data. The relations between FA and IRT parameterizations have been explored in previous studies (e.g., Asparouhov & Muthén, 2016; Bolt, 2005; Forero & Maydeu-Olivares, 2009; Kamata & Bauer, 2008; L. K. Muthén & Muthén, 2013; Raykov & Marcoulides, 2011; Takane & de Leeuw, 1987). However, the presentation here can still benefit applied researchers and graduate students who want to understand the relation between IRT FA in Mplus for three reasons. First, the level of mathematical abstraction used in those cited articles above may be challenging for some applied researchers and graduate students who are beginning to learn IRT and FA. Describing the relations between IRT and FA in a more readable fashion for unidimensional and multidimensional modeling can enhance the accessibility for a wider range of consumers of FA and IRT in education and psychology. Second, although trivial for those who are familiar with both logistic and normal ogive IRT modeling, the relation of FA with the logistic IRT modeling with the use of a scaling factor D (=1.7) is not always clearly delivered in previous works, which tends to be part of confusion experienced by applied researchers and graduate students in understanding the relation of FA and the logistic IRT model with or without D. Third, the provision of clearly understandable expressions of the relations between FA and IRT facilitates the interpretation of parameter estimates for either FA or IRT users. For example, a researcher who is mainly a user of FA but not familiar with IRT can convert the IRT slope parameters into more familiar FA parameterization, such as FA loadings and make sense of the magnitudes of IRT slope parameters.

Two-Parameter IRT Model in Mplus

In Mplus, categorical ordered item responses are modeled using the graded response model (GRM; Samejima, 1970). Suppose that item response k is scored $0,1,2,\dots ,K_i$, where the subscript $i$ represents the ith item ($i=1,2,\dots ,I$). In GRM, a cumulative response function is used to describe the probability of the response $k$ or higher. The cumulative response function in GRM is

$$P_{\mathrm{nik}}^{*}=f(\sum _{j=1}^M{a}_{\mathrm{ij}}{\mathrm{\theta }}_{\mathrm{nj}}-d_{\mathrm{ik}}),$$

where $P_{\mathrm{nik}}^{*}$ is the probability of the response k or higher for the nth person $(n=1,2,\dots ,N)$ with the ith item, ${\theta }_{\mathrm{nj}}$ is the nth person’s trait or ability parameter for the jth dimension $(j=1,2,\dots ,M)$, $a_{\mathrm{ij}}$ is the ith item slope parameter for the jth dimension, $d_{\mathrm{ik}}$ is the ith item category boundary location parameter, and $f^{-1}(·)$ is a link function. When $f^{-1}(·)$ is a logit link function, Equation 1 is the multidimensional logistic GRM. If a probit link function is chosen for $f^{-1}(·)$, Equation 1 becomes the multidimensional normal ogive GRM. Note that Mplus uses the negative sign for the $d_{\mathrm{ik}}$ parameter. The option response function when $0<k<K_i$ is obtained by

$$P_{\mathrm{nik}}=P_{\mathrm{nik}}^{*}-P_{\mathrm{ni}(k+1)}^{*},$$

where $P_{\mathrm{nik}}$ is the probability of response k. By the definition of the cumulative response function, $P_{\mathrm{nik}}^{*}=1$ when $k$ = 0, and $P_{\mathrm{ni}(k+1)}^{*}=0$ when $k=K_i$. Thus, $P_{\mathrm{nik}}=1-P_{\mathrm{ni}(k+1)}^{*}$ when $k$ = 0, and $P_{\mathrm{nik}}=P_{\mathrm{nik}}^{*}$ when $k=K_i$.

When item responses are dichotomous, the option response function or the cumulative response function above is reduced to the probability of a correct (or “yes”) answer, which is the IRF for the two-parameter IRT model. The unidimensional IRF for the dichotomous item response in Mplus is

$$P_{\mathrm{ni}}=f(a_i{\mathrm{\theta }}_n-d_i),$$

where $d_i$ is typically referred to as the ith item intercept parameter. A more conventional unidimensional two-parameter IRT IRF takes the form of

$$P_{\mathrm{ni}}=f\left[a_i({\mathrm{\theta }}_n-b_i)\right],$$

where $b_i=d_i/a_i$ is the ith item difficulty. Mplus estimates the parameters in the IRF of Equation (1) in general. In the case of the unidimensional modeling, Equation (3) is used for parameter estimation and the estimates of the model parameters are converted into the estimates of the parameters in Equation (4). The delta method (e.g., Casella & Berger, 2002) is used for the standard error estimation of item difficulty in Equation (4). Note that the delta method is a general statistical method to obtain a variance and does not refer to the “Delta” parameterization in Mplus. When the link function is the normal ogive, the model is called the two-parameter normal ogive IRT (2PN for short) or probit model. If the logistic link is used, it is called the two-parameter logistic IRT (2PL for short) or logistic model. Though not frequently used recently, a logistic link with scaling constant D = 1.7 has been used to approximate the 2PN. The logistic model with D in this case is

$$P_{\mathrm{ni}}=f\left[D{a}_i({\mathrm{\theta }}_n-b_i)\right],$$

where $D=1.7$ and $f^{-1}[·]$ is the logit link. The direct estimation of the model in Equation 5 is not available in Mplus.

Mplus IRT modeling may be classified by the estimation approach (full information vs. limited information), the link function (logit or probit), and the types of parameterization called “Theta” or “Delta” (see Asparouhov & Muthén, 2016; L. K. Muthén & Muthén, 2013, for the details of these parameterizations). Table 1 summarizes choices for the two-parameter IRT model estimation.

Table 1.

Item Response Theory Model Estimation Options in Mplus.

	Full information estimation
	Logit	Probit
ML	×	×
MLR	×	×
MLF	×	×
	Limited information estimation
	Logit	Probit
		“Theta” parameterization	“Delta” parameterization
WLS	NA	×	×
WLSM	NA	×	×
WLSMV	NA	×	×
ULSMV	NA	×	×

Note. ML = maximum likelihood; MLR = maximum likelihood with robust standard errors; MLF = maximum likelihood with standard error approximation using the first-order derivative; WLS = weighted least squares; WLSM = weighted least squares with mean-adjusted chi-square test; WLSMV = weighted least squares with mean- and variance-adjusted chi-square test; ULSMV = unweighted least squares with mean- and variance-adjusted chi-square test; NA = not applicable. “×” indicates that the estimation option is available.

Asparouhov and Muthén (2016) and L. K. Muthén and Muthén (2013) list three estimation options for the full information estimation and four options for the limited information estimation approach when using Mplus for the IRT model estimation. Full information estimation options are ML (maximum likelihood with conventional standard errors), MLR (maximum likelihood with robust standard errors, estimated by what is known as sandwich estimator), and MLF (maximum likelihood with standard error approximation using the first-order derivative). The four limited information estimation options are WLS (weighted least squares with conventional standard errors), WLSM (weighted least squares with mean-adjusted chi-square test for goodness of fit testing), WLSMV (weighted least squares with mean- and variance-adjusted chi-square test for goodness of testing), and ULS (unweighted least squares).

The full information estimation approach uses information contained in all item response patterns. Its objective function (which is a function optimized to obtain parameter estimates) is based on the strong principle of local independence (see McDonald, 1999, for strong and weak principles of local independence). The objective function is the MML function,

$$L_{\mathrm{MML}}=\int \underset{n}{\Pi }\underset{i}{\Pi }{P}_{\mathrm{ni}}\mathrm{dF}\left(\mathrm{\theta }\right),$$

where $\underset{n}{\Pi }\underset{i}{\Pi }{P}_{\mathrm{ni}}$ is the product of the IRF across items and person, and $F\left(\mathrm{\theta }\right)$ is the distribution function for $\mathrm{\theta }$. Model parameter are those estimates that maximize the MML function (see Bock & Aitkin, 1981; Baker & Kim, 2004 for the MML estimation. Point estimates for item parameters are the same across ML, MLR, and MLF methods. There are differences when calculating item parameters’ standard errors across the three options. One can choose either a probit or logit link when using the full information estimation approach in Mplus. The full information estimation approach does not involve “Theta” or “Delta” parameterization (this only becomes relevant when a limited information approach is used).

In the limited information estimation approach, the threshold for each item and the polychoric correlations between items are calculated. Note that the threshold is calculated based on the first order marginal or the univariate information, and the polychoric correlation is calculated using the second-order marginal or the bivariate information from data. Model parameters are obtained such that the difference between the sample-based first- and second-order statistics (sample threshold and polychoric correlation) and the model-based reproduced first- and second-order statistics (predicted threshold and polychoric correlation) is minimized. Simply speaking, the objective function is a weighted difference between observed and predicted first-order and second-order marginals. Differences among the four estimation options in the limited estimation approach are made via the choice of the weight based on the inverse of the covariance matrix of the threshold and polychoric correlations. WLS uses the full weight matrix, meaning the weight matrix does not have any element restrictions. Both WLSM and WLSMV use the same weight matrix, which is a diagonal matrix where all off-diagonal elements are zero. The weight matrix in ULS is the identity matrix that is the diagonal matrix where the diagonal elements are unity. Point estimates and their standard errors for item parameters are the same for both WLSM and WLSMV. ULS and WLS estimates and their standard errors are not necessarily the same as WLSM or WLSMV estimates due to differences in weight matrices.

In the limited information estimation approach, a continuous latent response variable is assumed to underlie observed categorical ordered responses for an item. The correlations of those latent continuous response variables for items are the polychoric correlations (or tetrachoric correlations when item responses are dichotomous). Furthermore, the relationship between a continuous latent response variable and the target construct (or dimension) is described as an additive linear form as in the traditional factor analysis that posits the linear relationship between the observed continuous variable and the target construct. Due to the introduction of those continuous latent response variables, extra constraints (compared to the traditional factor analysis for continuous variables) must be imposed to resolve the model identification. The “Theta” and the “Delta” parameterizations are connected to how to handle such constraints.

When using the limited information estimation approach, the “Theta” and the “Delta” parameterizations in Mplus are related to the constraint imposed on the residual (or unique) variance and the variance of a continuous latent response variable assumed to underlie the observed categorical ordered item responses, respectively. The “Theta” parameterization sets the residual variance equal to one. In the “Delta” parameterization, the variance of a latent continuous response variable is set to one. The appendix (Part I) provides a derivation of the normal ogive FA model and its relation with the IRT parameterization for a unidimensional dichotomous item response data. (Those readers mainly interested in the relations of the model parametrization between IRT and FA can skip Part I.). More important, Part II of the appendix provides a detailed summary of closed form expressions for the relations between IRT and “Theta” and “Delta” FA parameterizations for unidimensional, multidimensional, dichotomous, and polytomous item response modeling.

In this study, for full information estimation, ML-Logit, MLR-Logit, MLF-Logit, ML-Probit, MLR-Proit, and MLF-Probit were used because of their different standard error estimation procedures for a given link function. For the limited information estimation approach, WLS-Probit-Theta, WLSMV-Probit-Theta, and ULSMV-Probit-Theta were employed because WLSM and WLSMV are the identical estimators, and the “Theta” and “Delta” parameterizations produce the same results in terms of the IRT discrimination and difficulty parameter estimates. Also note that our study used ULSMV instead of ULS because the ULS option in Mplus does not permit the direct use of item response data, and ULSMV and ULS are the same estimator with the differences in the adjustment of the goodness of fit test statistic. Thus, among the 14 estimation options listed in Asparouhov and Muthén (2016) and L. K. Muthén and Muthén (2013), except for the MCMC estimation methods, there are essentially nine estimation options that may produce different results with regard to either point estimates or their standard errors (or both). The investigation of parameter recovery was always made in terms of the IRT parameterization of the item slope (or discrimination) and item difficulty (i.e., Equation 4). When estimating 2PN (probit) and 2PL (logit) models in Mplus, all the default options besides changing the estimation method were used.

Simulation Design

Item response data were generated following the standard IRT simulation technique: For the response of the ith item and the nth person, (1) calculate the IRF value (Equation 4 with the logit link and D = 1 or 1.7) with the assumed $\mathrm{\theta }$ and item parameter values, which are explained shortly; (2) draw a $u_{\mathrm{ni}}$ value, randomly from the standard uniform distribution; and (3) assign 1 (correct or yes response) if $u_{\mathrm{ni}}\le$ the IRF value and assign 0 (incorrect or no response) otherwise.

Test length and sample size varied in the data simulation: Test length of 11 (small), 22 (medium), and 44 (large), and sample sizes of 200 (small), 500 (medium), and 1,000 (large). These conditions were fully crossed, leading to nine data generation conditions. In each of the nine conditions, 4,000 replications were conducted. For a given replication, all nine estimation options (ML-Logit, MLR-Logit, MLF-Logit, ML-Probit, MLR-Proit, MLF-Probit, WLS-Probit-Theta, WLSMV-Probit-Theta, and ULSMV-Theta) were used.

The data-generating parameter values were randomly drawn from a log-normal distribution for the item slope parameters and the standard normal distribution for the difficulty parameters, respectively, $(a_i~\mathrm{logNormal}(.3,{.3}^2))$ and $(b_i~N(0,1))$. Person trait parameters were also randomly drawn from the standard normal distribution $(\mathrm{\theta }~N(0,1))$. For each replication, $\mathrm{\theta }$s were drawn at random anew while $a_i$ and $b_i$ were fixed once selected. Table 2 presents the summary statistics of the data-generating parameter values.

Table 2.

Summary of Data-Generating Parameter Values.

	Slope (a)
	Minimum	Median	M	Maximum	SD
11-item test	0.82	1.43	1.40	2.14	0.42
22-item test	0.77	1.35	1.33	2.01	0.31
44-item test	0.78	1.42	1.43	2.33	0.38
	Difficulty (b)
	Minimum	Median	M	Maximum	SD
11-item test	−1.52	−0.12	−0.04	1.67	1.02
22-item test	−1.93	0.18	−0.01	1.87	1.05
44-item test	−2.05	0.00	−0.04	1.98	0.87

For the item parameter recovery and standard error comparisons, bias, root mean squared error (RMSE), and mean absolute difference (MAD) were computed. For a given parameter,

$$\mathrm{Bias}=\left(\frac{1}{R}\right)\sum _{r=1}^R{\hat{\mathrm{\phi }}}_r-\mathrm{\phi },$$

$$\mathrm{RMSE}=\sqrt{\sum _{r=1}^R{({\hat{\mathrm{\phi }}}_r-\mathrm{\phi })}^2/R},\mathrm{and}$$

$$\mathrm{MAD}=\sum _{r=1}^R|{\hat{\mathrm{\phi }}}_r-\mathrm{\phi }|/R,$$

where $\mathrm{\phi }$ is the parameter of interest and $r$ is the replication number index ($r=1,2,\dots ,R$). In the item parameter recovery investigation, each of the data-generating parameters is $\mathrm{\phi }$. For the standard error investigation, the standard deviation (SD) of the $\hat{\mathrm{\phi }}$ values over all replications was used for $\mathrm{\phi }$ when calculating bias, RMSE and MAD. These indices were averaged across all items to compute summary indices for a given condition. The average of bias tended to be close to zero and both RMSE and MAD behaved similarly, preserving the same rank order of their values. As a result, averages of MAD were reported in the result section. The summary of bias and RMSE values are also available on request from the authors. MAD has a direct straightforward interpretation of how far an estimate is from a true (data-generating) parameter on average in absolute value.

Results

Mplus was used to estimate the two-parameter model with default convergence criteria. (Example files of Mplus IRT run syntax and output content are available on request from the authors or by accessing the following link: https://www.dropbox.com/sh/5x3vubg0j0ifz3w/AACNSJjxn-if82y8D-PSnIyBa?dl=0). First, nonconvergence in the model estimation was examined. Mplus full information estimation approaches had no convergence issue in any conditions, but the Mplus limited information approaches showed convergence problems in some conditions in this study. WLSMV-Probit-Theta (probit model with “Theta” parameterization in the WLSMV estimation) had two nonconvergent conditions: nonconvergence rates of 0.05% (2 out of 4,000 replications when test length = 11 with N = 200) and 0.2% (8 out of 4,000 when test length = 22 with N = 200). ULSMV-Probit-Theta (probit model with “Theta” parameterization in the ULSMV estimation) had one condition that showed 0.025% nonconvergence rate (1 out of 4,000) for the test length = 11 and N = 200. WLS-Probit-Theta (probit model with “Theta” parameterization in the WLS estimation) had eight conditions showing the nonconvergence rates of 32% (test length = 11 with N = 200), 0.65% (test length = 11 with N = 500), 10.95% (test length = 22 with N = 500), 0.23% (test length=22 and N = 1,000), and 100% (test length = 22 with N = 200; test length = 44 with N = 200; test length = 44 with N = 500; and test length = 44 and N = 1,000). In general, WLS-Probit-Theta had a tendency to show non- (or did not run at all) when the number of parameters in the model relative to the sample size increased, in which case Mplus sent out a message of “nonpositive definite” weight matrix.

The nonconvergence cases described above were excluded in the summary. Because of the relatively large number of the simulation samples (4,000 per condition) in the study, those simulation conditions with even high nonconvergence rates still provided a large number of converged replications for analysis (except for those four conditions addressed above for WLS-Probit-Theta). In the highest nonconvergence cases that had 32% and 10.95% nonconvergence rates (test length = 11 with N = 200 and test length = 22 with N = 500 with WLS-Probit-Theta), the numbers of the remaining converged replications were 2,720 and 3,562. Thus, all the results including WLS-Probit-Theta were summarized and compared. Again, WLS-Probit-Theta was not compared with other estimation methods in the four conditions showing 100% nonconvergence (test length = 22 with N = 200; test length = 44 with N = 200; test length = 44 with N = 500; and test length = 44 with N = 1,000).

Model Parameter Recovery

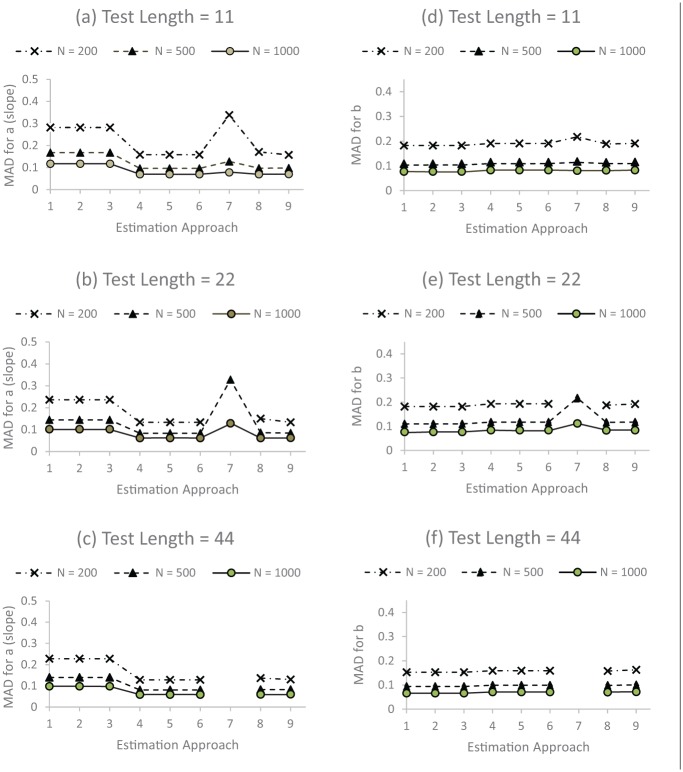
The recovery of item discrimination and difficulty parameters is presented in Figure 1.

Figure 1.

Recovery of item discrimination and difficulty parameters.

Note. MAD = mean absolute difference; ML = maximum likelihood; MLF = maximum likelihood with standard error approximation using the first-order derivative; MLR = maximum likelihood with robust standard errors; WLS = weighted least squares; WLSMV = weighted least squares with mean- and variance-adjusted chi-square test; ULSMV = unweighted least squares with mean- and variance-adjusted chi-square test. On the x-axis, 1 = ML-Logit, 2 = MLF-Logit, 3 = MLR-Logit, 4 = ML-Probit, 5 = MLF-Probit, 6 = MLR-Probit, 7 = WLS-Probit-Theta, 8 = WLSMV-Probit-Theta, and 9 = ULSMV-Probit-Theta.

On the x-axis in Figure 1, numbers indicate estimation approaches: 1 = ML-Logit, 2 = MLF-Logit, 3 = MLR-Logit, 4 = ML-Probit, 5 = MLF-Probit, 6 = MLR-Probit, 7 = WLS-Probit-Theta, 8 = WLSMV-Probit-Theta, and 9 = ULSMV-Probit-Theta. Numbers 1 through 3 represent the Mplus full information logit modeling and numbers 4 through 6 represent the Mplus full information probit modeling. The numbers 7 through 9 represent Mplus limited information probit modeling.

Again, ML-Logit, MLF-Logit, and MLR-Logit (1, 2, and 3 on the x-axis in Figure 1) produce the same point estimates in terms of item parameters, and therefore the same results. Also, ML-Probit, MLF-Probit, and MLR-Probit yield the same point estimates for item parameters (4, 5, and 6 on the x-axis in Figure 1), which lead to the same results.

Between the logistic and normal ogive (or probit) models for the full information estimation approaches in Mplus (1, 2, and 3 vs. 4, 5, and 6 on the x-axis in Figure 1), both produced almost the same results for the recovery of item difficulty, but the normal ogive (or probit) modeling (4, 5, and 6 on the x-axis in Figure 1) showed better recovery for the item slope parameters compared to the logistic modeling.

Between the full information probit modeling and the limited information probit modeling, except the WLS-Probit-Theta (4, 5, and 6 vs. 8 and 9 on the x-axis in Figure 1, without 7 which is the WLS-Probit-Theta), both exhibited similar recovery results. Of the three limited information probit modeling estimations, WLS-Probit-Theta was the worst, showing large nonconvergence rates compared to both WLSMV-Probit-Theta and ULSMV-Probit-Theta (which again showed very close performance to each other).

Standard Error Recovery

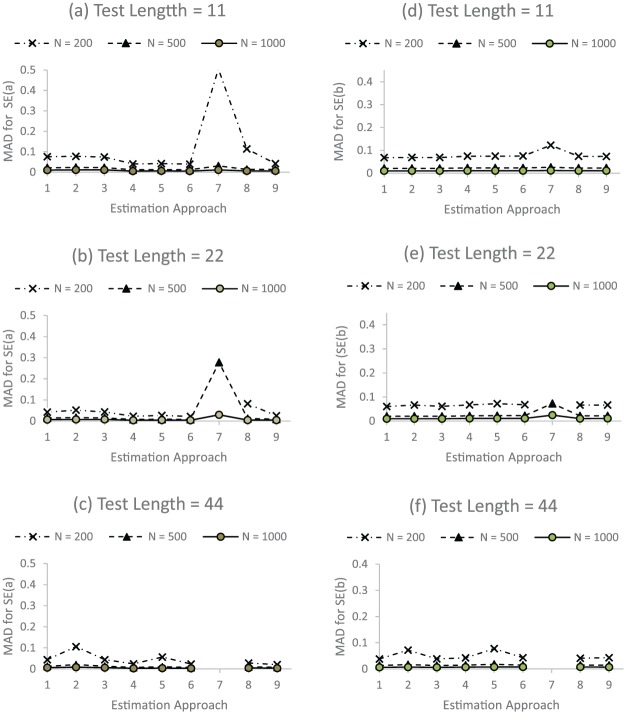
Figure 2 shows the recovery of SEs. The general patterns of the SE recovery across different estimation approaches resembled those of the item parameter recovery.

Figure 2.

Recovery of standard errors (SEs) of item discrimination and difficulty parameters.

Note. MAD = mean absolute difference; ML = maximum likelihood; MLF = maximum likelihood with standard error approximation using the first-order derivative; MLR = maximum likelihood with robust standard errors; WLS = weighted least squares; WLSMV = weighted least squares with mean- and variance-adjusted chi-square test; ULSMV = unweighted least squares with mean- and variance-adjusted chi-square test. On the x-axis, 1 = ML-Logit, 2 = MLF-Logit, 3 = MLR-Logit, 4 = ML-Probit, 5 = MLF-Probit, 6 = MLR-Probit, 7 = WLS-Probit-Theta, 8 = WLSMV-Probit-Theta, and 9 = ULSMV-Probit-Theta.

As in the item parameter recovery, WLS-Probit-Theta showed poor performance compared to other limited information approaches and the full information estimation approaches. The full and limited (except for WLS-Probit-Theta) information approaches showed comparable performance when N = 500 or 1,000.

Summary and Conclusion

The highly flexible nature of Mplus’ estimation approaches could raise a question of the comparability of the results from various estimation approaches of an IRT model. This study compared the performance of nine different estimation approaches in Mplus for the two-parameter IRT model in terms of item parameter and standard error estimation.

One limited information estimation approach, WLS-Probit-Theta often showed convergence problems across many simulation conditions. Unless the number of items is small with a large sample size (e.g., test length = 11 and N = 1,000 in this study), WLS-Probit-Theta showed either the poorest performance or serious nonconvergence problems. This seems to indicate difficulty in estimating the full weight matrix for the WLS approach. In terms of item discrimination parameter recovery, some noticeable differences were observed. The three full information probit and the two limited information probit modeling approaches outperformed other estimation approaches. Better performing methods in Mplus regarding the discrimination parameter recovery were ML-Probit, MLF-Probit, MLR-Probit, WLSMV-Probit-Theta, and ULSMV-Probit-Theta. Note again that the first three ML-Probit, MLF-Probit, and MLR-Probit produce the same point estimates for item parameters but different standard error estimates. WLSMV-Probit-Theta, and ULSMV-Probit-Theta yield different point estimates and standard errors. When the sample size was 500 or greater, all these five approaches in Mplus exhibited nearly the same results. When the sample size was small and the test length was not large (i.e., N = 200 and test length = 11 or 22 in this study), ULSMV-Probit-Theta (limited information approach) and the three full information approaches (ML-Probit, MLF-Probit, and MLR-Probit,) showed slightly better standard error recovery than WLSMV-Probit.

When the purpose of a latent variable modeling is to accurately estimate parameters and their standard errors for the 2-parmaeter IRT model via Mplus, our results show that, for a sample size of 500 or 1,000, one of the three full information probit modeling approaches (ML-Probit, MLF-Probit, or MLR-Probit) or one of the limited information probit modeling approaches (WLSMV-Probit-Theta or ULSMV-Probit-Theta) is preferred. However, if the sample size is small such as 200, and paired with a small or a moderate test length of 11 or 22, our findings show that ULSMV-Probit-Theta or one of the three limited information probit modeling is a better choice in terms of performance with regard to the standard error estimation of the discrimination parameters. Given that the WLSMV is a popular choice for ordinal item response data, the use of ULSMV-Probit-Theta or one of the three full information probit modeling approaches addressed above should be treated as a competitive choice or a better one when the sample size is small and test length is small in size. It is conjectured that using a larger sample than those used in this study (e.g., 5,000) would further decrease the differences between these estimation methods. Also, the performance of WLS-Probit-Theta may be expected to improve both when the number of items in a test is small (e.g., less than 10 items) and when samples are larger than those in this study, because of the provision of more data and the reduction of the burden in estimating the full weight matrix due to the decrease in the number of components in the weight matrix. All these conjectures leave room for future investigations, which may include different IRT models (e.g., Rasch model or GRM) and estimation methods (e.g., MCMC). Also, this study did not compare the Mplus IRT model estimation with more recently developed IRT programs such as flexMIRT (Cai, 2017) and SAS IRT Procedure (SAS Institute, 2015). This line of evaluative research could generate practical and helpful information for researchers and practitioners who use those programs.

As an additional didactic purpose, the appendix in this study also provides a clear presentation of the relations between IRT and the Theta/Delta FA parameterization in Mplus. The easily accessible closed form expressions in the appendix should help facilitate learning and understanding of IRT and the item factor analytic framework employed in the Mplus program for practitioners and graduate students in education and psychology.

Appendix

I. Normal Ogive Item Factor Analysis and IRT Parameterization for Unidimensional Dichotomous Response Data

For categorical ordered item response data, the limited information estimation approach assumes a (continuous) latent response variable for the observed categorical ordered response and a linear relationship between the latent response variable and the factors (or latent traits) as in the case of the traditional linear factor analysis with continuous observed variables. Part I of the appendix presents the relation between the item factor analytic model (FA) and IRT model parameterization for a unidimensional case. Those readers who want a more detailed treatment of the relations between FA and IRT are referred to, for example, Asparouhov and Muthén (2016), Bolt (2005), Forero and Maydeu-Olivares (2009), Kamata and Bauer (2008), L. K. Muthén and Muthén (2013), Raykov and Marcoulides (2011), and Takane and de Leeuw (1987).

For a dichotomously scored item response $u_i$ ($u_i=0\mathrm{or}1$), suppose a continuous latent variable $y_i^{*}$ and

$$u_i=0\mathrm{if}{y}_i^{*}<{\mathrm{\tau }}_i\mathrm{or}1\mathrm{if}{y}_i^{*}\ge {\mathrm{\tau }}_i.$$

There is some ${\mathrm{\tau }}_i$ (ith item threshold parameter) such that a response of 1 is observed when $y_i^{*}$ is equal to or greater than ${\mathrm{\tau }}_i$ and 0 is observed otherwise. Also assume

$$y_i^{*}=c_i+{\mathrm{\lambda }}_i\mathrm{\xi }+{\mathrm{ϵ}}_i,$$

where $c_i$ is the ith item intercept, ${\mathrm{\lambda }}_i$ is the ith item loading, $\mathrm{\xi }$ is a factor, and ${\mathrm{ϵ}}_i$ is the ith item residual. For the purpose of model identification, ${\mathrm{\tau }}_i$ is treated usually as free parameters but $c_i$ is fixed such that $c_i=0.$ Thus, the above equation is written usually as

$$y_i^{*}={\mathrm{\lambda }}_i\mathrm{\xi }+{\mathrm{ϵ}}_i.$$

Assume that the conditional distribution $y_i^{*}$ on $\mathrm{\xi }$ is normal with a constant variance, that is, $y_i^{*}|\mathrm{\xi }~N({\mathrm{\lambda }}_i\mathrm{\xi },{\mathrm{\psi }}_i^2)$, which implies $E({\mathrm{ϵ}}_i|\mathrm{\xi })=0$0 and $\mathrm{var}({\mathrm{ϵ}}_i|\mathrm{\xi })={\mathrm{\psi }}_i^2$. Imagine about a plot where the x-axis represents $\mathrm{\xi }$ and the y-axis is for $y_i^{*}$. ${\mathrm{\tau }}_i$ is a threshold (or cutoff) on the y-axis that decides the manifestation of a 0/1 response. Then, given $\mathrm{\xi }$, because of the assumption $y_i^{*}|\mathrm{\xi }~N({\mathrm{\lambda }}_i\mathrm{\xi },{\mathrm{\psi }}_i^2)$,

$$P(u_i=1|\mathrm{\xi })=\underset{{\mathrm{\tau }}_i}{\overset{\infty }{\int }}\frac{1}{\sqrt{2\mathrm{\pi }}{\mathrm{\psi }}_i}\exp [-\frac{1}{2}{\left(\frac{y_i^{*}-{\mathrm{\lambda }}_i\mathrm{\xi }}{{\mathrm{\psi }}_i}\right)}^2]{\mathrm{dy}}_i^{*}.$$

Let $y^{*}={\mathrm{\psi }}_{i}t+{\mathrm{\lambda }}_i\mathrm{\xi }\mathrm{and}{\mathrm{\tau }}_i<y^{*}<\infty$. $d{y}^{*}={\mathrm{\psi }}_i^{-1}\mathrm{dt}\mathrm{and}({\mathrm{\tau }}_i-{\mathrm{\lambda }}_i\mathrm{\xi })/{\mathrm{\psi }}_i<t<\infty$. Thus,

$$\begin{array}{cc}\multicolumn{1}{c}{P(u_i=1|\mathrm{\xi })}& =\underset{\frac{{\mathrm{\tau }}_i-{\mathrm{\lambda }}_i\mathrm{\xi }}{{\mathrm{\psi }}_i}}{\overset{\infty }{\int }}\frac{1}{\sqrt{2\mathrm{\pi }}}\exp [-\frac{t^2}{2}]\mathrm{dt}\hfill \\ \multicolumn{1}{c}{}& =\underset{-\infty }{\overset{\frac{{\mathrm{\lambda }}_i\mathrm{\xi }-{\mathrm{\tau }}_i}{{\mathrm{\psi }}_i}}{\int }}\frac{1}{\sqrt{2\mathrm{\pi }}}\exp [-\frac{t^2}{2}]\mathrm{dt}\hfill \\ \multicolumn{1}{c}{}& =\mathrm{\Phi }\left(\frac{{\mathrm{\lambda }}_i\mathrm{\xi }-{\mathrm{\tau }}_i}{{\mathrm{\psi }}_i}\right)=\mathrm{\Phi }(\frac{{\mathrm{\lambda }}_i}{{\mathrm{\psi }}_i}\mathrm{\xi }-\frac{{\mathrm{\tau }}_i}{{\mathrm{\psi }}_i})\hfill \\ \multicolumn{1}{c}{}& =\mathrm{\Phi }(a_i\mathrm{\theta }-d_i),\hfill \end{array}$$

where $a_i={\mathrm{\lambda }}_i/{\mathrm{\psi }}_i$ and $d_i={\mathrm{\tau }}_i/{\mathrm{\psi }}_i$, which shows the relation of IRT slope and intercept parameters with the FA parameters.

A typical FA parameterization assumes that the marginal variance, $\mathrm{var}\left(y_i^{*}\right)=1,$ which is the “Delta” parameterization, so that the residual variance ${\mathrm{\psi }}_i^2$ becomes a free parameter.

If we further assume the marginal variance, $\mathrm{var}\left(\mathrm{\xi }\right)=1$ in addition to $\mathrm{var}\left(y_i^{*}\right)=1$, then $\mathrm{var}\left({\mathrm{ϵ}}_i\right)={\mathrm{\psi }}_i^2=1-{\mathrm{\lambda }}_i^2$ under the “Delta” parameterization. If the “Theta” parameterization is used, that is, assuming $\mathrm{var}\left({\mathrm{ϵ}}_i\right)=1$, then $a_i={\mathrm{\lambda }}_i$ and $d_i={\mathrm{\tau }}_i$, which is the IRT parameterization. In order to provide the complete solution for resolving the scale indeterminacy in $y_i^{*}$ and $\mathrm{\xi }$, in practice the most popular assumptions are $y_i^{*}~N(0,1)$ and $\mathrm{\xi }~N(0,1)$, although the normality of $\mathrm{\xi }$ is not required in the derivation of the normal ogive model and its relation to the IRT parameterization.

II. Factor Analytic and IRT Parameterization in Unidimensional/Multidimensional Dichotomous/Polytomous Item Response Data

Part II of the appendix provides a summary of the expressions between FA (i.e, factor loading and threshold parameterization) and IRT (slope and intercept or discrimination and difficulty parameterization). All descriptions below are made in the context of the Mplus framework. IRT parameterization is related to the Mplus “Theta” and “Delta’ parameterizations. The “Theta” parameterization gives unbounded range for the value of the loadings in FA (or the slope parameter in IRT), while the “Delta” parameterization makes the range of the value of the loadings in FA within $\pm 1$. All equations below assume that the latent traits ($\mathrm{\theta }s$) follow a (multivariate) normal distribution and hold only when the errors (or residuals) in FA are uncorrelated. Estimation-wise, this involves the marginal maximum likelihood (MML) estimation with the usual local independence assumption in IRT modeling. The mean(s) of the normal distribution for the latent trait(s) is(are) set to zero(s) and variance(s) is(are) set to one(s) as part of the model identification. Fixing the parameters of the population distribution of $\mathrm{\theta }$ (e.g., as standard normal distribution) is a popular model identification solution in the unidimensional IRT when MML is employed in the full information estimation approach, as well as in the unidimensional FA.

Unidimensional Modeling

The “Theta” parameterization in the limited information approach leads to the normal ogive GRM (2PN model in the dichotomous response case). GRM has the slope parameter $a_i$ for item $i$ and the intercept parameter $d_{\mathrm{ik}}$ for the category $k$ in the item $i$, or the category step parameter $b_{\mathrm{ik}}$. For dichotomously scored data, GRM is the two-parameter IRT model either in the logistic version (2PL model) or the normal ogive version (2PN model). Also, the $d_{\mathrm{ik}}$ or $b_{\mathrm{ik}}$ parameter simply drops the category index $k$ in the dichotomous response modeling. (Thus, when $k=2$, $b_i$ for dichotomous response data is the item difficulty parameter in IRT.). Henceforth, FA with “Theta” parameterization and with “Delta” parameterization are denoted as “Theta” FA and “Delta” FA. In addition, let ${\mathrm{\lambda }}_i$ and ${\mathrm{\tau }}_{\mathrm{ik}}$ be the factor loading for item $i$ and the threshold for category $k$ in item $i$ in the FA parameterization.

From “Theta” FA to normal ogive IRT GRM (or logistic IRT GRM with D = 1.7)

$$a_i={\mathrm{\lambda }}_i$$

$$d_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}$$

$$b_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/{\mathrm{\lambda }}_i$$

From “Theta” FA to logistic IRT GRM without D

$$a_i=D{\mathrm{\lambda }}_i$$

$$d_{\mathrm{ik}}=D{\mathrm{\tau }}_{\mathrm{ik}}$$

$$b_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/{\mathrm{\lambda }}_i$$

From “Delta” FA to normal ogive IRT GRM (or logistic IRT GM with D = 1.7)

$$a_i={\mathrm{\lambda }}_i/\sqrt{1-{\mathrm{\lambda }}_i^2}$$

$$d_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/\sqrt{1-{\mathrm{\lambda }}_i^2}$$

$$b_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/{\mathrm{\lambda }}_i$$

From normal ogive IRT GRM (or logistic IRT GRM with D = 1.7) to “Delta” FA

$${\mathrm{\lambda }}_i=a_i/\sqrt{1+a_i^2}$$

$${\mathrm{\tau }}_{\mathrm{ik}}=d_{\mathrm{ik}}/\sqrt{1+a_i^2}=a_i{b}_{\mathrm{ik}}/\sqrt{1+a_i^2}$$

From “Delta” FA to logistic IRT GRM without D

$$a_i=D{\mathrm{\lambda }}_i/\sqrt{1-{\mathrm{\lambda }}_i^2}$$

$$d_{\mathrm{ik}}=D{\mathrm{\tau }}_{\mathrm{ik}}/\sqrt{1-{\mathrm{\lambda }}_i^2}$$

$$b_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/{\mathrm{\lambda }}_i$$

From logistic IRT GRM without D to “Delta” FA

$${\mathrm{\lambda }}_i=a_i/\sqrt{D^2+a_i^2}$$

$${\mathrm{\tau }}_{\mathrm{ik}}=d_{\mathrm{ik}}/\sqrt{D^2+a_i^2}=a_i{b}_{\mathrm{ik}}/\sqrt{D^2+a_i^2}$$

Multidimensional Modeling

In multidimensional modeling, the slope and intercept parameterization is a possible form in the IRT GRM, which has the intercept parameter $d_{\mathrm{ik}}$ and the slope parameter $a_{\mathrm{ij}}$ (dimension index $j=1,2,\dots ,M).$ Note that $d_{\mathrm{ik}}$ does not have a subscript for dimension because only one set of the $k-1$ intercept/step parameters is possible to estimate for an item regardless of a single or multiple dimensions. That is, $d_{\mathrm{ijk}}$ which depends on $j$ (dimension) is not estimable.

From “Theta” FA versus normal ogive multidimensional IRT (MIRT) GRM (or logistic MIRT GRM with D = 1.7)

$$a_{\mathrm{ij}}={\mathrm{\lambda }}_{\mathrm{ij}}$$

$$d_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}$$

From “Theta” FA to logistic MIRT GRM without D

$$a_{\mathrm{ij}}=D{\mathrm{\lambda }}_{\mathrm{ij}}$$

$$d_{\mathrm{ik}}=D{\mathrm{\tau }}_{\mathrm{ik}}$$

From “Delta” FA to normal ogive MIRT GRM (or logistic MIRT GM with D = 1.7)

Let ${\mathrm{\rho }}_{\mathrm{jj}\prime }$ be the correlation of dimension $j$ and $j\prime$$(j\prime =1,2,\dots ,M)$

$$a_{\mathrm{ij}}={\mathrm{\lambda }}_{\mathrm{ij}}/\sqrt{1-\sum _{j=1}^M\sum _{j\prime =1}^M{\mathrm{\lambda }}_{\mathrm{ij}}{\mathrm{\lambda }}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

$$d_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/\sqrt{1-\sum _{j=1}^M\sum _{j\prime =1}^M{\mathrm{\lambda }}_{\mathrm{ij}}{\mathrm{\lambda }}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

From normal ogive MIRT GRM (or logistic MIRT GRM with D = 1.7) to “Delta” FA

$${\mathrm{\lambda }}_{\mathrm{ij}}=a_{\mathrm{ij}}/\sqrt{1+\sum _{j=1}^M\sum _{j\prime =1}^M{a}_{\mathrm{ij}}{a}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

$$d_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/\sqrt{1+\sum _{j=1}^M\sum _{j\prime =1}^M{a}_{\mathrm{ij}}{a}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

From “Delta” FA to logistic MIRT GRM without D

$$a_{\mathrm{ij}}=D{\mathrm{\lambda }}_{\mathrm{ij}}/\sqrt{1-\sum _{j=1}^M\sum _{j\prime =1}^M{\mathrm{\lambda }}_{\mathrm{ij}}{\mathrm{\lambda }}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

$$d_{\mathrm{ik}}=D{\mathrm{\tau }}_{\mathrm{ik}}/\sqrt{1-\sum _{j=1}^M\sum _{j\prime =1}^M{\mathrm{\lambda }}_{\mathrm{ij}}{\mathrm{\lambda }}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

From logistic MIRT GRM without D to “Delta” FA

$${\mathrm{\lambda }}_{\mathrm{ij}}=a_{\mathrm{ij}}/\sqrt{D^2+\sum _{j=1}^M\sum _{j\prime =1}^M{a}_{\mathrm{ij}}{a}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$

$$d_{\mathrm{ik}}={\mathrm{\tau }}_{\mathrm{ik}}/\sqrt{D^2+\sum _{j=1}^M\sum _{j\prime =1}^M{a}_{\mathrm{ij}}{a}_{\mathrm{ij}\prime }{\mathrm{\rho }}_{\mathrm{jj}\prime }}$$