On the Origin of Compositional Features of Ribosomes

Abstract

Ribosomes are highly abundant in cells and comprise, besides RNAs of varying lengths, 55–80 similarly sized, short proteins. This seemingly unusual composition is thought to have resulted from selection for rapid autocatalytic ribosome production. Here, we demonstrate that ribosomal protein-splitting mutations cannot accelerate ribosome production. The autocatalytic explanation is also unnecessary, because protein lengths generally decline with expression levels. Although ribosomal proteins are shorter than expected from their expression levels, they are not outliers among members of large protein complexes in mean protein length or coefficient of variation. These observations are explainable because 1) shortening proteins lowers their synthetic cost and reduces the waste from mistranslation-induced protein dysfunction and degradation, 2) such benefits rise with expression levels, and 3) members of large complexes participate in more protein–protein interactions so are less tolerant to mistranslation. These and other considerations suggest that the compositional features of ribosomes originate from cellular energy economics.

Compositional Features of Ribosomes

Ribosomes synthesize peptides from amino acids according to the instruction of messenger RNAs and are one of the most important molecular machines of cellular life. A ribosome is made up of a large subunit and a small subunit, together consisting of three to four ribosomal RNAs (rRNAs) and dozens of ribosomal proteins (r-proteins). Ribosomes are highly abundant in cells. For instance, in rapidly growing cells, ∼80% of all RNAs belong to rRNAs and ∼30% of the total proteome is r-proteins (Warner 1999). As a result, ribosome production demands a large fraction of the energy budget of the cell. Reuveni et al. (2017) recently noted that 20–70% of the ribosome mass is in the few rRNAs of varying lengths, while the remaining mass is divided into 55–80 similarly sized, short r-proteins. Because dosage balance among members of a large complex is important and because the balance is more difficult to achieve with more proteins, these authors believed that ribosome’s unusual composition must have a special reason. They proposed that this reason is ribosome’s autocatalytic production; synthesizing many similarly short proteins instead of a few long ones minimizes the idle time of r-proteins (Reuveni et al. 2017). Here, we show that this model is neither valid nor needed. Instead, we propose general principles of protein length evolution governed by cellular energy economics and demonstrate that the compositional features of ribosomes are explainable by these principles.

Ribosome’s Compositional Features Cannot Result from Optimization for Autocatalytic Production

Autocatalytic production refers to the fact that the ribosome production rate rises as more ribosomes are made. Given that r-proteins have different lengths, the optimal state in Reuveni et al.’s model is when the synthesis time for each r-protein is short and the instantaneous production rates of all r-proteins are balanced such that amino acids incorporated into r-proteins quickly become part of an assembled functional ribosome for making new ribosomes (i.e., minimal idle time). Such balanced r-protein productions require a set of optimized relative translation initiation rates (measured by number of initiations per mRNA molecule per second) for the r-proteins, which are determined by the r-protein stoichiometry, lengths, translation elongation speeds (measured by number of codons per second), and corresponding mRNA concentrations. These optimized initiation rates are mechanistically realized by specific mRNA sequences, especially in the 5′-untranslated region (Gu et al. 2010; Mutalik et al. 2013).

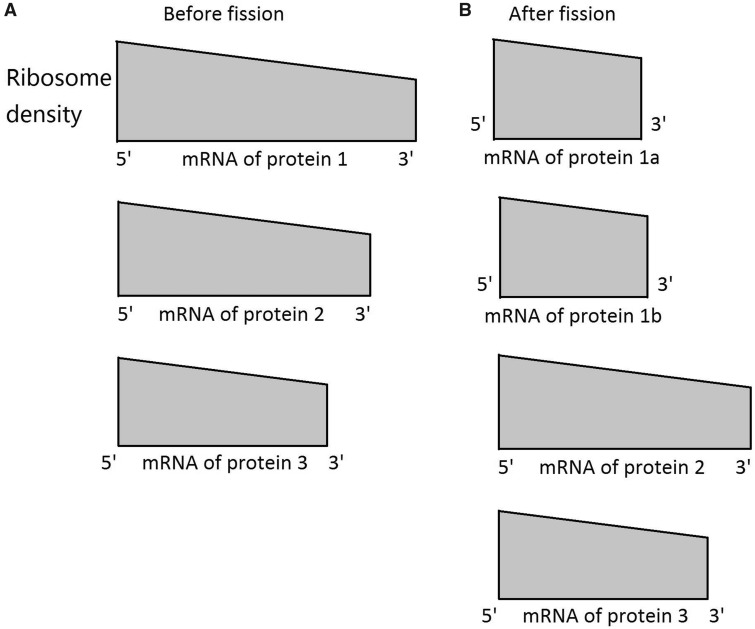
Now let us consider a mutation that divides one of the r-proteins into two shorter proteins without altering the sum of their functions (see below). This length change demands a new set of optimal relative initiation rates, which cannot be realized by the protein-fission mutation. It is reasonable to assume that, upon the protein-fission mutation, the two shorter r-proteins inherit their mother protein’s relative initiation rate, while all other r-proteins maintain their original relative initiation rates. These relative initiation rates ensure balanced amounts of production of all r-proteins, because the production rate equals the initiation rate under the assumption of no ribosome falloff during elongation. Thus, the dosages of all r-proteins remain overall balanced. However, because the newly created shorter proteins each take less time to synthesize than their mother protein, the synthesized shorter proteins must be idle until all of the other r-proteins are synthesized for new ribosomes to be assembled. In other words, because a ribosome is functional only when all of its components become available, a mutation must simultaneously split all r-proteins to be advantageous. Any mutation splitting only one of many r-proteins is neutral to the autocatalytic production of ribosomes, and an example involving breaking one of three r-proteins originally produced with equal rates is provided in figure 1 to illustrate the above argument. Note that, in eukaryotes, even splitting one protein likely requires multiple mutations. The most probable scenario would include duplication of an r-protein gene followed by subfunctionalization via degenerate mutations (Force et al. 1999; Zhang 2013). In prokaryotes, a gene may be broken into two functional genes in the same operon by one nonsense mutation at an appropriate position, if sequence elements necessary for translational initiation fortuitously exist downstream of the position experiencing the nonsense mutation. Regardless, the above analysis demonstrates that Reuveni et al.’s model does not work because no mutation spliting one r-protein can improve the autocatalytic production of ribosomes.

Fig. 1.

—The autocatalytic production of ribosomes is not accelerated by breaking one of the r-proteins into two shorter ones, illustrated by a toy example in which the ribosome comprises three r-proteins of equal doses, equal translation elongation speeds, but different lengths. The actual ribosome contains 55–80 r-proteins. (A) Ribosome densities before protein fission. Ribosome density (# of ribosomes per codon in all mRNAs of a gene) rises from the 3′ to 5′ of mRNAs, because the number of ribosomes in the cell is increasing with time due to the continuous production of ribosomes. At the optimal state, ribosome density at the 3′ end is the same among the three mRNA species, ensuring equal production rates of the three r-proteins at any time. The ribosome density at the 5′ end must be higher for longer proteins to ensure equal ribosome densities at the 3′ end among all r-proteins. (B) Ribosome densities after protein fission. When one r-protein is split into two, the ribosome densities at the 5′ end are equal for the two new proteins, because protein fission does not alter their relative translation initiation rates. Because the synthesis of each newly created short protein completes earlier than that of the original mother protein, these short proteins are useless until all other r-proteins complete synthesis. Hence, splitting one of the r-proteins does not accelerate the autocatalytic production of ribosomes. Regardless of the r-protein split, all existing ribosomes function continuously and the doses of all r-proteins synthesized are balanced, so r-protein fission does not decelerate ribosome production either. Ribosome densities can be compared within each panel but not between panels.

Ribosomal Proteins Follow Two General Trends of Protein Length

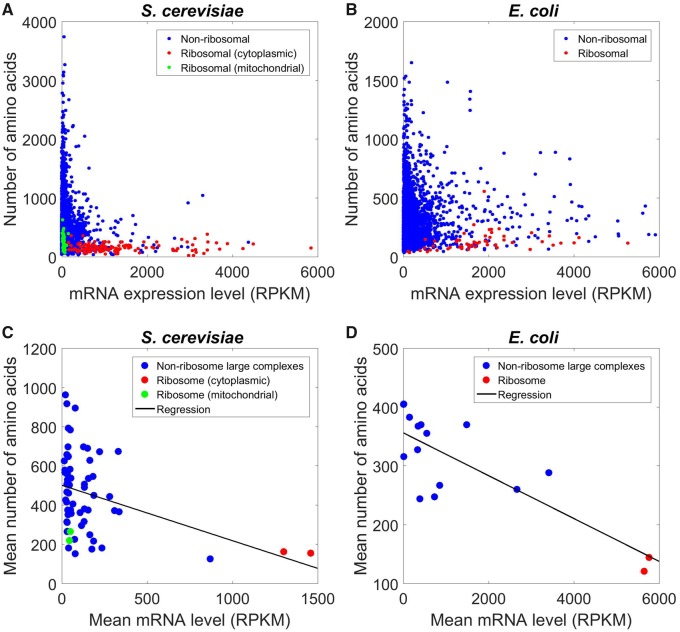
But do we need a ribosome-specific model to explain its compositional features aforementioned? Reuveni et al. showed that r-proteins are unusually short when compared with average proteins encoded in a genome. This comparison is, however, unfair, because highly expressed proteins tend to be shorter than lowly expressed ones (Akashi 2003; Urrutia and Hurst 2003; Subramanian and Kumar 2004). We thus ask whether r-proteins are significantly shorter than other proteins of similar expression levels. To this end, we first correlated protein length with its mRNA expression level among 5008 proteins of the budding yeast Saccharomyces cerevisiae, a well-studied eukaryotic model organism. We quantified the mRNA level by RNA sequencing read number per kilobase of transcript per million mapped reads (RPKM). Indeed, a significant, negative correlation is present (Spearman’s ρ = −0.16, P = 7.4 × 10⁻³²; fig. 2A). To examine if r-proteins are shorter than expected from their expression levels, we first artificially constructed the small subunit of the yeast cytoplasmic ribosome by randomly drawing from the entire pool of 5008 proteins (with replacement) the same number of proteins as the number of r-proteins in the subunit, under the condition that each protein drawn has <5% expression-level difference from the corresponding r-protein. This was repeated 1000 times, and each of the 1000 randomly constructed small subunit has a mean protein length greater than the observed mean length, suggesting that r-proteins of the small subunit are shorter than expected from their expression levels (P < 0.001). The same is true for the large subunit of the cytoplasmic ribosome (P < 0.001). Mitochondrial ribosomes do not make themselves, so are not subject to autocatalytic production. Yet, for both the small and large subunits of the yeast mitochondrial ribosome, the mean protein length is shorter than expected from their expression levels (both P < 0.001).

Fig. 2.

—Protein length tends to decline with its mRNA expression level. (A) Relationship between protein length and mRNA expression level in yeast. Each dot represents one protein. Red and green colors indicate cytoplasmic and mitochondrial r-proteins, respectively. (B) Relationship between protein length and mRNA level in Escherichia coli. Red color indicates r-proteins. (C) Relationship between mean protein length and mean mRNA level of members of large protein complexes in yeast. Each dot represents one complex. The two red dots indicate the two subunits of the cytoplasmic ribosome, whereas the two green dots indicate the two subunits of the mitochondrial ribosome. The black line shows the linear regression. (D) Relationship between the mean protein length and mean mRNA level of large protein complexes in E. coli. The two red dots indicate the two subunits of the ribosome.

Prokaryotic proteins are on an average substantially shorter than eukaryotic proteins (Zhang 2000). Yet, the negative correlation between protein length and mRNA expression level persists in the prokaryotic model organism Escherichia coli (ρ = −0.10, n = 3400 proteins, P = 2.0 × 10⁻⁸; fig. 2B). Furthermore, the r-proteins of E. coli are also significantly shorter than expected from their expression levels (P < 0.002 for both small and large subunits).

Because ribosomes are large protein complexes, we ask whether their unusually short r-proteins are related to this property. Following previous studies (Pessia et al. 2012; Chen and Zhang 2016), we define large protein complexes as those containing at least seven proteins. Indeed, 7 of the 59 nonribosome large protein complexes in yeast have a within-complex mean protein length smaller than that expected from their expression levels at the significance level of 0.001, despite that only 0.059 complex is expected to reach this level of significance by chance. Apparently, members of large complexes tend to be shorter than random proteins of similar expression levels.

The above finding suggests that r-proteins should be compared with members of large complexes upon the control for expression levels. To this end, we regressed the mean protein length with mean mRNA level of a complex across the 63 large complexes in yeast using a linear model (fig. 2C). We then computed the studentized residual in mean protein length for each complex (see Materials and Methods). A complex is considered to be an outlier at the 5% significance level if the absolute value of its studentized residual exceeds 1.96 (Belsley et al. 1980). The small and large subunits of the cytoplasmic ribosome have studentized residuals of 0.465 and 0.179, respectively, whereas those of the mitochondrial ribosome have studentized residuals of −1.194 and −1.450, respectively. Hence, none of them are outliers. We did observe three outliers from nonribosome large complexes, close to the expectation that 63 × 5% = 3.15 large complexes are outliers by chance. Similar results were obtained in E. coli (fig. 2D), although only 14 nonribosome large complexes are currently known in this species. Specifically, the small and large subunits of the E. coli ribosome, respectively, have studentized residuals of −0.052 and −0.707, so neither is an outlier. We observed one nonribosome large complex to be an outlier, close to the random expectation of 16 × 5% = 0.8. The yeast and E. coli results hold even when r-proteins are excluded from the linear regressions. To examine the robustness of our results, we repeated the linear regressions after taking logarithms of both mean protein length and mean expression level of protein complexes. We found the results to be qualitatively unchanged (supplementary fig. S1, Supplementary Material online). Together, these findings demonstrate that r-proteins are not special in mean protein length among large complexes upon the control of expression levels.

Reuveni et al. (2017) claimed that r-proteins are more similar in length than expected even after the control of the mean length. This control is inappropriate, because members of the same large complex tend to have similar expressions, which would predict similar protein lengths, while a random set of proteins of a fixed mean length can have widely different expressions and hence lengths. In other words, the length variation among r-proteins should be compared with that among members of the same large complex. We computed the coefficient of variation (CV) in protein length for each of the 59 nonribosome large protein complexes in yeast. We found that the CVs for the two cytoplasmic ribosomal subunits are not significantly different from those of nonribosome large complexes (P = 0.09; Wilcoxon rank-sum test). A similar result was obtained for the two mitochondrial ribosomal subunits (P = 0.11). The same is true in E. coli (P = 0.82) when the two ribosomal subunits are compared with the 14 nonribosome large complexes.

The Mechanistic Basis of the Two General Trends of Protein Length

Together, our results suggest that no ribosome-specific explanation is needed for the short and homogeneous lengths of r-proteins because they are not outliers among members of large complexes upon the control of expression levels. But why does the length of a protein generally decrease with its expression level and why are members of large protein complexes shorter than random proteins of similar expression levels? We propose two mechanisms, both related to cellular energy economics, to explain the origin of the negative correlation between protein length and expression level. First, a protein may contain unnecessary residues or segments; their presence/absence does not impact the protein function, but removing them saves the materials and energy in synthesizing the mRNA and protein. Because materials can be measured in terms of energy, hereinafter we use energy to refer to both materials and energy. For example, a 1% reduction in the length of a protein saves ∼1% of its synthesis energy. Note that the total energy savings resulting from the removal of such superfluous residues in a protein rises with the number of mRNA molecules and number of protein molecules synthesized, which in turn rise with the mRNA expression level. Hence, natural selection for the removal of superfluous residues intensifies with the expression level, resulting in a negative correlation between mRNA expression level and protein length (Akashi 2003; Urrutia and Hurst 2003). Protein length is of course influenced by many factors, including protein structure and function. That the length variation is much greater among lowly expressed proteins than highly expressed ones (fig. 2A and B) is consistent with the notation that selection arising from cellular energetics is especially strong on highly expressed proteins.

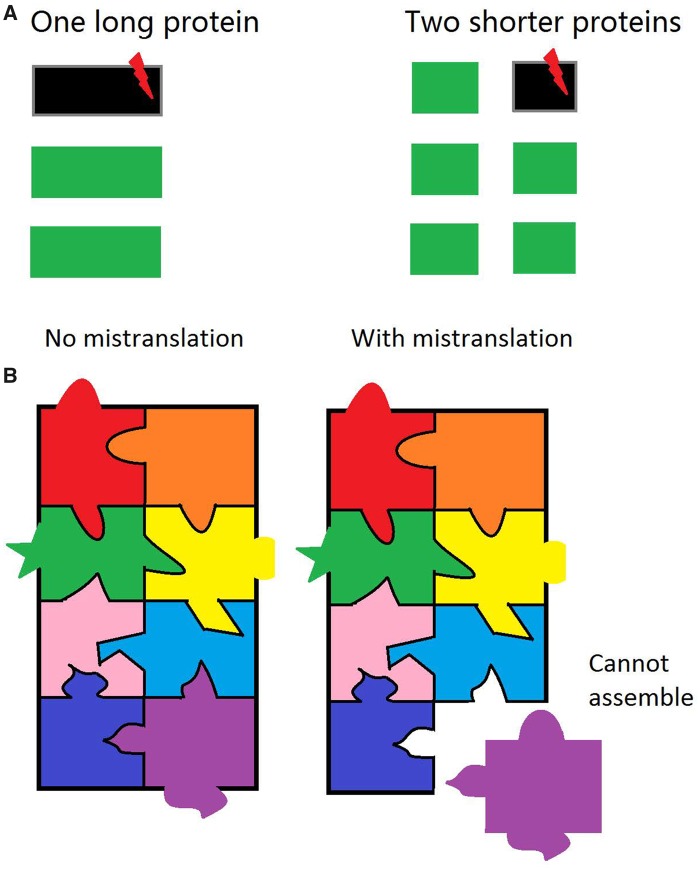
Second, it may be possible to divide a multidomain protein into two or more smaller proteins without impacting the protein function. While the total protein length is unaffected, having multiple shorter proteins instead of one long protein makes a difference in the presence of mistranslation, which either incorporates amino acids incorrectly or truncates the protein. In E. coli, yeast, and other species, mistranslation occurs at a rate of 10⁻⁵ to 10⁻² per codon, depending on the type of error (Drummond and Wilke 2009; Ribas de Pouplana et al. 2014). While some mistranslation events probably have minimal functional impacts, the rest can cause functional reduction, loss, or alteration (Yang et al. 2014). In addition, mistranslated proteins may be misfolded and subsequently degraded (Goldberg 2003). Regardless of the specific consequence, mistranslation wastes energy used in protein synthesis. Because the amount of energy wasted owing to mistranslation is proportional to the length of the mistranslated protein molecule, breaking a long protein into several smaller proteins can reduce the energy waste associated with protein dysfunction or degradation upon mistranslation (fig. 3A). To estimate this effect quantitatively, let us consider a mutation that breaks a protein with L amino acids into two proteins with βL and (1−β)L amino acids, respectively. Let the mistranslation rate be μ per codon. Before the protein fission, the expected number of translational errors per protein molecule equals μL, and the expected fraction of error-containing molecules is 1−e^−μL ≈ μL (when μL ≪ 1). If on average a mistranslated protein molecule is functionally equivalent to only f (f < 1) error-free molecules due to functional reduction, functional loss, or degradation, the energy waste owing to mistranslation is W = (1−f)μL(cEL) = (1 −f)μcEL², where c is the protein synthetic cost per amino acid and E is the mRNA expression level of the protein. Upon protein fission, the corresponding value becomes W′ = (1−f)μcE[β²L² +(1 −β)²L²]. So, the amount of energy savings caused by the fission is ΔW = W −W′ = 2(1−f)μcEβ(1−β)L² > 0. Apparently, protein fission reduces energy waste, so is beneficial. Furthermore, ΔW is maximized when β  =  0.5. In other words, breaking the protein into two equal-size proteins is most beneficial in terms of reducing mistranslation-associated energy waste. When L = 400, μ = 5 × 10⁻⁴, f = 0.9, β  =  0.5, ΔW equals 1% of the synthetic cost of the original protein. For a yeast gene with the median expression level, doubling the expression creates a selective disadvantage >10⁻⁵ (Wagner 2005). Therefore, saving 1% of its synthetic cost will have a selective advantage >10⁻⁷, approximately reciprocal of yeast’s effective population size (Wagner 2005). Hence, for highly expressed proteins, such a benefit is detectable by natural selection.

Fig. 3.

—Cellular energy economics explains why protein length declines with expression level and why members of large protein complexes are shorter than expected from their expression levels. (A) Protein fission reduces the mistranslation-associated energy waste. Each rectangle represents a protein molecule, with the length of the rectangle representing the protein length. Each red lightening symbol indicates a mistranslation event. Green rectangles are error-free molecules, whereas black rectangles are error-containing molecules. The left side shows a long protein with three newly synthesized molecules, including one that is error-containing. The right side shows the situation when the protein is split into two shorter ones (at the gene level). Now, a total of six molecules are synthesized, including an error-containing one. Although the total number of mistranslation events is unchanged, only one short protein is wasted in the right side compared with the waste of a long protein at the left side. Hence, energy waste is reduced by the protein fission. (B) Members of large protein complexes are less tolerant to mistranslation. Each piece of the jigsaw puzzle represents a protein, whereas the assembled jigsaw puzzle represents an assembled protein complex. To members of large protein complexes, mistranslation can not only impact its function but also its interactions with other members of the complex.

The above second mechanism can also explain why members of large complexes tend to be shorter than random proteins of comparable expression levels. Specifically, we propose that, compared with random proteins of similar expression levels, members of large complexes have lower f because they participate in more protein–protein interactions and hence are less tolerant to mistranslation (fig. 3B). For example, even when a translational error does not influence the catalytic function of a protein, it may affect its interaction with other members of the large complex and prevent the protein from incorporation into the complex. Because ΔW increases as f reduces, the selective pressure for protein fission is stronger for members of large complexes than random proteins of similar expressions, resulting in smaller lengths for the former than the latter. A large complex may also evolve by recruiting new members. Upon the recruitment, the new complex member will be subject to stronger selection from the above second mechanism than that when the protein is not part of any large complex.

Why Can Ribosomal RNAs Be Very Large?

Another compositional feature of ribosomes is the RNA content: three to four rRNAs with varying lengths. For instance, the three E. coli rRNAs contain 120, 1,542, and 2904 nucleotides, respectively. While rRNAs could be long because they are synthesized much faster than r-proteins (Reuveni et al. 2017), we investigated whether cellular energy economics also allows long rRNAs. rRNAs are transcribed by RNA polymerase I (RNAP I) and III that are thousands of times more accurate than RNAP II (Alic et al. 2007; Kuhn et al. 2007; Sydow and Cramer 2009), which is in turn much more accurate than translation (Lynch 2010). Hence, the error rate in synthesizing rRNAs is at least 10⁴ times lower than that in synthesizing r-proteins. In yeast, the median cost of precursor synthesis per nucleotide is 49.3 ATP molecules, whereas the combined biosynthesis and polymerization cost per amino acid is 30.3 ATP molecules (Wagner 2005). Comparing an rRNA of 3000 nucleotides with an r-protein of 300 amino acids, one can calculate using the ΔW formula derived earlier that the energy savings from splitting the r-protein is at least 60 times that from splitting the rRNA. This may explain the existence of much longer rRNAs than r-proteins. Having a long rRNA may even be preferable to having multiple short rRNAs, because dosage balance is easier to achieve in the former than the latter except when distinct rRNAs are encoded by genes of the same operon, as in many prokaryotes (Roller et al. 2016).

Conclusion

In summary, we demonstrated that the compositional features of ribosomes could not have resulted from potential selections for their faster autocatalytic production. We showed that no ribosome-specific hypothesis is necessary to account for the existence of many similarly sized, short r-proteins. Cellular energy economics explains not only the compositional features of ribosomes but also general relationships between mRNA expression levels and protein lengths, including for members of large protein complexes. Of particular interest is the role of transcriptional/translational errors in cellular energy economics. It appears to be a recurring theme that natural selection minimizing the impacts of molecular errors results in general patterns in genome, molecular, and cell biology (Warnecke and Hurst 2011; Lynch et al. 2014; Zhang and Yang 2015).

Materials and Methods

The gene expression data from wild-type yeast were obtained from Table S1 of a recent study (Chou et al. 2017). We averaged the RNA sequencing read counts among 12 replicates in computing the number of reads per kilobase of transcript per million mapped reads (RPKM). The RNA sequencing gene expression data of E. coli strain MG1655 in anaerobic growth were obtained from Data S6 of a previous study (Monk et al. 2016), and the averages from three replicates were used to compute RPKM. Yeast protein lengths were downloaded from Ensembl Biomart by choosing “cds length” followed by conversion to protein length. E. coli protein lengths were based on https://www.uniprot.org/docs/ecoli.txt, last accessed August 5, 2018. Yeast protein complex data were from an early study (Pu et al. 2009) and downloaded from http://wodaklab.org/cyc2008/downloads, last accessed August 5, 2018. E.coli protein complex data were downloaded from Table S8 of a previous study (Rajagopala et al. 2014); we removed ribosomal subunit L8 (a subset of ribosome large subunit and the only part of ribosome included in their table) and added information of ribosomal small and large subunits gathered from EcoCyc (Keseler et al. 2017). We performed linear regression using Matlab-embedded function “fitlm” and the option “linear.” Studentized residuals in linear regressions (Belsley et al. 1980) were computed following Matlab instructions (https://www.mathworks.com/help/stats/residuals.html, last accessed August 5, 2018). Other analyses used custom Matlab scripts.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.