Electro-optical chips promise a quantum link between electronic and optical circuits.
Abstract
Leveraging the quantum information-processing ability of superconducting circuits and long-distance distribution ability of optical photons promises the realization of complex and large-scale quantum networks. In such a scheme, a coherent and efficient quantum transducer between superconducting and photonic circuits is critical. However, this quantum transducer is still challenging because the use of intermediate excitations in current schemes introduces extra noise and limits bandwidth. We realize direct and coherent transduction between superconducting and photonic circuits based on the triple-resonance electro-optic principle, with integrated devices incorporating both superconducting and optical cavities on the same chip. Electromagnetically induced transparency is observed, indicating the coherent interaction between microwave and optical photons. Internal conversion efficiency of 25.9 ± 0.3% has been achieved, with 2.05 ± 0.04% total efficiency. Superconducting cavity electro-optics offers broad transduction bandwidth and high scalability and represents a significant step toward integrated hybrid quantum circuits and distributed quantum computation.
INTRODUCTION
The hybrid approach of combining superconducting and photonic quantum technologies promises to realize large-scale quantum networks (1–4). In superconducting quantum circuits, the low-loss single-quanta nonlinearity at microwave frequencies inherent to Josephson effect allows for efficient and fast quantum operations (5). However, it is challenging to directly transmit quantum states at microwave frequencies over long distances due to the high attenuation and thermal noise at room temperature. On the other hand, optical photons show complementary features. The weak single-photon nonlinearity prevents the development of high-fidelity quantum gates at optical frequency (6). However, low decoherence and dissipation rates make optical photons the ideal information carrier for quantum communication (2, 3). As a result, it is beneficial to develop a hybrid quantum platform where quantum information is processed by superconducting circuits and transmitted with optical photons. Thus, the quantum transducer, which can coherently interface superconducting and photonic circuits with high conversion efficiency, is highly demanded (7–20).
Coherent conversion of photons between microwave and optical frequencies has been proposed using various intermediate excitations, including collective spin in atom ensembles (18), phonon in electro-optomechanics (7–10), and magnon in magneto-optics (19, 20). Currently, the highest conversion efficiency is demonstrated on the basis of electro-optomechanical systems, where a compliant mechanical resonator couples to microwave and optical cavities simultaneously (7). The use of intermediate low-frequency (megahertz) excitations inevitably introduces extra noise channels, limits conversion bandwidth, and complicates operation with impedance matching between optical and microwave ports. The electro-optic approach can overcome these obstacles by excluding intermediate excitations in the conversion process, as proposed by Tsang recently (12, 13). Great improvement of electro-optic coupling strength is proposed by Javerzac-Galy et al. (15) using coplanar microwave structure and integrated optical resonators, showing the feasibility of near-unity conversion efficiency with practical device parameters. Although the conversion efficiency of electro-optic systems has been improved markedly, it is still limited to ~0.1% due to the large ohmic loss of nonsuperconducting material and small coupling rates resulting from large mode volumes (16). Moreover, the coherence and bidirectionality of the conversion process remain to be proved.
Here, we report the experimental demonstration of the coherent conversion between microwave and optical photons based on the electro-optic effect within a hybrid superconducting-photonic device, where planar superconducting resonators are integrated with aluminum nitride (AlN) optical cavities on the same chip. We observe the electromagnetically induced transparency effect in electro-optic systems as a signature of coherent conversion between microwave and optical photons. An internal conversion efficiency of 25.9 ± 0.3% and an on-chip efficiency of 2.05 ± 0.04% are realized. A major challenge we have addressed is to realize the energy and phase conservation of the triple-resonance condition with ultrasmall mode volumes, boosting the pump photon number and vacuum coupling rate simultaneously to enhance the coherent conversion. Moreover, our device is ready to incorporate other superconducting and photonic quantum devices on the same chip, providing the scalable platform for hybrid quantum network.
RESULTS
The principle of quantum transducers based on superconducting cavity electro-optics is illustrated in Fig. 1A. The optical cavity, consisting of materials with Pockels nonlinearity, is placed inside the capacitor of the LC microwave resonator. The electric field across the capacitor changes the refractive index of the optical cavity, thus modulating the optical resonant frequency. Reversely, modulated optical fields can generate microwave field due to the optical mixing (rectification) in Pockels materials (21). To implement the quantum transducer, we use integrated optical microring cavities made of AlN, which supports low-loss optical modes and provides high electro-optic coefficients simultaneously (Fig. 1B) (22). Superconducting microwave resonators are placed on top of a thin buffer layer, and the capacitor shape is designed to match the optical cavity to maximize the field overlap between microwave and optical modes (15, 17).
Fig. 1. Coherent conversion with cavity electro-optics.
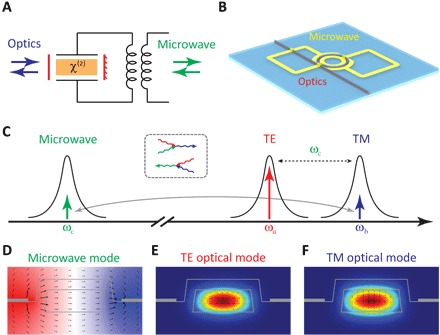
(A) Schematic of cavity electro-optic systems. The optical cavity is made of materials with Pockels nonlinearity (χ(2)) and placed in the capacitor of the LC circuit. At the same time, optical and microwave cavities are coupled to optical and microwave bus waveguides, respectively. (B) Integrated superconducting cavity electro-optic device. The red part is the optical cavity and coupling waveguide, and the yellow part is the superconducting microwave cavity. A buffer layer (semitransparent) is placed between optical devices and the superconducting cavity to prevent metallic absorption of optical photons. (C) Diagram of frequencies in the conversion process. Strong control light is applied to the TE optical mode (pump mode), and photons can be converted between the microwave mode and the TM optical mode (signal mode). Microwave photons are converted to optical photons through sum frequency generation, and optical photons are converted to microwave photons through difference frequency generation, as shown in insets. The mode distribution in the cross section is shown for (D) the microwave mode, (E) the TE optical mode, and (F) the TM optical mode. Arrow direction and length represent the electric field direction and strength in log scale, respectively. Colors in (D) represent the voltage distribution, and colors in (E) and (F) represent the energy density. In simulation, the optical waveguide is 2 μm wide and 800 nm thick, and the sidewall angle is 8°. The distance between microwave electrodes is 2.8 μm. The material boundary is plotted in gray.
We use the triple-resonance scheme to enhance the coupling, as shown Fig. 1C, with the interaction Hamiltonian written as
where a, b, and c are the annihilation operators for the pump and signal optical modes and microwave mode, respectively, and geo is the vacuum electro-optic coupling rate. Cavity electro-optic systems with triple resonances have been proposed and demonstrated recently (15, 16). However, the device geometry is limited to above several millimeters, as the pump and signal optical modes are from the same mode group, and the free spectral range (FSR) needs to match the microwave frequency. Large mode volume inevitably leads to a small vacuum coupling rate (thus low conversion efficiency) (section S1). In contrast, our integrated approach uses the transverse-electric (TE) and transverse-magnetic (TM) optical modes as pump and signal modes, respectively (Fig. 1, E and F), whose frequency difference equals the microwave frequency (23–26). Thus, the device size and mode volume can be further reduced without the limitation imposed by FSR. In this case, the r13 electro-optic coefficient is used, which also enables the use of TE-polarized microwave mode; that is, the heterogeneous integration of planar microwave resonators with optical cavities (Fig. 1D). During experiments, a strong coherent field is applied to the pump mode (a) to stimulate the coherent coupling between the signal mode (b) and the microwave mode (c), and photons can be bidirectionally converted between optical and microwave frequencies with on-chip efficiency
| (1) |
where κb,ex, κb, κc,ex, and κc are the external coupling and total loss rates for signal and microwave modes, respectively, and is the cooperativity, with na the photon number in the pump mode (section S1).
In experiments, the optical cavity is fabricated from an AlN layer on a silicon dioxide cladding on a silicon wafer (Fig. 2A). The optical ring cavity has a radius of 120 μm and a cross section of 2.0 μm × 0.8 μm (see section S2 for fabrication procedure and device cross section). An azimuthal number difference of 1 between the pump and signal optical modes is chosen to mitigate the optical mode mixing induced by the nonvertical waveguide sidewalls (see section S3 for the identification of azimuthal number difference and section S4 for the influence of TE/TM mode mixing). In Fig. 2B, we present the transmission of TE input light, where mode anti-crossing is observed arising from the structural asymmetry and fabrication imperfection. As TE and TM optical modes have opposite electro-optic coefficients, dc voltage is applied across the device to tune the frequency difference precisely in a wide spectrum range. Compared with using optical modes from the same group (15, 16), the large frequency tuning range of our device makes it easy to accommodate different microwave frequencies within a single device.
Fig. 2. Integrated superconducting cavity electro-optic device.
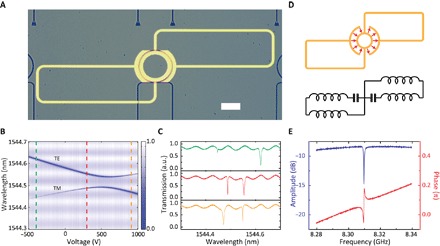
(A) Optical image of the superconducting cavity electro-optic device. Scale bar, 100 μm. (B) TE optical spectrum with different dc voltages. The azimuthal number difference between the TE and TM optical modes is 1. The mode anti-crossing gap is 2gx ~ 6.1 GHz, and the original dissipation rates for TM and TE optical modes without optical mode mixing are 190 and 480 MHz, respectively. (C) TE optical spectrum with dc voltages of −400 V (green), 300 V (red), and 900 V (orange), corresponding to the green, red, and orange dashed lines in (B), respectively. (D) Schematic of the microwave resonator and electric field distribution of the microwave mode, as well as the equivalent circuit. (E) Measured reflection spectrum of the microwave cavity. a.u., arbitrary units.
The microwave resonator is made of NbTiN superconducting film, with a critical temperature of about 14 K. The device is placed in a cryostat and cooled down to 2 K, and the device surface is covered by superfluid helium to introduce fast heat dissipation (27). To allow electro-optic phase matching, it is important to shape the microwave resonator to have an azimuthal number of 1 to match the azimuthal number difference between the pump and signal modes (Fig. 2D and section S5). The capacitance part of the microwave resonator has a radius of 120 μm to match the optical cavity, and the distance between electrodes is 2.8 μm. Each inductance arm has a length of 1.5 mm, allowing far-field magnetic coupling to an off-chip loop probe for broadband microwave signal input and readout. The microwave mode has a resonance of about ωc/2π = 8.31 GHz, with a decay rate of κc/2π = 0.55 MHz at 2 K (Fig. 2E). When the dc voltage is tuned to 297 V, the frequency difference between pump and signal modes is also about 8.31 GHz (Fig. 2C). Therefore, the phase matching and energy conservation are fulfilled simultaneously.
The coherent conversion of our device is first characterized with optical reflection spectrum. Strong control light is applied to the pump mode, and a weak probe light, derived from the control light by single sideband modulation, is sent to the signal mode (section S6). No obvious temperature change of the superconducting microwave resonator is observed (section S7). Figure 3A presents the probe light transmission spectrum sweeping across the signal mode, with a fixed control light on resonance with the pump mode. By tuning the dc voltage, the broad Lorentzian dip corresponding to the signal mode is shifted, with a sharp modification of the spectrum at a fixed frequency ω = ωc. This modification originates from the destructive interference between two pathways for the probe light: directly passing through the optical cavity and converting to microwave photons and then back to optical photons (28, 29). As shown in the enlarged spectrum (Fig. 3B), when the signal mode frequency matches ωc, there is a sharp transparency window, with the bandwidth equal to (1 + C)κc = (0.59 ± 0.01) MHz. If the signal mode is detuned, then the interference gives an asymmetric Fano-shaped spectrum. By fitting the transparency window, the conversion cooperativity can be extracted, and internal conversion efficiency can be inferred (Fig. 3, C and D) (30). An internal efficiency as high as (25.9 ± 0.3%) is achieved with our device under 8-dBm control light power (14 dBm total off-chip optical power with 6-dB insertion loss).
Fig. 3. Electromagnetically induced transparency with cavity electro-optics.
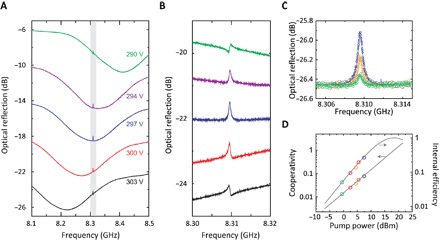
(A) Measured optical reflection spectrum as a function of the modulation frequency. (B) Zoom-in of the optical reflection spectrum centered at the transparency window. Each spectrum in (A) and (B) corresponds to a different dc voltage (thus different frequency detuning between pump and signal modes). Spectrums are offset for clarity. (C) Transparency window with the control light power of 8 dBm (blue), 5 dBm (orange), and 0 dBm (green). Circles are measured data, and solid lines are fitted spectra with eq. S13 in section S1. (D) Cooperativity and internal conversion efficiency versus control light power. The blue, orange, and green points correspond to the blue, orange, and green curves in (C), respectively. Gray lines are the fitted result based on measured data.
The bidirectional conversion is characterized by measuring the complete conversion matrix (Fig. 4A) with the dc voltage fixed at 297 V. By injecting the optical probe and monitoring the microwave output, we measure the microwave-to-optical coefficient Soe, which is a Lorentzian line shape centered at the microwave resonant frequency (Fig. 4C). The optical-to-microwave coefficient Seo is measured by reversing the input and output signal, which has the same spectrum shape with microwave-to-optical coefficient Soe, indicating that the conversion is bidirectional (Fig. 4D). The optical and microwave reflection spectra are also measured for calibration (Fig. 4, B and E), and the on-chip efficiency is estimated to be (2.05 ± 0.04%) (section S8). The main noise source during the conversion process is the thermal excitation of the microwave cavity, which can be reduced by working at a lower temperature. In addition, the noise generated by the parametric amplification process is negligible because of the deep resolved sideband condition (section S9).
Fig. 4. Bidirectional frequency conversion.
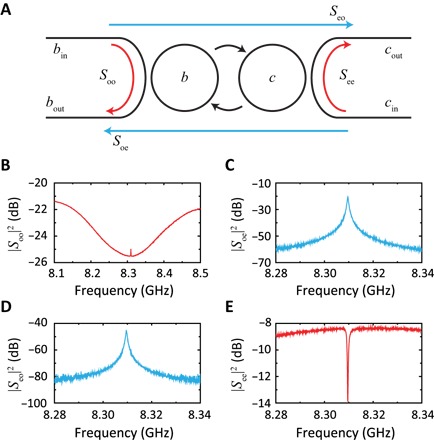
(A) Schematic showing the full conversion process. (B) The optical reflection Soo, (C) microwave-to-optical conversion Soe, (D) optical-to-microwave conversion Seo, (E) and microwave reflection See are measured to calibrate the on-chip conversion efficiency. The control light power is 8 dBm, and the dc voltage is 297 V. All conversion matrix coefficients are normalized to the radio frequency (RF) output power of the network analyzer (section S6).
DISCUSSION
An ideal quantum transducer demands the coherent conversion efficiency approaching 100%, when the cooperativity equals unity and both microwave and optical modes are deeply overcoupled. By optimizing the fabrication process and material properties, the efficiency of our device can be further increased. For instance, optical quality factors above 2 million have been demonstrated with single-crystalline AlN (31); therefore, intrinsic loss for optical modes can be reduced to κb,i = 2π × 100 MHz. Then, pump photon number can be increased by ~100 times with the same pump power, and the enhanced coupling rate geo can reach 16 MHz. With an improved microwave intrinsic loss rate of κc,i = 2π × 10 kHz (32), for example, by using sapphire substrate, the optimal on-chip efficiency exceeding η = 92% can be achieved by choosing the external optical coupling rate κb,ex = 2π × 2.9 GHz and the microwave coupling rate κc,ex = 2π × 0.29 MHz. Therefore, with the future development of single-crystalline AlN on sapphire system and its adaption for superconducting resonators, the approach presented here is promising to realize the high-fidelity quantum state transduction between superconducting and photonic circuits.
CONCLUSION
We have demonstrated the coherent photon transduction between integrated superconducting and photonic circuits. High transduction efficiency is realized on the basis of the triple-resonance electro-optic principle. Besides high efficiency, low noise, and large bandwidth, the large frequency tunability makes it easy to interface with different quantum systems, and the planar structure allows for the circuit-level integration of different quantum devices. All these features not only make our device an ideal quantum transducer but also provide a scalable platform to synthesize different quantum systems, paving the route toward large-scale hybrid quantum networks.
MATERIALS AND METHODS
Polycrystal AlN film preparation
The 800-nm AlN film was grown on a Si wafer with a 2-μm-thick SiO2 layer by the RF magnetron reactive sputtering, using pure aluminum (99.999%) targets in an argon and nitrogen gas mixture. The sputtered AlN film is polycrystal, with the c axis highly oriented perpendicular to the substrate. As AlN has a wurtzite crystal structure, the electro-optic coefficient has no direction dependence in the plain perpendicular to the c axis. Thus, the r13 coefficient in the sputtered AlN film can be used without considering the in-plane crystal direction change (22).
NbTiN film preparation
NbTiN films were sputtered by the RF magnetron method at room temperature using 70% Nb and 30% Ti alloy target in an argon and nitrogen gas mixture. The amorphous NbTiN film was formed uniformly on the surface, and a superconducting critical temperature Tc of about 13.8K was achieved.
Supplementary Material
Acknowledgments
We thank L. Jiang for the discussion and M. Power, M. Rooks, and L. Frunzio for the assistance in device fabrication. Funding: We acknowledge funding support from the Laboratory for Physical Sciences (LPS)/Army Research Office (ARO) (grant W911NF-14-1-0563), Air Force Office of Scientific Research (AFOSR) Multidisciplinary University Research Initiative (MURI) (grant FA9550-15-1-0029), NSF Emerging Frontiers in Research and Innovation (EFRI) (grant EFMA-1640959), and Defense Advanced Research Projects Agency (DARPA)/Optical Radiation Cooling and Heating in Integrated Devices (ORCHID) program through a grant from the AFOSR (FA9550-10-1-0297) and the Packard Foundation. Facilities used were supported by Yale Institute for Nanoscience and Quantum Engineering and NSF Materials Research Science and Engineering Center Division of Material Research 1119826. Author contributions: H.X.T., L.F., C.-L.Z., and X.H. conceived the experiment; L.F. fabricated the device; L.F., R.C., X.G., Z.G., and S.W. performed the experiment; and L.F. and C.-L.Z. analyzed the data. L.F. and C.-L.Z. wrote the manuscript, and all authors contributed to the manuscript. H.X.T. supervised the work. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/8/eaar4994/DC1
Section S1. Theory of cavity electro-optics and its utility for microwave-to-optical conversion
Section S2. Device fabrication procedure
Section S3. Identifying phase-matching conditions for optical modes
Section S4. Influence of optical mode mixing on the vacuum coupling rate geo
Section S5. Microwave resonator design
Section S6. Measurement setup
Section S7. Device temperature calibration
Section S8. Efficiency calibration
Section S9. Added noise during conversion
Fig. S1. Calculated internal conversion efficiency.
Fig. S2. Scanning electron microscopy picture of the cross section of a superconducting cavity electro-optic device.
Fig. S3. Anti-crossing between TE and TM optical modes.
Fig. S4. Measured spectrum signature of mixing between TE and TM modes.
Fig. S5. Wavelength difference between adjacent resonances.
Fig. S6. Phase-matching wavelength and anti-crossing strength.
Fig. S7. Vacuum coupling rate with hybrid optical modes.
Fig. S8. Microwave resonator simulation.
Fig. S9. Experiment setup for microwave-to-optical photon conversion.
Fig. S10. Microwave resonator performance under different temperatures.
REFERENCES AND NOTES
- 1.Schoelkopf R. J., Girvin S. M., Wiring up quantum systems. Nature 451, 664–669 (2008). [DOI] [PubMed] [Google Scholar]
- 2.O’Brien J. L., Furusawa A., Vučković J., Photonic quantum technologies. Nat. Photonics 3, 687–695 (2009). [Google Scholar]
- 3.Lvovsky A. I., Sanders B. C., Tittel W., Optical quantum memory. Nat. Photonics 3, 706–714 (2009). [Google Scholar]
- 4.Xiang Z.-L., Ashhab S., You J. Q., Nori F., Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623–653 (2013). [Google Scholar]
- 5.Clarke J., Wilhelm F. K., Superconducting quantum bits. Nature 453, 1031–1042 (2008). [DOI] [PubMed] [Google Scholar]
- 6.Kok P., Munro W. J., Nemoto K., Ralph T. C., Dowling J. P., Milburn G. J., Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007). [Google Scholar]
- 7.Andrews R. W., Peterson R. W., Purdy T. P., Cicak K., Simmonds R. W., Regal C. A., Lehnert K. W., Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 10, 321–326 (2014). [Google Scholar]
- 8.Bochmann J., Vainsencher A., Awschalom D. D., Cleland A. N., Nanomechanical coupling between microwave and optical photons. Nat. Phys. 9, 712–716 (2013). [Google Scholar]
- 9.Balram K. C., Davanço M. I., Song J. D., Srinivasan K., Coherent coupling between radio frequency, optical, and acoustic waves in piezo-optomechanical circuits. Nat. Photonics 10, 346–352 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Barzanjeh Sh., Abdi M., Milburn G. J., Tombesi P., Vitali D., Reversible optical-to-microwave quantum interface. Phys. Rev. Lett. 109, 130503 (2012). [DOI] [PubMed] [Google Scholar]
- 11.Lecocq F., Clark J. B., Simmonds R. W., Aumentado J., Teufel J. D., Mechanically mediated microwave frequency conversion in the quantum regime. Phys. Rev. Lett. 116, 043601 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Tsang M., Cavity quantum electro-optics. Phys. Rev. A 81, 063837 (2010). [Google Scholar]
- 13.Tsang M., Cavity quantum electro-optics. II. Input-output relations between traveling optical and microwave fields. Phys. Rev. A 84, 043845 (2011). [Google Scholar]
- 14.Huang S., Quantum state transfer in cavity electro-optic modulators. Phys. Rev. A 92, 043845 (2015). [Google Scholar]
- 15.Javerzac-Galy C., Plekhanov K., Bernier N. R., Toth L. D., Feofanov A. K., Kippenberg T. J., On-chip microwave-to-optical quantum coherent converter based on a superconducting resonator coupled to an electro-optic microresonator. Phys. Rev. A 94, 053815 (2016). [Google Scholar]
- 16.Rueda A., Sedlmeir F., Collodo M. C., Vogl U., Stiller B., Schunk G., Strekalov D. V., Marquardt C., Fink J. M., Painter O., Leuchs G., Schwefel H. G. L., Efficient microwave to optical photon conversion: An electro-optical realization. Optica 3, 597–604 (2016). [Google Scholar]
- 17.Soltani M., Zhang M., Ryan C., Ribeill G. J., Wang C., Loncar M., Efficient quantum microwave-to-optical conversion using electro-optic nanophotonic coupled resonators. Phys. Rev. A 96, 043808 (2017). [Google Scholar]
- 18.Hafezi M., Kim Z., Rolston S. L., Orozco L. A., Lev B. L., Taylor J. M., Atomic interface between microwave and optical photons. Phys. Rev. A 85, 020302(R) (2012). [Google Scholar]
- 19.Hisatomi R., Osada A., Tabuchi Y., Ishikawa T., Noguchi A., Yamazaki R., Usami K., Nakamura Y., Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93, 174427 (2016). [Google Scholar]
- 20.Williamson L. A., Chen Y.-H., Longdell J. J., Magneto-optic modulator with unit quantum efficiency. Phys. Rev. Lett. 113, 203601 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Bass M., Franken P. A., Ward J. F., Weinreich G., Optical rectification. Phys. Rev. Lett. 9, 446–448 (1962). [Google Scholar]
- 22.Xiong C., Pernice W. H. P., Sun X., Schuck C., Fong K. Y., Tang H. X., Aluminum nitride as a new material for chip-scale optomechanics and nonlinear optics. New J. Phys. 14, 095014 (2012). [Google Scholar]
- 23.Ilchenko V. S., Savchenkov A. A., Matsko A. B., Maleki L., Sub-microwatt photonic microwave receiver. IEEE Photonics Technol. Lett. 14, 1602–1604 (2002). [Google Scholar]
- 24.Ilchenko V. S., Savchenkov A. A., Matsko A. B., Maleki L., Whispering-gallery-mode electro-optic modulator and photonic microwave receiver. J. Opt. Soc. Am. B 20, 333–342 (2003). [Google Scholar]
- 25.Savchenkov A. A., Liang W., Matsko A. B., Ilchenko V. S., Seidel D., Maleki L., Tunable optical single-sideband modulator with complete sideband suppression. Opt. Lett. 34, 1300–1302 (2009). [DOI] [PubMed] [Google Scholar]
- 26.Strekalov D. V., Schwefel H. G. L., Savchenkov A. A., Matsko A. B., Wang L. J., Yu N., Microwave whispering-gallery resonator for efficient optical up-conversion. Phys. Rev. A 80, 033810 (2009). [Google Scholar]
- 27.Sun X., Zhang X., Schuck C., Tang H. X., Nonlinear optical effects of ultrahigh-Q silicon photonic nanocavities immersed in superfluid helium. Sci. Rep. 3, 1436 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Weis S., Rivière R., Deléglise S., Gavartin E., Arcizet O., Schliesser A., Kippenberg T. J., Optomechanically induced transparency. Science 330, 1520–1523 (2010). [DOI] [PubMed] [Google Scholar]
- 29.Safavi-Naeini A. H., Alegre T. P. M., Chan J., Eichenfield M., Winger M., Lin Q., Hill J. T., Chang D. E., Painter O., Electromagnetically induced transparency and slow light with optomechanics. Nature 472, 69–73 (2011). [DOI] [PubMed] [Google Scholar]
- 30.Hill J. T., Safavi-Naeini A. H., Chan J., Painter O., Coherent optical wavelength conversion via cavity optomechanics. Nat. Commun. 3, 1196 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Liu X., Sun C., Xiong B., Wang L., Wang J., Han Y., Hao Z., Li H., Luo Y., Yan J., Wei T., Zhang Y., Wang J., Aluminum nitride-on-sapphire platform for integrated high-Q microresonators. Opt. Express 25, 587–594 (2017). [DOI] [PubMed] [Google Scholar]
- 32.Bruno A., de Lange G., Asaad S., van der Enden K. L., Langford N. K., DiCarlo L., Reducing intrinsic loss in superconducting resonators by surface treatment and deep etching of silicon substrates. Appl. Phys. Lett. 106, 182601 (2015). [Google Scholar]
- 33.R. W. Boyd, Nonlinear optics, in Handbook of Laser Technology and Applications (Three-Volume Set) (Taylor & Francis, 2003), pp. 161–183. [Google Scholar]
- 34.Pernice W. H. P., Schuck C., Minaeva O., Li M., Goltsman G. N., Sergienko A. V., Tang H. X., High-speed and high-efficiency travelling wave single-photon detectors embedded in nanophotonic circuits. Nat. Commun. 3, 1325 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/8/eaar4994/DC1
Section S1. Theory of cavity electro-optics and its utility for microwave-to-optical conversion
Section S2. Device fabrication procedure
Section S3. Identifying phase-matching conditions for optical modes
Section S4. Influence of optical mode mixing on the vacuum coupling rate geo
Section S5. Microwave resonator design
Section S6. Measurement setup
Section S7. Device temperature calibration
Section S8. Efficiency calibration
Section S9. Added noise during conversion
Fig. S1. Calculated internal conversion efficiency.
Fig. S2. Scanning electron microscopy picture of the cross section of a superconducting cavity electro-optic device.
Fig. S3. Anti-crossing between TE and TM optical modes.
Fig. S4. Measured spectrum signature of mixing between TE and TM modes.
Fig. S5. Wavelength difference between adjacent resonances.
Fig. S6. Phase-matching wavelength and anti-crossing strength.
Fig. S7. Vacuum coupling rate with hybrid optical modes.
Fig. S8. Microwave resonator simulation.
Fig. S9. Experiment setup for microwave-to-optical photon conversion.
Fig. S10. Microwave resonator performance under different temperatures.


