Asymmetric Assembling of Iron Oxide Nanocubes for Improving Magnetic Hyperthermia Performance

Abstract

Magnetic hyperthermia (MH) based on magnetic nanoparticles (MNPs) is a promising adjuvant therapy for cancer treatment. Particle clustering leading to complex magnetic interactions affects the heat generated by MNPs during MH. The heat efficiencies, theoretically predicted, are still poorly understood because of a lack of control of the fabrication of such clusters with defined geometries and thus their functionality. This study aims to correlate the heating efficiency under MH of individually coated iron oxide nanocubes (IONCs) versus soft colloidal nanoclusters made of small groupings of nanocubes arranged in different geometries. The controlled clustering of alkyl-stabilized IONCs is achieved here during the water transfer procedure by tuning the fraction of the amphiphilic copolymer, poly(styrene-co-maleic anhydride) cumene-terminated, to the nanoparticle surface. It is found that increasing the polymer-to-nanoparticle surface ratio leads to the formation of increasingly large nanoclusters with defined geometries. When compared to the individual nanocubes, we show here that controlled grouping of nanoparticles—so-called “dimers” and “trimers” composed of two and three nanocubes, respectively—increases specific absorption rate (SAR) values, while conversely, forming centrosymmetric clusters having more than four nanocubes leads to lower SAR values. Magnetization measurements and Monte Carlo-based simulations support the observed SAR trend and reveal the importance of the dipolar interaction effect and its dependence on the details of the particle arrangements within the different clusters.

Magnetic hyperthermia (MH) is a novel noninvasive treatment, now undergoing clinical trials on patients with brain or prostate tumors,¹ that exploits the heat generated by magnetic nanoparticles (MNPs) when exposed to an alternating magnetic field.²⁻⁴ The use of MNPs as heat mediators in MH treatment impairs the monitoring of tumor progression by magnetic resonance imaging (MRI)¹ because it requires a substantial dose of MNPs to achieve the clinically relevant heating efficiency, incompatible with MRI imaging. Although several research studies have aimed at the design of optimal heat mediators that would allow reduction of the MNP dose, while maintaining the required heating performance, the low heating efficiency remains among the current limitations of MNPs used in clinical trials.⁵⁻⁷ In parallel to the direct synthesis of nanoparticles with optimized heat performances, the research focus was also directed toward the assembly of the same building blocks into controlled clusters in order to maximize their heating performance.⁸⁻¹¹ The aim behind this strategy is to achieve higher magnetic hyperthermia performances of defined MNPs used as building blocks by controlling the specific configuration of the MNPs in the final assembly.

The heating efficiency of the magnetic nanoparticles is expressed by their specific absorption rate (SAR). The SAR value is defined as the power absorbed per mass of the heat mediator in the case of MNPs. SAR depends on various factors, among them (i) the applied magnetic field characteristics (frequency and amplitude), (ii) the intrinsic magnetic properties (i.e., saturation magnetization, anisotropy) that depend on MNP features such as size, shape, composition, and arrangement, and (iii) the characteristics of the dispersing medium (i.e., viscosity, concentration, heat capacity).

Controlled or uncontrolled aggregation in a centrosymmetric 3D configuration—a bead-like assembly—was reported to lower SAR values.¹²⁻¹⁵ On the contrary, controlled aggregation in chain-like structures driven by anisotropic interactions of magnetic nanoparticles was reported to improve SAR values. For instance, bacterial magnetosome chains that are ca. 50 nm cubic-shape iron oxide nanoparticles individually coated with a lipid shell—naturally aligned in chain-like morphologies on protein filaments—are currently state-of-the-art in terms of hyperthermia performance.¹⁶ Similar findings were demonstrated by Serantes et al.,⁸ who have investigated the influence of dipolar interactions on the hysteresis loops in magnetic nanoassemblies by means of Monte Carlo simulations. Their Monte Carlo computational model predicted an increase in the area of the hysteresis loop by increasing the chain length as the key factor to improve SAR values. Alongside their mathematical calculations, their experimental calorimetric measurements—on 44 nm ferromagnetic spherical magnetite nanoparticles forming micrometer long chains in agarose upon applying 0.12 T magnetic fields—demonstrated the importance of chain alignment on the heating efficiency.⁸

Their model also showed how centrosymmetric assemblies composed of eight nanoparticles led to smaller hysteresis loops compared to the corresponding chain-like configuration.⁸ This indicates the importance of obtaining elongated assemblies of MNPs. Magnetic dipole–dipole interactions leading to the formation of chain-like structures under the action of external magnetic fields were also exploited by other groups to showcase the effect of the arrangement at the nanoscale on magnetic hyperthermia. Compared to the nonaligned samples, 40 nm magnetite nanoparticles—dispersed in agarose gel matrix and magnetically aligned in 40 mT fields—presented SAR values enhanced by a factor of 2.¹⁰

However, only relatively few studies have investigated the formation of particle arrangements of defined geometries—1D, 2D, or 3D structures—colloidally stable in a solution without the application of an external field and their correlation with magnetic hyperthermia measurements. In the work of Andreu et al.,⁹ in order to build clusters of different geometries, different encapsulating materials were exploited. Magnetic nanoparticles were embedded in silica nanoworms to obtain 1D chain arrangements, while poly(d,l-lactide-co-glycolic) acid (PLGA) was used for small 2D grouping of nanoparticles enwrapped in polymer spheres, showing that their magnetic properties and the hyperthermia response were governed by nanoparticle arrangement. The 1D and 2D nano-objects displayed an improved SAR behavior compared to that of single nanoparticles or agglomerates of NPs.⁹

Besides using PLGA polymer, known to be biocompatible and noncytotoxic,¹⁷ also many other polymers including dioleate-modified polyethylene glycol,¹⁸ poly(ε-caprolactone)-b-poly(ethylene glycol) (PCL-b-PEG),¹⁹ poly(trimethylammonium ethyl acrylate methyl sulfate)-b-poly(acrylamide),²⁰ poly(ethylene oxide-b-acrylate) (H₂N-PEO-b-PAA),²¹ poly(lactic-co-glycolic acid)-b-poly(ethylene glycol) (PLGA-b-PEG),²² and even triblock copolymers such as poly(ethylene imine)-b-poly(ε-caprolactone)-b-poly(ethylene glycol) (PEI-b-PCL-b-PEG)²³ were used in the literature to form polymeric colloidal clusters of nanocrystals. These soft colloidal nanocrystal clusters—a term introduced by Bakandritsos et al.(24)—have been evaluated as contrast agents for MRI, while no hyperthermia studies have been reported.¹⁸⁻²³

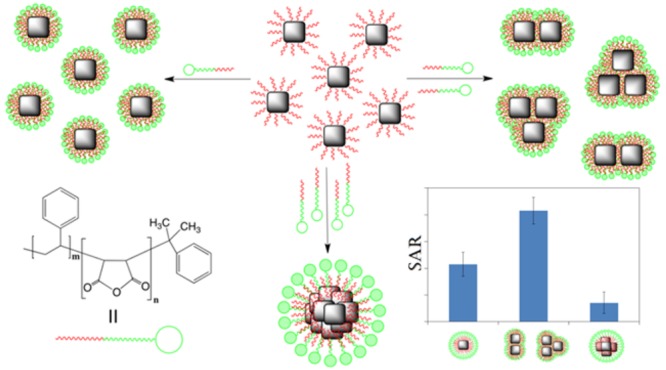
In this study, by using one type of nanocube and one specific amphiphilic polymer and by adjusting the polymer-to-nanoparticle parameter we controlled the formation of colloidally stable (i) single particles, (ii) dimer and trimer assemblies, and (iii) centrosymmetric structures. We then studied the evolution of SAR with the size and spatial arrangement of clusters and the corresponding magnetic parameters of the various soft colloidal clusters. The experimental SAR results are supported here by the theoretical simulations carried out by means of a kinetic Monte Carlo computational model on the clusters. We demonstrate that the primary factor responsible for the enhancement of SAR is, in fact, not the variation of M_s but rather the dipolar interaction effect induced by the arrangement of nanocubes into dimers, trimers, and centrosymmetric clusters. This work clearly shows that when working with one single type of MNP while promoting the anisotropic assembly of the MNPs, structured nanomaterials with enhanced heat performance are obtained.

Results and Discussion

The overall clustering process is schematically shown in Figure 1I. FeO/Fe₃O₄ core–shell iron oxide nanocubes²⁵ (IONCs, with an edge length of 20.2 ± 1.5 nm, Figure S1) were first used in this study. The choice of core–shell nanocubes was dictated by their magnetically noninteracting nature, alongside their initial stability in tetrahydrofuran (THF), as evidenced by the clear THF solution. Both conditions were considered prerequisites for a successful clustering protocol. Attempts done with noncompletely soluble nanoparticles were not successful (data not shown).

Figure 1.

Scheme of the clustering protocol using 20 nm core–shell iron oxide nanocubes. Representative TEM micrographs of IONCs@PScMA in water and just after they have been prepared at a ratio of (A) 16.5, (B) 33, (C) 50, and (D) 66 polymer chains/nm² of particle surface. (E–H) Collection of TEM images at higher magnification of dimers and trimers formed at the ratio of 33. (I) Schematic representation of the formation of soft colloidal nanoclusters.

In a typical clustering procedure for obtaining centrosymmetric clusters, taken as an example, as-synthesized oleic-acid-coated IONCs (m_Fe = 0.23 mg) were dispersed in 10 mL of THF together with the amphiphilic polymer poly(styrene-co-maleic anhydride) (PScMA), cumene-terminated (M_n = 1600 g/mol), at a ratio of 66 polymer chains/nm² of nanoparticle surface. Subsequently, the addition of 1 mL of H₂O by a syringe pump (0.5 mL/min), followed by sonication of the NP–polymer solution in an ice bath. During this step, the solution had to remain clear as the water transfer would fail if the THF/H₂O mixture became turbid during the water addition.

Interestingly, in the H₂O/THF mixture (ca. 1.5 mL), the nanocubes were not yet clustered; they still appeared as single nanocubes on the transmission electron microscopy (TEM) grid (data not shown), and the solution was clear. As the last 0.5 mL of THF evaporated, the solution became turbid. After full evaporation of THF, the IONCs were already clustered, and a thin layer of polymer was clearly evident on the clusters as checked by TEM characterization, even before the CHCl₃ addition (Figure S2a). These data suggest that the clustering was favored by the change in solubility of polymer and nanocubes as soon as the THF evaporated from THF/water mixture. The chloroform addition step promoted the extraction of the excess of polymer/surfactant molecules from the aqueous phase into the organic phase. This was clearly evident as a milky layer of polymer was found at the interface between CHCl₃ and water (Figure S3), and after CHCl₃ addition, no more extra polymer was visible on the TEM grid (Figure S2b).

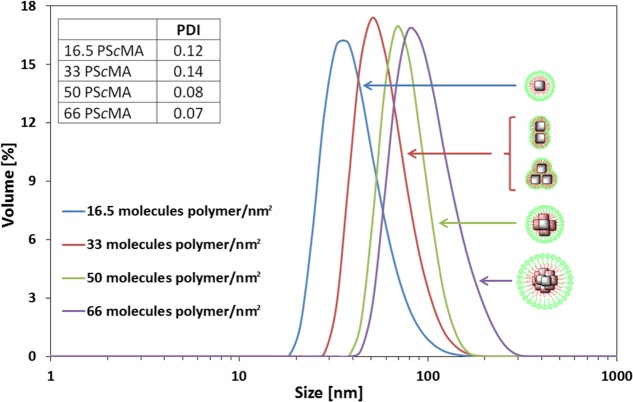
To set the clustering protocol, different parameters were investigated systematically. This list included the rate of THF evaporation, the ratio of water to THF, the total solution volume, and the amount of polymer. However, the main parameter that allowed a fine-tuning of the cluster size and the configuration of the nanoclusters was the number of molecules of amphiphilic polymer, poly(styrene-co-maleic anhydride), per square nanometer of particle surface. This ratio varied between 16.5 and 66 molecules/nm², corresponding to a change in size and configuration of the formed clusters. With an increase in polymer amount, the degree of clustering increased, as seen in the TEM micrographs in Figure 1. As judged by the distribution of nanoparticles on the TEM grid and from the interparticle distance (Figure 1A), with a ratio of 16.5 molecules of polymer/nm², the majority of the nanocubes were individually coated, whereas by doubling the amount of polymer to 33 molecules/nm², dimers and trimers were formed (Figure 1B). In this specific case, the dimer and trimer arrangements were even more evident by looking at a collection of TEM images in which isolated groups of two or three nanocubes were clearly seen. Often, on the same grid, different dimers and trimers were observed (Figure 1E–H). At 50 and 66 molecules of polymer/nm², the number of nanocubes per cluster increased, respectively, forming more tetramers or grouping of centrosymmetric clusters containing more than 5 nanocubes each (Figure 1C,D). The corresponding hydrodynamic volume distributions, as measured by dynamic light scattering (DLS), also reflected the size increase from ca. 40 to 100 nm (Figure 2). The mean hydrodynamic diameters by volume were 38 ± 2 nm (PDI 0.12), 51 ± 3 nm (PDI 0.14), 68 ± 4 nm (PDI 0.08), and 99 ± 2 nm (PDI 0.07) for 16.5, 33, 50, and 66 PScMA/nm², respectively. Note that the very low polydispersity index (PDI) values indicate a homogeneous distribution of the clusters obtained. Once formed, the cluster solutions could be kept for a very long time (more than a year) without showing any sign of aggregation (DLS and TEM characterization were the same as for freshly prepared samples).

Figure 2.

Tuning the mean hydrodynamic diameter of clusters by different polymer amounts. Volume distribution of hydrodynamic size d_H of soft colloidal clusters measured in water starting from 20 nm IONCs. The d_H was adjusted between 38 and 99 nm. No aggregation of clusters was detected as PDI values were between 0.07 and 0.14 (see inset).

Given that the hydrodynamic diameter obtained was an average value and that TEM images provide only qualitative images of the assemblies, in an attempt to quantify the percentage of individually coated nanoparticles, dimers, trimers, and clusters with more than four nanocubes for the different samples, we ran a statistical image analysis using ImageJ software. Numerous TEM micrographs were analyzed in order to obtain a statistical distribution of individually coated nanocubes versus 1D and 2D constructs (dimers and trimers, respectively) versus 3D constructs (bigger colloidal nanoclusters with n ≥ 4) so that at least 250 objects were analyzed for each sample (Figure S4). We focused on the three available samples: at 16.5, 33, and 66 polymer molecules/nm² samples (from now on, they will be referred to as 16.5PScMA, 33PScMA, and 66PScMA, respectively), as on those samples, further SAR measurements and magnetic characterizations were carried out. For sample 16.5PScMA, 255 objects were studied, corresponding to a total of 342 individual nanocubes, of which 66% were individually coated, 28% were dimers, 4% were trimers, and 2% were bigger clusters (Figure 3A). For sample 33PScMA, when doubling the amount of polymer with respect to the 16.5PScMA sample, out of 254 objects analyzed (Figure S4), corresponding to 493 IONCs, 70% consisted of an equal population of dimers and trimers (Figure 3B). The 30% remaining objects were 19% individually coated NPs and 11% 3D arrangements. For sample 66PScMA, when still doubling the polymer amount with respect to sample 33PScMA, almost only 3D clusters were obtained, representing 86% (Figure 3C) of the 259 objects inspected, corresponding to more than 1000 NPs (Figure S4). The remaining 14% of sample 66PScMA was equally distributed between single particles (5%), dimers (5%), and trimers (4%). Overall, we could statistically confirm that by increasing the polymer amount from 16.5 to 33 and further to 66 molecules of PScMA/nm² of NP surface, the resulting clusters evolved from a major population of individually coated nanoparticles to dimers and trimers and, last, to groups of more than 4 nanocubes per unit.

Figure 3.

Statistical analysis of fractions of different objects for samples (A) 16.5PScMA, (B) 33PScMA, and (C) 66PScMA indicated the presence of (A) 32% 1D and 2D constructs (28% dimers and 4% trimers) in sample 16.5PScMA, (B) majority of 70% (35% dimers and 35% trimers) in sample 33PScMA, and (C) only 9% (5% dimers and 4% trimers) 1D and 2D structures in sample 66PScMA, with a majority of clusters with a number of nanocubes higher than 4 (86%).

Thermogravimetric Analysis

Nanoparticle Surfactant Effect

In addition to the evaporation rate of THF, polymer amount, and initial stability of the nanocubes in THF, another crucial parameter for the successful water transfer and cluster formation was the surfactant amount associated with the nanocubes. We observed differences in the clustering procedure when changing the batch of core–shell IONCs (20.2 ± 1.5 nm) to a batch with a similar edge length of 20 ± 2 nm (Figure S5). Indeed, sometimes even if the initial cubes were soluble in THF, as for other batches of nanocubes, the procedure did not result in cluster formation. In order to elucidate the correlation between different batches of nanocubes and the clustering procedure, we carried out thermogravimetric analysis (TGA) on the two batches of nanocubes, as the amount of surfactant molecules, oleic acid (OA), stabilizing the nanocubes may have also contributed to cluster formation.

The thermogravimetric analysis of the IONC sample dispersed in CHCl₃ (sample A), for which the clustering process worked straightforwardly, showed a first weight loss of 26.4 wt % in the temperature range from 150 to 300 °C and a second weight loss of 31.2 wt % from 300 to 400 °C (Figure 4a, blue line). The first transition is mainly attributed to unbound or physisorbed OA,²⁶⁻²⁸ whereas the second transition is related to the oleate molecules chemisorbed on the particle surface.²⁶⁻²⁸ As a comparison, the TGA degradation profile of oleic acid is plotted showing a weight loss of ca. 90 wt % at 300 °C (Figure 4a, violet line), supporting the claim that the first weight loss is due to free oleic acid.

Figure 4.

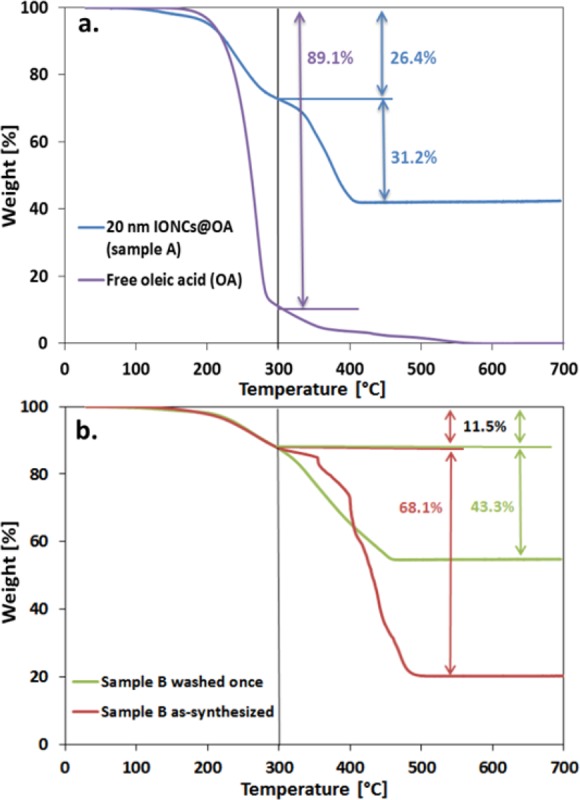
(a) TGA weight-loss profiles of oleic-acid-capped IONCs (sample A, blue curve) and free oleic acid (violet curve) performed in air. The first weight loss in the region between 150 and 300 °C corresponded to free oleic acid in solution, and the second weight loss in the region between 300 and 400 °C corresponded to oleate chemisorbed to the surface of the IONCs. (b) TGA weight-loss profiles of a new batch of as-synthesized oleic-acid-capped IONCs (sample B, red curve) and sample B after washing to remove excess of oleic acid (green curve). On sample B, before washing, no clusters were obtained. Upon one washing, the amount of oleate decreased from 68.1 to 43.3 wt %, re-establishing the cluster formation on sample B.

It should also be noted that, for this batch of IONCs, the amount of oleate chemisorbed to the surface of the IONCs—ligand density (ρ_l)—was much higher than the theoretical 5 ligands/nm².^29,30 The calculated ligand density was 27 ligands/nm² if only the second weight loss seen in TGA was considered. If instead the total weight loss of surfactant is considered—both decomposition steps between 150 and 400 °C—the surfactant density was 50 ligands/nm², with a 46 and 54% fraction corresponding to free oleic acid and oleate bound to the surface of the NPs, respectively. These results suggest a multilayer coating of surfactant on the particle (likely promoted by the hydrophobic interaction between the OA alkyl chains).

Next, TGA analysis was carried out on the core–shell IONC batch before and after the washing step, as for this batch the clustering process did not work initially (Figure 4b, sample B as-synthesized), but it did work after washing the excess surfactant (Figure 4b, sample B washed once). For the as-synthesized sample in CHCl₃ (Figure 4b), the organic layer accounted for a mass loss of 79.6 wt %, with 11.5 wt % corresponding to free oleic acid in solution and 68.1 wt % to oleate molecules (Figure 4b, red curve). The excess amount of oleate was due to a change in the amount of OA used for the synthesis of this batch. Interestingly, after centrifuging the sample in a mixture of chloroform/methanol (1:3 v/v), on the final sample, the total oleic acid amount associated with the IONCs was assessed to be 54.8 wt %, of which the oleate amount decreased to 43.3 wt % (Figure 4b, green curve). These results suggested that the amount of chemisorbed OA was crucial to the cluster formation: when too high, no clusters were formed, suggesting that the polystyrene branches of the amphiphilic PScMA could not intercalate with the surfactant layer, as the surfactant molecules were tightly packed close to one another. After the washing, as some of the OA molecules were stripped from the external layers, the decrease in the amount of chemisorbed OA facilitated the NP interaction with the polymer, and the water transfer proceeded. It is worth mentioning that there is a range of concentration of OA per nanoparticles in which the protocol works. We noticed, for instance, that an additional second washing step on the same sample did not result in cluster formation anymore. This indicated that by decreasing the chemisorbed OA amount from 124 (as-synthesized sample) to 29 (sample washed once) ligands/nm², the hydrophobic tail of the polymer, the PS units, could intercalate with the alkyl chain on the nanocube, while having even less oleate molecules, the interaction was no longer favorable.

Overall, the TGA data suggest that the balance between the oleate molecules chemically bound to the surface of the IONCs and the oleic acid molecules physisorbed or intercalated between the oleate molecules, forming additional outer layers of surfactant, was a crucial parameter to be controlled in order to obtain soft colloidal clusters.

It is interesting to note that the arrangement in chain configurations of nanoparticles has been observed in many phenyl-based polymers.³¹⁻³³ Polystyrene has been used, for instance, to cluster cobalt ferrite nanoparticles in chain assemblies of micrometer chain length³¹ and the same polymer has also been used to chain gold nanorods in a tip-to-tip configuration.³² Similar to the latter work, in our system, the cumene-terminated polymer and the nanocubes are both well soluble in THF; however, the addition of water as an antisolvent induces a different precipitation of the hydrophobic poly(styrene) moieties of the cumene-terminated polymer and the oleic-acid-capped nanocubes. We might speculate that the polymer–polymer interaction is more favorable compared to the polymer–nanoparticle interaction, likely because of their difference in solubility in the solvent mixture. Given that the nanocubes have multiple layers of OA, this shell (OA bears a carboxyl moiety) might provide a greater solubility of the IONCs compared to that of the amphiphilic PScMA in the THF/water mixture. This would likely provide a higher nanocube–nanocube affinity and drive the slow arrangement of the nanocubes in chains while the polymer molecules would tend to interact through phenyl rings. If this is the case, we would also explain why here, and in contrast to other works,²³ an increase in the polymer amount favors the clustering rather than the individual coating of nanocubes. If we compare our procedure to a previously reported procedure,²³ in which the authors reported that a high polymer/NP ratio favored the formation of discretely encapsulated MNPs, whereas at low ratio particle clustering was enforced by the relative depletion of polymer, we can underline that the main difference was the type of amphiphilic polymer chosen. Indeed, while we opted for the copolymer poly(styrene-co-maleic anhydride), in the work of Pöselt et al.,²³ the triblock polymer poly(ethylene imine)-b-poly(ε-caprolactone)-b-poly(ethylene glycol) was used for cluster formation.

Finally, it should be noted that our cluster procedure can be extended to other core–shell systems prepared by other methods³⁴⁻³⁶ (see, for instance, Figure S6 for another core–shell nanocube having a similar edge size and Figure S7 for iron oxide nanoparticle of 18 nm diameter and spherical shape). However, the procedure did not work when using Fe₃O₄ nanocubes that did not have a core–shell structure.⁶ For instance, Fe₃O₄ nanocubes of 20 nm were not soluble in THF, the initial solvent, and therefore, the procedure could not be tested. For 13 nm Fe₃O₄ nanocubes, being superparamagnetic and thus noninteracting, although the particles were soluble in THF, despite changing several reaction parameters in order to optimize them, only deformed groupings of nanocubes were obtained, but no dimers and trimers were properly formed (data not shown).

Magnetic Properties

Hyperthermia

The SAR measurements were performed on clustered samples that were prepared starting from core–shell nanoparticles which were subsequently aged for 1 year at room temperature. Under these conditions, the samples slowly changed from a core–shell structure to a quasi-one-phase material. The X-ray diffraction (XRD) pattern of the aged nanocubes is shown in Figure S8. The major reflections coincide with Fe_2.96O₄ (ICSD collection code: 82443). There exists 10–15 wt % FeO phase (Fe_0.942O, ICSD: 24696) in the nanocubes.

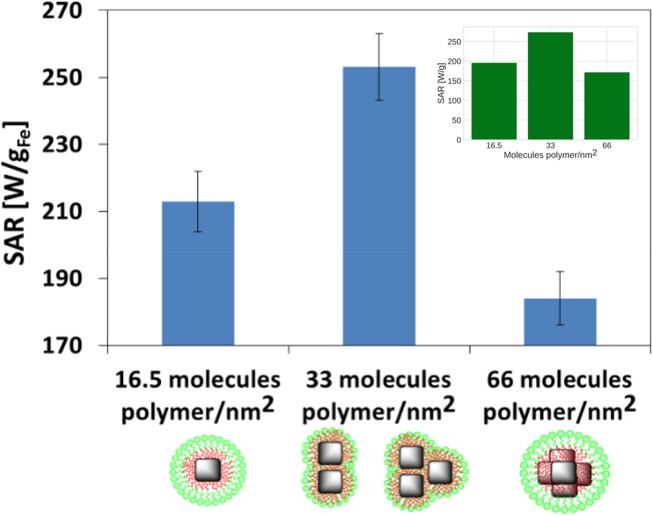
The SAR values were obtained at the highest frequency (302 kHz) and magnetic field (23.8 kA/m) of the instrument (nB Nanoscale Biomagnetics DM100 series) as the Fe concentration of the samples was in the range of 0.65–0.95 g/L in a volume of 200 μL. The values were 213 ± 9, 253 ± 10, and 184 ± 8 W/g_Fe for nanoconstructs formed at ratios of 16.5, 33, and 66 molecules PScMA/nm² of particle surface. By plotting (Figure 5) the trend observed for the different samples, we registered an increase in SAR for the mixture of dimers and trimers (33 molecules polymer/nm², Figure 1B,E–H) compared to both samples of individually coated nanoparticles (16.5 molecules polymer/nm², Figure 1A) and soft colloidal clusters with n ≥ 4 (66 molecules polymer/nm², Figure 1D), with n being the number of particles per cluster. When looking at the statistics, we could confirm that on the sample in which we have measured the highest SAR value (the 33 PScMA sample), the percentage of dimers and trimers was statistically higher. Individual nanocubes and clusters with n ≥ 4 were instead the predominant population for the samples 16.5PScMA and 66PScMA, respectively. As already reported by other groups, our data also suggest that centrosymmetric clusters significantly reduced the SAR value of the nanocubes (Figure 5). The inset in Figure 5 shows results of calculations based on the kinetic Monte Carlo modeling (see Materials and Methods section), which recovers the behavior observed experimentally for the different cluster types. Obtaining the agreement between the simulation and experiment (within the error bar) required setting the anisotropy constant value to K = 5 × 10⁴ erg/cm³. The single-particle values of the saturation magnetization were taken directly from the experimental data and corresponded to M_s of 367, 407, 407, and 314 emu/cm³ for the ensembles of, respectively, noninteracting, two-particle, three-particle, and six-particle clusters. The low value of K suggests that dipolar interactions dominate the anisotropy field of particles, as will be discussed later.

Figure 5.

SAR values for soft colloidal nanoclusters after 1 year aging time, formed at ratios of 16.5, 33, and 66 molecules PScMA/nm² of particle surface (f = 302 kHz, H = 23.8 kA/m). A higher SAR value was recorded for dimers and trimers compared to individual IONCs and clusters with n ≥ 4. Clustering the IONCs in centrosymmetric bead-like structures decreased their heating performance. Each experimental data point was calculated as the mean value of at least three independent measurements, with error bars indicating the mean deviation. Inset: SAR values obtained from kinetic Monte Carlo modeling of the structures as described in the text, reproducing the observed experimental trend within the error bar. Interparticle spacing for the simulation has been set to 1 nm gap as measured on the TEM images.

Magnetization Measurements

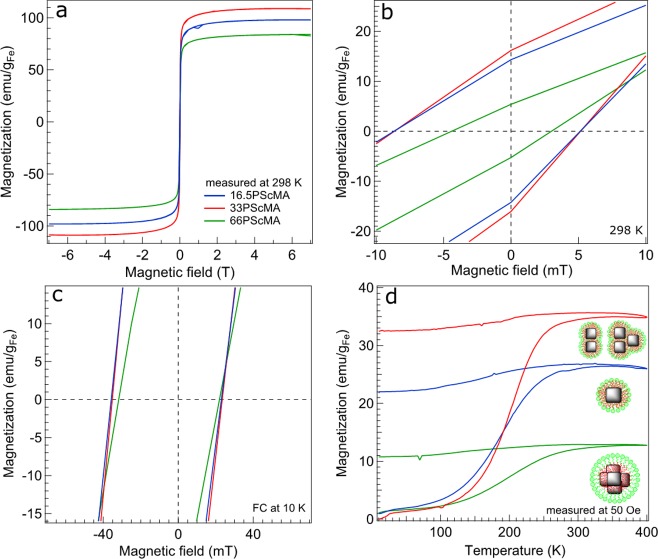
To gain a deeper knowledge about the magnetic properties of the fabricated constructs and also in an attempt to correlate static magnetic properties with dynamic features, here specifically the SAR, applied field and temperature-dependent magnetization measurements were carried out on all three samples. The magnetization hysteresis loops MversusH recorded at 298 and 10 K are shown in Figure 6. The formation of dimers is expected to enhance a collective magnetic behavior owing to the anisotropic alignment of nanoparticles and results in a significant enhancement of the hysteresis loop area. On the contrary, larger clusters (n ≥ 4) and also trimers experience a demagnetization effect due to their specific particle configuration with the tendency to form flux closure domains, thus causing a weakened coupling to external magnetic fields, that is, narrow hysteresis loops (see also our simulations Figure S13). At T = 298 K, both single nanoparticles and dimers and trimers reveal an identical remanent magnetization M_r and coercive field H_c (Figure 6b), while M_r and H_c decrease significantly in the 3D clusters (clusters with n ≥ 4). These results are supported by our numerical simulations, which show significant differences in the shape of dynamic hysteresis loops for different particle cluster structures (see Figures S13 and S14). Different behavior is observed at 10 K where the variation of H_c and M_r with a clustering state vanishes. This suggests that the increased anisotropy field and coercivity at the low temperature is sufficient to overcome the effects of interactions, an observation consistent with the interpretation of the room temperature magnetic properties in terms of different cluster structures. We also confirmed by using numerical simulations that increasing the values of M_s in magnetic nanostructures can lead to an improved overall heating performance; however, the dependence is nontrivial and significantly dependent on the particle cluster geometry (Figures S15 and S16).

Figure 6.

Magnetization hysteresis loops measured at room temperature (a,b), after cooling to 10 K in 5 T magnetic fields (c), and temperature-dependent zero-field-cooled and field-cooled magnetization measurements performed on aqueous suspension of nanoclusters after a year of aging time, solidified in gypsum matrix recorded at 50 Oe magnetic fields (d): 16.5PScMA (blue line, individual IONCs), 33PScMA (red line, dimers and trimers), and 66PScMA (green line, clusters with n ≥ 4).

It is tempting indeed to assume that large M_s values give rise to higher SAR because, given that the maximum magnetization of the system is directly proportional to M_s, intuitively higher M_s should imply a higher hysteresis loop area. However, a simple physical picture based on the Stoner–Wohlfarth particle theory suggests that given that the coercive field is inversely proportional to M_s (i.e., H_c ∝ 1/M_s), and the hysteresis loop area is related to M_s·H_c apart from a proportionality factor, the dependence of the loop area on M_s is eliminated (see (1) in the left columns in Figures S15 and S16). However, the value of M_s contributes to the heat dissipation indirectly, through determining the coercive field which, relative to the amplitude of the applied magnetic field, affects the size of minor or major hysteresis loops and thereby may induce significant differences in the heating output.³⁷ The value of M_s also determines the strength of the dipolar interactions, which also affects SAR, and the interaction effect may even dominate over the single-particle properties as suggested previously^38,39 and also by the present study (Figures 5, S15, and S16). Our numerical simulations assuming the same M_s = 450 emu/cm³ for all types of cluster structures clearly displays the same quantitative trend in SAR (Figure S15D,E). Moreover, at fixed K, varying the value of M_s in the range between 300 and 500 emu/cm³ preserves the overall trend of SAR for the different cluster types with minor difference between SAR versus clusters for different M_s values (Figure S16). These data support only a minor dependence on SAR of clusters over M_s and support the interpretation that the interparticle interactions and their dependence on the details of the particle arrangement within the clusters are an important factor in determining SAR.

We have also investigated using simulations the dependence of SAR on the interparticle edge to edge spacing as a way to control the dipolar interaction strength. Figure S17 suggests that while SAR is independent of the interparticle spacing for noninteracting particles, it decays monotonically with the spacing distance for dimers. This is expected because dipolar interaction weakens as particles are brought further apart. Interestingly, however, the spacing dependence of SAR is nonmonotonic for trimers and hexamers, which can be attributed to the effect of magnetic frustration and the collective magnetization behavior relevant for small spacing distances when particles are close and dipolar interactions strong. In addition, we have also used simulations to explore the cluster shape dependence of SAR, by considering six-particle clusters arranged into statistically different geometries quantified by a variable fractal dimension (Figure S18).⁴⁰ The values of SAR are the largest for statistically chain-like structures and continually decrease with the increasing degree of geometrical symmetry. Spherical cluster geometries lead to the lowest values of SAR. This confirms that tuning the cluster shape has profound consequences on SAR values.

It is well-known that such antiferromagnetic–ferrimagnetic (AFM–FiM) core–shell nanoparticles show so-called exchange bias identified by a shifted hysteresis loop 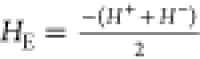, toward the opposite direction of the applied field in a field-cooled (FC) measurement. All three cluster samples, measured after 1 year aging time, show a slightly shifted loop with H_E of around 6 mT (Figure 6c). This means that all the samples have virtually the same phase composition and, yet after a year, show a small AFM–FiM interface volume. This feature was also confirmed by XRD data (Figure S8). The XRD pattern of aged nanocubes in CHCl₃ is identical to the nanocubes forming the clusters, as shown in Figure S8. The major reflections coincide with Fe_2.96O₄ (ICSD: 98-008-2443). Likely, the existence of 10–15 wt % FeO phase (Fe_0.942O, ICSD: 98-002-4696) in the particles, together with the structural defects, can account for the persistence of H_E. In a previous work,²⁵ we have found that similar core–shell nanocubes, which underwent thermal annealing at 130 °C and were thus fully transformed to the spinel phase, were still showing H_E of 5 mT. This was related to the existence of structural defects such as antiphase boundaries (APBs) as was also reported by other groups.³⁵

Broadly speaking, the magnetic energy barrier KV distribution, with K being the magnetocrystalline anisotropy constant and V the nanoparticle magnetic volume, can be qualitatively judged by looking at the steepness of zero-field-cooled (ZFC) curves as well as FC ones (Figure 6d). A steeper ZFC curve corresponds to a narrower KV distribution. At a first glance, it is seen that the dimers and trimers (33PScMA) and 3D constructs (66PScMA) show the steepest and the most gradually rising ZFC curve, proportional to the narrowest and broadest KV distribution, respectively. The superparamagnetic blocking temperature T_b, estimated from the maximum of ZFC curves, increases from 346 to 355 K and then to 379 K for singly coated particles, to dimers and trimers, and ultimately to 3D clusters, respectively. To a first approximation, knowing the T_b, the anisotropy constant is estimated by exploiting the Néel relaxation formula given by KV = 25k_BT_b (only valid at zero magnetic field, no magnetic interaction, and assuming typical measurement time at SQUID of 100 s), and K ∝ T_b/V holds that with both T_b and V increasing as dimers/trimers and 3D clusters are formed, it is plausible to assume that K constants of all three samples are comparable. Note that having assigned an identical K value (K = 5 × 10⁴ erg/cm³) to all three samples in the Monte Carlo simulations, a good numerical reproduction of the SAR results was achieved (Figure 5 inset and Figure S15).

SAR Value Improvement by Annealing

Having chosen FeO/Fe₃O₄ core–shell nanoparticles as starting materials, questions arose whether (i) the clusters, once formed, would be stable against a thermal oxidation transforming the initial biphasic core–shell system into a single phase material in a much shorter time, in comparison to the case of spontaneous room temperature oxidation discussed above, and (ii) whether the trend in SAR values of individual IONCs versus dimers and trimers and versus bigger soft colloidal clusters (n ≥ 4) would still be maintained.

We chose a freshly synthesized sample of core–shell iron oxide nanocubes with an edge length of 20 ± 2 nm (sample B, Figure S5) similar in size to the previous one studied for the clustering (Table S1). The XRD pattern of this sample reveals reflections of both Fe_2.96O₄ (ICSD: 82443) and Fe_0.942O (ICSD: 24696) phases, however dominated by the latter one (Figure S9a). Once the clusters were obtained (Figure S9b), the FeO core was oxidized to magnetite by thermal annealing in an oven at 80 °C for different time periods, each of them with an overnight duration up to a total of 52 h (Figure S9b). Hyperthermia experiments were carried out before and after each step of the annealing process, alongside XRD, DLS, and TEM characterization to follow the evolution of the phase composition, the morphology, and the colloidal stability of the clusters (Figures 7 and S10).

Figure 7.

Evolution of SAR values of soft colloidal nanoclusters by annealing in an oven at 80 °C. (A) SAR values (with standard deviation) for soft colloidal nanoclusters during the annealing process: individual IONCs, blue bars; dimers and trimers, red bars; and clusters with n ≥ 4, green bars. Only after 18 h of annealing did the sample of dimers and trimers show higher SAR values. The trend was maintained up to 52 h of annealing. (B) Schematic representation of the oxidation of the FeO core for clusters of different sizes in an oven at 80 °C.

The SAR values before annealing were below 50 W/g_Fe (Figure 7a and Table 1), which was expected for core–shell iron oxide nanocubes, due to a nearly noncontributing paramagnetic FeO core and small magnetite domains oriented differently on the outer layers.²⁵ As the first oxidation of the core by heat treatment started, the SAR values gradually increased up to a factor of 3.7 to 131 ± 5, 179 ± 1, and 97 ± 4 W/g_Fe for individual IONCs, dimers/trimers, and bigger clusters, respectively (Table 1). The dimer and trimer samples showed the highest SAR values compared to those of the other two samples after only 18 h of annealing. The trend was maintained throughout the whole annealing process, up to 52 h (Figure 7a and Table 1). After 52 h, the SAR values for all the samples did not improve any further. The XRD pattern of the 52 h annealed sample is dominated by the Fe_2.96O₄ (ICSD: 82443) phase, yet there is a detectable fraction of FeO (Figure S9b). It seems that in order to obtain completely oxidized particles, harsher oxidative conditions (e.g., higher temperatures, oxygen purging) have to be applied, compromising the stability and shape of the particles. In our previous work, we have observed that long oxidation times on individually coated nanocubes at 130 °C result in a full oxidation to maghemite, having a lower M_s and more aggregated state, with a marginal SAR improvement.²⁵

Table 1. SAR Values of Soft Colloidal Nanoclusters at 302 kHz Frequency and 23.8 kA/m Magnetic Field.

	individual IONCs@GaPEG SAR (W/gFe)	dimers and trimers SAR (W/gFe)	bigger clusters (n ≥ 4) SAR (W/gFe)
before annealing	46 ± 2	48 ± 3	42 ± 2
after 18 h annealing	131 ± 5	179 ± 1	97 ± 4
after 35 h annealing	180 ± 5	216 ± 1	142 ± 9
after 42 h annealing	183 ± 2	233 ± 1	138 ± 3
after 52 h annealing	162 ± 7	246 ± 8	150 ± 3

Remarkably, all the samples were stable during the annealing process as confirmed by DLS measurements (Figure S10). For example, for the sample of clusters with n ≥ 4, the volume weighted hydrodynamic diameter remained unchanged during the whole annealing process, with a Z-average of 98.1 ± 0.6 nm (PDI 0.07) before annealing and 96.5 ± 0.2 (PDI 0.08) after 52 h of annealing.

Similar static magnetic measurements have been performed on these samples (Figure S11). H_E of all three sample is ca. 6 mT (Figure S11c), similar to that of the other clusters (Figure 6c). This means that for all the colloidal assemblies the building block nanocubes have a similar phase composition, as also deduced from the XRD patterns (Figures S8 and S9b). Temperature-dependent magnetization curves reveal some interesting features (Figure S11d). It can be discerned that the dimers and trimers have the steepest ZFC curve rise, implying the narrowest KV distribution among all the samples. Strikingly, individual particles show a higher T_b (ca. 400 K) than dimers and trimers (i.e., 370 K), presumably caused by magnetic dipole–dipole interactions. It is known that slight particle–particle interactions can significantly shift T_b toward higher temperatures.⁴¹

Figure S15 shows results of simulations using the kinetic Monte Carlo modeling for variable value of effective anisotropy constant K. We set M_s = 450 kA/m of bulk Fe₃O₄. The right column of Figure S15 shows data similar to that in Figure 7, where Figure S15D resembles the 18 h annealed data well. This points to low effective anisotropy of particles K = 5 × 10⁴ erg/cm³, as the trend is in qualitative disagreement for higher value of the anisotropy constant. For this low effective anisotropy value, the dipolar interactions dominate the anisotropy, and therefore, the differences in SAR can be attributed to the presence of dipolar interactions, in agreement with previous studies.³⁵ They found significant reduction of the value of the effective anisotropy K with respect to the nominal value expected for cubic anisotropy K_c = −1.1 × 10⁵ erg/cm³. This is also supported by previous analysis, which estimates equivalent value of the effective uniaxial K to be equal to about 70% of K_c. The left column plots (a–d) in Figure S15 show the SAR before mixing the different fractions of the clusters according to Figure 3, which allows one to compare contributions to SAR from the distinct populations (i.e., only single cubes, only dimers, etc.).

Overall, these data suggest that for core–shell nanoparticles the assembly can be easily performed when the particles are in a noninteracting state, while their transformation to a more heat efficient material by annealing at moderate temperatures can occur after having obtained the clusters without losing their arrangement and colloidal stability. It is also worth highlighting that clustering the core–shell MNPs followed by the oxidation of the core is a promising method to achieve the highest yield of soft clusters with higher SAR values.

It may be worth mentioning here that other anisotropic nanomagnets, for example, nanowires or nanorods, could offer similar enhanced heating performances (with easier to tune aspect ratio).^42,43 Furthermore, such anisotropic structures can have also magnetomechanical actuation properties exploitable for cell damage.⁴⁴ However, it must be emphasized that the discrete nature of the dimers and trimers, reported by us, makes easier their disassembling and elimination after use, an important aspect to consider for clinically aimed approaches.⁴⁵

Conclusions

We have shown here that SAR values of core–shell IONCs were enhanced by forming anisotropic structures compared to both individually coated nanocubes and centrosymmetric clusters. The controlled clustering occurred during the water transfer of IONCs in the presence of the amphiphilic poly(maleic anhydride) polymer having poly(styrene) groups as hydrophobic chains. A few parameters were crucial to the cluster formation: while the anisotropic structures were dictated by the amount of amphiphilic polymer per nanoparticle surface, the rate of THF evaporation alongside the amount of surfactant determined the reproducibility of the protocol. The 1D and 2D structures formed with two and three IONCs, so-called dimers and trimers formed at the ratio of 33 molecules polymer per nanometer square of particle surface, showed higher SAR values than the individually coated nanoparticles and the centrosymmetric clusters, highlighting the importance of the arrangement of the nanoparticles at the nanoscale. For this study, we have selected freshly synthesized FeO/Fe₃O₄ core–shell nanocubes that, after cluster formation, underwent structural transformation in aqueous solution from FeO/Fe₃O₄ core–shell structure to mainly Fe₃O₄ phase either by slow aging at room temperature (time scale of a year) or by faster annealing process in an oven at 80 °C (time scale of few days). Remarkably, even in the latter case, the grouping of nanocubes in dimers and trimers presented higher SAR values than single cubes and centrosymmetric clusters, while their aqueous stability was not compromised upon annealing treatment. We also observed a variation of M_s between the different cluster structures, where the highest values of M_s corresponded also to the dimer and trimer cluster structures. Although this might suggest that the variation of M_s correlates with the observed enhanced values of SAR for dimer and trimer cluster structures, we demonstrated by means of a kinetic Monte Carlo computational model that the primary factor responsible for the enhancement of SAR is, in fact, not the variation of M_s but rather the magnetic dipolar effect induced by the particular arrangement of nanocubes into dimers, trimers, and centrosymmetric clusters (compare Figures S15 and S16). Finally, using the Monte Carlo simulation to numerically reproduce the high experimental values of SAR observed for the different cluster types required setting a rather low anisotropy constant K = 5 × 10⁴ erg/cm³ (Figure S15). This value agrees with the K value found experimentally for iron oxide nanocubes of the 19 nm cube edge.⁵ Increasing the value of K leads to a gradually diminishing effect of the clustering of nanocubes and ultimately to no real clustering-induced gain in SAR (Figure S15).

This work presents a versatile and smart strategy to use the same nanoparticle building blocks and achieve higher heat performances first by their controlled arrangement into anisotropic constructs made of two to three particles and second by promoting their phase transformation to Fe₃O₄.

Materials and Methods

Chemicals

All reagents were obtained from commercial suppliers and used without further purification. Iron pentacarbonyl (Fe(CO)₅, 98%), 1-octadecene (1-ODE, 99%), OA (90%), triethylamine (99%), chloroform (CHCl₃), ethanol, dichloromethane, poly(styrene-co-maleic anhydride), cumene-terminated (M_n = 1600 g/mol), α,ω-aminopropyl-poly(ethylene glycol) (M_n = 2000 g/mol), gallic acid, phosphate-buffered saline (150 mM NaCl, pH 7.4), and sodium hydroxide were purchased from Sigma-Aldrich. Sodium oleate (97%) was obtained from TCI. THF was purchased from Carlo Erba Reagents.

Synthesis of Nanocubes

Core–shell iron oxide nanocubes with an edge length of 20.2 ± 1.5 nm were synthesized following a recently published procedure²⁵ with a slight modification in order to obtain bigger nanoparticles. Briefly, in a typical synthesis of 20 nm nanocubes (Figure S1, sample A), OA (1.6 g, 5.7 mmol), sodium oleate (0.939 g, 3 mmol), and 1-ODE (5 mL) were added to a 50 mL three-neck flask connected to a reflux condenser and degassed for 30 min at 90 °C (the amounts for sample B were as follows: oleic acid (2.6 g, 9.2 mmol), sodium oleate (0.939 g, 3 mmol), and 1-octadecene (3 mL)). Subsequently, the solution was cooled to 60 °C and put under N₂ reflux. Then the precursor solution Fe(CO)₅ (0.597 g, 3 mmol, dissolved in 1 mL of 1-ODE) was injected, and the mixture was heated within 20 min to 320 °C. The solution reaction was stirred vigorously at 320 °C, and as nucleation started (the solution turned black), it was kept at that temperature for another 1.5 h and then cooled to room temperature. Finally, the IONCs were collected by centrifugation at 8000 rpm for 10 min and washed in a mixture of chloroform/methanol/acetone (1:6:1). The cleaning process was carried out three times, and the IONCs were finally dispersed in CHCl₃.

Controlled Clustering

For the formation of soft colloidal nanoclusters with hydrodynamic diameters around 100 nm, corresponding to 66 PScMA molecules/nm² for sample A, in a 20 mL vial, to 9 mL of THF solution was added 1 mL of stock solution of poly(styrene-co-maleic anhydride), cumene-terminated (PScMA, M_n = 1600 g/mol) polymer (obtained by dissolving 35 mg of polymer in 10 mL of THF, resulting in a [PScMA] = 2.19 mM). For 33 PScMA, to 9.5 mL of THF was added 0.5 mL of polymer stock solution. Instead, for 16.5 PScMA, to 9.75 mL of THF was added 0.25 mL of polymer stock solution. It followed the addition of 35 μL of iron oxide nanocubes solution ([Fe] = 6.09 g/L in CHCl₃, 0.33 μM in Fe) with a cube edge length of 20 nm. Subsequently, 1 mL of H₂O was added by a syringe pump, at the rate of 0.5 mL/min, while sonicating the solution in an ice bath. Next, the solution was placed on a horizontal shaker rotating at a speed of 100 rpm, and the vial was left uncapped overnight at room temperature (25 °C) to slowly evaporate the THF. The following day, the remaining 0.8–1 mL of solution was transferred to a 2 mL Eppendorf vial, and an equivalent volume of CHCl₃ was added. The Eppendorf vial was vigorously stirred at room temperature, and the two phases were left to separate for a couple of hours. Once the upper aqueous phase became clear, showing no sign of turbidity, it was transferred into a 1 mL HPLC vial. More in detail, to remove THF, allowing the final IONC dispersion in water, several evaporation methods were tried including (i) evaporation under reduced pressure (for roughly 1 h), (ii) atmospheric pressure evaporation of THF, while stirring the solution with a magnetic stirrer in an open beaker under the fume hood (for several hours), and (iii) nitrogen bubbling of the solution (for a couple of hours). When using evaporation under reduced pressure and nitrogen bubbling, although the clusters could be obtained, the reproducibility of the experiments was poor. This suggested that the rate of THF evaporation was crucial for cluster formation. Indeed, when slowly evaporating THF over 24 h by placing a 20 mL vial (without lid) on a horizontal shaker at a speed of 100 rotations per minute, the clusters were formed and the reproducibility of the cluster formation was significantly improved. At the last step, CHCl₃ was added to form a well-defined two-phase system, with the top layer being the aqueous phase containing the nanoclusters (colored phase on top, Figure S2).

Dynamic Light Scattering

Particle hydrodynamic size measurements were carried out using a Malvern Zetasizer Nano series instrument, operated in a 173° backscattered mode on diluted aqueous solutions of nanoclusters. The measurements were performed at 25 °C. An equilibration time of 2 min was allowed before each measurement, and at least three measurements were performed on each sample. The DLS sample was prepared by adding 25 μL of a cluster sample to 0.4 mL of water.

X-ray Diffraction

X-ray diffraction analysis was carried out on a Rigaku SmartLab diffractometer, equipped with a 9 kW Cu Kα rotating anode and operating at 40 kV and 150 mA. The patterns were acquired in Bragg–Brentano geometry, using a D\tex Ultra 1D silicon strip detector set in X-ray fluorescence reduction mode. The samples were prepared by drying concentrated drops of particle suspensions on zero diffraction silicon wafer.

Transmission Electron Microscopy

Conventional TEM images were obtained using JEOL JEM 1011 electron microscope, working at an acceleration voltage of 100 kV and equipped with a W thermionic electron source and a 11Mp Orius CCD camera (Gatan Company, USA). Samples were prepared by placing a drop of sample onto a carbon-coated copper grid, which was then left to dry before imaging.

Thermogravimetric Analysis

The weight loss of the oleic-acid-coated nanoparticles was determined using a TA Instruments Hi-Res TGA 2950 thermogravimetric analyzer under air atmosphere (60 cm³/min). The samples (5–10 mg) of the surfactant-coated nanocubes were heated from room temperature to 50 °C, and an isotherm was applied for 15 min and then heated to 700 °C at a heating rate of 10 °C/min.

The formula used for the calculation of ligand density (ρ_l) was described by Tong et al.:⁴⁶

where w_l is the weight fraction of the ligand, N_Av is Avogadro’s number, M_w,l is the molecular weight of the ligand, m_NP is the mass of one nanoparticle, w_NP is the weight fraction of the iron oxide nanoparticles, and A_NP is the surface area of one nanoparticle. The edge length of one nanocube was taken as 20 nm for area and volume calculations. For the nanoparticle mass calculation, the density of bulk magnetite was considered (5.18 g/cm³).

SAR Measurements

The calorimetric measurements to determine the specific absorption rate value of the iron oxide nanoclusters were carried out using the Nanoscale Biomagnetics instrument (DM100) operating over the range of frequencies from 105 to 302 kHz and fields up to 40 and 30 mT for 105 and 302 kHz, respectively. The SAR value was calculated using the formula:

where C is the specific heat capacity of dispersing medium (H₂O in most cases) per unit volume (J/K), and m is the concentration (g/L of Fe) of magnetic material in solution. The calorimetric measurements were carried out in quasi-adiabatic conditions, and the slope of the curve dT/dt was measured by taking into account only the first 20–25 s of the measurement. The measurements were done on samples of 200 μL at an Fe concentration ranging from 0.65 to 3.2 mg/mL.

Magnetic Characterization

Field-dependent static magnetic measurements performed on immobilized nanoclusters were carried out by employing magnetic property measurement system (MPMS-XL, Quantum Design) with EverCool technology. The samples were prepared by mixing 50 μL of nanoclusters dispersed in milli-Q water, at an iron concentration of 0.9 g/L, with 60 mg gypsum in the designated polycarbonate capsules and by drying the mixture thoroughly. The zero-field-cooled and field-cooled temperature-dependent magnetization measurements were performed on samples prepared in the same way in the cooling field of 5 mT. The residual magnetic field in the SQUID magnets was nulled using the designated low-field Hall sensor prior to ZFC measurements. All the presented magnetization data are corrected with respect to the diamagnetic and paramagnetic contributions of water and gypsum using the automatic background subtraction routine. The curves were normalized to the iron concentration as obtained from the elemental analysis.

Elemental Analysis

Elemental analysis was carried out via inductively coupled plasma atomic emission spectroscopy on a ThermoFisher iCAP 6000 series instrument. The samples were prepared by digesting 2.5–10 μL of sample in 1 mL of aqua regia in a 10 mL volumetric flask overnight. The next day, the flask was filled up to the graduation mark with milli-Q water and filtered through a 0.45 μm filter membrane prior to the measurement.

Magnetic Modeling Methodology

The kinetic Monte Carlo method used in this study systematically incorporates the complexity of realistic particle distributions, thermal fluctuations, and time varying external fields. The model assumes Stoner–Wohlfarth particles with uniaxial anisotropy k⃗_i = K_ik̂_i, where the unit vectors k̂_i for each nanocube are spherically distributed (i.e., following the uniform distribution on a unit sphere), and for simplicity, K_i is set to a constant K. We systematically explored the effect of the anisotropy constant K and found that the value 5 × 10³ J/m³ gives good qualitative agreement with the experimentally observed trends in SAR. Particles with cubic shape and cube edge of a = 20 nm and volume V_i = V = a³ are considered. The magnetic state of every individual particle is represented by a magnetic dipole moment m⃗_i = M_sm̂_i positioned in the center of its cube, where M_s is the saturation magnetization and m̂_i the particle moment normalized to unity. To reflect the slight degree of misalignment of nanocubes within clusters, which can be noted from the TEM image (Figure 1), the particle positions within elementary clusters were randomized using the fractal generating algorithm described previously⁴⁰ after setting the fractal dimension D_f = 3, which produces cluster structures, as illustrated in Figure S10. The chain-like and triangular clusters can also be obtained by the algorithm after setting D_f = 1 and D_f = 2, respectively, but given the small numbers of particles within the clusters, these can be obtained equivalently by setting D_f = 3, which allows one to systematically generate higher order clusters.

The Stoner–Wohlfarth energy of a cluster is

1

where the sum runs through particles i inside a cluster. The effective local field acting on particle i is given by the sum of the external applied field, H, and the dipolar interaction field described by the following equation:

2

Thermal fluctuations are accounted in the model by assuming the Néel–Arrhenius physical picture, where fluctuations—leading to frequency-dependent behavior—are described as a random hopping process over energy barriers ΔE separating the different states (magnetic moment configurations), defining the relaxation time scales as

3

where τ₀ = 10^–9 s, k_B is the Boltzmann constant, and T is the temperature. The essence of the kinetic Monte Carlo modeling is to solve the hopping dynamics via the master-equation formalism, including the interacting nature of particles, as given by eqs 1 and 2 and with realistic time scales as given by eq 3. Details of the method can be found in recent studies.^39,40

Throughout the present study, we consider systems of 3000 nanocubes, which were for simulation of the different ensembles split to 1500 dimers, 1000 trimers, and 500 six-particle centrosymmetric clusters. To study the noninteracting system, dipolar interactions H⃗_i^dip are set to zero for all particle pairs. We choose a parameter set consistent with the experimental conditions as discussed above, that is, the frequency of the applied field for calculations of SAR (determined from the hysteresis loop area) was set to f = 300 kHz, the field orientation was set along the z-axis of the coordinate system, and field amplitude was set to H₀ = 23.8 kA/m. For the inset of Figure 5, M_s values were set at 367, 407, 407, and 314 emu/cm³ for, respectively, single, dimers, trimers, and centrosymmetric clusters by converting M_s estimated from in Figure 6 from emu/g of Fe in emu/cm³ of Fe₃O₄. We also developed a case study with fixed M_s = 450 kA/m (450 emu/cm³, i.e., bulk magnetite-like particles) for all different types of cluster structures (see supplementary section, Figures S13–S15) consistent with the experiments on annealed systems (Figure 7 and Figure S11), which allows a straightforward comparison of the dipolar effects induced by the differences of the particle arrangement within the different cluster types. The particle temperature is set to constant T = 300 K, thus ignoring the self-heating effect, which is equivalent to assuming infinite heat capacity of particles.

The SAR was determined by evaluating the area of hysteresis loops computed for the ensembles of isolated particles and of two-particle, three-particle, or six-particle structures. Examples of the computed dynamic hysteresis loops are shown in Figure S13.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b05182.

• Additional TEM images of nanocubes and clusters, XRD spectra of the nanocube samples and DLS characterization of soft colloidal clusters, additional SQUID measurements of some samples, and additional images of the numerical Monte Carlo simulations (PDF)

Author Contributions

^¶ D.N. and A.L. contributed equally to this work.

The authors declare no competing financial interest.