Quantifying the effects of hydration on corneal stiffness with noncontact optical coherence elastography

Abstract

PURPOSE

To quantify the effects of the hydration state on the Young’s modulus of the cornea.

SETTING

Biomedical Optics Laboratory, University of Houston, Houston, Texas, USA.

DESIGN

Experimental study.

METHODS

Noncontact, dynamic optical coherence elastography (OCE) measurements were taken of in situ rabbit corneas in the whole eye–globe configuration (n = 10) and at an artificially controlled intraocular pressure of 15 mm Hg. Baseline OCE measurements were taken by topically hydrating the corneas with saline for 1 hour. The corneas were then dehydrated topically with a 20% dextran solution for another hour, and the OCE measurements were repeated. A finite element method was used to quantify the Young’s modulus of the corneas based on the OCE measurements.

RESULTS

The thickness of the corneas shrank considerably after topical addition of the 20% dextran solution (~680 μm to ~370 μm), and the OCE-measured elastic-wave speed correspondingly decreased (~3.2 m/s to ~2.6 m/s). The finite element method results showed an increase in Young’s modulus (500 kPa to 800 kPa) resulting from dehydration and subsequent thinning.

CONCLUSION

Young’s modulus increased significantly as the corneas dehydrated and thinned, showing that corneal geometry and hydration state are critical factors for accurately quantifying corneal biomechanical properties.

The cornea is a crucial part of vision because it provides physical protection to delicate inner elements of the eye and approximately two thirds of the total refractive power of the eye.¹ The structural integrity of corneal tissue is vital to its function and subsequent visual health by maintaining proper corneal geometry. It is well known that the corneal biomechanical properties and corneal geometry are tightly linked.² Diseases such as keratoconus³ and refractive procedures such as laser in situ keratomileusis⁴ and ultraviolet-A with riboflavin corneal crosslinking (CXL)⁵ can alter corneal biomechanical properties and geometry, leading to changes in visual acuity. For example, keratoconus causes degeneration of the cornea, leading to a highly irregular corneal geometry that results in distorted vision.^6,7 In general, keratoconus is diagnosed by techniques that rely on detecting these morphologic abnormalities and resulting visual aberrations.^7–9 However, techniques that can measure corneal biomechanical properties would enable earlier detection of disease onset by identifying underlying changes in corneal biomechanical properties before noticeable morphologic aberrations develop. Moreover, CXL is intended to stiffen the cornea; thus, evaluating corneal biomechanical properties could provide for planning and evaluating custom CXL therapies.^10,11 However, quantifying corneal biomechanical properties is not a simple process. Numerous confounding factors must be considered; these include corneal geometry, intraocular pressure (IOP), mechanical anisotropy, and nonlinearity.^12–21 Isolating and understanding the effects of these parameters is crucial for developing methods to accurately quantify corneal biomechanical properties.

Although the relationship between corneal hydration and thickness has been well studied, are fewer studies have assessed the relationship between corneal dehydration and biomechanical properties. Previous studies have used atomic force microscopy (AFM),²² inflation testing,²³ uniaxial mechanical testing,²⁴ and compression testing²⁵ to evaluate changes in corneal biomechanical properties resulting from altered hydration states. However, these modalities are not well suited to in vivo applications because of the destructive nature of mechanical and inflation testing, the long imaging times of AFM,²⁶ and the complications associated with assessments of compression.^27,28 Another reason to study the effects of dehydration on corneal biomechanical properties is the traditional CXL protocol,⁵ in which a 20% dextran solution is used. Previous studies have brought the effects of tissue dehydration as a compounding factor of the CXL stiffening into question^29,30 and have shown seemingly contradictory results of the effects of hydration on corneal stiffness.^22–25 Thus, understanding the effects of dehydration is crucial, not only for understanding inherent corneal biomechanical properties but also the effects of therapies such as CXL.

Measuring the biomechanical parameters of the cornea presents a challenge because of the cornea’s nonlinear viscoelastic behavior³¹ and noninvasive in vivo measurements are required. Traditional uniaxial testing of the cornea is impossible to perform in vivo because of its destructive nature and it is difficult to replicate in vivo conditions during such measurements.³¹ Similarly, other mechanical testing techniques, such as inflation testing,²³ are not viable in clinical applications. Clinically available instruments, such as the Ocular Response Analyzer (Reichert Technologies) and Corvis ST (Oculus Surgical, Inc.), use a large-force air puff to displace the cornea and quantify various parameters, such as inward deflection speed and corneal hysteresis. Although these parameters can be informative for disease detection, there is disagreement about their ability to detect changes in corneal biomechanical properties resulting from pathology, treatment, or both.^4,32–36 Brillouin microscopy can also assess the biomechanical properties of tissues noninvasively by measuring the Brillouin shift.^37,38 However, the link between material parameters and the Brillouin shift remains unclear.

Elastography was formalized in the early 1990s to quantify tissue mechanical properties by imaging displacements in tissues and then quantifying tissue biomechanical properties by linking the imaged displacements to mechanical models. Traditional elastographic techniques, such as ultrasound elastography³⁹ and magnetic resonance elastography,⁴⁰ have limited applications for the cornea because of their relatively large displacement amplitudes, poor spatial resolution, cost, and/or need for contact-based excitation. Optical coherence tomography (OCT)–based elastography,⁴¹ which is termed optical coherence elastography (OCE),^42,43 overcomes these limitations with micrometer-scale spatial resolution, nanometer-scale displacement sensitivity,⁴⁴ and noncontact excitation. Thus, OCE has been used to characterize the biomechanical properties of bioengineered tissue,⁴⁵ prostate cancer samples,⁴⁶ fibrotic mouse skin,⁴⁷ nephritic mouse kidneys,⁴⁸ and breast cancer biopsy samples,⁴⁹ among others. In general, the imaging depth of OCT is limited to a few millimeters in tissue; however, because the cornea is less scattering than most tissues and is usually thinner than 1.0 mm, OCT can image the entire thickness of the cornea. Moreover, the high spatial resolution and subnanometer displacement sensitivity make OCE well suited for characterizing corneal biomechanical properties.⁴³ Contact-based ocular OCE techniques have shown the heterogeneous properties of corneal tissue⁵⁰ under various conditions.^51,52 However, noncontact techniques are most favorable for corneal OCE because of their ease of use, lower risk for damaging tissue, and patient comfort.

In our previous studies,^21,53 we used the finite element method combined with OCE measurements of elastic-wave propagation to quantify the Young’s modulus of corneal tissue. The finite element method was chosen for its ability to easily adjust geometric parameters critical for accurately quantifying corneal biomechanical properties, such as thickness and curvature,²¹ and to integrate appropriate boundary conditions. We have also shown that the quantification of Young’s modulus of the cornea is strongly affected by the presence of the fluid–structure interface at the posterior corneal surface^53,54; therefore, the finite element method combined with OCE measurements shows potential for quantitatively assessing the effects of corneal hydration state on its biomechanical properties accurately.

In this study, we use a focused micro air pulse to induce elastic waves in fresh rabbit corneas in the whole eye–globe configuration. The elastic-wave propagation was detected by OCE, and the changes in corneal thickness and biomechanical properties, as quantified by OCE and the finite element method, during dehydration of the corneal tissue were analyzed.

MATERIALS AND METHODS

Ten fresh mature (>6 months) whole rabbit eye globes (Pel-Freez Biologicals) were shipped overnight on ice. Excess tissues, such as muscles, were removed from the globes, and the corneal epithelium was removed with a blunt surgical instrument. Because IOP can have a strong effect on the measured corneal biomechanical properties,^54,55 it was set with a closed-loop IOP control system to a physiologically relevant 15 mm Hg during all experiments.⁵⁶ The globes were placed in a home-built eye holder and were cannulated with 2 needles. One needle was connected via tubing to a pressure transducer, and the other needle was connected via tubing to a micro infusion pump to form the closed-loop IOP control system.

The short duration (<1 millisecond), low pressure (<10 Pa) focused micro air pulse was directed at the apex of the cornea and induced a low amplitude displacement (<10 μm), which then propagated as an elastic wave in the corneal tissue.⁵⁷ To ensure that the effects of corneal mechanical anisotropy were excluded,^58,59 all OCE measurements were taken along the nasal–temporal meridian. A 0.9% phosphate-buffered saline (PBS) solution was dropped on the corneas every 5 minutes, and the OCE measurements were taken every 20 minutes to establish a baseline. After the 60-minute measurement, 20% dextran in 0.9% PBS solution was dropped on the corneas every 5 minutes to dehydrate the corneas. The OCE measurements were then taken every 20 minutes for another 1 hour.

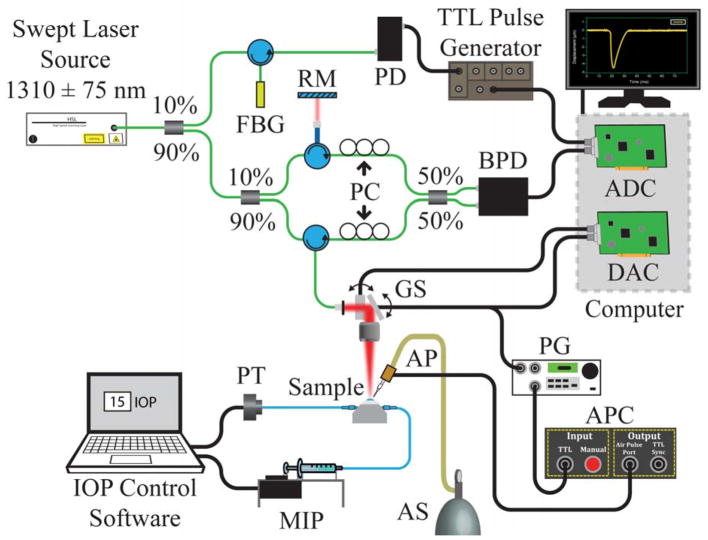
The elastic-wave propagation was detected with a phase-stabilized swept-source OCE system, which has been described in detail.⁶⁰ Briefly, the system has a central wavelength of approximately 1310 nm, a scan range of approximately 150 nm, a scan rate of 30 kHz, and a phase stability in the cornea of approximately 20 nm. Figure 1 shows a schematic of the system. The M-B-mode imaging was performed by synchronizing the air pulse with the OCT frame trigger, and 251 M-mode images were taken over an approximate 7.0 mm scan.⁶¹ Before any calculations, the phase data were corrected for the refractive index mismatch between the corneal tissue and air⁶² with the refractive index of the corneal tissue as 1.376.⁶³ The elastic-wave group velocity was quantified by cross-correlation analysis of the elastic-wave temporal displacement profiles. The elastic-wave propagation delays, which were determined by cross-correlation, were then linearly fitted to the wave-propagation distances, and the slope of the linear fit was used to calculate the velocity.⁶⁴ This procedure was repeated for each imaged in-depth layer, taking the curvature of the cornea into account as an accurate distance for the elastic-wave propagation path. The velocity was then averaged along the entire depth of the cornea for a given measurement. The central corneal thickness (CCT) was measured after the OCT structural image was rescaled to physical dimensions, again assuming a corneal refractive index of 1.376.⁶³

Figure 1.

Schematic of the experimental setup (ADC = analog-to-digital converter; AP = air-pulse port; APC = air-pulse controller; AS = air supply; BPD = balanced photodetector; DAC = digital-to-analog converter; FBG = fiber-Bragg grating; GS = galvanometer-mounted mirror scanners; IOP = intraocular pressure; MIP = microinfusion pump; PC = polarization controller; PD = photodetector; PG = pulse generator; PT = pressure transducer; RM = reference mirror; TTL = transistor–transistor logic).

Young’s modulus was estimated with the finite element method in the Ansys environment software (version 14.0, Ansys, Inc.).^21,53 Based on the OCT structural image obtained during the OCE measurements, the anterior and posterior surfaces of the rabbit cornea were well fitted by a circle. Hence, the finite element model was simplified as a spherical shell, with a curvature from an average of all samples. The mean fitted radius of the anterior surface was r_ant = 7.80 ± 0.05 mm, which indicated a negligible change in the corneal curvature during the experiments. In contrast, the CCT changed significantly, as expected, with a mean CCT of all samples at all timepoints of 571 ± 132 μm, where the error is the standard deviation (SD). The averaged CCTs from all samples for a given timepoint were used in the finite element models. During the simulation, the corneal tissue was assumed as linearly elastic and the Poisson ratio, mass density, aqueous humor density, and speed of sound in fluid were set at 0.49, 1062 kg/m^3,65 1000 kg/m³, and 1500 m/s, respectively. Fixed boundary conditions were considered at the corneoscleral limbus, and the OCE-measured displacement profile at the corneal apex was applied to the finite element model as an excitation, also at the apex. A fluid–structure interface was prescribed at the posterior surface to integrate the effect of the aqueous humor on the elastic wave in the cornea.⁵³ In the finite element model, a SOLID186-type element was used to mesh the cornea, and a FLUID220-type element was applied to the aqueous humor. The mesh sizes were 300 μm. The Young’s modulus of the finite element model was incrementally changed until the error between the finite element method–calculated velocity and the average OCE-measured velocity for that given timepoint was less than 5%.

RESULTS

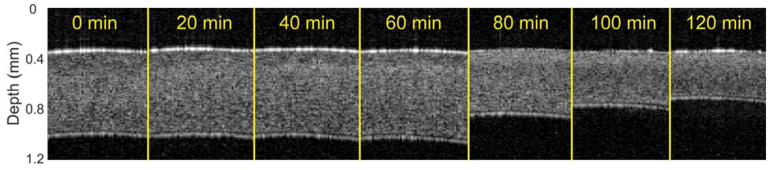
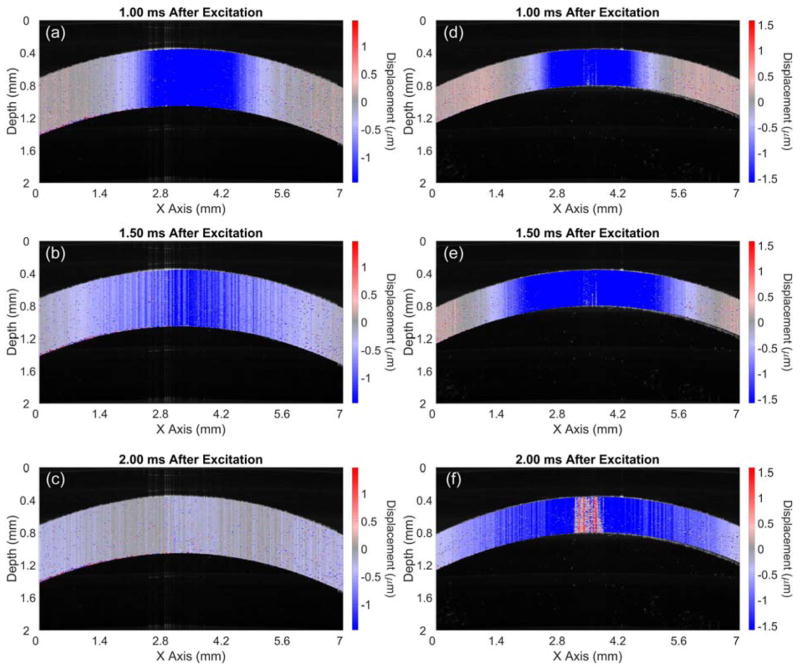
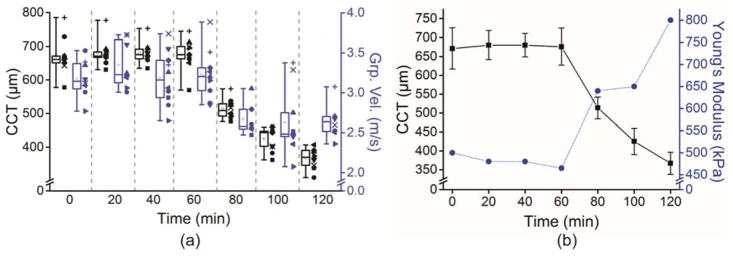
Figure 2 shows OCT structural images at the indicated times in a typical sample. There was a slight swelling resulting from the hydration by PBS in this sample; the cornea swelled from 672 μm at the 0-minute measurement to 713 μm at 60 minutes. After the topical addition of the 20% dextran solution, the CCT rapidly shrank from 713 μm at 60 minutes to 387 μm when the measurements were completed at 120 minutes. Figure 3 shows sample frames of the air pulse–induced elastic-wave propagating, as in the sample shown in Figure 2, at the initial 0-minute measurement and at the 100-minute measurement. Video 1 (available at: http://jcrsjournal.org) shows the propagation of the elastic wave at 1000 times slower than real time, with the 0-minute OCE measurement (top) and the 100-minute measurement (bottom). The times after excitation are shown at the top of each image in Figure 3 and Video 1 (available at: http://jcrsjournal.org). The red region at the apex of the 100-minute measurement is the result of phase-unwrapping errors and was excluded in calculations. The pale blue regions at the periphery of the cornea in Figure 3, c, show that the wave had mostly propagated out of the imaged region 2 milliseconds after excitation at the 0-minute measurement. In contrast, the wave is still clearly visible 2 milliseconds after excitation in the 100-minute measurement (Figure 3, f), showing that the wave was faster when the cornea was swollen than to when the cornea was dehydrated. Figure 4, a, plots the intersample mean CCT and elastic-wave velocity as a function time for all 10 samples with the error bars representing the inter-sample SD. The mean CCT slightly increased from 671 ± 54 μm at the initial 0-minute measurement to 676 ± 49 μm at the 60-minute measurement. After the addition of the 20% dextran solution, the thickness rapidly shrank to 367 ± 29 μm at the final measurement at 120 minutes. The average elastic-wave velocity decreased from 3.2 ± 0.2 m/s at the first OCE measurement to 2.6 ± 0.2 m/s at the final OCE measurement at 120 minutes.

Figure 2.

Optical coherence tomography structural images of the central region of approximately 2.0 mm a typical cornea after rescaling to physical dimensions. Topical PBS was dropped for the first 60 minutes, after which a 20% dextran solution was dropped on the corneas for an additional 60 minutes (PBS = phosphate-buffered saline).

Figure 3.

Air pulse–induced elastic-wave propagation in a typical sample at the initial 0-minute measurement (a to c) and the 100-minute measurement (d to f) (see Video 1, available at: http://jcrsjournal.org). The time after the air-pulse excitation for each frame is shown above the corresponding image.

Figure 4.

a: The CCT and elastic-wave group velocity of all 10 samples plotted as a function of time. The CCT is represented in black, and the elastic-wave group velocity is represented in blue. Each sample is coded by the shape of the datapoints plotted alongside the corresponding box-and-whisker plot. The boxes are the interquartile range, the central line is the median, the whiskers are the 5th and 95th percentiles, and the small inscribed box is the mean. b: Averaged CCT and Young’s modulus quantified by the finite element method. The CCT is represented by the black squares and solid black line, and the Young’s modulus is represented by the blue circles and dotted blue line. The error bars are the intersample SD. A 0.9% PBS solution was dropped on the corneas for the first 60 minutes, and a 20% dextran solution was dropped on the corneas for an additional 60 minutes (CCT = central corneal thickness; Grp. Vel. = group velocity; PBS = phosphate-buffered saline).

The finite element method was used to quantify the Young’s modulus of the cornea because it can accurately replicate the geometry and boundary conditions of the cornea. Quantifications were made on the averaged data shown in Figure 4, a. The mean error between the OCE-measured and finite element method–computed group velocity was 3.1% ± 5.7%, showing good agreement between the OCE measurements and finite element method results. Figure 4, b, plots the changes in CCT as well as the finite element method–assessed Young’s modulus as a function of time. From 0 to 60 minutes, when the PBS was dropped on the corneas, the CCT slightly increased and Young’s modulus decreased slightly from 500 kPa to 465 kPa. However, the addition of the 20% dextran solution caused the cornea to thin significantly, from approximately 680 μm at 60 minutes to approximately 370 μm at 120 minutes, which caused a corresponding increase in Young’s modulus from 465 kPa to 800 kPa.

DISCUSSION

In this study, we used a focused micro air pulse to induce low-amplitude elastic waves in the cornea; the waves were detected by a phase-stabilized OCE system. The OCE-measured elastic-wave velocity and OCT-measured corneal geometry were then used in finite element models to quantify the Young’s modulus of the cornea while it was dehydrated with a 20% dextran solution. The Young’s modulus of the cornea increased significantly as the corneas dehydrated and thinned. The main advantages of our work are that we (1) induced very small displacements (micrometer scale) to avoid global eye globe deformation during the OCE measurements,³¹ (2) used a constant IOP to eliminate variations in OCE-measured corneal biomechanical properties resulting from IOP changes,^{31,54,55, 66} (3) performed all measurements in the whole-globe configuration to avoid ambiguities resulting from different corneal tissue preparation methods,²² and (4) quantified the Young’s modulus of the cornea with a widely used engineering technique.^36–38,54

The corneas were topically hydrated with a 0.9% PBS solution, which is hypotonic to the corneal stroma and causes slight swelling. Normally, rabbit corneas are approximately 400 μm thick⁶⁷; however, they were approximately 670 μm after storage and hydration with PBS and deepithelialization. Previous studies^22,23 found positive correlations between corneal thickness and stiffness. Kling and Marcos²³ used inflation testing and found that the slope of the change in corneal thickness versus IOP was flatter in corneas stored in a 20% dextran solution than in untreated corneas, indicating a decrease in stiffness after storage in 20% dextran and subsequent thinning. However, inflation testing requires large changes in IOP that induce nonlinear biomechanical responses and no material parameters were quantified. Dias and Ziebarth²² used AFM to perform indentation testing and found that a 15% dextran solution thinned the corneas and caused the smallest increase in corneal stiffness compared with saline solutions. In contrast, Cherfan et al.⁶⁸ used mechanical extensiometry and found that riboflavin 0.1% in 20% dextran solution increased the Young’s modulus of the cornea by more than 2 times. Hatami-Marbini and Rahimi^24,69 showed that the tangential elastic modulus of corneal strips increased as thickness decreased (ie, the corneas were dehydrated) using mechanical extensiometry and that the in-plane and out-of-plane Young’s moduli increased as corneal tissue hydration decreased with mechanical compression testing.²⁵ The differences in the spatial and temporal scales of the measurement can bring about seemingly contradictory results. Cancer is the most notable example. Macrostructural elastography has shown that tumors are stiffer than surrounding tissue^70,71; however, microscale and nanoscale measurements have shown that malignant cells are softer than healthy cells.^72,73 Thus, the assessments of Dias and Ziebarth²² using AFM are not actually contradictory to the work by others showing that the bulk corneal stiffness increased when the cornea was dehydrated. Therefore, future study will require multiscale evaluation of corneal biomechanical properties to understand the changes at the tissue, cellular, and subcellular scales as a function of hydration.

Our previous work with OCE and the finite element method showed that as the thickness of agar phantoms increased, the OCE-measured and finite element method–simulated wave speeds increased when Young’s modulus was held constant.²¹ The results in this study show the same trend; however, Young’s modulus followed the opposite trend, indicating that wave speed alone is not truly indicative of the cornea’s material properties. If the Young’s modulus of the cornea were to remain constant, the changes in wave speed would perhaps be more dramatic. Additional simulations were performed by changing the thickness of corneal finite element models within the range observed in this study (~400 μm to ~800 μm) at a fixed Young’s modulus of 500 kPa (data not shown). These results showed a much more pronounced change in wave speed (~2.5 m/s at ~400 μm to ~4.5 m/s at ~800 μm) than the OCE-measured wave speed in the in situ porcine corneas. Thus, there was a change in the Young’s modulus of the cornea that compensated for the significant change in CCT. At the same IOP, a decrease in CCT could increase the stress on the corneal tissue. Because the cornea has a characteristic J- shaped stress–strain curve,³¹ the additional stress could cause an increase in Young’s modulus. Although the radius of curvature can also affect the measured wave speed,²¹ an analysis of variance test showed no significant variation in the radius of curvature as a function of CCT (P = .234); thus, no further analysis was performed.

An additional outcome of our results is the error that can be introduced when quantifying corneal biomechanical properties without accounting for the thickness. We performed finite element method simulations in which Young’s modulus and the thickness were altered so that the group velocity was equal (data not shown). The finite element method simulations matched results from our previously developed modified Rayleigh-Lamb wave model for the cornea^54,74 with the same parameters. Here, a small change in thickness of 80 μm resulted in a large difference in Young’s modulus of 210 kPa when the velocity was equal (at ~2.8 m/s). Therefore, even though a similar velocity is measured in the cornea, the Young’s modulus can be quite different for a different thickness.

The absolute values of Young’s modulus quantified in this study is higher than in our own previous work with rabbit corneas.^53,75 In fact, the reported values of Young’s modulus of the cornea vary by several orders of magnitude,⁷⁶ from a few kilopascals as assessed by AFM⁷⁷ to tens of megapascals as measured by tensile testing.⁷⁸ Multiple factors can account for this wide range of values, including the nonlinear stress–strain curve of the cornea,³¹ the testing conditions that can artificially raise the “equivalent IOP”³¹ and the temporal and spatial scale of the measurement.

In a live animal, the endothelial pumps, which help control corneal hydration and thickness, are still functioning. In ex vivo conditions, the pumps cease to function and various solutions have been tested to maintain corneal thickness.^22,79,80 In our future work, we will evaluate such solutions and their ability to control corneal thickness and their subsequent effects on corneal biomechanical properties as well as in vivo testing of how the corneal hydration state alters biomechanical properties. Moreover, the corneal hydration state and mass density are tightly linked.⁸¹ In this study, we kept the density constant, assuming its influence on the results would be minimal because of the relatively small influence of density on the Young’s modulus in many wave models.^54,82,83 We will integrate the changes in density to our future calculations.

A major limitation of this study is the quantification of corneal viscoelastic properties. At present, our combined technique of air-pulse OCE and the finite element method can only provide Young’s modulus but not the viscosity. We have shown that the elastic-wave group velocity depends on the thickness of the material, even when all other parameters, including the Young’s modulus, are equal.²¹ Group velocity has often been used to quantify the Young’s modulus of the cornea with simple models, primarily the shear-wave and surface-wave models. However, those models assume the sample is an infinitely thick plate,⁸³ which the cornea is not. We have developed a modified Rayleigh-Lamb wave model that uses the spectral dispersion of the elastic wave, considers the thickness of the sample, and integrates the fluid–structure interface at the corneal posterior surface to quantify the Young’s modulus and shear viscosity of the cornea, but this model assumes the cornea is a flat thin plate.^54,74 Hence, the finite element method was used because it can accurately replicate the corneal geometry, including curvature, which is an advantage of the finite element method over most analytical wave models. However, the OCE and finite-element method technique we present is based on group velocity only and cannot be used to obtain the viscosity of the cornea tissue because there would be 2 unknowns (Young’s modulus and viscosity) with only 1 known parameter (elastic-wave group velocity). The next step of our work is to integrate the OCE-measured elastic-wave spectral dispersion^84–86 into the finite element method simulations to obtain the viscoelasticity; however, this will increase the finite element method simulation time significantly.

Another limitation is the OCE acquisition time, which is tens of seconds. The extended acquisition time and need for multiple excitations would not be satisfactory for patient comfort. In additional, M-mode imaging means that corneal laser safety limits were exceeded. We developed an ultrafast technique capable of detecting the elastic-wave propagation within milliseconds, with only 1 excitation, and within corneal laser safety exposure limits.^66,87 However, the transverse spatial resolution is still limited. Nevertheless, this technique might be sufficient when combined with the finite element method or an accurate analytical wave model to quantify the biomechanical properties of the cornea within milliseconds in a completely noninvasive and safe manner.

In conclusion, this study found that the thickness of in situ rabbit corneas decreased along with the air pulse–induced elastic-wave velocity after the corneas were dehydrated with a 20% dextran solution. Quantification of Young’s modulus by the finite element method showed that the cornea stiffens as it dehydrates and reduces in thickness. The results indicate that the hydration state of the cornea plays a noticeable role in corneal biomechanical properties, which is particularly important for therapies such as CXL in which dextran solution is used.

Supplementary Material

supplement. Video 1.

Propagation of the air pulse–induced elastic wave in a sample rabbit cornea at 15 mm Hg. The top video is at the initial 0-minute optical coherence elastography (OCE) measurement, and the bottom video is at the 100-minute OCE measurement.

WHAT WAS KNOWN

• Corneal hydration alters the geometry and biomechanical properties of the cornea.

WHAT THIS PAPER ADDS

• Young’s modulus of the cornea increased as the cornea thinned as a result of dehydration.

Results show that Young’s modulus of the cornea is a factor of the thickness and hydration states that should be taken into account for proper quantification of the cornea’s biomechanical properties.