An automated technique to stage lower third molar development on panoramic radiographs for age estimation: a pilot study.

Abstract

Background

Automated methods to evaluate growth of hand and wrist bones on radiographs and magnetic resonance imaging have been developed. They can be applied to estimate age in children and subadults. Automated methods require the software to (1) recognise the region of interest in the image(s), (2) evaluate the degree of development and (3) correlate this to the age of the subject based on a reference population. For age estimation based on third molars an automated method for step (1) has been presented for 3D magnetic resonance imaging and is currently being optimised (Unterpirker et al. 2015).

Aim

To develop an automated method for step (2) based on lower third molars on panoramic radiographs.

Materials and methods

A modified Demirjian staging technique including ten developmental stages was developed. Twenty panoramic radiographs per stage per gender were retrospectively selected for FDI element 38. Two observers decided in consensus about the stages. When necessary, a third observer acted as a referee to establish the reference stage for the considered third molar. This set of radiographs was used as training data for machine learning algorithms for automated staging.

First, image contrast settings were optimised to evaluate the third molar of interest and a rectangular bounding box was placed around it in a standardised way using Adobe Photoshop CC 2017 software. This bounding box indicated the region of interest for the next step. Second, several machine learning algorithms available in MATLAB R2017a software were applied for automated stage recognition. Third, the classification performance was evaluated in a 5-fold cross-validation scenario, using different validation metrics (accuracy, Rank-N recognition rate, mean absolute difference, linear kappa coefficient).

Results

Transfer Learning as a type of Deep Learning Convolutional Neural Network approach outperformed all other tested approaches. Mean accuracy equalled 0.51, mean absolute difference was 0.6 stages and mean linearly weighted kappa was 0.82.

Conclusion

The overall performance of the presented automated pilot technique to stage lower third molar development on panoramic radiographs was similar to staging by human observers. It will be further optimised in future research, since it represents a necessary step to achieve a fully automated dental age estimation method, which to date is not available.

INTRODUCTION

Evaluating medical images for forensic age estimation is generally performed by expert human observers, such as radiologists or dentists. Their age estimations are mainly based on the developmental status of different anatomical structures depicted in the medical images. When teeth are still developing, the established methods mainly use panoramic radiographs for dental age estimation. In adolescents and subadults third molars are evaluated for age estimation, since the other elements of the permanent dentition are fully developed. (1) Numerous staging techniques have been developed to evaluate third molar growth and multiple methods have been reported that estimate age based on developmental stages allocated in reference populations. (2-5) Additionally, for age estimation in adolescents and subadults, it is recommended to evaluate a hand/wrist radiograph. In case the hand/wrist bones appear fully developed, the medial end of the clavicle should be assessed – either on radiographs or computed tomography. (6, 7) Although criteria have been described to discern one developmental stage from another, for teeth as well as for long bones or carpal bones, allocating a stage remains susceptible to inter- and intra-observer variability. (8-11)

Since variability in stage allocation is caused by the human eye and mind, automated staging techniques and related age estimation methods have been developed. Automated techniques require the software to (1) recognise the region of interest in the presented image(s) (12), (2) classify the presented degree of development into predefined stages and (3) estimate the age of the subject based on the allocated stage(s) and age related information from a reference population. (13) To develop software for automation or to teach existing software to recognise and classify specific shapes, a training data set is necessary.

Automatic third molar localisation software (step 1) has been developed for magnetic resonance imaging (MRI). (14) A regression random forest framework was used to predict the landmarks of the third molars in 3D MRI data. The aim of the current study was to find a way to develop automated algorithms for the second step, i.e. allocating an appropriate stage to the developing third molars. To simplify the problem in this pilot study, 2D data from panoramic radiographs were used and the focus was on the development of lower third molars.

MATERIALS AND METHODS

Study population and image analysis

Four hundred panoramic radiographs were collected from the patients’ files at Leuven University Hospital, Belgium. Radiographs were selected based on the development of the lower left third molars (FDI 38). Two observers (J.D.T. and P.R.) allocated developmental stages (Table 1, Figure 1) to each lower left third molar in consensus. In case of disputes, a third observer (P.W.T.) acted as referee to decide on the allocated stage. Observer 1 (J.D.T.) had 5 years of experience evaluating skeletal and dental radiographs for age estimation. Observer 2 (P.R.) was recently introduced to the field of age estimation. Observer 3 (P.W.T.) had over ten years of experience in dental and skeletal age estimation. Images were displayed on a Samsung HD television (model UE32E45300W, resolution 1920 x 1080 pixels) or Phillips HD television (model 65BDL4050D, resolution 1920 x 1080 pixels). Images were imported and enhanced for optimal visualization of the considered third molar in Adobe Photoshop CC 2017 software and saved as psd-files.

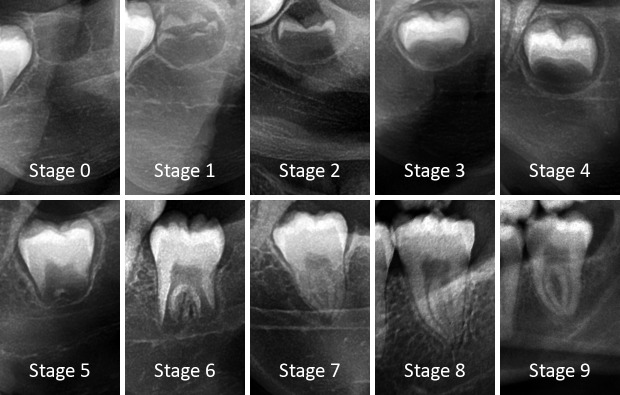
Table 1. Descriptive criteria for developmental stages of third molars (modification of stages defined by Demirjian (1973), Gleiser and Hunt (1955), Kullman (1992) and Moorrees (1963)).

Stage	Description
Stage 0	The crypt can be suspected in the jaw bone. Calcification of tooth tissue has not started.
Stage 1	A beginning of calcification is seen at the superior level of the crypt in the form of an inverted cone or cones. There is no fusion of these calcified points.
Stage 2	Fusion of the calcified points forms one or several cusps which unite to give a regularly outlined occlusal surface.
Stage 3	a) Enamel formation is complete at the occlusal surface. Its extension and convergence towards the cervical region is seen. b) The beginning of a dentinal deposit is seen. c) The outline of the pulp chamber has a curved shape at the occlusal border.
Stage 4	a) The crown formation is completed down to the cemento-enamel junction. b) The pulp chamber has a trapezoidal shape. The projection of the pulp horns gives an outline shaped like an umbrella top.
Stage 5	a) Beginning of root formation is seen in the form of a spicule. b) The root length is still less than the crown height. c) Initial formation of the radicular bifurcation is seen in the form of either a calcified point or a semi-lunar shape.
Stage 6	a) The calcified region of the bifurcation has developed further down from its semi-lunar stage to give the roots a more definite and distinct outline with funnel shaped endings. b) The root length is equal to or greater than the crown height.
Stage 7	The walls of the distal root canal are now parallel and its apical end is still partially open.
Stage 8	The walls of the root canal are now converging at the apex. The apical end is still partially open.
Stage 9	a) The apical end of the root canal is completely closed. b) The periodontal membrane has a uniform width around the root and the apex.

Figure 1.

Representative examples of lower left third molars in each developmental stage. Third molars are depicted within their bounding box.

A modified Demirjian’s staging technique was used. (15) Two additional stages were added to the eight Demirjian stages. First, a crypt stage was included, as suggested by Gleiser and Hunt (1955) (stage I). (16) Second, an additional stage was defined based on apical closure (cfr. Gleiser and Hunt (1955) stage XV, Moorrees (1963) stage A½ or Kullman (1992) root stage Aci). (17, 18) Moreover, Demirjian stage D was replaced with Gleiser and Hunt stage VII, crown completed. Finally, the order of criteria for Demirjian stage E was changed. Since some lower third molars are monoradicular, the presence of a calcified furcation was considered less important than relative root length.

Twenty radiographs per stage per sex were selected. Since only the radiographical appearance mattered, no restrictions were applied concerning age or biological origin of the subjects. Exclusion criteria for panoramic radiographs were insufficient image quality and severe bucco-lingual inclination of the considered third molar. The latter characteristic was most often encountered when third molars were suspected to be in stage 2 (Figure 2).

Figure 2.

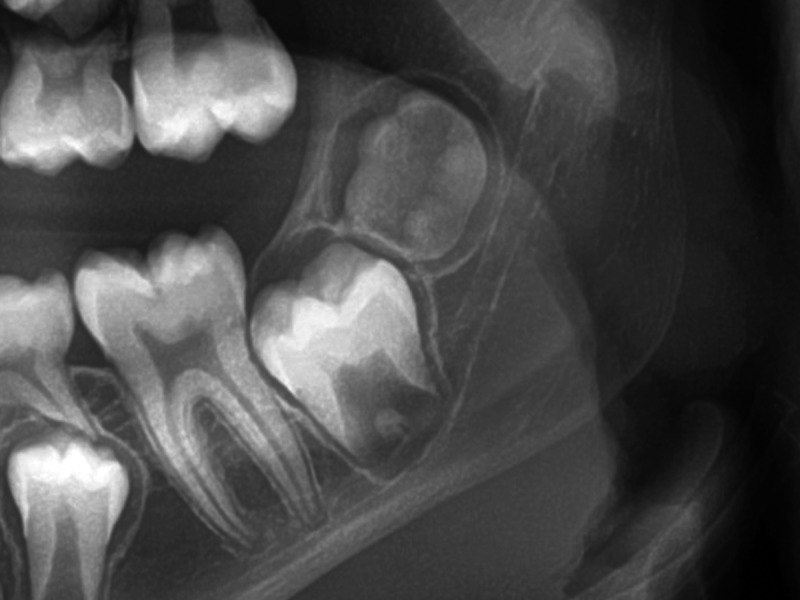
Excluded panoramic radiograph. The lower left third molar was suspected to be in stage 2, but it was expected that the software would not be able to recognise the stage due to its severe (out of plane) inclination.

Image processing and training of the software

A region of interest around the lower left third molar was delineated by manually placing a rectangular bounding box on each radiograph using Adobe Photoshop CC 2017. This enabled the staging software to only capture the image information of the considered third molar, disregarding the surrounding information. In fact, this step mimicked step 1 (recognise the region of interest in the presented image) of a fully automated technique. Dimensions of the bounding box were standardized to 240 pixels x 390 pixels, regardless of developmental stage. The long axis of the box was parallel to the tooth axis. The upper short side of the box was 2 mm cranially of the highest cusp tip. (Figure 3).

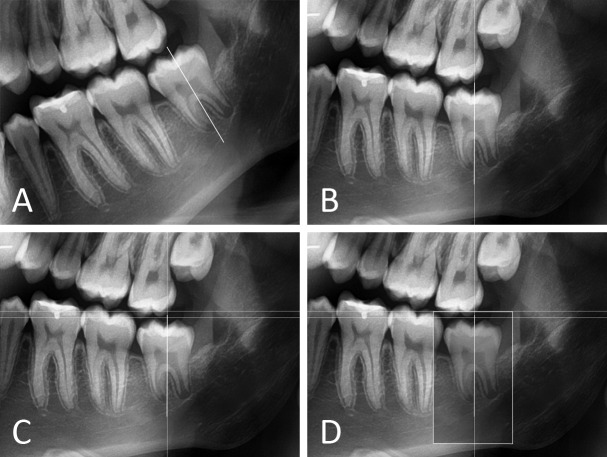
Figure 3.

Close-up of image processing using Adobe Photoshop CC 2017. (A) The long axis of the tooth was defined. (B) The image was rotated to orient the long axis vertically. (C) In succession, three guides were used to define the bounding box: (1) a vertical guide on the long axis of the third molar; (2) a horizontal guide touching the highest cusp tip; (3) a horizontal guide two millimetres occlusally from the previous guide. (D) The top of the bounding box was on guide 3. The width was symmetrically divided around guide 1. For all third molars, dimensions of the bounding box were 240 pixels x 390 pixels, regardless of the developmental stage.

Subsequently, the Photoshop psd-files were imported into MATLAB R2017a software, which only processed the image information in the bounding box. The image contrast was enhanced using contrast-limited adaptive histogram equalisation (19) (MATLAB function adapthisteq with default parameter settings). Several linear and non-linear multi-stage classifiers (Linear and Quadratic Discriminant Analysis, Decision Trees, Support Vector Machines, Nearest Neighbour Classifiers, Ensemble Classifiers) were tested using the Classification Learner App of MATLAB R2017a after preliminary feature extraction and reduction from the region of interest (ROI) (first 10 Principal Components of appearance, Histogram of Oriented Gradients (20)) as well as a Bag of Features approach using SURF features (21). Finally, a Deep Convolutional Neural Network approach was tested using transfer learning starting from AlexNet (22) (available as part of the MATLAB Neural Network Toolbox). AlexNet was originally trained on a subset of the ImageNet database (23), trained on more than a million images to classify images into 1000 object categories. As a result, the deeper layers of the network have learned a rich feature representation. The pre-trained AlexNet network was just adapted by replacing the final fully connected layer to train on the ten third molar stages. The weights were slightly retrained using stochastic gradient descent with momentum (momentum 0.9, initial learning rate 0.001, maximum number of training epochs 50 and a minibatchsize of 64).

Statistical analysis

For training and testing we used a 5-fold cross-validation, each round using 80% of the images for training and the remaining 20% for testing. Different metrics were calculated to measure the classification performance. The Rank-N recognition rate (Rank-N RR) measured how many times the correct stage (corresponding with the stage allocated by the human observers) was ranked first, second, … N^th in the automated stage allocation process. Accuracy was defined by the first rank recognition rate, reflecting the percentage of correctly allocated stages. The mean absolute difference between the automated and manual staging (numbered 1 to 10) was calculated. In order to account for the ordinal character of the staging, linearly weighted Cohen’s kappa and intra-class correlation coefficient (ICC) were calculated. Finally, confusion matrices obtained by cross-tabulation of the stages assigned by the software and the human observers (inter-observer agreement), allowed checking for systematic differences.

RESULTS

Using Transfer Learning as a type of Deep Learning Convolutional Neural Network approach outperformed all other tested approaches by at least 10% in classification accuracy. Table 2 shows the mean Rank-N RR, with a mean accuracy (Rank-1 RR) of 0.51. The mean absolute difference was 0.6 stages. The mean linearly weighted kappa was 0.82, ranging from 0.78 to 0.83 over the different cross-validation rounds. The mean ICC was 0.95, ranging from 0.93 to 0.96. From the cross tabulation (Table 3) it is clear that most frequently misclassified stages were in the neighbouring stages.

Table 2. Mean Rank-N recognition rate of automated stage allocation.

	The correct stage was ranked
	First	Second	Third	Fourth	Fifth	Sixth	Seventh	Eighth	Ninth	Tenth
Mean Rank-N RR	0.506	0.284	0.118	0.065	0.017	0.007	0.002	0	0	0

Table 3. Cross tabulation of allocated stages by the software (rows) and by the human observers (columns), normalised per row.

Stage	0	1	2	3	4	5	6	7	8	9
0	0.88	0.10	0.03	0	0	0	0	0	0	0
1	0.19	0.77	0.02	0.02	0	0	0	0	0	0
2	0	0.12	0.50	0.38	0	0	0	0	0	0
3	0	0.02	0.10	0.48	0.40	0	0	0	0	0
4	0	0.02	0	0.23	0.43	0.32	0	0	0	0
5	0	0	0	0	0.38	0.55	0.05	0.03	0	0
6	0	0	0	0	0	0.03	0.46	0.38	0.10	0.03
7	0	0	0	0	0	0.02	0.16	0.33	0.28	0.21
8	0	0	0	0	0	0	0.12	0.33	0.33	0.21
9	0	0	0	0	0	0	0	0.40	0.30	0.30

DISCUSSION

An automated technique to stage lower third molar development on panoramic radiographs was developed and its performance was tested. Inter-observer reliability (between automated and human observer staging) was similar to studies including only human observers. Although on average (only) 51% of the stages were correctly allocated, the mean absolute difference was 0.6 stages and the linearly weighted kappa coefficient 0.82, indicating that most misclassified stages were in the neighbouring stages only. Therefore, this novel approach looks promising and opens the perspective of countering variability in age estimation caused by intra- and inter-observer disagreement. After all, reproducibility was only in rare occasions reported to be perfect.

Observer- induced variability

In Table 4 statistics on intra- and inter-observer agreement were displayed for studies (2002-2017) that included assessments of developing third molars and that reported an appropriate statistic (more than merely the percentage of consistency). Notice that in these studies, staging as well as measuring was prone to disagreements. Whereas variability in measurements seems more random (24), variability in staging can be explained by multiple observer-related effects. First, systematic differences in allocated stages between research groups might be caused by a different calibration process. Kullman et al. (1996) reported that observers that were not calibrated showed significant variation in their registrations. (24) To our knowledge, no studies have been conducted to compare staging done by researchers from unrelated research groups.

Table 4. Reproducibility statistics for the assessment of third molar development.

Reference	Elements	Technique			Intra-observer agreement				Inter-observer agreement
					Statistic		N		Statistic		N
Altalie (2014) (42)	Lower left permanent teeth and all third molars	S	Demirjian and Köhler respectively		Weighted kappa	0.99	100		Weighted kappa	0.91	100
Boonpitaksathit (2011) (43)	All third molars	S	Demirjian		Kappa	0.85-0.94	30		Kappa	0.69	30
Cameriere (2008) (4)	Lower left third molar	M	Cameriere		CCC	0.95-0.97	30		CCC	0.95	30
		S	Demirjian		Kappa	1.00	30		Kappa	0.93	30
Cameriere (2014) (44)	Lower right third molar	M	Cameriere		ICC	1.00	50		ICC	1.00	50
Corradi (2013) (25)	All third molars	S	Demirjian		Reproducibility index	0.79-0.89	1560		Reproducibility index	0.65-0.71	1560
Dhanjal (2006) (10)	Both left third molars	S	Demirjian		Kappa	0.70-0.78	73		Kappa	0.68	73
		S	Solari		Kappa	0.65-0.71	73		Kappa	0.56	73
		S	Moorrees		Kappa	0.61-0.65	73		Kappa	0.52	73
		S	Haavikko		Kappa	0.70-0.73	73		Kappa	0.64	73
Duangto (2016) (45)	Both lower third molars	S	Demirjian (modified)		Kappa	0.96-0.97	100		Kappa	0.92-0.93	100
Elshehawi (2016) (46)	All left permanent teeth and all third molars	S	Demirjian		Kappa	0.91	10		Kappa	0.77	10
Gunst (2003) (47)	All third molars	S	Köhler		Simple kappa coefficient	0.13	50		Simple kappa coefficient	0.14	50
Harris (2007) (48)	One lower third molar	S	Moorrees		Fleiss' kappa	0.96	225		-
Hegde (2016) (49)	All third molars	S	Demirjian (modified)		Kappa	0.92	80		Kappa	0.94	80
Liversidge (2008) (50)	Lower left third molar	S	Moorrees		Kappa	0.77	100		-
Liversidge (2010) (5)	Lower left third molar	S	Demirjian		Kappa	0.95	30		-
		S	Moorrees		Kappa	0.91	30		-
Lucas (2016) (51)	Lower left third molar	S	Demirjian		Kappa	0.88	15		-
Maled (2016) (52)	All third molars	S	Demirjian		-				Kappa	0.85	167
Olze (2005) (53)	Lower left third molar	S	Demirjian		ICC	0.96	420		ICC	0.95-0.99	420
		S	Gustafson and Koch		ICC	0.89	420		ICC	0.87-0.98	420
		S	Gleiser and Hunt		ICC	0.98	420		ICC	0.95-0.97	420
		S	Kullman		ICC	0.94	420		ICC	0.92-0.98	420
		S	Harris and Nortje		ICC	0.90	420		ICC	0.83-0.93	420
Thevissen (2009) (54)	All third molars	S	Köhler		Weighted kappa	0.93	100		Weighted kappa	0.91-0.92	100
Thevissen (2011) (55)	Lower right third molar	M	Thevissen		WSCV	0.003-0.015	17		-
Zandi (2015) (56)	All third molars	S	Demirjian		Kappa	0.91-0.93	250		Kappa	0.87-0.88	250
Zelic (2016) (57)	Lower left third molar	M	Cameriere		ICC	0.85	60		ICC	0.82	60

CCC = Concordance correlation coefficient; ICC = Intra-class correlation coefficient; M = Measuring lengths and ratios; N = Number of participants; S = Staging; WSCV = Within-subject coefficient of variation.

Second, an observer might be uncertain about the stage to allocate. Corradi et al. (2013) attributed this to the tooth showing an intermediate stage of development or due to an unclear radiograph. (25) Instead of allocating the lowest stage – as originally proposed by Demirjian et al. (1973) (15) – they used artificial intelligence software to cope with what they called “soft evidence”. The observer would then indicate two adjacent stages with the relative degree of belief per stage. By contrast, allocating one stage was defined as “hard evidence”. Performance to discern minors from adults was better when soft evidence was incorporated than when only hard evidence was used. (25)

Finally, reproducibility is influenced by training. It has been stated that increasing experience, results in increasing reproducibility. (8, 24) To the limit, observer-induced variability could be circumvented by applying a deterministic automated staging technique. However, when supervised training of the neural network is applied – as was done in the current study – any errors in the supervised annotation of the training data will still be copied by the automated technique.

Automated age estimation methods

Automated methods imply exact reproducibility. (26) In the current study a staging technique was used, enabling a comparison between automated and human observer staging. However, when continuous data are considered (e.g. volumes of anatomical structures) and ROIs are determined automatically, this cannot be compared with any human observer action. In those studies, only the age estimation performance can be compared with that of methods based on human assessments. Some authors did study differences between volumes measured with different methods.

Dental age

Few studies on automated methods for dental age estimation have been conducted. None of them studied tooth development. Instead they were designed to estimate age in adults. Software for automated line-by-line scanning of tooth-cementum annulations (TCA) was presented by Czermak et al. (2006). (27) Segmentation was necessary and continuous data were used to estimate age. This method was tested on individuals of unknown age and compared with age estimation based on manual TCA counting, but no results on the comparison were reported. Since a comparison with a verified age was not possible, results were considered irrelevant for the current study.

Pulp/tooth volume ratios of monoradicular teeth were studied on cone beam computed tomography (CBCT) in patients between 10 and 65 years of age by Star et al. (2011). (28) Semi-automatic segmentation with Simplant Pro software allowed for the volumes to be defined. Differences between the real volumes and the volumes measured on the 3D images of the same teeth were calculated. For pulp and tooth respectively, they differed maximally 21% and 16%. Linear regression formulas were used with age as dependent variable and pulp/tooth ratio as predictor. The root mean squared errors from the regression model for incisors, canines, and premolars were respectively 12.86, 13.10, and 8.44 years.

Cameriere et al. (2015) studied canine pulp/tooth ratio in adults between 20 and 70 years old. (29) Using MATLAB, their method automatically segmented tooth and pulp tissue on radiographs of extracted teeth. It should be kept in mind that segmentation of in-situ teeth – especially at the root apex – becomes far more difficult due to the decrease in contrast, compared to extracted teeth. Age was estimated using a previously published formula (30), so it was not derived from the study sample. Mean absolute error was 3.05 years. (29)

The pulp chamber volume of upper and lower first molars was studied on CBCT by Ge et al. (2015). (31) Semi-automatic segmentation and voxel counting was performed using ITK-SNAP 2.4 software. A significant difference (p = 0.024) between the pulp volumes obtained from Micro CT and CBCT images was reported, with an average difference of 2.3%. The volume was incorporated into logarithmic regression to estimate age. Mean absolute error of 8.12 years and RMSE of 5.60 years were reported. (31) In a subsequent study the pulp of thirteen tooth types was studied in the same way. The pulp chamber volume of the upper second molar was found to be the most correlated with age. (32)

Skeletal age

Numerous fully automated (i.e. all steps in the process are computerised) methods for skeletal age estimation have been studied. Chang et al. (2003) developed an automatic bone age application that assessed phalangeal development in hand radiographs of patients aged 0.5 to 18 years. (33) Pre-processing (including segmentation) and assessment steps were fully automated. The software was trained using back propagation of neural network. The mean absolute error was less than 1.5 years in 84% of females and 79% of males.

Hand/wrist radiographs can also be evaluated using BoneXpert software (BoneXpert, v1.0; Visiana, Holte, Denmark, www.BoneXpert.com). (26) The software incorporates all three steps (feature recognition, stage allocation, age estimation) of the evaluation and can estimate age in girls from 2 to 15 years old and in boys from 2.5 to 17 years old. It automatically rejects images with abnormal bone morphology or insufficient image quality. The age estimation software was developed based on the findings of five human observers using the Greulich and Pyle atlas (GP) (34) or the Tanner and Whitehouse method (TW2). (35) Using leave-one-out cross-validation, they reported a standard deviation (SD) of 0.42 years between the chronological and estimated age for the GP method. (26) For the TW2 method, a corresponding SD of 0.80 years was reported. On average 68% of stages were allocated correctly to all bones by the software, ranging from 46% (ulna) to 83% (distal third phalanx).

Giordano et al. (2016) presented an alternative automated method based on TW2 for hand/wrist radiographs. (36) It was meant to estimate age in children up to six years old. Compared with two radiologists’ assessments, 87%-91% of stages were allocated correctly. Mean absolute error was 0.37-0.41 years (SD 0.29-0.33) between the automated age estimate and the estimated age based on the radiologists’ assessment.

Software to evaluate MR images is still being optimised. Since MRI provides a 3D depiction of the developing anatomical structures, analysis by the software is more complicated than based on 2D radiographs. To simplify the analysis Saint-Martin et al. (2014) predefined a limited region of interest at the epiphyseal-metaphyseal junction of the distal tibia on each MR image. (37) Their automatic method evaluated grey level variations in epiphyseal-metaphyseal fusion of the distal tibia and estimated age based on principal component analysis. Age estimation performance was only tested by checking whether or not individuals were correctly classified as minors or adults.

Urschler et al. (2015) developed an automated age estimation method based on the whole volumetric data of hand/wrist MRI. (38) It considers physeal fusion as a continuous process, so it does not use distinctive stages. A regression random forest framework is run by the software to pass decision trees taking the whole developmental process into account based on the training data. (13) Current medical computer vision and machine learning allows to process this complex data and use it for age estimation. Mean absolute error between chronological age and estimated age was 0.85 years (SD 0.58 years). (38)

Two major differences should be highlighted between the automated methods for skeletal age and those for dental age. In contrast to the dental age methods, the skeletal age methods were designed to estimate age in children, adolescents and subadults. Secondly, the performance regarding age estimation is better for the described skeletal methods than for the dental methods. A first explanation relates to the previous difference. Age estimation is more accurate and precise in younger individuals than in adults. A second explanation relates to the large variability in dental anatomy. Age related skeletal changes appear more homogenously on medical imaging than age related dental changes.

Limitations and future prospects

The presented automated technique to stage lower third molar development on panoramic radiographs still has some shortcomings. Although it avoided the need for manual or automatic segmentation, a bounding box was necessary to fix the ROI of the stage allocation software. This bounding box can be automatically determined by adapting the detection method by Unterpirker et al. (2015). (14) This requires retraining the Random Forest Regressors on our set of panoramic images of third molars. Alternatively, one can (re)train a Deep Convolutional Neural Network optimised for classification into third molar versus other objects and combine this with a sliding window object detection approach.

Another function that should be included in the process is automatic recognition of unsuitable images. As BoneXpert does (26), the software should be able to recognize images of insufficient quality and images in which the third molar appears extremely tilted.

Currently the highest stage difference between automated and human staging was three stages, but this only occurred once. It should be kept in mind that the current software analyses the image in a totally different way than the human observer does. It only relies on (implicit) non-localized appearance features that maximally distinguish the stages given the training set. This could be improved by replacing some of the fully convolutional layers by locally connected layers, taking positional differences into account. Furthermore, the current automated classification method does not explicitly consider the stage criteria (Table 1) as ordinal variables. Further improvements could be obtained by substituting the last classification layer using a classifier designed for ordinal classification. A two-step hierarchical/cascaded approach, first distinguishing between pre-root and root stages, followed by a final ordinal stage classification could be considered as well. This should be studied in future research, since large stage differences between automated assessment and human observer assessment are unacceptable for age estimation practice. Moreover, as with any Deep Convolutional Neural Network, the accuracy could certainly be increased when more panoramic radiographs are included to train the network. These additional radiographs could either be genuinely new training images or could be created through artificial data augmentation where data are added as transformed (translation, rotation, scale, contrast, etc.) copies of the original training data,.

Furthermore, the third step in the automated process, i.e. age estimation, needs to be implemented. Since the chronological age of the study population is known, the issue can be approached as a regression issue instead of a stage classification issue. This will allow to evaluate age estimation performance of the automated method, instead of stage allocation performance.

Finally, automated dental and skeletal methods should be integrated to further improve age estimation performance. (7, 39-41)

CONCLUSION

The overall performance of the presented automated pilot technique to stage lower third molar development on panoramic radiographs was similar to staging by human observers. Therefore, this novel approach looks promising. Optimisation of the technique will be conducted extending the current study sample and modifying the used software in further research. It represents a necessary step to render a fully automated dental age estimation method, which to date is not available.