Population projection accuracy: The impacts of sociodemographics, accessibility, land use, and neighbour characteristics

Abstract

Population projection is essential to governments, businesses, and research communities for many purposes. Although projection performance is often evaluated, we know very little about what factors affect projection accuracy. It is important to understand these factors in order to utilize the projections knowledgeably. This study fills this gap in the literature by comprehensively investigating the possible factors associated with population projection accuracy in 2010 for the continental US counties. The results indicate that the counties whose populations are more predictable tend to be desirable places—places with abundant employment opportunities, reliable public transportation infrastructure, easy access to work, and/or high land development potential; their neighboring counties tend to have a well-educated population and a higher income level. Also, projection accuracy is highly spatially associated. The findings provide important insights for population projection users to understand the characteristics of counties and their neighboring counties associated with their projection accuracy.

Introduction

Population projection is essential to governments, businesses, and research communities for various purposes (Swanson, 2016). Much of the research effort has been in developing new methods or refining existing methods for population projection (Smith et al., 2013). Such methods include extrapolation projections and time-series models, cohort component methods, postcensal population estimation models, conditional probabilistic models, structural models, population forecasting by grid cells, spatial Bayesian models, and knowledge-based regression models (Chi, 2009; Smith et al., 2013; Wilson & Rees, 2005). The effort in evaluating population projection has been much less (Simpson et al., 1996; Tayman et al., 2011). Although it is a typical practice that population projection is followed by projection evaluation, the latter is done mostly by assessing projection accuracy in different population size and growth categories.

The effort in understanding what factors affect projection accuracy is negligible—to our best knowledge, only three studies (Lenze, 2000; Tayman et al., 2011; Tayman et al., 1998) exist that examine population projection accuracy in association with possible factors; but they consider only three factors: population size, population growth rate, and region. That said, there are studies that identify associated factors of population estimation accuracy, the American Community Survey (ACS) estimates of the US, and population growth (or decline). These factors include demographic characteristics, socioeconomic conditions, transportation accessibility, the natural environment, land use and development, and neighbor characteristics (Chi, 2009; Simpson et al., 1996; Tayman et al., 2011). These factors may also affect population projection accuracy. However, there is a lack of a systemic evaluation of what factors affect projection accuracy and to what extent. Understanding what factors affect population accuracy is important because doing so will help users utilize the projections knowledgeably by knowing their performance and associated factors.

This study fills the gap in the population projection literature by evaluating a baseline population projection in 2010 at the county level in the continental United States using standard regression methods and spatial error models with spatially lagged responses (SEMSLRs [Chi & Voss, 2011]). This study contributes to the literature by investigating the associations of population projection accuracy with a relatively comprehensive list of possible factors, including the characteristics of neighboring spatial units.

In the next section, we briefly review the possible factors and the characteristics of neighboring spatial units that might be associated with population project accuracy; we also discuss the importance of including these factors for evaluating projection accuracy. The following section describes our data and analytical approach. We then report our findings in the results section. In the conclusion and discussion section, we provide a summary of this study and make recommendations for the use of population projections.

Population Projection Accuracy: Associated Factors and the Characteristics of Neighboring Spatial Units

Most of the existing studies that evaluate population projection accuracy focus on comparing the performance of different projection methods (Smith & Mandell, 1984; Wilson, 2015, 2016) or data sources (e.g., Simpson et al., 1996). We are aware of only three studies that investigate population projection accuracy in association with possible factors (Lenze, 2000; Tayman et al., 2011; Tayman et al., 1998). The factors these studies consider include population size, population growth rate, prior projection error, census division, and launch year. However, many other possible factors could affect population projection accuracy (Simpson et al., 1996; Tayman et al., 2011) but have not been investigated. To identify these potential factors, we expand the review of literature into four areas: evaluation of population estimates, evaluation of the ACS estimates of the US Census Bureau, the factors used for population forecasting, and the spatial effects of neighboring spatial units. Although estimating (past) population and projecting (future) population are two different endeavors, the methods for evaluating their performance are often the same. Therefore, we reviewed both the population estimation and projection literature in this paper.

First, some studies have examined the performance of population estimates in association with possible factors (Congdon, 1989; Dong, Ramesh, & Nepali, 2010; Lunn et al., 1998; Pursell, 1970). For example, Mckibben and Swason (1997) argue that it is important to understand and articulate the linkages between substantive socioeconomic factors with population estimation accuracy; they found that taking the de-industrialization trend into account reduced population estimation errors in Indiana, US. In a study of England and Wales, Simpson et al. (1996) note that for areas with highly mobilized populations (students, armed forces, and institutional populations) or for socially disadvantaged places (measured by unemployment rates, percentages of Blacks and Asians, and prevalence of multi-occupier households), it is more difficult to estimate their populations.

Second, some studies have evaluated the ACS estimates and identified potential factors that affect their accuracy (e.g., Folch et al., 2016; Hough & Swanson, 2006; US Census Bureau, 2009). This line of research reveals that the ACS estimation errors are not randomly distributed, instead they are subject to a place’s demographic, socioeconomic, and regional characteristics. For example, using Multnomah County, Oregon, as a test site, Hough and Swanson (2006) found that both the race category and the disability status are notably different between the ACS estimates and the decennial census. In a recent study, Folch et al. (2016) examined spatial variations of the ACS estimate errors. The results indicate that patterns of uncertainty vary across space and that the variations of estimation uncertainty cannot be entirely explained by place-specific economic, demographic, or geographic characteristics.

Third, many factors have been used for population projection. These include demographic characteristics (population size, previous population change rate, population density, age structure, racial and ethnic composition, institutional populations, educational attainment, migration, female-headed families with children, and sustenance organization), socioeconomic conditions (employment opportunities, crime rate, school performance, income growth and distribution, public infrastructure, housing conditions, housing prices, and local efforts to expand services), transportation accessibility (travel time to work, proximity to cities, public transportation, and accessibility to highways, airports, healthcare, and grocery stores), the natural environment (natural amenities such as water features, landscape aesthetics, and public parks and recreational areas as well as disamenities such as landfills, power plants, resource extractions, and propensity to natural disasters), and land use and development. These variables have previously been reviewed and used for population forecasting (e.g., in Chi, 2009) but not for projection evaluation.

Fourth, other factors, which are completely ignored in projection evaluation, are the characteristics of the neighboring units. Traditional population projection methods such as standard regression methods and cohort component methods treat each unit as independent from the others; i.e., what happens in one unit has nothing to do with its neighboring units. However, this independent distribution assumption cannot hold, as nowadays interactions among geographic units have increased dramatically. For example, suppose we have two neighboring towns, Town A and Town B. Most likely, their housing prices are related because convenient transportation (facilitated by personal vehicles or ride-sharing and a well-established transportation network) allows one to choose to work in one town but live in the other. When housing prices in Town A increase, a new equilibrium will be established once more newcomers choose to live in Town B, which has lower housing prices, which in turn increase. So the net gain in Town B is not because of its own “organic” growth but the “spillover” growth of Town A. This kind of spatial effect not only applies to the housing market but also to many of the factors mentioned previously. Spatial effects have been explicitly theorized in several demography-related theories, such as Tobler’s (1970) first law of geography and the spatial diffusion theory (Boyce, 1966). They have also been formally incorporated into demographic models and empirical studies (for a summary of the literature, see Chi & Zhu, 2008; Entwisle, 2007; Fossett, 2005; Reibel, 2007; Voss, 2007). In addition, spatial forecasting methods (e.g., Bracken, 1991; Chi & Voss, 2011; Chi & Wang, 2016; Hammer, Voss & Blakely, 1999) and structural methods (Smith et al., 2013) explicitly incorporate neighbor characteristics and the broader spatial context into population projection. In this study, we develop measures of neighbor characteristics based on the factors mentioned in the previous paragraph and a spatial weight matrix that quantifies the neighborhood structure.

Based on the review of the four areas of literature, we identified 20 factors that are possibly associated with population projection accuracy, falling into the categories of demographic characteristics, socioeconomic conditions, transportation accessibility, and land use and development. The 20 factors and their hypothesized impacts on projection accuracy are discussed in the next section. Specifically, we ask two questions. What characteristics do the predictable counties have? What characteristics do their neighbor counties have?

Data and Methods

We answer the two research questions by producing and evaluating a baseline population projection in 2010 at the county level in the continental United States using exploratory spatial data analysis techniques, standard regression methods, and SEMSLRs. Our baseline population projection is a 40-year extrapolation projection that is based on the arithmetic linear change of populations in 1970, 1980, 1990, and 2000 with the equal weight to project the population in 2010. Despite its simplicity, the extrapolation projection performs as well as sophisticated forecasting methods (Smith et al., 2013).

Data

We compare the projected 2010 population to the 2010 census-based population estimate to calculate the absolute percentage error (APE) and percentage error (PE) for each county. They are used as our two dependent variables to measure population projection accuracy. The PE is calculated as the percentage difference between the projected population and the census-based population estimate (Eq. 1). The APE is calculated as the absolute value of the PE (Eq. 2).

$$\text{PE}=\left(\frac{\mathit{Projected}\mathit{population}\mathit{size}-\mathit{Census}-\mathit{based}\mathit{population}\mathit{estimate}}{\mathit{Census}-\mathit{based}\mathit{population}\mathit{estimate}}\right)\times 100$$ (Eq. 1)

$$\text{APE}=\left|\frac{\mathit{Projected}\mathit{population}\mathit{size}-\mathit{Census}-\mathit{based}\mathit{population}\mathit{estimate}}{\mathit{Census}-\mathit{based}\mathit{population}\mathit{estimate}}\right|\times 100$$ (Eq. 2)

When evaluating population projection accuracy, the APE for each unit is used to calculate a mean APE for all units, which is a measure of projection precision, and the PE for each unit is used to calculate a mean PE for all units, which is a measure of projection bias (Smith et al., 2013). The mean APE and mean PE are two standard measures of population projection accuracy in the applied demography literature (Smith et al., 2013).

All counties in the continental United States are included in the analysis. However, from 1970 to 2010, the boundaries of the counties are not stable: boundaries change, new counties emerge, old counties disappear, and names change. In this study, we obtained population data from the IPUMS National Historical Geographic Information System, which harmonizes all data to the 2010 census geography.

Our independent variables are 20 factors that are possibly associated with population projection accuracy based on the review of relevant literature. The demographic and human capital variables include three conventional factors for evaluating projection accuracy (population growth rate from 2000 to 2010, population size in 2000, and population density in 2000), two age-related measurements (young and old), two race/ethnicity measurements (Black and Hispanic), and three education categories (high school, college, and bachelor’s degree). Economic conditions are measured by four variables: total employment, employment in the agricultural sector, employment in the retail sector, and median household income. Transportation accessibility is measured by three variables: public transportation, commuting time, and airport accessibility. We also include two crime-related statistics at the county level, total crime and violent crime. Land use and development is measured by the land developability index, which calculates the percentage of land available and suitable for future conversion and development (Chi, 2010a). The 20 independent variables represent a relatively comprehensive list of possible factors associated with population projection accuracy. These variables’ detailed descriptions, descriptive statistics, and data sources are presented in Table 1.

Table 1.

Variable descriptions, descriptive statistics, and data sources (N = 3,109)

Variable	Description	Mean	Std. Err.	Min	Max	Source
Absolute percentage error (APE) (APE)	Absolute value of the percentage error (%)	8.52	6.07	0.00	48.27	Decennial census 1970–2010
Percentage error (PE)	Percentage error (%)	4.40	9.49	−48.27	42.96	Decennial census 1970–2010
Population growth rate	Population growth rate, 2000–2010 (%)	5.24	13.13	−46.60	110.35	Decennial censuses 2000 and 2010
Population size	Population size, 2000 (natural log-transformed)	10.25	1.54	0.00	16.10	Decennial census 2000
Population density	Number of people per square kilometers	244.46	1675.61	0.10	66940.07	Decennial census 2000
Young	% young population (ages 12–18), 2000	25.48	3.22	9.57	45.30	Decennial census 2000
Old	% old population (age 65+), 2000	14.81	4.12	1.80	34.72	Decennial census 2000
Black	% Black population, 2000	8.84	14.56	0.00	86.49	Decennial census 2000
Hispanic	% Hispanic population, 2000	6.21	12.05	0.08	97.54	Decennial census 2000
High school	% population (age 25+) who finished high school, 2000	34.69	6.59	10.93	53.25	Decennial census 2000
Bachelor’s degree	% population (age 25+) with a bachelor’s degree, 2000	10.96	4.93	0.00	40.02	Decennial census 2000
College	% college population, 2000	26.11	5.65	9.87	44.89	Decennial census 2000
Employment	Employment rate, 2000	57.17	7.60	20.94	83.65	Decennial census 2000
Income	Median household income, 2000 (US dollars)	35456.74	8959.65	9333.00	82929.00	Decennial census 2000
Agriculture	% workers in agricultural industry, 2000	7.23	7.64	0.04	58.19	Decennial census 2000
Retail	% workers in retail industry, 2000	11.49	2.05	0.00	26.90	Decennial census 2000
Public transportation	% workers using public transportation to get to work, 2000	0.89	2.81	0.00	59.62	Decennial census 2000
Commuting time	% workers traveling 30 minutes or less to work, 2000	69.94	11.89	27.26	97.30	Decennial census 2000
Airport accessibility	Inverse distance from the centroid of a county to the nearest airport its nearest major airport	9142.46	10766.66	46.22	408524.80	Atlas of the United States
Total crime	Total crime per 100,000 population, 2000	535.74	385.76	0.00	3627.86	Uniform Crime Reports of FBI, 2000
Violent crime	Violent crime per 100,000 population, 2000	134.46	125.44	0.00	934.07	Uniform Crime Reports of FBI, 2000
Land developability	Land developability index	64.56	25.42	0.00	99.85	www.landdevelopability.org

Notes: FBI = Federal Bureau of Investigation.

Table 2 shows the expected association of each independent variable with the APE and PE. A positive (negative) coefficient suggests that the increase of an independent variable is associated with an increase (decrease) in APE, that is, lower (higher) projection precision. The interpretation of coefficients for PE, however, is not straightforward—for counties experiencing population growth, a positive coefficient indicates that the increase of an independent variable is associated with an increase in bias (i.e., an upward bias); for counties losing population, a positive coefficient indicates that the increase of an independent variable is associated with a reduction in bias (i.e., a downward bias) (Tayman, Smith, & Rayer, 2011).

Table 2.

Hypothesized relationships that each independent variable has with absolute percentage error (APE) and percentage error (PE)

Variable category	Variable measurements	APE	PE
Conventional factors for evaluating projection accuracy	Population growth rate	+	−
	Population size	−	+
	Population density	−	+
Age structure	Young Old	+	−
Racial/ethnic composition	Black Hispanic	+	−
Human capital	High school	−	−
	Bachelor’s degree
	College
Economic condition	Employment Income	−	−
	Agriculture Retail
Transportation	Public transportation Commuting time Airport accessibility	−	−
Crime	Total crime Violent crime	+	+
Land use and development	Land developability	−	−

To begin with, existing research has consistently found that population growth rate and population size are closely related with projection error (Lenze, 2000; Tayman et al., 2011). In particular, an increased population growth rate is observed to be linked with lower projection precision (higher APE) and higher bias (Smith, 1987; Tayman et al., 2011), whereas a higher population size is associated with improved precision (lower APE) but have little to do with projection bias. We also expect that higher population density is associated with higher precision but lower bias since more populous areas are easier to forecast than less populous areas. In addition, we expect that other demographic factors, such as age structure and racial composition, play a significant role in affecting projection accuracy. In particular, places with high percentages of elders, young people, Blacks, and Hispanics are harder to predict (Simpson et al., 1996), thus they would exhibit higher APEs and higher bias.

Also, human capital stock and local economic opportunities matter for projection accuracy. For human capital stock, we expect that places with higher percentages of better educated populations (measured by the percentages of the population with a high school degree and a bachelor’s degree as well as college population) are easier to predict and thus have lower APEs. In terms of local economic opportunities, we expect that places with better economic conditions (high employment rates and high median household incomes) are easier to predict; in other words, employment rate and median household income should be negatively associated with the APE. Previous work in regional science suggests that a place’s economic structure might have little to do with projection error (e.g., Lenze, 2000). Therefore, we expect to see insignificant associations of the percentages of employment in the agricultural and retail sectors with the APE and PE. We nevertheless still include these variables in our initial model.

Further, we hypothesize that a place’s living conditions (measured by transportation, crime rate, and the land available for conversion and development) matter for population projection accuracy. All else being equal, the desired living conditions would attract a constant population flow, which is more predictable and thus exhibits lower APEs.

Analytical Approach

We first adopted mapping and the local indicator of spatial association (LISA) to illustrate the distribution of APEs and PEs. We then used standard regression models and SEMSLRs to investigate what factors affect projection accuracy and what characteristics predictable counties’ neighbor counties have.

The LISA is an exploratory spatial data analysis method for detecting possible spatial clusters and/or outliers (Anselin, 1995). In this research, we used local Moran’s I to identify spatial clusters of APE and PE (i.e., counties with high APEs or PEs surrounded by counties with high APEs or PEs and counties with low APEs or PEs surrounded by counties with low APEs or PEs) as well as spatial outliers of APEs and PEs (i.e., counties with high APEs or PEs surrounded by counties with low APEs or PEs and counties with low APEs or PEs surrounded by counties with high APEs or PEs).

The standard regression models test if and how the two population projection accuracy variables—APE and PE—are associated with the 20 independent variables. The SEMSLRs include neighbor characteristics in addition to the variables used in the standard regression models (Chi 2010b). A SEMSLR is specified as:

$$\begin{gathered} Y=X\beta +\theta WY+u, \\ u=\rho Wu+\epsilon , \end{gathered}$$ (Eq. 3)

where Y is an n by 1 vector of response variables, X is an n by p design matrix of explanatory variables, W is an n by n spatial weight matrix, WY denotes a spatially lagged response variable in the sense that it is a weighted average of the response variables in the neighborhood, β is a p by 1 vector of regression coefficients for p explanatory variables, θ is a scalar coefficient for the spatially lagged response variables, u is an n by 1 vector of error terms, ρ is a scalar spatial error parameter, Wu denotes a spatially lagged error term in the sense that it is a weighted average of the error terms in the neighborhood, and ε is an n by 1 vector of error terms that are normally and independently but not necessarily identically distributed.

In this study, we define a county’s neighbor counties based on a first-order queen’s contiguity weight matrix, an often-used weight matrix in the demographic literature (Chi & Zhu, 2008). Any county that shares a portion or a point of County A’s boundary is County A’s neighbor county. A neighbor characteristic is measured as a weighted neighbor average of the corresponding independent variable. For example, County A’s neighbor income is the average of the income in its neighbor counties. We calculated a neighbor characteristic for each corresponding independent variable as well as the dependent variable (APE or PE). In total, we calculated 21 neighbor characteristics and used them in our SEMSLRs. It should be noted that the large number of independent variables in both the standard regression models and the SEMSLRs might cause a potential multicollinearity problem, which we used variance inflation factors (VIFs) to detect. The VIF values reflect how much of an independent variable’s variation is explained by the rest of the independent variables. Specifically, the VIF for independent variable i is defined as ${\mathit{VIF}}_i=\frac{1}{1-r_i^2}$, where $r_i^2$ is obtained by fitting a regression model for variable i on the rest of the independent variables (Craney & Surles, 2002). We use the maximum VIF value of 5 as an acceptable level (Rogerson, 2001).

For the standard regression models, we started with two full standard regression models with the two dependent variables. We used the backward elimination approach (Agresti & Finlay, 2009) based on the smallest Bayesian information criterion to remove the factors that do not have statistically significant associations with the dependent variable. For the SEMSLRs, we also started with two full models and then applied the backward elimination approach to refine the models.

Results

The Spatial Distribution of Projection Accuracy

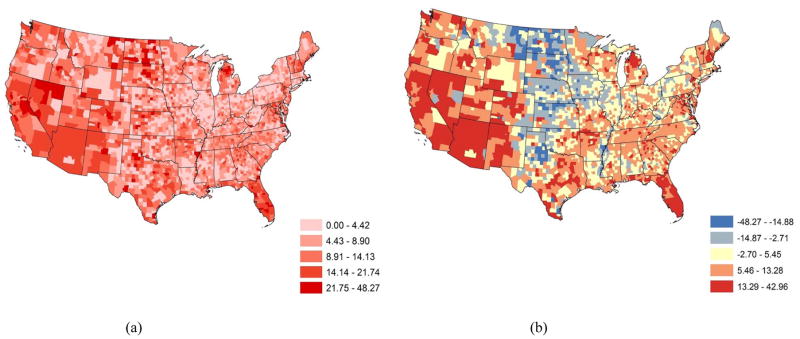
Figure 1 displays the spatial distribution of APEs (left panel) and PEs (right panel). The APE distribution suggests that population projections from the Midwest to New England are relatively precise. The precision decreases southward and westward generally. The precision fares the worst in Florida and the West, including California, Nevada, and Arizona. The PE distribution suggests that the projections are the least biased in two belts: one extending from Illinois to Indiana, Ohio, West Virginia, Pennsylvania, and New York, and the other across the three “Deep South” states of Alabama, Mississippi, and Louisiana. The Great Plains is underprojected while Florida, the West, and the Southwest are overprojected.

Fig. 1. Distributions of (a) absolute percentage errors and (b) percentage errors.

Notes: The values of APEs are non-negative. Large values of APEs indicate lower precision. A positive PE indicates that the 2010 population has been overprojected; a negative PE indicates that the 2010 population has been underprojected.

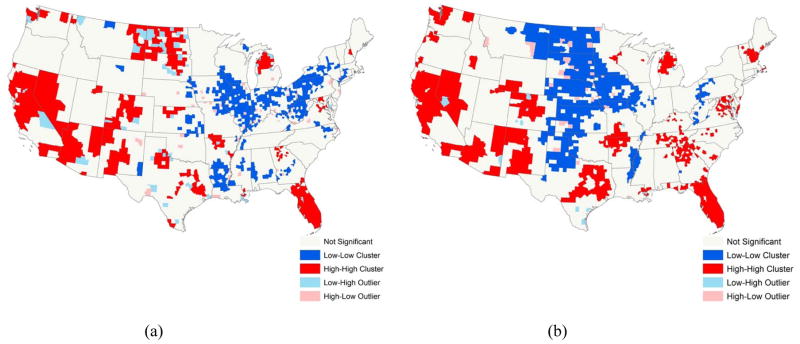
We further detect possible spatial clusters of APEs and PEs using the LISA statistics in Figure 2. The results of the LISA statistics echo those shown in Figure 1. The left panel of Figure 2 suggests that the projections are the most precise from Illinois to Indiana, Ohio, West Virginia, Pennsylvania, and New York, as well as for northern Louisiana. The projections are the least precise in Florida, California, Nevada, Arizona, and New Mexico. The right panel shows that the Great Plains has clusters of downward biases where populations are underprojected; clusters of upward biases (i.e., overprojected populations) dominate in Florida and scatter in the West and Southwest (California, Nevada, Arizona, New Mexico, and Utah), east Texas, part of Tennessee and Alabama, the D.C. region, New Hampshire, and northern Lower Michigan.

Fig. 2. Local clusters of spatial association of (a) absolute percentage errors and (b) percentage errors.

Note: Low-low clusters of APEs highlight counties with low APEs that are surrounded by counties with low APEs; the projections for these counties have high precision. High-high clusters of APEs highlight counties with high APEs that are surrounded by counties with high APEs; the projections for these counties have low precision.

Low-low clusters of PEs highlight counties with low PEs that are surrounded by counties with low PEs; these counties are underprojected and have high downward projection bias. High-high clusters of PEs highlight counties with high PEs that are surrounded by counties with high PEs; these counties are overprojected and have high upward projection bias.

Low-high outliers indicate counties with low APEs (or PEs) that are surrounded by counties with high APEs (or PEs). High-low outliers indicate counties with high APEs (or PEs) that are surrounded by counties with low APEs (or PEs).

The Predictable Counties’ Characteristics

To examine the associations between the projection accuracy and county characteristics, we fit standard regression models. Table 3 presents the results of the initial full models. Table 4 presents the results of standard ordinary least squares (OLS) models for both APE and PE as dependent variables in the reduced model after the backward elimination procedure. To facilitate the comparison on the relative magnitudes of the effects that the independent variables have on the dependent variables, we choose to present standardized beta coefficients rather than the unstandardized ones in both tables (Vittinghoff et al., 2012). We focus on explaining the signs and magnitudes in the reduced models.

Table 3.

Results of the initial standard regression models

	Model 1 (APE)	Model 2 (PE)
Population growth rate	0.33***	−0.87***
Population size	−0.13***	0.09***
Population density	0.01	0.02
Young	0.04	−0.01
Old	0.01	−0.20***
Black	0.12***	−0.14***
Hispanic	0.05*	0.03
College	0.08**	0.05**
High school	0.05	−0.09***
Bachelor’s degree	0.09*	−0.06*
Employment	−0.07*	−0.07***
Income	−0.01	−0.04*
Agriculture	0.16***	−0.15***
Retail	−0.01	0.07***
Public transportation	−0.00	−0.18***
Commuting time	−0.11***	−0.20***
Airport accessibility	0.05*	0.05**
Total crime	−0.04	−0.01
Violent crime	0.01	0.03
Land developability	−0.13***	−0.11***
Measurement of fit
Adjusted R2	0.16	0.53
AIC	−8718.02	−8414.15

Notes:

APE = Absolute percentage error; PE = Percentage error; AIC = Akaike information criterion.

Coefficients reported in the table are standardized coefficients.

^***p ≤ 0.001;

^**p ≤ 0.01;

^*p ≤0.05.

Table 4.

Results of the refined standard regression models

	Model 1 (APE)		Model 2 (PE)
	Coefficient	VIF	Coefficient	VIF
Population growth rate	0.32***	1.52	−0.87***	1.68
Population size	−0.13***	2.30	0.10***	2.48
Old	/		−0.20***	1.88
Black	0.12***	1.50	−0.14***	1.44
Hispanic	0.06**	1.54	/
College	0.09***	1.73	0.05**	1.85
High school	0.06*	3.15	−0.11***	2.77
Bachelor’s degree	0.08*	3.68	−0.07**	3.64
Employment	−0.05*	2.41	−0.08***	2.96
Income	/		−0.04***	1.70
Agriculture	0.18***	2.16	−0.14***	2.39
Retail	/		0.07***	1.44
Public transportation	/		−0.16***	1.41
Commuting time	−0.12***	1.32	−0.19***	1.49
Airport accessibility	0.05***	1.23	0.05***	1.24
Land developability	−0.13***	1.59	−0.11***	1.72
Measures of fit
Adjusted R2	0.16		0.53
AIC	−8727.46		−8418.17

Notes:

APE = Absolute percentage error; PE = Percentage error; VIF = Variance inflation factor; AIC = Akaike information criterion.

Coefficients reported in the table are standardized coefficients.

“/” means that the corresponding independent variable is not included in the regression model.

^***p ≤ 0.001;

^**p ≤ 0.01;

^*p ≤0.05.

Adjusted R² penalizes the model for including too many predictors. It is computed using the formula $R_{\mathit{adj}}^2=1-[\frac{\left(1-R^2\right)(n-1)}{n-k-1}]$, where n is the sample size and k is the number of predictors.

Sixteen percent of the variations of the APEs can be explained by twelve independent variables. The variables that have statistically significant negative associations with the APEs include population size, employment, commuting time, and land developability. The higher the values of these variables, the smaller the APE is (higher projection precision). In contrast, counties with higher growth rate and higher percentages of Blacks, Hispanics, residents with high school diplomas, college students, residents with bachelor’s degrees, agricultural employment, and/or easier access to airports have higher APEs (lower projection precision). In terms of coefficient magnitude, the increase of population growth rate has the largest effect on reducing projection precision (one standard unit increase of population growth rate is related with 0.32 unit increase of the APE), followed by agricultural employment (beta = 0.18), Black (beta = 0.12), and college (beta = 0.09). In contrast, population size and land developability have the largest effect on increasing projection precision—for every one standard unit increase in population size or land developability, the APE decreases by 0.13 standard unit. Also, commuting time also has relatively large effect on reducing the APE (beta = −0.12).

Fifty-three percent of the variation of the PEs can be explained by fifteen independent variables. The variables that have statistically significant negative associations with the PEs include population growth rate, old, Black, high school diplomas and bachelor’s degrees, employment, agricultural workers, income, public transportation, commuting time, and land developability. The higher the values of these variables, the smaller the PE is. An increase in any of these factors reduces projection upward bias for counties with overprojected populations but increases downward bias for counties with underprojected populations. Increased population growth rate has the largest effect on reducing the PE—with one standard deviation increase of population growth rate, the PE reduces by a 0.87 standard deviation. In contrast, counties with more people; higher percentages of Hispanics, college students, and retail employment; and/or higher airport accessibility have higher PEs. An increase in any of these factors increases projection upward bias for counties with overprojected populations but reduces downward bias for counties with underprojected populations.

By looking at both projection precision and projection bias, we find that the predictable counties have large populations and higher employment rates along with shorter commuting time, and/or higher land developability. These counties are those with ample employment opportunities, easy access to work, and/or high land development potential.

The Characteristics of Predictable Counties’ Neighboring Counties

To examine the possible associations of the projection accuracy with neighboring counties’ characteristics, we use SEMSLRs that specify APEs and PEs as a function of the county’s characteristics and their neighboring counties’ characteristics. The results of the initial full models are presented in Table 5. The results of the refined models after backward elimination are presented in Table 6.

Table 5.

Results of the initial spatial error regression models with spatially lagged responses

	Model 1 (APE)	Model 2 (PE)
Population growth rate	0.39***	−1.00***
Population size	−0.13***	0.08***
Population density	0.03	0.01
Young	0.04	0.03
Old	0.01	−0.25***
Black	0.11**	−0.26***
Hispanic	0.02	−0.12***
College	0.10**	0.04
High school	0.13**	0.02
Bachelor’s degree	0.11*	0.03
Employment	−0.06	−0.01
Income	0.01	−0.04*
Agriculture	0.16	−0.19***
Retail	−0.02	0.03
Public transportation	0.01	−0.13***
Commuting time	−0.11***	−0.12***
Airport accessibility	0.05*	0.02
Total crime	−0.03	0.01
Violent crime	0.01	−0.01
Land developability	−0.14***	−0.01
Neighbor average
Population growth rate	−0.04	0.1***
Population size	−0.10*	0.00*
Population density	−0.05	−0.07
Young	−0.02	−0.05*
Old	0.01	0.10***
Black	0.00	0.16***
Hispanic	0.02	0.15
College	−0.06	0.03
High school	−0.15**	−0.06
Bachelor’s degree	−0.05	−0.15***
Employment	0.00	−0.08*
Income	−0.08**	−0.05*
Agriculture	0.01	0.07
Retail	0.02	0.03*
Public transportation	−0.00	0.07
Commuting time	−0.01	−0.04
Airport accessibility	0.00	0.06***
Total crime	0.02	−0.05
Violent crime	−0.02	0.07**
Land developability	−0.01	−0.10***
Measurement of fit
Adjusted R2	0.17	0.58
AIC	−8721.98	−8741.36

Notes:

APE = Absolute percentage error; PE = Percentage error; AIC = Akaike information criterion.

Coefficients reported in the table are standardized coefficients.

^***p ≤ 0.001;

^**p ≤ 0.01;

^*p ≤0.05.

The neighbor averages are calculated based on the first-order queen’s continuity matrix.

Table 6.

Results of the refined spatial error models with spatially lagged responses

	Model 1 (APE)		Model 2 (PE)
	Coefficient	VIF	Coefficient	VIF
Population growth rate	0.39***	2.04	−0.99***	2.16
Population size	−0.11***	2.32	0.04**	2.63
Young	/		0.04**	2.28
Old	/		−0.22***	2.94
Black	0.09***	1.58	/
College	0.06*	1.88	0.05*	2.04
High school	0.10**	4.62	/
Bachelor’s degree	0.06*	3.66	0.09**	2.75
Employment	−0.05*	2.72	/
Income	/		−0.06**	1.69
Agriculture	0.19***	3.41	−0.21***	4.04
Retail	/		0.04*	1.51
Public transportation	/		−0.07***	1.51
Commuting time	−0.11***	1.74	−0.16***	2.25
Airport accessibility	0.05*	1.24	/
Land developability	−0.11***	1.71	/
Neighbor average
Population growth rate	−0.19***	2.29	0.57***	3.66
Young	/		−0.04*	2.72
Old	/		0.14***	3.93
Hispanic	0.04	1.69	/
High school	−0.07*	3.28	/
Bachelor’s degree	/		−0.10***	3.31
Employment	/		−0.06***	2.36
Agriculture	−0.05*	1.94	/
Income	−0.06*	3.91	0.21***	4.47
Commuting time	/		0.07**	2.93
Airport accessibility	/		0.03**	1.67
Spatially lagged APE	0.18***	1.28	/
Spatially lagged PE	/		0.43***	1.87
Measures of fit
Adjusted R2	0.19		0.64
AIC	−8842.80		−9288.47

Notes:

APE = Absolute percentage error; PE = Percentage error; VIF = Variance inflation factor; AIC = Akaike information criterion.

Coefficients reported in the table are standardized coefficients.

“/” means that the corresponding independent variable is not included in the regression model.

^***p ≤ 0.001;

^**p ≤ 0.01;

^*p ≤0.05.

Adjusted R² penalizes the model for including too many predictors. It is computed using the formula $R_{\mathit{adj}}^2=1-[\frac{\left(1-R^2\right)(n-1)}{n-k-1}]$, where n is the sample size and k is the number of predictors.

The neighbor averages are calculated based on the first-order queen’s continuity matrix.

Overall, the SEMSLRs improve model fit to data slightly: the adjusted R² increases from 0.16 to 0.19 for APEs and from 0.53 to 0.64 for PEs. The corresponding Akaike information criterion (AIC) values decrease for APEs and PEs, suggesting an improvement in model fit to data. The retained independent variables as well as their coefficients change modestly from the standard regression models.

The variables that have statistically significant negative associations with the APEs include population size, employment, commuting time, and/or land developability. The higher the values of these variables, the smaller the APE is, and the higher projection precision is. Similar to the results from the standard regression model, an increase in population size, employment, commuting time, and/or land developability increases projection precision; their effects are slightly less than those found from the standard regression model. In contrast, counties with higher growth rates and higher percentages of Blacks, residents with high school diplomas, college population, residents with bachelor’s degrees, and/or airport accessibility have lower projection precision; this is consistent with the results from the standard regression model.

In terms of neighboring counties’ characteristics, we found that if a county’s neighboring counties have a higher population growth rate, higher percentages of residents with high school diplomas and agricultural workers, and/or higher income, this county’s population projection has higher precision. For each standard unit increase in these factors of the neighboring counties, the APE decreases by 0.19, 0.07, 0.06, and 0.05 standard unit, respectively. In contrast, we found neighboring counties’ percentage of Hispanics is negatively associated with projection precision; for each standard unit increase in the neighboring’s counties’ Hispanic percentage, the APE increases by 0.05 standard unit. In addition, a county’s APE is positively and strongly associated with its neighboring counties’ APEs. For each standard unit increase in the latter, a county’s APE increases by 1.28 standard unit.

The variables that have statistically significant negative associations with the PE include population growth rate, old population, agricultural workers, income, public transportation, and commuting time. An increase in any of these variables reduces the upward projection bias for counties with overprojected populations but increases the downward projection bias for counties with underprojected populations. In contrast, counties with more people and/or higher percentages of young residents, college students, residents with bachelor’s degrees, and retail workers have higher PEs. An increase in any of these variables increases the upward projection bias for counties with overprojected populations but reduces the downward projection bias for counties with underprojected populations.

In terms of neighboring counties’ characteristics, a county’s PE is negatively associated with the percentages of young population, residents with bachelor’s degrees, and employment in its neighboring counties. For each standard unit increase in these variables, the PE decreases by 0.04, 0.10, and 0.06, respectively; these changes reduce the bias for counties with overprojected populations but increase the bias for counties with underprojected populations. In contrast, a county’s PE is positively associated with its neighboring counties’ population growth rate and percentages of old population, agricultural workers, commuting time, and airport accessibility. Each standard increase in the neighboring counties’ population growth rate is associated with 0.57 standard unit increase of PEs. In addition, a county’s PE is positively and strongly associated with its neighboring counties’ PEs. For each standard unit increase in the latter, a county’s PE increases by 1.87 standard unit.

Overall, we found that the predictable counties have more employment opportunities, easier access to work, and more available lands for development. Their neighboring counties have higher growth rates, higher percentages of residents with high school diplomas and bachelor’s degrees, more employment opportunities, and/or higher income.

Conclusion and Discussion

In this study, we investigate the possible factors associated with population projection accuracy in 2010 and the possible spatial variations of the associations for the continental US counties. The results indicate that the counties whose populations are more predictable tend to be desirable places—places with abundant employment opportunities, reliable public transportation infrastructure, easy access to work, and/or high land development potential; their neighboring counties tend to have a well-educated population and a higher income level. Because such places are desirable, they tend to experience stable population growth. For example, communities located in a good school district most likely have a strong housing market in a good or a weak economy. It is easier to conduct population projection in places with stable population growth than in places with unpredictable population change. Desirable places are more predictable.

The findings provide important insights for population projection users to understand projection accuracy associated with the characteristics of the counties and their neighboring counties. The findings of this research provide at least two implications. The first one is about how population projections can be used smartly for urban and regional planning purposes. Population projections have long been an important element in the urban and regional planning processes because, after all, it is population change that drives the change in demands for resources, which in turn requires an efficient coordination of resource allocations through urban and regional planning (Rayer & Smith, 2010). For example, comprehensive planning and the “smart growth” laws enacted in many states emphasize the importance of accurate population projections in urban and regional planning. Transportation planning is largely determined by predicted population change and traffic flows at local levels. However, the accuracy of population projections varies from one place to another. To use population projections smartly, it is important to know how well a projection performs, where it performs better, what affects its accuracy, and how it interacts with neighboring counties. Knowing parameters will help urban and regional planners use their expertise of local contexts to make the best judgements for planning purposes.

The second implication is that knowledge may not be able to help improve population projection accuracy, but it can definitely help with evaluating the projections. Keyfitz (1982) demonstrated that increasing knowledge does not necessarily help improve population projection accuracy and argued that the simplest method, extrapolating the past trend into the future, seems to perform the best. Despite this insight, efforts to improve projection accuracy have never stopped. This can be evidenced by the development of new methods, such as spatial regression models, geographically weighted regression methods, Bayesian methods, probabilistic methods, and many others, for improving population projections. Unfortunately, although some of these methods perform reasonably well based on some indicators of projection accuracy, overall they do not outperform the simplest extrapolation projection methods (Tayman et al., 2011). What does this mean? Should we stop pursuing knowledge? Is knowledge useless? Absolutely not. Our position is that knowledge is still useful, but its effectiveness depends upon how we use it. Although knowledge may not help with improving projection accuracy, it can be useful for us to understand why some areas are more predictable than others. Applied demographers (e.g., Smith & Tayman, 2003; Wilson, 2015) have long called for switching the focus of demographic forecasting from improving the methods to evaluating projection methods and accuracy. On the one hand, population projection accuracy from national and international scales to subcounty scales has not been improved much for at least the past half century (Chi, 2009). On the other hand, we see the rapidly increasing use of population projections in scenarios from urban planning to climate change research. Do we feel confident with the accuracy of the projections that we use? We are not saying we should not use population projection. For planning and climate change research purposes, we have to produce and use population projections. The point here is that we need to understand how the projections perform and when and where they work better than in other time periods and/or places.

It should be noted that the population projection accuracy assessed in this study is limited to the total population. To make the evaluation of population projection accuracy more useful, future research should examine what factors affect projection accuracy by different age, gender, and race/ethnicity groups. After all, different planning activities are targeted for different age groups. For example, education planners need school enrollment projections for ages 0–24. Labor force planners need population forecasts for ages 18–65. Health departments require forecasts of populations aged 50 and over. Businesses are more interested in the population estimates and forecasts of their targeted customers. For instance, women’s clothing stores are interested in estimates and forecasts of female populations at a certain age ranges. All of these different populations would require population forecasts produced by the cohort-component method (Smith et al., 2013). Future research could use the cohort-component method to project population by age, gender, and race/ethnicity, evaluate their projection accuracies, and identify factors that influence the accuracies. Such knowledge gained would be useful for different planning purposes.

It should also be noted that the “smaller” findings—in terms of what factors have what effects—might not be generalizable to other countries. On one hand, homogenous societies have little variation in terms of stratification (e.g., race and ethnicity) such as in Finland; the impact of neighboring spatial units’ characteristics in such societies would be much less than in the United States. On the other hand, in countries with a stratification system (e.g., based on wealth), population growth and population projection accuracy would be impacted by neighboring spatial units’ characteristics, but what characteristics make a place desirable place vary from country to country. That said, the “bigger” finding—that desirable places are based on different factors in different societies and that these differences reflect to a great extent how the stratification systems work in each society—is generalizable.