Ultra-high resolution blood volume fMRI and BOLD fMRI in humans at 9.4 T: Capabilities and Challenges

Abstract

Functional mapping of cerebral blood volume (CBV) changes has the potential to reveal brain activity with high localization specificity at the level of cortical layers and columns. Non-invasive CBV imaging using Vascular Space Occupancy (VASO) at ultra-high magnetic field strengths promises high spatial specificity but poses unique challenges in human applications. As such, 9.4 T B₁⁺ and B₀ inhomogeneities limit efficient blood tagging, the specific absorption rate (SAR) constraints limit the application of VASO-specific RF pulses, short T₂* values at 9.4 T require short readout duration, and long T₁ values at 9.4 T can cause blood-inflow contaminations.

In this study, we investigated the applicability of layer-dependent CBV-fMRI at 9.4 T in humans. We addressed the aforementioned challenges by combining multiple technical advancements: temporally alternating pTx B₁⁺ shimming parameters, advanced adiabatic RF-pulses, 3D-EPI signal readout, optimized GRAPPA acquisition and reconstruction, and stability-optimized RF channel combination. We found that a combination of suitable advanced methodology alleviates the challenges and potential artifacts, and that VASO fMRI provides reliable measures of CBV change across cortical layers in humans at 9.4 T. The localization specificity of CBV-fMRI, combined with the high sensitivity of 9.4 T, makes this method an important tool for future studies investigating cortical micro-circuitry in humans.

Graphical abstract

1. Introduction

A detailed understanding of the organization of macroscopic brain areas into distinct functional networks requires a detailed knowledge of the inter-area connections between the cortical layers (Hubei and Wiesel, 1972; Lund, 1988; Yacoub et al., 2015). The cortical grey matter (GM) ribbon consists of up to six of these histologically-defined cortical layers with thicknesses usually between 0.2 mm and 1 mm (Brodmann, 1909). Mapping the brain activity across the cortical layers and their differential functional connectivity to distant brain areas is highly valuable for human cognitive research (Lawrence et al., 2017; Stephan et al., 2017) and has the potential to become a valuable tool in clinical psychiatry. As such, many current theories of psychiatric and neurological diseases stress that they are primarily related to disorders of neural circuits (Gordon, 2016). Hence, mapping of layer-specific activity has the potential to serve as a missing link between preclinical animal research and clinical psychology.

The only non-invasive in-vivo imaging method currently capable of mapping brain activity at sub-millimeter resolutions across cortical layers is functional magnetic resonance imaging (fMRI).

While gradient echo (GE) blood oxygenation level-dependent (BOLD) fMRI is biased towards superficial cortical layers by locally unspecific veins (Menon et al., 1993; Polimeni et al., 2010; Uludag and Blinder, 2017), converging evidence suggests that alternative fMRI methods sensitive to cerebral blood volume (CBV) have a higher localization specificity (Goense et al., 2012; Huber et al., 2017a; Kennerley et al., 2005; Kim et al., 2013).

The only non-invasive CBV approach for high-resolution application in humans is Vascular Space Occupancy (VASO) (Lu et al., 2003). VASO measures CBV changes through selective detection of signal changes in the extravascular compartment, concurrent with changes in the nulled intravascular blood compartment. The VASO contrast is thus based on the difference between the longitudinal relaxation times (T₁) of tissue and blood and is generated by applying an inversion pulse before signal acquisition, effectively nulling the contribution of blood water magnetization at the time of signal excitation (so-called “blood-nulling time”), while keeping substantial tissue signal for detection.

The main disadvantage of VASO is the higher noise level compared to the GE-BOLD signal. The correspondingly low signal-to-noise ratio (SNR) and functional contrast-to-noise ratio (CNR) are particularly challenging at ultra-high spatial resolutions (voxel sizes < 1 mm³) (Huber et al., 2017c). The higher image SNR at ultra-high field strengths (9.4 T) (Pohmann et al., 2016) could theoretically counteract the limited sensitivity of sub-millimeter VASO. However, the application of VASO in humans at 9.4 T is associated with multiple VASO-specific technical challenges as follows:

a). Long T₁ values at 9.4 T increase the risk of unwanted blood-inflow contaminations.

The longer blood-T₁ at 9.4 T (Dobre et al., 2006) results in longer blood-nulling times, at which the VASO signal should be acquired (Jin and Kim, 2008). The correspondingly longer inversion time (TI) increases the risk of inflow of fresh (non-inverted) blood into the imaging slice (Donahue et al., 2009b).

b). Short T₂^* values at 9.4 T limit the EPI readout duration.

The faster T₂^* decay at 9.4 T is challenging for echo-planar readout schemes used in most fMRI applications (Kemper et al., 2017). It can limit the effective resolution and cause blurring in the phase-encoding direction (Huber et al., 2015b; Shmuel et al., 2007). For VASO applications, the fast T₂^* decay imposes an additional challenge of causing confounding BOLD contaminations that counteract the VASO contrast (Lu and van Zijl, 2005).

c). Specific absorption rate (SAR) limits constrain the RF power deposition.

The higher energy deposition at increasing field strengths (Vaughan and Griffiths, 2012) is accompanied by restrictive safety constraints for applications in humans. This is not only challenging with respect to the VASO-specific inversion pulses, but it also limits the number of fat saturation pulses and the flip angle of the excitation pulses preceding the image acquisition.

d). Variable signal stability of small RF elements in large channel count arrays.

Since the RF wavelength decreases with field strength, individual RF receive channels have a spatial sensitivity field that varies on a finer scale. This means that for the small elements in large channel count arrays, a given region of interest (ROI) in the brain has heterogeneous signal stability across the individual RF channels. While channels with close proximity to the ROI might capture the signal with high stability, other RF channels might be too far away from it and/or might be biased by signal fluctuations of other areas (e.g., the even closer skin).

e). B₁⁺ and B₀ inhomogeneities limit the efficient blood inversion in VASO.

B₁⁺ inhomogeneities at 9.4 T (Tse et al., 2016; Vaughan et al., 2006) are challenging in VASO because they limit the spatial homogeneity of the VASO-specific magnetization inversion efficiency. Insufficient blood magnetization preparation may introduce unwanted CBF contamination in large arteries (Donahue et al., 2009b). B₀ inhomogeneities can further limit the performance of inversion pulses (Bause et al., 2016) and result in larger distortions in EPI acquisitions.

In this paper, we discuss and investigate the limitations and the applicability of VASO fMRI at 9.4 T. Specifically, we focus on addressing the challenges listed above by means of advanced imaging technology. As such, we investigate the capabilities of temporally alternating pTx shimming parameters, advanced adiabatic RF pulses, 3D-EPI signal readout, optimized GRAPPA acceleration schemes, and stability-optimized locally specific RF channel combination schemes.

2. Materials and Methods

2.1. MR sequence and setup

Participants were scanned on a 9.4 T human MR scanner (Siemens Healthineers, Erlangen, Germany) using a head gradient set (AC84-mk2, maximum amplitude 80 mT/m, maximum slew rate 333 T/m/s, inner diameter 36 cm) in combination with a 16-channel parallel transmit system (1 kW per channel) and a dual-row (Kozlov and Turner, 2011) 16-channel transmit/31-channel receive array coil (Shajan et al., 2014). 9.4 T scanning was done in the Scannexus facilities (www.scannexus.nl) in Maastricht, The Netherlands. Online local SAR monitoring was achieved by a vendor-provided system (Gumbrecht et al., 2013). All in-vivo experiments at 9.4 T were approved by the local ethics committee and performed in accordance with internal safety guidelines. All participants gave informed consent.

2.2. Number of 9.4 T experiments

Seven experimental in-vivo sessions (N_session = 7) were conducted at 9.4 T. One experiment was discontinued due to hardware-related instabilities. N_functional = 9 functional experiments were performed across all participants at 9.4 T. For test-retest analysis, functional experiments were repeated at least two times. N_test-retest = 1 participant was invited twice. To investigate of the effect of pTX shimming on acquisition tSNR and inversion efficiency, a set of time series was acquired with varying inversion pulse amplitudes and flip angle sequences in four experiments of NpTx = 3 participants.

2.3. Functional task

The sensitivity to detect layer-dependent activity changes was investigated with a unilateral finger tapping task (thumb and index finger): blocks of 80 s (40 s rest and 40 s paced tapping a 0.75 Hz) were repeated 12 times, resulting in 16-minute acquisitions. During the task, the participants were watching a video of a moving hand and they were asked to mimic the tapping movement with the same speed. The motor cortex was chosen here as a model system for several reasons. A) The motor cortex has a particularly short arterial arrival time compared to other brain areas (Mildner et al., 2014). This means that it is strongly susceptible to blood inflow effects, and thus particularly suited to investigate the proposed methodology to account for them. B) The hand knob of the motor cortex has a consistent folding pattern across individuals. Hence, it is easy to target it with a small FOV and it is easy to adjust the imaging slices perpendicular to the cortical surface. C) The motor cortex has a unique double-layer structure of input and output layers (Mao et al., 2011; Papale and Hooks, 2017; Weiler et al., 2008). This makes it a well-suited model system to investigate the distinguishability of signal changes across cortical depth without large mixture effects.

2.4. Timing within TRs

Slice-selective slab inversion (SS-SI) VASO (Huber et al., 2014) with 3D-EPI readout was implemented in the vendor-provided IDEA environment (VB17A-UHF). The timing of the magnetization preparation and interleaved acquisition of VASO and BOLD data is schematically depicted in Fig. 1A. Sequence parameters were: TI/TR = 1025/2000 ms across all 9.4 T experiments. The TR here refers to the acquisition of one volume. Due to the interleaved acquisition of BOLD and VASO (see next section), the effective temporal resolution for each of the contrasts was TR_eff = 4000 ms. Due to the finite 3D-EPI readout duration, the k-space center is reached at an effective inversion time of TI_eff = 1414 ms.

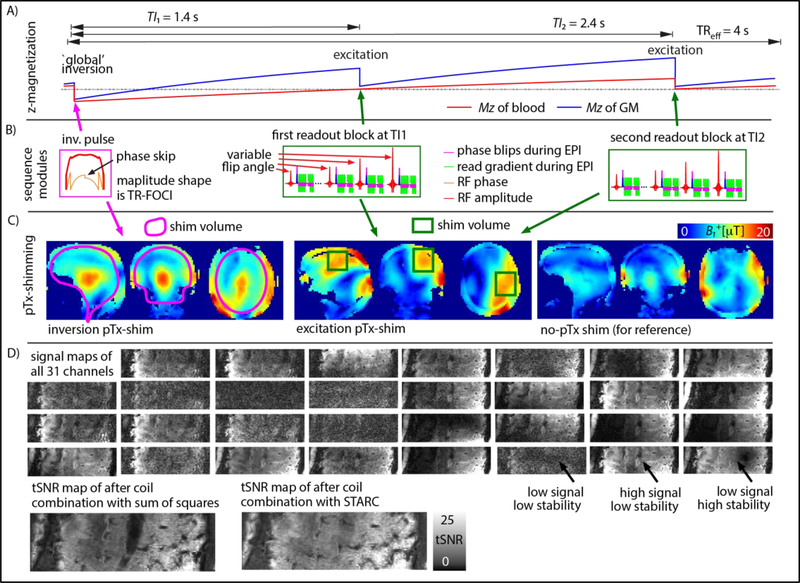
Fig. 1:

9.4 T VASO data acquisition and reconstruction. Panel A) shows the sequence timing and signal evolution of the blood and tissue compartments. Panel B) depicts those sequence modules that include RF-pulses; The adiabatic inversion pulse was applied with a phase skip and the excitation pulses had varying flip angles. Individual RF-modules shown in panel B) are played out with differently optimized local pTx shims. Panel C) exemplifies the varying pTx-shim modes used. Panel D) demonstrates that the different RF-receive channels have a very heterogeneous stability distribution. For instance, some channels with relatively large signal suffer from unstable GRAPPA fat ghosts (black arrow). Hence here, individual RF-channels are combined after being weighted by their stability with STARC. This increases the tSNR in areas of large fat-ghosts. Data in panels C-F) corresponds to one representative participant. (two columns, 8’’ width)

2.5. Technical strategies to account for challenges a)-e)

2.5.1. Accounting for challenge a): Shortening the blood-nulling time to minimize blood-inflow contaminations

VASO can be contaminated by inflow of non-inverted blood, especially when blood T₁ is not much shorter than the TR (Donahue et al., 2009c). These inflow effects can be minimized when the blood-nulling time is shorter than the time that blood needs to arrive from the arteries in the neck to the micro vessels of the imaging slice (Huber et al., 2016a). Here, a TI_eff = 1414 ms was chosen, which includes an additional temporal margin of 200 ms compared to the estimated arterial arrival time in the sensorimotor cortex (Mildner et al., 2014). The blood-nulling time was manipulated by means of an adjusted inversion efficiency of 76% in a B₁⁺-independent manner by using a phase skip (Fig. 1 (A)-(B)) of the RF field during inversion as described in (Huber et al., 2014). The inversion pulse shapes are based on the TR-FOCI pulse (Hurley et al., 2010) (Fig. 1 (A)-(B)). The blood-nulling time is calculated based on the literature value of blood T₁ = 2400 ms at 9.4 T (Dobre et al., 2006). A more comprehensive list of all important sequence parameters used here can be downloaded from as a protocol-pdf from Github (https://github.com/layerfMRI/SequenceGithub/blob/master/9.4T/Maastricht/1609/15/9T4/vaso%5B2%5D.pdf).

The TR-FOCI pulse was originally developed for applications at 7 T with pulse durations of 5 ms and bandwidth of 6.4 kHz. At 9.4 T, however, this is not achievable within the SAR constraints. Hence, we increased the pulse duration to 10 ms and reduced the bandwidth to 4.7 kHz. This increases the adiabaticity, but also makes it more susceptible to B₀ inhomogeneities (Norris, 2002). In three participants, the magnitude and bandwidth constraints were investigated within the practically achievable domain of advanced pTx B₁⁺ and B₀ shimming (Tse et al., 2016).

2.5.2. Accounting for challenge b): Estimating and correcting the BOLD contrast in VASO imaging

With increasing field strength, the positive BOLD signal change during neural activation increasingly counteracts the negative VASO signal change (Lu and van Zijl, 2005). The GE-BOLD effect typically has two components: intravascular and extravascular BOLD signal. At 9.4 T, the extravascular BOLD signal dominates the intravascular BOLD signal by more than 95% (Uludag et al., 2009). This extravascular BOLD contamination is considerably larger than the VASO signal of interest and needs to be corrected for to obtain quantitative CBV measurements. In SS-SI VASO, an interleaved, pair-wise acquisition (Fig. 1 (A)-(B)) of VASO and BOLD images is used to distinguish between BOLD and VASO signal components of the resulting signal. When the pure BOLD contrast contribution is known, the BOLD contamination in the VASO image can be factored out (Huber et al., 2014).

2.5.3. Accounting for challenge b): Fast EPI readout with small matrix to minimize the effect of fast T₂* decay

For fast EPI readout, a small anisotropic FOV was used: FOV_read = 32.8 mm, FOV_phase = 98.4 mm (300%). This was done to minimize aliasing artifacts with such small FOVs. The matrix size was adjusted to have the same asymmetry (44 × 132), yielding the corresponding nominal in-plane resolution of 0.74 × 0.74 mm². Ten axial slices were positioned to cover the left motor cortex. Slices were tilted until the major region of the index finger representation was acquired in slices perpendicular to the cortical surface. The nominal slice thickness was 1.5 mm.

2.5.4. Accounting for challenge c): 3D-EPI with low flip angles

In addition to the SNR advantage of 3D over 2D readouts at high resolution (Huber et al., 2018), the slab-selective nature of 3D requires the use of much lower flip angles and hence results in a much lower SAR footprint than conventional 2D-EPI. As in our previous work (Huber et al., 2018, 2017a), we used a VASO sequence based on 3D-EPI implementations from (Poser et al., 2010) with support for CAIPIRINHA sampling (Poser et al., 2013). 3D slab fold-over along the second phase-encoding direction was minimized by using a sharp slab-selective excitation pulse, with a bandwidth-time- product of 25.

VASO is an inversion recovery sequence. Hence, T₁-relaxation during the serial acquisition of 3D-EPI segments (k_x-k_y-planes) can result in blurring along the slice direction (Gai et al., 2011). To counteract this T₁-blurring, individual excitation pulse flip angles along the train of K_z-planes were optimized and varied so as to ensure an approximately equal signal for every shot. For the parameter used here, this resulted in a flip angle sequence of 21.8°, 22.5°, 23.4°, 24.3°, 25.5°, 26.8°, 28.4°, 30.5°, 33.3°, 37.3°, 43.7°, 57.4°, 90.0°. The flip angle distribution is schematically depicted in Fig. 1B. For further reduction in the energy-deposition of the RF-pulses, the pulse duration was adjusted to be D = 5 ms.

2.5.5. Accounting for challenge d) Coil combination based on respective stability

After the completion of the experiments, the time series of all 31 individual receive elements were exported from the scanner. The signal stability is very heterogeneous across elements and decoupled from the signal intensity (Fig. 1D), rendering the conventional approach of as Sum-of-Squares (SOS) reconstruction highly sub-optimal. Instead, we applied our recently introduced coil combination scheme called ‘STAbility- weighted RF-coil Combination’ (STARC) (Huber et al., 2017b). In contrast to SOS coil- combination, which combines the coil data with weights based on the signal magnitude, STARC combines the coil-specific data with weights based on their voxel- wise signal stability so as to maximize the temporal SNR in each voxel. The code implementing STARC is open source and can be downloaded from Github for Matlab https://github.com/diangraw/STARC-OptimalCoilCombo. In C++ https://github.com/layerfMRI/repository/tree/master/MYCOILCOMBINE and with GPU acceleration in Python https://github.com/cbclab/MCT (Harms et al., 2017; Kashyap et al., 2018).

2.5.6. Accounting for challenges b) and e): fast readout with advanced in-plane GRAPPA acceleration

For further acceleration of the data-acquisition compared to the fast T₂* decay and to minimize image distortions, in-plane GRAPPA (factor = 2) procedures were used.

For high-resolution EPI as used here, EPI acquisition bandwidth along the phase-encoding direction is comparatively low (here 1352 Hz/Px), as a result of the relatively long echo spacing (here 0.84 ms). In addition, B₀ inhomogeneities scale with field strength and are thus particularly large at 9.4 T. Hence, the segmented acquisition of the GRAPPA auto-calibration-signal (ACS) can result in phase inconsistencies in the GRAPPA kernel. This can be partly accounted for with the FLASH-GRAPPA ACS acquisition proposed by (Talagala et al., 2015).

Here, we implemented the FLASH-ACS approach and our pilot experiments suggested that FLASH-GRAPPA ACS provide higher tSNR as opposed to previously used LIN→PAR acquisition schemes at 7 T (Huber et al., 2018). For the reconstruction, the vendor’s GRAPPA (Griswold et al., 2006) reconstruction algorithms were applied, using a 3×4 (read direction × phase direction) kernel.

For further reduction of the echo time (TE), partial-Fourier acquisition with a factor of 6/8 was applied. To minimize corresponding signal blurring in the phase encoding direction, partial Fourier reconstruction (Jesmanowicz et al., 1998) was done with the projection onto convex sets (POCS) algorithm (Haacke et al., 1991) with 8 iterations. The resulting minimum TE was 21 ms and used in all experiments.

2.5.7. Accounting for challenge e): Homogenizing B₁⁺ with temporally alternating pTx shimming parameters

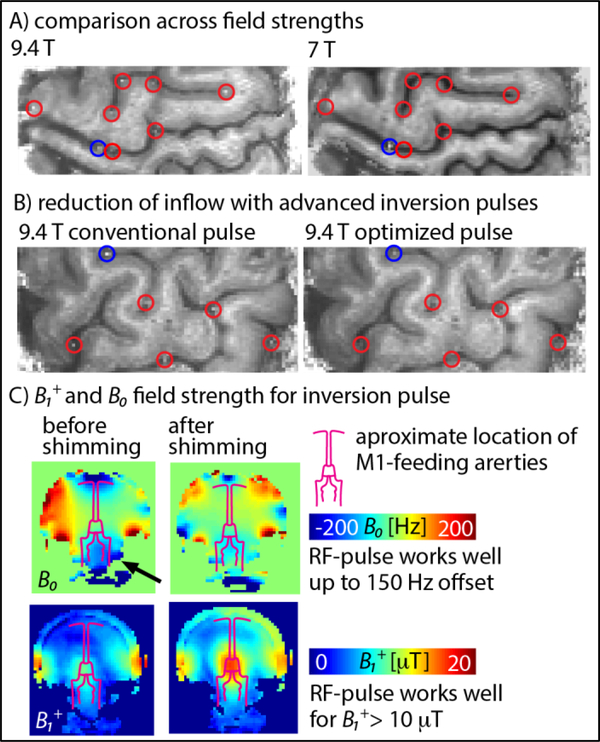
The B₀ and B₁⁺-fields were homogenized following setup and workflows (previously described in Fig. 1 of (Tse et al., 2016)): First, B₀ and B₁⁺ field maps were acquired with a dual-echo GRE and transmit phase-encoded DREAM sequences (Brink et al., 2014), respectively. Corresponding raw data were transferred and evaluated in real time for B₀ and B₁⁺ shimming on a computer next to the scanner host. There, ROIs could be selected and corresponding B₀ and B₁⁺shim values were estimated for subsequent application at the scanner. This followed the workflow described in (Tse et al., 2016) except that two sets of B₁⁺ shims were obtained. Since the global inversion and local slab excitation pulses have very different spatial extent (Fig. 1C), the pTx shim was optimized separately for the individual RF-pulses within one TR. While the adiabatic inversion pulse was played out with a pTx-shim optimized for the entire brain, the excitation pulses were applied with a pTx-shim optimized for the primary motor cortex. During the acquisition, the sequence toggled between these shims depending on whether an inversion or excitation pulse is utilized (Fig. 1C).

2.5.8. Accounting for challenge e) Layering-analysis in distorted EPI-space

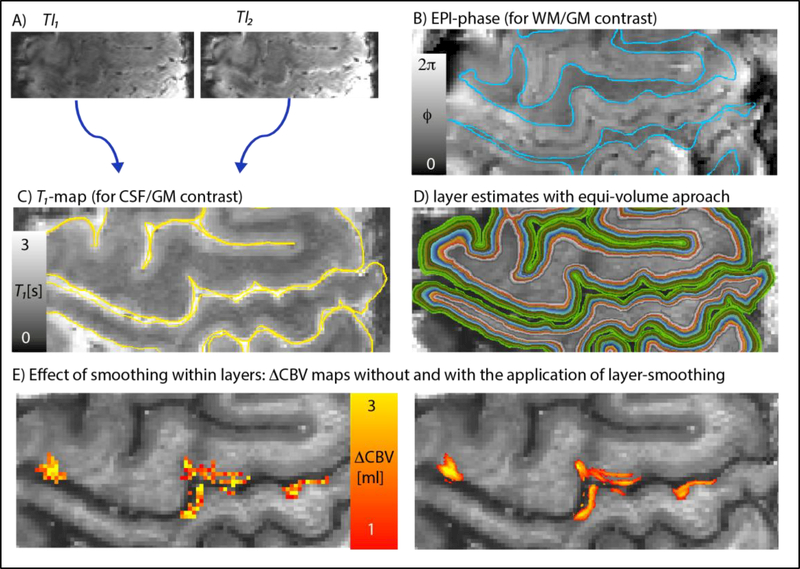
All layering analyses were conducted in EPI-space. This reduced the risk of inaccuracies and resolution loss of conventionally applied distortion correction and registration to so-called anatomical reference data (Kashyap et al., 2017; Renvall et al., 2016). Using the functional EPI data directly as anatomical reference makes these steps unnecessary. To obtain quantitative T₁-maps and corresponding T₁-weighted images (for tissue type classification) from the functional time series data, we normalized the signal intensities of the two inversion times in VASO (Fig. 2A) and fitted a forward Bloch model to the data, as described previously (Huber et al., 2016b). The cortical depth-dependent functional signal changes were calculated as previously described in (Huber et al., 2015a). In short: CSF-GM boundaries and GM-WM boundaries for the primary motor cortex ‘hand knob’ were manually delineated on T₁-weighted EPI images in FSLview (Fig. 2B-C). 20 cortical depths were calculated based on the equi-volume principle (Waehnert et al., 2014) (Fig. 2D). In order to avoid biases of variable detection thresholds across cortical depth (Goense et al., 2012), no significance-thresholding was applied. The corresponding evaluation code is open-source and can be downloaded from Github https://github.com/layerfMRI/LAYNII.

Fig. 2.

Layering of 9.4 T VASO data in EPI space. Images with different TIs (A) were divided to obtain T₁-maps from the functional EPI data. EPI-phase (B) and T₁-maps (C) were used for manual segmentation of GM. Panel D) depicts the corresponding estimates of cortical depths (a.k.a layers). Panel E) illustrates the effect of smoothing within layers. The expected double-layer-response is more clearly visible after smoothing. (two columns, 8’’ width)

For best visual depiction of the layer-dependent activation despite the relatively high noise level in single-participant single-slice activation maps, mild spatial smoothing within layers was applied (FWHM = voxel size) (Fig. 2E-F). No smoothing was applied across cortical depths. Note that the cortical profiles, however, were generated from the signal changes in the unsmoothed data.

2.6. Experiments at 7 T

To examine the potential inflow effects, the same experiments were also conducted on a 7 T scanner (SIEMENS Healthineers, Erlangen, Germany). For RF transmission and reception, a standard single-channel (birdcage, CP) transmit and a 32-channel receive head coil (Nova Medical, Wilmington, MA, USA) was used. Unlike the 9.4 T scanner, the 7 T scanner was equipped with a SC72 body gradient coil (max amplitude 70mT/m, max slew rate 200mT/m/ms). N = 6 participants were scanned at 7 T. One participant of those was scanned at both field strengths, at 9.4 T and 7 T, on two consecutive days. The scan parameters of the 7 T experiments (resolution, TR/TE, readout) and the stimulation protocol was identical to the 9.4 T experiments, with the exception of the a slightly shorter excitation pulse duration of 2 ms. It was necessary to reduce the pulse duration at 7 T in order to achieve the same echo-time at 7 T as at 9.4 T without resulting in nerve stimulation due to the 7 T body gradient coil. Use of the shorter pulse duration at 7 T was not a problem due to the reduced SAR restrictions at 7 T. Note that the same inversion time was used at 7 T and at 9.4 T. This was possible because the larger adjusted inversion-efficiency at 7 T (70% at 9.4 T vs. 80% at 7 T) resulted in a later blood-nulling time, despite the shorter blood-T₁ value.

2.7. Functional data analysis

All MR images were motion corrected using SPM12 (Functional Imaging Laboratory, University College London, UK). The outermost slices (one at each side) were excluded from the analysis to minimize and residual 3D-EPI related slab fold-over artifacts. Activation GLM analysis was done using FSL FEAT (Version 5.98) (Worsley, 2001) with a cluster threshold of 10 voxels (applied with AFNI (Cox, 1996)). tSNR was computed over 480 volumes after signal detrending with AFNI (Cox, 1996).

3. Results

We find that VASO at 9.4 T provides enough sensitivity to obtain reliable functional estimates of CBV change on a voxel-by-voxel level at 0.74 mm resolution (in-plane) within 16-min experiments, concurrently with BOLD fMRI. As specified below in more detail, we find that all the 9.4 T VASO-specific challenges could be addressed.

3.1. Functional results and their stability

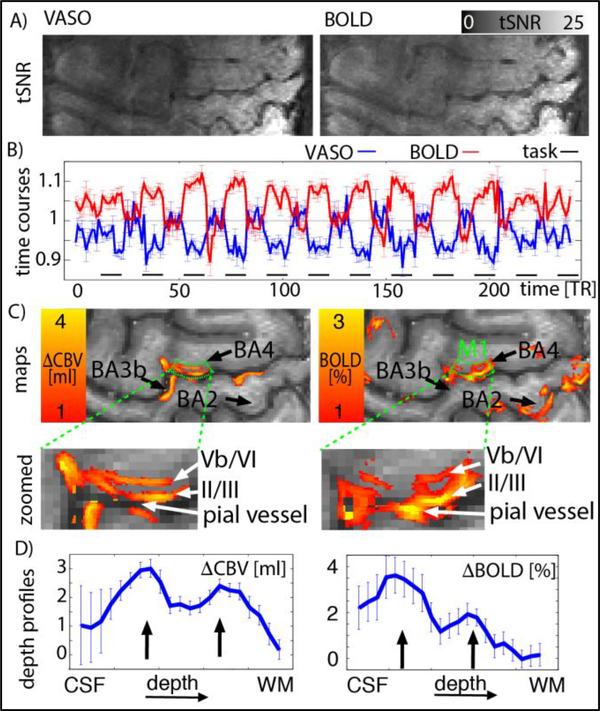
We find that the tSNR for VASO and BOLD in the GM of the motor cortex was 14±4 and 18±4, respectively (mean ± STD over participants). Representative maps of the spatial distribution of tSNR for BOLD and VASO are shown in Fig. 3 with corresponding maps of CBV and BOLD signal change. Due to the higher temporal stability of BOLD compared to VASO, more active voxels can be detected. This is especially the case in sensory areas BA3b and BA2. Within the index-finger area of M1 (BA4), both VASO and BOLD activation can be detected in all experiments. In BOLD activation maps, strong activity can often be seen above the cortical surface (see pial vessel arrow in Fig. 3c). As described before (Goense et al., 2012; Huber et al., 2015a; Uludag and Blinder, 2017), the secondary BOLD peak in deeper layers is slightly more superficial than the secondary CBV peak.

Fig. 3.

Measures of functional stability and sensitivity from one representative participant. Panel A) depicts tSNR for VASO and BOLD contrast. Panel B) depicts the time course of a GM ROI in M1 (BA4) (same for VASO and BOLD, green in panel C). It can be seen that the signal change between tapping and resting periods is larger than the noise between consecutive time points. Panel C) depicts layer-dependent activity maps for VASO and BOLD. It can be seen that GE-BOLD signal is dominated by activity from superficial layers. In VASO, however, a double stripe pattern can be seen in the index-finger region of M1. Panel D) presents the signal change as a function of cortical depth. The profile shows a double peak (black arrows). For BOLD, the double-peak feature is overlaid with a gradient of decreasing signal change towards deeper layers. (one-column, 4’’ width)

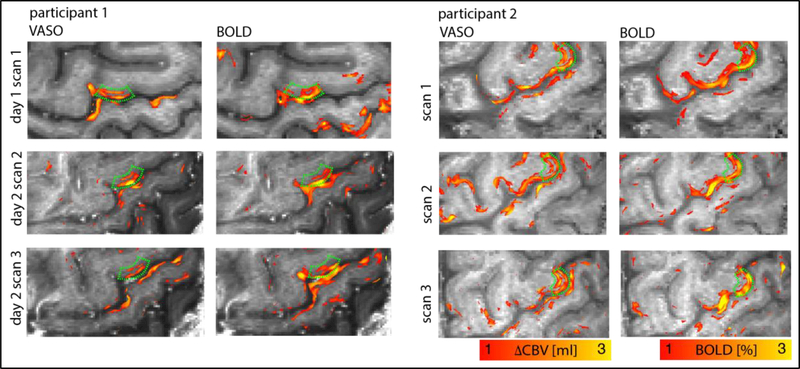
To test the stability and reproducibility of the method, we compared results of test- retest experiments across and within sessions from multiple days. Fig. 4 depicts that ∆CBV and BOLD signal change could be reliably detected across different experiments within and across scan sessions. Across experiments, VASO activation patterns (left columns in panels of Fig. 4) consistently reveal the feature of a double-stripe pattern in the index-finger region of M1 (green boxes).

Fig. 4:

Test-rest experiments to test the reproducibility of the methodology. It can be seen that in M1, VASO fMRI always reveals a double layer striping pattern (green ROIs), as expected. (two-columns, 8’’ width)

The average CBV change across all participants was is 2.6±0.7 ml per 100 ml of tissue (mean ± STD).

3.2. Inflow

We investigated the effect of the 9.4 T-optimized inversion pulse on inflow of fresh non-inverted blood in VASO at 9.4 T. In T₁-weighted sequences, such as VASO, inflow of fresh blood acts like a short T₁ component and results in easily visible isolated bright voxels (Van De Moortele et al., 2009). Here, we utilize this effect and quantify the occurrence of these voxels in order to investigate the effectiveness of the methodology proposed.

Fig. 5A illustrates the influence of inflow effects on VASO at 9.4 T and 7 T. At 7 T, with the 32ch-Nova coil, most large arteries are not refilled with fresh blood. Only isolated, very large arteries show inflow effects (blue circles in Fig. 5A). These very large arteries do not pose a problem in functional VASO, because they are not functionally engaged in the finger-tapping task. That is because these vessels are similarly refilled with fresh blood during rest and during tapping, so they do not mask the tapping-induced signal changes. For 9.4 T, additional smaller arteries are refilled during the inversion time (red circles in fig. 5A). While they are still too big to introduce flow contamination in the functional VASO contrast, their appearance suggests that the probability of arterial inflow-contaminations is increased.

Fig. 5:

Reduction of inflow contamination in VASO at 9.4 T with optimized adiabatic inversion pulses and advanced pTx- and B₀-shimming. Panel A) illustrates the influence of inflow effects on VASO at 9.4 T compared to 7 T. Panel B) shows that most of the inflow effects at 9.4 T can be minimized/removed by adjusting the inversion pulse parameters to the given B₁⁺ and B₀ constraints (C). Here, inflow effects could be reduced by adjusting the pulse parameters to be more conservative with respect to B₁⁺ inhomogeneities and less conservative with respect to B₀ inhomogeneities. (one-column, 4’’ width)

In three participants, the occurrence of inflow effects was investigated with 9.4 T-optimized inversion pulses (bandwidth = 4.7 kHz) compared to conventional inversion pulses (bandwidth = 6.4 kHz). It can be seen in Fig. 5B that the inflow effect in most of the feeding arteries (red circles in Fig. 5B) can be substantially reduced. This is most likely due to the larger inversion efficiency in areas of limited B₁⁺ field strengths and limited B₀ homogeneity below the Circle of Willis (black arrow in Fig. 5C). The fact that the inflow effects are reduced with inversion pulses of lower bandwidths, suggests that the application of VASO at 9.4 T is more limited by B₁⁺ amplitudes than by B₀ inhomogeneities. Across all functional runs, we did not encounter any significant functional inflow effects within the GM-ribbon.

4. Discussion

The results of this study suggest that the application of VASO at 9.4 T can be hindered by several potential technical constraints. However, when these challenges are addressed with advanced sequence methodology, ultra-high resolution CBV-weighted results allow reliable investigations of layer-dependent activity. The application of cortical depth-dependent VASO in humans at 9.4 T allows us to overcome the venous bias of GE-BOLD and achieve higher localization specificity across laminae.

4.1. Activity strengths

The average tapping-induced CBV change of 2.6±0.7 ml per 100 ml of tissue (mean ± STD) is in very good agreement with previous studies using the same task at slightly lower resolutions (0.78 mm - 0.8 mm) (Guidi et al., 2016; Huber et al., 2018, 2017a, 2015a). However, the measured value of 2.6±0.7 ml per 100 ml of tissue (mean ± STD) is significantly higher compared to studies using the same task at resolutions of 1.5 – 3 mm (Donahue et al., 2009a). This resolution-dependence of the measured CBV change is presumably coming from differing partial volume effects at different voxel sizes as estimated earlier (Huber et al., 2018).

4.2. Depth dependence of activity

Results shown in Fig. 3–4, suggest that the cortical depth-dependence of CBV changes has a double peak signature. This is visible as two peaks in profiles of Fig. 3 (black arrows) and it is visible as a double stripe pattern in M1 that follows the cortical ribbon in Fig. 4. Based on the known layer-dependent circuitry of primary motor cortex (Mao et al., 2011; Papale and Hooks, 2017; Weiler et al., 2008), this double-layer pattern is expected for a pinch-like finger-tapping task that also involves touching of the fingers. The superficial peak represents the ‘input’-activity of cortico-cortical connections (e.g. the touch-components from sensory areas), while the deeper peak represents the ‘output’-activity of cortico-spinal connections, as expected from the known layer-dependent micro-circuitry in M1 (Mao et al., 2011; Papale and Hooks, 2017; Weiler et al., 2008), discussed previously (Huber et al., 2017a).

GE-BOLD shows indications of a similar double-layer pattern. It is overlaid, however, with a much stronger bias towards superficial layers and voxels above the cortical surface. This bias in GE-BOLD is well known and comes from its unwanted sensitivity to large intracortical and pial veins (Kennerley et al., 2005; Kim et al., 2013).

4.3. VASO at 9.4 T compared to VASO at 7 T

Comparisons of fMRI methods across field strengths are not straightforward. Since scanners of different field strengths need to be equipped with different RF-coils (and often also gradient coils), the effect of the field strength cannot be isolated from effects of other hardware components. With this in mind, general trends of the different setups might still be of interest.

The reliability of 9.4 T shown in Fig. 4 suggests that, for the test case of small FOV in M1, 9.4 T VASO could achieve a comparable imaging quality as previously achieved at 7 T. Hence, despite the considerably more challenging environment of 9.4 T, activity could be measured across cortical depths as previously done at 7 T.

The application of VASO at 7 T was originally accomplished in 2011–2012 (Hua et al., 2011; Huber et al., 2012), but without significant improvements compared to 3 T. Only after several years of development work form multiple research groups (Hua et al., 2013; Huber et al., 2015a), it was finally possible to achieve the spatial resolution required for laminar investigations. We hypothesize that this will be similar at 9.4 T. Having achieved the leap forward to obtain the same resolution in 9.4 T VASO compared to 7 T VASO in this study, future developments of 9.4 T VASO will allow further improvements beyond the capabilities of 7 T. Specifically, we believe that the more spatially varying pattern of coil-sensitivities at 9.4 T compared to 7 T will enable higher parallel-imaging factors to further improve the resolution and the imaging coverage of high-resolution VASO (Poser and Setsompop, 2017).

4.4. Previous studies of VASO at 9.4 T

9.4 T VASO has been previously applied in cat visual cortex (Jin and Kim, 2008, 2006). In these publications, Jin and Kim already described the VASO-specific limitation of increased BOLD contaminations. Working in the controlled environment of animal research, they could account for BOLD contamination i) by means of short TEs, ii) by means of center-out trajectories, and iii) by means of in-plane k-space segmentation without the problem of variable respiration-induced B₀ EPI artifacts.

Jin and Kim also reported the challenge of inflowing fresh blood in VASO at 9.4 T. They could, however, not fully account for inflow effects. I.e., inflow effects could only be minimized by reducing TI below the blood-nulling time. This was at the cost of stronger, unwanted, inflow-weighting. Inflow effects could be further minimized by disregarding superficial cortical layers from the analysis, which rendered layer-dependent analysis impossible.

Working with animal models, SAR was not a major constraint for applications in cats. Thus, no additional measures needed to be taken to reduce the RF power. The smaller brain size of cats also resulted in relatively homogeneous B₁⁺ field, so the application of pTx was not necessary.

To the best of our knowledge, our experiments constitute the first application of VASO at 9.4 T in humans. With the advanced methodology proposed here, it is not only possible to fully account for inflow effects compared to previous 9.4 T VASO applications. It also accomplishes the leap forward to translate 9.4 T VASO from animals to humans.

5. Conclusion

In this study, layer-dependent CBV measurements at 9.4 T were achieved in humans. Prior to this study, this was only possible in animals. The combination of high sensitivity of UHF MRI with the high localization specificity of CBV-fMRI will be particularly valuable for future applications of laminar and columnar fMRI in humans.

Highlights:

• CBV-sensitive VASO was implemented at 9.4 T for layer-dependent fMRI in humans

• 9.4 T VASO is challenging due to: blood-inflow, SAR, T₂^*-decay, B₁⁺ and B₀ constraints

• Alternating pTx shimming and advanced adiabatic pulses can overcome these challenges

• Layer-dependent CBV changes can be reliably detected in human motor cortex at 9.4 T

• Submitted as Neuroimage technical Note

Abbreviations:

BOLD

blood oxygenation level dependent

CBV

cerebral blood volume

CNR

contrast-to-noise ratio

CSF

cerebrospinal fluid; ΔCBV = change in CBV

EPI

echo planar imaging

fMRI

functional magnetic resonance imaging

FOV

field of view

GE

gradient echo

GM

grey matter

ROI

region of interest

SAR

specific absorption rate

SNR

signal-to-noise ratio

SS-SI VASO

slice-selective slab inversion VASO

TE

echo time

Tl

inversion time

TR

repetition time

VASO

vascular space occupancy