Convex recovery of continuous domain piecewise constant images from nonuniform Fourier samples

Abstract

We consider the recovery of a continuous domain piecewise constant image from its non-uniform Fourier samples using a convex matrix completion algorithm. We assume the discontinuities/edges of the image are localized to the zero level-set of a bandlimited function. This assumption induces linear dependencies between the Fourier coefficients of the image, which results in a two-fold block Toeplitz matrix constructed from the Fourier coefficients being low-rank. The proposed algorithm reformulates the recovery of the unknown Fourier coefficients as a structured low-rank matrix completion problem, where the nuclear norm of the matrix is minimized subject to structure and data constraints. We show that exact recovery is possible with high probability when the edge set of the image satisfies an incoherency property. We also show that the incoherency property is dependent on the geometry of the edge set curve, implying higher sampling burden for smaller curves. This paper generalizes recent work on the super-resolution recovery of isolated Diracs or signals with finite rate of innovation to the recovery of piecewise constant images.

I. Introduction

The direct recovery of continuous domain signals by convex optimization is emerging as a powerful alternative to traditional discrete domain compressed sensing [1]–[3]. The ability of these continuous domain “off-the-grid” schemes to minimize discretization errors makes them attractive in practical applications, where only the low-pass measurements of the signal are available. The history of such continuous domain signal recovery algorithms dates back to Prony [4], where the recovery of a linear combination of exponentials from uniform samples is considered. Prony-like algorithms recover the signal by estimating an annihilating polynomial whose zeros correspond to the frequencies of the exponentials. Work by Liang et al. [5], [6] and the finite rate of innovation (FRI) framework [7] extended Prony-like methods to recover more general signals that reduce to a sparse linear combination of Dirac delta functions under an appropriate transformation (e.g., differential operators, convolution). Recently, several authors have further extended FRI methods to recover such signals from their non-uniform Fourier samples [3], [8]– [11] by exploiting the low-rank structure of an enhanced matrix built from Fourier data (e.g., a Hankel matrix in 1-D). Recovery guarantees exists for certain classes of these signals when the singularities are isolated and well-separated [2], [3], [12].

The signal models discussed above have limited flexibility in exploiting the extensive additional structure present in multi-dimensional imaging problems. In particular, the edges in multidimensional images are connected and can be modeled as smooth curves or surfaces. While discrete image representations to capture this structure have been the subject extensive research [13], [14], similar continuous domain representations have attracted less attention. We recently introduced a novel framework recover piecewise polynomial images, whose edges are localized to smooth curves, from their uniform [15], [16] and non-uniform [11] Fourier samples; our framework generalizes a recent extension of FRI models to curves [17]. We assume that the partial derivatives of the signal vanish outside the zero level-set of a bandlimited function, which is only true for piecewise smooth signals. This relation translates to a linear system of convolution equations involving the uniform Fourier samples of the partial derivatives, which can be compactly represented as the multiplication of a specific structured matrix with the Fourier coefficients of the bandlimited function. We have introduced theoretical guarantees for the recovery of such images from uniform samples [15], [16]. Our earlier work has shown that the structured matrix built from the Fourier coefficients of piecewise constant images is low-rank [11], [16], which we used to recover the image from its non-uniform Fourier samples with good performance in practical applications. We have also introduced an computationally efficient algorithm termed as GIRAF, which works on the original signal samples rather than the structured high-dimensional matrix [18], [19]; the computational complexity of this algorithm is comparable to discrete total variation regularization, which makes this scheme readily applicable to large-scale imaging problems, such as undersampled dynamic magnetic resonance image reconstruction [20].

The main focus of the present paper is to introduce theoretical guarantees on the recovery of continuous domain piecewise constant images from non-uniform Fourier samples via a convex structured low-rank matrix completion algorithm. Our main result shows number of non-uniform samples to recovery the image is proportional to the complexity of the edge set, as measured by the bandwidth of the edge set function, and an incoherence measure related to the edge set geometry. We additionally show that the recovery is robust to noise and model-mismatch.

The proof of the main result builds off of [3], which proved similar recovery guarantees for the recovery of multi dimensional isolated Diracs from non-uniform Fourier samples by minimizing the nuclear norm of an “enhanced” multi-level Hankel matrix. This work showed that the number of samples necessary for recovery depends the number of Diracs and on an incoherence measure of the signal, that can be defined solely in terms of the relative locations of the Diracs. However, the theory in [3] relies heavily on an explicit factorization of the enhanced matrix (e.g., Vandermonde factorization of a Hankel matrix in the 1-D case), which is only available when the number of singularities are isolated and finite. Since the singularities in the proposed class of piecewise constant images (i.e., the image edges) are not isolated nor finite, the recovery guarantees in [3] cannot be directly extended to our setting. Instead, to achieve our result, we give a new characterization of the row and column spaces of the structured matrix arising in our setting. We show this new characterization allows us to derive an incoherence measure based solely on geometric properties of the edge set. In particular, we derive an upper bound for the incoherence measure that is related to the size of edge set curve. The results show that high sampling burden is associated with the estimation of images with smaller piecewise constant regions, which is consistent with intuition.

We note that the signal models in [1]–[3] do not include the class of piecewise constant images considered in this work. In particular, all of the above models assume the discontinuities to be finite in number and well separated, unlike in our setting. Recently, [12] adapted the results in [3] to introduce recovery guarantees for Fourier interpolation of a variety of finite-rate-of-innovation signal models [7], including piecewise constant functions. However, these results are limited to the 1-D setting and share the assumption than the discontinuities/innovations of the signal are finite and isolated. Furthermore, the structured matrix lifting considered in this work is different than those considered in [3] and [12]. Specifically, the structured matrix lifting in this work consists of two vertically concatenated multi-level Toeplitz matrices (i.e., block Toeplitz with Toeplitz blocks), whose entries are built from the weighted Fourier coefficients of the images. This is substantially different from the structured matrix liftings considered in [3] (unweighted, one block, single block multilevel Hankel) and [12] (weighted, one block, single-level Hankel). Finally, we note that a preliminary version of the results presented in this has been published previously in the conference paper [21] without proofs. The present work includes considerably more details and proofs, and major improvements to the main theorem.

A. Notation

Bold lower-case letters x are used to indicate vector quantities, bold upper-case X to denote matrices, and calligraphic script 𝒳 for general linear operators. We typically reserve lower-case greek letters μ, γ, etc. for trigonometric polynomials (3) and upper-case greek letters Λ,Ω, etc. for their coefficient index sets, i.e. finite subsets of the integer lattice ℤ², with cardinality denoted by |Λ|. We write Λ+Ω for the dilation of the index set Ω by Λ, i.e. the Minkowski sum {k + ℓ: k ∈ Λ, ℓ ∈ Ω}, and write 2Λ to mean Λ + Λ, 3Λ = 2Λ + Λ, etc. We also denote the contraction of Ω by Λ by Ω:Λ = {ℓ ∈ Ω: ℓ − k ∈ Ω for all k ∈ Λ}.

II. Background

A. 2-D Piecewise Constant Images with Bandlimited Edges

In this work we consider a continuous domain piecewise constant model for images,

$$f(\mathit{r})=\sum _{i=1}^N{a}_i{1}_{U_i}(\mathit{r}),\text{for}\text{all}\mathit{r}=(x,y)\in {[0,1]}^2,$$ (1)

where a_i ∈ ℂ, 1_U denotes the characteristic function of the set U, and each U_i ⊂ [0, 1]² is a simply connected regions with piecewise smooth boundaries ∂U_i. We study the recovery of such an image from a sampling of its Fourier coefficients f̂ specified by

$$\widehat{f}[\mathit{k}]={\int }_{{[0,1]}^2}f(\mathit{r})e^{-j2\pi \mathit{k}·\mathit{r}};\mathit{k}\in \mathrm{\Omega }\subset {\mathbb{Z}}^2.$$ (2)

Following [16], we further assume that the edge set of the piecewise constant image, specified by E := ∪_i∂U_i, coincides with the zero set of a 2-D bandlimited function:

$$E=\{\mathit{r}\in {[0,1]}^2:\mu (\mathit{r})=0\},\text{with}\mu (\mathit{r})=\sum _{\mathit{k}\in \mathrm{\Lambda }}c[\mathit{k}]e^{j2\pi \mathit{k}·\mathit{r}},$$ (3)

where the coefficients c[k] ∈ ℂ, and Λ is a finite subset of ℤ². We call any function μ in the form (3) a trigonometric polynomial, and we say μ is bandlimited to Λ, i.e., the Fourier coefficients μ̂ are supported within Λ. For short, we will write {μ = 0} for the zero set of μ considered as a subset of [0, 1]².

Define the degree of a trigonometric polynomial μ, denoted by deg(μ) = (K,L) to be the linear dimensions of the smallest rectangle containing the support set {k : μ̂ [k] ≠ 0}. In [16] we proved that for every curve E given by the zero set of a trigonometric polynomial, there exists a unique minimal degree trigonometric polynomial¹ μ₀ such that E = {μ₀ = 0} and if μ is any other trigonometric polynomial with {μ₀ = 0} ⊂ {μ = 0}, then deg(μ₀) ≤ deg(μ) entrywise. By extension, we define the degree of a curve E to be equal to the degree of of its minimial degree polynomial μ₀. We also say the curve E is bandlimited to Λ₀ ⊂ ℤ², where Λ₀ is the minimal rectangular index set containing the support of μ̂. Intuitively, the degree/bandwidth of a curve gives a quantitative measure of its complexity. For example, in [16] we show the number of connected components of a curve is bounded in terms of its degree.

B. Recovery from uniform Fourier samples

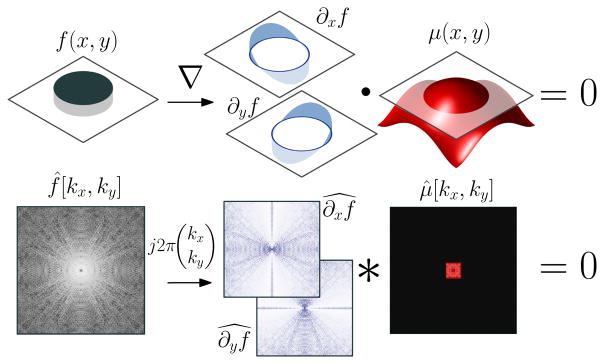
We have shown in [16] that when μ is any trigonometric polynomial that vanishes on the edge set of the piecewise constant image f, the gradient ∇f = (∂_xf, ∂_yf) satisfies the property

$$\mu \mathbf{\nabla }f=0,$$ (4)

where equality in (4) is understood in the sense of distributions (see, e.g., [22]). The spatial domain annihilation relation (4) translates directly to the following convolution annihilation relation in Fourier domain:

$$\sum _{\mathit{k}\in \mathrm{\Lambda }}\widehat{\mathbf{\partial }f}[\mathit{\ell }-\mathit{k}]\widehat{\mu }[\mathit{k}]=\mathbf{0},\forall \mathit{\ell }\in {\mathbb{Z}}^2.$$ (5)

Here $\widehat{\mathbf{\partial }f}[\mathit{k}]=j2\pi (k_x\widehat{f}[\mathit{k}],k_y\widehat{f}[\mathit{k}])$ for k = (k_x, k_y). Note the equations in (5) are linear with respect to the coefficients μ̂.

Suppose we have access to samples of the Fourier coefficients f̂ on a finite rectangular grid Γ ⊂ ℤ², and suppose μ is bandlimited to Λ₁ ⊂ Γ. Then we can build the system of equations in (5) for all ℓ belonging to the index set Λ₂ ⊂ Γ, where Λ₂ is the set of all integer shifts of Λ₁ contained in Γ. In this case (5) can be compactly represented in matrix form as

$$\mathcal{T}(\widehat{f})\mathit{h}=\left[\begin{array}{c}{\mathcal{T}}_x(\widehat{f})\\ {\mathcal{T}}_y(\widehat{f})\end{array}\right]\mathit{h}=\mathbf{0},$$ (6)

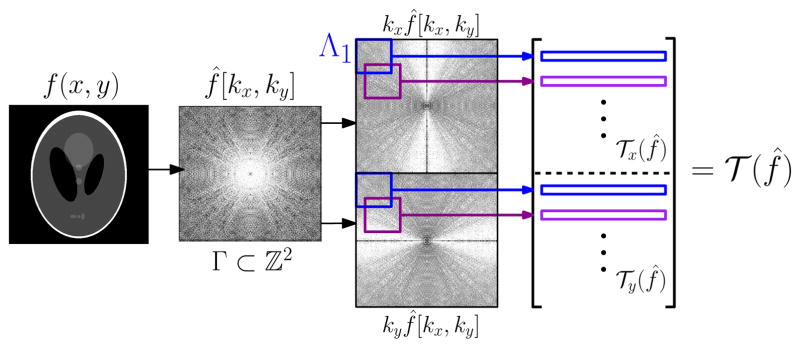
where 𝒯_x(f̂), 𝒯_y(f̂) ∈ ℂ^{|Λ₂|×|Λ₁|} are matrices corresponding to the discrete 2-D convolution with the arrays k_x f̂[k_x, k_y] and k_x f̂[k_x, k_y] for (k_x, k_y) ∈ Γ, respectively (after omitting the inconsequential factor j2π). Here we use h to denote the vectorized version of the filter (μ̂ [k] : k ∈ Λ₁), where the index set Λ₁ is called the filter support. The matrices 𝒯_x(f̂) and 𝒯_y(f̂) have a block Toeplitz with Toeplitz blocks structure. See Figure 2 for an illustration of the construction of 𝒯 (f̂).

Fig. 2.

Construction of the structured matrix lifting 𝒯 (f̂) considered in this work. From a rectangular array of the Fourier coefficients f̂ [k_x, k_y] of a continuous domain image f(x, y), the weighted arrays k_x f̂ [k_x, k_y] and k_y f̂ [k_x, k_y] are constructed. The matrices 𝒯_x(f̂) and 𝒯_y(f̂) are then obtained by extracting all vectorized patches from the weighted arrays, and loading these into the rows of 𝒯_x(f̂) and 𝒯_y(f̂). The resulting matrices 𝒯_x(f̂) and 𝒯_y(f̂) have a block Toeplitz with Toeplitz blocks structure. Finally 𝒯 (f̂) is formed by vertically concatenating the blocks 𝒯_x(f̂) and 𝒯_y(f̂).

Equation (6) shows that 𝒯 (f̂) is rank deficient, since it has the non-trivial vector h in its nullspace. In addition, when the filter support Λ₁ defining 𝒯 (f̂) is sufficiently big, we can also show 𝒯 (f̂) is low-rank. This is because if μ₀ is the minimal degree polynomial for the edge set, then any multiple of μ = γ · μ₀ bandlimited to Λ₁ will satisfy the annihilation equation (4). In Fourier domain, this means the vector

$$\mathit{h}=(({\widehat{\mu }}_0\ast \widehat{\gamma })[\mathit{k}]:\mathit{k}\in {\mathrm{\Lambda }}_1)$$ (7)

is in the nullspace of 𝒯 (f̂). Hence if the filter support Λ₁ is larger than support Λ₀ of μ₀, 𝒯 (f̂) has a large nullspace and is low-rank. The following result from [16] gives an exact characterization of the rank of 𝒯 (f̂), which will be important for this work:

Theorem 1

[16] Suppose f is a piecewise constant image (1) whose edge set E = {μ₀ = 0} is the zero set of a trigonometric polynomial μ₀ bandlimited to Λ₀. Let 𝒯 (f̂) be built with filter size Λ₁ ⊇ Λ₀, then

$$\mathit{rank}\mathcal{T}(\widehat{f})\le \mid {\mathrm{\Lambda }}_1\mid -\mid {\mathrm{\Lambda }}_1:{\mathrm{\Lambda }}_0\mid$$ (8)

where |Λ₁| is the number of indices in Λ₁ and |Λ₁: Λ₀| is the number of integer shifts of Λ₀ contained in Λ₁. Moreover, equality holds in (8) if Γ ⊇ 2Λ₁+Λ₀ and if the edge set does not contain any singular points. In this case, the nullspace of 𝒯 (f̂) consists of all vectors in the form (7).

Note that R := |Λ₁| − |Λ₁: Λ₀| is a measure of the bandwidth of μ₀ and hence is indicative of the complexity of the edge set curve E = {μ₀ = 0}. In the remainder of this work we assume the conditions in Theorem 1 that guarantee the equality rank 𝒯 (f̂) = R holds, in particular Γ ⊇ 2Λ₁+Λ₀.

If we take Λ₁ = Λ₀, the above result shows Fourier samples of f̂ in Γ ⊇ 3Λ₀ is sufficient for the recovery of the minimal degree polynomial μ₀, since in this case μ̂₀ can be identified as the unique non-trivial nullspace vector of 𝒯 (f̂). The following theorem states that once μ₀ is available, f is the unique solution to the annihilation equations (4) and (5):

Theorem 2

[16]. Suppose f is a piecewise constant image (1) whose edge set E = {μ₀ = 0} is the zero set of a trigonometric polynomial μ₀ bandlimited to Λ₀. Suppose the Fourier sampling set Γ ⊇ Λ₀. If g ∈ L¹([0, 1]²) satisfies

$${\mu }_0\nabla g=0\mathit{subject}to\widehat{g}[\mathit{k}]=\widehat{f}[\mathit{k}]\mathit{for}\mathit{all}\mathit{k}\in \mathrm{\Gamma },$$ (9)

then g = f almost everywhere.

In principle, this result allows us to solve for the amplitudes of regions of the piecewise constant function f by plugging in the known μ₀ into the equation (9) and solving a linear system, similar to Prony’s method. However, for complicated piecewise constant images with many regions, it may be more practical to use the approximations introduced in [16].

III. Recovery from non-uniform Fourier samples

The theory presented in Section I shows that the exact recovery of a continuous domain piecewise constant image with a bandlimited edge set is possible when we collect Fourier samples of the image on a sufficiently large uniform grid in Fourier domain. However, the recovery procedure breaks down when we have non-uniform or missing samples, which is often the case in practical settings, e.g., compressed sensing MRI [23]. Therefore, we propose and analyze a method to interpolate the missing samples to a uniform grid in Fourier domain, which guarantees full recovery of the image in spatial domain.

Recall that Theorem 1 says that the structured matrix 𝒯 (f̂) built from the Fourier coefficients f̂ [k], k ∈ Γ, where Γ ⊂ ℤ² is a uniform rectangular grid, is known to be low-rank precisely when f is a piecewise constant image with a bandlimited edge set. Hence we propose to recover f̂ [k], k ∈ Γ from its samples at non-uniform locations Ω ⊂ Γ as the solution to the convex matrix completion problem: min

$$\underset{\widehat{g}[\mathit{k}],\mathit{k}\in \mathrm{\Gamma }}{min}{\Vert \mathcal{T}(\widehat{g})\Vert }_{\ast }\text{subject}\text{to}\widehat{g}[\mathit{k}]=\widehat{f}[\mathit{k}]\text{for}\text{all}k\in \mathrm{\Omega }$$ (10)

where ||·||^* denotes the nuclear norm, i.e., the sum of the singular values of a matrix, which is the convex relation of the rank functional. Note that (10) is different than the standard low-rank matrix completion setting studied in [24], [25] in that the low-rank matrix 𝒯 (f̂) is structured and parameterized by the coefficient vector f̂. Similar structured low-rank matrix completion schemes have been proposed for the recovery of signals from non-uniform Fourier samples [3], [12] and used with empirical success in MRI applications [10], [11], [26]. The main focus of this paper is to determine the sufficient number of samples that will ensure exact recovery of the Fourier coefficients of f on the reconstruction grid Γ with high probability.

A. Role of incoherence

Several authors have shown that the sufficient number of samples for low-rank matrix recovery by nuclear norm minimization to succeed is dependent on the incoherence of the sampling basis with respect to the matrix to be to be recovered [3], [25]. Similarly, our results depend on an incoherence measure derived from the structure of the matrix 𝒯 (f̂) and properties of the piecewise constant image f. In particular, define ℘_U and ℘_V to be the orthogonal projections onto the column space and row space of 𝒯 (f̂), respectively, i.e., if 𝒯 (f̂) = UΣV^* is the rank-R singular value decomposition then ℘_UX = UU^*X, ℘_VX = XVV^*. In Appendix B, we show that the structured matrix 𝒯 (f̂) can be expanded using orthonormal basis of matrices A_k such that

$$\mathcal{T}(\widehat{f})=\sum _{\mathit{k}\in \mathrm{\Gamma }/\{0\}}\widehat{f}[\mathit{k}]w[\mathit{k}]{\mathit{A}}_{\mathit{k}}$$ (11)

where w[k], k ∈ Γ/{0} are a set of positive weights that do not depend on f̂. Similar to results in [3], [12], [25], we prove that nuclear norm minimization (10) recovers the exact low-rank solution with high probability provided we can uniformly bound the norms of the projections of the sampling basis matrices A_k onto the row and column spaces of 𝒯 (f̂):

Proposition 3

Consider 𝒯 (f̂) of rank R corresponding to a piecewise constant function f whose edge set coincides with the zero set of μ₀, let ρ be the incoherency measure associated with μ₀ to be defined in the sequel, and set c_s = |Γ|/|Λ₁|. Then we have

$$\underset{\mathit{k}\in \mathrm{\Gamma }}{max}{\Vert {\mathcal{P}}_U{\mathit{A}}_{\mathit{k}}\Vert }_F^2\le \frac{\rho R{c}_s}{\mid \mathrm{\Gamma }\mid },$$ (12)

$$\underset{\mathit{k}\in \mathrm{\Gamma }}{max}{\Vert {\mathcal{P}}_V{\mathit{A}}_{\mathit{k}}\Vert }_F^2\le \frac{\rho R{c}_s}{\mid \mathrm{\Gamma }\mid }$$ (13)

The proof in Section VIII-F relies on the row and column spaces of 𝒯 (f̂) derived in Lemma 8 and Lemma 6 in the next section. These results will be used in the derivation of the main theorem in Section IX.

B. Main Results

We now present our main results, which determine the sufficient number of random Fourier samples for the convex structured low-rank matrix completion program (10) to succeed with high probability. Our first theorem addresses the case of recovery from noiseless Fourier samples:

Theorem 4

Let f be a continuous domain piecewise constant image (1), whose edge-set is described by the zero-set of the trigonometric polynomial μ₀ bandlimited to Λ₀ (see (3)). Let Ω ⊂ Γ be an index set drawn uniformly at random within Γ. Then there exists a universal constant c > 0 such that the solution to (10) is f̂ with probability exceeding 1 − |Γ|⁻², provided

$$\mid \mathrm{\Omega }\mid >c\rho c_{s}R{log}^4\mid \mathrm{\Gamma }\mid ,$$ (14)

where R = |Λ₁| − |Λ₁ : Λ₀| = rank 𝒯 (f̂), c_s = |Γ|/|Λ₁|, c is a universal constant, and ρ ≥ 1 is an incoherence measure depending on the geometry of the edge-set, to be defined in the sequel.

To better understand the dependence of the bound in (14) on the filter size Λ₁ and the edge set bandwidth Λ₀, assume for simplicity that Λ₁ is some dilation of Λ₀, that is, Λ₁ = αΛ₀, where α > 1 is an integer. In this case, the factor c_s R in (14) simplifies to

$$\left(\frac{\mid {\mathrm{\Lambda }}_1\mid -\mid {\mathrm{\Lambda }}_1:{\mathrm{\Lambda }}_0\mid }{\mid {\mathrm{\Lambda }}_1\mid }\right)\mid \mathrm{\Gamma }\mid \le \left(\frac{{\alpha }^2-{(\alpha -1)}^2}{{\alpha }^2}\right)\mid \mathrm{\Gamma }\mid \le \frac{2\mid \mathrm{\Gamma }\mid }{\alpha }.$$ (15)

Therefore, assuming the other constants in (14) are fixed, the number of measurements sufficient for exact recovery is proportional to the reciprocal of the dilation factor α. This suggests taking the filter size Λ₁ to be as large as allowed by Theorem 4. Namely, Λ₁ should satisfy 2Λ₁ + Λ₀ = Γ, i.e., the side-lengths of filter support Λ₁ should be roughly half those of the reconstruction grid Γ. Fixing the filter support Λ₁ to obey this bound, then Γ = (2α + 1)Λ₀, and so |Γ| ≤ (2α + 1)²|Λ₀|. Inserting this bound into (15) gives

$$c_{s}R=O(\alpha \mid {\mathrm{\Lambda }}_0\mid ).$$ (16)

Combined with (14), this shows that the number of measurements sufficient for exact recovery is on the order of |Λ₀|, up to incoherence and log factors.

The proof of Theorem 4, detailed in Appendix B, is in line with the approach of [3]. In particular, we prove the result by constructing an approximate dual certificate using the well-known “golfing scheme” of [25]. The main differences between in the proof of the above result and that in [3] results from the differences in the matrix structure and hence the characterization of the incoherency between the row and column subspaces of 𝒯 (f̂) with the sampling basis. In particular, the matrix 𝒯 (f̂) we consider is obtained by stacking two block Toeplitz with Toeplitz blocks (BTTB) matrices whose entries are the weighted Fourier coefficients of f, as opposed to a single unweighted BTTB matrix in [3]. The approach in [3] relies on an explicit low-rank factorization of a BTTB matrix in terms of Vandermonde-like matrices². Since this factorization is not available in our setting, we use algebraic properties of trigonometric polynomials to give a new characterization of the row and column spaces of the matrix. In particular, we show in Section IV that similar Vandermonde-like basis matrices exist for the row and column space of the lifted matrix, and use these to derive a related incoherence measure that satisfies the bounds in Prop. 3.

C. Recovery in the presence of noise and model-mismatch

We now generalize (66) to the setting where we have noisy or corrupted Fourier samples

$${\widehat{f}}_n[\mathit{k}]=\widehat{f}[\mathit{k}]+\eta [\mathit{k}],\mathit{k}\in \mathrm{\Omega },$$ (17)

where η[k] ∈ ℂ is a vector of noise. In this case, we pose recovery as

$$\underset{\widehat{g}}{min}{\Vert \mathcal{T}(\widehat{g})\Vert }_{\ast }\text{subject}\text{to}{\Vert {\mathcal{P}}_{\mathrm{\Omega }}({\widehat{f}}_n-\widehat{g})\Vert }_2\le \delta .$$ (18)

where δ > 0 is an estimate of the ℓ²-norm of the error ||η||, and ℘_Ω denotes projection onto Ω. We make no assumptions on the statistics of the noise η. In particular, η can represent errors due to model-mismatch, such as when the image is not perfectly piecewise constant, or when the edge set of the image does not coincide perfectly with the zero level-set of a bandlimited function.

The following theorem shows that when the deviation of f̂_n from f̂ is small, the modified recovery program (18) recovers a solution that is close in norm to f̂ under the same sampling conditions as Theorem 4.

Theorem 5

Let f be specified by (1), whose edge-set is described by the zero-set of the trigonometric polynomial μ₀ bandlimited to Λ₀ with associated incoherence measure ρ. Let Ω ⊂ Γ be an index set drawn uniformly at random within Γ such that |Ω| satisfies the bound (14) in Theorem 4. If the measurements f̂_n satisfy ||℘_Ω(f̂_n − f̂)||₂ ≤ δ, then the solution ĝ to (18) satisfies

$${\Vert \mathcal{T}(\widehat{f})-\mathcal{T}(\widehat{g})\Vert }_F\le 5{\mid \mathrm{\Gamma }\mid }^2\delta .$$ (19)

with probability exceeding 1 − |Γ|⁻².

See Section IV in the Supplementary Materials for proof. The bound (19) allows us to quantify the effect of model-mismatch on recovery. In particular, suppose the image f_n represents a perturbation from an ideal piecewise constant image f such that their difference in L²-norm is δ-small:

$${\Vert f_n-f\Vert }_{L^2}^2={\left({\int }_{{[0,1]}^2}{\mid f_n(r)-f(\mathit{r})\mid }^{2}d\mathit{r}\right)}^{\frac{1}{2}}\le \delta .$$ (20)

Then by Parseval’s theorem, the measurements of f̂_n satisfy ||℘_Ω(f̂_n − f̂)||² ≤ δ, hence Theorem 5 applies. From (19) we obtain the bound ||𝒯 (f̂) − 𝒯 (ĝ)||_F ≤ 5|Γ|²||f_n − f||_L². This shows that if the image f_n is close to the ideal piecewise constant image f in spatial domain L²-norm, then the matrix 𝒯 (ĝ) we recover using (18) will be close in norm to 𝒯 (f̂) with high probability.

IV. Row and column spaces of 𝒯 (f̂) and incoherence

In this section we define an incoherence measure ρ that satisfies the desired bounds in Prop. 3. We show that the incoherence measure depends only on the geometry of the edge set of the image. The incoherence measure is derived from a new characterization of the row and column spaces of the matrix 𝒯 (f̂) in terms of Vandermonde-like basis matrices.

A. Row and column spaces of 𝒯 (f̂)

Our first lemma gives a basis for the row space of 𝒯 (f̂):

Lemma 6

A basis of the row space of 𝒯 (f̂) is given by the columns of the |Λ₁| × R Vandermonde-like matrix

$${\mathit{E}}_{\mathit{row}}(P):=\frac{1}{\sqrt{\mid {\mathrm{\Lambda }}_1\mid }}\left(\begin{array}{ccc}{e}^{j2\pi {\mathit{k}}_1·{\mathit{r}}_1}& \dots & e^{j2\pi {\mathit{k}}_1·{\mathit{r}}_R}\\ ⋮& & ⋮\\ e^{j2\pi {\mathit{k}}_{\mid {\mathrm{\Lambda }}_1\mid }·{\mathit{r}}_1}& \dots & e^{j2\pi {\mathit{k}}_{\mid {\mathrm{\Lambda }}_1\mid }·{\mathit{r}}_R}\end{array}\right)$$ (21)

where {k₁, …, k_|Λ1|} is a linear indexing of elements in Λ₁, and P = {r₁, …, r_R} is a set of R = |Λ₁|−|Λ₁ : Λ₀| distinct points on the edge set curve {μ₀ = 0} chosen such that the columns of E_row are linearly independent.

The careful reader will have noticed that Lemma 6 takes for granted the existence of a set of points P = {r₁, ...., r_R} ⊂ {μ₀ = 0} such that the columns of E_row(P) is linearly independent. Call such a set P a set of admissible nodes for the curve {μ₀ = 0}. The following result shows that sets of admissible nodes always exist and are easy to construct:

Lemma 7

Let μ₀ be bandlimited to Λ₀. Any set of M ≥ R + |Λ₀| distinct points on the curve {μ₀ = 0} contains a subset of R points that are a set of admissible nodes.

The next lemma shows that we can characterize the column space of 𝒯 (f̂) in a similar way as the row space:

Lemma 8

A basis of the column space of 𝒯 (f̂) is given by the columns of the 2|Λ₂| × R weighted Vandermonde-like matrix:

$${\mathit{E}}_{\mathit{col}}(P)=\frac{1}{\sqrt{\mid {\mathrm{\Lambda }}_2\mid }}\left(\begin{array}{ccc}\frac{w_{1,x}}{\Vert {\mathit{w}}_1\Vert }{e}^{j2\pi {\mathit{k}}_1·{\mathit{r}}_1}& \dots & \frac{w_{R,x}}{\Vert {\mathit{w}}_R\Vert }{e}^{j2\pi {\mathit{k}}_1·{\mathit{r}}_R}\\ ⋮& & ⋮\\ \frac{w_{1,x}}{\Vert {\mathit{w}}_1\Vert }{e}^{j2\pi {\mathit{k}}_{\mid {\mathrm{\Lambda }}_2\mid }·{\mathit{r}}_1}& \dots & \frac{w_{R,x}}{\Vert {\mathit{w}}_R\Vert }{e}^{j2\pi {\mathit{k}}_{\mid {\mathrm{\Lambda }}_2\mid }·{\mathit{r}}_R}\\ \frac{w_{1,y}}{\Vert {\mathit{w}}_1\Vert }{e}^{j2\pi {\mathit{k}}_1·{\mathit{r}}_1}& \dots & \frac{w_{R,y}}{\Vert {\mathit{w}}_R\Vert }{e}^{j2\pi {\mathit{k}}_1·{\mathit{r}}_R}\\ ⋮& & ⋮\\ \frac{w_{1,y}}{\Vert {\mathit{w}}_1\Vert }{e}^{j2\pi {\mathit{k}}_{\mid {\mathrm{\Lambda }}_2\mid }·{\mathit{r}}_1}& \dots & \frac{w_{R,y}}{\Vert {\mathit{w}}_R\Vert }{e}^{j2\pi {\mathit{k}}_{\mid {\mathrm{\Lambda }}_2\mid }·{\mathit{r}}_R}\end{array}\right),$$ (22)

where where {k₁, …, k_|Λ2|} is a linear indexing of elements in Λ₂ and P = {r₁, ...., r_R} is a set of admissible nodes for the curve {μ₀ = 0}. The weight vectors w_i = (w_i,x, w_i,y), are described by the formula (52) in Appendix VIII, and depend only on the edge set {μ₀ = 0}, the nodes P, and the filter support Λ₁.

See Section VIII-C for the proofs of Lemmas 6 and 7, and Section VIII-E for the proof of Lemma 8.

B. Incoherence measure

We now show how to define an incoherence measure ρ that satisfies the desired bounds in Prop. 3. Consider the Gram matrix G(P) = [E_row(P)]^*E_row(P), where P is any set of R points r₁, …, r_R on the edge set curve {μ = 0}. It is easy to see from the definition (21) that the entries of G(P) are specified by

$${(\mathit{G}(P))}_{i,j}=\frac{1}{\mid {\mathrm{\Lambda }}_1\mid }{D}_{{\mathrm{\Lambda }}_1}(r_i-r_j),1\le i,j\le R,$$ (23)

where D_Λ1(r) := Σ_k∈Λ1e^j2πk·r is the Dirichlet kernel supported on Λ₁. Note that G(P) has ones along the diagonal, and the magnitude of the off-diagonal entries is dictated by the distances |r_i − r_j | and the filter support Λ₁. We now define the incoherence measure ρ associated with the edge set E = {μ₀ = 0} in terms of G(P).

Definition 9

Suppose the edge set curve E = {μ₀ = 0} has bandwidth Λ₀ (see (3)), and set R = |Λ₁| − |Λ₁: Λ₀|. Define the incoherence measure ρ by

$$\rho =\underset{\begin{array}{c}P\subset \{{\mu }_0=0\}\\ \mid P\mid =R\end{array}}{min}\frac{1}{{\lambda }_{\mathit{min}}[\mathit{G}(P)]},$$ (24)

where λ_min[G(P)] is the minimum eigenvalue of G(P).

Put in words, among all possible arrangements of R points along the edge-set {μ₀ = 0}, we seek the arrangement such that the minimum eigenvalue G(P) is as large as possible. Intuitively, the optimal arrangement will maximize the minimum separation distance among the R points, and ρ can be thought of as a measure of this geometric property. In particular, edge set curves that enclose a small area, and hence require the points P to be closely spaced along the curve, will result in a large value of ρ. According to Theorem 4, the measurement burden will be high for such curves.

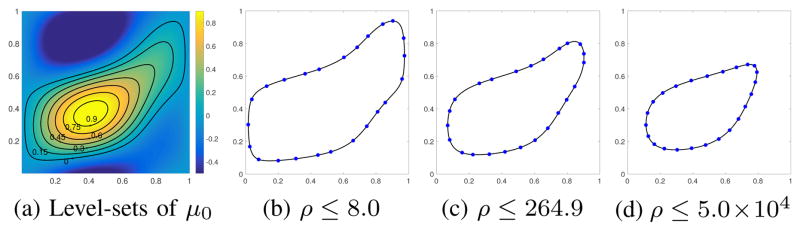
Note that curves corresponding to a particular bandwidth can come in different sizes. Specifically, for a fixed μ₀ with bandwidth Λ₀ consider the family of curves {μ₀ = α}, where α is a scalar. One can change α to obtain multiple curves with exactly the same bandwidth, each of which correspond to a different levelset of μ₀. These level-sets will have different incoherence measures, depending on how large or small the level-set curves are. This shows the incoherence of an edge set captures something besides its bandwidth. See Figure 3 for an illustration.

Fig. 3.

Illustration of edge set incoherence measure ρ. In (a) are the level-sets of trigonometric polynomial μ₀ bandlimited to Λ₀ of size 3×3. These curves all have the same bandwidth, Λ₀, but come in different sizes. In (b)–(d) we show R = 24 nodes on the curve giving the indicated bound on incoherence parameter ρ defined in (24), assuming a filter Λ₁ of size 7×7. Observe that the incoherence measure increases as the curve gets smaller. This indicates the smaller curves have a significant sampling burden.

We can give incoherency measure of an edge set a more precise geometric interpretation based on the minimum separation distance of a set of admissible nodes. We generalize a bound on the condition number of Vandermonde matrices derived in [27] to the case of the Vandermonde-like matrix (21), and use this to derive a bound for the incoherence parameter ρ.

Theorem 10

Assume that the points $P={\{(x_i,y_i)\}}_{i=1}^R$ belonging to the curve {μ₀ = 0} satisfy |x_i − x_j | > Δ and |y_i − y_j | > Δ for all i ≠ j. Assume the filter support Λ₁ ⊂ ℤ² is a square region symmetric around the origin of size $\sqrt{\mid {\mathrm{\Lambda }}_1\mid }\times \sqrt{\mid {\mathrm{\Lambda }}_1\mid }$. Then

$$\rho \le {\left(1-\frac{1}{\sqrt{\mid {\mathrm{\Lambda }}_1\mid }\mathrm{\Delta }}\right)}^{-2},$$ (25)

where ρ is the incoherence parameter (24) associated with the curve {μ₀ = 0}.

See Section I of the Supplementary Materials for the proof. The bound in (25) shows that the incoherence is close to one (i.e., is as small as possible) when $\mathrm{\Delta }\gg 1/\sqrt{\mid {\mathrm{\Lambda }}_1\mid }$. Since Δ is the spacing between each pair of points on the curve, to achieve a larger Δ spacing, and hence a smaller ρ, requires a larger curve. This suggests that fewer measurements are required to recover a larger curve, which is consistent with the findings in the isolated Dirac setting [27], [28].

V. Numerical Experiments

A. Algorithms

For small to moderate problem sizes the nuclear norm minimization problem (10) can be solved efficiently with the alternating directions method of multipliers (ADMM) algorithm, which results in a modification of the singular value thresholding (SVT) algorithm [29]. This approach has been proposed for related structured low-rank matrix completion problems in several works, e.g., [3], [11], [12], [30]. We adopt this approach here as well for our small-scale numerical experiments. A detailed implementation of this algorithm can be found in, e.g., [28]. However, we note that for large scale problems, such as those encountered in realistic imaging applications, more efficient approaches need to be adopted, because often in these cases the lifted matrix is too large to be held in memory. A fast algorithm for solving an approximation to (10) for large-scale problems is given in [19].

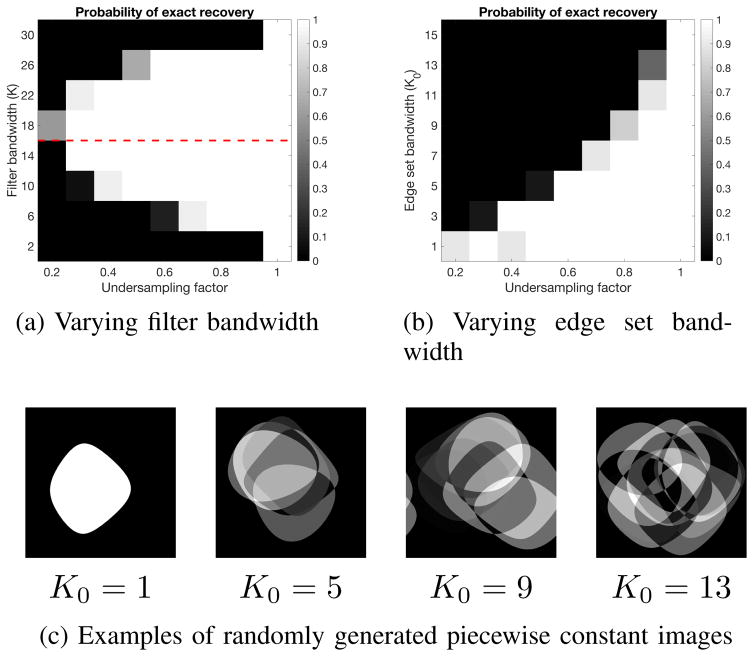
B. Phase transitions

In Fig. 4, we study the probability of exact recovery under different assumptions on the filter size and edge set of the image. For these experiments the reconstruction grid Γ was of size 65 × 65. We generated synthetic random piecewise constant functions with known edge set bandwidth (see Fig. 3(c)), and attempted to recover their Fourier coefficients in Γ from random samples in Ω at the specified undersampling factor. For each set of parameters we ran 10 random trials. We count the recovery as “exact” if the recovered coefficients f̂ satisfied ||f̂ − f₀||/||f̂₀|| < 10⁻³, where f̂₀ is the ground truth. The exact recovery rate was then obtained by averaging over the 10 trials.

Fig. 4.

Phase transition experiments. We generated random piecewise constant images with known edge-set bandwidth and study the success rate proposed structured low-rank matrix completion scheme under two conditions: in (a) we vary the filter size Λ₁ while keeping the edge-set bandwidth K₀ fixed, in (b) we vary the edge-set bandwidth K while keeping the filter size fixed. Examples of the randomly generated data are shown in (c).

First, in Fig. 4(a), we studied the effect of changing the filter size Λ₁ on the recovery while keeping other parameters constant. We fixed the edge-set bandwidth to |Λ₀| = 9×9 and varied the filter size as |Λ₁| = (2K +1)×(2K +1) for K = 1, …, 30. We call K the filter bandwidth. Note that Theorem 4 has restrictions on how large Λ₁ can be. The maximum filter bandwidth for which Theorem 4 holds in this case was K = 15 (red line in Figure 4(a)), however we extended the filter size to observe the behavior of the algorithm outside of this regime. As predicted by Theorem 4, we find that the optimal performance is obtained when Λ₁ is the largest as allowed by Theorem 4 (roughly half the size of Γ in each dimension).

Next, in Fig. 4(b), we study the recovery as a function of the bandwidth of the edge-set of the image. The filter bandwidth was fixed at K = 15, and we varied the edge-set bandwidth as |Λ₀| = (2K₀ +1)×(2K₀ +1). The phase transition shows dependence |Ω| = O(|Λ₀|) as predicted by Theorem 4.

C. Comparison with TV minimization on real MRI data

We also compare the proposed Fourier domain interpolation scheme against standard discrete TV minimization in spatial domain:

$$\underset{\mathit{u}\in {ℂ}^N}{min}TV(\mathit{u})\text{subject}\text{to}{P}_{\mathrm{\Omega }}(\mathit{Fu})=P_{\mathrm{\Omega }}(\mathit{F}{\mathit{u}}_0).$$ (26)

Here u ∈ ℂ^N with N = N_xN_y is a 2-D array representing a discrete N_x × N_y image, u₀ ∈ ℂ^N is the image to be recovered, F ∈ ℂ^N×N denotes the unitary 2-D discrete Fourier transform (DFT) matrix acting on N₁ × N₂ arrays, P_Ω is projection onto the index of sampling locations Ω ⊂ [N_x]×[N_y], and TV (·) denotes the (isotropic) total variation semi-norm:

$$TV(\mathit{u})=\sum _{i=1}^N{({\mid {({\mathit{\partial }}_1\mathit{u})}_i\mid }^2+{\mid {({\mathit{\partial }}_2\mathit{u})}_i\mid }^2)}^{\frac{1}{2}}$$ (27)

where ∂₁ and ∂₂ are finite difference operators in the horizontal and vertical directions, respectively. The problem (26) has been studied extensively [31]–[36] as a model for undersampled MRI reconstruction and other inverse problems in imaging.

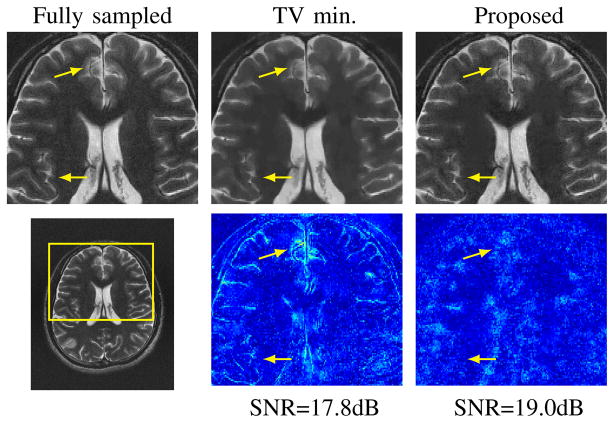
In Fig. 5 we perform an experiment comparing against TV minimization and the proposed approach on real MRI data. For this experiment we used a fully-sampled four-coil single-slice acquisition consisting of 256 × 256 Cartesian k-space samples, which was compressed to a single virtual coil using an SVD-based technique [37]. The data in the single virtual coil was observed to have smoothly varying complex phase in image domain. To compensate for this source of model-mismatch, we further pre-preprocessed the data by removing the complex phase in image domain. We note that this preprocessing step is unrealistic for a true MRI experiment. However, the optimization problem (10) could be modified to incorporate an estimate of the smoothly varying phase in the measurement model; we omit this step for simplicity. Finally, we retrospectively undersampled the pre-processed virtual single coil data, taking 50% uniform random samples. We find that the proposed structured low-rank recovery shows significant improvement recovery error over standard total variation as measured by SNR = 20log₁₀(||f̂||/||f̂^* − f̂||), where f̂^* is the recovered data and f̂ is the ground truth. The error images indicate the proposed method more faithfully recovers the true edges of the image.

Fig. 5.

Recovery of MRI data from 2-fold random uniform undersampling. Error images shown in bottom right.

VI. Discussion

Discrete domain total-variation minimization has played a central role in compressed sensing from its inception [31], [32], which models the image to be recovered as (approximately) piecewise constant. Since the present work can be thought of as an extension of compressed sensing type guarantees to the continuous domain setting, it is fruitful to explore the connections between our continuous domain model and discrete domain total variation.

At first glance, the structured low-rank matrix completion problem (10) may seem far removed from the TV-minimization problem (26). But, in fact, one can show TV-minimization (26) is equivalent to nuclear norm minimization of a related structured matrix lifting in Fourier domain. Specifically, (26) is equivalent to

$$\underset{\mathit{v}}{min}{\Vert \mathcal{C}(\mathit{Fu})\Vert }_{\ast }\text{subject}\text{to}{P}_{\mathrm{\Omega }}(\mathit{Fu})=P_{\mathrm{\Omega }}(\mathit{F}{\mathit{u}}_0).$$ (28)

Here

$$\mathcal{C}(\mathit{Fu})=\left[\begin{array}{c}{\mathcal{C}}_x(\mathit{Fu})\\ {\mathcal{C}}_y(\mathit{Fu})\end{array}\right]\in {ℂ}^{2N\times N}$$ (29)

and 𝒮_x(Fu), 𝒮_y(Fu) are block circulant with circulant blocks matrices whose first column is specified by the arrays v_x = F∂_xu and v_y = F∂_xu. Assuming circular boundary conditions, we can write (v_x)[k_x, k_y] = (1 − e^j2πk_x/N_x)(Fu)[k_x, k_y] and (v_y)[k_x, k_y] = (1 − e^j2πk_y/N_y)(Fu)[k_x, k_y].

We find it interesting to use this re-formulation of TV-minimization to better understand the proposed approach. In Table I we summarize the similarities and differences. One essential difference is the dimensions of the matrix liftings. In particular, the matrix lifting we propose has dimensions 2|Λ₂| × |Λ₁|, with |Λ₁| ≪ |Λ₂| whereas the matrix lifting associated with TV in (28) has dimensions 2N × N. If the reconstruction grid size is the same in both cases, i.e., |Γ| = N, then the proposed matrix lifting has substantially fewer columns than the one associated with TV. This is due to our assumption that edge set of the image has low bandwidth. In other words, we restrict the degrees of freedom of the model by constructing a lifting with fewer columns. We believe this difference may explain the success of the proposed method over TV-minimization observed empirically in Section V.

TABLE I.

Comparison of proposed scheme with discrete total variation minimization

	TV-minimization	Proposed
Spatial domain	discrete	continuous
Derivative operator	finite differences	exact derivative
Singularity set	discrete points	connected curves
Frequency domain	discrete	discrete
Frequency weighting wi[k]	1 − ej2πki/Ni	j2πki
Lifted matrix structure	two-level circulant	two-level Toeplitz
Rank of lifted matrix	sparsity of discrete gradient	bandwidth of edge set

VII. Conclusion

We derived performance guarantees for the recovery of piecewise constant images from random non-uniform Fourier samples via a convex structured low-rank matrix completion problem. This was achieved by adapting results in [3] to the case of a low-rank block two-fold Toeplitz matrix with an additional weighting scheme that arises naturally when considering piecewise constant images. We also define incoherence measures that rely only on geometric properties of the edge set, which indicate that the sampling burden is higher for images with smaller piecewise constant regions.

The recovery guarantees in this work studied the case of uniform random samples. However, in practice we observe that recovery works well with when considering other types of variable density random sampling, where the low spatial frequencies are more heavily sampled. It would be interesting to adapt our results to a wider variety of sampling distributions, and to identify the optimal sampling strategy for signals belonging to our image model.

Fig. 1.

Annihilation of a piecewise constant function as a multiplication in spatial domain (top) and as a convolution in Fourier domain (bottom). The partial derivatives of a piecewise constant function are supported on the edge set. If there is a bandlimited function μ that is zero along the edge set, then the spatial domain product of μ with the gradient ∇f = (∂_xf, ∂_yf) is identically zero. In Fourier domain, this is equivalent to the annihilation of the arrays j2πk_xf[k_x, k_y] and j2πk_yf[k_x, k_y] by 2-D convolution with a finite filter determined by the Fourier coefficients μ̂.

VIII. Appendix A: Incoherence Bounds

A. Notation and Preliminaries

To simplify our arguments, we will convert the linear operators 𝒯(f̂) and 𝒯(f̂)* defined in Fourier domain to linear operators acting on spaces of trigonometric polynomials (3) in spatial domain. Specifically, for any index set Ω ⊂ ℤ², let B_Ω denote the vector space of all trigonometric polynomials that have coefficients supported within Ω. Similarly, we denote the space of vector fields ρ = (ρ₁, ρ₂) with components ρ₁, ρ₂ ∈ B_Ω as $B_{\mathrm{\Omega }}^2$. We set 𝒮(f) = ℱ𝒯(f̂) ℱ⁻¹, where ℱ is the Fourier transform of a periodic function on [0, 1]². For any index set Λ, define the Dirichlet kernel D_Λ1 (r) := Σ_k∈Λ1 e^j2πk·r. For all φ ∈ B_Λ1, the action of the linear operator $\mathcal{S}(f):B_{{\mathrm{\Lambda }}_1}\to B_{{\mathrm{\Lambda }}_2}^2$ can be expressed compactly as

$$\mathcal{S}(f)\phi =D_{{\mathrm{\Lambda }}_2}\ast (\phi \nabla f)\in B_{{\mathrm{\Lambda }}_1}^2,$$ (30)

where φ∇f is understood as a tempered distribution, and the convolution is applied separately to each vector field component. Here convolution with D_Λ2 is a bandlimiting operation. Simliarly, for $\mathit{\rho }=(\rho ,{\rho }_2)\in B_{{\mathrm{\Lambda }}_2}^2$, the adjoint 𝒮(f)^* acts as

$$\mathcal{S}{(f)}^{\ast }\mathit{\rho }=D_{{\mathrm{\Lambda }}_1}\ast (\mathit{\rho }·\nabla f)\in B_{{\mathrm{\Lambda }}_1}$$ (31)

which is the spatial domain equivalent of the adjoint matrix 𝒯(f̂)^*. More expliclty, if f = 1_U where U is a simply connected region with smooth boundary ∂U, a straightforward argument using the divergence theorem shows that the function 𝒮(f)φ is given pointwise as the weighted curve integral

$$(\mathcal{S}(f)\phi )(\mathit{r})={\oint }_{\partial U}{D}_{{\mathrm{\Lambda }}_2}(\mathit{r}-{\mathit{r}}^{\prime })\mathit{n}({\mathit{r}}^{\prime })ds(r^{\prime }),$$ (32)

for all r ∈ [0, 1]², where n(r′) is the outward unit normal to the curve ∂U at r′, and ds is the arc-length element. Likewise, 𝒮(f)^*ρ is the function given pointwise by

$$(\mathcal{S}{(f)}^{\ast }\mathit{\rho })(\mathit{r})={\oint }_{\partial U}{D}_{{\mathrm{\Lambda }}_1}(\mathit{r}-{\mathit{r}}^{\prime })[\mathit{\rho }({\mathit{r}}^{\prime })·\mathit{n}({\mathit{r}}^{\prime })]ds(r^{\prime }),$$ (33)

for all r ∈ [0, 1]². These formulas can be generalized to an arbitrary piecewise constant function f = Σ_i a_i1_Ui by linearity. However, in the remainder we focus on the case where f = 1_U to simplify our arguments.

B. Fundamental subspaces of 𝒮(f) and dimensions

Under the conditions of Theorem 1, the nullspace of 𝒯(f̂) is spanned by shifts of the minimal annihilating filter, $\widehat{{\mu }_0}$. In spatial domain, this space consists of all multiples of the minimal degree polynomial γ = η μ₀ such that γ is bandlimited to Λ₁. We denote this space by

$${({\mu }_0)}_{{\mathrm{\Lambda }}_1}:=\{\eta {\mu }_0:\eta \in B_{{\mathrm{\Lambda }}_1:{\mathrm{\Lambda }}_0}\}.$$ (34)

Note that (μ₀)_Λ1 is a subspace of B_Λ1 with dimension |Λ₁: Λ₀|. Therefore, the dimension of the kernel of 𝒮(f), denoted by ker 𝒮(f), is given by

$$dimker\mathcal{S}(f)=\mid {\mathrm{\Lambda }}_1:{\mathrm{\Lambda }}_0\mid .$$ (35)

By the rank-nullity theorem, the dimension of the image of 𝒮(f), denoted by im 𝒮(f), is

$$dim\text{im}\mathcal{S}(f)=\mid {\mathrm{\Lambda }}_1\mid -\mid {\mathrm{\Lambda }}_1:{\mathrm{\Lambda }}_0\mid =R.$$ (36)

Likewise, the dimension of the coimage im 𝒮(f)^* is also R. Furthermore, since im 𝒮(f)^* = [kerS(f)]^⊥, we have

$$\text{im}\mathcal{S}{(f)}^{\ast }={({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$$ (37)

This means that any γ ∈ B_Λ1 is in the row space if and only if γ is orthogonal to every trigonometric polynomial of the form η μ₀ ∈ B_Λ1, or equivalently,

$$\langle \gamma ,\eta ,{\mu }_0\rangle ={\int }_{{[0,1]}^2}\gamma (\mathit{r})\overline{\eta (\mathit{r}){\mu }_0(\mathit{r})}d\mathit{r}=0$$ (38)

for all η ∈ B_{Λ1: Λ0}.

C. Basis for the coimage of 𝒮(f) (corresponding to the row space of 𝒯(f̂))

Let s ∈ [0, 1]², and set φ_s ∈ B_Λ1 to be the translated Dirichlet kernel:

$${\phi }_{\mathit{s}}(\mathit{r})=D_{{\mathrm{\Lambda }}_1}(\mathit{r}-\mathit{s})\text{for}\text{all}\mathit{r}\in {[0,1]}^2.$$ (39)

Equivalently, φ_s ∈ B_Λ1 is the trigonometric polynomial specified in Fourier domain as

$$\widehat{{\phi }_{\mathit{s}}}[\mathit{k}]=\{\begin{array}{ll}{e}^{-j2\pi \mathit{s}·\mathit{k}}\hfill & \text{if}\mathit{k}\in {\mathrm{\Lambda }}_1\hfill \\ 0\hfill & \text{if}\mathit{k}\notin {\mathrm{\Lambda }}_1\hfill \end{array}.$$ (40)

Observe that the inner product of φ_s with any other trigonometric polynomial η ∈ B_Λ1 is given by the point-evaluation of η at s:

$$\langle \eta ,{\phi }_{\mathit{s}}\rangle =\sum _{\mathit{k}\in {\mathrm{\Lambda }}_1}\widehat{\eta }[\mathit{k}]e^{j2\pi k·\mathit{s}}=\eta (\mathit{s}).$$ (41)

Suppose now that the point s satisfies μ₀(s) = 0. In this case, we see that φ_s is necessarily in the coimage $\text{im}\mathcal{S}{(f)}^{\ast }={({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$ since we have

$$\langle \gamma {\mu }_0,{\phi }_{\mathit{s}}\rangle =\gamma (\mathit{s}){\mu }_0(\mathit{s})=0.$$ (42)

for any multiple of the minimal polynomial γμ₀ ∈ B_Λ1, i.e., any element in ker 𝒮(f) = (μ₀)_Λ1.

We will now show how to construct a basis for the coimage of 𝒮(f) out of elements having the form φ_ri for some r_i, i = 1, …,R belonging to the zero set of μ₀. For an arbtirary collection of R points ${\{{\mathit{r}}_i\}}_{i=1}^R\subset \{{\mu }_0=0\}$, we are not guaranteed that the set of functions ${\{{\phi }_{{\mathit{r}}_i}\}}_{i=1}^R$ is linearly independent. However, we will show that there exists a constant M = M(Λ₀,Λ₁) such that for any M distinct points ${\{r_i\}}_{i=1}^M\subset \{{\mu }_0=0\}$ we can always find a subset of R linearly independent basis functions from the collection ${\{{\phi }_{{\mathit{r}}_i}\}}_{i=1}^M$. The constant M is related the maximum number of isolated zeros that a system of two trigonometric polynomials can have. The following lemma, which is a consequence of the BKK bound in enumerative algebraic geometry (see, e.g., [38]), puts a bound on M. See section II of the supplementary material for proof.

Lemma 11

Let Λ₁ and Λ₀ be rectangular index sets such that Λ₀ ⊂ Λ₁, and set R = |Λ₁| − |Λ₁: Λ₀|. For any μ₀, μ₁ trigonometric polynomials bandlimited to Λ₀ and Λ₁, respectively, the maximum number M of isolated solutions of μ₀(r) = μ₁(r) = 0 is bounded as

$$M<R+\mid {\mathrm{\Lambda }}_0\mid .$$ (43)

We now prove equivalents of Lemma 6 and Lemma 7 in terms of the spatial domain operator 𝒮(f):

Lemma 12

Let {r₁, …., r_N} be any collection of N distinct points on the curve {μ₀ = 0}, where N ≥ R + |Λ₀|. Then the coimage space $im\mathcal{S}{(f)}^{\ast }={({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$ is spanned by the set of shifted Dirichlet kernels φ_i(r) = D_Λ1 (r − r_i) for all i = 1, …,N, i.e.,

$$\mathit{span}{\{{\phi }_{{\mathit{r}}_i}\}}_{i=1}^N={({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }.$$ (44)

In particular, there exists a subset of R = |Λ₁| − |Λ₁: Λ₀| elements of ${\{{\phi }_{{\mathit{r}}_i}\}}_{i=1}^N$ that is a basis for the coimage space ${({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$.

Proof

All the functions φ_ri are in ${({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$ since we have ≪φ_i, γμ₀〉 = γ(r_i)μ₀(r_i) = 0 because each r_i belong to the zero set of μ₀. This implies that

$$\text{span}{\{{\phi }_{{\mathit{r}}_i}\}}_{i=1}^M\subseteq {({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }.$$ (45)

Our focus is on proving (44) with equality. For this, it is sufficient to show that any vector orthogonal to $\text{span}{\{{\phi }_i\}}_{i=1}^N$ is in (μ₀)_Λ. Assume that there is a vector η(r) ∈ B_Λ1 that is in the orthogonal complement space of $\text{span}{\{{\phi }_i\}}_{i=1}^N$. This is only possible if

$$\langle \eta ,{\phi }_i\rangle =\eta ({\mathit{r}}_i)=0,\text{for}\text{all}i=1,\dots ,N.$$ (46)

Therefore, both η and μ₀ have N zeros in common. By Lemma 11 this is only possible if η contains μ₀ as a factor. This implies that all vectors in the orthogonal complement space of $\text{span}{\{{\phi }_i\}}_{i=1}^M$ are in (μ₀)_Λ1, or equivalently

$$\text{span}{\{{\phi }_{{\mathit{r}}_i}\}}_{i=1}^M\supseteq {({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp },$$ (47)

which together with (45) proves (44).

Finally, we also know that the dimension of ${({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$ is equal to R <M. Thus, one can select a subset of R basis functions φ_i that are linearly independent and hence a basis for ${({\mu }_0)}_{{\mathrm{\Lambda }}_1}^{\perp }$.

Translating this result to Fourier domain, we see that the row space of 𝒯(f̂) is spanned by the vectors of Fourier coefficients $(\widehat{{\phi }_i}[\mathit{k}]:\mathit{k}\in {\mathrm{\Lambda }}_1)\in {ℂ}^{\mid {\mathrm{\Lambda }}_1\mid }$, for i = 1, …,R. Equivalently, this can be expressed as the columns of the Vandermonde-like matrix E_row specified by (21), which proves Lemma 6 and 7.

D. Discretization of curve integrals: quadrature formula

Using the results from the previous subsection, we now introduce a quadrature formula for curve integrals, which we will use to determine the range space im 𝒮(f) in the next subsection.

Let γ be any function in B_Λ for any Λ ⊇ Λ₀. Then from the orthogonal decomposition $B_{\mathrm{\Lambda }}={({\mu }_0)}_{\mathrm{\Lambda }}\oplus {({\mu }_0)}_{\mathrm{\Lambda }}^{\perp }$ we can decompose γ as

$$\gamma (\mathit{r})=\sum _{i=1}^S{a}_i{D}_{\mathrm{\Lambda }}(\mathit{r}-{\mathit{r}}_i)+\phi (\mathit{r}){\mu }_0(\mathit{r}),$$ (48)

where S = |Λ|−|Λ: Λ₀|, and where ${\{D_{\mathrm{\Lambda }}(\mathit{r}-{\mathit{r}}_i)\}}_{i=1}^S$ defines a basis of ${({\mu }_0)}_{\mathrm{\Lambda }}^{\perp }$. Here, the coefficients a_i in (48) are obtained uniquely as

$$\left[\begin{array}{c}{a}_1\\ ⋮\\ a_S\end{array}\right]={\mathit{D}}^{-1}\left[\begin{array}{c}\gamma ({\mathit{r}}_1)\\ ⋮\\ \gamma ({\mathit{r}}_S)\end{array}\right],$$ (49)

where D ∈ ℝ^S×S is the symmetric matrix with entries [D]_i,j = D_Λ(r_i − r_j) for 1 ≤ i, j ≤ S. The above expression can be compactly expressed as a = D⁻¹g, where g = (γ(r₁), …, γ(r_S))^T.

Lemma 13

Let f = 1_U where U is a simply connected region with smooth boundary ∂U, which is the zero levelset of μ₀ ∈ B_Λ0 and let γ ∈ B_Λ. Consider the curve integral of the form

$$\mathit{q}={\oint }_{\partial U}\gamma (\mathit{r})\mathit{n}(\mathit{r})ds(\mathit{r}),$$ (50)

where n(r) = ∇f(r)/|∇f(r)| is the unit normal on the curve ∂U. The curve integral can be evaluated using the quadrature formula

$$\mathit{q}=\sum _{i=1}^S\gamma ({\mathit{r}}_i){\mathit{w}}_i,$$ (51)

where the S = |Λ| − |Λ : Λ₀| points ${\{r_i\}}_{i=1}^S$ belong to the curve {μ₀ = 0}, and the cooresponding weight vectors w_i ∈ ℝ², i = 1, .., S, are specified by

$$\left[\begin{array}{c}{\mathit{w}}_1\\ ⋮\\ {\mathit{w}}_S\end{array}\right]={\mathit{D}}^{-1}\left[\begin{array}{c}{\mathit{v}}_1\\ ⋮\\ {\mathit{v}}_S\end{array}\right].$$ (52)

where v_i = ∮_∂U D_Λ(r − r_i)n(r)ds(r) ∈ ℝ².

Proof

Decomposing γ(r) using (48), we obtain

$${\oint }_{\partial U}\gamma (\mathit{r})\mathit{n}(\mathit{r})ds(\mathit{r})=\sum _{i=1}^S{a}_i\underset{:={\mathit{v}}_i}{\underbrace{{\oint }_{\partial U}{D}_{\mathrm{\Lambda }}(\mathit{r}-{\mathit{r}}_i)\mathit{n}(\mathit{r})ds(\mathit{r})}}$$ (53)

The above sum can be expressed in the vector form as

$$\sum _{i=1}^S{a}_i{\mathit{v}}_i={\mathit{a}}^{\ast }\mathit{V}={\mathit{g}}^{\ast }{\mathit{D}}^{-1}\mathit{V}$$ (54)

where $\mathit{V}={[{\mathit{v}}_1^T,\dots ,v_S^T]}^T\in {ℂ}^{R\times 2}$. Setting $\mathit{W}={\mathit{D}}^{-1}\mathit{V}={[{\mathit{w}}_1^T,\dots ,{\mathit{w}}_S^T]}^T\in {ℂ}^{R\times 2}$ we obtain (51).

E. Basis for the range of 𝒮(f) (corresponding to the column space of 𝒯(f̂))

We now introduce a basis set for im 𝒮(f), which will be used to prove Lemma 8.

Lemma 14

The range of 𝒮(f), denoted by im 𝒮(f) is specified by

$$\text{im}\mathcal{S}(f)=\mathit{span}{\{{\mathit{w}}_i{D}_{{\mathrm{\Lambda }}_2}(\mathit{r}-{\mathit{r}}_i)\}}_{i=1}^R$$ (55)

for an appropriate choice of points ${\{{\mathit{r}}_i\}}_{i=1}^R\subset \{{\mu }_0=0\}$ with R = |Λ₁| − |Λ₁: Λ₀|, and where the weight vectors w_i are specified by (52).

Proof

Consider an arbitrary element ρ = (ρ, ρ₂) ∈ im 𝒮(f). We can express ρ as ρ = 𝒮(f)ψ = ℬ_Λ2 (ψ∇f) = D_Λ2 * (ψ∇f) for some ψ ∈ B_Λ1. By the definition in (33), we have

$$\begin{gathered} \mathit{\rho }(\mathit{r})={\oint }_{\partial U}\psi (\mathit{s})D_{{\mathrm{\Lambda }}_2}(\mathit{r}-\mathit{s})\mathit{n}(\mathit{s})ds \\ =\sum _{i=1}^S\psi ({\mathit{r}}_i)D_{{\mathrm{\Lambda }}_2}(\mathit{r}-{\mathit{r}}_i){\mathit{w}}_i, \end{gathered}$$ (56)

where we Lemma 13 in the last step with S = |Γ| − |Γ : Λ₀| since the integrand ψ(s)^* D_Λ2 (r − s) belongs to B_Γ. The above relation shows that any ρ(s) ∈ im 𝒮(f) can be expressed as the linear combination of the functions D_Λ2 (s − r_i)w_i, for i = 1, .., S. Thus, we have $\text{im}\mathcal{S}(f)\subset \text{span}{\{D_{{\mathrm{\Lambda }}_2}(\mathit{r}-{\mathit{r}}_i){\mathit{w}}_i\}}_{i=1}^S$. We also know that dim (im 𝒮(f)) = R < S. This implies that we can select a subset of R vectors from the set ${\{D_{{\mathrm{\Lambda }}_2}(\mathit{r}-{\mathit{r}}_i){\mathit{w}}_i\}}_{i=1}^S$ that are linearly independent, which will span im 𝒮(f), and hence define a basis.

Correspondingly, the column space of 𝒯(f̂) is spanned by the Fourier coefficients of the basis vectors w_iD_Λ2 (r − r_i), or the columns of the 2|Λ₂| × R weighted Vandermonde-like matrix E_col specified by (22).

F. Incoherence Bounds

1) Projection onto row subspace

Let E_row = E_row(P) be any basis for the row space V of 𝒯(f̂) specified by (21), whose columns are vectorized Fourier coefficients of the translated and normalized Dirichlet kernels ${\phi }_i(\mathit{r})=\frac{1}{\sqrt{\mid {\mathrm{\Lambda }}_1\mid }}{D}_{{\mathrm{\Lambda }}_1}(\mathit{r}-{\mathit{r}}_i)$, i = 1, …,R, for some set of admissible nodes P = {r₁, …, r_R} ⊂ {μ₀ = 0}. Projecting the measurement basis matrix A_k onto V, we have

$$\begin{gathered} {\Vert {\mathcal{P}}_V{\mathit{A}}_{\mathit{k}}\Vert }_F^2={\Vert {\mathit{A}}_{\mathit{k}}{\mathit{E}}_{\text{row}}{({\mathit{E}}_{\text{row}}^{\ast }{\mathit{E}}_{\text{row}})}^{-1}{\mathit{E}}_{\text{row}}^{\ast }\Vert }_F^2 \\ \le {[{\lambda }_{\mathit{min}}({\mathit{E}}_{\text{row}}^{\ast }{\mathit{E}}_{\text{row}})]}^{-1}{\Vert {\mathit{A}}_{\mathit{k}}{\mathit{E}}_{\text{row}}\Vert }_F^2 \end{gathered}$$

Since A_k selects |ω(k)| rows of E_row, each of which has R entries of magnitude $1/\sqrt{\mid {\mathrm{\Lambda }}_1\mid }$, we have

$${\Vert {\mathit{A}}_{\mathit{k}}{\mathit{E}}_{\text{row}}\Vert }_F^2=\frac{1}{\mid \omega (\mathit{k})\mid }·R·\mid \omega (\mathit{k})\mid ·\frac{1}{\mid {\mathrm{\Lambda }}_1\mid }=\frac{R}{\mid {\mathrm{\Lambda }}_1\mid }=\frac{R{c}_s}{\mid \mathrm{\Gamma }\mid }$$ (57)

where c_s = |Γ|/|Λ₁|. Hence,

$${\Vert {\mathcal{P}}_V{\mathit{A}}_{\mathit{k}}\Vert }_F^2\le {[{\lambda }_{\mathit{min}}({\mathit{E}}_{\text{row}}^{\ast }{\mathit{E}}_{\text{row}})]}^{-1}\frac{R{c}_s}{\mid \mathrm{\Gamma }\mid }.$$ (58)

Minimizing over all sets of admissible nodes P in the construction of E_row gives the final bound

$${\Vert {\mathcal{P}}_V{\mathit{A}}_{\mathit{k}}\Vert }_F^2\le \frac{\rho R{c}_s}{\mid \mathrm{\Gamma }\mid }.$$ (59)

2) Projection onto column space

Let E_col = E_col(P) be a basis for the column space of 𝒯(f̂) specified by (22), whose columns are vectorized Fourier coefficients of the translated and weighted Dirichlet kernels $\frac{1}{\sqrt{\mid {\mathrm{\Lambda }}_2\mid }}\frac{{\mathit{w}}_i}{\Vert {\mathit{w}}_i\Vert }{D}_{{\mathrm{\Lambda }}_2}(\mathit{r}-{\mathit{r}}_i)$, for some set of admissible nodes P = {r₁, …, r_R} ⊂ {μ₀ = 0}. Observe the columns of E_col are defined to have unit ℓ²-norm. Following the same steps as in the row space bound, we have

$$\begin{gathered} {\Vert {\mathcal{P}}_U{\mathit{A}}_{\mathit{k}}\Vert }_F^2={\Vert {\mathit{E}}_{\text{col}}{({\mathit{E}}_{\text{col}}^{\ast }{\mathit{E}}_{\text{col}})}^{-1}{\mathit{E}}_{\text{col}}^{\ast }{\mathit{A}}_{\mathit{k}}\Vert }_F^2 \\ \le {[{\lambda }_{\mathit{min}}({\mathit{E}}_{\text{col}}^{\ast }{\mathit{E}}_{\text{col}})]}^{-1}{\Vert {\mathit{E}}_{\text{col}}^{\ast }{\mathit{A}}_{\mathit{k}}\Vert }_F^2 \end{gathered}$$

Expanding the norm ${\Vert {\mathit{E}}_{\text{col}}^{\ast }{\mathit{A}}_{\mathit{k}}\Vert }_F^2$ gives

$$\begin{gathered} {\Vert {\mathit{E}}_{\text{col}}^{\ast }{\mathit{A}}_{\mathit{k}}\Vert }_F^2=\frac{1}{\mid {\mathrm{\Lambda }}_2\mid }\sum _{i=1}^R\frac{1}{\mid \omega (\mathit{k})\mid }\sum _{\mathit{\ell }\in \omega (\mathit{k})}{\left|\langle \frac{\mathit{\ell }}{\Vert \mathit{\ell }\Vert },\frac{{\mathit{w}}_i}{\Vert {\mathit{w}}_i\Vert }\rangle \right|}^2 \\ \le \frac{R}{\mid {\mathrm{\Lambda }}_2\mid }\le \frac{R{c}_s}{\mid \mathrm{\Gamma }\mid }. \end{gathered}$$

Hence, we have

$${\Vert {\mathcal{P}}_U{\mathit{A}}_{\mathit{k}}\Vert }_F^2\le \frac{{\rho }^{\prime }R{c}_s}{\mid \mathrm{\Gamma }\mid }.$$ (60)

where ρ′ is defined similarly to ρ as:

$${\rho }^{\prime }=\underset{\begin{array}{c}P\subset \{{\mu }_0=0\}\\ \mid P\mid =R\end{array}}{min}\frac{1}{{\lambda }_{\mathit{min}}[{\mathit{E}}_{\text{col}}(P)\ast {\mathit{E}}_{\text{col}}(P)]},$$ (61)

Finally, we show how to bound ρ′ by ρ in (60). Observe that we can re-define ρ and ρ′ in terms of the minimum singular value of the basis matrices E_row(P) and E_col(P), according to the correspondences:

$$\begin{gathered} {\lambda }_{\mathit{min}}({\mathit{E}}_{\text{col}}{(P)}^{\ast }{\mathit{E}}_{\text{col}}(P))={\sigma }_{\mathit{min}}^2({\mathit{E}}_{\text{col}}(P)), \\ {\lambda }_{\mathit{min}}({\mathit{E}}_{\text{row}}{(P)}^{\ast }{\mathit{E}}_{\text{row}}(P))={\sigma }_{\mathit{min}}^2({\mathit{E}}_{\text{row}}(P)). \end{gathered}$$

We will show ${\sigma }_{\mathit{min}}^2({\mathit{E}}_{\text{row}}(P))\le {\sigma }_{\mathit{min}}^2({\mathit{E}}_{\text{col}}(P))$, or equivalently, [λ_min(E_col(P)^*E_col(P))]⁻¹ ≤ [λ_min(E_row(P)^*E_row(P)]⁻¹, for any set P consisting of R points on the edge set. The claim then follows immediately by taking the minimum over all such sets P.

To ease notation, we drop the dependence on the set P in the following. Observe that we can express E_col as

$${\mathit{E}}_{\text{col}}=\left[\begin{array}{c}{\stackrel{\sim }{\mathit{E}}}_{\text{col}}{\mathit{W}}_x\\ {\stackrel{\sim }{\mathit{E}}}_{\text{col}}{\mathit{W}}_y\end{array}\right]$$ (62)

where ${\mathit{W}}_x=\text{diag}(\frac{w_{1,x}}{\Vert {\mathit{w}}_1\Vert },\dots ,\frac{w_{R,x}}{\Vert {\mathit{w}}_R\Vert }),{\mathit{W}}_y=\text{diag}(\frac{w_{1,y}}{\Vert {\mathit{w}}_1\Vert },\dots ,\frac{w_{R,y}}{\Vert {\mathit{w}}_R\Vert })$, and Ẽ_col ∈ ℂ^|Λ₂|×R is the Vandermonde-like matrix given entrywise by [Ẽ_col]_i,j = e^j2πk_i·r_i, for all k_i ∈ Λ₂, 1 ≤ j ≤ R. In other words, Ẽ_col has the same structure as E_row, but is built with respect to Λ₂ instead of Λ₁. In particular, since we always assume Λ₁ ⊂ Λ₂, the matrix E_row can be embedded as a submatrix of Ẽ_col by restricting the rows of Ẽ_col to those indexed by Λ₁. By the variational characterization of the minimum singular value of a matrix, we have

$$\begin{gathered} {\sigma }_{\mathit{min}}^2({\mathit{E}}_{\text{col}})=\underset{\Vert \mathit{u}\Vert =1}{min}{\Vert {\mathit{E}}_{\text{col}}\mathit{u}\Vert }^2 \\ =\underset{\Vert \mathit{u}\Vert =1}{min}{\Vert {\stackrel{\sim }{\mathit{E}}}_{\text{col}}{\mathit{W}}_x\mathit{u}\Vert }^2+{\Vert {\stackrel{\sim }{\mathit{E}}}_{\text{col}}{\mathit{W}}_y\mathit{u}\Vert }^2 \\ \ge {\sigma }_{\mathit{min}}^2({\stackrel{\sim }{\mathit{E}}}_{\text{col}})\underset{=1}{\underbrace{({\Vert {\mathit{W}}_x\mathit{u}\Vert }^2+{\Vert {\mathit{W}}_y\mathit{u}\Vert }^2)}} \end{gathered}$$ (63)

Finally, since E_row is a submatrix of Ẽ_col, we also have ${\sigma }_{\mathit{min}}^2({\mathit{E}}_{\text{row}})\le {\sigma }_{\mathit{min}}^2({\stackrel{\sim }{\mathit{E}}}_{\text{col}})$, which together with (63) gives the desired inequality.

IX. Appendix B: Proof of Main Theorem

A. Reformulation in lifted domain

We now reformulate the recovery of f̂ as a matrix recovery problem in the lifted domain. The matrices 𝒯_x(f̂) and 𝒯_y(f̂) contain several copies of the weighted entries k_x f̂[k] and k_y f̂ [k], respectively. We use ω(k) to denote the set of locations (α₁, α₂) in the matrix 𝒯_x(f̂) or 𝒯_y(f̂) that contain the entry k_x f̂[k] or k_y f̂[k] (this set is the same in either case).

We define the sampling matrices ${\mathit{A}}_{\mathit{k}}=\left[\begin{array}{c}{\mathit{A}}_{1,\mathit{k}}\\ {\mathit{A}}_{2,\mathit{k}}\end{array}\right]\in {ℂ}^{2\mid {\mathrm{\Lambda }}_2\mid \times \mid {\mathrm{\Lambda }}_1\mid }$, for each k = (k₁, k₂) ∈ Γ, where

$${({\mathit{A}}_{i,\mathit{k}})}_{\mathit{\alpha }}=\{\begin{array}{ccc}\frac{k_i}{\Vert \mathit{k}\Vert \sqrt{\mid {\omega }_i(\mathit{k})\mid }},& \text{if}& \mathit{\alpha }=({\alpha }_1,{\alpha }_2)\in \omega (\mathit{k})\\ 0& \text{else}& \end{array}$$ (64)

for i = 1, 2. The matrices {A_k}_k∈Γ form an orthonormal basis for the space of matrices defined by the range of the matrix lifting 𝒯; we will call any matrix in the range of 𝒯 a structured matrix. For any set of coefficients {ĝ[k]}_k∈Γ we can expand the structured matrix 𝒯(ĝ) as

$$\mathcal{T}(\widehat{g})=\sum _{\mathit{k}\in \mathrm{\Gamma }}\widehat{g}[\mathit{k}]\Vert k\Vert \sqrt{\mid w_i(k)\mid }{\mathit{A}}_{\mathit{k}}.$$ (65)

We denote the projection operator corresponding to a single sampling location k by 𝒜_k(X) = 〈A_k,X〉 A_k. Since {A_k}_k∈Γ is an orthonormal basis, for any structured matrix X, we have Σ_k∈Γ 𝒜_k(X) = 𝒜(X) = X. Since A_k is not the basis for a general X ∈ ℂ^{2|Λ₂|×|Λ₁|}, we also define the projection operator to the space orthogonal to the space of structured matrices by 𝒜_⊥(X) = (ℐ − 𝒜)(X), where ℐ is the identity operator. In particular, the constraint 𝒜_⊥(X) = 0 implies that X is a structured matrix.

The recovery of f from its partial Fourier samples f̂[k], k ∈ Ω, can thus be reformulated as the completion of a structured matrix X from its measurements 𝒜_k, k ∈ Ω. Since the matrix is structured, we have 𝒜_⊥(X) = 0. We thus reformulate (10) as the structured low-rank recovery problem:

$${\text{minimize}}_{\mathit{X}}{\Vert \mathit{X}\Vert }_{\ast }\text{subject}\text{to}{\mathcal{Q}}_{\mathrm{\Omega }}(\mathit{X})={\mathcal{Q}}_{\mathrm{\Omega }}(\mathcal{T}(\widehat{f})),$$ (66)

where 𝒬_Ω that satisifies 𝔼[𝒬_Ω] = ℐ is defined as:

$${\mathcal{Q}}_{\mathrm{\Omega }}=\frac{\mid \mathrm{\Gamma }\mid }{\mid \mathrm{\Omega }\mid }{\mathcal{A}}_{\mathrm{\Omega }}+{\mathcal{A}}^{\perp }$$ (67)

B. Conditions for perfect recovery

The tangent space T of the matrix X is defined as $T:=\{\mathbf{U}{\mathbf{X}}_1^H+{\mathbf{X}}_2{\mathbf{V}}^H:{\mathbf{X}}_1\in {ℂ}^{\mid {\mathrm{\Lambda }}_2\mid \times R},{\mathbf{X}}_2\in {ℂ}^{\mid {\mathrm{\Lambda }}_1\mid \times R}\}$ where X = UΛV^H is the singular value decomposition of X. The orthogonal complement of T is denoted by T^⊥. We first show that if ℘_T ≈ ℘_T𝒬_Ω℘_T, and if an approximate dual certificate that satisfies certain conditions exist, we obtain perfect recovery.

Lemma 15

Consider a multiset Ω that contains m random indices. Suppose the sampling operator 𝒬_Ω obeys

$$\Vert {\mathcal{P}}_T-{\mathcal{P}}_T{\mathcal{Q}}_{\mathrm{\Omega }}{\mathcal{P}}_T\Vert \le \frac{1}{2}$$ (68)

and there exists a dual certificate matrix W satisfying

$${\mathcal{Q}}_{\mathrm{\Omega }}^{\perp }(\mathit{W})=0$$ (69)

$${\Vert {\mathcal{P}}_T(\mathit{W}-\mathit{U}{\mathit{V}}^{\ast })\Vert }_F\le \frac{1}{6n}$$ (70)

$$\Vert {\mathcal{P}}_T^{\perp }(\mathit{W})\Vert \le \frac{1}{2}.$$ (71)

Then, 𝒯(f̂) is the unique solution to (66), where n = |Γ| and m = |Ω|.

See Section III-A of supplementary material for proof. Equation (68) suggests that 𝒬_Ω ≈ ℐ on the tangent space. The conditions (69), (70), and (71) indicates the existence of a W, which approximates the exact dual certificate UV^*. The above lemma is in line with [3, lemma 1], with the exception of the third condition, indicated by (70). To satisfy (68), we bound the deviation of ℘_T𝒬_Ω℘_T from ℘_T in the following lemma.

Lemma 16

Suppose (12) holds. Then we have

$$\Vert {\mathcal{P}}_T-{\mathcal{P}}_T{\mathcal{Q}}_{\mathrm{\Omega }}{\mathcal{P}}_T\Vert \le \epsilon \le \frac{1}{2}$$ (72)

with probability exceeding 1 − n⁻⁴, provided that m > c₁ρR c_s log(n).

We prove this using [39, Theorem 1.6]. (See Section III-B of supplementary material)

C. Construction of the approximate dual certificate W

We will now use the golfing scheme of [3], [25] to construct an approximate dual certificate W, which satisfies (69), (70), and (71). In particular, we generate j₀ independent random sampling sets Ω_i; 1 ≤ i ≤ j₀, each containing m̃ = m/j₀ samples corresponding to sampling with replacement. We start with F₀ = UV*, and follow the following steps:

1. F₀ = UV^* and set $j_0-3{log}_{\frac{1}{\epsilon }}n$.

2. ∀i(1 ≤ i ≤ j₀), F_i = ℘_𝒯(ℐ − 𝒬_Ωi)℘_T (F_i−1)

3. $\mathit{W}={\sum }_{j=1}^{j_0}{\mathcal{Q}}_{{\mathrm{\Omega }}_i}{\mathit{F}}_{j-1}$

Step 3 ensures that W satisfies (69) since each term W_i = 𝒬_ΩiF_j−1 satisfies ${\mathcal{Q}}_{\mathrm{\Omega }}^{\perp }({\mathit{W}}_i)=0$. The recursive construction also satisfies (70). In particular,

$$\begin{gathered} {\Vert {\mathcal{P}}_T(\mathit{W}-\mathit{U}{\mathit{V}}^{\ast })\Vert }_F={\Vert {\mathcal{P}}_T{\mathit{F}}_{j_0}\Vert }_F \\ \le {\epsilon }^{j_0}{\Vert {\mathit{F}}_0\Vert }_F={\epsilon }^{j_0}\sqrt{R}\le {\epsilon }^{j_0}n \end{gathered}$$

Now we focus on showing that W satisfies (71). Note that if j₀ is chosen as $3{log}_{\frac{1}{\epsilon }}n$, assuming n > 6, we have ${(\epsilon )}^{j_0}n<\frac{1}{6n}$.

Lemma 17

For any matrix M, there exists some numerical constant c₂ such that

$$\Vert (\mathcal{I}-{\mathcal{Q}}_{\mathrm{\Omega }})(\mathit{M})\Vert \le c_2\sqrt{\frac{\mathit{n}logn}{m}}{\Vert \mathit{M}\Vert }_{\mathcal{A},2}+\frac{c_2\mathit{n}logn}{m}{\Vert \mathit{M}\Vert }_{\mathcal{A},\infty },$$ (73)

with probability at least 1 − n⁻¹⁰. Here,

$${\Vert \mathit{M}\Vert }_{\mathcal{A},\infty }=\underset{\mathit{k}\in \mathrm{\Gamma }}{max}\left|\frac{\langle {\mathbf{A}}_{\mathit{k}},\mathbf{M}\rangle }{\mid {\omega }_k\mid }\right|$$ (74)

$${\Vert \mathit{M}\Vert }_{\mathcal{A},2}=\sqrt{\sum _{\mathit{k}\in \mathrm{\Gamma }}\frac{{\mid \langle {\mathbf{A}}_{\mathit{k}},\mathbf{M}\rangle \mid }^2}{\mid {\omega }_k\mid }}$$ (75)

See Section III-C of supplementary material for proof.

Lemma 18

Assume that there exists a constant μ₅ such that ${\omega }_{\mathit{k}}{\Vert {\mathcal{P}}_T({\mathit{A}}_{\mathit{k}})\Vert }_{\mathcal{A},2}\le \frac{{\mu }_{5}R}{n}$. For any matrix M, we have

$${\Vert {\mathcal{P}}_T[(\mathcal{I}-{\mathcal{Q}}_{\mathrm{\Omega }})(\mathit{M})]\Vert }_{\mathcal{A},2}\le c_3\sqrt{\frac{{\mu }_5\mathit{R}logn}{m}}\left({\Vert \mathit{M}\Vert }_{\mathcal{A},2}+\sqrt{\frac{\mathit{n}logn}{m}}{\Vert \mathit{M}\Vert }_{\mathcal{A},\infty }\right),$$

with probability at least 1 − n⁻¹⁰.

See Section III-D of the Supplementary Materials for proof.

Lemma 19

For any matrix M ∈ T, there exists some numerical constant c₄, such that

$${\Vert {\mathcal{P}}_T[(\mathcal{I}-{\mathcal{Q}}_{\mathrm{\Omega }})(\mathit{M})]\Vert }_{\mathcal{A},\infty }\le c_4\sqrt{\frac{\rho c_s\mathit{R}logn}{m}}\sqrt{\frac{\rho c_{s}R}{n}}{\Vert \mathit{M}\Vert }_{\mathcal{A},2}+\frac{c_4\rho c_s\mathit{R}logn}{m}{\Vert \mathit{M}\Vert }_{\mathcal{A},\infty },$$ (76)

with probability at least 1 − n⁻¹⁰.

See Section III-F of the Supplementary Materials for proof. From the golfing scheme, we have $\Vert {\mathcal{P}}_{T^{\perp }}(\mathit{W})\Vert \le {\sum }_{j=1}^{j_0}\Vert {\mathcal{P}}_{T^{\perp }}{\mathcal{Q}}_{{\mathrm{\Omega }}_i}{\mathcal{P}}_T{\mathit{F}}_{j-1}\Vert$. Using lemma 17 and substituting from lemma 18 and lemma 19, we have

$$\Vert {\mathcal{P}}_{T^{\perp }}{\mathcal{Q}}_{{\mathrm{\Omega }}_i}{\mathit{F}}_{j-1}\Vert \le {\left(\frac{1}{2}\right)}^{j_0-1}{c}_2\left\{\sqrt{\frac{\mathit{n}logn}{\stackrel{\sim }{m}}}{\Vert {\mathit{F}}_0\Vert }_{\mathcal{A},2}+\frac{\mathit{n}logn}{\stackrel{\sim }{m}}{\Vert {\mathit{F}}_0\Vert }_{\mathcal{A},\infty }\right\}$$

The last inequality holds if m̃ = m/j₀ ≫ max (μ₅, ρc_s)Rlog n. Substituting for $j_0=3{log}_{\frac{1}{\epsilon }}(n)$ assumed in the golfing scheme, we require m ≫ c₆ max (μ₅, ρc_s)Rlog² n to satisfy the above inquality. See Section III-G of the Supplementary Materials for details. We will now present the lemmas bounding ||F₀||_𝒜,2 and ||F₀||_𝒜,∞, where F₀ = UV^*.

Lemma 20

With the incoherence measure ρ, one can bound

$${\Vert \mathit{U}{\mathit{V}}^{\ast }\Vert }_{\mathcal{A},\infty }\le \frac{\rho c_{s}R}{n}$$ (77)

$${\Vert \mathit{U}{\mathit{V}}^{\ast }\Vert }_{\mathcal{A},2}^2\le \frac{c_7{\mu }_3{c}_s{log}^2(n)R}{n}$$ (78)

$${\Vert {\mathcal{P}}_T(\sqrt{{\omega }_{\alpha }}{\mathbf{A}}_{\alpha })\Vert }_{\mathcal{A},2}^2\le \frac{c_7{\mu }_3{c}_s{log}^2(n)R}{n},\forall \mathit{\alpha }\in \mathrm{\Gamma }$$ (79)

for μ₃ = 3ρ and c₇ is some constant.

See Section III-H of the Supplementary Materials for proof. From (79), we see that the constant μ₅ in lemma 19 can be chosen as μ₅ = c₇ μ₃ c_s log²(n) such that ${\omega }_{\mathit{k}}{\Vert {\mathcal{P}}_T({\mathit{A}}_{\mathit{k}})\Vert }_{\mathcal{A},2}\le \frac{{\mu }_{5}R}{n}$. Substituting for μ₅, we observe that the dominant term has its dependence on log⁴(n). Thus, ||℘_T^⊥ 𝒬_ΩiF_j−1||< 1/2 if m > c₆c₇ c_s (3ρ) R log₄(n).