Revealing the distinct folding phases of an RNA three-helix junction

Abstract

Remarkable new insight has emerged into the biological role of RNA in cells. RNA folding and dynamics enable many of these newly discovered functions, calling for an understanding of RNA self-assembly and conformational dynamics. Because RNAs pass through multiple structures as they fold, an ensemble perspective is required to visualize the flow through fleetingly populated sets of states. Here, we combine microfluidic mixing technology and small angle X-ray scattering (SAXS) to measure the Mg-induced folding of a small RNA domain, the tP5abc three helix junction. Our measurements are interpreted using ensemble optimization to select atomically detailed structures that recapitulate each experimental curve. Structural ensembles, derived at key stages in both time-resolved studies and equilibrium titrations, reproduce the features of known intermediates, and more importantly, offer a powerful new structural perspective on the time-progression of folding. Distinct collapse phases along the pathway appear to be orchestrated by specific interactions with Mg ions. These key interactions subsequently direct motions of the backbone that position the partners of tertiary contacts for later bonding, and demonstrate a remarkable synergy between Mg and RNA across numerous time-scales.

INTRODUCTION

Decades of research revealed the dynamics that enable protein folding and conformational transitions, propelling the development of novel biomaterials (1,2), drug design (3,4) and therapeutics (5,6). Despite the growing recognition of its central biological roles as mediators and catalysts of numerous biological reactions (7–9), no similar picture exists for RNA (10). Understanding how RNA structures fold to accomplish these various roles can unlock new strategies for drug design and treatment (11–13). However, as the RNA folding landscape is rugged, involving many intermediates, pathways and co-existing states (11,14,15), experimental results are scarce and challenging to interpret. This richness and complexity demands an experiment that embraces an ensemble view of the process (11).

RNA folding has been studied by many powerful experimental techniques, including those which provide site specific information about folding intermediates (16–20), interconverting species (21–24), and yield intricate frameworks for the reaction (10,25,26). While critical to our full understanding of the process, these experiments provide a limited window into a complete visualization of folding, which also relies on crucial, large scale structural re-arrangements (27).

Small-angle X-ray scattering reports large scale, as well as subtle, changes in global molecular shapes in an ensemble measurement. Time resolution can be achieved by integrating either stopped- or continuous- flow mixing (28–31). These challenging experiments are small in number and, to date, have yielded an incomplete picture of RNA’s route(s) from unfolded to native states. Limitations of previous SAXS experiments reflect difficulties associated with measuring high quality scattering profiles on the shortest time scales and/or over a broad range of scattering angles that reflect both small and large scale changes in conformation. In addition, previous studies relied on the application of standard methods for data interpretation which allow only general statements and rough conformational properties to be discerned.

Here, we reveal the Mg-dependent folding pathway of a ubiquitous RNA motif, the three helix junction (32), using ensemble decomposition methods and atomically detailed models to interpret both static, and time-resolved SAXS data. The latter were acquired with a new type of microfluidic mixer, which is based on a novel design (33). The former relied on advanced, molecular dynamics based simulation techniques to offer comprehensive information on structures and dynamics, charting plausible and consistent folding pathways for this RNA. Experimental refinement of these simulation results is carried out by ensemble optimization methods (EOM), an essential step, and provides atomically detailed structures for evaluation. This tightly coupled approach alleviates the above limitations for interpreting SAXS data. It provides unique insight into the structures that populate the folding pathway of this RNA, offering never-before-seen intermediates that underscore the unique role(s) of Mg²⁺ in sculpting the folding landscape. The properties of known reaction intermediates are recognized in this analysis, validating the approach.

Our work focuses on the tP5abc three-helix junction (Figure 1) a truncated subdomain from the Tetrahymena ribozyme. At 56 nucleotides in length, tP5abc is ideally sized for these studies. It is small enough to model with atomic detail, yet displays a rich variety of interactions that often characterize RNA folding: electrostatic repulsion (31,34), Mg²⁺ binding (35–39), both non-specific and specific compactions (28), helix-docking (40), tertiary contact formation (14) and secondary structure shifts (41). Furthermore, previous studies of this molecule using a variety of techniques provide complementary data on which to benchmark and compare our results (e.g. (16,34,41–43)), though past measurements of the rates of P5abc folding show a clear dependence on the ionic conditions employed (44,45). Together with new intermediates presented here, we identify a clear trajectory across the landscape, as the RNA evolves from extended to native structures.

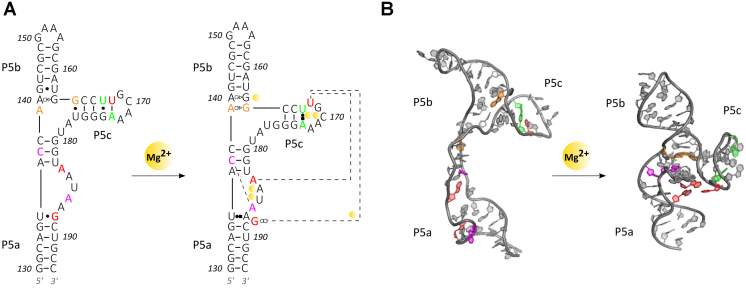
Figure 1.

Structures of the tP5abc three helix junction in both unfolded and folded representations. Secondary (A) and 3D (B) structure(s) of tP5abc. In (A), site bound Mg²⁺ ions are shown as orange spheres and non-Watson Crick base pairs are represented as Leontis/Westhof symbols (59). In the folded structure two helix docking interactions occur (purple and orange residues), two hinge interactions form (red triplet) and a secondary structural switch in P5c is observed (green residues). The nucleotide numbering convention is chosen to remain consistent with the larger P5abc domain, although this truncated molecule contains only 56 nucleotides. 3D Structures rendered with PyMOL (DeLano Scientific LLC).

MATERIALS AND METHODS

Detailed descriptions of all experiments, simulations and data analysis are provided in the Supporting Information. Here, we briefly outline the methods employed.

RNA synthesis

TP5abc was synthesized in vitro using PCR amplified DNA and purified by size exclusion chromatography using a Superdex HiLoad 16/600 200 pg column on an AKTA FPLC purifier. After purification, the RNA was buffer exchanged into a solution containing 20 mM KCl, 10 mM KMOPS, 20 μM EDTA, pH 7 (we refer to this as buffer A) using Amicon Ultra-0.5 10KdA concentrators before being stored.

SAXS experiments

For experimental conditions with varying KCl concentrations, the samples were buffer exchanged five times into solutions containing the stated amount of monovalent salt in addition to 10 mM KMOPS and 20 μM EDTA, pH 7. Samples intended for studies as a function of divalent ion concentration were initially prepared in buffer A. For static measurements, Mg was added to the quoted concentration immediately before exposure to X-rays. Details about sample preparation, experimental setup and interpretation of SAXS data for static experiments are provided in the Supporting Information, text and Supplementary Figures S1 and S2.

For the time-resolved experiments, tP5abc in buffer A was rapidly mixed with Mg to reach a concentration of 1 mM at the end of the mixing region for all time points, via rapid diffusion. Details about the time-resolved experiments, including the design, fabrication and testing of the microfluidic mixer, experimental setup and data collection, are provided in the Supporting Information text, Supplementary Figures S3–S7 and Results and Discussion: Time-resolved SAXS Experiments.

Static and time-resolved SAXS data were acquired at beamline G1 of the Cornell High Energy Synchrotron Source (CHESS). The RNA was annealed at 65°C for 5 minutes and subsequently slow cooled to room temperature before both experiments. For static experiments, RNA concentrations of 80, 60 and 40 μM were used. At each salt condition, data were acquired at multiple RNA concentrations to remove the effects of interparticle interference in the data. Buffer subtracted SAXS curves for a given salt condition but different sample concentrations were matched in the range q > 0.1 A⁻¹, and either averaged together, or extrapolated to the zero concentration limit to give the final curves. Time-resolved experiments were carried out at [RNA] of 80 μM. All SAXS data were analyzed using MATLAB (MathWorks, Natick, MA, USA) with code written in-house. The SAXS data for the static and time-resolved experiments are available through the SASBDB, codes are given at the end of the manuscript.

Simulations

Simulations used the known structures of the beginning and ending states of the folding reaction. A minimum energy pathway is computed, connecting the two, and serves as the starting point for extensive MD simulations of the pool of possible structures, including waters and ions. Detailed descriptions of structural pool generation from simulation is provided in the Simulations section within the Supporting Information.

Ensemble optimization

SAXS profiles for all MD structures were calculated with CRYSOL (46), with maximum harmonic order 15, Fibonacci grid of order 18 and default hydration parameters. Ensemble optimization was run to fit the calculated SAXS curves from the pool to the experimental SAXS data using GAJOE 2.0 (47). For each experimental condition, the program was run for 2000 generations, eight ensembles were selected for each generation, each ensemble had a self-optimizing size, and the scheme was iterated 100 times to accumulate statistics with constant subtraction allowed. Selections made in the final rounds of ensemble optimization were interpreted to provide the results and landscapes presented here.

Thus, for each condition (every SAXS curve), 800 ensembles of structures were interpreted, where each ensemble independently fits the experimental SAXS data. The mean number of structures required to fit the data at each condition (in each ensemble) varies between 6 and 10 on average, depending on the experimental condition. Multiple ensembles of structures that equally fit the data (as assessed through a chi-square analysis) are included to accumulate statistics, and to account for slight variations in structures that recapitulate the data.

RESULTS AND DISCUSSION

Static SAXS experiments

RNA folding occurs in several steps or phases, with molecules populating a variety of intermediate, partially folded conformations (40). To assess the global structural properties of these differing states we first performed static SAXS experiments over a range of ionic conditions. To accentuate differing interactions and ion-specific conformations, experiments were carried out in solutions containing various amounts of either KCl or MgCl₂. The former promotes the effects of electrostatic screening and non-specific collapse (28), while the latter is used to stabilize tertiary contact formation (48). These studies can also reveal intermediates that rely on the presence of Mg (40).

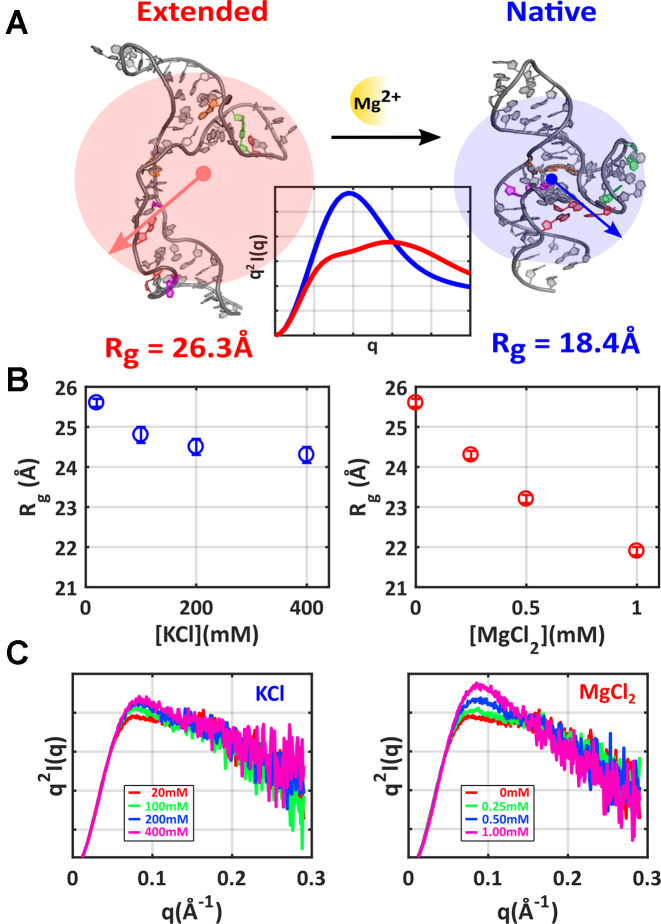
SAXS profiles display the intensity of scattered X-rays (I) as a function of momentum transfer q, which equals 4πsin θ/λ, where λ is the X-ray wavelength and 2θ is the scattering angle. Scattering into the smallest angles, where the signal is largest, reflects the global size of a molecule through its radius of gyration (R_g). The expected/computed R_g’s of purely extended (unfolded) or native tP5abc, shown in Figure 2A, vary significantly. Interesting differences are observed following the addition of the two different salts. As [KCl] increases, a gradual decrease in R_g is measured, reflecting changes in the screening length of the phosphate charges by additional salt. In contrast, Mg is far more efficient in compacting the RNA, consistent with its role in stabilizing tertiary contacts. While R_g values and trends with increasing salt provide limited insight into the folding landscape, they contain some important information: Mg specific interactions have global consequences for structures in the tP5abc ensemble.

Figure 2.

SAXS reports global structural features of tP5abc: shape and size. (A) Structures of the extended (unfolded) and native tP5abc conformations are shown, along with their calculated R_g’s and theoretically derived Kratky plots (center). Kratky plots of q²I versus q emphasize high angle scattering and provide finer details of molecular conformations. (B) Measured R_g’s assess the mean size of the RNA ensemble at varying concentrations of KCl (left plot, blue) and MgCl₂ (right plot, red). (C) Kratky plots reveal more details of molecular conformations during KCl (left) and MgCl₂ titrations (right). The static SAXS curves are available through the SASBDB under accession codes: SASDCF4, SASDCG4, SASDCH4, SASDCJ4, SASDCK4, SASDCL4 and SASDCM4.

Additional information about RNA’s conformations can be inferred through inspection of the scattering at higher q values than those used to determine R_g. Higher q scattering is emphasized through Kratky plots of the SAXS data, shown in Figure 2C, which display q²I versus q. The height of the mid-q peak (q ∼ 0.1 Å⁻¹) and the slope of the higher q scattering (q > 0.1 Å⁻¹) are important features of the Kratky plots and reveal subtle details of molecular conformations. A pronounced peak in the mid-q regime followed by a negatively sloped tail generally indicates ‘folded’ or compact conformations (49). A shallower peak followed by a less strongly sloped tail signifies ‘unfolded’ or extended conformations. Changes in the higher q portions of the curve are interpreted to indicate subtle structural changes such as extension/expansion for a shallower slope, or compaction for a steeper slope. These trends are illustrated in Figure 2A, using computed profiles for extended and native tP5abc generated from pdb coordinates.

Turning to the data, scattering profiles acquired at the lowest salt conditions display ‘unfolded’ behavior in Kratky plots, with a low mid-q peak and flat slope at higher q. The mid-q peak rises slightly with increasing [KCl], but no discernible trend is seen in the high q tail. These curves display few signatures of the folded state. In contrast, Kratky plots of profiles acquired as a function of increasing [Mg] show a more definitive increase in peak height at mid-q, paired with a gradually declining tail. At the highest Mg concentrations, the curve's features hint that a fraction of the population may be occupying native (or at least highly compact) states.

Ensemble modeling

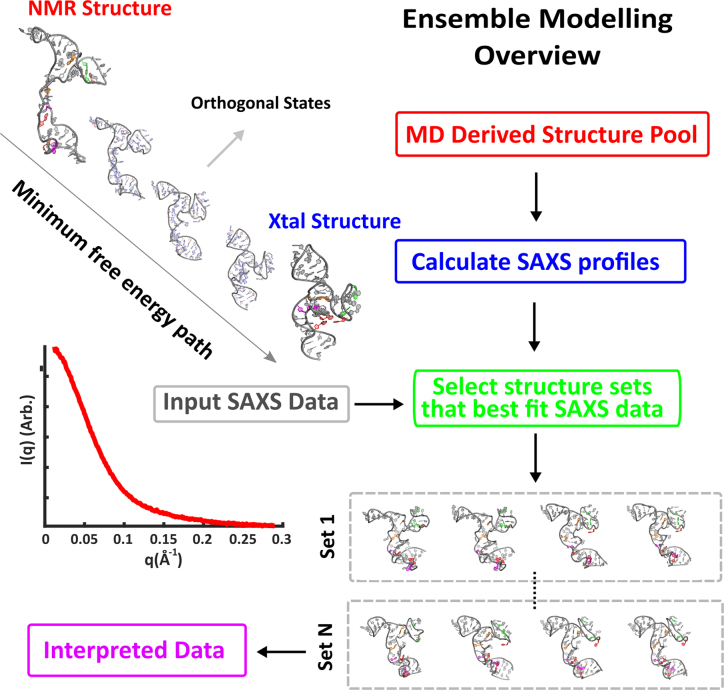
The complex and subtle behavior of the curves at high q is difficult to interpret by visual inspection. The analysis is further complicated by the possible presence of coexisting states under any given condition. A more quantitative interpretation of these changes can be obtained through a deconvolution of the SAXS profiles into curves that describe representative RNA conformations, using an ensemble optimization method (50). Ensemble optimization identifies sets of model structures, selected from a vast pool representing many potential states, whose summed SAXS profiles best fit the input experimental curve. This method is especially powerful for capturing nucleic acids conformations, as the phosphates along the backbone provide the majority of scattering contrast (51). However, a large and physically reasonable pool of models is required as a starting point.

To generate this pool we performed MD simulations, starting from the NMR derived (no Mg) structure (41), and ending at the native state, truncated from the P4P6 crystal structure (52). Subsequently, we used MD simulations with varying solution conditions to refine the two end state structures (see SI for details). We used the reaction path (RP) approach (53–55) to generate plausible pathways between these states. Given the coordinates of these two states, we sought a curve in configuration space that connects them, with a minimal free energy barrier. We added the structures along this pathway to the pool, and in addition explored and added conformations orthogonal to this path (see Supporting Information, ‘Structure Pool’ section for more discussion on pool design, and Supplementary Figure S8). The theoretical SAXS profiles of each model conformation is then calculated (46). As a next step, sets of structures are selected from this pool through a well-defined iterative refinement procedure (50). The summed scattering profile of each set recapitulates the given input experimental SAXS curve, as assessed by a chi square analysis. The selection of multiple sets (800 for each condition) accounts for variations in structures that can adequately fit the data. With this approach, the MD generated pool is refined against experimental SAXS data for each experimental condition, circumventing challenges associated with current MD force-fields and ion modelling (56). The structures selected from the pool are interpreted to be representative of the underlying folding landscape at each experimental condition. This procedure is summarized in Figure 3 and fully described in the Supporting Information, including a critical assessment of the ensemble approach (the section title).

Figure 3.

Conformations of tP5abc can be elucidated by comparing measured SAXS profiles with those computed from selected groups of MD derived structures. A large potential pool of tP5abc states is generated by identifying the lowest free energy path between the unfolded and native tP5abc conformations, and considering states along and orthogonal to this path. The underlying RNA landscape can be assessed by examining sets of structures selected from this large pool whose computed and summed scattering profiles best fit the experimental data.

Static RNA landscapes

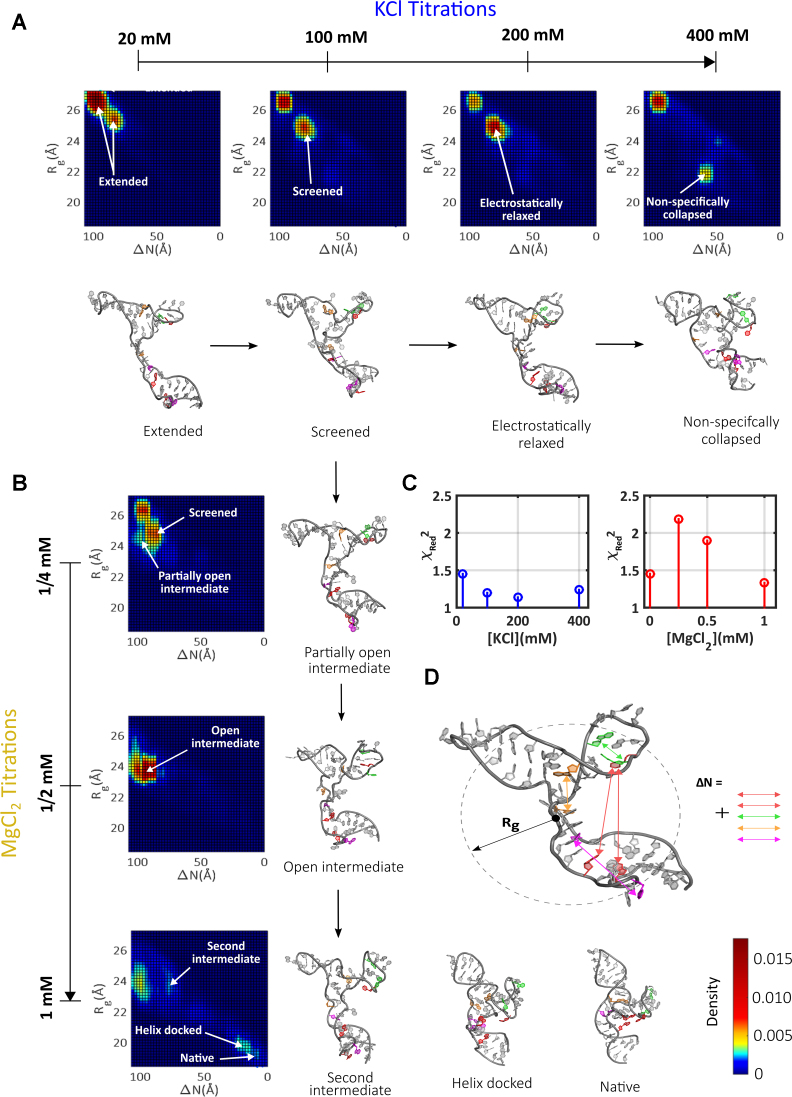
The fits achieved using this method show excellent agreement between the computed profiles of selected states and raw SAXS curves (Figure 4C and Supplementary Figure S9). Having identified sets of structures from the pool that match each experimental condition (mean ensemble size shown in Supplementary Figure S10), we developed a parameterization to aid in visualizing the selected conformations. We compute two metrics for each model structure: its R_g and the distance to native state (ΔN). The latter parameter (defined in Figure 4D and Supplementary Figure S11) is computed by summing the distance between all pairs of tertiary contacts in a given model structure, and subtracting from this sum the distances measured in the native structure. The residues that contribute to each tertiary contact are pictured in color in Figure 1. To compute ΔN for one tertiary contact (for example the contact between A139 and G164, depicted in orange in Figure 1), the distance between them is computed within each model and the corresponding distance measured in the native structure subtracted. Thus, the overall value of ΔN drops to zero for the native structure, while high value of ΔN suggests lack of native contact formation. This metric provides a quantitative measure of proximity to the native state.

Figure 4.

The evolution of the folding landscape in static titrations. (A) The landscapes derived from KCl titrations are shown, along with representative structures (full sets of structures are shown in SI). (B) The landscapes derived from MgCl₂ titrations are shown along with representative structures (full sets of structures are shown in SI). (C) The quality of fitting using the selected models is assessed through computation of the reduced chi-square. (D) The metrics R_g and ΔN, illustrated for an example conformation, are used to locate each structure on the folding landscape.

Each selected model is represented by a point placed on a landscape, whose axes correspond to these two metrics. This landscape is also a heat map, where the density of selected structures within a 0.5 Å circle centered about each point is represented by color. To aid the presentation, these maps are smoothed by a 5-point rolling mean. Landscapes derived from the static salt titrations are shown in Figure 4A and B (with more details in Supplementary Figure S12). A representative structure is shown near highly populated clusters to illustrate the shared conformational properties of these groups of states (to aid in evaluating the range of structures present, an expanded number of structures for each cluster and landscape is given in Supplementary Figures S13–S19).

At the lowest salt condition probed, extended RNA conformations result from repulsive interactions between locally unscreened phosphates along the charged backbone. The majority of selected models populate the large R_g, large ΔN corner, in the upper left of the conformational landscape. These expanded states are consistent with the measured Kratky plot (signalling an ‘unfolded’ rather than ‘folded’ ensemble), as well as the relatively large measured R_g. The more effective backbone screening that occurs with increasing [KCl] enables some compaction, and the nature of the selected models shifts from extended to so-called screened or electrostatically relaxed states. These latter conformations are defined by R_g and ΔN values that are intermediate between the limiting values for tP5abc. They are consistent with a measured decrease in R_g, and a slight increase in the mid-q region of the Kratky plot found in the raw data. A careful examination of the locations of the colored bases in the models, representing the two sides of a potential tertiary contact (Figure 1A), suggests a lack of tertiary interactions. Thus, the reduction in ΔN relative to the lower salt, extended states is a natural consequence of an electrostatic relaxation or collapse. Finally, states with smaller R_g appear at the largest [KCl] probed. Model structures that recapitulate the data suggest that these states lack tertiary contacts, and the backbone conformation in the ensembles suggests that these molecules are non-specifically collapsed. The native tP5abc structure is never achieved in this range of [KCl], nor is evidence found for tertiary contact formation. These findings are consistent with previous studies of tP5abc in KCl, which show no indication of native structure at any concentration of KCl (57).

Taken together, the landscapes are well described by two classes of states at low to moderate [KCl]: extended and screened/electrostatically relaxed. A new class of conformations, non-specifically collapsed states, appear only at the highest salt concentrations. This classification is reinforced by the application of singular value decomposition (SVD) analysis to the KCl salt series. In this analysis, at least three basis states are required to fit the entire set of experimental data with χ² ≤ 1 (Supplementary Figure S20). The EOM fitting not only captures this behavior, but provides an interpretation in terms of model structures, in place of SVD-derived basis curves that may not be physically relevant.

Completely different sets of states are required to provide a comparable analysis of conformations in a MgCl₂ titration, reflected by the appearance of the heat maps (Figure 4B). In Mg, more distinct patches of states are present, with vastly varying R_g and ΔN values, suggesting a more rugged energy landscape. The states identified at the smallest [Mg] studied are similar to those found at low [KCl]. These states have smaller R_g and ΔN values than the extended states. As [Mg] increases to 0.5 mM conformations with similar R_g values to the electrostatically relaxed states appear to funnel toward a region of the landscape which represents states with surprisingly large ΔN values. Structures in this cluster display distinct, expanded orientations of the P5c and P5a helices about the molecular core. Insight from the model conformations suggests the absence of tertiary contacts. The absence of these states at all measured [KCl] and at lower [Mg] suggests that a critical number of Mg ions is required to stabilize these conformations. The unique arrangement of P5a, and the location of P5c relative to P5b would be consistent with specific Mg²⁺ interactions with both the A-rich bulge and P5c, regions with known Mg²⁺ binding sites (41,52,58). Given their characteristic structural features, we name these states 'open intermediates’. The properties of these Mg dependent open intermediates are consistent with the intermediate proposed in (43).

At the highest [Mg], the selected populations shift from open intermediates to clusters of states found in the bottom right corner of the landscape, a region with small R_g and ΔN values (Figure 4B). This shift reflects the trends in the raw data: smaller R_g values are measured, and the peaks become enhanced in Kratky plots. The P5a and P5b helices in the selected model conformations are stacked on the molecular core, with orange (A139–G164) and purple (C137–A186) pairs of tertiary contacts formed. The red colored tertiary contact is not detected in the states on the left side of this cluster. We call these states ‘helix-docked’. In contrast, structures that populate the right side of this cluster, with smaller R_g, do display interactions in the red ‘hinge’ region. We call these the native tP5abc states, as all pairs of tertiary contacts have formed. It is interesting that both of these clusters are absent in lower [Mg]. Even at 1 mM Mg, a large percentage of the population still resides in the open intermediates. Thus, these states appear to be promoted from the open intermediates through additional interactions with Mg. Only 12% of the population reaches the native state in 1 mM Mg (Supplementary Figure S21) with the remainder residing either in the helix-docked, or open intermediate states. This relatively small number is in good agreement with NMR studies that report 8% native state population under similar conditions (16). These trends are once again recapitulated in an SVD analysis, where a minimum of 3 basis states are required to define the Mg series (Supplementary Figure S20).

Time-resolved SAXS (TR-SAXS) experiments

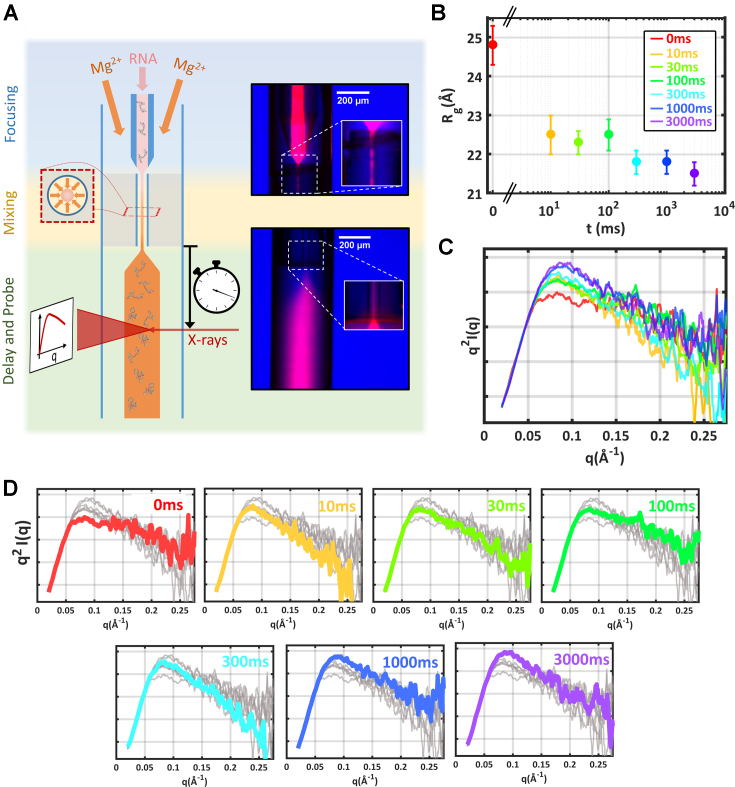
With the landscapes of tP5abc established for static salt titrations, the next step is to carry out a folding experiment to study the kinetic pathway from initially extended conformations to the native state. A microfluidic assembly that addresses the shortcomings of previous mixers for TR-SAXS utilizes mixing technology developed for time-resolved crystallographic experiments (33), delivering high signal-to-noise data with low sample consumption on time scales that span the folding reaction (for details, see Supporting Information). The experimental arrangement is sketched in Figure 5A. Extended tP5abc in a low salt state (20 mM KCl) was rapidly combined with Mg²⁺ to induce folding and subsequently probed at time-points ranging from 10 ms to 3 s after mixing. These time scales were selected to capture both early phase electrostatic collapse and late stage secondary structural shifts (16,34). The final [Mg²⁺] after mixing was 1 mM, sufficient to yield the native structure (16).

Figure 5.

Schematic of mixer used to trigger Mg-induced folding of tP5abc and the full time course acquired. (A) Cartoon schematic of the microfluidic device used in these experiments (left). Fluorescent images of each device region are shown (right). Using this device, we followed the folding pathway of tP5abc after mixing with sufficient MgCl₂ to induce the native state. (B) The measured R_g’s report on the mean global size of the RNA ensemble. (C) Kratky plots highlight more subtle structural details. These curves have been smoothed for presentation purposes. The color scheme is identical to panel B. (D) Expanded view of the Kratky plots shown in panel c. Here, each time point is individually highlighted in color, while the remaining time-points are shown in gray to illustrate the significant variation in scattering at high q. The TR-SAXS curves are available through the SASBDB under accession codes: SASDC74, SASDC94 SASDCA4, SASDCB4, SASDCC4, SASDCD4 and SASDCE4.

Results of the TR-SAXS experiments are shown in Figure 5B–D. Changes in the profiles are detected within 10ms after mixing to a final concentration of 1 mM Mg²⁺. The raw data show a large reduction in R_g, and the emergence of a peak in the Kratky plot as the high angle tail drops significantly. Between 10 and 100 ms, the average size of the RNA (R_g) remains constant within error. However, subtle conformational rearrangements during this period are indicted by gradual, upward shifts in the high q region of the Kratky plot.

A second collapse is detected 300 ms after the initiation of folding. A measurable reduction in R_g, is accompanied by an increased negative slope at the largest q in the Kratky plots. Native-like features in the scattering profiles begin to appear on time scales of 1000–3000 ms. A pronounced peak in the mid-q region of the Kratky plot, as well as a moderately downwards slope at higher q are reminiscent of the profile acquired in static titrations, at 1 mM Mg (Figure 2C), and the R_g’s agree within error.

In summary, the raw SAXS data reveal two distinct collapse phases, on short (10 ms) and medium (300 ms) time-scales. More subtle conformational re-arrangements are observed throughout the remaining time-course.

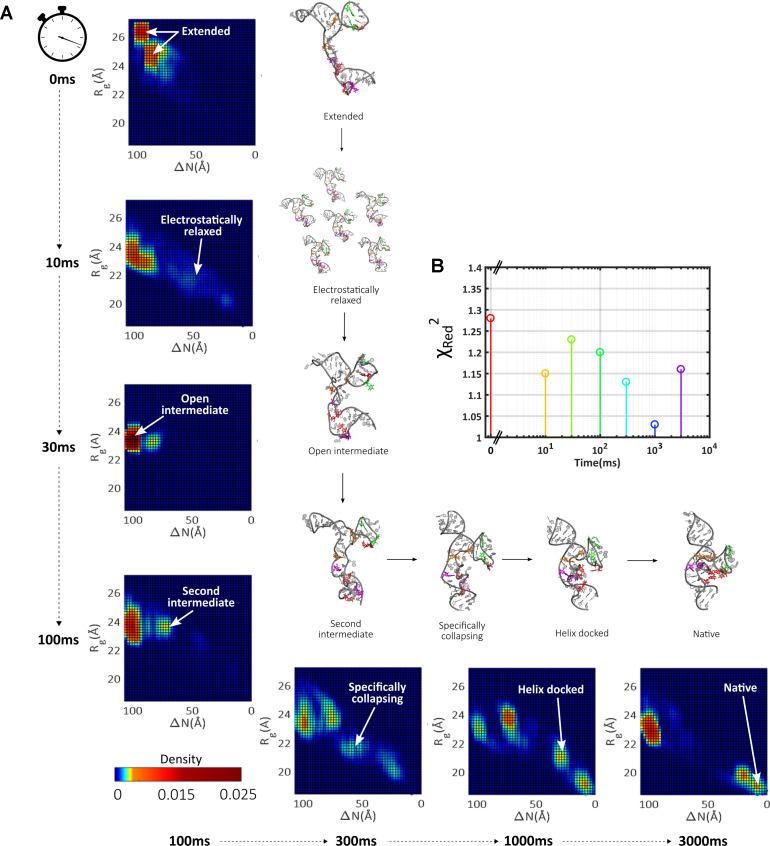
Time-resolved RNA landscapes

To interpret the TR-SAXS data, we performed the same EOM analysis employed for the static titrations, using the full structural pool for all time points. The fits achieved using this pool are in excellent agreement with the data (Figure 6B and Supplementary Figures S22–S24 contain more details of ensemble parameters, including the mean ensemble size), though the reduced signal-to-noise in the TR experiments results in smaller chi-square values for all conditions. The time evolution of the derived landscapes is shown in Figure 6A. A different heat-map color scheme was used for the time-resolved data to increase the dynamic range so that all seven time points can be simultaneously displayed. An expanded structure set for each cluster and time point is shown in Supplementary Figures S25–S31.

Figure 6.

The evolution of the RNA folding landscape in time after mixing with sufficient MgCl₂ to induce the native state. (A) Landscapes for each time point are shown, along with representative structures populating specific regions on these maps. (B) Fits achieved to the time-resolved data are assessed by calculating the reduced chi-square for each condition.

In the low salt starting condition for the TR series (20 mM KCl), the majority of selected EOM structures represent extended states. This landscape closely resembles the corresponding static point. Minor differences result from slight structure factor present in the time-resolved SAXS data at this time point, reflecting slight interparticle interference at the higher [RNA] of these studies.

Within 10ms after initiation of folding, dramatic changes to the landscape are already apparent. Although a cluster is visible on the left side of the landscape, a large fraction of EOM-derived structures populate an ill-defined swath of space covering a wide range of R_g and ΔN values (electric blue). Native contacts are sparse within this ensemble: the reduction of ΔN relative to the t = 0 state signals a non-specific (electrostatic) collapse. Surprisingly, no comparable set of structures is found in the ensembles derived from static SAXS experiments. The electrostatically relaxed, non-specifically collapsed states detected in titrations of KCl or MgCl₂ reveal preferred conformations that reflect deep, narrow electrostatic wells (Figure 4A and B). In contrast, few preferred conformations are observed in the ensemble measured 10 ms after mixing. The presence of these transient structures likely explains the distinctive behavior observed in the Kratky plots for the TR series, which is absent from the static data.

From 10 to 30 ms, electrostatically relaxed states funnel to globally compact states with large ΔN. After 30ms, the population coalesces into a single cluster, suggestively co-located in the landscape with the open intermediates observed in the static Mg titrations. These highly stable states feature prominently in the TR landscapes, and persist throughout the remaining time series.

At 100 ms after mixing, the selected structures reveal a dramatic backbone reorganization and another cluster of states appears, which we call the second intermediates. In this cluster, models assume a distinct ‘T’ shape as the P5a helix adopts a more vertical orientation under the molecular core in our representation. Close inspection of structures reveals that a twisting of the backbone between P5a and P5b helices appears to induce this re-arrangement. As a result of this global shift, one pair of helix docking interactions (G164–A139 orange bases) appears primed for association.

The Kratky plots shown in Figure 5D reveal that the subtle expansion reverses at ∼300 ms into folding, when a second compaction is detected. The SAXS profiles that follow this compaction begin to resemble those acquired in 1 mM Mg. The selected structures shift out of the open intermediate cluster, and more heavily weight the second intermediates and new states in the middle of the conformational landscape. Examination of these new models, discussed below, reveals the presence of tertiary contacts, thus we name them ‘specifically collapsed’. States in this region show a bowing of P5c helix towards the molecular core, as the P5b helix becomes more vertical. Such an arrangement places the tandem G-A pairs (orange residues) in close proximity. As a result, this pair likely form first. This re-arrangement simultaneously moves one side of the P5c hinge interaction closer to its partners in P5a (red residues), suggesting cooperative formation of tertiary contacts.

The subsequent transition of this specifically collapsed intermediate to an even more compact state is reflected in the EOM structures selections at 1000 ms. A population of molecules show the P5a and P5b helices docked about the molecular core, with both orange and purple residue pairs formed. Interestingly, the selected models still lack both the P5c secondary structure switch (green pair) and hinge interactions (red pairs) that define the native fold. From its position on the landscape, this state is recognizable as the helix docked state (1 mM Mg static landscape). The occupation of the helix-docked and native conformations at this time point and beyond are evident from the Kratky plots of the raw SAXS curves: a high mid q peak is paired with a downward sloping tail.

From 1000 to 3000 ms, the population shifts to occupy more of the native state, suggesting that the final conformational re-arrangement represents a transition from the helix docked to the native state. This shift may proceed through a concurrent P5c switch (green pairs) and hinge formation (red pairs), as has been previously suggested (43). At the final time-point for these experiments, the native state comprises 15% of the population, consistent with our static measurements and close to the results of NMR studies carried out under similar conditions, as previously discussed (Supplementary Figure S32). The majority of remaining molecules either reside in the helix-docked state or revert to the open intermediate cluster. The distribution of molecules on the landscape for this final time point closely resembles that derived for the static titrations (1D projections are compared in Supplementary Figure S34). While the signal-to-noise in the TR SAXS experiments makes it more challenging to distinguish basis components in SVD analysis, at least three states are required to span the space occupied by the seven time points (Supplementary Figure S33).

Distinct collapse phases reflect interactions with Mg

The application of ensemble methods to analyze SAXS data enriches our understanding of the symbiotic relationship between Mg and RNA: Mg ions sculpt the RNA backbone into structures that precisely position the different sides of tertiary contacts for interaction. Notably, although these intermediates are primed for tertiary contact formation, our models suggest that most lack stable tertiary contacts. Strikingly, many of the structures found in Mg titrations are absent from titrations in KCl.

The analysis of time resolved studies, in conjunction with atomistic models, provides additional evidence highlighting the importance of Mg–RNA interactions at all stages of folding. States found in the electrostatically relaxed ensemble have no analogue in static salt titrations. In the next phase of folding (10–100 ms) this unwieldly collection of states funnels rapidly into an open intermediate, collections of structures which are relatively similar to each other. These states are never found in static titrations with KCl, requiring a certain threshold of Mg for formation. Their prevalence in all conditions exceeding this threshold, (and throughout later TR series) suggests that the Mg ions surround RNA in a diffuse manner. The distinct conformations of helices within these states, coupled with MD computations of Mg ion density around these structures (see Supporting Information, Supplementary Figure S35 and accompanying text), suggests that locally high concentrations of ions within the A-rich bulge and P5c stabilize these intermediates. The emergence of these states early in the folding pathway hints that such interactions are crucial in directing the molecule away from the deep, non-specifically collapsed wells found in the KCl titration, maintaining the RNA in folding competent conformations.

Folding proceeds from this open intermediate through states found at higher [Mg] in static titrations, including the second intermediates, helix-docked and native states. Additional Mg mediated events are therefore required to evolve out of the open intermediates, and induce the specific collapse transition. Atomistic models, selected to recapitulate the SAXS data, suggest that each structural re-arrangement is designed to bring the distant sides of tertiary contacts into closer proximity. Transitions between these distinctly structured intermediates illustrate that large scale conformational re-arrangements occur as a direct result of small scale shifts in the molecular backbone.

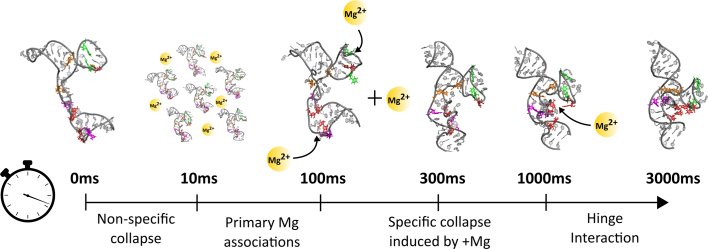
The final conformational switch, from the helix-docked to the native state, occurs at long time points (1000–3000 ms). Although we cannot directly visualize Mg ions in the experiment, simulations suggest that this re-arrangement is triggered by ion occupation of a phosphate lined pocket in the helix docked state, as observed in the P5abc subdomain from the P4P6 crystal structure (52). This pocket is created by the orientations of the P5a, b and c helices in this late stage intermediate. Interestingly, the ion occupying this pocket is partially dehydrated (52), thus would require the highest degree of RNA ordering to capture (36). Figure 7 shows a cartoon summary of the time-scales, kinetic phases, key intermediates and (inferred) Mg associations.

Figure 7.

Summary of the distinct phases of collapse observed on the route to the native state. The key phases of collapse are named and illustrated, along with a cartoon representation of the inferred Mg associations triggering each phase. Mg ions are schematically depicted as orange spheres; arrows suggest their suspected interaction regions with RNA.

CONCLUSION

The combination of TR- and static SAXS, ensemble decomposition and atomistic structures generated by MD simulations has elucidated an intricate folding landscape for an RNA three helix junction. This approach grants a wide description of RNA folding for this ubiquitous structural motif, revealing an array of intermediates, their roles in the folding pathway, and suggests a complex interplay of tertiary contact formation and distinct collapse phases with Mg²⁺ associations. Given the modularity of RNA folding, the themes we have outlined in this work are likely echoed in the folding of many other RNAs.

DATA AVAILABILITY

The SAXS data along with analysis and metrics is deposited in the SASBDB under accession codes: SASDC74, SASDC94 SASDCA4, SASDCB4, SASDCC4, SASDCD4 and SASDCE4 for the time-resolved data and SASDCF4, SASDCG4, SASDCH4, SASDCJ4, SASDCK4, SASDCL4 and SASDCM4 for the static data.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [R01-GM085062 to L.P. and R.E., R01-GM059796 to R. E., R35-GM122514 to L.P.]; National Science Foundation through a Science and Technology Center [1231306 to L.P.]; Welch Foundation [F-1896 to R.E.]; AD181 faculty research grant (to S.K.); S.K. acknowledges the NYU Abu Dhabi High Performance Computing Center for computational resources; Cornell High Energy Synchrotron Source (CHESS), National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF [DMR-1332208]. Funding for open access charge: National Institutes of Health.

Conflict of interest statement. None declared.