On the importance of negative controls in viral landscape phylogeography

Abstract

Phylogeographic reconstructions are becoming an established procedure to evaluate the factors that could impact virus spread. While a discrete phylogeographic approach can be used to test predictors of transition rates among discrete locations, alternative continuous phylogeographic reconstructions can also be exploited to investigate the impact of underlying environmental layers on the dispersal velocity of a virus. The two approaches are complementary tools for studying pathogens' spread, but in both cases, care must be taken to avoid misinterpretations. Here, we analyse rice yellow mottle virus (RYMV) sequence data from West and East Africa to illustrate how both approaches can be used to study the impact of environmental factors on the virus’ dispersal frequency and velocity. While it was previously reported that host connectivity was a major determinant of RYMV spread, we show that this was a false positive result due to the lack of appropriate negative controls. We also discuss and compare the phylodynamic tools currently available for investigating the impact of environmental factors on virus spread.

1. Introduction

In recent years, phylogeographic inference has become a routine tool for analysing the history of spread in virus epidemics (Bloomquist, Lemey, and Suchard 2010; Faria et al. 2011; Pybus, Tatem, and Lemey 2015; Holmes et al. 2016; Baele et al. 2017). In part, this has been stimulated by computationally efficient implementations of different diffusion models in the popular Bayesian phylogenetic software BEAST (Lemey et al. 2009, 2010). A large number of studies have employed these models to perform either discrete (e.g. Su et al. 2015; de Bruycker-Nogueira et al. 2016; Al-Qahtani et al. 2017; Magee, Suchard, and Scotch 2017) or continuous (e.g. Torres et al. 2014; Groseth et al. 2015; Streicker et al. 2016) phylogeographic reconstruction of virus epidemics.

The discrete diffusion model requires an a priori and often arbitrary grouping of locations that, although sometimes relevant (e.g. when considering virus movements across larger or even at global scales), often represents an unrealistic or oversimplified division of the space in which virus spread is reconstructed. In addition, sampling bias is a strong limitation of the discrete phylogeographic approach (De Maio et al. 2015; Baele et al. 2017): over- and under-sampling will affect estimates of transition rates between locations, hence impacting ancestral reconstructions. Finally, the restriction that all ancestors of the sampled viruses can only have existed at the sampled locations can further limit the realism of reconstructed phylogeographic processes. For these reasons, the continuous phylogeographic approach, in which latitude and longitude changes are modelled as a (relaxed) bivariate Brownian diffusion process, can provide a more realistic alternative. On the other hand, the continuous approach remains restricted to dispersal processes that maintain some relationship with geographic distance. This may not be the case for human viruses, such as influenza migration at the global scale, which has been demonstrated to follow air transportation (Lemey et al. 2014).

Landscape genetics is a general field that ‘aims to inform on the interactions between landscape features and evolutionary processes’ (Manel and Holderegger 2013). In practice, classical landscape genetic approaches often consist in comparing genetic clusters or inter-individual/population distances with environmental factors to investigate their impact on gene flow. By comparison, we here define ‘landscape phylogeography’ as a subfield of landscape genetics, which specifically aims to relate phylogenetically informed dispersal frequency or velocity to environmental factors. Yet, landscape phylogeographic analyses are most often applied to rapidly evolving organisms such as pathogens, and especially viruses, that allow for time-calibrated phylogenies to infer the dispersion history (see also Fountain-Jones et al. 2018 for a more global review of what they term ‘eco-phylogenetic’ methods). In this context, and bearing their specific limitations in mind, discrete, and continuous phylogeographic approaches represent complementary tools for studying the impact of environmental factors on virus spread. Specifically, with the recently introduced generalised linear model (GLM) parameterisation of the discrete phylogeographic model available in BEAST (Lemey et al. 2014), it is possible to jointly estimate the spread history and the relevance and contribution of potential predictors to the ‘transition frequencies’ among discrete locations. For continuous phylogeographic reconstructions, posterior trees can be mapped in a geographical context to investigate the impact of underlying environmental rasters on the virus dispersal velocity (Dellicour, Rose, and Pybus 2016; Jacquot et al. 2017). However, it is imperative to take cautionary measures in landscape phylogeographic approaches. For instance, we here argue that it is important to include appropriate negative controls in landscape phylogeographic testing. The present study specifically focuses on the importance of such negative controls in order to avoid false positive results.

Recently, Trovão et al. (2015) presented a comprehensive study of the history of rice yellow mottle virus (RYMV) spread. RYMV is a single-stranded RNA virus classified within the Sobemovirus genus (Truve and Fargette 2011) and responsible of one of the economically most important plant diseases in Africa (Abo, Sy, and Alegbejo 1998). RYMV is transmitted by various biotic and abiotic means, but there is no evidence of seed-borne transmission (Bakker 1974; Traoré et al. 2009). The natural host range of RYMV is limited to the two cultivated rice species (Oryza sativa and O. glaberrima), some wild rice species (O. barthii and O. longistaminata) and a few wild grasses (Konaté, Traoré, and Coulibaly 1997). RYMV is a fast evolving virus (Fargette et al. 2008) and its diversity has a marked geographical distribution that is not blurred by repeated long-range movements (Abubakar et al. 2003). Because of the restricted host range and the limited mobility of its biotic transmission vectors (Bakker 1974) it has been suspected that the intensification of rice cultivation underlies the RYMV emergence, a hypothesis that was further reinforced by field surveys (Traoré et al. 2009).

Trovão et al. (2015) used both the discrete and continuous phylogeographic models to reconstruct the RYMV dispersal history in Africa. In addition, they also applied the GLM extension of the discrete phylogeographic model to study the impact of several factors on the dispersal frequency between countries. Using this approach, they found strong support for host connectivity, i.e. geographic distances scaled by the intensity of rice production (measured as the area harvested per hectare), as an important predictor of RYMV dispersal frequency. In an attempt to assess whether the intensity of rice production also left an imprint on the dispersal velocity of the virus, we were confronted with conflicting results that prompted a more extensive investigation of how environmental factors impacted RYMV dispersal frequency and velocity in West and East Africa. Based on the analysis of both the original and an updated data set of RYMV sequences, we here aim to (1) perform a comprehensive investigation of environmental factors impacting RYMV dispersal frequency and velocity, (2) compare the related discrete and continuous approaches, and (3) discuss the importance of negative controls when analysing the impact of environmental factors on virus spread.

2. Methodology

2.1 The original and extended RYMV data sets

All analyses detailed below were performed on two data sets: the data set analysed by Trovão et al. (2015) and an extension thereof including additional sequences. The Trovão et al. data set was composed of 180 sequences from West Africa and 117 sequences from East Africa. Since the study of Trovão et al., additional time- and geo-referenced RYMV sequences were made available and these were included to arrive at 210 sequences from West Africa and 240 sequences from East Africa. Analysing the Trovão data set allowed a direct comparison with the results reported by Trovão et al., while the extended data set served to investigate the robustness of results to the sampling.

2.2 Discrete and continuous phylogeographic analyses

All phylogeographic inferences were performed using BEAST 1.8.4 (Drummond et al. 2012) and the BEAGLE library (Ayres et al. 2012) to improve computational performance. Discrete and continuous phylogeographic inferences were performed using the same settings previously used in Trovão et al. (2015) and described below. Because of the clear separation between the East and West African lineages (Trovão et al. 2015), the East and West African data were treated as separate partitions that evolve according to independent phylogenies. Accordingly, the discrete and continuous phylogeographic reconstructions were performed for each clade separately (but within the same BEAST analysis). The substitution process was modelled according to the SRD06 parametrisation (Shapiro, Rambaut, and Drummond 2006), and the skygrid model was specified as tree topology prior (Gill et al. 2013). Separate relaxed clock models with rates drawn from an underlying lognormal distribution (Drummond et al. 2006) were fit to both the East and West African clade, but with a shared lognormal mean to optimally use the time signal in both clades. Discrete phylogeographic inferences were performed at the country level using the continuous-time Markov chain process (Lemey et al. 2009) implemented in BEAST. This method reconstructs the dispersion history between discrete locations and infers a posterior distribution of trees whose internal nodes are associated with an estimated ancestral location. Continuous phylogeographic inferences were performed using the relaxed random walk (RRW) diffusion model (Lemey et al. 2010) also available in BEAST. Following Trovão et al. (2015), we used a lognormal distribution to model among-branch heterogeneity in diffusion velocity. This continuous character trait mapping allows to reconstruct the dispersal history in a continuous space and generates a posterior distribution of trees whose internal nodes are associated with geographic coordinates. Markov chain Monte Carlo analyses were run for 500 million and 1 billion iterations for the discrete and continuous phylogeographic inference, respectively. The chains were sampled every 100 000 generations, and the first 10 per cent of the samples in each chain was removed as burn-in. BEAST XML files corresponding to these analyses are available as Supplementary Files S1 and S2. For both methods, maximum clade credibility (MCC) trees were obtained with TreeAnnotator 1.8.4 (Drummond et al. 2012) and convergence and mixing properties were inspected using Tracer 1.6 (http://tree.bio.ed.ac.uk/software/tracer).

2.3 Landscape analyses: GLM and post hoc approaches

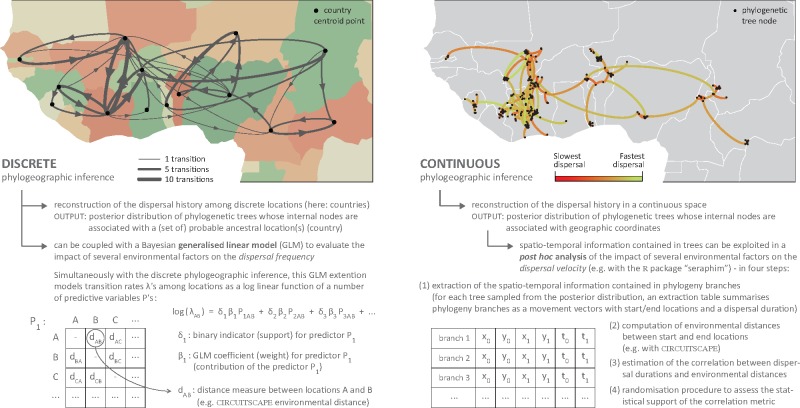
Following Trovão et al. (2015), the contribution of potential predictive variables of RYMV spread was first assessed with the GLM extension of the discrete phylogeographic method implemented in BEAST (Lemey et al. 2014), to which we further refer as the ‘discrete-GLM’ approach. As summarised in Fig. 1, this results in estimates of the contribution (the GLM coefficient) and statistical support (expressed by a Bayes factor (BF) calculated from inclusion probability estimates) for each predictive variable included in the model. By identifying the combination of predictors that best explain the transition rates between discrete locations, the discrete-GLM approach allows to investigate the impact of environmental factors on the dispersal ‘frequency’.

Figure 1.

Schematic overview of the discrete and continuous phylogeographic approaches that can be used to study the impact of environmental factors on a viral epidemic. Dispersion histories reported in both cases were informed by a consensus tree inferred from the discrete and continuous phylogeographic analyses based on the initial data set of Trovão et al. (2015) for West Africa (180 sampled RYMV sequences; see Section 2 for further details).

Secondly, we also used a post hoc univariate approach that capitalises on the outcome of continuous phylogeographic reconstructions (Fig. 1; Dellicour, Rose, and Pybus 2016), which became available only after the study by Trovão et al. The first step in this ‘continuous post hoc’ approach is the extraction of the spatio-temporal information contained in trees sampled from the posterior distribution. After this step, each phylogenetic branch can be treated as a distinct movement vector associated with start/end locations and a dispersal duration (Pybus et al. 2012). In a second step, an environmental distance is computed for each phylogenetic branch and environmental factor considered in the study. Environmental distances can be computed with different path-taken models such as the least-cost path algorithm (Dijkstra 1959) or with circuit theory (McRae 2006, McRae et al. 2008; see below). In a third step, we can then estimate the correlation between phylogeny branch durations and associated environmental distances. The final step consists in a randomisation procedure to assess the support of the correlation statistic. This procedure is based on the randomisation of tree branch positions while maintaining the tree topology and the inferred location of the most ancestral node (Dellicour, Rose, and Pybus 2016). In addition, randomisations are performed within a minimum convex hull defined by all node positions and while avoiding that nodes fall in non-accessible cells (e.g. sea areas). These four steps are implemented in R scripts available within the package ‘seraphim’ (Dellicour et al. 2016). As the post hoc analysis tests the correlation between dispersal durations and environmental distances, it explicitly investigates the impact of tested environmental factors on the dispersal ‘velocity’. We consider this post hoc approach as univariate because, contrary to discrete-GLM approach, each environmental factor is treated individually in the current implementation.

2.4 Computing environmental distances with circuit theory

All environmental distances were computed with the programme CIRCUITSCAPE 4.0.5 (McRae 2006; McRae et al. 2008) that implements a method based on circuit theory. This method treats environmental rasters as grids of electric resistance or conductance to study the connectivity among locations. In this framework, pairwise connectivity is approximated by estimating pairwise electric resistance measures between locations. When the underlying environmental raster is treated as a resistance grid, raster cells associated with higher values are less permeable to movement. On the opposite, if the raster acts as a conductance grid, the same cells will be more permeable to movement. For the continuous post hoc approach, pairwise effective resistances were thus computed between point locations defined by the start and end node coordinates of each phylogenetic branch. In order to estimate the resistance between two nodes, one of the two node locations is arbitrarily connected to a 1-A current source and the other one is connected to ground. For the discrete-GLM approach, pairwise resistances were computed between discrete locations, which are defined, in the context of this study, as the different countries in the West and East African study areas. Because multiple samples may have been obtained at different locations within a specific country, a single resistance distance between two countries was computed as the average distance between all possible pairs of locations from the different countries, thus treating all sampling locations from one country as current sources and all sampling locations from the other country as ‘ground’ (Supplementary Fig. S2). Note that for the GLM analyses, the environmental distances were all log-transformed and standardised prior to their inclusion in the model (Lemey et al. 2014).

2.5 Including a ‘null’ raster in both approaches

In order to study the impact of a particular environmental variable on the dispersal frequency and velocity, we consider two different types of rasters: the environmental rasters and their corresponding ‘null’ rasters that serve as negative controls. The null raster is a copy of the environmental rasters but with a value of ‘1’ assigned to all cells (Supplementary Fig. S2). To allow a comparison with the null raster, all the cell values of the environmental rasters were preliminary increased by ‘1’. This also ensures that the absence of the environmental feature in a given cell is coded by the minimum value of ‘1’ in both environmental and null rasters. When computing pairwise environmental distances on the null raster, there is no environmental heterogeneity impacting the connectivity among locations (Supplementary Fig. S2). Therefore, on this homogeneous raster, only the spatial distance between sampling locations impacts the pairwise resistance values, which are thus correlated with geographic distances. The interest here is to obtain pairwise geographic distance measures as estimated with circuit theory, i.e. environmental distances computed in the absence of environmental heterogeneity. Indeed, pairwise distances computed on a null raster can be more realistic measures of spatial connectivity than simple great-circle geographic distances for two reasons: (1) movements are not allowed across inaccessible areas (coded with no-data value in the null raster), and (2) by accommodating uncertainty in the route taken, the path model based on circuit theory integrates the contribution of several possible pathways.

In the discrete-GLM approach, we include pairwise distances computed on the null raster as an additional predictor. This allows to directly compare the relevance and effect of the environmental rasters with their corresponding null raster, and also avoids interpretation difficulties. If the null raster distances are not included, it is difficult to unambiguously attribute a potentially significant impact of an environmental factor to the model used to compute distances on environmental rasters or to the environmental raster’s heterogeneity.

For the continuous post hoc approach, environmental distances computed on the null raster were used to estimate the correlation statistic Q = R²_env − R²_null, where R²_env is the coefficient of determination obtained when branch durations are regressed against environmental distances computed on the environmental raster, and R²_null is the coefficient of determination obtained when branch durations are regressed against environmental distances computed on the null raster. An environmental factor can only be considered as potentially explanatory if both its distribution of regression coefficients and associated distribution of Q values are positive (Jacquot et al. 2017). Indeed, negative regression coefficients indicate that branch durations are negatively correlated with environmental distances, and negative Q values indicate that considering environmental distances computed on the environmental raster rather than on the null raster does not improve the linear regression fit. The statistical support for the Q distribution was therefore only tested (with the randomisation procedure described above) when at least 90 per cent of the estimated Q values were positive. In that case, each of the trees sampled from the posterior distribution was randomised once to generate null distributions of Q values that can be compared directly with the posterior distributions of estimated Q values. As described in Dellicour et al. (2017), each estimated Q value (Q_estimated) was then compared with its corresponding randomised value (Q_randomised) to compute a BF support. Such a support for a particular environmental factor was approximated by the posterior odds that Q_estimated > Q_randomised (see Dellicour et al. 2017 for further details). As described in the scale of interpretation of BF’s defined by Kass and Raftery (1995), BF values higher than three and twenty can be, respectively, considered as ‘positive’ and ‘strong’ evidences of the statistical significance of Q_estimated.

2.6 The tested environmental factors

Following Trovão et al. (2015), we tested as environmental factor the spatially disaggregated rice production (area harvested in hectares) obtained using the spatial production allocation model (HarvestedChoice 2011). We evaluated both the rice harvested area as estimated in 2000 and in 2005 and a log-transformed version of this raster. In addition to the rice harvested area (Fig. 2), we also tested the impact of additional environmental factors: elevation, annual mean temperature, annual precipitation, and the main rivers on the two study areas (Supplementary Fig. S1; see Supplementary Table S1 for the source of original raster files). Rice harvested area rasters as well as rasterised main rivers were here tested as potential conductance factors, meaning that raster cells associated with relatively higher rice harvested area values are more permeable to movement. For the main rivers raster, a value equal to (1+k) was assigned to each cell crossed by a main river. We tested three different values for the parameter k: 10, 100, and 1,000. As the raster cells that are not crossed by a main river were assigned a uniform value of 1, k thus defines the additional conductance associated with raster cell crossed by a main river (see Laenen et al. 2016 for a similar approach). The other environmental factors (elevation, temperature and precipitation) were tested once as potential resistance and once as potential conductance factors, which is a cautious approach when no obvious prior assumption can be made about the impact of an environmental factor on the dispersal velocity. The null raster was treated as a resistance factor but, because of its uniformity, the same results would be obtained if treated as a conductance factor.

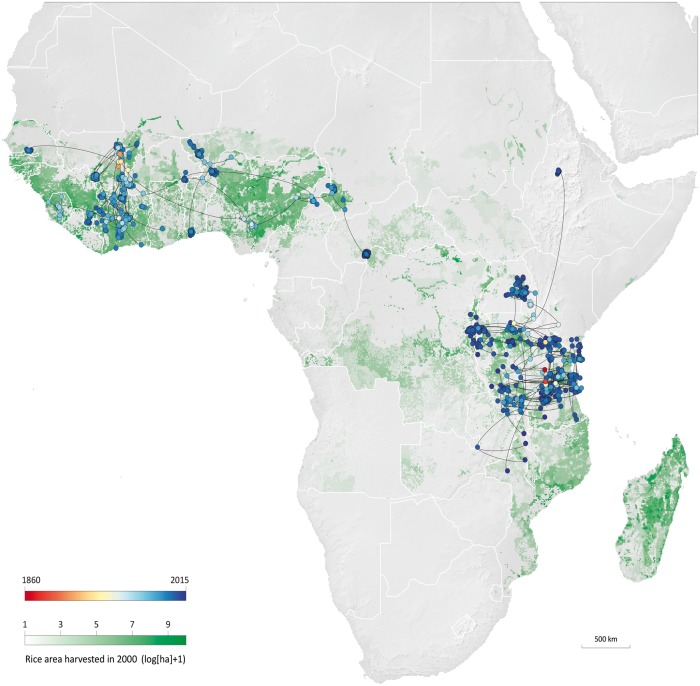
Figure 2.

Consensus trees estimated from the continuous phylogeographic reconstructions of the RYMV dispersal in West and East Africa, and which were based on the updated data set made of 210 and 240 RYMV sequences, respectively. The MCC consensus trees are superimposed on a raster of rice harvested areas and tree nodes are coloured according to their time of occurrence.

To explicitly investigate the impact of including a negative control, the following combinations of environmental factors were tested with the discrete-GLM approach: (1) the great-circle geographic distances and the environmental distances computed on the rice harvested area in 2000, (2) environmental distances computed on the null raster and the raster based on rice harvested area in 2000, (3) the great-circle geographic distances and the environmental distances computed on the null and rice harvested area in 2000 rasters, (4) the great-circle geographic distances and the environmental distances computed on the null and log-transformed rice harvested area in 2000 rasters, and (5) the great-circle geographic distances and the environmental distances computed on the null and rice harvested area in 2005 rasters. We note that in this case, pairwise great-circle distances were not computed between country centroid points, but by averaging pairwise great-circle distances between all possible pairs of sampling locations in the two different countries. Finally, we also performed a global GLM analysis involving all the different environmental factors listed above. For the latter analysis, we also included as predictors environmental values either measured at the location of origin or at the destination of each dispersal event.

3. Results and discussion

Continuous and discrete phylogeographic reconstructions based on the extended data set are reported in Fig. 2 and in Supplementary Files S3 and S4, respectively (see Trovão et al. 2015 for corresponding results based on the initial data set). Results for the five discrete-GLM analyses focusing on the role of geographic distance and rice harvested area on the spread of RYMV are reported in Table 1. Environmental distances computed on a rice harvested area raster are only identified as a reasonably well supported predictor (BF >15) for West Africa when environmental distances computed on the null raster are not included as a predictor (see the first GLM analysis in Table 1). The BF support for the importance of environmental distances computed on the rice harvested area raster, however, drops below 10 when including more data, and the support becomes negligible in both datasets when the negative control under the form of environmental distances computed on the null raster is included. Instead, pairwise distances computed on the null raster are the only consistently supported predictor. Combined, these results reveal that environmental distances computed on the rice harvested area raster does not represent a better predictor of the transition rates among discrete locations than the corresponding distances computed on the homogeneous null raster. As for the continuous post hoc analyses, the low proportion of positive Q values associated with this environmental raster also indicates that the related environmental heterogeneity is not a better predictor of the dispersal velocity than a homogeneous null raster.

Table 1.

Analysis of the impact of rice harvested areas on RYMV dispersal frequency (based on discrete diffusion inference) and velocity (based on continuous diffusion inference).

Discrete phylogeographic reconstruction + GLM analyses	Data set of Trovão et al. (180 + 117 sequences)				Extended data set (210 + 240 sequences)
	West Africa		East Africa		West Africa		East Africa
	GLM coefficient	BF	GLM coefficient	BF	GLM coefficient	BF	GLM coefficient	BF
1° GLM analysis:
Geographic distance	−0.76 [−1.78, 1.61]	16	0.05 [−3.66, 4.01]	0.3	−0.85 [−1.53, 0.66]	32	−0.15 [−3.82, 3.76]	0.8
Rice harvested area 2000 (C)	−0.47 [−1.62, 1.55]	16.5	−0.18 [−3.56, 3.54]	0.9	−0.39 [−2.55, 2.35]	7.2	−0.49 [−2.74, 2.88]	5.6
2° GLM analysis:
Null raster (R)	−1.09 [−1.4, −0.75]	>99	−0.33 [−3.66, 3.66]	1.2	−1.15 [−1.5, −0.82]	>99	−0.83 [−1.98, 2.34]	13.7
Rice harvested area 2000 (C)	−0.01 [−3.61, 3.84]	0.3	−0.16 [−3.66, 3.52]	0.9	0.03 [−3.59, 3.85]	0.3	−0.07 [−3.66, 3.59]	0.9
3° GLM analysis:
Geographic distance	−0.02 [−3.58, 3.96]	0.6	−0.06 [−3.98, 3.96]	0.3	0.01 [−3.61, 3.90]	0.5	−0.19 [−3.78, 3.77]	0.9
Null raster (R)	−1.06 [−1.4, −0.68]	>99	−0.17 [−3.62, 3.84]	0.9	−1.12 [−1.5, −0.75]	>99	−0.82 [−2.11, 2.01]	16.7
Rice harvested area 2000 (C)	0.01 [−3.89, 3.78]	0.2	0.00 [−3.62, 3.94]	0.6	0.01 [−3.87, 3.75]	0.2	−0.04 [−3.63, 3.75]	0.8
4° GLM analysis:
Geographic distance	−0.09 [−3.91, 3.92]	0.6	−0.02 [−3.85, 3.9]	0.3	−0.03 [−3.67, 3.71]	0.5	−0.10 [−3.64, 3.75]	0.9
Null raster (R)	−0.97 [−2.02, 1.18]	34.8	−0.21 [−3.87, 3.73]	0.8	−1.08 [−1.95, 0.75]	62	−0.77 [−3.26, 2.47]	7.8
Rice harvested area 2000 (log, C)	−0.22 [−3.68, 3.35]	0.9	−0.11 [−3.88, 3.91]	0.6	−0.04 [−3.68, 3.77]	0.7	−0.35 [−3.73, 3.37]	2.1
5° GLM analysis:
Geographic distance	0.00 [−3.62, 3.87]	0.6	−0.04 [−3.74, 3.77]	0.3	−0.02 [−3.8, 3.73]	0.5	−0.13 [−3.85, 3.77]	0.9
Null raster (R)	−1.04 [−1.4, −0.59]	>99	−0.17 [−3.80, 3.78]	0.9	−1.11 [−1.5, −0.74]	>99	−0.73 [−2.67, 2.74]	10.4
Rice harvested area 2005 (C)	0.09 [−3.71, 3.91]	0.3	−0.22 [−3.68, 3.76]	1.1	0.02 [−3.72, 3.76]	0.2	−0.18 [−3.63, 3.63]	1.3
Continuous phylogeographic reconstruction +  post hoc analyses	Data set of Trovão et al. (180 + 117 sequences)				Updated data set (210 + 240 sequences)
	West Africa		East Africa		West Africa		East Africa
	Q statistic	Q > 0 (per cent)	Q statistic	Q > 0 (per cent)	Q statistic	Q > 0 (per cent)	Q statistic	Q > 0 (per cent)
Rice harvested area 2000 (C)	−0.07 [−0.15, 0.05]	11	−0.03 [−0.07, 0.00]	3	−0.11 [−0.2, −0.03]	0	−0.07 [−0.11, 0.02]	6
Rice harvested area 2000 (log, C)	0.02 [−0.04, 0.10]	7	−0.02 [−0.04, 0.01]	17	−0.02 [−0.1, 0.03]	27	−0.01 [−0.06, 0.04]	33
Rice harvested area 2005 (C)	−0.09 [−0.15, 0.00]	3	−0.01 [−0.06, 0.05]	36	−0.13 [−0.2, −0.05]	1	−0.01 [−0.08, 0.05]	45

For GLM coefficients and Q statistics, we report both the median value and 95 per cent HPD interval. ‘BF’ refers to ‘Bayes factor’ and, according to the scale of interpretation defined by Kass and Raftery (1995), BF >3 and >20 can, respectively, be considered as ‘positive’ and ‘strong’ (in bold) evidences of the GLM coefficient or Q statistic significance. ‘C’ and ‘R’ indicate if the considered environmental raster was, respectively, treated as a conductance or resistance factor (see the text for further details).

In the case of the discrete-GLM analyses, it is not straightforward to understand why considering environmental distances computed on the null raster, instead of great-circle geographic distances, has such a large impact on the result. A first important difference between the two measures is that pairwise distances computed with path models such as the least-cost or CIRCUITSCAPE algorithms take inaccessible areas into account. However, there are no pronounced inaccessible areas on the null raster. The second important difference is that CIRCUITSCAPE integrates the contribution of multiple pathways. Therefore, when applied on a null raster, this algorithm does not only account for geographic proximity as computed by Euclidean or great-circle geographic distances. Taking this source of uncertainty into account appears to influence the correlation between the two geographic distance measures (Supplementary Fig. S4): while the correlation remains high, they do not maintain a linear relationship, in particular for short distances.

It is important to underline that these results only indicate that the currently available data does not hold any signal for an impact of rice density on the dispersal frequency and velocity of RYMV spread. As rice crops constitute the primary host of the virus, we still expect their distribution to be a key factor for the presence of the virus. Furthermore, as acknowledged by the authors of this map, the rice harvested area raster is a ‘plausible crop distribution map’ (You, Wood, and Wood-Sichra 2009) that approximates the situation in the field by integrating information from various sources such as production statistics, land use, satellite imagery, or prior knowledge about the spatial distribution. As such, there is little guarantee that it provides a good estimate of the actual rice harvested map in Africa. It would therefore be interesting to use more accurate maps to test the relationship between host density and RYMV dispersal frequency/velocity.

In addition to the five discrete-GLM analyses and the continuous post hoc results reported in Table 1, we also report, in Supplementary Table S2, the results of the analyses involving a larger number of predictors. In a first attempt, this global GLM analysis included three predictors per environmental raster: the pairwise environmental distances computed on the raster, as well as the environmental values measured at the location of origin and at the destination. Yet, due to the important correlation among pairwise environmental distances computed on different rasters, we had to discard most of these predictors to avoid collinearity problems in the GLM analysis. Eventually, and for consistency with the above environmental analysis, among the predictors based on environmental distances, only those derived from the null raster and the rice harvested area rasters were kept (see Supplementary Table S2 for the final list of selected predictors). This extended discrete-GLM analysis further corroborates the importance of incorporating an appropriate null raster as a predictor: for both clades and both data sets, only the negative control had a BF support >20 (or even 10). Consistently, none of the predictors tested with the continuous post hoc approach is associated with a BF support >20 (Supplementary Table S2). We can only note that environmental distances computed on the annual mean temperature raster treated as a resistance factor have an associated BF support of 8.1, which corresponds to a ‘positive’ evidence according to the scale of interpretation of Kass and Raftery (1995). Yet, with a 95 per cent highest posterior density (HPD) interval of [0.00–0.01], the associated Q distribution remains very small, implying that this environmental raster hardly increases the correlation between dispersal duration and environmental distances.

The collinearity problems in the discrete-GLM approach are due to the high correlation among environmental and spatial distances. Collinearity in multiple regressions is a well-known issue in spatial/landscape genetics (e.g. Balkenhol, Waits, and Dezzani 2009; Blair et al. 2013). As reviewed in Prunier et al. (2015), several approaches have been proposed to tackle this problem. The simplest approach, which was used in this study, is to exclude variables based on a threshold value (here 0.7) for Pearson’s correlation coefficient (Dormann et al. 2013). An obvious disadvantage of this approach can be the arbitrariness in deciding which of the highly correlated variables to exclude. Alternatively, computation of orthogonal predictors can be used to obtain derived independent predictors, but their interpretation may be challenging. Finally, commonality analysis, a detailed variance-partitioning procedure (Newton and Spurrell 1967), could represent a promising solution. By decomposing the unique and common contribution of each predictor to the overall model fit, commonality analysis can provide insights for interpreting GLMs in the context of multicollinearity (Prunier et al. 2015). The implementation of commonality analyses or similar approaches represents an interesting perspective to also improve the interpretation of GLM results (Jacquot et al. 2017).

The continuous phylogeographic method employs an RRW model that allows the diffusion velocity to vary among branches, and that is flexible enough to allow an imprint of environmental heterogeneity through diffusion rate heterogeneity. Yet, in the continuous post hoc approach, the phylogeographic reconstruction and environmental factor testing remain separate steps. Consequently, and in order to take into account the uncertainty associated with Bayesian phylogeographic inference, the environmental factors analysis has to be performed on several trees sampled from the posterior distribution. The development of an alternative approach that integrates the landscape analysis within the phylogeographic reconstruction could avoid the computational burden of the post hoc approach. Furthermore, the history of spread and the impact of environmental factors should, ideally, be co-estimated to coherently accommodate estimation uncertainty, allowing for cross-talk between the model components (Vrancken et al. 2015; Gräf et al. 2015) and avoiding the risk of error propagation (e.g. Vrancken et al. 2015; Cuypers et al. 2017). Whereas the discrete-GLM approach can already incorporate time-variable predictors using an epoch extension (Bielejec et al. 2014), another conceptual drawback of the continuous-post hoc approach is that environmental/external factors are assumed to be constant in time, and the incorporation of time-variable predictors (e.g. temperature measures averaged by month) is currently not supported. In the context of the present study, considering the rice harvested area as constant in time was indeed a limiting assumption, which could explain why no significant impact was detected for this environmental factor. Finally, it is important to emphasise that the discrete-GLM and continuous post hoc approaches use different criteria, respectively, the dispersal frequency and velocity, to assess the impact of external factors. The choice of one approach over the other thus depends on the initial research question or, alternatively, both approaches can be used in parallel and in a complementary way. Indeed, it is possible that in some situations a particular environmental factor has an impact on the dispersal frequency but not on the velocity, or vice versa.

In this work, we highlight the importance of including a negative control when investigating the impact of external factors on pathogen spread with the discrete-GLM and continuous post hoc approaches. This negative control is an additional potential predictor that measures pairwise connectivity in the absence of environmental heterogeneity. Its relevance stems from the fact that the connectivity between locations can be more realistically captured by simultaneously considering all possible pathways across a landscape as compared to proportioning the connectivity between locations to the involved pairwise spatial (great-circle) distances. As a consequence, an external factor that does not have an impact on the spread, but for which environmental distances have been computed using an advanced movement model (e.g. the one implemented in CIRCUITSCAPE), can yield a false positive result in the absence of an appropriate negative control. We believe this is the most likely explanation for the support of distances computed on the rice harvested area raster as a predictor for the migration frequency that was reported in Trovão et al. (2015).

Conflict of interest: None declared.