Resurrecting the individual in behavioral analysis: Using mixed effects models to address nonsystematic discounting data

Abstract

Delay and probability discounting functions typically take a monotonic form, but some individuals produce functions that are nonsystematic. Johnson and Bickel (2008) developed an algorithm for classifying nonsystematic functions on the basis of two different criteria. Type 1 functions were identified as nonsystematic due to random choices and Type 2 functions were identified as nonsystematic due to relatively shallow slopes, suggesting poor sensitivity to choice parameters. Since their original publication, the algorithm has become widely used in the human discounting literature for removal of participants, with studies often removing approximately 20% of the original sample (Smith & Lawyer, 2017). Because subject removal may not always be feasible due to loss of power or other factors, the present report applied a mixed effects regression modeling technique (Wileyto, Audrain-Mcgovern, Epstein, & Lerman, 2004; Young, 2017) to account for individual differences in DD and PD functions. Assessment of the model estimates for Type 1 and 2 nonsystematic functions indicated that both types of functions deviated systematically from the rest of the sample in that nonsystematic participants were more likely to show shallower slopes and increased biases for larger amounts. The results indicate that removing these participants would fundamentally alter the properties of the final sample in undesirable ways. Because mixed effects models account for between-participant variation with random effects, we advocate for the use of these models for future analyses of a wide range of functions within the behavioral analysis field, with the benefit of avoiding the negative consequences associated with subject removal.

Delay and probability discounting are widely employed choice paradigms (e.g., Green & Myerson, 2004; Myerson, Green, Hanson, Holt, & Estle, 2003) within the behavioral analysis field. Delay discounting (DD) refers to the reduction in subjective reward value with increases in reward delay, and probability discounting (PD) refers to the reduction in value with increases in the odds against receipt (or decreases in probability). Discounting paradigms are often used to assess individual differences in discounting (e.g., Odum, 2011a), contextual effects on individuals’ performance (DeHart & Odum, 2015; Dixon, Jacobs, & Sanders, 2006; Odum, 2011b), and group-level differences associated with drug abuse (de Wit, 2009; Kirby & Petry, 2004), smoking (Bickel, Odum, & Madden, 1999), pathological gambling (Madden, Petry, & Johnson, 2009), and obesity (Bruce et al., 2011; Weller, Cook, Avsar, & Cox, 2008). Thus, an analysis at the level of both the group and the individual is often desirable.

There are two main types of discounting tasks: adjusting and fixed. In adjusting DD tasks in humans, a participant is presented a series of questions, inquiring whether s/he would prefer a small amount of money soon versus a relatively larger amount later. These questions are used to determine the parameters of a smaller-sooner (SS) reward that equate its value to that of a larger-later (LL) reward. Similarly, PD tasks determine the parameters of a certain-smaller (CS) reward that make its value subjectively equivalent to that of an uncertain-larger (UL) reward. Similar tasks can be used in animals by providing different amounts of food at different delays or odds of occurrence. These tasks yield indifference points as the primary dependent variable. Changes in LL delay (or odds of UL receipt) result in a monotonic function relating the delay/odds to the indifference point.

Fixed DD and PD tasks involve delivering a common set of items to all participants. One of the most common fixed tasks in humans is the Monetary Choice Questionnaire (MCQ; Kirby, Petry, & Bickel, 1999), which delivers a set of 27 items that are specific pairings of amounts and delays (or odds), designed to have set values equating to specific discounting rates. All participants receive the full set of items in a random order so that the participants’ choices do not have any effect on item delivery. Fixed tasks have also been developed for use in animals by delivering fixed pairs of food amounts and delays (or odds) for several trials within a session (Evenden & Ryan, 1996) or for several sessions (Green & Estle, 2003; Marshall & Kirkpatrick, 2013). Changes in food amount, delay, or odds often occur in an ascending or descending order. Typically the dependent variable on the MCQ is the discounting rate associated with a change in preference from SS/CS to LL/UL, but the proportion of LL/UL choices can also be analyzed (Myerson, Baumann, & Green, 2014). In animals, the typical dependent variable is the mean proportion LL/UL choices as a function of amount of, delay until, or odds against LL/UL occurrence.

In both the adjusting and fixed tasks, nonlinear regression models can be used to fit functions to the discounting data to determine how quickly rewards lose value with increases in delay or odds against (e.g., Doyle, 2013). The most common functions that are utilized for this purpose are the hyperbolic (e.g., Myerson & Green, 1995) and hyperboloid (Myerson & Green, 1995). For DD, the hyperbolic function is given in Equation 1; the function for PD is given in Equation 2.

$$V=A/(1+kD)$$ (1)

$$V=A/(1+hƟ)$$ (2)

Here, A is the amount of reward, D is reward delay, Ɵ is odds against, and V is the discounted reward value. The free parameters, k and h, are discounting rates (i.e., slopes) of the hyperbolic functions. The hyperboloid function is identical to the hyperbolic, except for the addition of a sensitivity parameter, S, as an exponent to the entire denominator. The discounting rates from the hyperbolic and hyperboloid functions are usually the target for analyses designed to predict and explain important psychological phenomena at the individual and group level.

Despite its popularity, an underrecognized problem with fitting nonlinear functions to discounting data is the assumption that the functions must be monotonically related to changes in delay or odds. This is, in fact, an issue with a wide array of tasks within the behavioral analysis field in which behavior is measured in response to stimuli occurring along a continuum such as psychophysical functions, generalization gradients, and demand curves in behavioral economics. Within the discounting tasks, functions with random deviations may be flagged as Type 1 nonsystematic functions. Nonsystematic data may also refer to non-decreasing, or Type 2 nonsystematic functions. Nonsystematic functions meeting either of these criteria could justifiably be excluded from the final analysis (Johnson & Bickel, 2008), which may result in upwards of 20% of the data being removed (Smith & Lawyer, 2017). Such exclusion has been justified by suggesting that these patterns are due to careless, random, and/or rule-oriented responding (Johnson & Bickel, 2008). However, Type 1 nonsystematic functions may be due to a single errant data point rather than some inattention to the task. Indeed, some reports that have retained individuals with Type 1 nonsystematic functions in which this appears to be the case (see, for example, Johnson & Bruner, 2013; Lawyer, Williams, Prihodova, Rollins, & Lester, 2010).

Type 2 nonsystematic functions may also imply inattentiveness as the discounting rate approximates zero. However, consistent preference for the larger outcome across LL delays and UL odds may be due to delay or risk insensitivity, which could explain Type 1 nonsystematic data. Delay processing deficits have been shown in schizophrenia, attention deficit hyperactivity disorder, and substance abuse (Allman & Meck, 2012; Barkley, Edwards, Laneri, Fletcher, & Metevia, 2001; Wittmann & Paulus, 2008), such that exclusion of Type 2 nonsystematic functions could reduce our understanding of choice behaviors in these individuals by eliminating many of them from the final sample. Although a primary impetus of psychological science is to identify and explain individual differences in behavior, exclusion criteria such as those proposed by Johnson and Bickel (2008) effectively eliminate idiosyncratic behavior in favor of data that are easier to fit with hyperbolic discounting functions and less likely to inflate error variance estimates in subsequent statistical models conducted on the k- and h-values. The data exclusion due to difficulties in curve fitting indicates that this analytical approach is not well-equipped to handle the wide array of individual differences present in both human and animal data, indicating the need for a fundamental transformation in discounting analyses. While the present report focused on discounting analyses, the proposed analytical framework can apply to a wide array of tasks within the behavioral analysis field, as noted in the General Discussion.

Traditionally, discounting researchers calculate individual’s discount rates (k or h values) via hyperbolic model fitting and then use general linear models (e.g., t-tests, ANOVA, correlation coefficients) to test group differences or correlations of individual differences. However, there are inherent problems with this two-stage approach (Moscatelli, Mezzetti, & Lacquanti, 2012; Young, 2016, 2017). For example, it assumes that all individuals contribute equal weighting, while it is possible (and often likely in adjusting procedures) that different numbers of trials were delivered to different individuals. Accordingly, discount rates may not be as precisely measured in some individuals as in others. This approach also assumes that all participants within groups behaved comparably as the models only compute estimates at the group level and the remaining variance is lumped into the error term. Mixed effects regression models circumvent these issues, as they estimate group effects of the model’s predictors (i.e., fixed effects), while simultaneously accounting for the variance in individual functions via random effects (Bolker et al., 2008; Hoffman & Rovine, 2007; Pinheiro & Bates, 2000; Schielzeth & Nakagawa, 2013). Random effects estimates are computed with respect to both the individual’s data and the population estimates, a technique called partial pooling (Gelman & Hill, 2006). More extreme functions, such as those identified as nonsystematic, are pulled toward the estimated population mean, a process known as shrinkage. Individuals with fewer data points also contribute less weight to the model’s estimates compared to individuals with relatively more data points. Together, these factors reduce the impact of outliers on the fixed effects estimates. Accordingly, individual differences become informative rather than erroneous (Bolker et al., 2008). Given the strength of mixed effects models in handling individual differences, there is considerable motivation to adapt the use of these models for analyzing discounting data (Wileyto et al., 2004; Young, 2017), a strategy that effectively resurrects the individual in discounting analyses of group data. Thus, individual differences can be collectively appreciated while still gaining valuable insight into group effects.

The goal of this report was to assess the treatment of nonsystematic data in mixed effects models. Data were collected using an online version of the MCQ (Kirby et al., 1999), and both PD and DD tasks were delivered to all participants. In addition to examining general model performance, we examined the estimates for nonsystematic individuals to better understand the implications of removing participants based on the Type 1 and Type 2 algorithm proposed by Johnson and Bickel (2008). The results clearly advocate for the adoption of mixed effects models as a preferable tool for analyzing discounting data in future studies.

Method

Participants

The participants were 106 (58 male, 48 female) undergraduate psychology students (mean age = 20; range = 19–34) recruited through the SONA System. They completed the study on line. Students received class credit for participating in the project.

Procedures

Participants were directed to the Qualtrics Survey Software tool (Provo, UT) to complete the informed consent, a demographics form, and the DD and PD tasks. After completion of the survey, participants received a debriefing statement.

Informed consent

All procedures used in this study were approved by the Kansas State University Institutional Review Board (Protocol 8220). At the beginning of the online session, participants reviewed a message of confidentiality. Participants could select “yes” to enter the study or “no” to exit. Participants were reminded of their right to withdraw from the study at any time by closing the survey. They were informed that they would only receive course credit if they completed all the items in the questionnaire.

Demographics

After reading the informed consent disclosure, participants were given demographics questions to ascertain background information including age, gender, years of education, marital status, and socioeconomic status.

Money choice questionnaire

Choice of delayed and probabilistic rewards were accomplished using the MCQ (Kirby et al., 1999). The 27 items and their corresponding k- and h-values are displayed in Tables 1 and 2 for the DD and PD tasks, respectively. There were three questions at each k- or h-value, each with different magnitudes. The items for the two tasks were delivered in a random order with DD and PD items intermixed. The choice options were presented horizontally and centered on the screen. The SS (or CS) and LL (or UL) options were randomly located on the left or right side of the question. Participants could indicate their selection by ticking a radio button next to their preferred choice and then advanced to the next question. At the start of the MCQ, participants received the following instructions:

Table 1.

Individual items for the Monetary Choice Questionnaire (Kirby et al., 1999) used for the delay discounting task. The smaller-sooner (SS) and larger-later (LL) delays were in days. The log k-values are the natural logarithm of the original k-values. The items were delivered in a random order. Items 28–30 were catch trials in which the rewards were both available now but the SS and LL magnitudes differed.

Item	SS Amount	SS Delay	LL Amount	LL Delay	k	log k
1	$34	0	$35	186	0.00016	−8.74
2	$28	0	$30	179	0.0004	−7.82
3	$22	0	$25	136	0.001	−6.91
4	$25	0	$30	80	0.0025	−5.99
5	$19	0	$25	53	0.006	−5.12
6	$24	0	$35	29	0.016	−4.14
7	$14	0	$25	19	0.041	−3.19
8	$15	0	$35	13	0.1	−2.30
9	$11	0	$30	7	0.25	−1.39
10	$54	0	$55	117	0.00016	−8.74
11	$47	0	$50	160	0.0004	−7.82
12	$54	0	$60	111	0.001	−6.91
13	$49	0	$60	89	0.0025	−5.99
14	$40	0	$55	62	0.006	−5.12
15	$34	0	$50	30	0.016	−4.14
16	$27	0	$50	21	0.041	−3.19
17	$25	0	$60	14	0.1	−2.30
18	$20	0	$55	7	0.25	−1.39
19	$78	0	$80	162	0.00016	−8.74
20	$80	0	$85	157	0.0004	−7.82
21	$67	0	$75	119	0.001	−6.91
22	$69	0	$85	91	0.0025	−5.99
23	$55	0	$75	61	0.006	−5.12
24	$54	0	$80	30	0.016	−4.14
25	$41	0	$75	20	0.041	−3.19
26	$33	0	$80	14	0.1	−2.30
27	$31	0	$85	7	0.25	−1.39
28	$21	0	$30	0
29	$39	0	$55	0
30	$56	0	$80	0

Table 2.

Individual items for the Monetary Choice Questionnaire used for the probability discounting task. The log h-values are the natural logarithm of the original h-values. The items were delivered in a random order. CS = certain-smaller; UL = uncertain-larger. Items 28–30 were catch trials in which the reward chances were both 100% but the CS and UL magnitudes differed.

Item	CS Amount	CS Chance	UL Amount	UL Chance	h	log h
1	$34	100	$35	5	0.0016	−6.44
2	$28	100	$30	6	0.0048	−5.34
3	$22	100	$25	10	0.0144	−4.24
4	$25	100	$30	18	0.0432	−3.14
5	$19	100	$25	30	0.1296	−2.04
6	$24	100	$35	47	0.3888	−0.94
7	$14	100	$25	60	1.1664	0.15
8	$15	100	$35	72	3.4992	1.25
9	$11	100	$30	85	10.4976	2.35
10	$54	100	$55	7	0.0016	−6.44
11	$47	100	$50	7	0.0048	−5.34
12	$54	100	$60	12	0.0144	−4.24
13	$49	100	$60	16	0.0432	−3.14
14	$40	100	$55	26	0.1296	−2.04
15	$34	100	$50	45	0.3888	−0.94
16	$27	100	$50	57	1.1664	0.15
17	$25	100	$60	72	3.4992	1.25
18	$20	100	$55	86	10.4976	2.35
19	$78	100	$80	5	0.0016	−6.44
20	$80	100	$85	7	0.0048	−5.34
21	$67	100	$75	11	0.0144	−4.24
22	$69	100	$85	16	0.0432	−3.14
23	$55	100	$75	26	0.1296	−2.04
24	$54	100	$80	45	0.3888	−0.94
25	$41	100	$75	59	1.1664	0.15
26	$33	100	$80	71	3.4992	1.25
27	$31	100	$85	86	10.4976	2.35
28	$21	100	$30	100
29	$39	100	$55	100
30	$56	100	$80	100

“In the task that follows, you will have the opportunity to choose between different amounts of money available after different delays or with different chances. The questionnaire contains about 60 questions, such as the following:

• Would you rather have (a) $10 in 30 days or (b) $2 now

• or

• Would you rather have (a) $5 for sure or $10 with a 25% chance

You will not receive any of the rewards you choose, but you should make your decisions as though you were going to get the rewards you choose.”

In addition to the 27 primary choice items, there were catch trials that assessed magnitude discrimination on the DD and PD tasks (see Tables 1 and 2, items 28–30). These were included as an additional measure for detecting potential nonsystematic performance. The choice task required about 20 min to complete and there was a time limit of 90 min for study completion. If participants did not complete on time, their session timed out and they had to restart the questionnaire from the beginning and complete all items within the 90-min time frame to receive course credit.

Debriefing statement

Participants who completed all items received a debriefing statement in which they were informed that they had completed a study that intended to examine how choices about money relate to other life choices and were then thanked for their participation. They were then provided a link for claiming their course credit.

Modeling Approach

All participants were included in all analyses. The DD and PD questionnaires were analyzed separately and included all choices made to the 27 items. An examination of the catch trials indicated that there were four participants (Pps 91, 95, 102, and 106) in the DD task and seven participants (Pps 31, 38, 40, 48, 67, 95, and 102) in the PD task who made “incorrect” choices by selecting the smaller amount on one or two of the trials. However, performance on catch trials did not predict performance on the other choice trials. Most importantly, catch trial performance was not a reliable predictor of nonsystematic choice behavior, so the catch trials were not included in the analyses.

Computation of k and h-values

The computation of the natural logarithm of the k- and h-values followed the procedure described in Kirby, Petry, and Bickel (1999). Values were computed for each of the three magnitude ranges and the mean log k- or h-value was determined from these values for each participant. When participants made a single transition from SS (CS) to LL (UL) the k-value (or h-value) was the average of the two values surrounding the transition. When participants did not make a transition (i.e., they preferred the SS/CS or LL/UL for all questions), then the k- or h-value was set at the endpoint of the range (either on the SS/CS or LL/UL side). If participants made multiple transitions, a signature of nonsystematic responding, then their k- or h-value was the average of the values surrounding these transitions. The k- and h-values served as reference values for comparison to the mixed effects regression model.

Identification of nonsystematic functions

Each participant was assessed for possible nonsystematic discounting by applying the algorithm proposed by Johnson and Bickel (2008). First, the choices for each participant (SS = 0, LL = 1 for DD; CS = 0, UL = 1 for PD) were averaged across the three questions that assessed each k- or h-value within the DD and PD tasks (one question for each magnitude range; see Tables 1 and 2). The mean proportion of LL (or UL) choices as a function of k- or h-value was used for the determination of nonsystematic discounting. When applied to an adjusting procedure, as in their original article, there are two types of nonsystematic discounting functions that can be identified. Type 1 functions were identified as individuals with any indifference point (after the first one) that was greater than the preceding indifference point by more than 20% of the larger-later reward. For the current data set, because the individual values were the proportion of LL (or UL) choices and could only take limited values between 0 and 1, and because our functions increased as a function of k (or h), we adapted the Type 1 criterion. Individual discounting functions were identified as Type 1 nonsystematic if there was a .33 or greater decrease in the proportion of LL choices between the previous k- (or h-) value and the successive k- (or h-) value. Type 2 nonsystematic functions were identified in the original algorithm as individuals whose behavior did not change appreciably over the choice function. For the adjusting procedure, this involved identifying participants for which the last indifference point was not less than the first indifference point by at least 10% of the larger-later reward. To adapt this criterion, we identified Type 2 functions when the change in the proportion of LL (or UL) choices associated with the largest k- (or h-) versus the smallest k- (or h-) value was less than .33. It is worth noting that the criteria adopted here, out of necessity due to the measurement tool employed, are more liberal than the original algorithm, and thus we would anticipate potentially identifying more nonsystematic participants.

Mixed effects logistic regression models

The raw choice data were analyzed using mixed effects logistic regression models conducted in MATLAB R2016a (The Mathworks, Natick, MA). All 27 choices for each task from the MCQ for all participants were entered into the model and coded as binary variables (SS = 0, LL = 1; CS = 0, UL = 1). Separate models were conducted on the DD and PD tasks. The fixed effects were the k- or-h-values for DD and PD, respectively. The k- and h-values were log-transformed and were entered as both intercept and slope parameters. This is similar to the logistic regression approach espoused by Wileyto et al. (2004; see also Young, 2017), who utilized a two-parameter model with relative magnitude and delay as parameters for a Kirby DD task. We choose to instead enter the k- and h-values to provide better correspondence of the models across the DD and PD tasks. The intercept was set at the middle k- and h-value so that the model’s estimates reflect the mean choice of the LL (or UL) option in the middle of the choice function. For the slope, the estimates for the k- and h-values reflect the steepness of the discounting function, which indicates sensitivity to changes in k or h. Thus, the intercept can be used as an estimate of bias in choice and the slope as an estimate of sensitivity to changes in choice parameters. The intercept and slope were also entered as random effects, so that estimates were computed for each participant as well as for the overall group. The estimates for the participants assess deviations from the group (fixed effects) estimates, and MATLAB supplies test statistics for the degree of deviation. Due to the use of logistic regression, all effect size estimates from the mixed effects models are reported as b-values, which are unstandardized regression coefficients in the form of log odds ratios.

Model correspondence assessments

The random effects parameters from the mixed effects models were assessed for correspondence to the traditional Kirby MCQ measurement by computing a Pearson’s correlation coefficient. Both the intercept and slope from the mixed effects models were correlated with the mean k- and h- values from the DD and PD tasks.

We also conducted assessments of correspondence with the nonsystematic algorithm by examining the test statistics for the random effects (both the intercept and slope parameters) for significant deviations from the overall estimates. Participants were deemed as significantly deviating from the overall estimate if their slope and/or intercept estimate differed significantly from the overall estimates (p < .05). We then assessed the degree to which these estimates of deviation concorded with the algorithm.

Terminology

For simplicity of exposition from here forward, the characterizations of the data using the Kirby computation are referred to simply as “Kirby,” and characterizations from the nonsystematic algorithm are referred to as “Algorithm Type 1” and “Algorithm Type 2.” The estimates (b-values) from the mixed model are referred to as “Model Intercept” and “Model Slope” for the intercept and slope parameters, respectively.

Results

Delay discounting

Based on the fitting of the algorithm to each participant’s data, there were 32 discounting functions identified as Algorithm Type 1 and 9 identified as Algorithm Type 2. There were 6 functions that jointly met the criteria for Algorithm Types 1 and 2. Thus, there were 35 nonsystematic functions out of the 106 participants, or 33% of the individuals. The incidence of nonsystematic functions is on the high end of what is typically observed (Smith & Lawyer, 2017), most likely due to the use of more liberal criteria than the original algorithm. However, using a more liberal criterion is advantageous to achieving our goal of thoroughly analyzing the full range of potential nonsystematic functions.

Algorithm-Model agreement

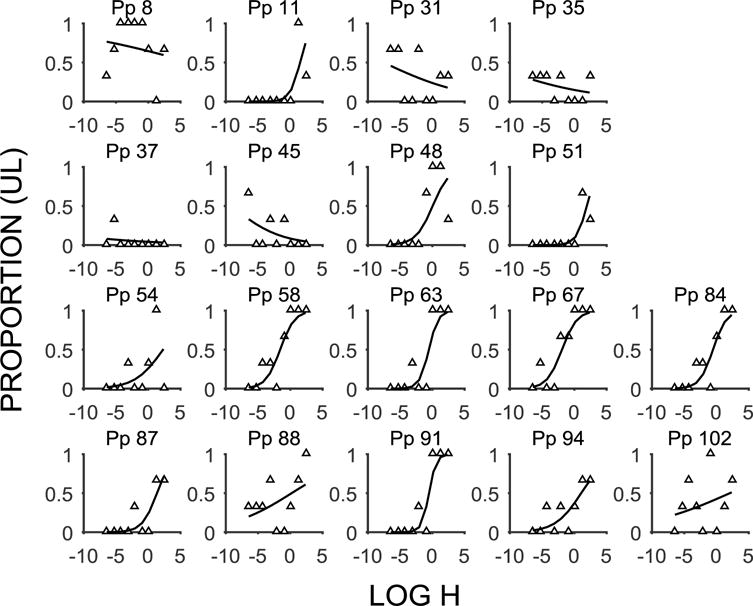
An examination of the random effects estimates indicated that the mixed effects model identified 16 of the Algorithm Type 1 and 6 of the Algorithm Type 2 participants as deviating significantly from the overall estimates on either the intercept or the slope estimate. Figure 1 displays the discounting functions for the Algorithm Type 1 participants and Table 3 displays the corresponding estimates for the intercept and slope (note that Pps 35, 54, 59, and 102 also met the criterion for Algorithm Type 2 functions). There are some clear patterns evident in the estimates. Specifically, the Algorithm Type 1 functions deviated in the Model Intercept alone (Pps 8, 17, 33, and 49), the Model Slope alone (Pp 100), or both estimates (Pps 35, 37, 39, 48, 51, 54, 59, 63, 65, 79, and 102). All these participants had slopes that were flatter than the overall estimate (overall b = 1.93), indicating that they showed impaired sensitivity to changes in k-value. The intercept estimates were less consistent, with some participants making more LL choices (Pps 8, 17, 33, 37, 48, 51, and 63), indicated by positive estimates, and some making more SS choices (Pps 35, 39, 49, 54, 59, 65, 79, 100, and 102), indicated by negative estimates, at the intercept. However, all the participants made more LL choices at the intercept in comparison to the overall estimate (overall b = −2.19). Thus, all participants had flatter functions that were characterized by relatively increased LL choices.

Figure 1.

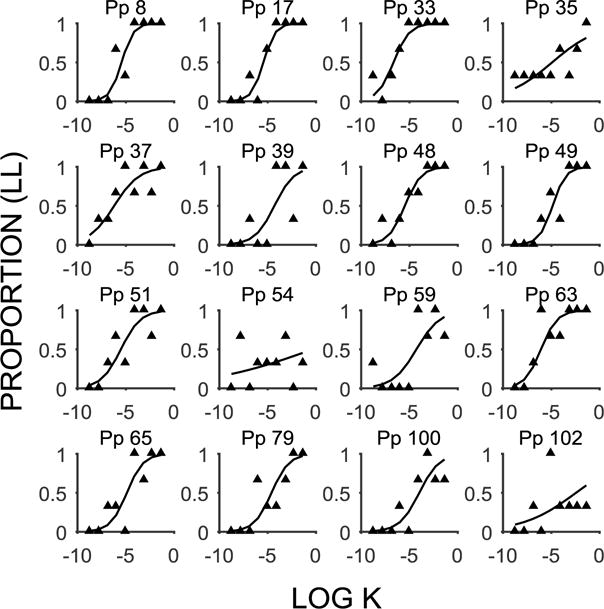
Delay discounting functions (mean proportion of LL choices as a function of the log k-value) for individuals identified as Type 1 nonsystematic by the algorithm and identified as having deviant estimates by the mixed effects model. The filled triangles are the individual data points and the lines are the model fits for individual participants (Pp).

Table 3.

The random effects estimates (b-values) for participants that met the algorithm criterion for Type 1 nonsystematic functions, and had estimates that deviated significantly from the overall estimates in the mixed effects regression model. The mixed effects model included log k-value entered as an intercept and slope parameter for both fixed and random effects determination. For the fixed effects, the intercept indicated that participants were significantly SS-preferring at the middle k-value, t(2847) = −7.08, p < .001, b = −2.19, [−2.80, −1.59]. LL choices increased significantly overall as a function of log k-value, t(2847) = 18.65, p < .001, b = 1.93, [1.73, 2.13]. The b-values for the individuals are the model estimates from the individual fit of the random effects parameters, with positive intercepts indicating more LL preferring and negative intercepts indicating more SS preferring (0 indicates indifference). Higher positive slopes indicate steeper discounting functions. Significant (p < .05) deviations from the overall intercept (−2.19) and slope (1.93) are indicated in bold text and non-significant deviations are indicated in italics.

Participant	Intercept	Slope
8	0.52	1.64
17	0.52	1.63
33	1.88	1.22
35	−0.09	0.42
37	0.84	0.77
39	−0.81	0.99
48	0.44	1.18
49	−0.35	1.46
51	0.39	0.99
54	−0.85	0.18
59	−0.69	0.83
63	1.14	1.20
65	−0.26	1.18
79	−0.57	1.11
100	−1.10	0.98
102	−0.97	0.36

The Type 2 algorithm is designed to detect individuals that are nonsystematic due to a failure to show sensitivity to the task parameters. Figure 2 shows the six participants that met the Algorithm Type 2 criterion and were also deviant in the mixed effects model (see Table 4 for accompanying estimates). All Algorithm Type 2 participants were gauged as deviating significantly on both the Model Intercept and Slope parameters, and all participants had functions that were flatter and relatively more LL preferring compared to the overall estimates (overall b = 1.93 for slope and overall b = −2.19 for intercept). In comparing the estimates with the Algorithm Type 1 results, it seems that the Algorithm Type 2 participants exhibited similar patterns as the Algorithm Type 1 participants, but were more extreme.

Figure 2.

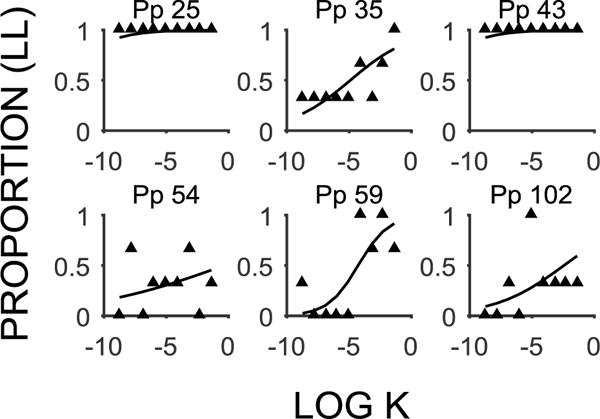
Delay discounting functions (mean proportion of LL choices as a function of the log k-value) for individuals identified as Type 2 nonsystematic by the algorithm and identified as having deviant estimates by the mixed effects model. The filled triangles are the individual data points and the lines are the model fits for individual participants (Pp).

Table 4.

The random effects estimates (b-values) for participants that met the algorithm criterion for Type 2 delay discounting functions, and had estimates that deviated significantly from the overall estimates in the mixed effects regression model. The b-values for the individuals are the model estimates from the individual fit of the random effects parameters, with positive intercepts indicating more LL preferring and negative intercepts indicating more SS preferring (0 indicates indifference). Higher positive slopes indicate steeper discounting functions. Significant (p < .05) deviations from the overall intercept (−2.19) and slope (1.93) are indicated in bold text.

Participant	Intercept	Slope
25	4.36	0.51
35	−0.09	0.42
43	4.36	0.51
54	−0.85	0.18
59	−0.69	0.83
102	−0.97	0.36

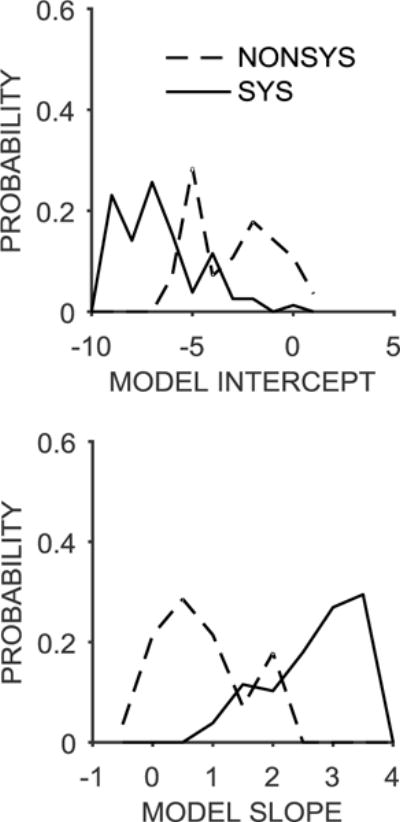
These results suggest that the characterization by the mixed effects model of the Algorithm Type 1 and Type 2 functions do not necessarily qualify as separate categories of discounting function, but instead are more extreme values along the continuum of the intercept and slope estimates. To characterize this continuum, Figure 3 depicts histograms for the model intercepts and slopes. Due to the small number of Algorithm Type 2 participants (and the observation that their estimates showed the same general pattern as the Algorithm Type 1 participants), the all nonsystematic (NONSYS) participants (n = 35) are combined and compared to the remaining participants who had systematic (SYS) functions (n = 71). The distribution of Model Intercepts was shifted to the right for the nonsystematic functions, consistent with the observation of relatively higher incidence of LL choices. There was also a leftward shift in the distribution of Model Slopes (Figure 3, bottom panel), in that the nonsystematic functions had flatter slopes (see also Tables 3 and 4). Here, the shift in the distribution was more pronounced, suggesting that the primary factor discerning the systematic and nonsystematic functions is sensitivity to k, which should reflect the discounting rate. To confirm these patterns, the variable of function type (nonsystematic versus systematic) was added to the original mixed effects regression model as an interaction term with log k and was effects coded (−1 vs. +1, with systematic as the reference group). The nonsystematic participants displayed significantly greater LL choices at the intercept, t(2845) = 3.17, p = .002, b = 1.07, [0.41, 1.73] and had significantly shallower slopes, t(2845) = −8.24, p < .001, b = −0.72, [−0.89, −0.55]. It is worth noting, however, that there is considerable overlap in the distributions of the intercepts and slopes, suggesting that the differences between these sub-groups is due to a distributional shift. Thus, it may be more valuable to characterize individual discounting functions quantitatively accordingly to the slope and intercept rather than attempting to discern different categories of discounting functions.

Figure 3.

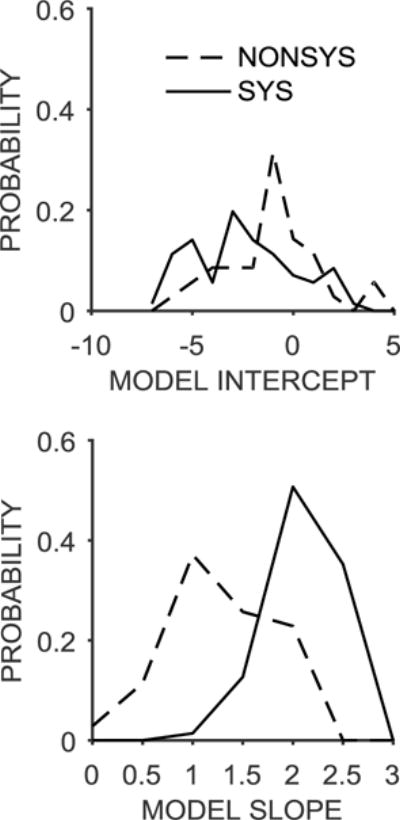
Top: The distribution of model intercept estimates for participants with nonsystematic (NONSYS; Algorithm Type 1 and Type 2 combined) and systematic (SYS) delay discounting functions. Bottom: The distribution of model slope estimates for participants with nonsystematic and systematic delay discounting functions.

Algorithm-Model discrepancies

There were an additional 17 Pps that were identified as Algorithm Type 1 (Pps 11, 14, 18, 28, 36, 44, 55, 58, 67, 72, 80, 87, 92, and 94), Type 2 (Pp 81), or both Algorithm Type 1 and 2 (Pps 62 and 86), but who were not identified by the model estimates as deviating significantly (see Table 5); these participants’ functions are displayed in Figure 4. Many of these functions had one errant data point (Pps 11, 14, 28, 36, 44, 55, 58, 67, 80, 87, 92, and 94), but otherwise displayed a systematic function. The modest noise in the data from these participants did not skew the estimates either for slope or intercept, so their estimates were not deviant. Participants 62, 81 and 86 are interesting as their functions are flatter and more SS preferring, but the model did not detect them as deviating significantly. Because most of participants were SS preferring at the intercept (b = −2.19), the data from these three Algorithm Type 2 participants are more in line with the group than, for example, Pps 25 and 43 (see Figure 2), and therefore were not identified as deviant.

Table 5.

The random effects estimates (b-values) for Algorithm Type 1 and Type 2 delay discounting functions that had model estimates that did not deviate significantly from the overall intercept or slope. The b-values for the individuals are the model estimates from the individual fit of the random effects parameters, with positive intercepts indicating more LL preferring and negative intercepts indicating more SS preferring (0 indicates indifference). Higher positive slopes indicate steeper discounting functions. These participants did not display any significant deviation from the overall intercept (−2.19) or slope (1.93).

Participant	Intercept	Slope
11	−4.04	1.78
14	−2.25	1.59
18	−1.10	1.35
28	−0.97	1.78
36	−5.18	1.81
44	−1.68	1.98
55	−0.97	1.78
58	−3.98	2.01
62	−4.59	1.22
67	−2.58	1.82
72	−1.76	1.24
80	−0.83	1.56
81	−6.26	1.29
86	−3.94	0.98
87	−3.44	1.73
92	−1.22	1.50
94	−2.58	1.82

Figure 4.

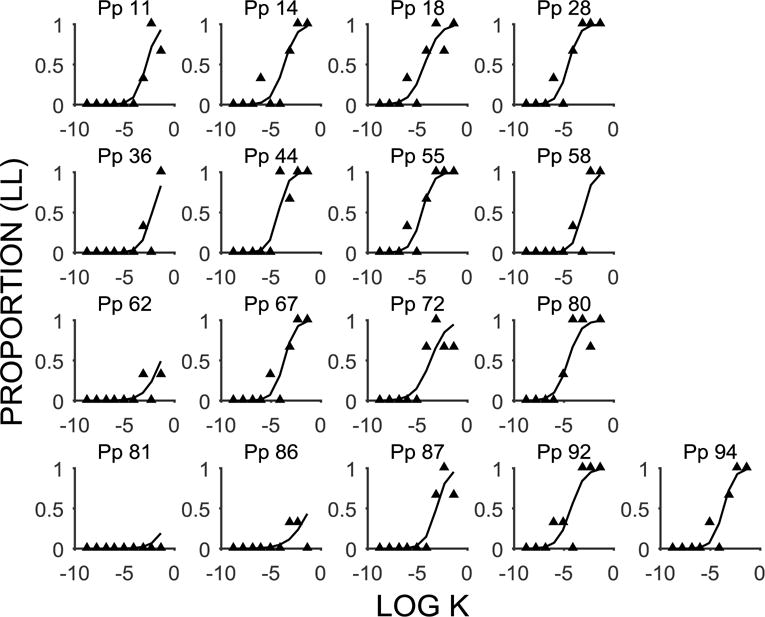
Delay discounting functions (mean proportion of LL choices as a function of the log k-value) for individuals identified as nonsystematic by the algorithm, but were not deviant in the mixed effects model. Participants (Pp) 11, 14, 18, 28, 36, 44, 55, 58, 67, 72, 80, 87, 92, and 94 were identified as Algorithm Type 1, Pp 81was identified as Algorithm Type 2, and Pps 62 and 86 were identified as Algorithm Type 1 and 2. The filled triangles are the individual data points and the lines are the model fits for individual participants.

An interesting and diagnostic model fit is Participant 81, who had a nearly-significant deviation of the intercept (b = −6.26, p = .063), and showed a flat function in the observed data range. The model fit an increasing function that was shifted far to the right and with a flatter than average slope. This is because the mixed effects model uses information from the population estimates to inform the fits to the individuals. The model determined that it is unlikely that the true function for the individual would be flat across the whole discounting space, but rather the function should increase. This is an important feature of mixed effects models that promotes generalization to the population means, in that individual fits are not driven solely by the individual function but are instead informed by a combination of the population estimates as well as the features of the individual (Boisgontier & Cheval, 2016; Moscatelli et al., 2012).

An additional discrepancy between the model and algorithm was that the model identified 31 participants who had either intercept or slope parameters that deviated significantly, but that were systematic functions (data not shown). These participants systematically increased their LL choices as a function of k-value (without any reversals), but slope and/or intercept deviated from the overall estimate. These deviant functions, therefore, could be characterized as variance of interest that we would ultimately wish to account for, explain, and predict with other variables.

Kirby-Model agreement

In addition to assessing the model treatment of nonsystematic data, we examined the correlation between the random effects parameters and the log k-values computed using the Kirby method (see Data Analysis). Figure 5 displays the correlations between the Kirby k and the Model Intercept (top panel) and Model Slope (bottom panel). There was a strong correlation of the Kirby k with the Model Intercept, r = −.97, p < .001, and a weaker but significant correlation with the Model Slope, r = .42, p < .001. Thus, the model estimates, particularly the intercept, were consistent with the Kirby computation. One would expect to see a higher correlation with the intercept because the Kirby computation measures the point of choice transition rather than the slope of the choice function. The intercept provides an index of bias in choices, whereas the slope provides an index of sensitivity to changes in k. The Model Slope was partially independent from the Kirby k-value. Both model estimates are informative and provide somewhat different information in assessing individual differences. This suggests that the use of the two parameters that distinguish bias versus sensitivity may be a significant refinement in the analysis of discounting function, providing a more thorough analysis of the nature of the discounting function and the potential underlying mechanisms that drive choice behavior.

Figure 5.

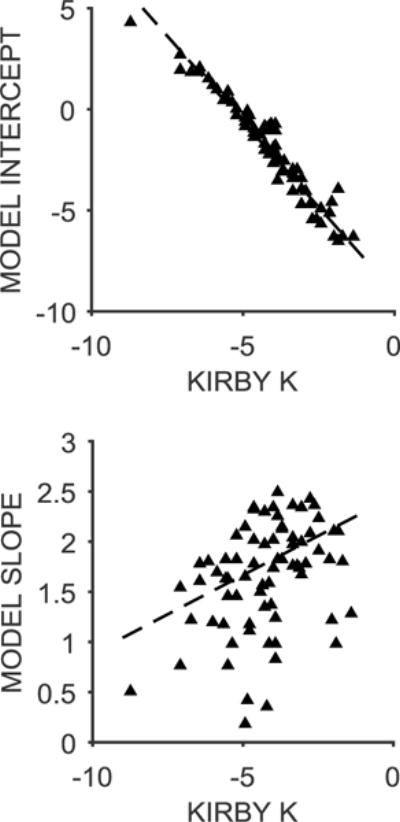
Top: The relationship between log k-value computed using the Kirby method and the random effects model intercept. Bottom: The relationship between log k-value and the model slope. The triangles are data from individual participants and the dashed lines are the best-fitting linear regression fits through the data.

Probability discounting

Analysis of the PD functions utilized the same approach as the DD data. There were 22 discounting functions identified as Algorithm Type 1 and 11 identified as Algorithm Type 2, of which 5 of these were also categorized as Algorithm Type 1. Thus, there were 28 nonsystematic functions, or 26% of the individuals.

Algorithm-Model agreement

An examination of the random effects estimates from the mixed effects model indicated strong agreement between the algorithm and model; the model identified 18 of the 22 Algorithm Type 1 participants and all 11 of the Algorithm Type 2 participants as deviant on the intercept and/or the slope estimate. Figure 6 displays the Algorithm Type 1 functions, and Table 6 provides the random effects estimates (note that Pps 31, 35, 37, 45, and 54 also met the criterion for Algorithm Type 2 functions). All but one participant (Pp 8) showed a CS preference at the intercept (indicated by negative estimates), but all participants showed relatively lower CS preference compared to the overall estimate (b = −6.51), indicating that the Algorithm Type I participants were relatively more risk prone. Most participants were deviant in the slope estimates due to having flatter discounting functions compared to the overall estimate, b = 2.49 (Pps 11, 48, 51, 54, 58, 63, 67, 84, 87, 88, 94, and 102), and a few participants (Pps 8, 31, 35, 37, and 45) exhibited negative slopes due to decreasing UL choices as a function of h-value. Participant 91 displayed a slope that was not deviant (although their slope was flatter than the overall estimate), but they were relatively less CS preferring at the intercept compared to the overall estimate. Thus, the Algorithm Type 1 participants were characterized by having flatter (or even slightly negative) discounting functions indicating poor sensitivity to changes in h and were relatively less CS preferring (i.e., relatively more risk prone).

Figure 6.

Probability discounting functions (mean proportion of UL choices as a function of the log h-value) for individuals identified as Type 1 nonsystematic by the algorithm and identified as having deviant estimates by the mixed effects model. The white triangles are the individual data points and the lines are the model fits for individual participants (Pp).

Table 6.

The random effects estimates (b-values) for Algorithm Type 1 participants that had estimates that deviated significantly from the overall model estimates. The mixed effects model included log h-value entered as an intercept and slope parameter for both fixed and random effects determination. For the fixed effects, the intercept indicated that participants had a strong bias for certainty (CS preference) at the middle h-value, t(2846) = −14.26, p < .001, b = −6.51, [−7.40, −5.61]. UL choices increased significantly overall as a function of log h-value, t(2846) = 13.83, p < .001, b = 2.49, [2.14, 2.84]. The b-values for the individuals are the random effects estimates, with positive intercepts indicating more UL preferring and negative intercepts indicating more CS preferring (0 indicates indifference). Higher positive slopes indicate steeper discounting functions, and negative values indicate decreasing discounting functions. Significant (p < .05) deviations from the overall intercept (−6.51) and slope (2.49) are indicated in bold text and non-significant deviations are indicated in italics.

Participant	Intercept	Slope
8	0.79	−0.09
11	−4.52	1.27
31	−0.85	−0.15
35	−1.50	−0.12
37	−2.91	−0.11
45	−1.86	−0.26
48	−1.60	0.77
51	−4.83	1.22
54	−1.99	0.46
58	−0.42	0.90
63	−2.07	1.39
67	−0.10	0.86
84	−1.47	0.98
87	−2.97	0.88
88	−0.47	0.21
91	−2.69	1.79
94	−1.55	0.50
102	−0.60	0.15

Figure 7 shows the 11 participants that met the Algorithm Type 2 criterion and were also deemed as deviant in the mixed effects model (see Table 7 for accompanying estimates). The Algorithm Type 2 participants were gauged as deviating significantly in the slope estimate only (Pps 43, 52, 57, 73, 80, and 90) or in both estimates (Pps 31, 35, 37, 45, 54). All participants had functions that were CS preferring, but relatively less CS preferring than the overall intercept, and had flat or negative slopes. In comparing the estimates with the Algorithm Type 1 results, it seems that the Algorithm Type 2 participants exhibited similar patterns. There were six Algorithm Type 2 participants that did not also meet the criterion for Algorithm Type 1 (Pps 43, 52, 57, 73, 80, and 90). These participants had very flat and CS-preferring functions, with the strongest negative intercept estimates (−5.26), but were still relatively less CS preferring than the overall sample. The model fit the same function to these participants, which was characterized by a modest positive slope, reflecting the influence of the overall population estimates in the model.

Figure 7.

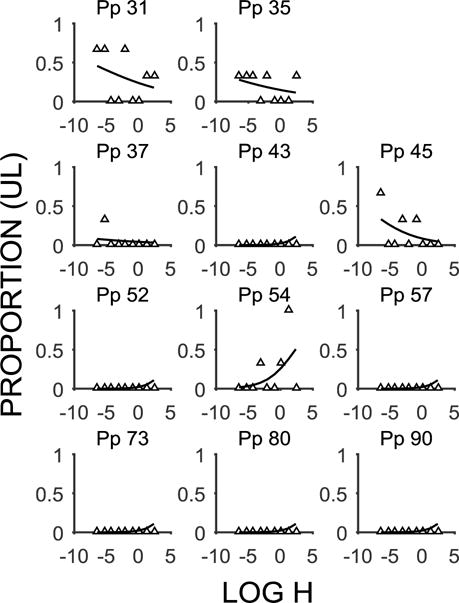
Probability discounting functions (mean proportion of UL choices as a function of the log h-value) for individuals identified as Type 2 nonsystematic by the algorithm and identified as having deviant estimates by the mixed effects model. The white triangles are the individual data points and the lines are the model fits for individual participants (Pp).

Table 7.

The random effects estimates (b-values) for participants that met the algorithm criterion for Algorithm Type 2 probability discounting functions, and had estimates that deviated significantly from the overall estimates in the mixed effects regression model. The b-values for the individuals are the model estimates from the individual fit of the random effects parameters, with positive intercepts indicating more UL-preferring and negative intercepts indicating more CS-preferring (0 indicates indifference). Higher positive slopes indicate steeper discounting functions, and negative values indicate decreasing discounting functions. Significant (p < .05) deviations from the overall intercept (−6.51) and slope (2.49) are indicated in bold text and non-significant deviations are indicated in italics.

Participant	Intercept	Slope
31	−0.85	−0.15
35	−1.50	−0.12
37	−2.91	−0.11
43	−5.26	0.72
45	−1.86	−0.26
52	−5.26	0.72
54	−1.99	0.46
57	−5.26	0.72
73	−5.26	0.72
80	−5.26	0.72
90	−5.26	0.72

As with DD, these results suggest that Algorithm Type 1 and Type 2 individuals’ characterization by the mixed effects model does not constitute a separate category of discounting function, but rather are simply more extreme values along a continuum. Figure 8 shows the distribution of the Model Intercepts (top panel) and Model Slopes (bottom panel) for the systematic (n = 78) and nonsystematic (all Algorithm Type 1 and Type 2, n = 28) participants. The intercepts were shifted to the right for the nonsystematic participants, indicating that they were relatively less CS-preferring and this was confirmed by a main effect in the regression model, t(2844) = 6.36, p < .001, b = 2.34, [1.62, 3.06]. The slope estimates were shifted to left in the nonsystematic participants, indicating flatter discounting functions, t(2844) = −9.37, p < .001, b = −1.16, [−1.40, −0.92].

Figure 8.

Top: The distribution of model intercept estimates for participants with nonsystematic (NONSYS; Algorithm Type 1 and Type 2 combined) and systematic (SYS) probability discounting functions. Bottom: The distribution of model slope estimates for participants with nonsystematic and systematic probability discounting functions.

Algorithm-Model discrepancies

There were four additional Algorithm Type 1 participants that were not identified by the model estimates as deviant; these participants are displayed in Figure 9 and their estimates appear in Table 8. These participants were characterized as having one errant data point that did not skew the estimates of slope or intercept, and otherwise displayed a systematic function. Accordingly, these participants did not have deviant estimates, although they met the criterion for potential exclusion and in many studies, would have been excluded from the final analysis (but see Johnson & Bruner, 2013; Lawyer et al., 2010). An additional discrepancy between the model and algorithm was that the mixed effects model identified 8 participants who had either intercept or slope parameters that deviated significantly from the overall estimates, but that were systematic functions according to the algorithm (data not shown).

Figure 9.

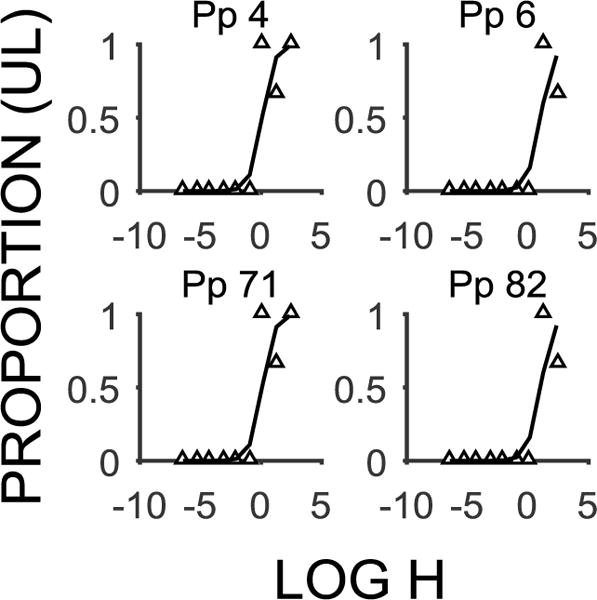
Probability discounting functions (mean proportion of UL choices as a function of the log h-value) for individuals identified as Algorithm Type 1, but who were not deviant in the mixed effects model. All Algorithm Type 2 participants were identified as having deviant estimates. The white triangles are the individual data points and the lines are the model fits for individual participants.

Table 8.

The random effects estimates (b-values) for Algorithm Type 1 delay discounting functions that had estimates that did not deviate significantly from the overall intercept or slope. The b-values for the individuals are the model estimates from the individual fit of the random effects parameters, with positive intercepts indicating more UL preferring and negative intercepts indicating more CS preferring (0 indicates indifference). Higher positive slopes indicate steeper discounting functions. These participants did not display any significant deviation from the overall intercept (b = −6.51) or slope (b = 2.49).

Participant	Intercept	Slope
4	−4.31	2.02
6	−5.79	1.88
71	−4.31	2.02
82	−5.79	1.88

Kirby-Model agreement

Figure 10 shows the correlations between the Kirby h and the Model Intercept (top) and Model Slope (bottom). There was a significant correlation with the Model Intercept, r = −.60, p < .001, and a non-significant correlation with the Model Slope, r = .09, p = .384. Overall, the model intercept was consistent with the Kirby computation, but the model slope was largely independent from the Kirby computation.

Figure 10.

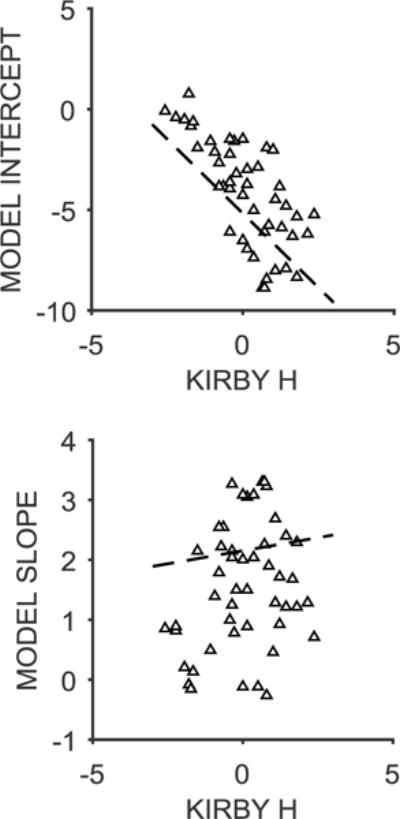
Top: The relationship between log h-value computed using the Kirby method and the random effects model intercept. Bottom: The relationship between log h-value and the model slope. The white triangles are data from individual participants and the dashed lines are the best-fitting linear regression fits through the data.

Internal reliability analyses

One possible reason for the lower correlation between the Model Intercept and the Kirby computation in the PD task may be due to poor internal reliability in responding on that task. To assess this possibility, k- and h-values were determined for each set of 9 questions (i.e., for each magnitude range) within the two tasks, and Cronbach’s alpha was computed to assess internal reliability. This provides a metric of agreement in the participant’s responding to the three sets of questions within each task, with a values greater than .7 indicating good reliability within a task. For the DD task, there was strong internal reliability, a = .91. For the PD task, there was moderately strong internal reliability, a = .81, but the level of agreement was weaker than in the DD task. This may explain the weaker correlation in the PD task as there was more variation in responses, leading to less stability in choice functions overall.

Cross-task analyses

It is possible that there may have been some consistency in the performance across the DD and PD tasks, particularly where the two sets of items were intermixed. To assess this possibility, we first conducted a Pearson’s correlation on the individual k- and h-values. This revealed no significant correlation, r = .05, p = .691. Next, we examined the degree of correspondence between the nonsystematic participants in the two tasks. Of the 18 participants that were identified as nonsystematic (Type 1 or Type 2) in the DD task and who also had deviant estimates, 9 were also identified as nonsystematic and had deviant estimates in the PD task. Of the remaining 17 participants identified as nonsystematic in the DD task, but who had non-deviant model estimates, there was no correspondence with nonsystematic participants in the PD task. Thus, it appears that individuals with non-systematic, deviant functions overlapped to a degree (50% of individuals) in their performance of the two tasks, suggesting that these individuals may possess a common trait that is expressed across both DD and PD tasks.

Discussion

Individuals make choices every day, and suboptimal choice behavior is a hallmark of drug abuse (de Wit, 2009; Kirby & Petry, 2004), smoking (Bickel et al., 1999), pathological gambling (Madden et al., 2009), and obesity (Bruce et al., 2011; Weller et al., 2008). Therefore, understanding DD and PD, especially in populations of interest, is critical. The present report sought to investigate the effectiveness of mixed effects models in analyzing discounting data to effectively resurrect the individual in behavior analysis and resolve underappreciated issues with current analytical approaches in the field. Existing approaches to analyzing choice behavior within DD and PD tasks often result in the removal of around 20% of the participants who are flagged as nonsystematic (Smith & Lawyer, 2017). Therefore, an alternative approach to analyzing DD and PD data is necessary to address the issue of nonsystematic data, hence the reason for exploring mixed effects models in the current study.

Algorithm-model summary and implications

For any response function that should relate systematically to a variable along a continuum, such as discounting functions, there are two primary sources of variance that may potentially be observed – nuisance variance and variance of interest. Nuisance variance presumably emerges from random noise in functions that may be due to inconsistent or biased performance. Variance of interest can then be conceived of as systematic variance that is presumably due to some underlying trait or process that we ultimately want to account for with other variables. The Johnson and Bickel (2008) algorithm was created to provide an objective approach for identifying nonsystematic participants that could potentially be removed from subsequent analyses. The nonsystematic Type 1 algorithm is designed to detect nuisance variance in the data but should not be skewed towards detecting variance of interest. However, the current results indicate a clear bias in the detection of Algorithm Type 1 participants that are reasonably shifted along the same continuum as the Algorithm Type 2 participants (Figures 3 and 8). These findings raise questions as to whether eliminating such participants could systematically change study outcomes by altering the final sample characteristics for analysis. While the application of this type of analysis to more data sets is certainly necessary before drawing general conclusions, the present findings raise potential concerns that eliminating participants based on the nonsystematic algorithm could reduce and/or skew the variation in the final sample for analysis. If this is the case, then the final reported sample would not be adequately representative of the original sample.

A comparison of participants flagged as nonsystematic by the algorithm and who also deviated in the mixed effects model indicated moderate correspondence in DD and strong correspondence in PD. In cases where the nonsystematic participants had deviant model estimates, these participants’ random effects estimates differed systematically from the overall estimates. In both tasks, the algorithm identified participants who had flatter functions, indicating reduced sensitivity to changes in k- or h-values, indicative of lower discounting rates. This is not surprising because noisy Type 1 functions should be flatter on average and the Type 2 algorithm by its definition is designed to detect flatter slopes. Interestingly, the Algorithm Type 1 and 2 participants in the DD task were relatively more LL preferring (less impulsive) whereas in the PD task, the participants were relatively less CS preferring (risk prone). One common factor may be a relatively increased preference for larger rewards (LL and UL) in the nonsystematic participants. The origins of these biases are less obvious as there is no inherent reason why nonsystematic participants should prefer larger rewards. It is possible that these nonsystematic individuals may be performing the task in a slightly different but equally valid way, an interesting possibility for future research.

It is also worth noting that the nonsystematic algorithm identified 17 additional participants in the DD task and 4 additional participants in the PD task that had model estimates that did not deviate significantly from the overall estimates. With the more liberal algorithm criterion used here, these participants would have been identified for potential removal from the study even though their functions were not deviant from the group. This raises a serious issue relating to the use of the nonsystematic algorithm for data removal purposes. There were several participants with single preference reversals. In some cases (e.g., Pps 8 and 17 in DD; Figure 1), the functions were deviant from the group, but in other cases (e.g., Pps 11 and 14 in DD; Figure 4), they were not. The algorithm is insensitive in differentiating between these types of participants even though they are performing differently on the task, although some previous papers have applied a more conservative version of the algorithm and kept these individuals within their samples (Johnson & Bruner, 2013; Lawyer et al., 2010). One advantage of the mixed model is that all participants can be included in the analysis, and deviations in performance due to variance of interest factors or nuisance variance can be accounted for with the fixed and random effects, respectively. This is a more powerful and unbiased approach as the analysis is driven by the properties of the data set rather than a pre-supposition about participant’s performance.

Kirby-model summary and implications

Traditionally, a hyperbolic discounting curve is fit to discounting functions, and the free parameter k (or h) is considered the individual difference parameter that is used in basic and clinical research. Mixed effects models do not determine k (or h), but rather determine an intercept and slope. Intercept represents bias, and slope represents sensitivity to changes in delay (or odds), an analytical distinction that has been adopted in other approaches to fit discounting functions to individuals’ data (see Wilhelm & Mitchell, 2008, 2009). The correspondence between the Kirby k- and h-values and the Model Intercept estimates for individual participants was generally good (Figures 5 and 10). This suggests that the modelling approach largely captured the information provided by the Kirby k- and h-values. The correlation was higher for the DD task, and this may have been due to stronger internal reliability compared to the PD task. Generally, although there were fewer nonsystematic participants in the PD task, individual’s choice behavior was less consistent across the three sets of questions within the task. One possible factor that could affect choice stability in PD is that individuals can show framing effects based on the format of risk-related information (e.g., frequencies, probabilities, percentages) that could potentially affect choice behavior across different ranges of amounts (e.g., Brase, 2002).

While bias was highly correlated with k and h, sensitivity was weakly correlated with k in the DD task and uncorrelated with h in the PD task. This suggests that the slope and intercept detected different aspects of the data. Further, the slope provided additional information that was not fully captured by the traditional Kirby computation of k- and h-values. In fact, participants with shallower slopes were often flagged as nonsystematic and would be removed from analysis if using the algorithm. However, these participants may have instead exhibited poor sensitivity to changes in delay and/or odds, and this could be variance of interest that should be captured and analyzed instead of ignored. Removing these participants could inhibit understanding of populations of interest that may exhibit this choice pattern. Using slope and intercept estimates derived from mixed effects models provides an avenue to include and better understand these individuals. Mixed effects models not only maintain the information provided by the traditional approach, as this is captured by the intercept, but also provide additional information captured by the slope.

Conclusions

Using mixed effects models allows for nonsystematic individuals to remain in the analysis. Thus, even data from nonsystematic individuals can be restored to the forefront of behavior analysis instead of treating these individuals as noise. This can be done in an integrated fashion with group-level analyses. Overall, mixed effects models provide an alternative method of analyzing DD and PD data that can parse out additional aspects of the data (bias and sensitivity) without excluding individuals, thus avoiding the worrisome possibility of skewing, biasing, or reducing important sources of variance within the final sample for analysis. The modeling approach applied here can be adapted for use with a range of different tasks, experimental designs, and dependent variables within the behavioral analysis domain simply by selecting different model distributions and link parameters. Thus, mixed effects models are a powerful new methodology that can be added to the behavior analyst’s tool kit, for applications well beyond discounting choice tasks.

Skinner (1956) objected to the use of group means to create smoothness in data because this ultimately eliminated the individual differences of interest, and obscured any evidence of the factors involved in producing variation among individuals. Harzem (1984, p. 387) later argued that the experimental analysis of behavior should explicitly turn its attention to the “study of individual differences as distinct behavioral phenomena.” It seems that modern statistical techniques have finally paved the way to realize the ability to embrace individuals while also simultaneously analyzing those individuals within the context of the groups to which they belong. Thus, by utilizing mixed effects models, we can truly resurrect the individual in the study of the experimental analysis of behavior.