The equivalent medium of cellular substrate under large stretching, with applications to stretchable electronics

Abstract

The concepts of open, cellular substrates for stretchable electronic systems are of interest partly due to their ability to minimize disruptions to the natural diffusive or convective flow of bio-fluids in advanced, bio-integrated implants. The overall elastic properties, and in particular the stretchability, of such systems are difficult to determine, however, because they depend strongly on the alignment and position of the serpentine interconnects relative to the openings in the cellular substrate, which is difficult to precisely control, even with the assistance of precision stages and visualization hardware. This paper establishes an analytic constitutive model for an equivalent medium for a cellular substrate under finite deformation. Results demonstrate that the elastic stretchability of a serpentine interconnect bonded to this equivalent medium represents a lower-bound estimate for the case of the actual cellular substrate, where the bonding adopts different alignments and positions. This finding provides a simple, conservative estimate of stretchability, which has general utility as an engineering design rule for platforms that exploit cellular substrates in stretchable electronics.

1. Introduction

Recent progress in advanced materials and mechanics design concepts has led to rapid development of diverse types of stretchable electronics technologies in which high performance inorganic electronic materials are exploited to yield systems with impressive levels of mechanical flexibility and stretchability, for wide range of biological and medical applications from eye-like digital cameras (Ko et al., 2008), to devices that integrate with or deploy inside blood vessels (Klinker et al., 2015; Lee et al., 2015) to circuits that softly laminate onto brain (Kang et al., 2016; Zhang et al., 2016), heart (Lu et al., 2015; Xu et al., 2015) and skin (Jang et al., 2016; Koh et al., 2016; Li et al., 2017b; Webb et al., 2015). The fundamental approach is to exploit deformable interconnects to isolate brittle materials from strains associated with overall system deformation, thereby allowing complex combinations of stretching, bending and twisting without fracture or degradation in properties (Avila and Xue, 2017; Chen et al., 2016a; Chen et al., 2016b; Yang et al., 2017).

Significant efforts have been devoted to designs in stretchable devices (Rogers et al., 2010). The most common approach is for all functional components to reside on rigid device “islands” that are electrically and mechanically linked by stretchable/deformable interconnects (Choi et al., 2016; Lu and Yang, 2015; Ma et al., 2017; Song, 2015; Zhang et al., 2015). These interconnects can either adopt an out-of-plane arc shape formed by buckling due to release of substrate pre-strain (Jones et al., 2004; Khang et al., 2006; Lacour et al., 2005; Ma et al., 2016b; Su et al., 2012; Wang et al., 2017), or an in-plane serpentine shape (Gonzalez et al., 2008; Huyghe et al., 2008; Liu and Lu, 2016; Xu et al., 2017; Zhang and Parnell, 2017), to achieve stretchability at the system level. Such systems with islands and interconnects are always integrated on or encapsulated into solid substrates that support and protect the systems when mounted on biological tissues (Li et al., 2017a).

A disadvantages of such an approach is that this type of solid substrate/encapsulation disrupts the natural diffusive or convective flows of bio-fluids (Dou et al., 2015) through the stretchable electronics. Lee et al. (Lee et al., 2017) proposed a bio-inspired honeycomb cellular substrate to achieve high permeability as a solution to this problem. In addition, the cellular substrate has much lower equivalent modulus than a solid substrate made of the same material (Jang et al., 2015), thereby allowing it to achieve much larger stretchability, as discussed in the following.

Stretchability is one of the most important defining properties of such classes of electronics, where the values range from ~30% for epidermal applications (Kim et al., 2011b) and multifunctional integumentary membranes for cardiac measurements and stimulation (Xu et al., 2014; Xu et al., 2015), to ~125% for catheter-based devices for cardiac ablation therapy (Kim et al., 2011a). One major challenge with stretchable electronics that exploit cellular substrates is the difficulty associated with precisely positioning the interconnects and other features of the electronics relative to the cellular substrates. Consequently, the degree of stretchability of the integrated systems cannot be accurately determined because, as shown in this paper, the stretchability depends on the alignment and position of interconnects. This paper aims to establish the lower-bound estimates of the stretchability with respect to all alignments and positions of a representative interconnect on cellular substrate. An analytic constitutive model for the equivalent medium of the cellular substrate under finite deformation is established in Section 2, which agrees well with direct numerical simulations even at 100% applied strain. Section 3 compares the elastic stretchability of the serpentine interconnect bonded to the equivalent medium to that bonded to the cellular substrate with 32 different alignments, positions and directions. It is shown that the elastic stretchability for the equivalent medium is a lower bound of that for the cellular substrate with different alignments. The resulting values represent a simple, conservative estimate of the elastic stretchability, and is useful to the design of stretchable electronics bonded to cellular substrate.

It should be pointed out that there exist extensive studies on mechanics of the cellular structure under infinitesimal deformation (e.g., Chen et al., 2016c; Giboson and Ashby, 1997; Giboson et al., 1982; Hasanyan and Waas, 2016; Mora and Waas, 2007; Okumura et al., 2004; Zhu, 2010), and few studies under finite deformation based on the neo-Hookean constitutive model (e.g., Mihai and Goriely, 2015; Mihai et al., 2017) For stretching beyond 20%, the neo-Hookean models deviate substantially from the direct numerical simulations, therefore fall short for applications to stretchable electronics involving very large stretching (e.g., 100%).

2. An analytic, constitutive model of a cellular substrate under finite deformation

Let E₀ denote the linear elastic modulus of the cell walls. In general, the relation between the nominal stress and engineering strain of the virgin material for the cellular walls can be written as σ = E₀f (ε), where the function f satisfies df/dε∣_ε=0 = 1. This section aims to establish the stress-strain relation of the equivalent medium for the cellular substrate in terms of f and the porosity ϕ of the cellular substrate.

The cellular substrate used in stretchable electronics has high porosity (> 70%) (Lee et al., 2017) to offer both high permeability and stretchability. Figure 1a shows a schematic illustration of the hexagonal cellular substrate with the (center-to-center) cell size d. The cell walls have length $l=d/\sqrt{3}$ and width $\delta =d(1-\sqrt{\varphi })$. For a high porosity such as 80% as in experiments (Lee et al., 2017), the cell wall width δ is much smaller than its length l such that cell walls can be modeled as beams. For uniaxial stretching along the x-direction of the global coordinate system {x, y} (parallel to the cell wall), the basic unit for the cellular substrate, as shown in Fig. 1b, consists of three beams of length l/2 and 120° apart. Let 2P denote the force (per unit thickness along the out-of-plane direction) in the cell wall along x-direction (Fig. 1b), which gives the nominal stress in this wall, normalized by E₀, as ${\widehat{T}}_{\mathrm{h}}=2P/\left(E_0\delta \right)=\widehat{T}/(1-\sqrt{\varphi })$, where T̂ = 2P/(E₀ d) is the nominal stress in the equivalent medium of the cellular substrate, also normalized by E₀. From the uniaxial stress-strain curve σ = E₀ f (ε) of the virgin material for the cell walls, the engineering strain in the cell walls parallel to the stretching direction is

$${\epsilon }_{\mathrm{h}}=f^{-1}\left({\widehat{T}}_{\mathrm{h}}\right)=f^{-1}\left(\frac{\widehat{T}}{1-\sqrt{\varphi }}\right).$$ (1)

Figure 1.

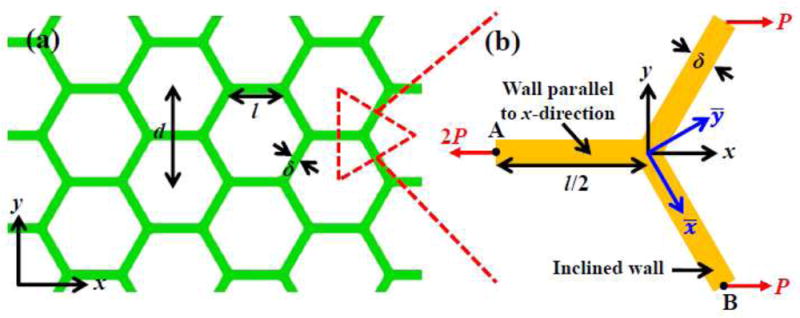
(a) Schematic illustration of cellular substrate, and (b) mechanics model of a unit cell.

Finite element analysis (Lee et al., 2017) shows that the strains in the inclined cell walls (not parallel to the stretching direction x) are much smaller than the strain along the x direction. Therefore, the linear elastic relation is used for the inclined cellular walls. A local coordinate system {x̄, ȳ} is introduced with x̄ axis parallel to an inclined cellular wall, as shown in Figs. 1b and 2. Let S and s denote the arc length along the axis of the inclined cellular wall before and after the deformation, respectively, and φ=φ (s) the angle between the tangent and the x̄ axis (Fig. 2). The shear force Q and axial force N in the inclined cellular wall (Fig. 2) are related to P and φ as

$$N=P\cos (\pi /3-\phi ),$$ (2a)

$$Q=-P\sin (\pi /3-\phi ).$$ (2b)

Figure 2.

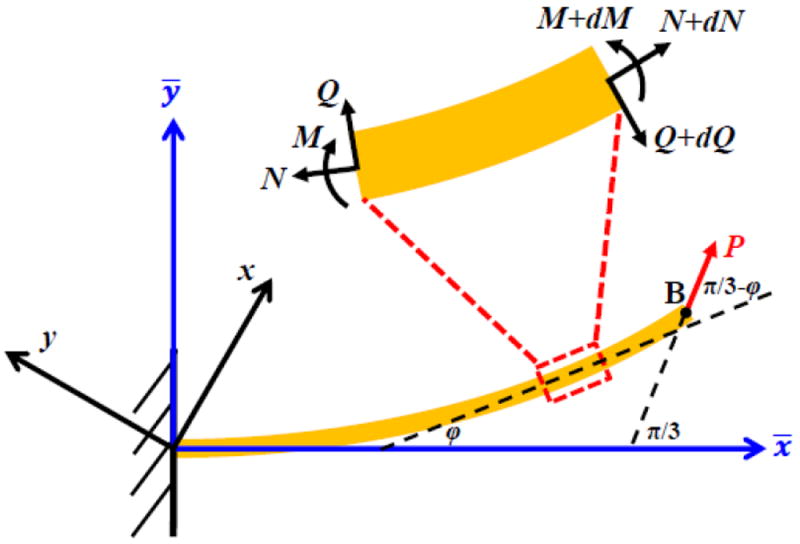
Beam model for the inclined cell wall under finite deformation, and the global and local coordinate systems.

Equilibrium of force in the inclined wall gives (Ma et al., 2016a; Ma and Zhang, 2016)

$$\frac{\mathrm{d}Q}{\mathrm{d}s}-N\frac{\mathrm{d}\phi }{\mathrm{d}s}=0,\mathrm{or}\frac{\mathrm{d}Q}{\mathrm{d}S}-N\frac{\mathrm{d}\phi }{\mathrm{d}S}=0,$$ (3a)

$$\frac{\mathrm{d}N}{\mathrm{d}s}+Q\frac{\mathrm{d}\phi }{\mathrm{d}s}=0,\mathrm{or}\frac{\mathrm{d}N}{\mathrm{d}S}+Q\frac{\mathrm{d}\phi }{\mathrm{d}S}=0,$$ (3b)

where ds and dS are related to the strain N/(E₀δ) in the inclined wall by ds/dS =1+N/(E₀ δ) Fan et al., 2017). Equilibrium of moment M in the inclined wall (Fig. 2) gives

$$Q=\frac{\mathrm{d}M}{\mathrm{d}s},\mathrm{or}\left(1+\frac{N}{E_0\delta }\right)Q=\frac{\mathrm{d}M}{\mathrm{d}S}.$$ (3c)

Substitution of Eq. (2) into the moment equilibrium in Eq. (3c), together with the moment-curvature relation M = E₀ Idφ/dS (Ma et al., 2016a), give

$$\frac{{\mathrm{d}}^2\phi }{\mathrm{d}{S}^2}=-\frac{P}{E_{0}I}\left[\sin \left(\frac{\pi }{3}-\phi \right)+\frac{1}{2E_0\delta }P\sin \left(\frac{2\pi }{3}-2\phi \right)\right],$$ (4)

where E₀ I= E₀ δ³/12 is the bending stiffness of cellular walls. The above equation, together with T̂ = 2P/(E₀d), $\delta =d(1-\sqrt{\varphi })$ and the moment free condition (dφ/dS)∣_S=l/2 due to symmetry, give

$${\left(\frac{\mathrm{d}\phi }{\mathrm{d}S}\right)}^2=\frac{12\widehat{T}}{{\left(1-\sqrt{\varphi }\right)}^3{d}^2}\left\{\cos \left(\frac{\pi }{3}-\phi \right)-\cos \beta +\frac{\widehat{T}}{8(1-\sqrt{\varphi })}\left[\cos \left(\frac{2\pi }{3}-2\phi \right)-\cos 2\beta \right]\right\},$$ (5)

where ${\beta =\pi /3-\phi \mid }_{s=l/2}={\pi /3-\phi \mid }_{s=\sqrt{3}d/6}$ is determined from the following equation obtained by integrating Eq. (5) from S = 0 to S = l/2, i.e.,

$${\int }_0^{\pi /3-\beta }\frac{\mathrm{d}\phi }{\sqrt{\left\{\cos \left(\frac{\pi }{3}-\phi \right)-\cos \beta +\frac{\widehat{T}}{8(1-\sqrt{\varphi })}\left[\cos \left(\frac{2\pi }{3}-2\phi \right)-\cos 2\beta \right]\right\}}}=\sqrt{\frac{\widehat{T}}{{\left(1-\sqrt{\varphi }\right)}^3}},$$ (6)

which gives β in terms of the porosity ϕ and normalized nominal stress T̄. The local coordinates of the end of the inclined wall (Point B in Figs. 1b and 2) can be obtained from φ in Eq. (5), and dx̄/ds= cosφ and dȳ/ds = sinφ, as

$$\left\{\begin{array}{c}{\widehat{\overline{x}}}_{\mathrm{B}\_\mathrm{end}}\\ {\widehat{\overline{y}}}_{\mathrm{B}\_\mathrm{end}}\end{array}\right\}\equiv \frac{1}{d}\left\{\begin{array}{c}{\overline{x}}_{\mathrm{B}\_\mathrm{end}}\\ {\overline{y}}_{\mathrm{B}\_\mathrm{end}}\end{array}\right\}={\int }_0^{\pi /3-\beta }\frac{\left[1+\frac{\widehat{T}\cos (\pi /3-\phi )}{2\left(1-\sqrt{\varphi }\right)}\right]\left\{\begin{array}{c}\cos \phi \\ \sin \phi \end{array}\right\}\mathrm{d}\phi }{2\sqrt{\frac{3\widehat{T}}{{\left(1-\sqrt{\varphi }\right)}^3}\left\{\cos (\pi /3-\phi )-\cos \beta +\frac{\widehat{T}}{8\left(1-\sqrt{\varphi }\right)}[\cos (2\pi /3-2\phi )-\cos 2\beta ]\right\}}}.$$ (7)

The global coordinates {x, y} of the end of the inclined wall, normalized by d, are obtained as

$$\left\{\begin{array}{c}{\widehat{x}}_{\mathrm{B}\_\mathrm{end}}\\ {\widehat{y}}_{\mathrm{B}\_\mathrm{end}}\end{array}\right\}=\left\{\begin{array}{cc}\cos \frac{\pi }{3}& \sin \frac{\pi }{3}\\ -\sin \frac{\pi }{3}& \cos \frac{\pi }{3}\end{array}\right\}\left\{\begin{array}{c}{\widehat{\overline{x}}}_{\mathrm{B}\_\mathrm{end}}\\ {\widehat{\overline{y}}}_{\mathrm{B}\_\mathrm{end}}\end{array}\right\}.$$ (8)

Equation 1 gives the coordinates {x, y} (normalized by d) of the end of the cellular wall parallel to the stretching direction (Point A in Fig. 1a) as

$${\widehat{x}}_{\mathrm{A}\_\mathrm{end}}=-\frac{1}{2\sqrt{3}}\left[1+f^{-1}\left(\frac{\widehat{T}}{1-\sqrt{\varphi }}\right)\right],$$ (9a)

$${\widehat{y}}_{\mathrm{A}\_\mathrm{end}}=0.$$ (9b)

Equations 8 and 9, together with the initial coordinates ( ${{\widehat{x}}_{\mathrm{B}\_\mathrm{end}}\mid }_{\widehat{T}=0}=1/4\sqrt{3}$, ${{\widehat{y}}_{\mathrm{B}\_\mathrm{end}}\mid }_{\widehat{T}=0}=-1/4$, ${{\widehat{x}}_{\mathrm{A}\_\mathrm{end}}\mid }_{\widehat{T}=0}=1/2\sqrt{3}$, ${{\widehat{y}}_{\mathrm{A}\_\mathrm{end}}\mid }_{\widehat{T}=0}=0$), give the equivalent engineering strains of the cellular substrate parallel and perpendicular to the stretching direction (x- and y-direction, respectively) as

$${\epsilon }_{\mathrm{x}\_\mathrm{cellular}}\equiv \frac{{\widehat{x}}_{\mathrm{B}\_\mathrm{end}}-{\widehat{x}}_{\mathrm{A}\_\mathrm{end}}}{{{\widehat{x}}_{\mathrm{B}\_\mathrm{end}}\mid }_{\widehat{T}=0}-{{\widehat{x}}_{\mathrm{A}\_\mathrm{end}}\mid }_{\widehat{T}=0}}=\frac{4({\widehat{x}}_{\mathrm{B}\_\mathrm{end}}-{\widehat{x}}_{\mathrm{A}\_\mathrm{end}})}{\sqrt{3}},$$ (10a)

$${\epsilon }_{\mathrm{y}\_\mathrm{cellular}}\equiv \frac{{\widehat{y}}_{\mathrm{B}\_\mathrm{end}}-{\widehat{y}}_{\mathrm{A}\_\mathrm{end}}}{{{\widehat{y}}_{\mathrm{B}\_\mathrm{end}}\mid }_{\widehat{T}=0}-{{\widehat{y}}_{\mathrm{A}\_\mathrm{end}}\mid }_{\widehat{T}=0}}=­4{\widehat{y}}_{\mathrm{B}\_\mathrm{end}},$$ (10b)

where x̂_{A_end}, x̂_{B_end} and ŷ_{B_end} are obtained from Eqs. 7, 8 and 9, and they depend on the porosity ϕ, normalized nominal stress T̄ and uniaxial stress-strain curve σ = E₀f (ε) of the virgin material. The equivalent Poisson’s ratio of the cellular substrate is defined from the increments of ε_{x_cellular} and ε_{y_cellular} as

$${\nu }_{\mathrm{cellular}}\equiv \frac{d{\epsilon }_{\mathrm{y}\_\mathrm{cellular}}}{d{\epsilon }_{\mathrm{x}\_\mathrm{cellular}}}=-\frac{d{\epsilon }_{\mathrm{y}\_\mathrm{cellular}}/d\widehat{T}}{d{\epsilon }_{\mathrm{x}\_\mathrm{cellular}}/d\widehat{T}},$$ (11)

where dε_{x_cellular}/dT̄ and dε_{x_cellular}/dT̄ are obtained from Eq. 10.

The incompressible Mooney-Rivlin constitutive relation (Mooney, 1940) is adopted in the following to illustrate the analytic constitutive model above. It gives analytically the uniaxial stress-strain curve σ = E₀ f (ε), where f (ε) is given by

$$f(\epsilon )=\frac{1}{15}\left(4+\frac{1}{1+\epsilon }\right)\left[1+\epsilon -\frac{1}{{\left(1+\epsilon \right)}^2}\right],$$ (12)

and the only material property is the linear elastic modulus E₀. Equations (10a) and (11) then give the nominal stress (normalized by E₀) and Poisson’s ratio of the equivalent medium of the cellular substrate, which are shown versus the engineering strain (up to 100%) in Figs. 3a and b, respectively, at different high porosities (ϕ = 50%, 60%, 70%, 80% and 90%). Figures 3a and b also show the stress-strain curve and Poisson’s ratio of the cellular substrate directly obtained from finite element analysis (FEA). It is clear that, for ϕ ≥ 50%, the analytic constitutive model for the equivalent medium of the cellular substrate agrees well with the numerical results without any parameter fitting.

Figure 3.

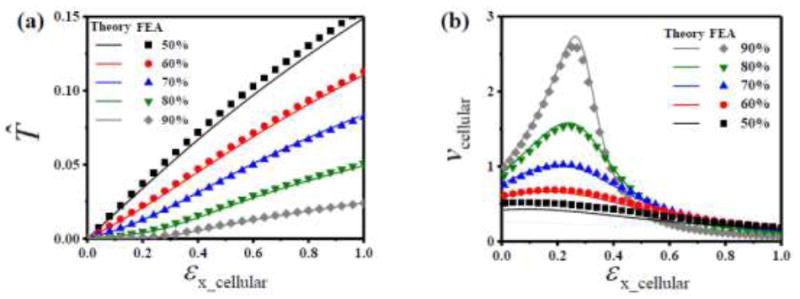
(a) Normalized equivalent nominal stress (T̄) and (b) equivalent Poisson’s ratio (ν_cellular) versus equivalent engineering strain (ε_{x_cellular}) of the equivalent medium for the cellular substrate, obtained by FEA and beam model at different porosities ϕ = 50%, 60%, 70%, 80% and 90%.

The stress-strain curves are obtained by FEA for the cellular substrates stretched along x-, 45° and y-directions, as shown in Fig. 4a. The incompressible Mooney-Rivlin constitutive model is used for the cellular walls. The normalized stress-strain curves of the equivalent medium for the cellular substrate are shown in Fig. 4b. At each porosity ranging from ϕ =50% to 90%, the normalized stress-strain curves are essentially the same for stretching along different directions. Therefore, the equivalent medium for the cellular substrate can be approximated as isotropic, and the analytic model above derived for stretching along the cell wall direction is applicable for any direction.

Figure 4.

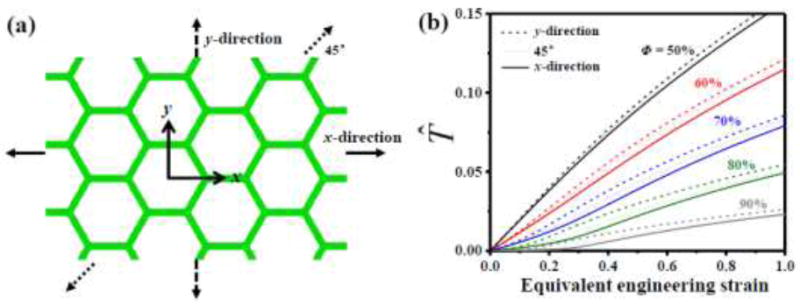
Normalized equivalent nominal stress (T̂) versus equivalent engineering strain of the equivalent medium for the cellular substrate, obtained by FEA, for different stretch directions (x-, 45° and y-directions) and different porosities (ϕ= 50%, 60%, 70%, 80% and 90%).

3. Stretchability of serpentine interconnect on a cellular substrate

For a serpentine interconnect bonded to a cellular substrate, FEA can define the stretchability for three representative shapes that have the same width (w = 50 μm), same cross section [0.1 μm-thick Cu (elastic modulus 119 GPa, Poisson’s ratio 0.34) sandwiched by two 1.2 μm-thick layers of PI (elastic modulus 2.5 GPa, Poisson’s ratio 0.34)], same radius $R=\sqrt{3}d/2=0.45\mathrm{mm}$ for the circular part but different lengths L [1.04 mm (Figs. 5a and d), 0.52 mm (Figs. 5b and e) and 0 (Figs. 5c and f), respectively] of the straight part of the serpentine interconnect, as in Fig. 5. The cellular substrate consists of a 0.35 mm thick layer of PDMS with a porosity ϕ = 80% and cell size d = 0.52 mm, where the elastic modulus and Poisson’s ratio of PDMS are 500 kPa and 0.5 (Lee et al., 2017), respectively.

Figure 5.

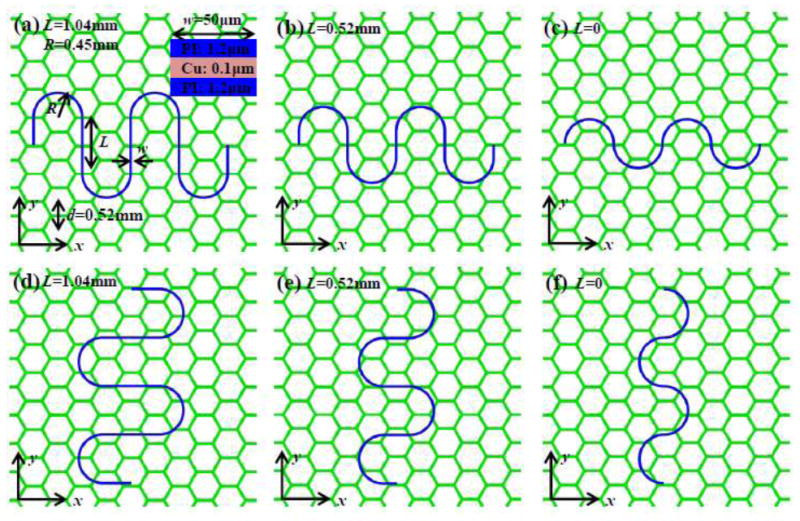
Three representative shapes of the serpentine interconnects, with different lengths of the straight part, bonded to the cellular substrate along (a-c) x- and (d-f) y-directions, respectively.

In practice, it can be difficult to precisely control the alignment and position of the serpentine interconnect on the cellular substrate. Finite element analysis is used to study the stretchability of three representative shapes of serpentine interconnects in Fig. 5, which are bonded to the cellular substrate along x- (Figs. 5a-c) and y-directions (Figs. 5d-f). For each shape and each direction of the serpentine interconnect, 16 alignments with all combinations of offset by 0, $\sqrt{3}d/6$, $\sqrt{3}d/3$ and $\sqrt{3}d/2$ along x-direction (parallel to cell wall, Fig. 5), and 0, d/6, d/3 and d/2 along y-direction (perpendicular to cell wall) are studied. The elastic stretchability, defined for 0.3% yield strain of Cu, has a large variation among all 32 alignments for each shape in Fig. 5. For the serpentine interconnect with long straight part L = 1.04 mm (Figs. 5a and d), the mean elastic stretchability is 85% for all 32 alignments, with the standard deviation 18%. For the serpentine interconnects with medium straight part L = 0.52 mm (Figs. 5b and e) and no straight part L = 0 (Figs. 5c and f), the mean elastic stretchabilities are 74% and 45%, with the standard deviations 13% and 4%, respectively. It is clear that the elastic stretchability increases with the length of the straight part of serpentine interconnect.

Finite element analysis is also used to study the elastic stretchability of serpentine interconnect bonded to a solid substrate, which has the analytic constitutive model in Section 2 for the equivalent medium of the cellular substrate with porosity ϕ = 80%. For three shapes of the serpentine interconnect in Fig. 5, the elastic stretchabilites are 73%, 65% and 34%, respectively, which are the lower bound of the elastic stretchabilites obtained for 32 alignments and directions discussed above, as shown in Fig. 6. This is because the cellular substrate allows the serpentine interconnect to buckle freely in the open space, while the equivalent medium, even though it has a low elastic modulus, still constraints the serpentine interconnect. Therefore, the equivalent medium in Section 2 yields an effective way to estimate the lower bound of elastic stretchability of the serpentine interconnect bonded to a cellular substrate. This lower-bound estimate is useful to design stretchable electronics on cellular substrate without the need to accurately determine the alignment.

Figure 6.

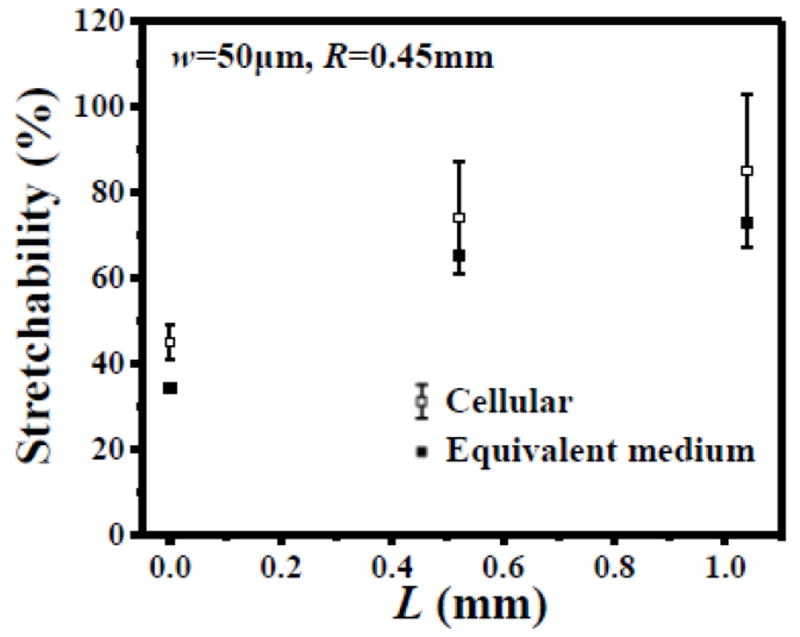
The elastic stretchability of the serpentine interconnect bonded to a cellular substrate, which has a large range of variation due to different alignments, positions and directions of the interconnect on the substrate. The elastic stretchability of the serpentine interconnect bonded to the equivalent medium of the cellular substrate is also shown. Three lengths of the straight part of the serpentine interconnect are taken, L = 1.04mm, 0.52mm and 0.

In the following the substrate is fixed as a 0.35 mm-thick solid, equivalent medium for cellular PDMS with porosity ϕ = 80%. The cross-section thicknesses and materials (1.2 μm-thick PI/ 0.1 μm-thick Cu/ 1.2 μm-thick PI) of the serpentine interconnect are also fixed in order to study effects of width w and length L of the straight part. Figure 6 shows the elastic stretchability versus the width w for the length of straight part L = 1.04 mm and the radius $R=\sqrt{3}d/2=0.45$ mm of circular part of the serpentine interconnect. A narrow serpentine interconnect (w = 50 μm) yields significantly larger stretchability than those for wider ones (w from 75 μm to 175 μm). This is because, for wide serpentine interconnects, the outer edge of the arc wrinkles with large amplitude when under stretching, as shown in the inset in Fig. 7, which leads to a large local strain in Cu, therefore a low elastic stretchability.

Figure 7.

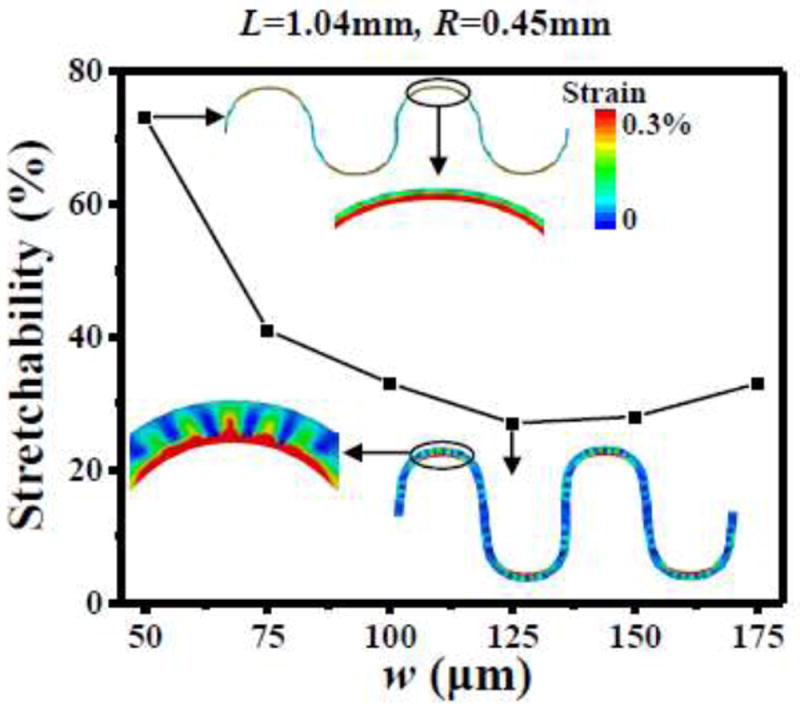
The elastic stretchability of the serpentine interconnect, bonded to the equivalent medium of the cellular substrate, versus the interconnect width w for the fixed length of the straight part L = 1.04mm and radius of the circular part R = 0.45mm.

Figure 6 suggests that the elastic stretchability increases with length L of the straight part of serpentine interconnect, but this increase saturates as L reaches approximately twice the radius R of the circular part. With the width w = 50 μm (as suggested by Fig. 7), the elastic stretchability of serpentine interconnect on the solid, equivalent medium of the cellular substrate is shown versus the length-to-radius ratio L/R in Fig. 8 for two radii R = 0.45 mm and 0.25 mm. The elastic stretchability clearly increases with the radius R because, for small radius, the outer edge of the arc also wrinkles with large amplitude when under stretching, as shown in the inset in Fig. 8, therefore a low elastic stretchability. The elastic stretchability increases with L/R, and saturates once L/R = ~2, which is the suggested ratio for the design of serpentine interconnect.

Figure 8.

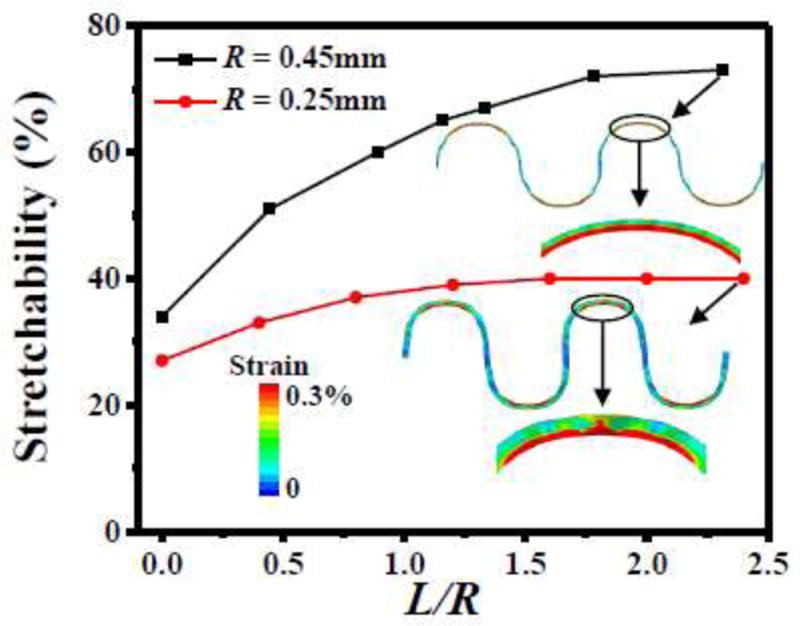
The elastic stretchability of the serpentine interconnect, bonded to the equivalent medium of the cellular substrate, versus the length-to-radius ratio L/R of the serpentine interconnect for the fixed width and w = 50 μm and two radii R = 0.45mm and 0.25mm.

4. Concluding remarks

1. An analytic constitutive model is established for an equivalent medium for a cellular substrate under finite deformation. For porosity ϕ ≥ 50%, the effective properties (e.g., nonlinear stress-strain relation under finite deformation, Poisson’s ratio) of the equivalent medium predicted by this analytic constitutive model agree well with those of the cellular substrate, without any parameter fitting.

2. The elastic stretchability of the serpentine interconnect bonded to the equivalent medium is a lower-bound estimate of that bonded to the cellular substrate. This lower-bound estimate is important to the design of stretchable electronics that use cellular substrates because its stretchability depends strongly on the alignment and position of interconnects on the cellular substrate, which are difficult to precisely control.