Quantification of Muscle Tissue Properties by Modeling the Statistics of Ultrasound Image Intensities using a Mixture of Gamma Distributions in Children With and Without Cerebral Palsy

Abstract

Objective

To investigate whether quantitative ultrasound (QUS) imaging, based on the envelope statistics of the backscattered ultrasound signal, can describe muscle properties in typically developing children and those with cerebral palsy (CP).

Methods

Radiofrequency ultrasound data were acquired from the rectus femoris muscle of children with CP (N=22) and an age-matched cohort without CP (N=14) at rest and during maximal voluntary isometric contraction. A mixture of gamma distributions was used to model the histogram of the echo intensities within a region of interest in the muscle.

Results

Muscle in CP exhibited a heterogeneous echotexture significantly different from healthy controls (p<0.001) with larger deviations from Rayleigh scattering. A mixture of two gamma distributions showed an excellent fit to the ultrasound intensity, and the shape and rate parameters were significantly different between CP and control groups (p<0.05). The rate parameters for both the single gamma distribution and mixture of gamma distributions were significantly higher for contracted muscles compared to resting muscles, but there was no significant interaction between these two factors (CP and muscle contraction) for a mixed-model ANOVA analysis.

Conclusions

Ultrasound tissue characterization indicates a more disorganized architecture and increased echogenicity in muscles in CP consistent with previously documented increases in fibrous infiltration and connective tissue changes in this population. Our results indicate that quantitative ultrasound can be used to objectively differentiate muscle architecture and tissue properties.

Introduction

It is well established that size, tissue composition, and architecture of skeletal muscle is a major determinant of its function^1-3. The connective tissue architecture and infiltration of fibrous tissue and fat alter the mechanical properties of muscle, and these in turn affect the ability of the muscle to generate force^4-6. The quantitative characterization of muscle composition and architecture can be an important clinical diagnostic and outcome measure in disorders with primary muscle pathology, such as muscular dystrophy, and neuromuscular disorders with associated muscle spasticity and paresis, such as cerebral palsy, stroke and spinal cord injuries⁷. Quantitative muscle tissue characterization is also important for more fundamental studies investigating the linkages between tissue properties and dynamic function⁸.

The current gold standard for characterization of muscle tissue composition and distribution of fiber type is through muscle biopsy⁹, which is invasive and carries the risks of infection, bleeding, and patient discomfort. Biopsies are often impractical when longitudinal measurements are desirable, and for dynamic studies. In recent years, a number of imaging methods have been developed that provide quantitative estimates of muscle tissue properties. Magnetic resonance Imaging (MRI) and computed tomography (CT) imaging can be used to quantify fatty infiltration¹⁰. Ultrasound is attractive for musculoskeletal imaging because it is portable and readily available for clinical or research use, can be used for real time imaging during dynamic tasks, and is well suited for longitudinal monitoring because it is inexpensive and safe¹¹. Ultrasound imaging is routinely used to measure anatomical muscle dimensions such as thickness, cross sectional area, fascicle length, and pennation angle^12-15, and more recently to quantify mechanical properties of muscle using elastography¹⁶. However, there continues to be a need to develop objective ultrasound-based methods for quantifying muscle microarchitecture and composition. Such a method for ultrasonic tissue characterization of muscle would have clinical utility by providing a noninvasive assessment of muscle characteristics (such as fatty and fibrous tissue infiltration, and fiber architecture) without the need for muscle biopsy.

The objective of this paper is to investigate the use of statistical models to quantitatively analyze ultrasound echotexture in muscle. As a feasibility study, we investigated the differences between muscle characteristics in children with cerebral palsy and a cohort of healthy children. Cerebral palsy (CP) is the most common physical disability originating in childhood¹⁷. Muscles in CP are known to have structural differences in muscle fibers and connective tissues within the muscle^18,19. In particular, weaknesses in the knee extensor muscles, such as the rectus femoris, which are important for maintaining an upright posture during gait, has been implicated in poor mobility and crouch gait, which is a common gait problem in CP²⁰.

Quantitative ultrasound (QUS) methods for characterizing tissue composition and tissue properties have a long history²¹. However, the application of quantitative ultrasound methods for characterizing muscle tissue has been limited primarily to analysis of gray scale levels²². Previous work has shown that fibrosis and fatty infiltration in skeletal muscle in a number of neuromuscular disorders can be assessed using ultrasound, with abnormal muscle showing increased echogenicity compared to normal control^23,24. Furthermore, quantitative ultrasound methods have been used to quantify intramuscular fat content in animals^25,26. In addition to echogenicity, the echotexture, or speckle pattern, is a unique signature of the underlying tissue microstructure, and a quantitative analysis can reveal useful acoustic properties of the underlying medium that can be related to biological properties and tissue characteristics^27-29.

In previous work, typically two approaches have been pursued to quantitatively extract information about tissue composition and microarchitecture from backscattered ultrasound echoes²¹. The first approach utilized a spectral analysis of the raw radiofrequency (RF) data, and derived QUS parameters such as attenuation coefficient and mean scatterer spacing from fitting a theoretical model to the normalized spectrum of the backscattered ultrasound signal^30,31. A second approach modeled the envelope of the backscattered ultrasound signal using different statistical models, where the model parameters could be related to underlying tissue properties^32-35. The spectral approach traditionally has been used in conjunction with careful calibration with a reference phantom to eliminate the transfer function of the ultrasound imaging system, while the envelope statistics are calculated after normalization of image intensities with image-based reference intensity without using a reference phantom, and does not require access to raw radiofrequency data. However, it can be shown from theoretical considerations that both approaches are fundamentally related³⁶. In this paper, our focus is on quantitative ultrasound based on envelope statistics, since it can be performed more readily in a clinical setting with conventional imaging instruments.

In this study, we investigated two questions: (1) what are the statistical properties of ultrasound scattering from muscle tissue; and (2) what quantitative technique for analysis of echo statistics better differentiates between the abnormal muscle of children with CP compared to normal muscle in healthy controls. The backscattered ultrasound signal from muscle tissue contains mixture of diffuse and coherent scattering and strongly specular reflections from fascia and fascicular boundaries. Ultrasound scattering occurs primarily at interfaces, such as connective tissues of the endomysium, perimysium and fascia and other components, including muscle cells, fat and fibrous tissue, with a mismatch of acoustic impedance³⁷. In practice, this heterogeneous scattering cannot be easily modeled using a single distribution, even accounting for a combination of coherent and diffuse scattering³⁵. In previous work, mixtures of distributions have been used as an effective method of overcoming this problem³⁸. Therefore, we investigated a mixture of distributions to model scattering from muscle tissue. A mixture model introduces additional model parameters, and therefore can better fit situations with heterogeneous scattering. A mixture of various different probability distributions can be considered for modeling the backscattered envelope statistics. Previous work has shown that the homodyne-K distribution³⁵ is the most generalized model for ultrasound envelope statistics. However, the homodyne-K distribution does not have a closed-form expression for the probability distribution function, and is therefore not convenient for parameter estimation in a mixture model. The Nakagami distribution is an approximation of the homodyne K-distribution, has been used in a number of applications, since the distribution parameters can be more readily estimated³⁹. We utilized the gamma distribution to model echo intensities, which is identical to the use of a Nakagami distribution to model echo amplitudes. Parameter estimation of a mixture of gamma distributions can be performed robustly using well-established approaches⁴⁰.

Experimental Methods

Study subjects

Children with CP were recruited at the National Institutes of Health Clinical Center, following procedures approved by the IRB. Informed consent for the study was obtained from all human subjects. The inclusion criteria were a diagnosis of spastic bilateral CP, premature birth (<34 weeks), periventricular white matter injury on a previous MRI, ability to walk with or without external assistance for 20 feet without stopping, and, mild to moderate gross motor dysfunction (Gross Motor Functional Classification System (GMFCS) levels I, II, or III). Participants were excluded if they were receiving oral or intrathecal baclofen, had undergone surgery to the lower extremities in the past year or any major surgery within the past 6 months, had any major medical illness, or were currently using an exercise device regularly. In this study, we analyzed data from 22 children with CP (mean age = 10.6 yrs.; range 5.1-17.6 yrs.; body mass index = 19.26; range 13.45-31.13) for whom raw radiofrequency ultrasound data were available. Of the 22 children, 2 were at GMFCS level I, 12 were at level II, and 8 were at level III. We also analyzed data from 14 healthy volunteers who were matched to the CP cohort in terms of age (mean age = 12.2 yrs.; range 6.9-17.1 yrs.; body mass index: 19.99; range 15.78-26.78) and for whom raw radiofrequency ultrasound data were available.

Data acquisition

Ultrasound imaging was performed using a SonixTouch ultrasound system (BK Ultrasound, Richmond, BC, Canada) with an L14-5W transducer, with a frequency range of 5-14MHz, and 60 mm width. The subject was seated comfortably on an isokinetic dynamometer (Biodex Medical Systems, Shirley, NY, USA) with the knee was flexed at a 60° angle (Figure 1). A tape measure was used to measure the length of the rectus femoris muscle between the origin and insertion points on the leg ipsilateral to non-dominant upper extremity, and the midpoint of the muscle (50% of the muscle length) was marked on the skin surface with the muscle relaxed. All images were acquired with the same ultrasound system settings. The musculoskeletal imaging preset (MSK) was used, with a 10MHz center frequency, 3 cm depth, and 76 dB dynamic range. The rectus femoris muscle was visualized in cross section at the location of the skin mark. Images were acquired at baseline with the subject’s muscle relaxed, and during a maximal voluntary isometric contraction (MVIC) for 5 seconds. The ultrasound transducer was held steadily at the same anatomical location based on the skin mark for both relaxed and MVIC conditions, in a direction perpendicular to the skin surface. Raw RF ultrasound data were saved with a sampling frequency of 40 Msamples/sec.

Figure 1.

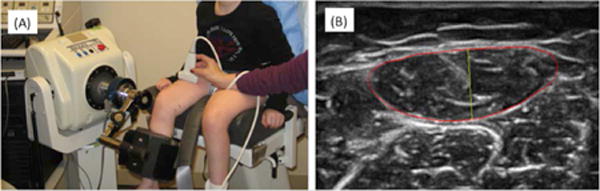
(A) Experimental setup for data acquisition. (B) Ultrasound image of the rectus femoris, with the muscle boundary outlined in red, and the thickness indicated in yellow.

Data analysis

The intensity of the raw RF ultrasound data was calculated using the Hilbert transform. For each subject, a single B-mode image frame, at rest and during MVIC, respectively was selected. The MVIC frame was selected at the peak of sustained contraction.

We performed two different types of analysis. First, we created spatial parameter maps by estimating the statistical model parameters from the histogram of echo intensities within a moving rectangular window. The window size was varied from 3 times the acoustic wavelength to 7 times the wavelength. Second, we selected the entire muscle as the region of interest for estimating the model parameters. For this analysis, the rectus femoris muscle was identified manually in the corresponding B-mode images. The muscle boundary was manually marked by identifying the hyperechoeic fascia boundaries. The entire muscle was considered the region of interest (ROI) for analysis. The fascia outside the muscle was not included in the ROI, but all fascia interfaces inside the muscle boundaries were included in the analysis. The backscattered intensities within this muscle ROI were normalized by the maximum value within the ROI. The statistical properties of the normalized backscattered intensities were analyzed using statistical models described in the next section.

Theoretical Methods

Theoretical model of the envelope statistics of the backscattered signal

Different theoretical models of the envelope statistics of backscattered ultrasound echoes from a heterogeneous medium have been critically reviewed elsewhere³⁵. A common formulation considers ultrasound scattering from a volume of tissue to be analogous to a random walk with N steps, where each step has a step size of a_i, and a direction ${\overrightarrow{r}}_i$^41,42. The step size corresponds to the scattering amplitude, and the direction depends upon the positions of the scatterers, and affects the phase of the returned echo. For an unbiased random walk, a_i, and ${\overrightarrow{r}}_i$are assumed to be uniformly distributed, corresponding to the case of incoherent (diffuse) scatterers in a homogeneous medium. Assuming N to be infinitely large, the backscattered amplitude of the echo follows a Rayleigh distribution for a 2-dimensional random walk with variance ${\sigma }^2=\raisebox{1ex}{${\overline{a}}^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, where ${\overline{a}}^2$ is the variance of the scatterer amplitudes⁴¹. The Rayleigh distribution is applicable in the case of well-developed speckle without coherent scattering. In this case, the signal to noise ratio (SNR), defined as the ratio of the mean to the standard deviation, is 1.91⁴³.

To account for coherent scattering, a number of extensions of the Rayleigh distribution has been proposed, including the Rice distribution³⁵ and the homodyne-K distribution⁴¹. The homodyne-K distribution is the most generalized model for envelope statistics³⁵, since it can account for the effects of a small number of scatterers in a resolution cell, and a coherent scattering component and the parameters can be associated with physical tissue characteristics. However, since the homodyne-K distribution does not have a closed-form expression for the probability distribution function, other distributions are often used in practice. For a random variable × representing the amplitude of the backscattered ultrasound echo, the Nakagami distribution is an approximation of the homodyne K-distribution, and accounts for both coherent as well as diffuse scattering³⁹.

$$P_{\mathit{Nakagami}}(x|m,\mathrm{\Omega })=\frac{2}{\mathrm{\Gamma }\left(m\right)}{\left(\frac{m}{\mathrm{\Omega }}\right)}^m{x}^{2m-1}{e}^{-\left(\frac{m{x}^2}{\mathrm{\Omega }}\right)}.$$ Eq. 1

The parameters Ω and m can be interpreted as the mean intensity and the square of the SNR, respectively. If the envelope statistics follow a Nakagami distribution, then the square of the envelope, or the intensity, I=x², of the backscattered ultrasound signal, follows a gamma distribution,

$$P_{\mathit{Gamma}}(I|\alpha ,\beta )=\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }(\alpha )}{I}^{\alpha -1}{e}^{-\beta I},$$ Eq. 2

where α is the shape parameter and β is the rate parameter. The shape parameter can be interpreted as the square of the SNR (α = m), and the rate parameter is the ratio of the square of SNR and mean intensity ( $\beta =\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\Omega }$}\right.$).

Based on the above theoretical formulation, we can see that the use of a gamma distribution to model the intensity (square of amplitude) of the backscattered ultrasound signals can account for both coherent and diffuse scattering. The above formulation holds for envelope statistics within small regions of interest corresponding to the size of the speckle. As the region of interest is increased and different tissue types contribute to the envelope statistics, a single distribution may no longer be a suitable model. In such situations, a mixture of two distributions can provide more flexibility in modeling the observed statistics. In this paper, we investigated the suitability of three distributions: Rayleigh, gamma and mixture of gamma, to model the envelope statistics from muscle.

Estimation of model parameters for mixture of gamma distributions

In the most general case, we assume that the squared envelope of the backscattered ultrasound echoes from heterogeneous muscle tissue follows a mixture of two gamma distributions with probability density function:

$$f(I|p,{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2)=p{P}_{\mathit{Gamma}}(I|{\alpha }_1,{\beta }_1)+(1-p)P_{\mathit{Gamma}}(I|{\alpha }_2,{\beta }_2),$$ Eq. 4

where $p\in (0,1),{\alpha }_1>0,{\alpha }_2>0,{\beta }_1>0,{\beta }_2>0.$

To ensure model identifiability and obtain a unique solution to the parameter estimation problem, we impose the constraint such that ${\alpha }_2>{\alpha }_1$.

Suppose there are n independent and identically distributed (i.i.d.) observations $I_1,\cdots ,I_n$. The likelihood function for the unknown parameters $\theta \equiv (p,{\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2)$is given by

$$L_n(\theta )={\displaystyle \prod _{i=1}^{n}f(I_i|p,{\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2)}.$$ Eq. 5

We maximize the above likelihood function to obtain the maximum likelihood estimators of θ, denoted by $\widehat{\theta }\equiv (\widehat{p},{\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\beta }}_1,{\widehat{\beta }}_2)$. The optimization can be accomplished using the quasi-Newton algorithm⁴⁰. Specifically, we used an implementation of the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, which is an efficient algorithm for solving nonlinear optimization problems.

Statistical Analysis

The model parameters (SNR, shape and rate of the single gamma distribution and shape, rate and mixture probability of the two gamma distributions) were estimated from the muscle images at rest and during MVIC in both healthy volunteers and children with CP. We utilized the SNR parameter to investigate the deviation from purely diffuse scattering. We then investigated whether the gamma distributions were a good fit to the underlying data using descriptive statistics and the ${\chi }^2$ goodness of fit statistic. The estimated parameters were then compared between the two groups (healthy volunteers and children with cerebral palsy) using descriptive statistics. Log-transformations were applied to the rate parameters to approximate normality. A mixed model ANOVA (with a subject-specific random intercept) analysis was performed to investigate sources of variation due to CP and due to muscle contraction, and any interaction between these effects. Residual analysis was performed to evaluate the suitability of the mixed effects model. Bonferroni correction (for two parameters for the single Gamma distribution and five parameters for the mixture of Gamma distributions) was applied for multiple comparisons when evaluating significant differences. The statistical software SAS (version 9.4; SAS Institute, Cary, NC) was used for all analyses.

Results

Exemplary images from the rectus femoris muscle of a healthy volunteer and a child with CP, at rest and during MVIC, show that the muscle in the child with CP is more echogenic and has a qualitatively different echotexture (Figures 2 and 3).

Figure 2.

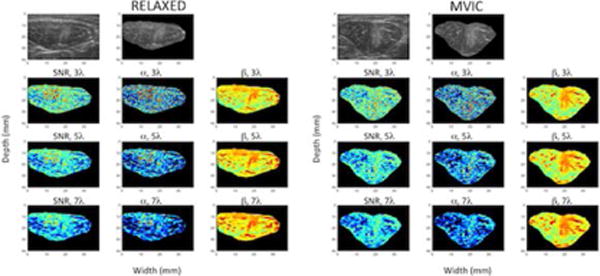
B-mode and spatial parameter maps of the rectus femoris muscle in a healthy volunteer at rest (columns 1, 2 and 3) and during maximum voluntary isometric contraction (MVIC) (columns 4, 5 and 6). The top row shows the envelope of the raw radiofrequency signal in gray scale without any further processing, with values normalized by the maximum value in the image. The second and fifth columns of the top row shows the B-mode image masked by the region of interest for the muscle at rest and during MVIC, respectively. The second row shows the estimated parameter maps for SNR and the shape and rate parameters of a single gamma distribution estimated using a moving window of size 3 times the wavelength (i.e., 0.46 mm). The third and fourth rows show the same parameters estimated using moving windows of increasing size: 5 times the wavelength (0.77 mm) and 7 times the wavelength (1.08 mm). The SNR and shape parameters are shown on the same scale for all window sizes. The rate parameter is log compressed for display to better visualize the dynamic range of values.

Figure 3.

B-mode and spatial parameter maps of the rectus femoris muscle in a child with CP at rest (columns 1, 2 and 3) and during maximum voluntary isometric contraction (MVIC) (columns 4, 5 and 6). The top row shows the envelope of the raw radiofrequency signal in gray scale without any further processing, with values normalized by the maximum value in the image. The second and fifth columns of the top row shows the B-mode image masked by the region of interest for the muscle at rest and during MVIC, respectively. The second row shows the estimated parameter maps for SNR and the shape and rate parameters of a single gamma distribution estimated using a moving window of size 3 times the wavelength (i.e., 0.46 mm). The third and fourth rows show the same parameters estimated using moving windows of increasing size: 5 times the wavelength (0.77 mm) and 7 times the wavelength (1.08 mm). The SNR and shape parameters are shown on the same scale for all window sizes. The rate parameter is log compressed for display to better visualize the dynamic range of values.

The depths of the centroid of the manually marked region of interest for the rectus femoris muscle were not significantly different between the CP and healthy volunteer groups (15.98 ± 2.81 mm vs. 16.56 ± 2.62 mm, respectively; p=0.6). As expected, the size of the rectus femoris muscle was significantly larger in the healthy volunteers vs. those in CP (547.44 ± 127.28 mm² vs. 273.43 ± 91.15 mm², respectively; p<0.0001).

We created parametric maps of the SNR parameter calculated within moving windows of different sizes (Figures 2 and 3). These parametric maps highlighted the large variability of the parameter within the muscle. The SNR parameter was low in regions where fascia tissue interfaces were present. The SNR parameter also varied with the size of the window used for estimation. Similar variability was observed for the Gamma parameters as well. It can be seen that as expected the shape parameter of the single Gamma distribution closely tracks the SNR as expected.

The large variability of the parameters within the muscle is a barrier in using spatial parameter maps in adequately and compactly describing the characteristics of the muscle. While the mean and standard deviation of the parameters showed differences between the groups, the values were dependent upon the choice of window used for parameter estimation. For the analysis in this paper, we therefore chose the entire muscle as the region of interest and used a mixture of gamma parameters to describe the statistics.

A scatterplot of the mean and standard deviation of the amplitudes (normalized by the maximum value) within the entire muscle region of interest shows that the estimated SNR (corresponding to the slope) in the case of healthy volunteers is significantly lower than that of children with CP, both during rest and MVIC (p<0.001 using a two-sample t-test on the SNR estimates) (Figure 4). The SNR for the case of controls during MVIC is closest to that of the expected value of 1.91 for a Rayleigh distribution, whereas in the other cases the SNR is larger than that for a Rayleigh distribution, indicating heterogeneous scattering. The R² statistics for the linear regression for healthy volunteers are 0.74 and 0.92, respectively for rest and MVIC, while for CP are 0.76 and 0.83, respectively for rest and MVIC.

Figure 4.

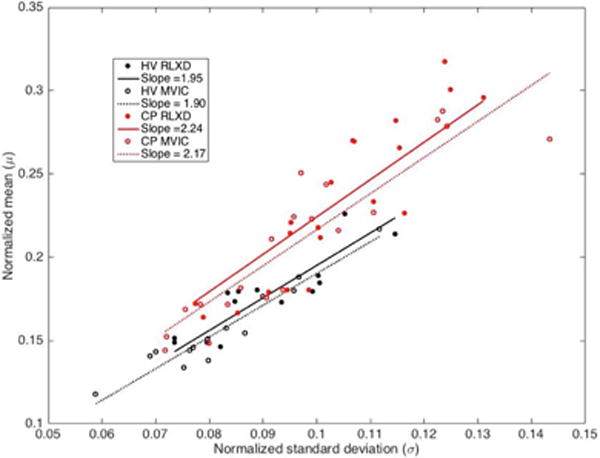
Scatterplot of normalized mean vs. standard deviation of the distribution of scatterer amplitudes within the rectus femoris muscle in healthy volunteers (HV) and subjects with cerebral palsy (CP), in the relaxed state (RLXD) and during maximum voluntary isometric contraction (MVIC). The slopes of the regression lines, which corresponds to the signal to noise ratio (SNR), are significantly higher for the subjects with CP compared to the healthy volunteers (p<0.001). The SNR for the case of healthy volunteers during isometric contraction is closest to that expected for a Rayleigh distribution (1.91), whereas in the other cases they are larger, indicating the presence of significant amounts of coherent scattering. The R² statistics for the linear regression for HV are 0.74 and 0.92, respectively for RLXD and MVIC, while for CP are 0.76 and 0.83, respectively for RLXD and MVIC.

The histogram of the normalized intensity in the same muscles, overlaid with the maximum likelihood models for a single gamma distribution and a mixture of two gamma distributions show that the mixture of gamma distributions provide an excellent fit with the underlying data (Figure 5). By looking at the two separate components of the mixture, we notice that the component with the smaller value of the shape parameter models the distribution of low and intermediate intensities (green dashed curve), whereas the component with the larger value of the shape parameter models the distribution of higher intensities that contribute to the heavy tail of the distribution (blue dashed curve). It can further be seen that the heavy tail of the underlying distribution is a factor that explains why the single gamma distribution underestimates the contribution of low and intermediate intensities. The goodness of fit evaluated using the ${\chi }^2$statistic confirms that the mixture of gamma distributions is consistently a better fit to the data for all subjects, both healthy volunteers and children with CP (Figure 6).

Figure 5.

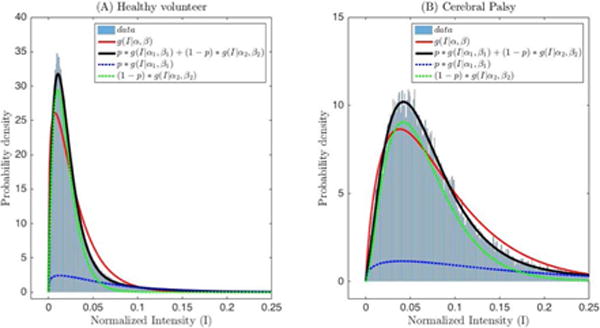
(A) Histogram of backscattered ultrasound intensities in Figure 3(A) normalized by the maximum value, overlaid with the model fits for a single gamma (red, solid line) and mixture of two gamma distributions (black solid line). (B) Histogram of backscattered ultrasound intensities in Figure 3(C) normalized by the maximum value, overlaid with the model fits for a single gamma (red, solid line) and mixture of two gamma distributions (black, solid line). Blue and green dashed lines show the partial contribution of the two gamma distributions weighted by p and (1-p), respectively. g(I|α,β) is the probability density function of the gamma distribution.

Figure 6.

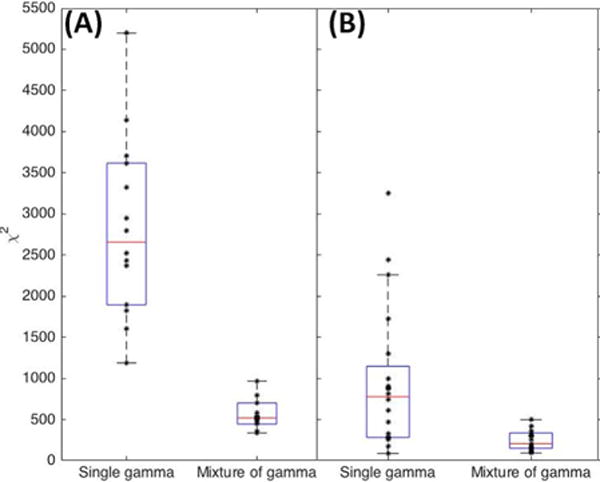
(A) Goodness of fit evaluation using the χ² statistic. (A) Healthy volunteers at rest and (B) Subjects with cerebral palsy (CP) at baseline at rest. The central line in the boxplot corresponds to the median, the edges correspond to 25^th and 75^th percentiles, and whiskers correspond to extremal values not considered outliers.

The estimated QUS model parameters of the single gamma distribution are significantly different between healthy volunteers and subjects with CP at baseline, as are the estimated parameters of the mixture of gamma distributions (Tables 1-3; Figures 7-8). A mixed model ANOVA (Tables 2-3) analysis shows that all the parameters (shape and rate parameters for both the single gamma distribution and mixture of gamma distributions) are significantly different between healthy volunteers and CP. There was no significant difference in the mixture probability of the two gamma distributions between the groups. The rate parameters for both the single gamma distribution and mixture of gamma distributions are significantly higher for contracted muscles compared to resting muscles (Tables 1-3), but there is no significant interaction between these two factors (CP and muscle contraction). This implies that the difference in tissue characteristics between relaxed and contracted states in CP is similar to the difference between relaxed and contracted states in healthy volunteers, even though the tissue characteristics in relaxed and contracted states in CP are both significantly different from those in healthy volunteers.

Table 1.

Shape and Rate parameters for single gamma distribution and a mixture of two gamma distributions fitted to the backscattered echo intensity of the rectus femoris muscle from healthy volunteers and children with CP, with the muscle relaxed and during MVIC.

		Healthy Volunteers (N=14)		Patients with CP (N=22)
		Relaxed	MVIC	Relaxed	MVIC
Single gamma	α	1.24±0.13	1.19±0.10	1.49±0.22	1.44±0.19
	β	33.0±8.6	41.1±13.8	25.1±8.1	29.9±11.4
Mixture of gamma	α1	1.21±0.09	1.17±0.10	1.39±0.22	1.32±0.17
	α2	2.00±0.15	2.03±0.17	2.25±0.21	2.31±0.23
	β1	13.6±3.6	17.1±5.7	11.3±2.6	12.6±2.5
	β2	77.4±16.9	108.8±34.1	53.5±18.4	69.0±23.1
	p	0.19±0.04	0.22±0.08	0.23±0.11	0.24±0.12

Table 3.

Mixed model ANOVA (with a subject-specific random intercept) for the shape parameters, (α₁,α₂) and the rate parameters, (β₁,β₂), for a mixture of two gamma distributions fitted to the backscattered echo intensity of the rectus femoris muscle. The two factors considered are abnormalities due to CP compared to healthy volunteers, and muscle contraction (MVIC) compared to relaxed muscle. Significant differences are seen in all parameters for CP compared to healthy volunteers at the 5% level after Bonferroni correction for multiple comparisons. Significant differences are seen in the rate parameters for muscle contraction at the 5% level after Bonferroni correction for multiple comparisons. No significant interaction is observed. Log-transformations were applied to the rate parameters to approximate normality. Residual analysis shows that the mixed effects model fits the data well.

Source of variation	α1	β1	α2	β2
CP	0.0016*	0.0038*	<1E-4*	0.0001*
MVIC	0.0775	0.0002*	0.2294	<1E-4*
Interaction CP*MVIC	0.6696	0.2326	0.6925	0.5932

Figure 7.

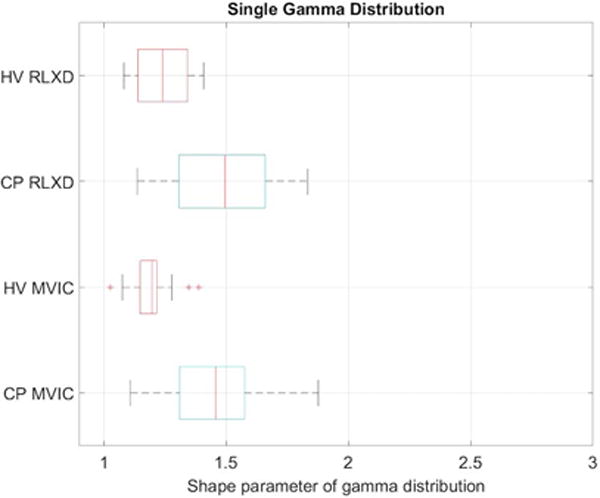
Boxplots of the shape parameter for a single gamma distribution fitted to the speckle envelope in the rectus femoris muscle of healthy volunteers (HV) and subjects with cerebral palsy (CP) when the muscle is relaxed (RLXD) and during maximal voluntary isometric contraction (MVIC). The central line in the boxplot corresponds to the median, the edges correspond to 25^th and 75^th percentiles, and whiskers correspond to extremal values not considered outliers.

Figure 8.

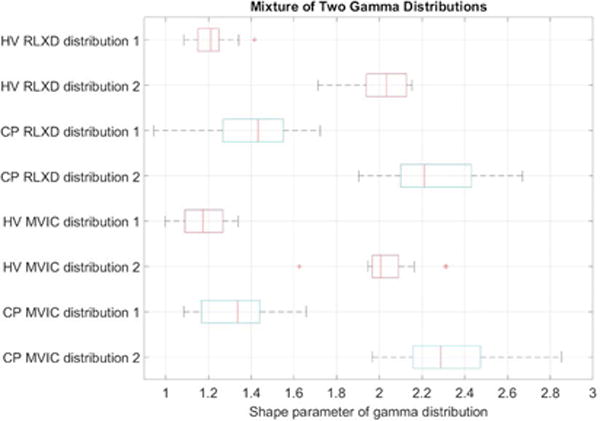
Boxplots of the shape parameters for dual gamma distributions fitted to the speckle envelope in the rectus femoris muscle of healthy volunteers (HV) and subjects with cerebral palsy (CP) when the muscle is relaxed (RLXD) and during maximal voluntary isometric contraction (MVIC). The central line in the boxplot corresponds to the median, the edges correspond to 25^th and 75^th percentiles, and whiskers correspond to extremal values not considered outliers.

Table 2.

Mixed model ANOVA (with a subject-specific random intercept) for the shape parameter, (α) and the rate parameter, (log(β)), for a gamma distribution fitted to the backscattered echo intensity of the rectus femoris muscle. The two factors considered are abnormalities due to CP compared to healthy volunteers, and muscle contraction (MVIC) compared to relaxed muscle. Significant differences are seen in both parameters for CP compared to healthy volunteers at the 5% level after Bonferroni correction for multiple comparisons. Significant differences are seen in the rate parameter for muscle contraction at the 5% level after Bonferroni correction for multiple comparisons. No significant interaction is observed. Log-transformation was applied to the rate parameter to approximate normality. Residual analysis shows that the mixed effects model fits the data well.

Source of variation	α	β
CP	<1E-4*	0.0061*
MVIC	0.0617	0.0015*
Interaction CP*MVIC	0.9539	0.5854

Discussion

The objective of our study was to investigate two questions: (1) what are the statistical properties of heterogeneous ultrasound scattering from muscle tissue and whether a mixture of Gamma distributions can adequately describe the statistics of ultrasound scattering from muscle; and (2) what quantitative technique for analysis of echo statistics better differentiates between the abnormal muscle of children with CP compared to normal muscle in healthy controls.

Our results show that, as expected, scattering from muscle is heterogeneous. Within the rectus femoris muscle, there is significant regional variability in the envelope statistics (Figures 2 and 3). The parameter estimates are also sensitive to the size of the window used to calculate the envelope statistics (Figures 2 and 3). The parameter maps might provide a visualization of the heterogeneity of the muscle, and provide complementary information to that obtained using the B-mode alone. However, in many applications it would be useful to obtain a single representative measure of the muscle quality and tissue characteristics⁹.

To address this issue, we selected the entire cross-sectional view of the muscle in a 2D image plane as the region of interest. Our results indicate that a mixture of gamma distributions can be used to adequately describe the envelope statistics of backscattered ultrasound from the entire muscle (Figure 5). In healthy muscle, ultrasound waves are scattered by highly organized tissue. It can be seen from Figures 5 and 6, that the single gamma distribution cannot adequately describe the mixture of normal muscle tissue and fascia boundaries, but a mixture of two gamma distributions can model the scattering with an excellent goodness of fit in all subjects studied (Figure 6).

Our results indicate that the values of the shape parameters of the gamma distribution (both single as well as the mixture of two gamma distributions) are significantly lower in healthy volunteers compared to children with CP, (Tables 2 and 3). As described in the Methods, the shape parameter of a gamma distribution is related to the square of the SNR. From Figure 4, it can be seen that the SNR for the case of controls is closest to that of the expected value of 1.91 for a Rayleigh distribution, whereas in CP the SNR is larger than that for a Rayleigh distribution, indicating heterogeneous scattering from muscle in children with CP with a larger proportion of coherent scatterers. Conversely, our results indicate that the rate parameters of the gamma distribution (both single as well as the mixture of two gamma distributions) are significantly higher in healthy volunteers compared to children with CP, (Tables 2 and 3). This implies that the distributions in children with CP have higher mean intensities and a heavier-tailed distribution compared to that in healthy volunteers, as shown in Figure 5 (i.e., the cumulative probability of brighter echo intensities is higher in children with CP than in healthy children). These findings can be interpreted based on histological evidence of muscle changes in CP. Muscles in CP have been shown to be weaker and smaller, with structural differences in muscle fibers and connective tissues within the muscle^18,19. In the case of CP, muscle spasticity has been related to changes in distribution of muscle fiber type⁴⁴, increased total collagen content⁹, and poor organization of extracellular matrix material⁴⁵, and an increase in the amount of fibrous tissue in muscle²³. These changes in muscle structure may cause the ultrasound image to appear more echogenic (bright) in children with CP, as shown in Figure 3. For example, a high correlation exists between ultrasound echo intensity and fibrous tissue infiltration²³. In controls, the coherent scatterers are primarily the fascia and connective tissue interfaces that are well separated from the normal muscle tissue. As a result, a single gamma distribution is not a good fit to the data (Figure 5). Indeed, the parametric maps clearly show that the parameter estimates for normal muscle and fascia tissue interfaces visible on B-mode images are markedly different. On the other hand in CP, the coherent scattering could be due to fibrous tissue infiltration into the muscle microarchitecture, and therefore a single gamma distribution shows a qualitative better fit for these muscles compared to controls (Figure 5). Quantitatively, the goodness of fit evaluated using the ${\chi }^2$statistic confirms that the mixture of gamma distributions is consistently a better fit to the data for all subjects (Figure 6). Our results indicate that a single gamma model is sufficient if the goal is to differentiate between the two groups, but a mixture model better describes the underlying scattering statistics and may be more suitable for quantitative ultrasound analysis of muscle.

Our results also show that the rate parameter is significantly higher in contracted muscle compared to relaxed muscle in both controls and CP, whereas the shape parameter is not different (the significant effect of MVIC on β in Tables 2 and 3). The rate parameter is inversely proportional to the mean intensity (Eq. 3); therefore an increase in the rate parameter of the gamma distribution would correspond to a decrease in the mean echo intensities. It is well known that when muscles contract, their echogenicity decreases⁴⁶. The decrease in echogenicity during contraction can be caused by both an increase in the thickness of muscle fascicles that increases the separation between the echogenic fascicular boundaries, as well as a change in the pennation angle of the muscle fibers that changes the angle of reflection of the ultrasound echoes. Our results show that this change is more pronounced in healthy volunteers compared to CP, consistent with the fact that children with CP are not able to contract their muscles effectively.

There are a number of limitations of this study that must be acknowledged. Our sample size was small, and these results need to be confirmed in a larger study. The study was not designed to investigate whether the ultrasound measures are predictive of functional improvement. We did not systematically evaluate the trial-to-trial reproducibility of the echotexture measurements. While we attempted to control for the position of the probe relative to anatomical landmarks, we did not systematically evaluate what effect variations in probe placement of the ultrasound probe may have on the results. We also did not evaluate whether the results depend upon the choice of ultrasound scanner and transducer. During isometric muscle contraction, the region of interest in the muscle could be at a slightly different location compared to the rest state. Although repeatability was not evaluated in this study, several previous studies have shown that ultrasound echogenicity and echotexture analysis is a repeatable and valid method for quantifying skeletal muscle characteristics and for differentiating between normal and pathological muscle tissue ^23,24,47,48. A previous study in children⁴⁹ showed that muscle heterogeneity evaluated using texture analysis is a sensitive method to differentiate between healthy and pathological muscle tissue. In this study, we did not evaluate the effect of age on echotexture. While muscle size increases with age, previous studies have shown no significant effect of age on echotexture⁴⁹. In our study, we compared children with CP to a healthy age-matched cohort. Therefore, we do not think that age dependence is a significant limitation in interpretation of our study results. A limitation of using a mixture of gamma distributions is that the QUS model parameters cannot directly be linked to some tissue characteristics such as effective scatterer size, or coherent scatterer power, which may be possible using more sophisticated model fits such as the homodyne-K distribution. However the parameters of the gamma distribution do relate to tissue characteristics that affect coherent and diffuse scattering, and changes in the parameters are directly related to changes in tissue composition and microarchitecture. One advantage of using the mixture of gamma distributions is that the parameter estimation can be performed robustly using well-established approaches.

Conclusion

Quantitative ultrasound imaging of muscle is feasible, and a mixture of gamma distributions can describe the envelope statistics with an excellent goodness of fit. To the best of our knowledge, this is the first study that describes the use of a mixture of gamma distributions to perform quantitative ultrasound imaging of muscle for tissue characterization.