Abstract
Evidence for the Crabtree effect was first reported by H. Crabtree in 1929 and is defined as the glucose-induced decrease of cellular respiratory flux. This effect was observed in tumor cells and was not detected in most non-tumor cells. A number of hypotheses on the mechanism underlying the Crabtree effect have been formulated. However, to this day, no consensual mechanism for this effect has been described. In a previous study on isolated mitochondria, we have proposed that fructose-1,6-bisphosphate (F1,6bP), which inhibits the respiratory chain, induces the Crabtree effect. Using whole cells from the yeast Saccharomyces cerevisiae as a model, we show here not only that F1,6bP plays a key role in the process but that glucose-6-phosphate (G6P), a hexose that has an effect opposite to that of F1,6bP on the regulation of the respiratory flux, does as well. Thus, these findings reveal that the Crabtree effect strongly depends on the ratio between these two glycolysis-derived hexose phosphates. Last, in silico modeling of the Crabtree effect illustrated the requirement of an inhibition of the respiratory flux by a coordinated variation of glucose-6-phosphate and fructose-1,6-bisphosphate to fit the respiratory rate decrease observed upon glucose addition to cells. In summary, we conclude that two glycolysis-derived hexose phosphates, G6P and F1,6bP, play a key role in the induction of the Crabtree effect.
Keywords: mitochondria; respiration; respiratory chain; yeast; glycolysis; Crabtree effect; fructose1,6-bisphosphate; glucose-6-phosphate; oxidative phosphorylation
Introduction
The Crabtree effect was first described by H. Crabtree in 1929 and is defined as the glucose-induced decrease of cellular respiratory flux (1). This effect was observed in tumor cells and had no occurrence in most non-tumor cells (1). Consequently, studies aiming to decipher the molecular mechanism leading to the Crabtree effect were mostly conducted by comparing tumor cell lines and their non-tumorigenic counterpart. The origin of the glucose-induced repression of cellular respiratory flux has long been sought and even though a number of hypotheses have been formulated, its triggering mechanism(s) is still unknown. It is possible that its induction may be due to a combination of several factors (2). In some tumor cells, a drastic decrease in phosphate (Pi) was observed upon glucose addition and the Crabtree effect was eliminated by adding an excess of Pi. This led the authors to propose that a decreased cytosolic Pi concentration was the actual trigger of this phenomenon (3). Another hypothesis is that the glycolytic enzymes (phosphoglycerate kinase and pyruvate kinase) compete with mitochondria for free cytoplasmic ADP (2, 4). Addition of glucose would trigger an overactive glycolysis that would outcompete mitochondria for ADP uptake. ADP being one of the substrates of the mitochondrial ATP synthase, the activity of this enzyme would decrease and so would mitochondrial respiration. However, this hypothesis might not hold true in vivo because the mitochondrial adenine nucleotide translocase Km is almost 100 times lower than that of the glycolytic enzymes (5). Consequently mitochondria would still import cytosolic ADP regardless of glycolysis activation. In the same line of thought, it has been shown that the thermodynamic phosphate potential (i.e. [ATP/ADPxPi]) changes in response to glucose addition to sarcoma ascites tumor cells (6), due to a decrease in both ADP and Pi.
Cytoplasmic Ca2+ levels have also been proposed as being responsible for the Crabtree effect. Indeed, one study showed that glucose addition increased mitochondrial Ca2+ uptake inhibiting the ATP synthase (7). However, such a regulation cannot be proposed as an unequivocal mechanism of induction of the Crabtree effect because in a hepatoma cell line Ca2+ levels did not change in response to glucose (2).
It has also been proposed that because the mitochondrial outer membrane regulates the access of substrates to the intermembrane space, it could regulate the oxidative phosphorylation rate (8). Indeed if ADP or the respiratory substrates were kept in the cytoplasm this would induce a decrease in respiratory flux. In agreement with this hypothesis, it has been shown that, in proteoliposomes, physiological concentrations of NADH close reconstituted porin (the external mitochondrial membrane main permeability barrier) (9). It has also been shown that within normal adult cardiomyocytes and in the HL-1 cardiac cell line, intracellular local diffusion restrictions of adenine nucleotides and metabolic feedback regulation of respiration via phosphotransfer networks are different, most probably as a result of differences in structural organization of these cells (10). Cardiomyocytes contain tight complexes where mitochondria and Ca2+/Mg2+-ATPases are organized to ensure effective energy transfer and feedback signaling via specialized pathways. In contrast, these complexes do not exist in HL-1 cells, which exhibit less organized energy metabolism (11). Hence diffusion restrictions are most likely not involved in the induction of the Crabtree effect.
Some years ago work from our laboratory pointed to a possible induction of the Crabtree effect by glycolysis-derived hexose phosphate, namely F1,6bP3 (12). We showed that on isolated mitochondria, F1,6bP inhibits the mitochondrial respiratory chain, whereas G6P stimulates it. More precisely, at physiological levels, F1,6bP inhibits mitochondrial complexes III and IV (12). This inhibition was shown on mitochondria isolated from the yeast Saccharomyces cerevisiae and on mitochondria isolated from rat liver (mammalian mitochondria). However, no inhibition from F1,6bP was observed on mitochondria isolated from Crabtree negative yeast–yeast that do not harbor an inhibition of cellular respiration when glucose is added to the culture medium. These results led us to propose that F1,6bP that accumulated within the cell upon glucose addition was responsible for the induction of the Crabtree effect.
We show here on whole cells of S. cerevisiae that glycolysis hexose phosphate, namely glucose-6-phosphate that activates the respiratory chain and fructose-1,6-bisphosphate that inhibits the respiratory chain, play a crucial role in the induction of the Crabtree effect. We show that not only the F1,6bP-induced inhibition of the respiratory chain plays a role in the induction of the Crabtree effect but also, the activation of the respiratory chain by G6P is important. In comparable stoichiometries, both hexose phosphates have opposite effects on the respiratory chain activity. Thus, the induction of the Crabtree effect depends on the ratio between these two hexose phosphates. Last, in silico modeling of the Crabtree effect taking into account our experimental results shows that the hexose phosphates-induced kinetic regulation of respiratory chain activity is mandatory to observe the Crabtree effect.
Results
The Crabtree effect is due to an inhibition of the mitochondrial respiratory chain
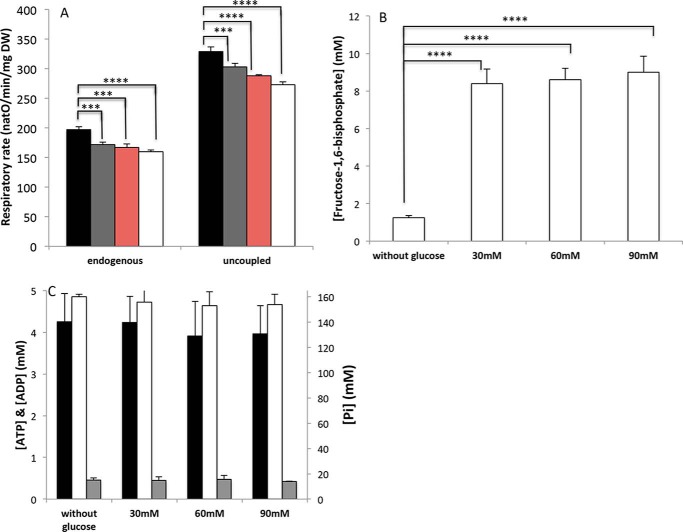
We investigated the induction of the Crabtree effect in our model S. cerevisiae. As previously shown (12), glucose addition to yeast cells grown on non-fermentative substrate induced a decrease in respiratory rate (Fig. 1A). To determine whether this inhibition was due to a respiratory chain inhibition or to a decrease in the phosphorylation processes at the mitochondrial level, we assessed the respiratory rate under uncoupled conditions, where the respiratory chain flux is at a maximal rate. Upon glucose addition, the uncoupled respiratory rate of WT cells decreased (Fig. 1A), pointing to respiratory chain inhibition. Glucose addition did not modify significantly adenine nucleotides or Pi (Fig. 1C). These results rule out an involvement of ADP or Pi on the induction of the Crabtree effect in the S. cerevisiae WT strain.
Figure 1.
Study of the Crabtree effect in WT cells. A, glucose-induced decrease in respiratory rate. Glucose concentrations were as follows: none (black), 30 mm (gray), 60 mm (red), and 90 mm (white). B, fructose-1,6-bisphosphate accumulation. C, ATP (black), ADP (gray), and Pi (white). Respiratory rates, fructose-1,6-bisphosphate, adenine nucleotides, and Pi determination were performed as described under “Experimental procedures.” Results are mean ± S.E. of at least three separate experiments.
To this day, the only mechanism proposed for the glucose-induced respiratory chain inhibition is the effect of fructose-1,6-bisphosphate, a glycolysis intermediary that accumulates upon glucose addition to cells (12). We thus measured this intermediate in WT cells upon glucose addition. Fig. 1B shows that although in cells grown on lactate as a carbon source fructose-1,6-bisphosphate concentration is quite low, it significantly rises up eight times upon glucose addition.
Deletion of hexokinase 2 prevents the induction of the Crabtree effect
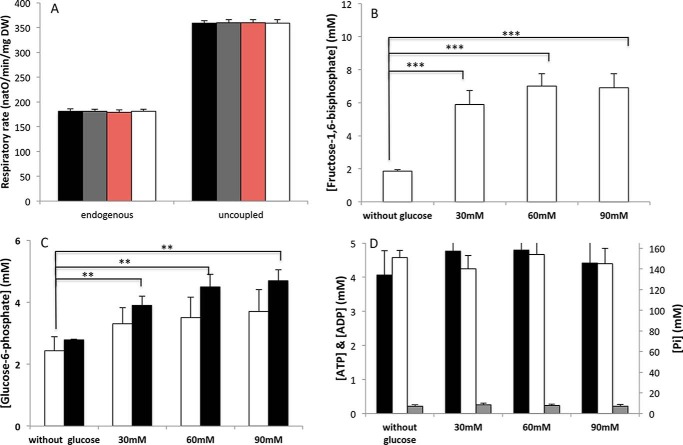
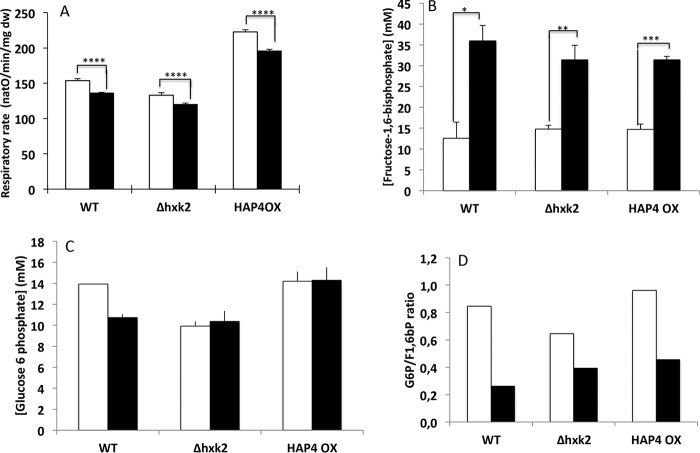
To further investigate the role of F1,6bP on the induction of the Crabtree effect we explored means to alter the accumulation of glycolysis metabolites in response to glucose addition. Hexokinase is the first enzyme of the glycolysis pathway. There are a number of isoenzymes in both yeast and mammalian cells. However, hexokinase2 (hxk2) is the predominant hexokinase during growth on glucose. It is the yeast homolog of glucokinase, which is overexpressed in tumor cells and it is not inhibited by its product, glucose-6-phosphate. As a consequence its activity should result in high accumulation of glycolysis intermediates in response to glucose addition (13). We thus studied the induction of the Crabtree effect in a hxk2-deletion strain. In the Δhxk2 strain, no inhibition of the respiratory rate was observed upon glucose addition (Fig. 2A). In the Δhxk2 strain neither adenine nucleotides nor Pi concentrations were significantly affected upon glucose addition (Fig. 2D).
Figure 2.
Study of the Crabtree effect in Δhxk2 cells. A, respiratory rate. Glucose concentrations were as follows: none (black), 30 mm (gray), 60 mm (red), and 90 mm (white). B, fructose-1,6-bisphosphate accumulation in Δhxk2 cells upon glucose addition. C, glucose-induced glucose-6-phosphate modulations in WT (white) and Δhxk2 (black) cells and D, ATP (black), ADP (gray), and Pi (white) in Δhxk2 cells. Respiratory rates and fructose-1,6-bisphosphate, glucose-6-phosphate, adenine nucleotides, and Pi determination were performed as described under “Experimental procedures.” Results are mean ± S.E. of at least three separate experiments.
To ensure that in Δhxk2 cells the absence of respiratory rate inhibition was not due to no variation or decreased F1,6bP accumulation in response to glucose addition, we measured the fructose-1,6-bisphosphate concentration. Fig. 2B shows that whereas the fructose-1,6-bisphosphate concentration is low in cells grown on lactate as a carbon source, upon glucose addition its concentration rises significantly in the Δhxk2 cells. However, upon glucose addition the overall concentration remains slightly lower in the Δhxk2 cells as compared with the WT cells (see Fig. 1). It has previously been shown that glucose-6-phosphate antagonizes the fructose-1,6-bisphosphate effect on respiratory chain activity: it activates the respiratory chain (12). We thus determined the glucose-6-phosphate concentration change in response to glucose addition both in WT and Δhxk2 cells. Glucose addition induced a significant increase in glucose-6-phosphate in Δhxk2, whereas the increase of G6P in WT cells is lower and not statistically significant (Fig. 2C).
Not only F1,6bP but also G6P plays a crucial role in the induction of the Crabtree effect
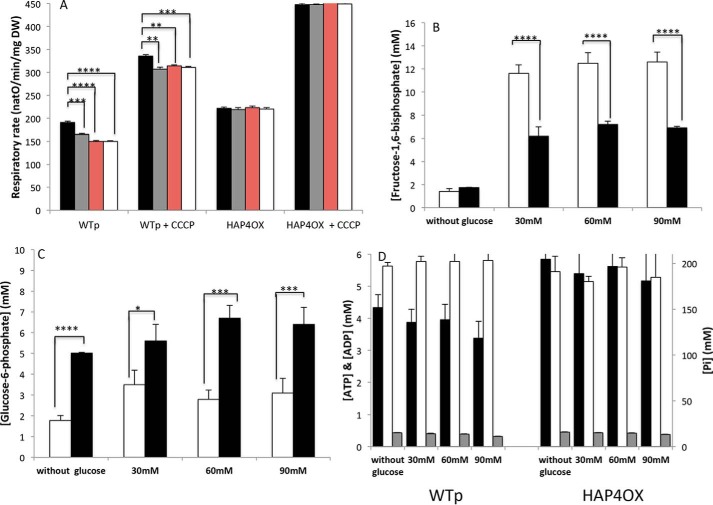
HAP4p (master regulator of the HAP transcription complex) plays a crucial role in the orientation of fermentative metabolism in the yeast S. cerevisiae (14). Hap4p is the activator subunit of the transcriptional complex involved in carbon source-dependent regulation of respiratory function (15, 16). Transcription of this subunit is glucose repressible (16), suggesting that Hap4p is the key component of the complex in terms of its control of transcriptional activity in response to carbon source. Thus a strain overexpressing HAP4p should exhibit an increased mitochondrial content and a strong orientation of energetic metabolism toward respiratory metabolism, altering the relationship between glycolysis intermediates and respiratory rate. In this strain, glucose addition did not inhibit the respiratory rate (Fig. 3A), whereas the Crabtree effect was present in the WT cells (control cells harboring an empty plasmid). Measurements of both adenine nucleotides and Pi showed that these parameters were mostly unaffected upon glucose addition in both the WT strain and the strain overexpressing the HAP4p subunit (Fig. 3D).
Figure 3.
Study of the Crabtree effect in HAP4p-overexpressing cells. A, respiratory rate. Glucose concentrations were as follows: none (black), 30 mm (gray), 60 mm (red), and 90 mm (white). B, fructose-1,6-bisphosphate accumulation in WT (white) and HAP4p-overexpressing (black) cells upon glucose addition. C, glucose-induced glucose-6-phosphate modulations in WT (white) and HAP4p-overexpressing cells (black) cells. D, ATP (black), ADP (gray), and Pi (white) in WT and HAP4p-overexpressing cells. Respiratory rates, fructose-1,6-bisphosphate, glucose-6-phosphate, adenine nucleotides, and Pi determination were performed as described under “Experimental procedures.” Results are mean ± S.E. of at least three separate experiments. HAP4OX: Δhap4 strain harboring a plasmid overexpressing HAP4p.
Whereas fructose-1,6-bisphosphate concentration is quite low in cells grown on lactate as a carbon source, it increases upon glucose addition in both the WT and HAP4p overexpressing cells (Fig. 3B). The absence of an induction of the Crabtree effect in the HAP4p-overexpressing cells is thus not due to an absence of fructose-1,6-bisphosphate accumulation upon glucose addition even though in the HAP4p-overexpressing cells, F1,6bP never reaches a concentration comparable with the one in the WT cells. We next investigated the effect of glucose on glucose-6-phosphate (which stimulates the respiratory chain) concentration in WT cells and in cells overexpressing HAP4p. For each strain, glucose-6-phosphate does not vary significantly upon glucose addition (Fig. 3C). However, its concentration is significantly doubled in the HAP4p-overexpressing cells as compared with the WT cells (see Fig. 3C). This result could imply an increase in the antagonist effect of glucose-6-phosphate on the activity of the respiratory chain in HAP4p-overexpressing cells.
The sensitivity of mutant cells to F1,6bP-mediated inhibition is maintained
The results described above raised the question of whether the respiratory chain from Δhxk2 and HAP4p-overexpressing cells remained sensitive to F1,6bP. To address this question, we studied the respiratory chain F1,6bP-mediated inhibition on the respiratory activity of nystatin-permeabilized spheroplasts from each of the strains of interest (17).
Fig. 4, A and B, clearly shows that there are no significant differences in the F1,6bP-mediated inhibition between the WT and mutant cells. Thus the absence of Crabtree effect induction in the Δhxk2 and HAP4p-overexpressing cells was not due to a modulation of the respiratory chain response to F1,6bP.
Figure 4.
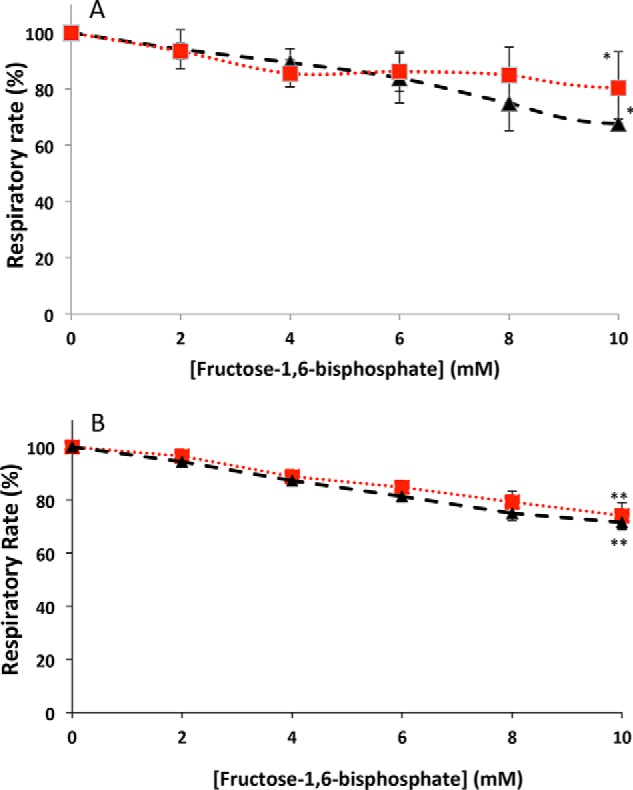
Fructose-1,6-bisphosphate-induced inhibition of respiration on permeabilized spheroplasts. A, fructose-1,6-bisphosphate-induced inhibition of respiration on permeabilized spheroplasts isolated from WT (black) and Δhxk2 (red) cells. B, fructose-1,6 bisphosphate-induced inhibition of respiration on permeabilized spheroplasts isolated from WT (black) and HAP4p-overexpressing (red) cells. Respiratory rates were measured as described under “Experimental procedures.” Results are mean ± S.E. of at least three separate experiments. The values at F1,6bp = 10 mm are statistically significantly different from the value at F1,6bP = 0 mm for each strain (WT, hxk2, and ΔHAP4OX).
A similar experiment was performed with G6P to ensure that respiratory chains in mutant cells were indeed stimulated by this hexose phosphate (data not shown). However, upon its addition to spheroplasts, G6P was steadily metabolized into F1,6bP making such a control experiment impossible.
Both glucose-6-phosphate and fructose-1,6-bisphosphate play a crucial role in the induction of the Crabtree effect
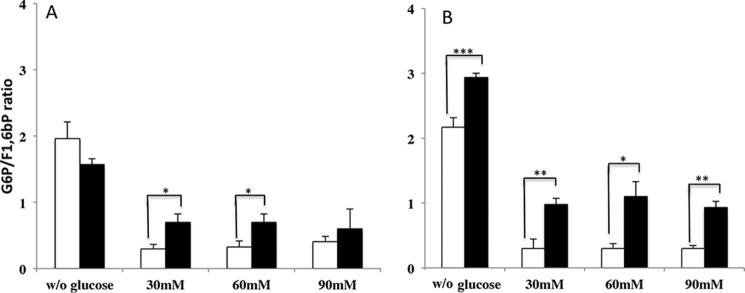
As mentioned above, whereas F1,6bP has been shown to inhibit mitochondrial respiratory chain, G6P stimulates it. In our previous paper, on isolated mitochondria (12), we showed that, in the presence of G6P, F1,6bP inhibited the mitochondrial respiratory chain only above the point where a stoichiometric amount of each hexose was required, i.e. the respiratory chain is inhibited when the G6P/F1,6bP ratio drops below 1. To determine whether in whole cells the G6P/F1,6bP ratio rather than the F1,6bP concentration alone was the key inducer of the Crabtree effect, we assessed this ratio in WT, Δhxk2, and HAP4-overexpressing cells. Fig. 5 clearly shows that whereas the G6P/F1,6bP ratio drops well below 1 in WT cells upon glucose addition, it stays pretty close to this value in the Δhxk2 and HAP4-overexpressing cells.
Figure 5.
G6P/F1,6bP ratio in WT and Δhxk2 (A) and WTp and HAP4OX (B) overexpressing cells. The ratios were calculated from the date of Figs. 1–3. WT (white) and mutants (black) are represented.
The G6P/F1,6bP ratio is the key player for the induction of the Crabtree effect
If our hypothesis stands true, i.e. the induction of the Crabtree effect relies upon the G6P/F1,6bP ratio, this ratio may be manipulated in our mutant cells to trigger the Crabtree effect. To perform this experiment, yeast cells were grown in galactose medium, where the glycolysis pathway is active and the glycolytic enzymatic content is higher than in a non-fermentable medium (used in our previous experiments). The reasoning behind this is that to accumulate more F1,6bP in our mutant cells, and thus decrease the G6P/F1,6bP ratio, active glycolytic enzymes are required. Consequently, WT and mutant cells were grown on galactose medium and the Crabtree effect was induced by the addition of 60 mm glucose. Fig. 6A shows that upon glucose addition, WT and mutant (Δhxk2 and HAP4-overexpressing) cells exhibit a statistically significant Crabtree effect as well as a consequent increase in F1,6bP concentration in WT and mutant cells (Fig. 6B), whereas variations of the G6P concentration are not statistically significantly different (Fig. 6C). So in galactose-grown WT or mutant cells, glucose induced both a Crabtree effect and a decrease in the G6P/F1,6bP ratio, even if the effect of glucose addition was lower than the one observed in cells grown in non-fermentative medium (Fig. 1A). It should be stressed here that the respiratory rate inhibition upon glucose addition when cells are grown on galactose medium is lower (but still statistically significant) than the one assessed when cells are grown on non-fermentative medium (Fig. 1A); this stands true for all three strains. However, in these cells and in the absence of glucose, the G6P/F1,6bP ratio is already below 1 (Fig. 6D), due to an active glycolysis. Thus in this experimental setup, the respiratory chain is most likely already slightly inhibited due to a concentration of F1,6bP a bit higher than the G6P concentration.
Figure 6.
Study of the Crabtree effect in galactose-grown cells without (white) or with (black) glucose. A, glucose-induced decrease in respiratory rate. B, fructose-1,6-bisphosphate accumulation. C, glucose-6-phosphate modulation in cells. D, data from B and C were used to calculate the G6P/F1,6bP ratio. Respiratory rates, fructose-1,6-bisphosphate, and glucose-6-phosphate were measured as described under “Experimental procedures.” Results are mean ± S.E. of at least three separate experiments.
An in silico study of the Crabtree effect confirms a role for glycolysis-derived hexose phosphate
There are good models of yeast metabolism with an accurate representation of the kinetics of glycolytic enzymes. It was thus tempting to see whether these models, developed for other purposes, would reproduce the experimental features of the Crabtree effect. We choose the recent model of Smallbone et al. (21) developed to fit the experimental glycolytic metabolites concentrations and to calculate the control coefficients of the glycolytic enzymes on the glycolytic flux. Two questions were addressed here: (i) do we reproduce in silico the experimental variations of F1,6bP and G6P and (ii) is a regulation by these metabolites necessary to obtain the Crabtree effect or could the Crabtree effect be obtained independently of such a regulation? To do so, as described under “Experimental procedures” and considering our previous experimental results (12), we introduced a regulatory function that is a Hill function of the G6P/F1,6bP ratio. Because the ATP and ADP concentrations did not appreciably change experimentally, we fixed their values in the model to the experimental values.
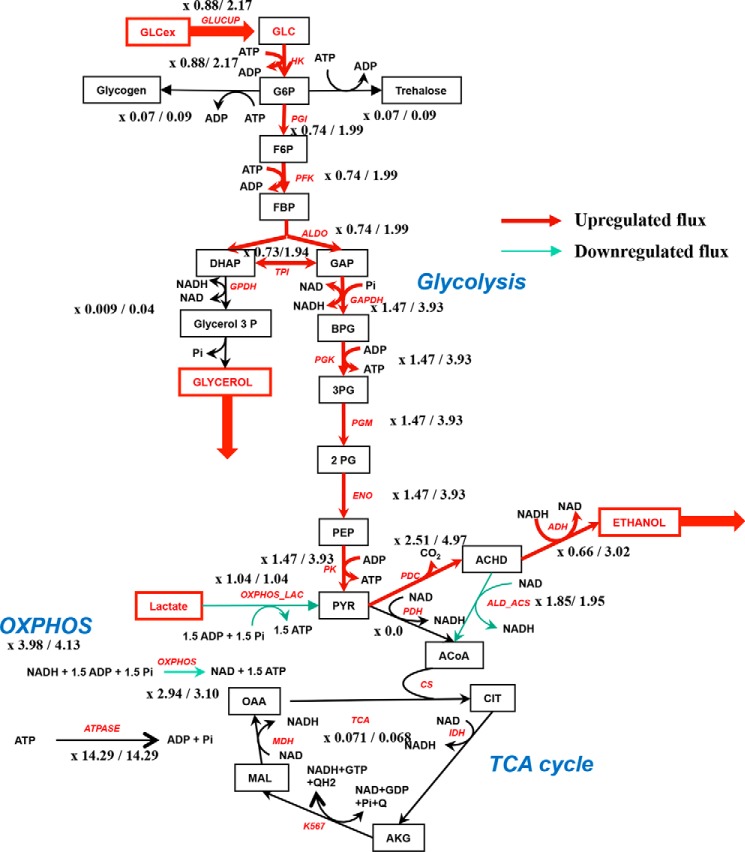
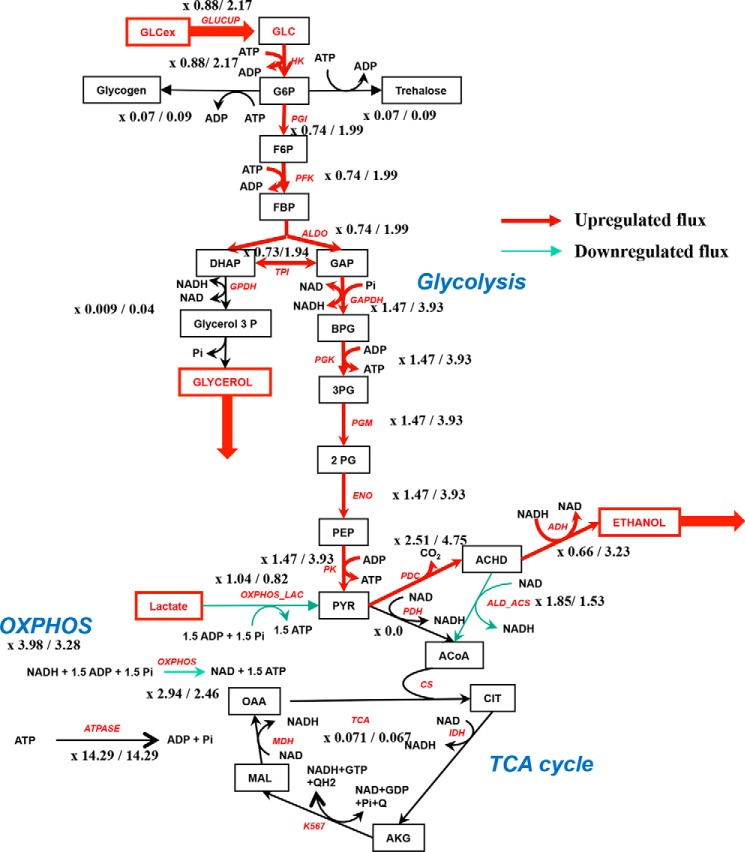
Concerning the effect on respiratory rate (VO2 = OXPHOS_NADH + OXPHOS_LAC), in the absence of regulation of the OXPHOS rate by the G6P/F1,6bP ratio, the addition of a high concentration of glucose (60 mm) slightly increases the respiratory rate about 4%. This increase is entirely due to an increase in OXPHOS_NADH as expected (NADH increases upon glucose addition to cells). OXPHOS_LAC is fixed due to the fixed ratio of ATP/ADP (Table 1 and Fig. 7). In the presence of a regulation of the OXPHOS rate by the G6P/F1,6bP ratio, both OXPHOS_NADH and OXPHOS_LAC decrease when glucose increases (up to 60 mm) (Table 2). OXPHOS_NADH shows a lower value at a high glucose concentration due to a low G6P/F1,6bP value, despite the higher concentration of NADH. The respiratory rate (VO2 = OXPHOS_NADH + OXPHOS_LAC) decreases by about 20% (Table 2 and Fig. 8), in accordance with experimental values (see Fig. 4, for example).
Table 1.
Simulation results without modulation of the respiratory rate by the ratio G6P/F1,6bP
| Glucose mm | G6P | F1,6bP | G6P/F1,6bP | OXPHOS_NADH | OXPHOS_LAC | VO2 | ATPase | NADH | Pyr |
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.81 | 0.61 | 2.96 | 2.94 | 1.04 | 3.98 | 14.29 | 0.015 | 1.99 |
| 60 | 3.16 | 7.49 | 0.42 | 3.10 | 1.04 | 4.13 | 14.29 | 0.08 | 5.13 |
Figure 7.
Theroretical fluxes in the metabolic network with 0.5/60 mm external glucose in the absence of G6P/F1,6BP modulation. The first value of flux corresponds to 0.5 mm external glucose and the second value to 60 mm external glucose. The red steps have their flux increased after addition of 60 mm glucose and the green ones decreased. The ratio G6P/F1,6bP goes from 2.95 (0.5 mm glucose) to 0.42 (60 mm glucose). A slight OXPHOS activation is observed in this case.
Table 2.
Simulation results with OXPHOS modulation by the ratio G6P/F1,6bP
| Glucose mm | G6P | F1,6bP | G6P/F1,6bP | OXPHOS_NADH | OXPHOS_LAC | VO2 | ATPase | NADH | Pyr |
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.81 | 0.61 | 2.96 | 2.94 | 1.04 | 3.98 | 14.29 | 0.015 | 1.99 |
| 60 | 3.15 | 8.50 | 0.37 | 2.46 | 0.82 | 3.28 | 14.29 | 0.09 | 4.78 |
Figure 8.
Theroretical fluxes in the metabolic network with 0.5/60 mm external glucose in the presence of G6P/F1,6BP modulation. The red steps have their flux increased after addition of glucose and the green ones decreased. An OXPHOS inhibition is observed in this case.
Fig. 9, A and B, shows that the concentrations of F1,6bP and G6P obtained in the model are close to the experimental values. They do not depend much upon the presence of the regulatory Hill function of the G6P/F1,6bP ratio. At low glucose concentrations, F1,6bP is equal to 0.6 as compared with an experimental value of 1 and the G6P value is equal to 1.8 as compared with an experimental value of 2, which gives a G6P/F1,6bP ratio of 2.6 as compared with the experimental value of 2. In the presence of high concentrations of glucose, both concentrations reach values between 7.8 and 8.7 mm for F1,6bP and between 3.12 and 3.16 for G6P (the experimental values being between 8 and 9 and between 3.3 and 3.7, respectively, which gives G6P/F1,6bP values around 0.4 as compared with experimental values between 0.3 and 0.4). Consequently, the results of Fig. 9 show that the model actually fits the experimental values of F1,6bP and G6P and their increase in the presence of glucose. Thus, modeling illustrates the need to consider the G6P- and F1,6bP-mediated modulation of oxidative phosphorylation to simulate the decrease in the respiratory rate observed after glucose addition.
Figure 9.

Experimental (blue, values are from the WT) and simulated (orange, without inhibition and green, with inhibition) values of F1,6bP (A) and G6P (B) at various glucose concentrations.
Last, we plotted the relationship between the rate of respiration and the G6P/F1,6bP ratio with the values obtained throughout this work (Fig. 10). The points, coming from Figs. 1–3 (summarized in Fig. 5) and Fig. 6 are remarkably gathered, which substantiate our hypothesis of an apparent regulation of the Crabtree effect induction by the G6P/F1,6bP ratio. In optimizing the parameters K of the model to fit the experimental results drawn in Fig. 10, we found that K = 0.27 gives a good fit of the experimental results, perfectly describing the inhibition of respiration for G6P/F1,6bP values below 0.7–0.8. As stressed previously, we show that when this ratio is above 0.8, no inhibition of the respiratory rate is observed. Furthermore, the calculation of the G6P/F1,6bP ratio from the literature on ascites tumor cells (2, 6) shows that it decreases upon glucose addition to cells and the plot of the first values corresponding to ascites tumor cells is in accordance with our values in yeast (Fig. 10). Of note, these authors respiratory rate inhibition is higher than what is seen in yeast, most likely due to the synergistic effects of hexose phosphate and phosphate potential.
Figure 10.
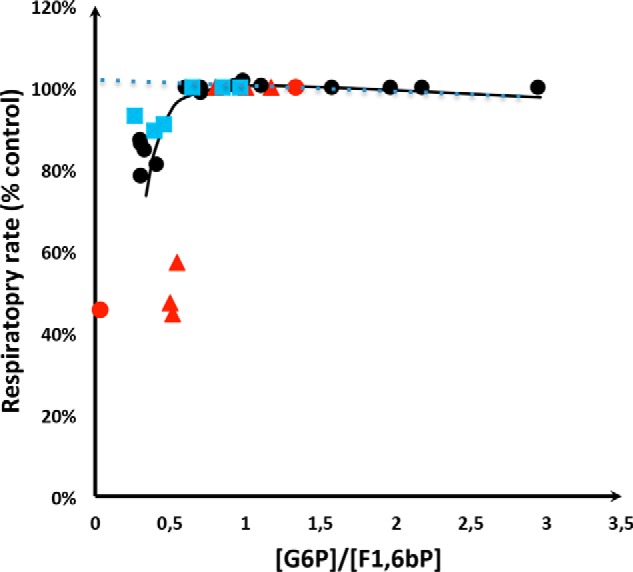
Respiratory rate as a function of the [G6P]/[F1,6bP] ratio. Black filled circles correspond to the WT, Δhxk2, and HAP4p-overexpressing cells grown on lactate medium (Figs. 1–3 and 5). Blue filled squares correspond to the same strains grown on galactose medium (Fig. 6). The red triangles correspond to values from the literature on ascites tumor cells. Red circles are derived from Ref. 2 and the red triangles are derived from Ref. 6. The full curve is drawn according to the model described under “Experimental procedures” with K = 0.27 in the regulatory Hill's curve as a function of the G6P/F1,6bP ratio (Hill's n = 4). The dotted line corresponds to an absence of regulatory Hill's function.
Discussion
The Crabtree effect was first evidenced by H. Crabtree in 1929 (1). Ever since then a number of studies were conducted on different models to decipher the molecular mechanisms responsible for the inhibition of the respiratory rate upon glucose addition. A number of hypotheses were formulated, depending on the cellular model and the experimental conditions used. However, to this day, no unifying mechanism has been evidenced. We have previously shown that glycolysis-derived hexose phosphates were able to stimulate (G6P) or inhibit (F1,6bP) the mitochondrial respiratory chain. This previous work was done on mitochondrial isolated either from yeast or rat liver. The F1,6bP-induced inhibition of the respiratory chain led us to propose that the accumulation of this metabolite upon glucose addition to cells was a key player in the induction of the Crabtree effect. However, these experiments were mostly conducted on isolated mitochondria as a model system. In this paper, we used whole yeast cells, which are a more physiological model to study the molecular events leading to the Crabtree effect.
We assessed a number of parameters upon induction of the Crabtree effect. Parameters that were proposed to be responsible for this effect, such as ADP, Pi, and the phosphate potential did not vary appreciably under our experimental conditions, regardless of the glucose concentration used to induce the Crabtree effect. Furthermore, the fact that the uncoupled respiratory rate is decreased upon glucose addition clearly points to a respiratory chain inhibition as the source of the Crabtree effect. Should ADP and Pi be responsible for this effect, they would decrease the cellular respiratory rate and yet have no effect on the uncoupled respiratory rate. G6P concentration varied only marginally upon glucose addition in WT cells. In contrast, F1,6bP accumulated widely, whereas the respiration is inhibited. To strengthen our hypothesis that the increase in F1,6bP and G6P are one of the causes of the Crabtree effect induction, we used a different means to vary their concentrations, including culture media and mutations. The assessment of G6P and F1,6bP concentrations in the WT as well as in the mutant strains demonstrated that not only was F1,6bP accumulation mandatory for the induction of the Crabtree effect but that the G6P intracellular concentration plays a key role too. Indeed, G6P stimulates the mitochondrial respiratory chain, antagonizing the F1,6bP-mediated inhibition in such a way that the ratio between G6P and F1,6bP has to be below 0.7–0.8 to trigger a Crabtree effect (Fig. 10), i.e. the cytoplasmic concentration of F1,6bP has to be slightly higher than that of G6P. It should be stressed here that on isolated mitochondria the ratio between these hexoses also has to be below 1 to inhibit the respiratory chain (12). Finally an in silico model developed (21) predicts an increase in the hexose phosphate concentrations following the addition of glucose and the simulated G6P/F1,6BP ratio changes in response to glucose addition were quantitatively in good agreement with our experimental results. However, the main interest of the model was to show that it is mandatory to implement the G6P/F1,6bP ratio-induced modulation of oxidative phosphorylation to reproduce the glucose-mediated decrease in respiratory rate observed after the addition of glucose to cells.
To summarize our study we plotted the rate of respiration as a function of the G6P/F1,6bP ratio for all our experimental conditions (see Fig. 10). The fact that all points are remarkably gathered drawing a smooth curve with a threshold around 0.7–0.8 indicates that the G6P/F1,6bP ratio is a rather good variable to express the antagonist effect of G6P and F1,6bP on the respiratory chain (12). Moreover, tumor cell lines exhibit the Crabtree effect (1, 2) and previous work from the literature on ascites tumor cells have shown that the concentrations of hexose phosphate increase upon glucose addition (2, 6). The calculation of the G6P/F1,6bP ratio from these data shows that it decreases upon glucose addition to cells and the plot of the first values corresponding to ascites tumor cells is in accordance with our values corresponding to yeast cells (see Fig. 10). This further reinforces both our results and our hypothesis of a role of the G6P/F1,6bP ratio in the induction of the Crabtree effect. We propose that hexose phosphates that arise from glycolysis, namely G6P and F1,6bP, play a key role in the induction of the Crabtree effect. Further studies will be necessary to determine whether such a mechanism applies to a number of cell types.
Experimental procedures
Yeast strains, culture medium, and growth conditions
The following yeast strains were used in this study BY4742 (MATα; his3Δ1; leu2Δ0; lys2Δ0; ura3Δ0), BY4742 Δhap4 (MATα; his3Δ1; leu2Δ0; lys2Δ0; ura3Δ0; hap4::kanMX4), and BY4742 ΔHxk2 (MATα; his3Δ1; leu2Δ0; lys2Δ0; ura3Δ0; Hxk2::kan MX4). Cells were grown aerobically at 28 °C in the following medium: 0.175% yeast nitrogen base without sulfate (Difco), 0.2% casein hydrolysate (Merck), 0.5% (NH4)2SO4, 0.1% KH2PO4, 2% lactate (w/v) (Prolabo), pH 5.5, 20 mg liter−1 of l-tryptophan (Sigma), 40 mg liter−1 of adenine hydrochloride (Sigma), and 20 mg liter−1 of uracil (Sigma). When cells carried a plasmid (pTET-HAP4 (18)), the relevant amino acid was omitted from the medium. Growth was measured at 600 nm in a Safas spectrophotometer (Monaco). Dry weight determinations were performed on samples of cells harvested throughout the growth period and washed twice in distilled water. Cellular volume determination was performed measuring the median cell volume of asynchronous yeast cell cultures using a Coulter counter apparatus (Beckman-Coulter). The volumes stipulated in Table 3 were determined.
Table 3.
Cellular volumes of the different strains used in this study
Cellular volume determination was performed as described under “Experimental procedures.” Results are means ± S.D. of at least three separate experiments.
| Strain | Volume (fentoliter/cell) | ± |
|---|---|---|
| WT | 32 | 1 |
| ΔHxk2 | 33 | 1 |
| WTp | 37 | 2 |
| HAP4 | 63 | 4 |
Oxygen consumption assays
Oxygen consumption was measured polarographically at 28 °C using a Clark oxygen electrode in a 1-ml thermostatically controlled chamber. Respiratory rates (JO2) were determined from the slope of a plot of O2 concentration versus time. Respiration assays of growing cells were performed in the growth medium except in the case of uncoupled respiration (10 μm carbonyl cyanide p-chlorophenylhydrazone), where 100 mm ethanol was added to avoid any kinetic control upstream the respiratory chain.
Adenine nucleotide measurements
Cellular extracts were prepared by an ethanol extraction method adapted from the one described in Ref. 19. Briefly, cells were harvested by rapid filtration on nitrocellulose filter (1 μm). The filter was immediately dropped into a glass tube containing 5 ml of ethanol, 10 mm Hepes, pH 7.2 (4/1), and the tube was then incubated at 80 °C for 3 min. The mixture was cooled down on ice for at least 3 min, and the ethanol/Hepes solution was eliminated by evaporation using a rotavapor apparatus. The residue was suspended in 500 μl of water. Insoluble particles were eliminated by centrifugation (12,000 × g, 10 min, 4 °C) and adenine nucleotide content was determined on the supernatant. ATP and ADP were measured using a luciferin/luciferase enzymatic kit (ATPlite One-step, PerkinElmer Life Sciences). For ADP content determination, the extract was incubated for one-half hour at 28 °C in the following buffer: 75 mm KH2PO4, 15 mm MgSO4, 0.1 mm phosphoenolpyruvate, and 1 unit of pyruvate kinase to transform ADP into ATP, then quantified using the ATPlite kit.
Pi determination
Pi was determined according to the method of Sumner (20).
Hexose phosphate measurements
Glycolysis hexose phosphates were measured in the following buffer: 50 mm triethanolamine, 7.5 mm MgCl2, 3.75 mm EDTA. G6P was measured in the presence of 1 mm NAD+ and 0.3 unit/ml of glucose-6-phosphate dehydrogenase. NADH absorbance was followed at 340 nm and the signal was calibrated with standard NADH of known concentration.
F1,6bP was measured in the following buffer: 50 mm triethanolamine, 7.5 mm MgCl2, 3.75 mm EDTA, 1 mm NAD+, 1 mm Pi, 1 mm ADP, 0.6 units/ml of phosphoglycerate kinase, and 0.3 unit/ml of aldolase. The reaction was started by adding 0.3 unit/ml of glyceraldehyde-3-phosphate dehydrogenase. NADH absorbance was followed at 340 nm and the signal was calibrated with standard NADH.
Spheroplast preparation
Spheroplasts were obtained according to Avéret et al. (17) and were suspended in the following buffer: 1 m sorbitol, 1.7 mm NaCl, 0.5 mm EGTA, 10 mm KCl, 1 mm potassium phosphate, 10 mm Tris-HCl, 10 mm NH4Cl, 6 mm iodoacetate, whenever required and 1% BSA, pH 6.8. Protein determination was done using the biuret method with BSA as a standard.
Model description
To further investigate the role of glycolysis hexose phosphates in the induction of the Crabtree effect, we performed an in silico study of the induction of this effect. We started from a yeast glycolysis model as developed in Ref. 21. This model involved a detailed description of all glycolysis reactions as well as the pathway from pyruvate to ethanol through acetaldehyde (pyruvate decarboxylase and alcohol dehydrogenase) and two branches: one toward acetate (acetate branch: acetaldehyde → acetate) and the other toward succinate thus summarizing most of the TCA cycle (succinate branch: pyruvate → succinate).
We adapted this model to our experimental conditions by suppressing the acetate branch and replacing the succinate branch by a more detailed representation of the TCA cycle involving pyruvate dehydrogenase and the TCA cycle reactions: acetyl-CoA + 4 NAD + ADP + Pi → 4 NADH + ATP, both modeled by an irreversible mass action equation. For the sake of simplicity, the reduction of quinone Q within the TCA cycle was replaced by the reduction of an extra molecule of NAD, which has the same proton stoichiometry in yeast because S. cerevisiae does not contain a proton pumping complex I. Instead of the acetate branch we added a reaction called ALD_ACS (acetaldehyde dehydrogenase and acetyl-CoA synthase) that represents the production of acetyl-CoA from acetaldehyde: acetaldehyde + NAD + ATP → acetyl-CoA + NADH + ADP + Pi, also modeled by an irreversible mass action equation. Pyruvate decarboxylase and ALD_ACS is the major pathway of pyruvate entry in the TCA cycle in our experimental conditions in which two substrates (NADH and lactate) are feeding the respiratory chain in different entry points. Thus the OXPHOS modeling involves two equivalent reactions with different stoichiometries: 1) OXPHOS_NADH: NADH + 1.5 ADP + 1.5 Pi → NAD + 1.5 ATP and 2) OXPHOS_LAC: lactate + ADP + Pi → pyruvate + ATP. Both reactions are considered as irreversible and modeled by a Henri-Michaelis-Menten equation (22) with two inhibitor terms (INH_ATP and GF_Inhib),
| (Eq. 1) |
| (Eq. 2) |
with
| (Eq. 3) |
| (Eq. 4) |
where Vmax_NADH = 50 mm/s, Vmax_lactate = 33 mm/s and KADP = 1 mm; and Klactate = 1 mm; KNADH = 1 μm.
INH_ATP function is a decreasing hyperbola representing the OXPHOS inhibition at high ATP concentrations (KA = 1).
The GF_Inhib term summarizes the activation and inhibition by G6P and F1,6bP, respectively (K = 0.005). It is a sigmoid function of the ratio G6P/F1,6bP taking values between 0 and 1.
The concentration and flux values at steady-state are obtained using Copasi (http://copasi.org/)4 (23).
Data analysis
Data are presented as mean ± S.E. Differences between substrate conditions were analyzed by t test, with the following code in the figures: (*) for p < 0.05, (**) for p < 0.01, (***) for p < 0.001, and (****) for p ≪ 0.001. When comparing different values obtained in the same experiment (typically the value without glucose and the value with glucose added in the same sample) the mean of the differences was compared with 0 (matched pairs differences) with the same representation code in the figures.
Author contributions
M. R. L., E. R., N. H., S. R., R. I., and J.-P. M. formal analysis; M. R. L., E. R., N. H., A. M., S. U.-C., and M. R. investigation; S. R., J.-P. M., S. U.-C., M. R., and A. D. writing-review and editing; J.-P. M. and A. D. validation; J.-P. M. and A. D. methodology; S. U.-C., M. R., and A. D. supervision; A. D. conceptualization; A. D. resources; A. D. data curation; A. D. funding acquisition; A. D. writing-original draft; A. D. project administration.
Acknowledgments
We thank Cyrielle Bouchez and Louise Injarabian for technical help. We thank Dr. Manuel Rojo and Dr. Arnaud Mourier for careful proofreading of the manuscript and constructive discussions.
This work was supported by the CNRS (Conseil National de la Recherche Scientifique), the Comité de Dordogne and Gironde de la Ligue Nationale Contre le Cancer, The Fondation ARC pour la recherche sur le Cancer, the Plan Cancer 2014–2019 number BIO 2014 06, the French Association against Myopathies, and the European Commission (to H. N.). The authors declare that they have no conflicts of interest with the contents of this article. This publication reflects the view only of the authors and the European Commission cannot be held responsible for any use which may be made of the information contained therein.
Please note that the JBC is not responsible for the long-term archiving and maintenance of this site or any other third party hosted site.
- F1,6bP
- Fru-1,6-P
- G6P
- Glc-6-P
- hxk2
- hexokinase2
- OXPHOS
- oxidative phosphorylation
- LAC
- lactate.
References
- 1. Crabtree H. G. (1929) Observations on the carbohydrate metabolism of tumours. Biochem. J. 23, 536–545 10.1042/bj0230536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Rodríguez-Enriquez S., Juárez O., Rodríguez-Zavala J. S., and Moreno-Sánchez R. (2001) Multisite control of the Crabtree effect in ascites hepatoma cells. Eur. J. Biochem. 268, 2512–2519 10.1046/j.1432-1327.2001.02140.x [DOI] [PubMed] [Google Scholar]
- 3. Koobs D. H. (1972) Phosphate mediation of the Crabtree and Pasteur effects. Science 178, 127–133 10.1126/science.178.4057.127 [DOI] [PubMed] [Google Scholar]
- 4. Weinhouse S. (1972) Glycolysis, respiration, and anomalous gene expression in experimental hepatomas: GHA Clowes memorial lecture. Cancer Res. 32, 2007–2016 [PubMed] [Google Scholar]
- 5. Veech R. L., Lawson J. W., Cornell N. W., and Krebs H. A. (1979) Cytosolic phosphorylation potential. J. Biol. Chem. 254, 6538–6547 [PubMed] [Google Scholar]
- 6. Sussman I., Erecińska M., and Wilson D. F. (1980) Regulation of cellular energy metabolism: the Crabtree effect. Biochim. Biophys. Acta. 591, 209–223 10.1016/0005-2728(80)90153-X [DOI] [PubMed] [Google Scholar]
- 7. Wojtczak L., Teplova V. V., Bogucka K., Czyż A., Makowska A., Więckowski M. R., Duszyński J., and Evtodienko Y. V. (1999) Effect of glucose and deoxyglucose on the redistribution of calcium in Ehrlich ascites tumour and Zajdela hepatoma cells and its consequences for mitochondrial energetics. Eur. J. Biochem. 263, 495–501 10.1046/j.1432-1327.1999.00522.x [DOI] [PubMed] [Google Scholar]
- 8. Saks V., Belikova Y., Vasilyeva E., Kuznetsov A., Fontaine E., Keriel C., and Leverve X. (1995) Correlation between degree of rupture of outer mitochondrial membrane and changes of kinetics of regulation of respiration by ADP in permeabilized heart and liver cells. Biochem. Biophys. Res. Commun. 208, 919–926 10.1006/bbrc.1995.1422 [DOI] [PubMed] [Google Scholar]
- 9. Zizi M., Forte M., Blachly-Dyson E., and Colombini M. (1994) NADH regulates the gating of VDAC, the mitochondrial outer membrane channel. J. Biol. Chem. 269, 1614–1616 [PubMed] [Google Scholar]
- 10. Anmann T., Guzun R., Beraud N., Pelloux S., Kuznetsov A. V., Kogerman L., Kaambre T., Sikk P., Paju K., Peet N., Seppet E., Ojeda C., Tourneur Y., and Saks V. (2006) Different kinetics of the regulation of respiration in permeabilized cardiomyocytes and in HL-1 cardiac cells: Importance of cell structure/organization for respiration regulation. Biochim. Biophys. Acta 1757, 1597–1606 10.1016/j.bbabio.2006.09.008 [DOI] [PubMed] [Google Scholar]
- 11. Eimre M., Paju K., Pelloux S., Beraud N., Roosimaa M., Kadaja L., Gruno M., Peet N., Orlova E., Remmelkoor R., Piirsoo A., Saks V., and Seppet E. (2008) Distinct organization of energy metabolism in HL-1 cardiac cell line and cardiomyocytes. Biochim. Biophys. Acta 1777, 514–524 10.1016/j.bbabio.2008.03.019 [DOI] [PubMed] [Google Scholar]
- 12. Díaz-Ruiz R., Avéret N., Araiza D., Pinson B., Uribe-Carvajal S., Devin A., and Rigoulet M. (2008) Mitochondrial oxidative phosphorylation is regulated by fructose 1,6-bisphosphate: a possible role in Crabtree effect induction? J. Biol. Chem. 283, 26948–26955 10.1074/jbc.M800408200 [DOI] [PubMed] [Google Scholar]
- 13. Aiston S., Trinh K. Y., Lange A. J., Newgard C. B., and Agius L. (1999) Glucose-6-phosphatase overexpression lowers glucose 6-phosphate and inhibits glycogen synthesis and glycolysis in hepatocytes without affecting glucokinase translocation: evidence against feedback inhibition of glucokinase. J. Biol. Chem. 274, 24559–24566 10.1074/jbc.274.35.24559 [DOI] [PubMed] [Google Scholar]
- 14. van Maris A. J., Bakker B. M., Brandt M., Boorsma A., Teixeira de Mattos M. J., Grivell L. A., Pronk J. T., and Blom J. (2001) Modulating the distribution of fluxes among respiration and fermentation by overexpression of HAP4 in Saccharomyces cerevisiae. FEMS Yeast Res. 1, 139–149 10.1016/S1567-1356(01)00022-8,10.1111/j.1567-1364.2001.tb00025.x [DOI] [PubMed] [Google Scholar]
- 15. de Winde J. H., and Grivell L. A. (1993) Global regulation of mitochondrial biogenesis in Saccharomyces cerevisiae. Prog. Nucleic Acids Res. Mol. Biol. 46, 51–91 10.1016/S0079-6603(08)61018-1 [DOI] [PubMed] [Google Scholar]
- 16. Forsburg S. L., and Guarente L. (1989) Identification and characterization of HAP4: a third component of the CCAAT-bound HAP2/HAP3 heteromer. Genes Dev. 3, 1166–1178 10.1101/gad.3.8.1166 [DOI] [PubMed] [Google Scholar]
- 17. Avéret N., Fitton V., Bunoust O., Rigoulet M., and Guérin B. (1998) Yeast mitochondrial metabolism: from in vitro to in situ quantitative study. Mol. Cell. Biochem. 184, 67–79 10.1023/A:1006830810440 [DOI] [PubMed] [Google Scholar]
- 18. Chevtzoff C., Yoboue E. D., Galinier A., Casteilla L., Daignan-Fornier B., Rigoulet M., and Devin A. (2010) Reactive oxygen species-mediated regulation of mitochondrial biogenesis in the yeast Saccharomyces cerevisiae. J. Biol. Chem. 285, 1733–1742 10.1074/jbc.M109.019570 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Loret M. O., Pedersen L., and François J. (2007) Revised procedures for yeast metabolites extraction: application to a glucose pulse to carbon-limited yeast cultures, which reveals a transient activation of the purine salvage pathway. Yeast 24, 47–60 10.1002/yea.1435 [DOI] [PubMed] [Google Scholar]
- 20. Sumner J. B. (1944) A method for the colorimetric determination of phosphorus. Science 100, 413–414 10.1126/science.100.2601.413 10.1126/science.100.2601.413 [DOI] [PubMed] [Google Scholar]
- 21. Smallbone K., Messiha H. L., Carroll K. M., Winder C. L., Malys N., Dunn W. B., Murabito E., Swainston N., Dada J. O., Khan F., Pir P., Simeonidis E., Spasić I., Wishart J., Weichart D., et al. (2013) A model of yeast glycolysis based on a consistent kinetic characterisation of all its enzymes. FEBS Lett. 587, 2832–2841 10.1016/j.febslet.2013.06.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Cornish-Bowden A., Mazat J.-P., and Nicolas S. (2014) Victor Henri: 111 years of his equation. Biochimie 107, 161–166 10.1016/j.biochi.2014.09.018 [DOI] [PubMed] [Google Scholar]
- 23. Hoops S., Sahle S., Gauges R., Lee C., Pahle J., Simus N., Singhal M., Xu L., Mendes P., and Kummer U. (2006) COPASI–a COmplex PAthway SImulator. Bioinformatics 22, 3067–3074 10.1093/bioinformatics/btl485 [DOI] [PubMed] [Google Scholar]