Tensorial Spherical Polar Fourier Diffusion MRI with Optimal Dictionary Learning

Abstract

High Angular Resolution Diffusion Imaging (HARDI) can characterize complex white matter micro-structure, avoiding the Gaussian diffusion assumption inherent in Diffusion Tensor Imaging (DTI). However, HARDI methods normally require significantly more signal measurements and a longer scan time than DTI, which limits its clinical utility. By considering sparsity of the diffusion signal, Compressed Sensing (CS) allows robust signal reconstruction from relatively fewer samples, reducing the scanning time. A good dictionary that sparsifies the signal is crucial for CS reconstruction. In this paper, we propose a novel method called Tensorial Spherical Polar Fourier Imaging (TSPFI) to recover continuous diffusion signal and diffusion propagator by representing the diffusion signal using an orthonormal TSPF basis. TSPFI is a generalization of the existing model-based method DTI and the model-free method SPFI. We also propose dictionary learning TSPFI (DL-TSPFI) to learn an even sparser dictionary represented as a linear combination of TSPF basis from continuous mixture of Gaussian signals. The learning process is efficiently performed in a small sub-space of SPF coefficients, and the learned dictionary is proved to be sparse for all mixture of Gaussian signals by adaptively setting the tensor in TSPF basis. Then the learned DL-TSPF dictionary is optimally and adaptively applied to different voxels using DTI and a weighted LASSO for CS reconstruction. DL-TSPFI is a generalization of DL-SPFI, by considering general adaptive tensor setting instead of a scale value. The experiments demonstrated that the learned DL-TSPF dictionary has a sparser representation and lower reconstruction Root-Mean-Squared-Error (RMSE) than both the original SPF basis and the DL-SPF dictionary.

1 Introduction

Diffusion MRI (dMRI) is a unique non-invasive imaging technique to explore white matter in human brain by measuring the diffusion of water molecules. The diffusion process is fully characterized by the diffusion propagator P(R), called the Ensemble Average Propagator (EAP), in the displacement R-space [1]. With the narrow pulse assumption, the diffusion signal attenuation E(q) is the 3D Fourier transform of P(R), i.e., P(R) = ∫_ℝ³ E(q) exp(−2πq^TR)dq. A hot topic in dMRI is to recover the continuous signal E(q) and the EAP P(R) from a limited number of signal samples with noise.

Diffusion Tensor Imaging (DTI) [2] is the most popular method for diffusion data reconstruction. With the Gaussian diffusion assumption, E(q) = exp(−4π²τq^TDq) where τ is the diffusion time and D is the 3 × 3 diffusion tensor. Many other methods, categorized as High Angular Resolution Diffusion Imaging (HARDI), were proposed to avoid the Gaussian assumption and characterize more general diffusion processes due to complex microstructure. Diffusion spectrum imaging [3] does not impose any assumption on diffusion signal, but it requires a long scan time, and only estimates diffusion signal and propagator in discretized samples, not in a continuous domain. MAP-MRI [4,5] and Spherical Polar Fourier Imaging (SPFI) [6,7] are two state-of-the-art methods, which estimate continuous E(q) and P(R) from arbitrary sampling schemes by representing E(q) using orthonormal basis functions with analytic Fourier transform.

The Compressed Sensing (CS) technique recovers a signal from measurements by considering the sparsity of the signal under a dictionary. CS methods have been proposed in dMRI to recover diffusion signal and propagator using both discretized [8] and continuous bases [7]. The most important advantage of the continuous basis representation is that it allows the analytical Fourier transform without numerical error. In CS reconstruction, a dictionary that yields sparse representation of diffusion signals plays an important role. MAP-MRI was first proposed using an isotropic tensor in its basis [4], then using a general tensor [5]. SPFI first used SPF basis [9,6], then learned an adaptive sparser dictionary based on SPF basis from continuous Gaussian signal space [7]. All those evolutions make the dictionaries in MAP-MRI and SPFI sparser and more suitable for CS reconstruction. However, existing MAP-MRI in [5] still uses manually devised basis without performing dictionary learning, and existing SPFI in [6] and DL-SPFI in [7] use isotropic Gaussian diffusion in its dictionary, which is limited to represent diffusion signals with high anisotropy.

In this paper, we propose Tensorial SPFI which generalizes SPFI [6] by considering a general adaptive tensor setting instead of using just a simple scalar value, and we also propose TSPFI with optimal dictionary learning, called DL-TSPFI, to learn an even sparser dictionary from only a small subspace of SPF coefficients of Gaussian diffusion signals. The learned dictionary is proven to be capable to sparsely represent an arbitrary mixture of Gaussian diffusion signals, by considering an adaptive tensor setting. The learned dictionary is then adaptively applied to all voxels using a weighted LASSO optimization with adaptive tensor setting from DTI for CS reconstruction. Experiments demonstrated that TSPFI and DL-TSPFI provide sparser representation and yield low RMSE in CS reconstruction than the state-of-the-art SPFI [6] and DL-SPFI [7].

2 Tensorial Spherical Polar Fourier Imaging (TSPFI)

The SPF basis is a continuous orthonormal basis that can sparsely represent Gaussianlike 3D signal [9,6]. In SPFI, the diffusion signal is represented by the SPF basis { $B_{nlm}(\mathbf{q}|\zeta )=G_n(q|\zeta )Y_l^m(\mathbf{u})$}, i.e.,

$$\begin{array}{cc}E(q\mathbf{u}|\zeta )=\sum _{n=0}^N\sum _{l=0}^L\sum _{m=-l}^l{a}_{nlm}{G}_n(q|\zeta )Y_l^m(\mathbf{u}),& G_n(q|\zeta )={\left[\frac{2n!}{{\zeta }^{3/2}\Gamma (n+3/2)}\right]}^{1/2}exp(-\frac{q^2}{2\zeta })L_n^{1/2}(\frac{q^2}{\zeta })\end{array}$$ (1)

where q = qu, u ∈ 𝕊², ζ is the scale parameter and $Y_l^m(\mathbf{u})$ is the real spherical harmonic basis. It was proven that the EAP can be analytically represented by dual SPF basis [6]:

$$\begin{array}{cc}P(R\mathbf{r}|\zeta )=\sum _{n=0}^N\sum _{l=0}^L\sum _{m=-l}^l{a}_{nlm}{F}_{nl}(R|\zeta )Y_l^m(\mathbf{r})& B_{nlm}^{\text{dual}}(\mathbf{R}|\zeta )=F_{nl}(R|\zeta )Y_l^m(\mathbf{r})\end{array}$$ (2)

where R = Rr, r ∈ 𝕊², and the definition of F_nl(R|ζ) can be found in [6]. It can be seen that B₀₀₀(q) is just an isotropic Gaussian function, which makes the SPF representation sparse for isotropic Gaussian signal E(q) = exp(−4π²τq^TDq). However it requires more basis elements to represent a Gaussian signal with a highly anisotropic tensor. The representation error is actually inevitable for any finite order N and L, although increasing the orders can reduce the representation error. DL-SPFI was proposed in [7] to learn a sparser dictionary from Gaussian diffusion signals with different mean dif-fusivity and fractional anisotropy (FA), and adaptively set the scale value ζ based on the mean diffusivity. [7] also demonstrated that the DL-SPF dictionary keeps the same level of sparsity for Gaussian diffusion with different FA, while the sparsity in SPF dictionary decreases for signals with higher FA.

Theorem 1 (TSPF Basis and Dual TSPF Basis). Let D be 3 × 3 positive definite matrix with eigen-decomposition D = Q∧²Q^T, Q^TQ = I, then { $\sqrt{|\Lambda |}{B}_{nlm}(\Lambda Q^T\mathbf{q}|\zeta )$} is an orthonormal basis set, called the Tensorial SPF (TSPF) basis. Its Fourier transform is { $\frac{1}{\sqrt{|\Lambda |}}{B}_{nlm}^{\mathit{\text{dual}}}({\Lambda }^{-1}{Q}^T\mathbf{R}|\zeta )$} called the dual TSPF basis, which is also complete and orthonormal in the dual Fourier space.

We propose Tensorial SPFI (TSPFI) to further sparsely represent Gaussian-like signals. Theorem 1 demonstrates TSPF basis and dual TSPF basis which are the affinely transformed SPF basis and dual SPF basis¹. TSPFI represents diffusion signal E(q) using TSPF basis in Eq. (3), then the diffusion propagator is analytically represented as dual TSPF basis in Eq. (4), where we set ζ₀ = (8π²τ)⁻¹ such that $\sqrt{|\Lambda |}{B}_{000}(\Lambda Q^T\mathbf{q}|{\zeta }_0)$ is proportional to Gaussian function exp(−4π²τq^TDq).

$$E(q\mathbf{u}|\mathbf{D})=\sqrt{|\Lambda |}\sum _{n=0}^N\sum _{l=0}^l\sum _{m=-l}^l{a}_{nlm}{G}_n(q)(q\sqrt{{\mathbf{u}}^T\mathbf{D}\mathbf{u}}|{\zeta }_0)Y_l^m\left(\frac{\Lambda Q^T\mathbf{u}}{\Vert \Lambda Q^T\mathbf{u}\Vert }\right)$$ (3)

$$P(R\mathbf{r}|\mathbf{D})=\frac{1}{\sqrt{|\Lambda |}}\sum _{nlm}{a}_{nlm}{F}_{nl}(R\sqrt{{\mathbf{r}}^T{\mathbf{D}}^{-1}\mathbf{r}}|{\zeta }_0)Y_l^m\left(\frac{{\Lambda }^{-1}{Q}^T\mathbf{r}}{\Vert {\Lambda }^{-1}{Q}^T\mathbf{r}\Vert }\right)$$ (4)

The representation using TSPF basis is sparse for Gaussian-like diffusion signals when we set tensor D appropriately, and the first basis is enough to represent Gaussian diffusion signals. Note that MAP-MRI basis [5] also uses an anisotropic Gaussian function as the zero order basis, while it can be proven that MAP-MRI basis can be linearly represented by the TSPF basis with a finite order, but the opposite is not true, which means TSPF basis is more general than MAP-MRI basis.

Similarly with [7], considering E(0) = 1, we have ${\sum }_0^N{a}_{nlm}{G}_n(0)=\sqrt{4\pi }{\delta }_l^0$, 0 ≤ l ≤ L, −l ≤ m ≤ l. Then we can separate the coefficient vector a into $\mathit{a}={({\mathit{a}}_0^T,{\mathit{a}\prime }^T)}^T$, where a₀ = (a₀₀₀, …, a_0LL)^T, a′ = (a₁₀₀, …, a_NLL)^T, and represent a₀ using a′, i.e.,

$$\begin{array}{ccc}{a}_{0lm}=\frac{1}{G_0(0)}(\sqrt{4\pi }{\delta }_l^0-\sum _{n=1}^N{a}_{nlm}{G}_n(0)),& 0\le l\le L,& -l\le m\le l\end{array}$$ (5)

Then based on Eq. (3), a′ can be estimated from measurements of E(q) via weighted LASSO.

$$\underset{\mathit{a}\prime }{min}{\Vert \mathbf{M}\prime \mathit{a}\prime -\mathit{e}\prime \Vert }_2^2+{\Vert \mathbf{H}\mathit{a}\prime \Vert }_1$$ (6)

$$\begin{array}{cc}\mathbf{M}\prime =\left[\begin{array}{ccc}\sqrt{|\Lambda |}(B_{100}(\Lambda Q^T{\mathbf{q}}_1|{\zeta }_0)-\frac{G_1(0|{\zeta }_0)}{G_0(0|{\zeta }_0)}{B}_{000}(\Lambda Q^T{\mathbf{q}}_1|{\zeta }_0))& \cdots & \sqrt{|\Lambda |}(B_{NLL}(\Lambda Q^T{\mathbf{q}}_1|{\zeta }_0)-\frac{G_N(0|{\zeta }_0)}{G_0(0|{\zeta }_0)}{B}_{0LL}(\Lambda Q^T{\mathbf{q}}_1|{\zeta }_0))\\ ⋮& \ddots & ⋮\\ \sqrt{|\Lambda |}(B_{100}(\Lambda Q^T{\mathbf{q}}_s|{\zeta }_0)-\frac{G_1(0|{\zeta }_0)}{G_0(0|{\zeta }_0)}{B}_{000}(\Lambda Q^T{\mathbf{q}}_S|{\zeta }_0))& \cdots & \sqrt{|\Lambda |}(B_{NLL}(\Lambda Q^T{\mathbf{q}}_S|{\zeta }_0)-\frac{G_N(0|{\zeta }_0)}{G_0(0|{\zeta }_0)}{B}_{0LL}(\Lambda Q^T{\mathbf{q}}_S|{\zeta }_0))\end{array}\right],& \mathit{e}\prime =\left[\begin{array}{c}{E}_1-exp(-4{\pi }^2\tau {\mathbf{q}}_1^T\mathbf{D}{\mathbf{q}}_1)\\ ⋮\\ E_S-exp(-4{\pi }^2\tau {\mathbf{q}}_S^T\mathbf{D}{\mathbf{q}}_S)\end{array}\right],\end{array}$$

where {E_i} are signal measurements in q-space, e′ is the measurement vector removing its Gaussian part, M′ is the basis matrix used for reconstruction, H is the regularization matrix. After estimating a′, a₀ can be obtained using Eq. (5), then E(0) = 1 is automatically satisfied. For Gaussian diffusion signal, if D is estimated correctly, then e′ = 0, a′ = 0, and only a₀₀₀ is non-zero. Thus Eq. (6) mainly focus on the non-Gaussian fitting.

3 TSPFI with Optimal Dictionary Learning (DL-TSPFI)

Based CS theory [10], a dictionary with sparser representation gives better reconstruction. Following DL-SPFI in [7], we consider a more general formulation:

$$\underset{\mathit{c}}{min}{\Vert \mathbf{M}\prime \mathbf{W}\mathit{c}-\mathit{e}\prime \Vert }_2^2+{\Vert \mathbf{V}\mathit{c}\Vert }_1.$$ (7)

Note that Eq. (7) actually considers a general dictionary represented as a linear combination of TSPF basis, i.e., M′W, where W is the combination matrix and c is the new coefficient vector under transformed dictionary. When W is identity, Eq. (7) becomes TSPFI in Eq. (6). As we discussed that MAP-MRI basis can be linearly represented by TSPF basis, W can be specifically designed such that M′W is the MAP-MRI basis removing its Gaussian part, then Eq. (7) becomes MAP-MRI.

Instead of using specific W in TSPFI and MAP-MRI, we would like performing dictionary learning to learn a good W as well as a good dictionary M′W from a set of given signals { ${\mathit{e}}_i^{\prime }$}. such that the representation {c_i} are all sparse, i.e.

$$\begin{array}{cc}\underset{\mathbf{C},\mathbf{W},\mathbf{D}}{min}\sum _i{\Vert {\mathit{c}}_i\Vert }_1& \text{s.t}.{\Vert \mathbf{M}\prime \mathbf{W}{\mathit{c}}_j-{\mathit{e}\prime }_j\Vert }_2\le \in ,\forall j.\end{array}$$ (8)

Considering real data always suffers from noise and a limited number of samples, similarly with [7], we perform dictionary learning in synthetic mixture of Gaussian signals. Considering simulated signals can be generated in continuous q-space and TSPF basis is an orthonormal basis showed in Theorem 1, Eq. (8) is equivalent to Eq. (9), where the dictionary learning can be performed in the space of TSPF coefficients with a small dimension, not the space of simulated measurements of E(q) with infinite dimension.

$$\begin{array}{cc}\underset{\mathbf{C},\mathbf{W},\mathbf{D}}{min}\sum _i{\Vert {\mathit{c}}_i\Vert }_1& \text{s.t}.{\Vert \mathbf{W}{\mathit{c}}_j-{\mathit{a}\prime }_j\Vert }_2\le \in ,\forall j.\end{array}$$ (9)

The learned result (W*, D*) is actually determined by the chosen space of diffusion signals. We have several theoretical results to design a small space for training data to learn a general dictionary. 1) Theorem 2 proved that the single tensor model { $E(\mathbf{q})=exp(-4{\pi }^2\tau {\mathbf{q}}^T\mathbf{D}\mathbf{q})|\mathbf{D}\in {\text{Sym}}_{+}^3$}, where ${\text{Sym}}_{+}^3$ is the space of 3 × 3 positive definite matrices, is sufficient to learn a dictionary to sparsely represent signals from mixture of tensor models. The theorem works for both DL-SPFI in [7] and DL-TSPFI. 2) Theorem 3 shows that the dictionary (W*, D*) can be learned from a small space $S_0\subset {\text{Sym}}_{+}^3$, then the learned dictionary can be affinely transformed to another tensor space. Note that for every single Gaussian signal, the sparsest c is 0 once we set the tensor D correctly. However this does not help us to handle arbitrary mixture of Gaussian signals with noise where a single tensor D cannot fully represent all Gaussian components. Thus we have to learn a common dictionary for a subspace of ${\text{Sym}}_{+}^3$, such that even when the tensor D is not correctly set, the learned dictionary still yields a sparse representation. 3) Theorem 4 demonstrated that we can fix a tensor D₀ and learn a sparse dictionary W* from Gaussian signals with D in a geodesic ball d(D₀, D) < Δ[11]. Then the learned dictionary can be adaptively applied to Gaussian signals with D in another geodesic ball d(D₁, D) < Δ by adaptively setting tensor in TSPF basis as D₁. The geodesic ball actually mimics the difference between the tensor used in TSPF basis and the ground truth tensor in each Gaussian component in the mixture of Gaussian model.

Theorem 2 (Sparsity of Mixture of Tensors [7]). A dictionary learned from signals generated by single tensor model can sparsely represent signals generated by arbitrary mixture of tensor model.

Theorem 3 (Optimal Dictionary). For signals generated from the single tensor model with tensors {exp(−4π²τq^TDq) | D ∈ S₀}, if the dictionary {W*, D*} is the optimal solution for (9), then for another space {exp(−4π²τq^TADA^Tq) | D ∈ S₀} with non-singular A, {W*, AD*A^T} is still the optimal solution.

Theorem 4 (Traning Space and Adaptive Tensor). Let D₀ be a fixed tensor. If training signals are from {exp(−4π²τq^TDq) | d(D₀, D) < Δ}, where d(D₀, D) is the Riemannian distance between D₀ and D [11], and if we set D* = D₀ and estimate W* in dictionary learning, then (W, D₁) can sparsely represent signals from {exp(−4π²τq^TDq) | d(D₁, D) < Δ}

Because of Theorem 4, it is possible to choose any D₀ and generate signals from the geodesic ball of D₀. In practice, in order to better mimic the representation error of tensors, we simply set D₀ = 0.7 × 10⁻³I as a typical isotropic tensor in human brain, and then generated Gaussian signals with mean diffusivity (MD) in range [0.5, 0.9] × 10⁻³mm²/s, FA in range [0, 0.9], uniformly orientated in 321 directions from sphere tessellation. Note that we used a relatively small range of MD, while a relatively large range of FA. It is because when using a tensor model to fit a mixture of Gaussian signal, the MD value of the tensor model normally has relatively less error than its FA value compared to the ground truth MD and FA in each Gaussian component. For example, considering a mixture of three Gaussian functions with FA = 0.9 and MD = 0.7 × 10⁻³ respectively along x, y and z axises, after DTI fitting, the estimated MD is still close to 0.7 × 10⁻³, but the estimated FA is close to 0. Note that when choosing isotropic D₀, the TSPF coefficients {a_i} become SPF coefficients with the corresponding scale, and the dictionary learning process is the same as the one used in DL-SPFI [7]. The SPF coefficients of the Gaussian signals were calculated via numerical inner product with N = 4, L = 8. Then we performed an efficient online learning method implemented in the SPAMS toolbox [12] to learn W with 250 atoms using the initialization of identity matrix. We added the atoms ${\{B_{n00}(\mathbf{q})\}}_{n=1}^N$ back to sparsely represent isotropic signals. Thus we have total 254 columns in the learned W. Then we estimated the energy {h_j} of dictionary atoms via the coefficients {c_i}, and set V in Eq. (7) as a diagonal matrix with elements $V_j=\frac{S}{h_j}\lambda$, where λ is a tuning regularization parameter, S is the dimension of measurements. This is to penalize the dictionary atom with low energy of coefficients. With the learned W and V, Eq. (7) first performs DTI to estimate a tensor D for TSPF basis matrix M′, then performs weighted LASSO for CS reconstruction of c, then a′ = Wc, and a can be obtained accordingly based on Eq. (5).

4 Experiments

Signal Sparsity in Miture of Gaussian Model

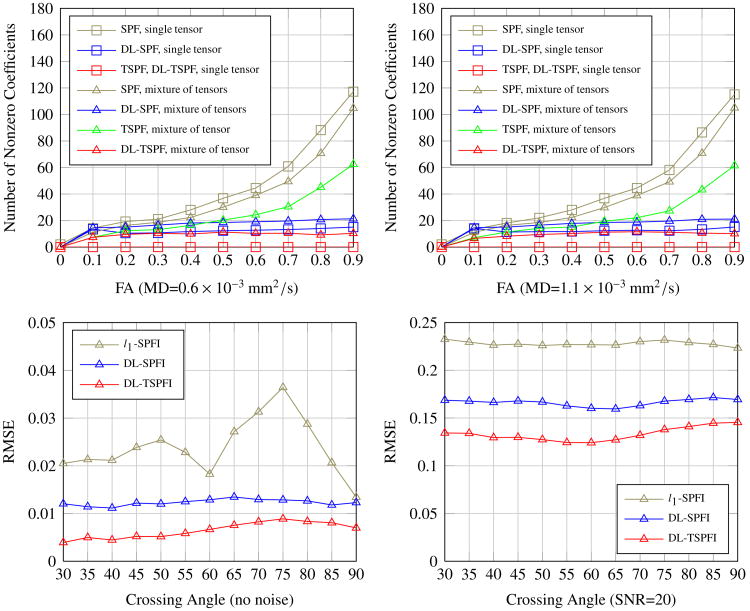
We would like to demonstrate the importance of adaptive tensor setting and validate the theorems. We generated Gaussian diffusion signals with different FA in range [0, 0.9], along different directions, and with two MD values respectively 0.6 × 10⁻³ and 1.1 × 10⁻³. These signals from single tensor model with the same FA and MD but different orientations were also randomly mixed to obtain mixture of Gaussian signals. Then with N = 4, L = 8, we performed adaptive scale setting to obtain adaptive SPF basis and DL-SPF basis, and performed adaptive tensor setting to obtain adaptive TSPF basis and DL-TSPF basis. Then for each signal, we calculated the coefficients a′ respectively for SPF basis and TSPF basis using numerical inner product, then calculated the coefficients c respectively for DL-SPF and DL-TSPF basis using Eq. (9). For the obtained coefficients under each basis, we calculated the number of non-zero values as the sparsity of the representation. The value in a′ or c is considered to be non-zero if its absolute value is larger than 0.01‖a′‖ or 0.01 ‖c‖. The sparsity of signals with two MD values were showed in the top two subfigures of Fig. 1. The top left subfigure showed that although DL-TSPF basis was learned from signal Gaussian diffusion signals, it can sparsely represent signals from mixture of Gaussian functions, which validated Theorem 2 The top right subfigure showed that although the MD value 1.1 × 10⁻³ is outside of the MD range used in dictionary learning, the sparse representation still holds by adaptively setting diffusion tensor in DL-TSPF basis, which validates Theorem 3 and 4. Both subfigures demonstrated the DL-TSPF basis obtains sparser representation than DL-SPF basis [7], and TSPF basis is sparser than SPF basis.

Fig. 1. Synthetic Experiments.

First row: the average number of non-zero coefficients for SPF, DL-SPF, TSPF and DL-TSPF basis. Second row: RMSE of different methods using the Söderman cylinder model with and without noise.

RMSE in Cylinder Model

We evaluated the different basis using the Soderman cylinder model [13] which is different from the Gaussian signals used in dictionary learning. Using the DSI sampling scheme in [8] with b_max = 8000s/mm², 514 measurements, we generated ground truth DWI signals from the cylinder model with the default parameters in [13]. Then we estimated the coefficients under different basis from an under-sampled dataset with 170 samples and reconstructed the DWI signals in all 514 samples. Root-Mean-Square Error (RMSE), which is defined based on the difference of the estimated signal and ground truth signal in these 514 samples, was used to quantify the reconstruction accuracy. We also added Rician noise with signal-to-noise ratio (SNR) of 20 and performed Monte-Carlo simulation. We set λ = λ_l = λ_n = 10⁻⁸ for the noise-free dataset and 10⁻⁵ for the noisy dataset for all methods. The second row of Fig. 1 indicates that DL-TSPFI yields the lowest RMSE than DL-SPFI and L1-SPFI in both noiseless and noisy conditions.

RMSE in Real Data

We also tested CS reconstruction using DL-TSPFI on a real DSI data set released by Bilgic ², which was also used to validate DL-SPFI [7]. This dataset uses the same DSI sampling scheme as the above cylinder data experiment. With DL-SPFI and DL-TSPFI, we perform CS reconstruction with λ = 10⁻⁶ respectively using full 514 measurements and a subset of 170 samples, then we calculated two RMSEs, one is based on the difference of coefficients using full measurements and the subset of measurements, and the other one is based on the difference of recovered DWI signals in these 514 points using full samples and subsamples. Fig. 2 showed that DL-TSPFI obtains less RMSE than DL-SPFI, especially for RMSE defined using coefficients in white matter area.

Fig. 2. Real Data Experiment.

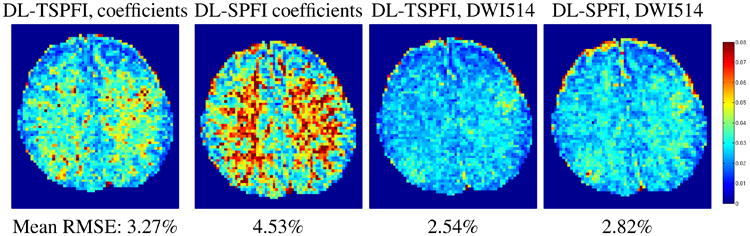
RMSE calculated from estimated SPF coefficients and recovered 514 DWI samples.

5 Conclusion

In this paper, we propose a novel Tensorial SPFI (TSPFI) which allows a continuous representation for both the diffusion signal and the diffusion propagator. TSPFI is a combination of existing DTI and SPFI. We also propose a dictionary learning strategy, called DL-TSPFI, to learn a sparser dictionary from mixture of Gaussian signals. The learned dictionary can be optimally and adaptively applied to different voxels by adaptive tensor setting. The proposed TSPFI and DL-TSPFI yield a sparser representation with lower CS reconstruction error than existing SPFI and DL-SPFI. The source codes of TSPFI and DL-TSPFI will be available in the DMRITool package³.