Summary
Mounting neural evidence suggests that, in situations in which there are multiple potential targets for action, the brain prepares, in parallel, competing movements associated with these targets, prior to implementing one of them. Central to this interpretation is the idea that competing viewed targets, prior to selection, are rapidly and automatically transformed into corresponding motor representations. Here, by applying target-specific, gradual visuomotor rotations, and dissociating, unbeknownst to participants, the visual direction of potential targets from the direction of the movements required to reach the same targets, we provide direct evidence for this provocative idea. Our results offer strong empirical support for theories suggesting that competing action options are automatically represented in terms of the movements required to attain them. The rapid motor encoding of potential targets may support the fast optimization of motor costs under conditions of target uncertainty and allow the motor system to inform decisions about target selection.
Keywords: action, decision-making, motor planning, parallel encoding, reaching, visuomotor adaptation
Introduction
During the course of any given day, we make myriad decisions about which action, from among those immediately available to us, to perform next. It has been shown, in the context of goal-directed reaching (Cisek and Kalaska, 2005; Cui and Andersen, 2011; Klaes et al., 2011), that competing potential targets elicit separate neural representations in sensorimotor brain areas prior to one of the targets being selected. One influential but controversial idea, which resonates with Gibson’s notion of action affordances (Gibson, 1979), is that this activity represents competing motor representations associated with the targets (Cisek, 2007; Cisek and Kalaska, 2010). However, given that these brain areas exhibit both sensory- and motor-related response properties, it is also possible, and difficult to rule out, that this neural activity instead represents purely visual or spatial information about the targets (Ochiai et al., 2002; Pesaran et al., 2006; Pearce and Moran, 2012).
Behavioural studies have investigated the encoding of competing reach targets using variants of the ‘go-before-you-know’ task, in which individuals are required to launch a movement towards two or more potential targets before knowing the final target. In such tasks, participants often exhibit spatial averaging behaviour whereby reaches are initially aimed towards the midpoint of the distribution of potential targets (Ghez et al., 1997; Chapman et al., 2010a; Gallivan et al., 2011), which is effective in terms of reducing the cost of the in-flight corrective actions required once the target is selected following movement (Hudson et al., 2007; Stewart et al., 2013; Haith et al., 2015a). A fundamental question, with important ramifications for understanding the mechanisms underlying both movement planning and decision making, is how spatial averaging behaviour emerges. One possibility is that, when presented with competing potential targets, the brain prepares and then executes a movement in the average visual direction of these targets. From a computational perspective, this ‘visual encoding’ strategy could be viewed as advantageous, as it would not require that the brain devote further resources to forming motor representations of each potential reach target. However, it is also possible that the brain does, in fact, form motor representations of each potential target and then prepares a movement based on these representations. According to this alternative ‘motor encoding’ account, spatial averaging could arise either from averaging the movement parameters (i.e., the initial movement directions or the final hand positions) of reach plans formed for each potential target, or from computing an optimal movement based on motor representations of these targets. In instances in which the target is selected prior to movement onset, such motor encoding may facilitate the rapid launching of the associated movement (Cisek, 2007; Gallivan et al., 2015, 2016a). Moreover, the motor encoding of potential targets could also provide a mechanism through which movement-related parameters (e.g., costs) are factored into decisions among competing options (Cos et al., 2012).
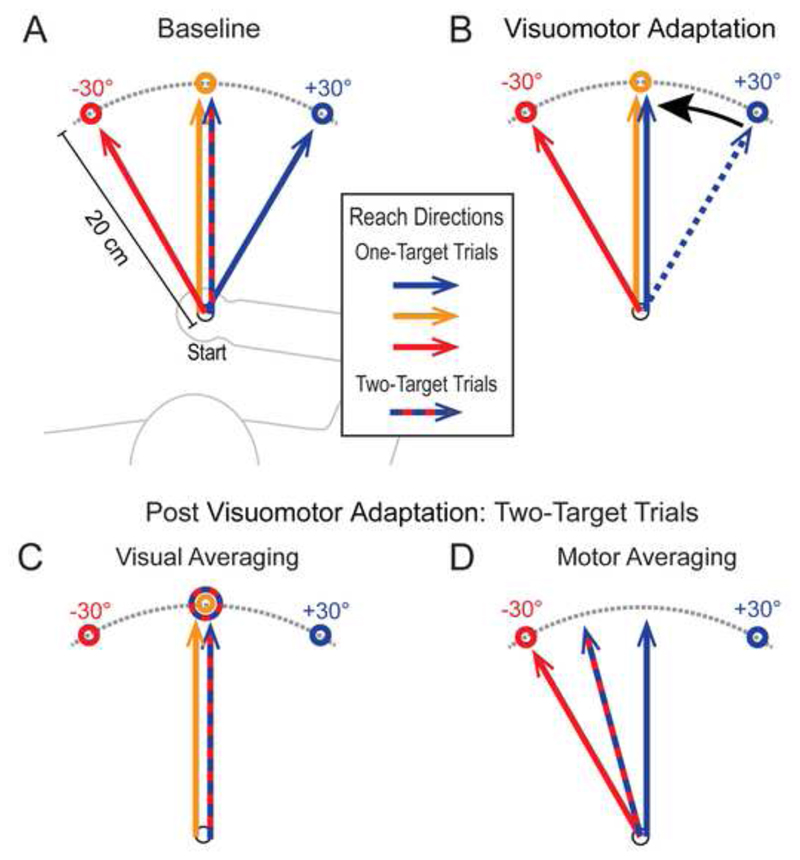
To determine which of these above accounts is correct (i.e., visual versus motor encoding of potential targets), we designed an experimental task in which participants moved the handle of a robotic manipulandum in a horizontal plane to move a virtual cursor from a start position towards one or two potential targets (see Methods for details). In the key trials in our experiment, participants performed reaching movements toward single targets located at -30, 0 and +30°, as well as ‘go-before-you-know’ reaches towards two potential targets located at -30° and +30°. In the baseline condition, we found that participants reached directly towards single targets (solids lines, Fig. 1A), and launched reaches in the spatially averaged direction in two-target trials (striped arrow, Fig. 1A). Such behavior, as noted above, is consistent with both the visual and motor encoding of potential targets. So, to directly test between these alternate accounts, we then gradually adapted participants to visuomotor rotations such that they unwittingly produced identical straight ahead (~0°) one-target movements for both the 0° and +30° targets (Fig 1B, see also Hirashima and Nozaki, 2012). Here, following adaptation, the visual and motor encoding hypotheses now make different predictions with respect to the initial movement direction in two-target trials. The visual encoding hypothesis predicts that the initial direction will be towards the spatial midpoint of the targets (striped arrow, Fig. 1C), because the visually averaged direction is ~0° and reaches to the 0° target are unaffected by the applied visuomotor rotations. In contrast, the motor encoding hypothesis predicts that the initial direction (striped arrow, Fig. 1D) should be midway between the adapted one-target movement towards the +30° target (blue arrow, Fig. 1D) and the (non-adapted) one-target movement towards the -30° target (red arrow, Fig. 1D). Critically, we applied the visuomotor rotations gradually so that participants were unaware of the dissociation between their visual and motor space. In addition, participants were required to initiate reaches as soon as the targets were presented. These two features of the task, importantly, guard against the use of deliberate cognitive strategies (Stewart et al., 2014; c.f. Gallivan et al., 2015), and allow us to assess whether putative motor encoding is automatic (i.e., non-conscious) in nature. We also removed performance feedback in these two-target trials so as to prevent any error feedback learning (c.f. Stewart et al., 2014).
Figure 1. Experimental paradigm and hypotheses.
(A) Predicted initial reach directions for one- and two-target trials involving the -30°, 0° and +30° targets prior to adaptation to visuomotor rotations (Day 1 of testing). A straight ahead initial movement in -30/+30° two-target trials (striped arrow) is expected regardless of whether participants aim for the average target position (visual averaging) or execute an average of movement paths for the two potential targets (motor averaging). (B) Predicted initial reach directions following adaptation to visuomotor rotations gradually applied to the 0 and +30° targets and designed such that participants moved their hands straight ahead (~0°) for both the 0 and +30° targets, and directly to the -30° target, in one-target trials (Day 2 of testing). (C) Under visual averaging, the initial movement direction in -30/+30° two-target trials should be straight ahead if participants aim for the average visual target position (striped arrow) (D) Under motor averaging, due to this compression of motor space, the initial movement direction in -30/+30° two-target trials (striped arrow) should be rotated leftward if participants execute an average of the potential motor paths.
Results
On Day 1 of testing, the purpose of which was to obtain baseline performance measures, participants completed the pre-adaptation phase. Here, in each trial, either one target (-30, -15, 0 and +30°) or two potential targets (with the left target at -30° and the right target at -20, -10, 0, +10, +20, or +30°) were presented and, immediately following target presentation, an auditory beep cued participants to initiate a movement towards the target(s). Importantly, the actual target (randomly selected in two-target trials) was only cued (filled-in) at movement onset. For each target display, visual feedback was removed on half of the trials.
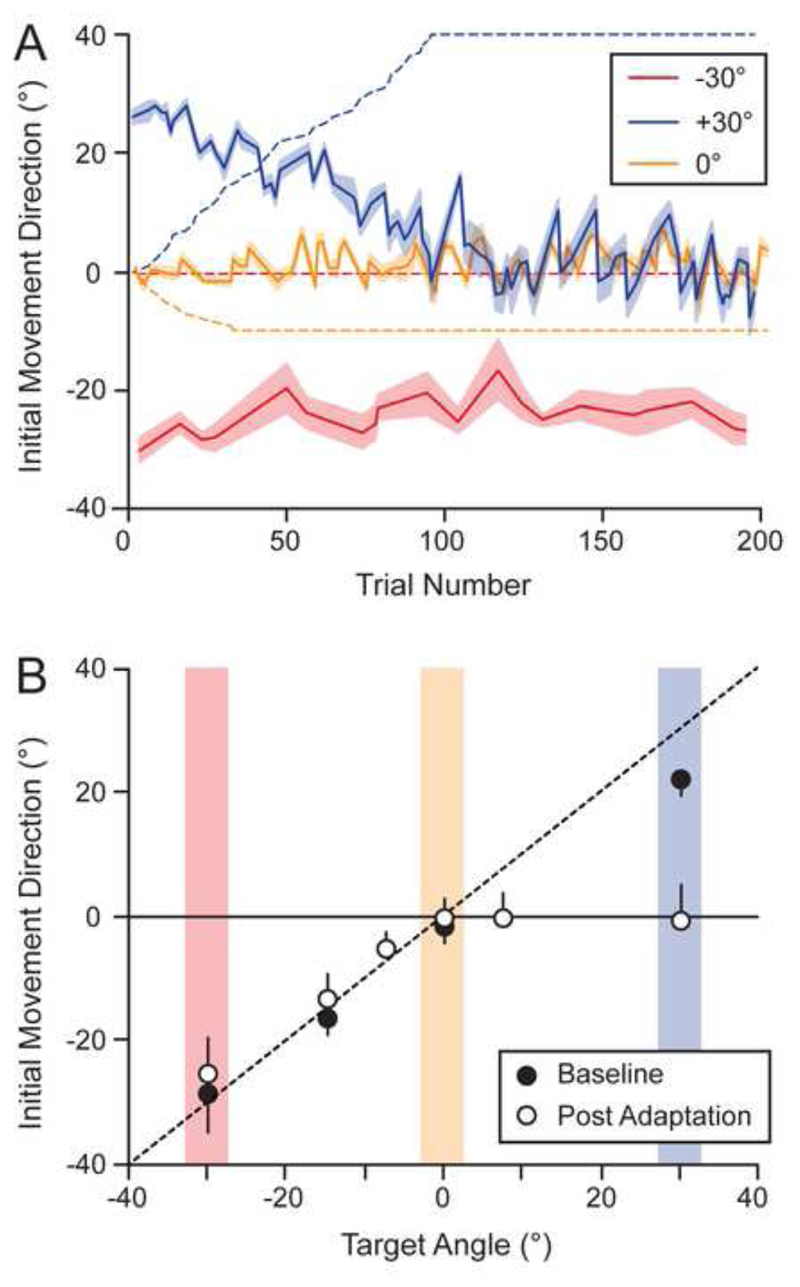
On Day 2 of testing, participants completed the adaptation and post-adaptation phases. During the adaptation phase, we gradually applied opposing visuomotor rotations (up to +40 and -10°, respectively) to the +30 and 0° targets (dashed lines, Figure 2A). This caused the participants to adapt the initial direction of their movements for the 30° target while maintaining the initial reach direction for the -30 and 0° targets (solid lines, Figure 2A). Critically, we found that during the latter half of the adaptation trials, during which the visuomotor rotations were held constant, participants’ initial movement directions were approximately straight ahead (0°) for both the 0° and +30° targets and approximately in the direction of the target for the -30° target. Notably, during post-experiment debriefing, participants reported being unaware of the visuomotor rotations being applied.
Figure 2. Initial movement directions during and after visuomotor adaptation.
(A) Direction of the robot handle, relative to the start position, at 30% of the distance to the targets as a function of trial number during the adaptation phase. The red, orange and blue lines represent one-target trials involving the -30, 0, and +30° targets, respectively. Each line represents the mean across participants and the shaded region represents ±1 SE. The colour-matched dashed lines show the visuomotor rotations applied to each target. Note that the +40° and -10° rotations were increased linearly over each trial of the +30° and 0°, respectively, and the rotations applied appear jagged in the plot due to the spacing of these trials among the other trials (B) Average initial movement direction for one-target trials (based on participant medians) as a function of target angle during baseline testing on Day 1 (black circles) and after adaptation on Day 2 (white circles). The dashed line is the unity line and the vertical black lines represent either plus or minus 1 SD.
During the post-adaptation phase, participants then completed two-target trials, all without visual feedback of the cursor, and one-target trials (at -30, -15, -7.5, 0, +7.5, and +30° targets) both with and without this visual feedback (see Supplemental Results and Fig. S1). Figure 2B shows the average initial movement direction for one-target trials as a function of target angle during baseline testing on Day 1 (black circles) and after adaptation on Day 2 (white circles). On Day 1, we found that movements were aimed approximately in the direction of the targets. On Day 2, following adaptation to the visuomotor rotations applied to the +30 and 0° targets, we instead found that movements to the 0, +7.5, and +30° targets tended to be directed straight ahead (0°) whereas movements to the -30, -15 and -7.5° targets were approximately in the direction of the target (Fig. 2B).
The fact that participants learned to produce similar straight-ahead movements for separate visual target locations (i.e., the 0° and +30° targets) allowed us to critically test whether, when simultaneously presented with competing +30° and -30° targets, initial movement directions correspond to the average visual direction of the potential targets (visual averaging) or, rather, the average direction of the movement paths towards the potential targets (motor averaging). That is, if a participant aimed to the average target position, we would expect the initial movement direction to be roughly straight ahead because movements towards the 0° target location were not rotated away from that position (striped arrow, Fig. 1C). Conversely, if the initial movement corresponds to an average of the constituent single-target movement directions, we would expect the initial direction to be biased to the left (i.e., rotated counter clockwise) because of the visuomotor rotation applied to the +30° target (striped arrow, Fig. 1D).
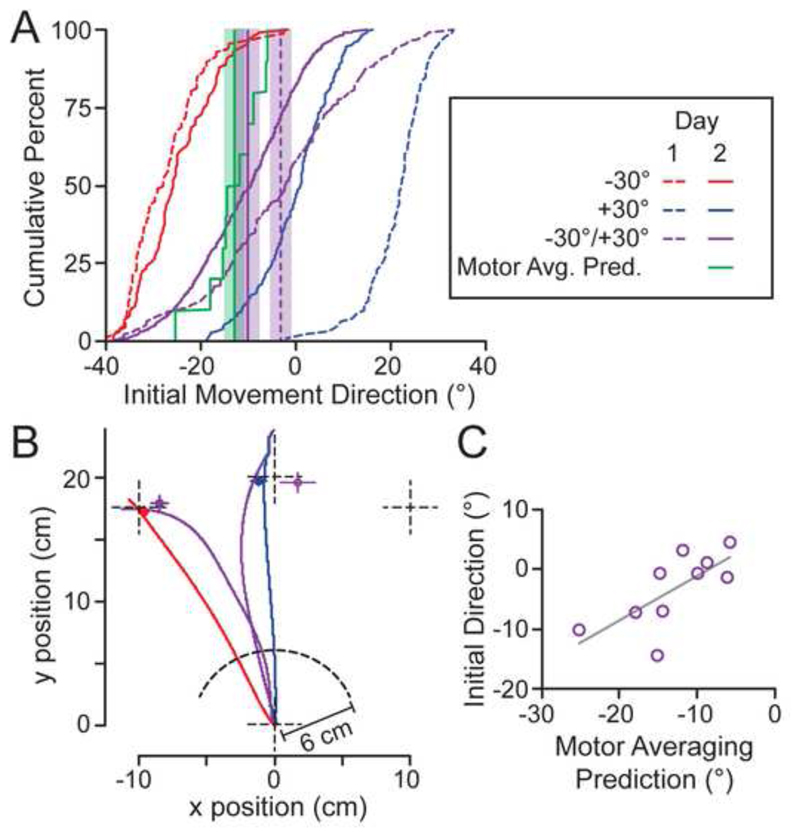
Figure 3A shows cumulative distributions, combining data from all participants and trials, of initial movement directions in one- and two-target non-visual feedback trials involving the -30 and +30° targets, with separate distributions shown for the Day 1 baseline (dashed lines) and Day 2 post-adaptation phases (solid lines). Consistent with previous work, we found that the distribution of initial directions in -30/+30° two-target trials on Day 1 (dashed purple line) was centered close to 0° (Chapman et al., 2010a; Gallivan et al., 2011; Stewart et al., 2014). Critically, however, the distribution for these trials on Day 2 (solid purple line) was shifted significantly leftward (i.e., counterclockwise). Figure 3B shows representative Day 2 hand paths, from a single participant, for -30 and +30° one-target trials, and for -30/+30° two target trials in which either the -30 or +30° target was selected. The open circles show, for each of these trial types, the mean endpoint positions, averaged across participant medians, at which participants ‘clicked’ the handle, believing they had reached the target. To quantify the shift in the initial direction of -30/+30° two-target trials, we computed, for each participant, the median direction in these trials on Days 1 and 2 (see dashed- and solid-lined vertical purple lines in Fig. 3A, respectively). A paired t-test using these median values revealed that the direction on Day 2 (M = -10.25°; SE = 2.12°) was significantly less (t9 = -2.79; p = 0.021) than on Day 1 (M = -3.26°; SE = 1.92°). This shift in initial direction is consistent with the motor averaging hypothesis. Furthermore, this shift is inconsistent with the visual averaging hypothesis, if we assume (under the visual averaging hypothesis) that movements directed towards the visual averaged target are largely unaffected by the visuomotor rotations. [See the Supplemental Information and Fig. S2, where directly test the visual averaging hypothesis and show that this hypothesis is not consistent with our results].
Figure 3. Test of the motor averaging hypothesis.
(A) Cumulative distributions of initial movement directions (i.e., handle direction at 30% of the target distance) and the predicted initial movement direction on Day 2 assuming motor averaging. Note that the distribution for the motor averaging prediction is based on a single value per participant (N=10). The vertical lines show mean initial directions for the -30/+30° trials on Days 1 and 2 and the predicted motor average on Day 2. The width of the shaded regions represent ± 1 SD. The legend applies to all panels. (B) Representative hand paths from a single participant in trials without visual feedback following adaptation on Day 2. Note that movement corrections in 2-target trials (purple traces) occurred after the hand travelled 6 cm or 30% of the distance to the targets. The circles represent the mean reach endpoint locations (i.e., handle ‘click’ positions), based on participant medians, for the four trial types; the x and y error bars represent ± 1 SE. The dashed cross-hairs indicate the locations of the -30, 0, and +30° targets and the start position. (C) Relation between median initial movement direction in -30/+30° trials on Day 2 and the Day 2 motor averaging prediction. Each point represents a participant and the grey line is the linear regression line (r = 0.70, p = 0.024).
To directly test the idea that the reaches executed towards multiple potential targets are predicted by a weighted average of the movement paths to each single target individually (i.e., a motor average), we computed, from the one-target trials, the initial reach direction that we would expect to observe in -30/+30° two-target post-adaptation trials if this was indeed the case. To derive this predicted direction, we first developed a weighting, for each participant, based on their initial directions in -30° and +30° one-target pre-adaptation trials without cursor feedback (from Day 1). The weighting (w), which captures participants’ inherent trajectory biases in the -30°/+30° two-target trials, was computed as follows: w = (Θ-30/+30° – Θ-30°)/(Θ30° – Θ-30°), where Θ is the initial direction and a value above 0.5 indicates a rightward (or clockwise) bias. We then applied this subject-specific weighting to the initial directions in post-adaptation –30° and +30° one-target trials without cursor feedback (from Day 2) to obtain the predicted motor average direction for each participant. (Note that in carrying out this procedure for each participant, we used median values for each trial type.) The weights across participants ranged from 0.34 to 0.62, with an average of exactly 0.50.
The green curve in Fig. 3A shows the cumulative distribution of this predicted motor average on Day 2. Note that, because this distribution is based on a single value per participant, this distribution is composed of 10 unique values, equaling the total number of participants analyzed. Overall, we found that the predicted motor average (mean = -13.04°, SE = 1.85, see green vertical line in Fig. 3A) was highly similar to the initial movement direction (mean = -10.25°) in -30/+30° two-target Day 2 trials, and a paired t-test failed to reveal any significant difference (t9 = 1.79, p = 0.11) between the two. Further analysis showed a significant linear relationship (r = 0.70, p = 0.024) between this predicted motor average and the actual reach movements executed towards the competing targets (Fig. 3C). This finding, combined with all the results presented above, provides compelling evidence for the idea that individuals, when presented with multiple action options, generate initial reach vectors that closely resemble an average vector of the movements toward each target individually.
Because the visuomotor rotations were introduced gradually, such that participants would not be aware of the rotations, adaptation should be driven by implicit processes without a contribution from explicit or cognitive processes (McDougle et al., 2015, 2016). As a consequence, we would not expect to observe an increase in reaction time (i.e., the time from target presentation to reach onset) from the baseline phase on Day 1 to the post-adaptation phase on Day 2 (Fernandez-Ruiz et al., 2011; Haith et al., 2015b). To assess this prediction, for each participant we computed, for each phase, the median reaction time in one-target trials (-30, 0 and 30° trials) and two-target trials (-30°/+30° trials). A phase by target number repeated measures ANOVA revealed that, in fact, reaction time was significantly shorter (F1, 9 = 18.3; p = 0.002) in the post-adaptation phase (M = 271 ms, SE = 9 ms) than in the baseline phase (M = 307 ms, SE = 9 ms). We found no effect of target number (F1, 9 = 1.54; p = 0.246) and no interaction (F1, 9 = 4.10; p = 0.074). The decrease in reaction time across days, which may reflect general learning of the task, clearly supports the idea that participants adapted to the visuomotor rotations implicitly and without conscious awareness.
Discussion
Here we found, using a visuomotor adaptation task that dissociated the viewed spatial locations of potential targets from their corresponding reach directions, that the initial direction of reaches rapidly launched towards two potential targets (i.e., under conditions of target uncertainty), constitutes a weighted average of the reach directions associated with the two targets when presented individually (i.e., under conditions of target certainty). This finding indicates that the competing potential targets were rapidly and automatically mapped onto the corresponding motor representations prior to movement selection.
There are several key features of the current task that allow for a robust conclusion that the mapping of viewed potential targets into motor coordinates occurs both rapidly and automatically. First, because the visuomotor rotations were applied gradually, participants were unaware of the dissociation between target and reach directions. Second, participants were required to launch reaches immediately after target presentation. These two features make it highly unlikely that participants would have implemented a deliberate strategy to handle the visuomotor dissociation. Third, because of the large number of different one- and two-target configurations employed, it is improbable that participants could have developed rote responses to the two-target configurations. Finally, participants never received visual feedback of the cursor in two-target trials following adaptation to the visuomotor rotations, and therefore we can rule out the possibility that they learned to generate motor averaged responses based on error feedback. Note that the current task has several advantages over a previous study we carried out in which we dissociated target and initial reach directions using an obstacle (Stewart et al., 2014). Whereas the previous results were consistent with motor encoding, other possible interpretations could not be ruled out (see Supplemental Discussion).
We suggest that, under conditions of target uncertainty, the rapid, automatic motor encoding of targets can support the specification of initial movement directions that tend to optimize motor costs. One possibility, consistent with optimal feedback control models (Todorov and Jordan, 2002), is that the motor system computes an initial movement, based on motor representations of the targets (e.g., the hand positions associated with the targets), that minimizes the ultimate cost of corrected movements to the targets once they are selected (Hudson et al., 2007; Stewart et al., 2013; Haith et al., 2015a). Another possibility is that the motor system averages components of the reach plans specified for the potential targets, such as the initial directions or final hand positions, when generating an initial movement towards these targets. This latter ‘multiple plans’ account could provide an approximate optimization of the motor costs. In addition, in situations in which the target is selected before movement onset, forming multiple plans may facilitate the rapid launching of reaches once the target is selected (Gallivan et al., 2015), and may provide key information for deciding which reach option to select in the first place (Cos et al., 2011, 2012; Cisek and Pastor-Bernier, 2014). (Note that whereas spatial averaging behaviour in the context of eye movements may arise from the simultaneous execution of competing movement plans (McPeek et al., 2000, 2003), because of the inherent complexity of arm movement planning and control, we do not believe this is a plausible account of averaging in the case of reaching.)
Our results are consistent with a recently described model in which, under similar conditions of target uncertainty, an optimal feedback control policy is calculated for each potential target and a weighted average of these policies is computed, for each moment in time, based on the relative desirability of the competing targets (Christopoulos and Schrater, 2015). This model not only predicts the averaging of feedback gains for competing targets (as shown in Gallivan et al., 2016b) but also the trajectory averaging frequently observed during both eye and hand movements (e.g. Chou et al., 1999; e.g. Chapman et al., 2010b). In summary, our findings support the hypothesis that, prior to target selection and subsequent movement execution, competing potential reach targets are rapidly and automatically transformed into corresponding motor representations (Cisek, 2007). These behavioural findings provide for a strong interpretation of the results of recent neurophysiological studies showing that multiple spatial goals are represented in sensorimotor regions of the brain (Klaes et al., 2011; Grent-’t-Jong et al., 2015; Dekleva et al., 2016); namely that this activity directly reflects movement-related parameters associated with these goals.
Experimental Procedures
Participants
Sixteen right-handed individuals (5 males) between 18 and 26 years of age completed the full experiment after providing informed written consent. The participants were recruited from the population of undergraduate and graduate students at Queen’s University and received financial compensation for their time. The Queen’s University General Ethics Board approved all experimental procedures.
On Day 1 of testing, participants completed the pre-adaptation phase of the experiment in which they performed one-target trials and two-target ‘go-before-you-know’ trials. Previous studies have shown that when initiating reaches toward two potential targets, many participants aim towards the midpoint and then make a correction towards the cued target (Chapman et al., 2010a, 2010b; Stewart et al., 2013, 2014; Gallivan and Chapman, 2014). However, a third to a half of all participants do not exhibit consistent trial-to-trial averaging behaviour and, instead, will at least occasionally adopt a strategy that involves picking one of the two potential targets to aim towards (Stewart et al., 2013, 2014). Because spatial averaging behaviour is a prerequisite for testing our hypotheses (noted above), we screened 28 participants on Day 1 and continued with those who, based on visual appraisal, exhibited robust trial-to-trial spatial averaging, resulting in 16 participants. Given the importance of participants properly adapting to the applied visuomotor rotations on Day 2 for testing our hypotheses (also noted above), only individuals who successfully adapted and maintained this adaptation throughout post-adaptation phase, as assessed by examining cumulative distributions of initial movement directions (see Stewart et al., 2014), were included for analysis (10 participants). Although we selected participants whose performance characteristics allowed for a clear and unambiguous test of our hypotheses, it is important to emphasize that the basic conclusions drawn from the current study are not limited to these participants and the selection criteria by which the participants were selected cannot bias the results.
Apparatus
Seated participants used the right hand to grasp the handle of a robotic manipulandum (WristBOT, Howard et al., 2009) that could be moved in a horizontal plane. The circular start position (diameter 20 mm), circular cursor representing the handle position (diameter 20 mm), and target(s) (diameter 20 mm) were displayed on a 30-inch monitor located above the plane of movement. Participants viewed these stimuli in a mirror located halfway between the monitor and movement plane, such that they appeared to be in the plane of movement. Participants could not see their hand or arm.
Procedure
To begin each trial, the participant moved the cursor into the start position (at body midline, 20 cm below the 0° target) and held it there for 200 ms. After this period of time elapsed, either one target or two potential targets were presented (at 20 cm distance), which together with an auditory ‘beep’ delivered at the same time, provided the cue to initiate a reaching movement. If the cursor moved from the start position less than 100 ms after the beep or more than 325 ms after the beep, the message “too early” or “too late” was displayed, respectively, and the trial was aborted. In two-target trials, the participant had to begin moving before knowing which of the two potential targets would be cued as the actual target. In these trials, one of the targets was cued (filled in) once the cursor moved 20 mm from the start position. For consistency, the target was also filled in at this point in one-target trials. In all trials, the participant was required to move the cursor to the cued target and click on it with the button located on the top of the manipulandum within 500 ms of leaving the start position. If the participant took longer than 500 ms to click on the target the message “too slow” was displayed. A trial was considered a “hit” if any part of the cursor contacted any part of the target at the time the button was pressed. The trial was considered a “miss” if the cursor was not in contact with the target when the button was clicked.
Day 1: Practice and Baseline Phases
Participants on Day 1 first completed 64 practice trials with visual feedback of the cursor. These included 4 trials for each of 4 one-target displays (with targets at -30, -15, 0 and 30°) and 8 trials for each of 6 two-target displays (with the left target at -30° and the right target at -20, -10, 0, 10, 20, or +30°), presented in random order. Participants then completed an additional set of 160 practice trials with 10 trials for each of the same 4 one-target displays and 20 trials for each of same six two-target displays, with visual feedback of the cursor randomly removed for half of the trials for each display type and with the order of all trials randomized. After these practice trials, participants completed 320 pre-adaptation phase trials, which included 20 trials for each of the 4 one-target displays and 40 trials for each of the 6 two-target displays. For each display, visual feedback was removed on half of the trials and the order of all trials was randomized. Participants were given an optional break after every 50 trials during the pre-adaptation phase as well as the post-adaptation phase described below. Note that the removal of cursor feedback on some Day 1 trials was done so as to allow for direct comparison with Day 2 trials, in which the removal of cursor feedback on two-target trials was necessary for testing our hypotheses (see below).
Day 2: Adaptation and Post-Adaptation Phases
Participants began the Day 2 session by completing 96 practice trials to reacquaint them with the task. These included 6 and 12 trials for each of the 4 one-target displays and each of the 6 two-target displays, respectively, used on Day 1. These practice trials were followed by the adaptation phase, in which we gradually applied opposing visuomotor rotations to the +30 and 0° targets so that, by the end of the phase, participants would generate roughly straight ahead (0°) hand movements when moving the cursor to either target (Fig. 1B). The adaptation phase consisted of 192 one-target trials with visual feedback of the cursor. This consisted of 81 trials with the +30° target, 81 trials with the 0° target, 20 trials with the -30° target, and 10 trials with the -15° target (all presented in random order). For the +30° target trials, a visuomotor rotation of +40° was gradually introduced, in 1-degree increments, over the first 40 +30° target trials and then held at 40° (see blue dashed line in Fig. 2A). For the 0° target trials, a visuomotor rotation of -10° was gradually introduced, in the same 1-degree increments, over the first ten 0° target trials and then held at -10° (see orange dashed line in Fig. 2A). No rotations were applied to the -30 and -15° targets. We applied 40 and -10° rotations to the +30 and 0 degree targets, respectively, to compensate for two factors associated with adaptation to visuomotor rotations: incomplete adaptation, seen even when adapting to a single target, and generalization of adaptation across targets; i.e., from the +30° target to the 0° target and vice versa (Krakauer et al., 2000; Hirashima and Nozaki, 2012). As can be clearly seen in Fig. 2A, the application of these rotations resulted in our group of participants generating similar, straight-ahead movement directions for both target locations.
Following this adaptation phase, participants then completed 720 post-adaptation phase trials, which contained two-target trials, all without visual feedback of the cursor, and one-target trials with and without visual feedback of the cursor. In the one-target trials with vision of the cursor, the +40 and –10° visuomotor rotations were applied to the +30 and 0° targets, respectively, with no rotation being applied to other targets. Single targets were presented at one of six possible target locations: -30, -15, -7.5, 0, +7.5, and +30°. Through pilot testing we determined that it was necessary to include a high proportion of one-target trials with visual feedback involving the 0 and +30° targets in order to maintain the visuomotor adaptation achieved during the earlier adaptation phase. Accordingly, there were 200 trials each for the 0 and +30° one-target displays, with 20 of those trials having visual feedback of the cursor removed. Also, there were 100 trials each for the -30 and -15° one-target displays, with again 20 of those trials having cursor feedback removed. Finally, we had 20 trials each for the -7.5 and +7.5°, with half of those having the visual feedback removed.
Three two-target displays, all without visual feedback of the cursor, were presented during the post-adaptation phase: -30/0°, 0/+30°, and -30/+30° trials. Since we were primarily interested in the -30/+30° two-target trials—trials in which we expected to observe our maximal effects and that would serve as the critical test between the motor and visual averaging hypotheses—we included sixty -30/+30° trials and only ten each of -30/0° and 0/+30° trials. If a participant, when presented with -30/+30° trials, aimed towards the averaged target position (i.e., visual averaging, Fig. 1C), we would expect the initial movement direction to be roughly straight ahead (i.e., ~0°). Conversely, if a participant instead executed an initial reach movement consistent with the average of the two movements to the potential target (i.e., motor averaging, Fig. 1D), then we would expect the initial direction to be biased leftward (i.e., rotated counter clockwise) because of the influence of the learned visuomotor rotation on the movement direction to the +30° target. Note that we never included visual cursor feedback on any of the two-target trials as this would have necessarily biased the outcome. Following the completion of Day 2 testing and immediately prior to experiment debriefing, participants were asked as to whether they noticed any mismatch between their hand movements and the cursor position during testing. None reported being aware of any incongruence.
Data Analysis
The position of the handle was sampled at 1000 Hz and digitally smoothed using a fourth-order, zero-phase lag Butterworth filter with a cut-off frequency of 14 Hz. To obtain a measure of the direction of the initial movement vector, prior to when corrections could occur in two-target trials, we determined the direction of the handle, relative to the start position, when the handle reached 30% of the distance (i.e., 6 cm) from the start position to the arc along which the targets were located. We refer to this as the initial movement direction.
Supplementary Material
Acknowledgments
The authors would like to thank Martin York, Justin Caldwell, and Sean Hickman for technical support and assistance, as well as Stephen Scott and Douglas Munoz for helpful discussions. Funding from the Natural Sciences and Engineering Research Council of Canada (NSERC), the Wellcome Trust; the Royal Society Noreen Murray Professorship in Neurobiology (DW); the Canadian Foundation for Innovation, and the Ontario Innovation Trust supported this study. J.P.G was supported by an NSERC Banting Postdoctoral Fellowship and CIHR Postdoctoral Fellowship. B.M.S. was supported by an NSERC graduate scholarship.
Footnotes
Author Contributions
All authors contributed to the study design, interpreted the data, and approved the final version of the manuscript for submission. B.M.S. performed the testing and data collection. B.M.S., J.P.G, and J.R.F. performed the data analysis. J.P.G., B.M.S., D.M.W., and J.R.F. drafted the manuscript and L.A.B. provided critical revisions.
Competing financial interests
The authors declare no competing financial interests.
References
- Chapman CS, Gallivan JP, Wood DK, Milne JL, Culham JC, Goodale MA. Short-term motor plasticity revealed in a visuomotor decision-making task. Behav Brain Res. 2010a;214:130–134. doi: 10.1016/j.bbr.2010.05.012. [DOI] [PubMed] [Google Scholar]
- Chapman CS, Gallivan JP, Wood DK, Milne JL, Culham JC, Goodale MA. Reaching for the unknown: multiple target encoding and real-time decision-making in a rapid reach task. Cognition. 2010b;116:168–176. doi: 10.1016/j.cognition.2010.04.008. [DOI] [PubMed] [Google Scholar]
- Chou IH, Sommer MA, Schiller PH. Express averaging saccades in monkeys. Vision Res. 1999;39:4200–4216. doi: 10.1016/s0042-6989(99)00133-9. [DOI] [PubMed] [Google Scholar]
- Christopoulos V, Schrater PR. Dynamic Integration of Value Information into a Common Probability Currency as a Theory for Flexible Decision Making. PLoS Comput Biol. 2015;11:e1004402. doi: 10.1371/journal.pcbi.1004402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P. Cortical mechanisms of action selection: the affordance competition hypothesis. Philos Trans R Soc Lond B Biol Sci. 2007;362:1585–1599. doi: 10.1098/rstb.2007.2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Kalaska JF. Neural correlates of reaching decisions in dorsal premotor cortex: specification of multiple direction choices and final selection of action. Neuron. 2005;45:801–814. doi: 10.1016/j.neuron.2005.01.027. [DOI] [PubMed] [Google Scholar]
- Cisek P, Kalaska JF. Neural mechanisms for interacting with a world full of action choices. Annu Rev Neurosci. 2010;33:269–298. doi: 10.1146/annurev.neuro.051508.135409. [DOI] [PubMed] [Google Scholar]
- Cisek P, Pastor-Bernier A. On the challenges and mechanisms of embodied decisions. Philos Trans R Soc Lond B Biol Sci. 2014;369 doi: 10.1098/rstb.2013.0479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cos I, Belanger N, Cisek P. The influence of predicted arm biomechanics on decision making. J Neurophysiol. 2011;105:3022–3033. doi: 10.1152/jn.00975.2010. [DOI] [PubMed] [Google Scholar]
- Cos I, Medleg F, Cisek P. The modulatory influence of end-point controllability on decisions between actions. J Neurophysiol. 2012;108:1764–1780. doi: 10.1152/jn.00081.2012. [DOI] [PubMed] [Google Scholar]
- Cui H, Andersen RA. Different representations of potential and selected motor plans by distinct parietal areas. J Neurosci. 2011;31:18130–18136. doi: 10.1523/JNEUROSCI.6247-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekleva BM, Ramkumar P, Wanda PA, Kording KP, Miller LE. Uncertainty leads to persistent effects on reach representations in dorsal premotor cortex. Elife. 2016;5 doi: 10.7554/eLife.14316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Ruiz J, Wong W, Armstrong IT, Flanagan JR. Relation between reaction time and reach errors during visuomotor adaptation. Behav Brain Res. 2011;219:8–14. doi: 10.1016/j.bbr.2010.11.060. [DOI] [PubMed] [Google Scholar]
- Gallivan JP, Barton KS, Chapman CS, Wolpert DM, Randall Flanagan J. Action plan co-optimization reveals the parallel encoding of competing reach movements. Nat Commun. 2015;6 doi: 10.1038/ncomms8428. 7428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallivan JP, Bowman NAR, Chapman CS, Wolpert DM, Flanagan JR. The sequential encoding of competing action goals involves dynamic restructuring of motor plans in working memory. J Neurophysiol. 2016a;115:3113–3122. doi: 10.1152/jn.00951.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallivan JP, Chapman CS. Three-dimensional reach trajectories as a probe of real-time decision-making between multiple competing targets. Front Neurosci. 2014;8:215. doi: 10.3389/fnins.2014.00215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallivan JP, Chapman CS, Wood DK, Milne JL, Ansari D, Culham JC, Goodale MA. One to four, and nothing more: nonconscious parallel individuation of objects during action planning. Psychol Sci. 2011;22:803–811. doi: 10.1177/0956797611408733. [DOI] [PubMed] [Google Scholar]
- Gallivan JP, Logan L, Wolpert DM, Flanagan JR. Parallel specification of competing sensorimotor control policies for alternative action options. Nat Neurosci. 2016b;19:320–326. doi: 10.1038/nn.4214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghez C, Favilla M, Ghilardi MF, Gordon J, Bermejo R, Pullman S. Discrete and continuous planning of hand movements and isometric force trajectories. Exp Brain Res. 1997;115:217–233. doi: 10.1007/pl00005692. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. The Ecological Approach to Visual Perception. 1979.
- Grent-’t-Jong T, Oostenveld R, Medendorp WP, Praamstra P. Separating Visual and Motor Components of Motor Cortex Activation for Multiple Reach Targets: A Visuomotor Adaptation Study. J Neurosci. 2015;35:15135–15144. doi: 10.1523/JNEUROSCI.1329-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haith AM, Huberdeau DM, Krakauer JW. Hedging your bets: intermediate movements as optimal behavior in the context of an incomplete decision. PLoS Comput Biol. 2015a;11:e1004171. doi: 10.1371/journal.pcbi.1004171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haith AM, Huberdeau DM, Krakauer JW. The influence of movement preparation time on the expression of visuomotor learning and savings. J Neurosci. 2015b;35:5109–5117. doi: 10.1523/JNEUROSCI.3869-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirashima M, Nozaki D. Distinct motor plans form and retrieve distinct motor memories for physically identical movements. Curr Biol. 2012;22:432–436. doi: 10.1016/j.cub.2012.01.042. [DOI] [PubMed] [Google Scholar]
- Howard IS, Ingram JN, Wolpert DM. A modular planar robotic manipulandum with end-point torque control. J Neurosci Methods. 2009;181:199–211. doi: 10.1016/j.jneumeth.2009.05.005. [DOI] [PubMed] [Google Scholar]
- Hudson TE, Maloney LT, Landy MS. Movement planning with probabilistic target information. J Neurophysiol. 2007;98:3034–3046. doi: 10.1152/jn.00858.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaes C, Westendorff S, Chakrabarti S, Gail A. Choosing goals, not rules: deciding among rule-based action plans. Neuron. 2011;70:536–548. doi: 10.1016/j.neuron.2011.02.053. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Pine ZM, Ghilardi MF, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci. 2000;20:8916–8924. doi: 10.1523/JNEUROSCI.20-23-08916.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDougle SD, Bond KM, Taylor JA. Explicit and Implicit Processes Constitute the Fast and Slow Processes of Sensorimotor Learning. J Neurosci. 2015;35:9568–9579. doi: 10.1523/JNEUROSCI.5061-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDougle SD, Ivry RB, Taylor JA. Taking Aim at the Cognitive Side of Learning in Sensorimotor Adaptation Tasks. Trends Cogn Sci. 2016 doi: 10.1016/j.tics.2016.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPeek RM, Han JH, Keller EL. Competition between saccade goals in the superior colliculus produces saccade curvature. J Neurophysiol. 2003;89:2577–2590. doi: 10.1152/jn.00657.2002. [DOI] [PubMed] [Google Scholar]
- McPeek RM, Skavenski AA, Nakayama K. Concurrent processing of saccades in visual search. Vision Research. 2000;40:2499–2516. doi: 10.1016/s0042-6989(00)00102-4. [DOI] [PubMed] [Google Scholar]
- Ochiai T, Mushiake H, Tanji J. Effects of image motion in the dorsal premotor cortex during planning of an arm movement. J Neurophysiol. 2002;88:2167–2171. doi: 10.1152/jn.2002.88.4.2167. [DOI] [PubMed] [Google Scholar]
- Pearce TM, Moran DW. Strategy-dependent encoding of planned arm movements in the dorsal premotor cortex. Science. 2012;337:984–988. doi: 10.1126/science.1220642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesaran B, Nelson MJ, Andersen RA. Dorsal premotor neurons encode the relative position of the hand, eye, and goal during reach planning. Neuron. 2006;51:125–134. doi: 10.1016/j.neuron.2006.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart BM, Baugh LA, Gallivan JP, Flanagan JR. Simultaneous encoding of the direction and orientation of potential targets during reach planning: evidence of multiple competing reach plans. J Neurophysiol. 2013;110:807–816. doi: 10.1152/jn.00131.2013. [DOI] [PubMed] [Google Scholar]
- Stewart BM, Gallivan JP, Baugh LA, Flanagan JR. Motor, not visual, encoding of potential reach targets. Curr Biol. 2014;24:R953–R954. doi: 10.1016/j.cub.2014.08.046. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.